Формулы (математический анализ)
шпаргалка
Формулы дифференцированияВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Таблица основных интегралов

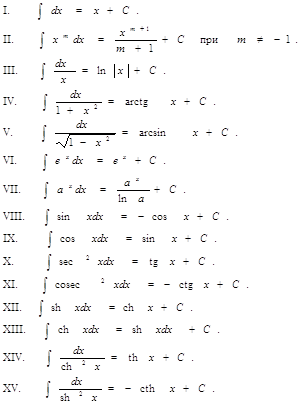
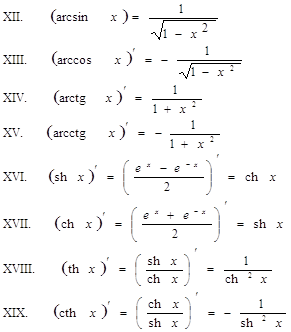
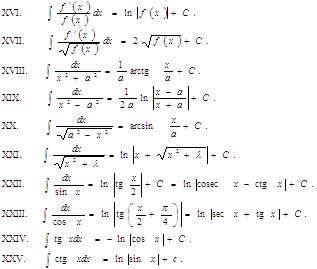
Правила интегрирования
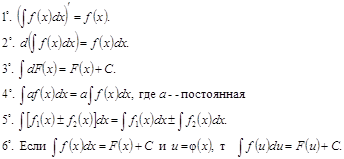
Основные правила дифференцирования
Пусть СтАФпостоянная, u=u(x), v=v(x) тАУ функции, имеющие
производные.
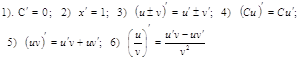
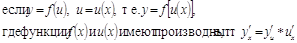
7)

Интегрирование по частямВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВа
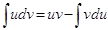
Основные свойства определённого интеграла
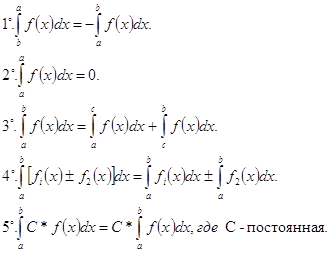
Интегрирование простейших дробей
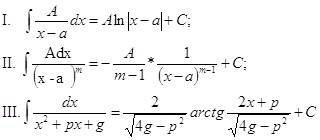
Замена переменной вВа неопределенном интеграле
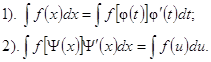
Площадь плоской фигуры
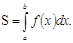 Площадь криволинейной трапеции, ограниченной кривой
Площадь криволинейной трапеции, ограниченной кривой 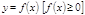 , прямыми
, прямыми 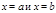 и отрезком[a,Ваb] оси Ox,Вавычисляется по формуле
и отрезком[a,Ваb] оси Ox,Вавычисляется по формуле
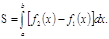 Площадь фигуры, ограниченной кривыми
Площадь фигуры, ограниченной кривыми 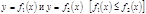 и прямыми
и прямыми 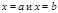 , находится по формуле
, находится по формуле
Если кривая задана параметрическими уравнениями 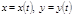 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми 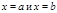 и отрезком[a,Ваb] оси Ox,Вавыражается формулой
и отрезком[a,Ваb] оси Ox,Вавыражается формулой
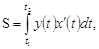
где 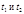 определяются из уравнений
определяются из уравнений 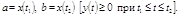
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением 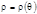 и двумя полярными радиусами
и двумя полярными радиусами 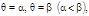 находится по формуле
находится по формуле
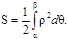
Длина дуги плоской кривой
Если кривая y=f(x) на отрезке [a, b] тАУ гладкая (т.е. производная 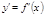 непрерывна), то длина соответствующей дуги этой кривой находится по формуле
непрерывна), то длина соответствующей дуги этой кривой находится по формуле
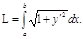
При параметрическом задании кривой x=x(t),Ва y=y(t) [x(t) иВаy(t) тАУ непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра 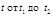 , вычисляется по формуле
, вычисляется по формуле
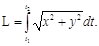
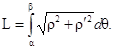 Если гладкая кривая задана в полярных координатах уравнением
Если гладкая кривая задана в полярных координатах уравнением 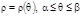 , то длина дуги равна
, то длина дуги равна
Вычисление объема тела
Вычисление объема тела по известным площадям поперечных сечений.
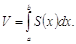 Если площадь сечения тела плоскостью, перпендикулярной оси Ox, можетВабыть выражена как функция от x, т.е. в виде
Если площадь сечения тела плоскостью, перпендикулярной оси Ox, можетВабыть выражена как функция от x, т.е. в виде 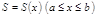 , то объем части тела, заключенной между перпендикулярными оси OxВаплоскостями x=a иВаx=b, находится по формуле
, то объем части тела, заключенной между перпендикулярными оси OxВаплоскостями x=a иВаx=b, находится по формуле
Вычисление объема тела вращения. Если криволинейная трапеция, ограниченная кривой 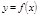 и прямыми
и прямыми 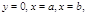 вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле
вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле
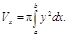
Если фигура, ограниченная кривыми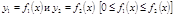 и прямыми x=a, x=b, вращается вокруг оси Ox, то объем тела вращения
и прямыми x=a, x=b, вращается вокруг оси Ox, то объем тела вращения
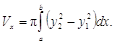
Вычисление площади поверхности вращения
Если дуга гладкой кривой 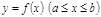 вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле
вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле
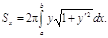
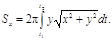 Если кривая задана параметрическими уравнениями
Если кривая задана параметрическими уравнениями 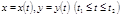 , то
, то
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://" onclick="return false">
Вместе с этим смотрят:
"Инкарнация" кватернионов
* Алгебры и их применение
*-Алгебры и их применение
10 способов решения квадратных уравнений
Bilet