Новое о гравитационном константе G

НОВОЕ О ГРАВИТАЦИОННОЙ КОНСТАНТЕ G: ПЯТНАДЦАТЬ ЭКВИВАЛЕНТНЫХ ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ КОНСТАНТЫ G

Аннотация

Показано, что гравитационная константаG является составной константой, содержит в себе постоянную Планка h, скорость света c и другие константы и функционально с ними связана. В частности константа G имеет функциональную зависимость от следующих важнейших физических констант:

G=f (h,c, R_∞, α, π

На основе группы универсальных суперконстант h_{u ,} l_u , t_u , α , π получены 15 эквивалентных формул для вычисления гравитационной константы G[2,3,5,6]. Найденное по этим формулам новое значение константы G равно:

G=6,67286741(89)тАв 10^-11 m³ kg^-1s^-2.

Новое значение константы G вместо четырех цифр содержит 9 цифр [2,3,6]. Полученные результаты указывают на фундаментальную связь электромагнетизма и гравитации и на существование единого онтологического константного базиса, который является основой физических и астрофизических констант.

1. ВАЖНЕЙШАЯ КОНСТАНТА ФИЗИКИ И АСТРОФИЗИКИ

Большинство физических констант связаны законами физики с другими константами. Это является решающим фактором для определения каждой константы [17]. Однако такие константы как: гравитационная константа < FONT>G, отношение масс протон-электрон m_p/m_e, постоянная Хаббла H₀ считаются не связанн ыми вообще ни с какими другими константами. В отношении важнейшей физической константы G остается надежда на то, что удастся выявить ее связь с чем-либо в рамках будущей единой теории, которая должна объед инить все четыре взаимодействия.

Гравитационная константа G широко используется как в физических теориях,так и в практике, начиная с астрофизики и кончая космонавтикой [19]. Однако ее значение определено с недостаточной точностью. Как отмечает автор в [19]: "повышение точности знания G способствует углублению понимания физики гравитации и уточнению фундаментальных закономерностей смежных с ней отраслей знаний." Кроме того, все е ще остается открытым вопрос о природе гравитации и о сущности гравитационной константы G. Как известно, сама форма закона всемирного тяготения Ньютона тАУ пропорциональность силы массам и обратная пр опорциональность квадрату расстояния, проверена с гораздо большей точностью, чем точность гравитационной константы G. Поэтому основное ограничение на точное определение гравитационных сил наклады вает константа G. Эта константа определена экспериментально. Науке пока неизвестно существует ли аналитическое соотношение для определения гравитационной константы, существует ли связь между кон стантой G и другими фундаментальными физическими константами. В теоретической физике эту важнейшую константу пытаются использовать совместно с константой Планка h и скоростью света c для создания квантовой теории гравитации и для разработки единых теорий. Поэтому, вопрос о первичности и независимости константы G выходит на первый план. Важно выяснить в какой степени зависимы или независимы другие фундаментальные константы. В этом клубке проблем работы по уточнению значения гравитационной константы приобретают особую актуальность. Одним из путей для решения этой задачи являются орбитальные гравитационные эксперименты. Космические исследования открывают тут новые возможности. Однако, как отмечается в [19], для этого потребуются "и компенсация сноса корабля, и высокая точность диагноза температурного и гравитационного полей, и наконец, очень высокая точность определения пространственного положения пробных тел. Кроме того, могут потребоваться дополнительные усилия по доставке корабля в либрационные точки и по обеспечению связи с ним". Сложность экспериментальных работ по уточнению гравитационной константы G заставляет искать другие способы определения ее точного значения.

2. СОСТАВНАЯ СУЩНОСТЬ КОНСТАНТЫ G

В [5-12] проведены исследования константы G и других фундаментальных физических констант. Ставилась задача выявить константы, которые могут претендовать на роль тАЬистинно фундаментальныхтАЭ констант. В результате была открыта группа первичных, независимых констант, из которых состоят важнейшие фундаментальные константы [2-9]. Таких первичных, независимых констант пять:

• фундаментальный квант действия h_u (h_u=7,69558071(63)тАв10^-37 J s),
• фундаментальная длина l_u (l_u=2,817940285(31)тАв10^-15 m),
• фундаментальный квант времени t_u (t_u=0,939963701(11)тАв10^-23 s),
• постоянная тонкой структуры α (α =7,297352533(27)тАв10^-3 ),
• число π (π=3,141592653589).

Эти пять констант являются тАЬистинно фундаментальнымитАЭ константами и имеют онтологический статус. Константы, входящие в эту группу, являются первичными и независимыми константами. Чтобы подчеркнуть их тАЬист инную фундаментальностьтАЭ они были названы универсальными суперконстантами [2]. Универсальные суперконстанты проистекают из свойств физического вакуума [2 - 12].

Размерные суперконстанты h_u, l_u, t_u определяют физические свойства вакуума и являются константами фундаментального состояния материи [3 - 8]. Суперконстанты π и α определяют геометрические свойства пространства-времени. Суммой геомет рических(π , α) и физических(h_u, l_u, t_u ) супер констант представлен онтологический базис фундаментальных физических констант (Рис.1).

Рис.1 Онтологический базис фундаментальных физических констант.

Группа, состоящая из пяти первичных суперконстант [2,8], позволила выявить важнейшую особенность гравитационной константы G. Оказалось, что эта константа является сос тавной константой и содержит в себе постоянную Планка h, скорость света c, постоянную тонкой структурыα и другие константы. Таким образом, гравитационная константа Ньютона функционально зависима от других фундаментальных констант. В частности, одной из функциональных зависимостей является следующ ая: G=f(h,c, R_∞, α, π). Дальнейшие исследования показали, что константа G, как и другие фундаментальные константы, наиболее просто может быть выражена посредством единой группы констант тАУ универсальных суперконстант [2-9]:

{G, m_pl, c, h, тАж e, m_e, R_∞, μ_B,Ф_о} = f (h_{u ,} l_u , t _u , α , π).

Таким образом, подтверждается подход А.Пуанкаре, согласно которому утверждается дополнительность физики и геометрии [13]. Согласно этому подходу в реальных экспериментах мы всегда наблюдаем некую тАЬсуммутАЭ физики и геометрии. Это значит, что экспериментально измеренные значения физических констант также должны содержать в себе "что-то от физики" и "что-то от геометрии". Как показано в [2 - 8], универсальные суперконстанты являются составляющими важ нейших физических констант. "Что-то от физики" и "что-то от геометрии" как раз несут в себе эти составляющие (универсальные суперконстанты) своим составом геометрических и физических суперконстант.

3. ПЯТНАДЦАТЬ ЭКВИВАЛЕНТНЫХ ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ КОНСТАНТЫ G.

Группа универсальных суперконстант (h_{u ,} l_u, t_u, α, π) позволила выявить глобальную взаимосвязь фундаментальных констант и получить математические формулы для вычисления гравитационной константы G[2,3.5]. Ниже приведены 15 эквивалентных формул для вычисления гравитационной константы G. Часть из них ранее были опубликованы в [5, 6, 15]:

G = l_u⁵/t_u³h_uD_o, G = l_u³/t_u² m_e D_o ,

G = l_pl² l_u α/t_u² m_e, G = 2πc³lu²/αhD_o,

G = c³α²l_u/2h R_∞ D_o G = c³l_pl²α/h_u,

G = t_pl²c²l_u α/t_u² m_e, G = c⁵t_pl²α/h_u,

G = l_u⁴10⁷/e²t_u²D_o, G = h_uα²/4πt_u m_pl²R_∞,

Из приведенных формул видно, что константа Gвыражается с помощью других фундаментальных констант очень компактными и простыми соотношениями. Все формулы для гравитационной константы сохраняют когерентность. В числе констант, с помощью которых представлена гравитационная константа, использованы такие константы: фундаментальный квант h_u, скорость света c, постоянная тонкой структуры α, постоянная Планка h , число π, фундаментальная метрика пространства-времени (l_u,t_u), элементарная масса m_e, элементарный заряд e,большое космологическое число D_o[2, 14], планковскиеединицы длины l_pl, массы m_pl< /FONT>, времени t_pl. Это указывает на единую сущность электром агнетизма и гравитации и на существование единого фундаментального базиса у всех физических констант. Это же подтверждают пять приведенных ниже дополнительных формул.

Используя константы h, c, R_∞, απ, получим следующую формулу:

G =с³ α⁵/8 πh R_∞²D0

Используя константы h_u, l_u , t_u,m_e, α, π, получим следующую формулу:

G = h_ul_u/t_um_e²D₀

Используя константы h_u, c, α, m_pl, пол учим следующую формулу:

G = h_u c/α m_pl²

Используя константы l_u, магнетон Бора μ_B, m_e, α, π, получим следующую формулу:

G = 4μ_B²α²В·10^-7/l_u ²m_e²D_o

Используя константы l_u, постоянную Хаббла H, t_u, h_u,α, получим следующую формулу:

G = 2l_u⁵α H/t_u² h_u

Все 15 формул являются эквивалентными. Отметим, что каждая из 14 формул допускает редукцию к формуле:

G = l_u⁵/t_u³h_uD_o

Таким образом, формулы показывают, что гравитационная константа G не является независимой. Она связана с важнейшими фундаментальными конста нтами.

4. ЭКСПЕРИМЕНТАЛЬНЫЕ ЗНАЧЕНИЯ КОНСТАНТЫ G.

Значение G было определено впервые английским физиком Г.Кавендишем в 1798 г. на крутильных весах путем измерения силы притяжения между дву мя шарами. Значение, полученное Г.Кавендишем:

G=6,740(50)тАв 10^-11 m³kg^-1s^-2 .

В последующие годы измерения гравитационной константы продолжались. В 1982 году G.Luther и W.Towler получили значение [20]:

G=6,67260(50)тАв 10^-11 m³kg^-1s^-2 .

Значение гравитационной константы, рекомендованное Комиссией по фундаментальным физическим константам CODATA в 1986 г.:

G = 6,67259 (85)тАв 10^-11 m³kg^-1s^-2 .

В [20] приведены результаты измерений гравитационной константы, полученные разными авторами. Значения, полученные разными авторами, значительно отличаются. Эти значения представлены тремя-шестью цифрами. При этом лучшие экспериментальные значения не превышают пять-шесть знаков. Очевидно, это связано с тем, что измерение значений гравитационной константы сопряжено с большими трудностями. На точность измерения оказывает влияние множество факторов. В частности , на точность измерения константы G влияют некоторые космические ритмы (солнечные, лунные, звездные), которые пока не нашли какого-либо объяснения [20]. В 1996 году О.В.Карагиоз и В.П.Измай лов получили значение:

G=6,67290(50)тАв 10^-11 m³kg^-1s^-2 .

Современное значение константы G, рекомендованное CODATA 1998 [1]:

G=6,673(10)тАв 10^-11 m³kg^-1s^-2 .

5. НОВОЕ ЗНАЧЕНИЕ КОНСТАНТЫ G, ПОЛУЧЕННОЕ РАiЕТОМ.

Рекомендованное значение гравитационной константы претерпело такую метаморфозу: сначала CODATA 1986 предложил более точное значение, затем CODATA 1998 рекомендует менее точное значение. Из всех универсальных физических констант точность в определении G остается сам ой низкой. Среднеквадратическая погрешность для G на несколько порядков превышает погрешность других констант. Точность в три-пять десятичных знаков для важнейшей физической констант ы нельзя считать нормальным положением дел. На важность исследований, целью которых должно быть повышение точности фундаментальных физических констант, обратили внимание Тейлор и Коэн [18]: "Мы считаем, что в области фундаментальных констант должна бы ть проведена большая работа и что романтике следующего десятичного знака нужно отдаться со всей страстью не ради ее самой, но ради новой физики и более глубокого понимания природы, которая здесь еще скрывается от нас". Это в полной мере относится к г равитационной константе.

Используя приведенные выше формулы, значение гравитационной константы можно получить расчетом. При этом точность ее можно повысить сразу на несколько десятичных знаков и приблизить к точно сти электромагнитных констант. Все приведенные выше формулы дают новое значение константы G, которое по точности на четыре порядка(!) выше принятого на сегодня значения. Наибол ее точное значение гравитационной константы можно получить на основе использования следующих физических констант: скорости света в вакууме c, постоянной Планка h , постоянной Ридберга R_∞, постоянной тонкой структуры α, числа π. Такое же точное значение гравитационной константы получается при использ овании универсальных суперконстант (h_{u ,} l_u , t_u , α , π). Новое значение константы G содержит 9 цифр [2]:

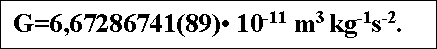
Таким образом, более чем за 200 лет своего существования гравитационная константа прошла несколько этапов, на которых ее значение считалось разным:

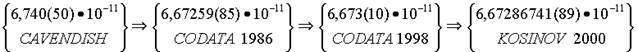
Значение гравитационной константы, полученное расчетом по приведенным выше формулам, оказалось наиболее точным.

6. СРАВНЕНИЕ РАiЕТНЫХ ЗНАЧЕНИЙ КОНСТАНТЫ G

Все приведенные 15 формул дают практически одинаковые значения гравитационной постоянной. Отклонения очень незначительные и наблюдаются в седьмом-девятом знаках, что связано с различной точностью тех констан т, посредством которых представлена гравитационная константа G.

По мере того, как будет возростать точность рекомендованных значений констант, можно будет с еще большей точностью вычислять значение грав итационной константы G. Отметим, что для этого достаточно иметь более точные значения двух констант - h и α [16].

В таблице приведены экспериментальные результаты [20] и расчетные значения константы G, полученные по приведенным выше формулам:

Кем и когда получено	Формула	Значение
Cavendish, 1798	Нет	6,740(50)тАв 10-11 m3kg-1 s-2
Luther, Towler, 1982	Нет	6,67260(50)тАв 10-11 m3kg-1 s-2
CODATA 1986	Нет	6,67259(85)тАв 10-11 m3kg-1 s-2
Karagioz, Izmaylov, 1996	Нет	6,67290(50)тАв 10-11 N m2 kg-2
CODATA 1998	Нет	6,673(10)тАв 10-11 m3kg-1 s-2
Kosinov, 2000	G = lu5/tu3huDo	6,67286741(93)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = lu3/tu2 me Do	6,67286741(91)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = c5tpl2α/hu	6,67286742(97)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = hulu/tume2D0	6,6728674(20)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = hu c/α mpl2	6,6728674(22)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = c3α2lu/2h R∞ Do	6,6728674(16)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = lu4107/e2tu2Do	6,6728674(13)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = lpl2 lu α/tu2 me	6,6728674(11)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = c3lpl2α/hu	6,67286742(97)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = 2πc3lu2/αhDo	6,67286741(93)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = tpl2c2lu α/tu2 me	6,6728674(11)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = huα2/4πtu mpl2R∞ ;	6,6728674(13)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G =с3 α5/8 πh R∞2D0	6,67286741(89)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = 4μB2α2В·10-7/lu2 me2Do	6,6728674(22)тАв 10-11m3kg-1 s-2
Kosinov, 2000	G = 2lu5α H/tu2 hu	6,6728674(11)тАв 10-11m3kg-1 s-2

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Bilet