Рациональные уравнения и неравенства

Содержание

I. Рациональные уравнения.

1) Линейные уравнения.

2) Системы линейных уравнений.

3) Квадратные уравнения и уравнения, сводящиеся к ним.

4) Возвратные уравнения.

5) Формула Виета для многочленов высших степеней.

6) Системы уравнений второй степени.

7) Метод введения новых неизвестных при решении уравнений и систем уравнений.

8) Однородные уравнения.

9) Решение симметрических систем уравнений.

10) Уравнения и системы уравнений с параметрами.

11) Графический метод решения систем нелинейных уравнений.

12) Уравнения, содержащие знак модуля.

13) Основные методы решения рациональных уравнений

II. Рациональные неравенства.

1) Свойства равносильных неравенств.

2) Алгебраические неравенства.

3) Метод интервалов.

4) Дробно-рациональные неравенства.

5) Неравенства, содержащие неизвестное под знаком абсолютной величины.

6) Неравенства с параметрами.

7) Системы рациональных неравенств.

8) Графическое решение неравенств.

III. Проверочный тест.

Рациональные уравнения

Функция вида

P(x) = a₀xⁿ + a₁x^{n тАУ 1}+ a₂x^{n тАУ 2}+ тАж + a_{n тАУ 1}x + a_n,

где n тАФ натуральное, a₀, a₁,тАж, a_n тАФ некоторые действительные числа, называется целой рациональной функцией.

Уравнение вида P(x) = 0, где P(x) тАФ целая рациональная функция, называется целым рациональным уравнением.

Уравнение вида

P₁(x) / Q₁(x) + P₂(x) / Q₂(x) + тАж + P_m(x) / Q_m(x) = 0,

где P₁(x), P₂(x), тАж ,P_m(x), Q₁(x), Q₂(x), тАж, Q_m(x) тАФ целые рациональные функции, называется рациональным уравнением.

Решение рационального уравнения P (x) / Q (x) = 0, где P (x) и Q (x) тАФ многочлены (Q (x) ¹ 0), сводится к решению уравнения P (x) = 0 и проверке того, что корни удовлетворяют условию Q (x) ¹ 0.

Линейные уравнения.

Уравнения вида ax+b=0, где a и b тАФ некоторые постоянные, называется линейным уравнением.

Если a¹0, то линейное уравнение имеет единственный корень: x = -b /a.

Если a=0; b¹0, то линейное уравнение решений не имеет.

Если a=0; b=0, то, переписав исходное уравнение в виде ax = -b, легко видеть, что любое x является решением линейного уравнения.

Уравнение прямой имеет вид: y = ax + b.

Если прямая проходит через точку с координатами X₀ и Y₀, то эти координаты удовлетворяют уравнению прямой, т. е. Y₀ = aX₀ + b.

Пример 1.1. Решить уравнение

2x тАУ 3 + 4(x тАУ 1) = 5.

Решение. Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x тАУ 3 + 4x тАУ 4 = 5, 2x + 4x = 5 + 4 + 3,

6x = 12, x = 2.

Ответ: 2.

Пример 1.2. Решить уравнение

2x тАУ 3 + 2(x тАУ 1) = 4(x тАУ 1) тАУ 7.

Решение. 2x + 2x тАУ 4x = 3 +2 тАУ 4 тАУ 7, 0x = тАУ 6.

Ответ: Æ.

Пример 1.3. Решить уравнение.

2x + 3 тАУ 6(x тАУ 1) = 4(x тАУ 1) + 5.

Решение. 2x тАУ 6x + 3 + 6 = 4 тАУ 4x + 5,

тАУ 4x + 9 = 9 тАУ 4x,

-4x + 4x = 9 тАУ 9,

0x = 0.

Ответ: Любое число.

Системы линейных уравнений.

Уравнение вида

a₁x₁ + a₂x₂+ тАж + a_nx_n = b,

где a₁, b₁, тАж ,a_n, b тАФнекоторые постоянные, называется линейным уравнением с n неизвестными x₁, x₂, тАж, x_n.

Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными. Если система из n неизвестных, то возможны следующие три случая:

1) система не имеет решений;

2) система имеет ровно одно решение;

3) система имеет бесконечно много решений.

Пример 2.4. решить систему уравнений

2x + 3y = 8,

3x + 2y = 7.

Решение. Решить систему линейных уравнений можно способом подстановки, который состоит в том, что какого-либо уравнения системы выражают одно неизвестное через другие неизвестные, а затем подставляют значение этого неизвестного в остальные уравнения.

Из первого уравнения выражаем: x= (8 тАУ 3y) / 2. Подставляем это выражение во второе уравнение и получаем систему уравнений

x = (8 тАУ 3y) / 2,

3(8 тАУ 3y) / 2 + 2y = 7.

Из второго уравнения получаем y = 2. С учётом этого из первого уравнения x = 1.

Ответ: (1; 2).

Пример 2.5. Решить систему уравнений

x + y = 3,

2x + 2y = 7.

Решение. Система не имеет решений, так как два уравнения системы не могут удовлетворяться одновременно (из первого уравнения x + y = 3, а из второго x + y = 3,5).

Ответ: Решений нет.

Пример 2.6. решить систему уравнений

x + y = 5,

2x + 2y = 10.

Решение. Система имеет бесконечно много решений, так как второе уравнение получается из первого путём умножения на 2 (т.е. фактически есть всего одно уравнение с двумя неизвестными).

Ответ: Бесконечно много решений.

Пример 2.7. решить систему уравнений

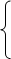x + y тАУ z = 2,

2x тАУ y + 4z = 1,

тАУ x + 6y + z = 5.

Решение. При решении систем линейных уравнений удобно пользоваться методом Гаусса, который состоит в преобразовании системы к треугольному виду.

Умножаем первое уравнение системы на тАУ 2 и, складывая полученный результат со вторым уравнением, получаем тАУ 3y + 6z = тАУ 3. Это уравнение можно переписать в виде y тАУ 2z = 1. Складывая первое уравнение с третьим, получаем 7y = 7, или y = 1.

Таким образом, система приобрела треугольный вид

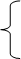
x + y тАУ z = 2,

y тАУ 2z = 1,

y = 1.

Подставляя y = 1 во второе уравнение, находим z = 0. Подставляя y =1 и z = 0 в первое уравнение, находим x = 1.

Ответ: (1; 1; 0).

Пример 2.8. при каких значениях параметра a система уравнений

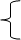2x + ay = a + 2,

(a + 1)x + 2ay = 2a + 4

имеет бесконечно много решений?

Решение. Из первого уравнения выражаем x:

x = тАУ (a / 2)y + a / 2 +1.

Подставляя это выражение во второе уравнение, получаем

(a + 1)( тАУ (a / 2)y + a / 2 +1) + 2ay = 2a + 4.

Далее умножим обе части уравнения на 2 и упростим его:

(a + 1)(a + 2 тАУ ay) + 4ay = 4a + 8,

4ay тАУ a(a + 1)y = 4(a + 2) тАУ (a + 1)(a + 2),

ya(4 тАУ a тАУ 1 ) = (a + 2)(4 тАУ a тАУ 1),

ya(3 тАУ a) = (a + 2)(3 тАУ a).

Анализируя последнее уравнение, отметим, что при a = 3 оно имеет вид 0y = 0, т.е. оно удовлетворяется при любых значениях y.

Ответ: 3.

Квадратные уравнения и уравнения, сводящиеся к ним.

Уравнение вида ax² + bx + c = 0, где a, b и c тАФ некоторые числа (a¹0);

x тАФ переменная, называется квадратным уравнением.

Формула решения квадратного уравнения.

Сначала разделим обе части уравнения ax² + bx + c = 0 на a тАФ от этого его корни не изменятся. Для решения получившегося уравнения

x² + (b / a)x + (c / a) = 0

выделим в левой части полный квадрат

x² + (b / a) + (c / a) = (x² + 2(b / 2a)x + (b / 2a)²) тАУ (b / 2a)² + (c / a) =

= (x + (b / 2a))² тАУ (b²) / (4a²) + (c / a) = (x + (b / 2a))² тАУ ((b² тАУ 4ac) / (4a²)).

Для краткости обозначим выражение (b² тАУ 4ac) через D. Тогда полученное тождество примет вид

x² + (b / a)x + (c / a) = (x + (b / 2a))² тАУ (D / (4a²)).

Возможны три случая:

1) если число D положительно (D > 0), то в этом случае можно извлечь из D квадратный корень и записать D в виде D = (ÖD)². Тогда

D / (4a²) = (ÖD)² / (2a)² = (ÖD / 2a)², потому тождество принимает вид

x² + (b / a)x + (c / a) = (x + (b / 2a))² тАУ (ÖD / 2a)².

По формуле разности квадратов выводим отсюда:

x² + (b / a)x + (c / a) = (x + (b / 2a) тАУ (ÖD / 2a))(x + (b / 2a) + (ÖD / 2a)) =

= (x тАУ (( -b + ÖD) / 2a)) (x тАУ (( тАУ b тАУ ÖD) / 2a)).

Теорема: Если выполняется тождество

ax² + bx + c = a(x тАУ x₁)(x тАУ x₂),

то квадратное уравнение ax² + bx + c = 0 при X₁ ¹ X₂ имеет два корня X₁ и X₂, а при X₁ = X₂ тАФ лишь один корень X₁.

В силу этой теоремы из, выведенного выше, тождества следует, что уравнение

x² + (b / a)x + (c / a) = 0,

а тем самым и уравнение ax² + bx + c = 0, имеет два корня:

X₁=(-b + Ö D) / 2a; X₂= (-b - Ö D) / 2a.

Таким образом x² + (b / a)x + (c / a) = (x тАУ x1)(x тАУ x2).

Обычно эти корни записывают одной формулой:

где b² тАУ 4ac = D.

2) если число D равно нулю (D = 0), то тождество

x² + (b / a)x + (c / a) = (x + (b / 2a))² тАУ (D / (4a²))

принимает вид x² + (b / a)x + (c / a) = (x + (b / 2a))².

Отсюда следует, что при D = 0 уравнение ax² + bx + c = 0 имеет один корень кратности 2: X₁ = тАУ b / 2a

3) Если число D отрицательно (D < 0), то тАУ D > 0, и потому выражение

x² + (b / a)x + (c / a) = (x + (b / 2a))² тАУ (D / (4a²))

является суммой двух слагаемых, одно из которых неотрицательно, а другое положительно. Такая сумма не может равняться нулю, поэтому уравнение

x² + (b / a)x + (c / a) = 0

не имеет действительных корней. Не имеет их и уравнение ax² + bx + c = 0.

Таким образом, для решения квадратного уравнения следует вычислить дискриминант

D = b² тАУ 4ac.

Если D = 0, то квадратное уравнение имеет единственное решение:

X=-b / (2a).

Если D > 0, то квадратное уравнение имеет два корня:

X₁=(-b + ÖD) / (2a); X₂= (-b - ÖD) / (2a).

Если D < 0, то квадратное уравнение не имеет корней.

Если один из коэффициентов b или c равен нулю, то квадратное уравнение можно решать, не вычисляя дискриминанта:

1) b = 0; c ¹ 0; c / a <0; X1,2 = В±Ö(-c / a )

2) b ¹ 0; c = 0; X1 = 0, X2= -b / a.

Корни квадратного уравнения общего вида ax² + bx + c = 0 находятся по формуле

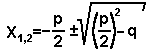
Квадратное уравнение, в котором коэффициент при x² равен 1, называется приведённым. Обычно приведённое квадратное уравнение обозначают так:

x² + px + q = 0.

Теорема Виета.

Мы вывели тождество

x² + (b / a)x + (c / a) = (x тАУ x1)(x тАУ x2),

где X₁ и X₂ тАФ корни квадратного уравнения ax² + bx + c =0. Раскроем скобки в правой части этого тождества.

x² + (b / a)x + (c / a) = x² тАУ x₁x тАУ x₂x + x₁x₂ = x² тАУ (x₁ + x₂)x +x₁x₂.

Отсюда следует, что X₁ + X₂ = тАУ b / a и X₁X₂ = c / a. Мы доказали следующую теорему, впервые установленную французским математиком Ф. Виетом (1540 тАУ 1603):

Теорема 1 (Виета). Сумма корней квадратного уравнения равна коэффициенту при X, взятому c противоположным знаком и делённому на коэффициент при X²; произведение корней этого уравнения равно свободному члену, делённому на коэффициент при X².

Теорема 2 (обратная). Если выполняются равенства

X₁ + X₂ = тАУ b / a и X₁X₂ = c / a,

то числа X₁ и X₂ являются корнями квадратного уравнения ax² + bx + c = 0.

Замечание. Формулы X₁ + X₂= тАУ b / a и X₁X₂= c / a остаются верными и в случае, когда уравнение ax² + bx + c = 0 имеет один корень X₁ кратности 2, если положить в указанных формулах X₂ = X₁. Поэтому принято считать, что при D = 0 уравнение ax² + bx +c = 0 имеет два совпадающих друг с другом корня.

При решении задач, связанных с теоремой Виета, полезно использовать соотношения

(1 / X₁) + (1/ X₂)= ( X₁ + X₂)/ X₁X₂ ;

X₁² + X₂²= (X₁ + X₂)² тАУ 2 X₁X₂;

X₁ / X₂ + X₂ / X₁ = (X₁² + X₂²) / X₁X₂ = ((X₁ + X₂)² тАУ 2X₁X₂) / X₁X₂;