Экономико-математическое моделирование

Сидин Э.Ф.

Экономико-математическое моделирование.

Учебное пособие. Электронный вариант-дискета.

Учебное пособие написано на базе материала лекций, которые читаются студентам дневной формы обучения.

Пособие содержит краткое изложение теоретических вопросов и конкретные экономико-математические модели по каждой теме рабочей программы.

В начале пособия помещено содержание электронного курса, что облегчает поиск необходимого материала.

В конце пособия приведен обзор пакетов прикладных программ, позволяющих реализовать те или иные экономико-математические модели.

Учебное пособие может быть использовано студентами при написании курсовых и дипломных работ.

Содержание

Тема
1. Предмет и структура курса. Основные принципы системного подхода.

1.1. Предмет и структура курса.

1.2. Понятие сложной системы.

1.3. Взаимодействие системы с внешней средой

1.4. Особенности сложных систем.

1.5. Основные понятия системного подхода и анализа.

1.6. Классификация систем и их моделей.

1.7. Особенности экономических систем.

Тема 2. Метод математического моделирования в экономике.

2.1. Понятие тАЬмодельтАЭ и тАЬмоделированиетАЭ.

2.2. Классификация моделей.

2.3. Этапы практического моделирования.

2.4. Оптимальность управления и достаточность системы ограничений.

2.5. Формальная классификация моделей.

Тема 3. Матричные ЭММ. Модель межотраслевого баланса.

3.1. Основные соотношения и понятия модели.

3.2. Коэффициенты прямых и полных материальных затрат.

3.3. Разновидности матричных балансовых моделей.

Тема 4. Оптимизационные ЭММ

1.1. Особенности ЭММ оптимизации.

4.2. ЭММ оптимизации производственного плана отрасли.

4.3. ЭММ оптимизации выпуска продукции предприятиями отрасли.

4.4. ЭММ распределения финансовых ресурсов по оптимизации прироста мощностей (отрасли, предприятия, ..).

4.5. Распределение капитальных вложений по проектам.

4.6. ЭММ составления оптимальных смесей, сплавов, соединений и выбор оптимального рациона питания (кормления).

4.7. ЭММ оптимизации раскроя материала.

4.8. Экономическая интерпретация двойственных задач линейного программирования.

Тема 5. Методы моделирования стохастических (вероятностных) систем. Имитационное моделирование.

5.1. Понятие о вероятностных системах и процессах.

5.2. Имитационное моделирование систем и процессов.

5.3. Имитационная модель и ее структура.

5.4. Метод Монте-Карло (метод статистических испытаний).

Тема 6. Методы и модели управления запасами.

6.1. Основные определения и понятия теории управления запасами.

6.2. Классификация систем снабжения и их моделей.

6.3. Стратегия управления запасами.

6.4. Детерминированная ЭММ управления запасами с фиксированным спросом.

6.5. Модель управления запасами при случайном спросе.

6.6. ЭММ управления запасами с ограничениями на складские помещения.

Тема 7. ЭММ систем массового обслуживания.

7.1. Основные понятия и определения.

7.2. Классификация и обозначение СМО.

7.3. Основные характеристики системы массового обслуживания.

Тема 8. ЭММ и модели АСУ.

8.1. Основные характеристики и классификация АСУ

8.2. ЭММ расчета эффективности АСУ.

Тема 9. Эконометрические модели и их применение в экономике.

9.1. Основные понятия об эконометрических моделях и корреляционном анализе.

9.2. Метод наименьших квадратов (МНК).

9.3. Использование качественных показателей в эконометрических моделях.

Тема 10. Обзор прикладных пакетов программ

Тема 1. Предмет и структура курса. Основные принципы системного подхода.

1.1. Предмет и структура курса.

ЭММ тАУ это комплекс экономических и математических дисциплин. Научной основой являются основные положения диалектики, экономики, теории сложных систем, законы математики.

Цель изучения курса - получение знаний об экономике, построении ЭММ и их оптимизации на ЭВМ.

1.2. Понятие сложной системы.

Сложная система тАУ комплекс подсистем, обладающих общими сложными свойствами.

Элемент системы при данном подходе тАУ это тот объект, который не подлежит расчленения, и внутренняя структура которого не исследуется. Сложные системы, их структура и иерархия определяются целями исследования.

Подсистема тАУ самостоятельно функционирующий объект, не подлежащий декомпозиции.

Принципы выделения системы:

- наличие управляющего центра;

- обладает общей целью;

- состоит из компонентов;

- система работает при взаимодействии с окружающей средой;

- система жизнеспособна при наличии достаточных ресурсов.

1.3. Взаимодействие системы с внешней средой

Любая техническая, биологическая система работает в окружении среды, которая оказывает внешнее воздействие на систему с параметрами возмущения, искажающими результаты управления.

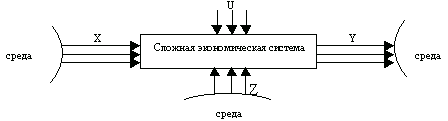
Параметры:

X тАУ входные параметры, факторные признаки, экзогенные параметры;

Y тАУ выходные параметры, результативные признаки, эндогенные параметры;

Z тАУ параметры возмущения, случайные факторы, случайные составляющие;

U тАУ параметры управления. Системы бывают открытые (взаимодействующие с внешней средой) и закрытые (невзаимодействующие с внешней средой).

1.4. Особенности сложных систем.

Сложная система тАУ комплекс отдельных подсистем, функционирующих в тесном взаимодействии, решающих общую задачу.

Основные особенности:

- наличие большого количества связанных между собой отдельных подсистем;

- наличие иерархической структуры управления, как по горизонтали, так и по вертикали;

- обязательной присутствие информационной сети;

- функционирование связано с воздействием случайных факторов.

Эффективность системы определяется функционалом:

W = F₀(f(x₀), f(x₁),тАж,f(x_n))

1.5. Основные понятия системного подхода и анализа.

При анализе сложных экономических систем (СЭС) придерживаются системного подхода. Это предполагает максимальный охват всех взаимосвязей и анализ последствий принятого решения.

Основные моменты:

а) Уточнение предметной области исследования, ее структуризация на задачи;

б) выбор параметров и критериев оценки эффективности системы;

в) Подбор нужных ЭММ;

г) Уточнение деталей и целей анализа системы;

д) Синтезирование математических моделей, обеспечивающих достижение поставленных целей.

Системы в своем структурном строении бывают одноуровневые и многоуровневые.

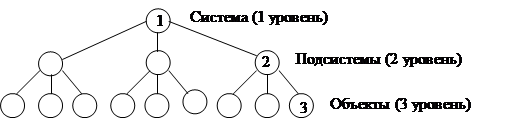
1.6. Классификация систем и их моделей.

В зависимости от признаков системы, сами системы и их модели классифицируются на:

1) динамические и статические;

2) стохастические (вероятностные) и детерминированные (регулярные);

3) непрерывные и дискретные;

4) линейные и нелинейные.

По наличию обратных связей системы подразделяются на открытые, закрытые, комбинированные.

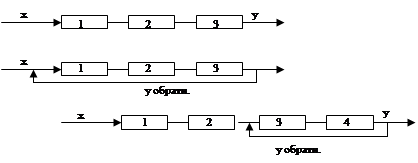
Открытые:

Закрытые:

Комбинированные:

1.7. Особенности экономических систем.

Экономическая система является частью более сложной системы тАУ социально-экономической, и представляет собой вероятностную, динамическую, адаптивную систему, охватывающую процессы производства, обмена, распределения и потребления материальных благ, а также предоставления различных сервисных услуг. Как правило, входные параметры экономических систем тАУ это материальные вещественные потоки производственных и природных ресурсов, то есть Х. Входные параметры тАУ это материальные вещественные потоки, оборудование, военная продукция, продукция накопления, возмещения и экспорта, то есть У.

Экономические системы тАУ многоступенчатые, многоуровневые системы, и любая неопределенность, случайность во входных параметрах в нижних уровнях приводит к неопределенностям и случайностям в выходных параметрах подсистем более высокого порядка и системы в целом.

Структурная схема простой экономической системы

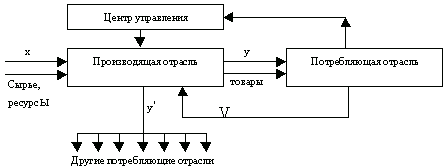
ЭММ оптимизации обычной экономической системы

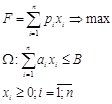
где p_iтАУ прибыль от реализации единицы продукции;

x_i- объем выпуска продукции;

a_i- расход сырья на единицу продукции;

B - общий запас сырья;

W - область допустимых ограничений;

Тема 2. Метод математического моделирования в экономике.

2.1. Понятие тАЬмодельтАЭ и тАЬмоделированиетАЭ.

С понятием тАЬмоделирование экономических системтАЭ (а также математических и др.) связаны два класса задач:

1) задачи анализа, когда система подвергается глубокому изучению ее свойств, структуры и параметров, то есть исследуется предметная область будущего моделирования.

2) Задачи, связанные с задачами синтеза (получения ЭММ данной системы).

Модель тАУ изображение, представление объекта, системы, процесса в некоторой форме, отличной от реального существования.

Различают физическое и математическое моделирование.

2.2. Классификация моделей.

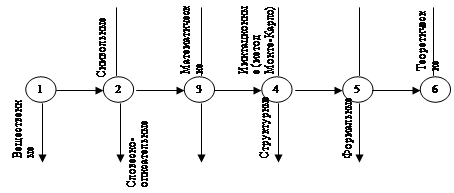
Модели

2.3. Этапы практического моделирования.

1) Анализ экономической системы, ее идентификация и определение достаточной структуры для моделирования.

2) Синтез и построение модели с учетом ее особенностей и математической спецификации.

3) Верификация модели и уточнение ее параметров

4) Уточнение всех параметров системы и соответствие параметров модели, их необходимая валидация (исправление, корректирование).

Этап подгонки модели многократный.

2.4. Оптимальность управления и достаточность системы ограничений.

В экономических системах (моделях) критерием оптимальности выбирают параметры, как правило, определяющие наилучшим образом эффективность данной системы. Такими параметрами могут быть максимальная прибыль и затраты, минимальное время достижения цели и т.д.

Вектор оптимального управления тАУ набор тех параметров, которые обеспечивают оптимальную траекторию функционирования данной ЭС. В любой модели (ЭС) имеются ограничения по ресурсам, по фондам и т.д. Поэтому система ограничений W тАУ запись условий в виде уравнений, неравенств, в которых существует единственное оптимальное решение. Совместимость ограничений тАУ обязательное условие разрешимости любой модели. На практике тАУ это запасы ресурсов, сырья, трудовые ресурсы, финансовые ресурсы, др.

тАЬСмягчить ограничениетАЭ - значит, получить показатель оптимизации оптимистичным.

тАЬУжесточить ограничениятАЭ - сделать более строгими, значит получить показатель оптимизации пессимистичным.

Ограничения могут встречаться в разных комбинациях.

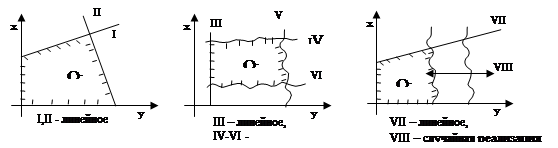
ЭММ линейна тогда и только тогда, когда целевая функция и система ограничений линейны. Любая комбинация:

- целевая функция линейна - W нелинейна;

- целевая функция нелинейна - W линейна;

- целевая функция нелинейна - W нелинейна;

приводит к нелинейности модели.

2.5. Формальная классификация моделей.

Признак классификации	Модель
1. Целевое назначение	Прикладные, теоретико-аналитические
2. По типу связей	Детерминированные, стохастические
3. По фактору времени	Статические, динамические
4. По форме показателей	Линейные, нелинейные
5. По соотношению экзогенных и эндогенных переменных	Открытые, закрытые
6. По типу переменных	Дискретные, непрерывные, смешанные
7. По степени детализации	Агрегированные (макромодели), детализированные (микромодели)
8. По количеству связей	Одноэтапные, многоэтапные
9. По форме представления информации	Матричные, сетевые
10. По форме процесса	Аналитические, графические, логические
11. По типу математического аппарата	Балансовые, статистические, оптимизационные, имитационные, смешанные

Тема 3. Матричные ЭММ. Модель межотраслевого баланса.

3.1. Основные соотношения и понятия модели.

Матричные экономико-математические модели предназначены для анализа и планирования производства и распределения проВндукции на различных уровнях тАФ от отдельного предприятия до народного хозяйства в целом.

Положительными и ценными качествами данной модели являются общность расчетов, которые опираются на знание коэффициентов прямых и полных материальных затрат.

Основу баланса составляет совокупность всех отраслей матеВнриального производства; их число равно п. Каждая отрасль дважды фигурирует в балансе: как производящая и как потребляющая. Отрасли какпроизводителю продукции соответВнствует определенная строка, а отрасли какпотребителю проВндукции тАФ определенный столбец.

Если номер любой производящей отрасли обозначить через i, а номер любой потребляющей отрасли тАФ через j, то находящиеся на пересечении отраслей (т. е. соответственно строк и столбцов) величины х_ij нужно понимать как стоимость средств производства, произведенных в i-й отрасли и потребленных в качестве материальных затрат в j-и отрасли.

х_ij тАУ технологический коэффициент.

Матричная модель межотраслевого баланса

Производящая отрасль	Потребляющая отрасль					Продукция, тыс.грн.
Производящая отрасль	1	2	3	j	N	Конечная	Валовая
1	x₁₁	x₁₂	x₁₃	тАж	x_1n	y₁	X₁
2	x₂₁	x₂₂	x₂₃	тАж	x_2n	y₂	X₂
3	x₃₁	x₃₂	x₃₃	тАж	x_3n	y₃	X₃
I	тАж	тАж	тАж	тАж	тАж	..	тАж
N	x_n1	x_n2	x_n3	тАж	x_nn	y_n	X_n
Оплата труда	v₁	v₂	v₃	тАж	v_n	v_кон	-
Чистый доход, тыс. грн.	m₁	m₂	m₃	тАж	m_n	m_кон	-
Валовая продукция, тыс. грн.	X₁	X_2`	X₃	тАж	X_n	-	X

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Bilet