Исследование движения центра масс межпланетных космических аппаратов
2. ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ
2.1. ВВЕДЕНИЕ
В данной работе проводится исследование движения центра масс МКА под действием различных возмущающих ускорений (от неВнцентральности гравитационного поля Земли, сопротивления атмоВнсферы, притяжения Солнца и Луны, из-за давления солнечных луВнчей) и создание математической модели движения ЦМ МКА, поВнзвоВнляющей учесть при интегрировании уравнений движения ЦМ МКА эволюцию орбиты МКА.
В работе разрабатывается алгоритм коррекции, ликвидирующий ошибки выведения МКА и рассчитывается масса топлива, необхоВндимая для проведения коррекции, необходимой из-за эволюции паВнраметров орбиты и из-за ошибок выведения МКА на рабочую орВнбиту.
Точность проведения коррекции зависит от точности направлеВнния корректирующего импульса, заданной в ТЗ. Было проведено модеВнлирование системы коррекции в режиме стабилизации углоВнвого поВнложения при работе корректирующей двигательной устаВнновки.
В работе приводятся программы, реализующие интегрирование уравнений движения ЦМ МКА, процесс осуществления коррекции и расчет топлива для коррекции.
2.2. КРАТКИЕ СВЕДЕНИЯ ОБ ОРБИТЕ
Основными показателями эффективности космической группировки, являются:
- предельная производительность МКА в сутки на освещенной стороне Земли не менее 400-500 объектов.
- периодичность наблюдения районов съемки не реже одного раза в сутки.
Расположение плоскости орбиты по отношению к Солнцу выбрано таким образом, чтобы угол между линией узлов и следом терминатора на плоскости экватора Земли составлял Dт = 30В°. При этом северный полувиток орбиты должен проходить над освещенной частью земной поверхности. Для определенности углу Dт приписывается знак Вл+В» в том случае, если восходящий узел орбиты находится над освещенной частью Земли, и знак Вл-В», если ВУ находится над неосвещенной частью. При выборе баллистического построения оперируют углом D, однозначно определяющимся прямым восхождением Солнца a0 и долготой восходящего узла орбиты в абсолютном пространстве W: D = a0 - W. Соотношение между углом Dт и углом D: DiDт - 90В°.
2.2.1. ХАРАКТЕРИСТИКА ОРБИТЫ
Для решения задач наблюдения Земли из космоса с хорошим разВнрешением при жестких ограничениях на массу КА и минимизации затрат на выведение целесообразно использовать низкие круговые орбиты. В этом классе орбит выделяют солнечно-синхронные орВнбиты со следующими свойствами:
- скорость прецессии плоскости орбиты в пространстве составВнляет примерно 1В° в сутки, что практически обеспечивает постоянВнство ориентации ее относительно терминатора Земли в течении всего срока активного существования КА.
- близость наклонения плоскости орбиты к полярному, что обесВнпечивает глобальность накрытия полюсами обзора поверхности Земли.
- возможность наблюдения районов на поверхности Земли приВнмерно в одно и то же местное время при незначительном изменении углов места Солнца в точке наблюдения.
Всем этим условиям удовлетворяют солнечно-синхронные орВнбиты с высотами от нескольких сот до полутора тысяч километров. На больших высотах наклонение солнечно-синхронной орбиты отВнлиВнчается от полярного, и глобальность накрытия поверхности Земли не обеспечивается. Для повышения эффективности наблюдеВнния цеВнлесообразно выбрать орбиты с изомаршрутной трассой, у которых следы орбит ежесуточно проходят на одними и теми же районами Земли, что позволяет обеспечивать периодичность наВнблюдения одВнного и того же объекта, как минимум, раз в сутки с одного КА.
Предварительные расчеты показали, что целесообразно испольВнзовать орбиту с высотой Н = 574 км и наклонением плоскости орВнбиты к плоскости экватора Земли i = 97,6В°.
Масса МКА может составить от 500 до 800 кг (что зависит от вида целевой аппаратуры, устанавливаемой на борту МКА). Для выведения МКА на орбиту используется РН СС-19 (ВлРокотВ») с разгонным блоком ВлБризВ».
2.2.3. СВЯЗЬ МКА С НАЗЕМНЫМИ ПУНКТАМИ УПРАВЛЕНИЯ
Управление МКА осуществляется с наземных пунктов управления на территории России. Их количество и место расположения выбирается таким образом, чтобы на любом витке можно было организовать сеанс связи с МКА хотя бы с одного пункта управления. Угол возывшения МКА над горизонтом наземного пункта управления должен быть не менее 7В°, а дальность до МКА не должна превышать 2200 км.
В расчете зон связи были использованы следующие исходные данные:
- высота орбиты - 574 км.
- наклонение орбиты - 97,6В°.
- географическая долгота восходящего узла первого витка - 4В° в.д.
- минимальный угол возвышения МКА над местным горизонтом - 7В°.
Из рассматривавшихся возможных наземных пунктов управления (Москва, Новосибирск, Хабаровск, Мурманск, Калининград, Диксон, Комсомольск-на-Амуре, Петропавловск-Камчатский), было выбрано три (Москва, Диксон, Петропавловск-Камчатский), обеспечивающие возможности связи с МКА на любом витке орбиты. При этом зоны связи с МКА составляют от 3 до 9 минут на витке.
Интергральные характеристики возможности связи с МКА:
- высота орбиты - 574 км.
- число витков, видимых из Москвы, вит/сутки - 6.
- суммарное время видимости из Москвы, мин - 41.
- суммарное время видимости с трех пунктов, мин - 153.
- максимальное время видимости одного витка, мин - 9,1.
2.2.4. ВЫВЕДЕНИЕ МКА НА РАБОЧУЮ ОРБИТУ
Выведение МКА на орбиту с наклонением i = 97,6В° и высотой Н = 574 км осуществляется ракетой-носителем ВлРокотВ» с разгонным блоком ВлБризВ». При выведении для каждой отделяющейся части РН (отработанная первая ступень, обтекатель, отработанная вторая ступень) существует свой район падения.
Возможные варианты старта:
1. Полигон Байконур.
Из-за отсутствия зон падения отделяющихся частей возможно сформировать опорную орбиту с наклонением i порядка 65В°. Для формирования опорной орбиты с наклонением близким полярному при использовании трассы с азимутом стрельбы более 180В° (направление стрельбы на юг) - первая ступень падает в районе Ашхабада, обтекатель сбрасывается на высоте Н порядка 100 км, вторая ступень падает за Аравийским полуостровом. С точки зрения энергетики, выведение осуществляется не по оптимальной схеме, в результате чего на круговую орбиту высотой Н порядка 700 км выводится МКА массой менее 600 кг.
2. Полигон Ледяная (Свободный).
Из-за отсутствия зон падения отделяющихся частей возможно сформировать опорную орбиту с наклонением i порядка 54В° и 65В°. При северном запуске РН первая ступень падает в районе заповедника в устье реки Олейма (приток Лены).
3. Космодром Плесецк.
Азимуты пуска с космодрома Плесецк обеспечивают наклонения орбит i от 72В° до 93В°. Формирование требуемового наклонения i = 97,6В° осуществляется с помощью разгонного блока ВлБризВ».
В результате работы двух ступеней РН формируется баллистическая траектория с наклонением i = 93В°. Высота в момент окончания работы двигателя второй ступени составляет Н = 190 км, наклонная дальность L = 300 км. Приблизительно через 1,2 секунды после прохождения команды на выключение двигателя второй ступени проходит команда на запуск ДУ РБ. После выключения двигателя второй ступени РН происходит отделение от ракеты связки РБ с КА. Время расцепки t = 318 секунд. Абсолютная скорость в момент отделения V = 5550 м/с. Отделяемая масса 6700 кг.
Двигательная установка РБ ВлБризВ» выполняет задачу доразгона КА при формировании опорной орбиты.
Характеристики двигателя РБ ВлБризВ»:
- тяга R, кг - 2000.
- удельный импульс Rуд, сек - 324.
- количество включений, р - 7.
- интервал между включениями, сек - 20.
- время функционирования, час - 7.
В результате работы двигателя РБ ВлБризВ» при первом включении происходит увеличение высоты баллистической траектории с Н = 190 км до Н = 270 км и к моменту окончания работы двигателя (t = 905,5 сек) в точке с аргументом широты u = 104,1В° формируется опорная эллиптическая орбита с параметрами:
- высота в перигее Нп, км - 190.
- высота в апогее На, км - 574.
- большая полуось орбиты а, км - 6747.
- эксцентриситет e - 0,02548
- наклонение i, В° - 93,4.
- период обращения Т, час - 1,53.
- аргумент перигея w, В° - 128,38.
- долгота восходящего узла в гринвичской СК, фиксированной на момент старта Wг, В° - 48,37.
Величина импульса характеристической скорости, отрабатываемого при первом включении ДУ РБ dV1 = 2,36 км/с, время работы порядка 600 сек.
Работа двигателя при первом включении происходит вне зоны видимости НПУ на территории России. Географические координаты, соответствующие этому моменту:
- широта jВ» 76В°.
- долгота lВ» 238В°.
В момент прохождения МКА перигея опорной эллиптической орбиты (t = 1231 сек) географические координаты составляют:
- широта jВ» 53В°.
- долгота lВ» 227В°.
На опорной эллиптической орбите МКА совершает пассивный полет до апогея. В районе апогея (t = 1,12 час) осуществляется второе включение ДУ РБ.
В результате приложения второго компланарного импульса характеристической скорости dV2 = 0,12 км/с, при втором включении (время работы 20 сек) формируется круговая орбита с параметрами:
- высота Н, км - 574.
- наклонение i, В° - 93,4.
- период обращения Т, час - 1,6.
Работа двигателя при втором включении происходит вне зоны видимости НПУ на территории России. Географические координаты, соответствующие этому моменту:
- широта jВ» 1,5В°.
- долгота lВ» 35,8В°.
Для создания круговой, солнечно-синхронной орбиты необходимо изменить наклонение до i = 97,6В°. С этой целью осуществляется третье включение ДУ РБ при первом прохождении восходящего узла орбиты (t = 1,3 час).
В результате приложения ортогонального импульса характеристической скорости dV3 = 0,62 км/с, при третьем включении (время работы 90 сек) формируется солнечно-синхронная круговая орбита с параметрами:
- высота Н, км - 574.
- наклонение i, В° - 97,6.
- период обращения Т, час - 1,6.
- число оборотов в сутки N - 15.
Работа двигателя при третьем включении происходит вне зоны видимости НПУ на территории России. Географические координаты, соответствующие этому моменту:
- широта jВ» 0В°.
- долгота lВ» 28,1В°.
После выключения двигателя при третьем запуске происходит отделение МКА от РБ ВлБризВ».
Кинематические параметры в гринвичской СК, фиксированной на момент старта РН и оскулирующие элементы орбиты на момент отделения от РБ:
Параметр | Значение |
t, сек | 4946,5 |
X, м | 4638800 |
Y, м | 5120280 |
Z, м | 689680 |
Vx, м/с | 241,23 |
Vy, м/с | -1233 |
Vz, м/с | 7473,5 |
l, В° | 28,1 |
T, c | 5761,67 |
e | 0,0009 |
i, В° | 97,595 |
Ra, м | 6940000 |
Rп, м | 6952000 |
2.3. ИСХОДНЫЕ ДАННЫЕ И ЦЕЛИ РАБОТЫ
2.3.1. ИСХОДНЫЕ ДАННЫЕ
Номинальная орбита, необходимая для выполнения задач МКА, имеет следующие параметры:
- круговая, e = 0.
- солнечно-синхронная, скорость прецессии линии узлов орбиты W равна скорости обращения Солнца относительно Земли
W = 2p / 365,2422 = 0,0172 рад/сут = 0,98 В°/сут.
- изомаршрутная, за сутки МКА совершает целое количество оборотов (n = 15).
Это обеспечивает прохождение МКА над одними и теми же райВнонами в одно и тоже местное время.
- период Т = 5765 с.
- высота орбиты Н = 574 км.
- наклонение орбиты i = 97,6В°.
- географическая долгота восходящего узла орбиты lэ = 28,1В°.
Долгота восходящего узла в геоцентрической экваториальной (абсолютной) системе координат OXYZ определяется как разность
lэ - s0,
где s0 - часовой угол, отсчитывающийся от гринвичского мериВндиана до оси X, направленной в точку весеннего равноденствия.
Часовой угол зависит от даты старта и выбирается из астроноВнмиВнческого ежегодника. В данной задаче для моделирования выВнбран часовой угол = 0.
Следовательно долгота восходящего узла орбиты W = lэ = 28,1В°.
Исходя из ТЗ, начальная точка выведения имеет следующие коВнорВндинаты в гринвичской системе координат, фиксированной на момент старта РН:
Параметр | Значение |
t, сек | 4946.5 |
X, м | 4638800 |
Y, м | 5120280 |
Z, м | 689506,95 |
Vx, м/с | 241,23 |
Vy, м/с | -1233 |
Vz, м/с | 7472,65 |
Элементы орбиты:
l, В° | 28,1 |
T, c | 5761,67 |
e | 0,0009 |
i, В° | 97,595 |
Ra, м | 6940000 |
Rп, м | 6952000 |
Кинематические параметры в геоцентрической экваториальной системе координат:
t, сек | 4946.5 |
X, м | 6137262,9 |
Y, м | 3171846,1 |
Z, м | 689506,95 |
Vx, м/с | -201,3 |
Vy, м/с | -1247,03 |
Vz, м/с | 7472,65 |
l, В° | 28,1 |
Точность выведения:
- предельная ошибка по координате (3s) - 7 км.
- предельная ошибка по скорости (3s) - 5 м/с.
Пересчитав ошибку по координате на ошибку по периоду вывеВндения орбиты получим предельную ошибку по периоду DT - 10 сек.
Корреляционная матрица ошибок выведения на момент выведеВнния составляет:

Члены, стоящие на главной диагонали представляют собой квадВнраты предельных ошибок - (3s)2.
K11 = K22 = K33 = (3s)2 = 72 = 49 км.
K44 = K55 = K66 = (3s)2 = 52 = 25 м/с.
Остальные члены представляют собой вторые смешанные моВнменты Kij = Kji = rijsisj или Kij = Kji = rjj(3si)(3sj), где rjj - коэффициВненты связи величин i и j. В данном случае вторые смешанные моВнменты Kij = Kji = 0.
Кинематические параметры в геоцентрической экваториальной системе координат на момент выведения с учетом ошибок выведеВнния:
t, сек | 4946.5 |
X, м | 6144262,9 |
Y, м | 3178846,1 |
Z, м | 696506,95 |
Vx, м/с | -206,3 |
Vy, м/с | -1252,03 |
Vz, м/с | 7477,65 |
l, В° | 28,1 |
Параметры орбиты с учетом ошибок выведения:
l, В° | 28,13 |
T, c | 5795,7 |
W, В° | 28,13 |
p, км | 6973,5 |
а, км | 6973,6 |
e | 0,00314 |
i, В° | 97,637 |
2.3.2. ЦЕЛИ РАБОТЫ
1) Исследование и моделирование движения ЦМ МКА при возВндействии на КА возмущающих ускорений.
2) Разработка алгоритмов проведения коррекции траектории МКА, моделирования процесса, и расчет потребного топлива для проведения коррекции траектории.
3) Исследование динамики системы коррекции траектории при стабилизации углового положения в процессе проведения коррекВнции траектории МКА.
2.4. МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС МКА
2.4.1.УРАВНЕНИЕ ДВИЖЕНИЯ КА
Рассмотрим невозмущенное движение материальных точек М и m в некоторой инерциальной системе координат. Движение соверВншаВнется под действием силы притяжения Fz. Сила Fz для материальВнной точки m определяется формулой:
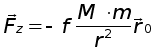 ,
,
где Вж - постоянная притяжения,
ro- единичный вектор, направленный от М к m,
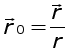 ,
,
где 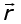 - радиус-вектор, проведенный из т.М до т.m.
- радиус-вектор, проведенный из т.М до т.m.
r - относительное расстояние от М до m.
На точку М действует сила Fz, равная по величине и направленВнная в противоположную сторону.
На основе второго закона Ньютона уравнения движения материВнальных точек М и m имеют вид:
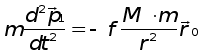 (1),
(1), 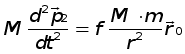 (2)
(2)
или
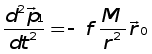 (3),
(3), 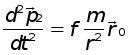 (4)
(4)
где 1 - радиус-вектор, проведенный из начала инерциальной сисВнтемы координат в точку m.
2- радиус-вектор, проведенный из начала инерциальной сисВнтемы координат в точку М.
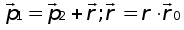 .
.
Вычитая из уравнения (3) уравнение (4), получим уравнение двиВнжения матеВнриальной точки m относительно притягивающего ценВнтра М:
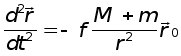

Так как m<<М, следовательно, можно пренебречь ускорением, которое КА с массой m сообщает притягивающему центру М. ТоВнгда можно совместить начало инерциальной системы координат с приВнтягивающим центром М. Следовательно,  .
.
Таким образом, уравнение невозмущенного движения КА отноВнсительно притягивающего центра М в инерциальной системе коорВндинат, центр которой находится в М, имеет вид
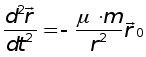 ,
,
где m = fM - гравитационная постоянная Земли.
Рассмотрим возмущенное движение КА в геоцентрической экваВнториальной (абсолютной) системе координат OXYZ:
- начало О - в центре масс Земли.
- ось X направлена в точку весеннего равноденствия g.
- ось Z совпадает с осью вращения Земли и направлена на СеверВнный полюс Земли.
- ось Y дополняет систему до правой.
Движение КА в абсолютной системе координат OXYZ происхоВндит под действием центральной силы притяжения Земли Fz, а также под действием возмущающих сил Fв. Уравнение движения имеет вид
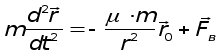 или
или 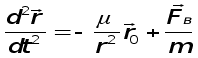
где m = 597 кг - масса КА.
В проекциях на оси абсолютной системы координат OXYZ полуВнчим
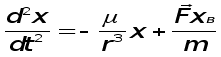 или
или 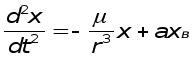
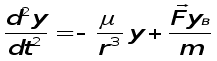 или
или 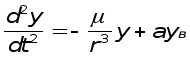
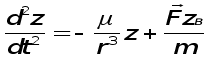 или
или 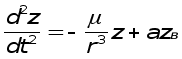
где axв, ayв, azв- возмущающиеся ускорения.
Основные возмущающиеся ускорения вызываются следующими причинами:
- нецентральностью поля притяжения Земли.
- сопротивлением атмосферы Земли.
- влиянием Солнца.
- влиянием Луны.
- давлением солнечного света.
2.4.2. ВОЗМУЩАЮЩИЕ УСКОРЕНИЯ, ДЕЙСТВУЮЩИЕ НА МКА
1) Возмущающееся ускорение, вызванное нецентральностью граВнвитационного поля Земли.
Рассмотрим потенциал поля притяжения Земли. При точном расВнчете параметров орбиты спутников, в качестве хорошего приблиВнжеВнния к действительной поверхности Земли принимают геоид. Геоид - это гипотетическая уровенная поверхность, совпадающая с поверхВнностью спокойного океана и продолженная под материком.
Иногда в баллистике под геоидом понимают не поверхность, а тело, которое ограничено поверхностью мирового океана при неВнкоВнтором среднем уровне воды, свободной от возмущений. Во всех точках геоида потенциал притяжения имеет одно и то же значение.
Потенциал притяжения Земли можно представить в виде разлоВнжеВнния по сферическим функциям.
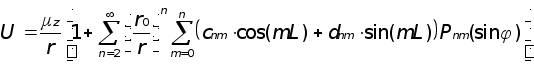
где mz = fMz - гравитационная постоянная Земли.
r0- средний экваториальный радиус Земли.
сnm, dnm - коэффициенты, определяемые из гравиметрических данВнных, а также по наблюдениям за движением ИСЗ.
L - долгота притягивающей точки.
j - широта притягивающей точки.
Pnm(sinj) - присоединенные функции Лежандра степени m и поВнрядка n (при m № 0).
Pnm(sinj) - многочлен Лежандра порядка n (при m = 0).
Составляющие типа (mz/r)(r0/r)cn0Pn0(sinj) - называют зональВнными гармониками n-поВнрядка. Т.к. полином Лежандра n-го поВнрядка имеет n действительных корней, функция Pn0(sinj) будет меВннять знак на n широтах, сфера делится на n+1 широтную зону, где эти составляюВнщие имеют попеременно Вл+В» или Вл-В» значения. ПоВнэтому их называют зональными гармониками.
Составляющие типа
(mz/r)(r0/r)cnmcos(mL)Pnm(sinj) и (mz/r)(r0/r)dnmsin(mL)Pnm(sinj)
- называют тессеральными гармониками n-порядка и степени m. Они обращаются в 0 на 2m меридианах, где cos(mL) = 0 и sin(mL)= 0 и на n-m параллелях, где Pnm(sinj)= 0 или dmPnm(sinj)/d(sinj)m = 0, сфера делится на n+m+1 трапецию, где эти составляющие сохраВнняют знак.
Составляющие типа и
(mz/r)(r0/r)ccos(nL)P(sinj) и (mz/r)(r0/r)dsin(nL)P(sinj)
- называют секториальными гармониками n-порядка и степени m. Эти составляющие меняю знак только на меридианах, cos(nL) = 0 и sin(nL)= 0, на сфере выделяют 2n меридиональных секторов, где эти составляющие соВнхраняют знак.
Многочлен Лежандра степени n находится по следующей форВнмуле:
Pn0(z) = 1/(2n!)ТС(d(z2 - 1)/dz)
Присоединенная функция Лежандра порядка n и степени m нахоВндится по следующей формуле:
Pnm(z) = (1-z2)m/2ТСdmPn0(z)/dzm
Возмущающая часть гравитационного потенциала Земли равна
Uв= U’ + DU’ = (U - mz/r) + DU’
где DU’ - потенциал аномалий силы тяготения Земли.
U’ - часть потенциала Земли, которая учитывает несферичность Земли.
Следовательно,
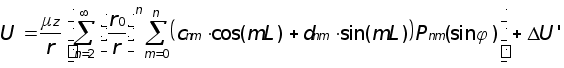
Первая зональная гармоника в разложении потенциала учитыВнвает полярное сжатие Земли.
Зональные гармоники нечетного порядка и тессеральные гармоВнники, где n-m нечетное число - учитывают ассиметрию Земли отноВнсительно плоскости экватора.
Секториальные и тессеральные гармоники - учитывают ассиметВнрию Земли относительно оси вращения.
Первая зональная гармоника имеет порядок 10-3, а все остальные - порядок 10-6 и выше. Поэтому будем учитывать в разложении поВнтенВнциала притяжения только зональную гармонику (n=2, m=0) и секторальную гармонику (n=2, m=2). Также не будем учитывать потенциал аномалий силы тягоВнтения Земли DU’.
Таким образом,
Uв = (mz/r)(r0/r)2[c20P20(sinj) + (c22cos(2L) + d22sin(2L))P22(sinj)],
где c20= - 0,00109808,
c22= 0,00000574,
d22 = - 0,00000158.
P20(x) = 1/222!ТСd2(x2 - 1)2/dx2.
Следовательно P20(x) = (3x2 - 1)/2.
Так как sinj = z/r, следовательно P20(sinj) = (3(z/r)2 - 1)/2.
P22(x) = (1 - x2)2/2ТСd2P20(x)/dx2 = 1/2ТС(1 - x2)ТСd2(3x2 - 1)/dx2
Следовательно P22(x) = 3(1 - x2).
Так как sinj = z/r, следовательно P22(sinj) = 3(1 - (z/r)2).
Значит
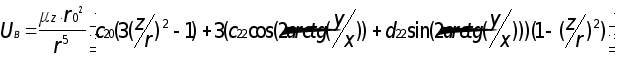
Чтобы найти возмущающее ускорение от нецентральности поля тяготения Земли в проекциях на оси абсолютной системы коордиВннат OXYZ, надо взять производные от возмущающего потенциала Uв по координатам X, Y, Z, причемr = Ц(x2 + y2 + z2).
Следовательно,
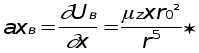
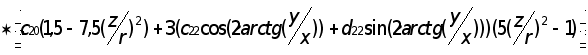
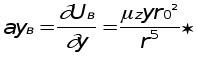
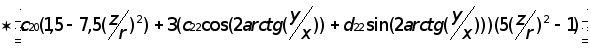
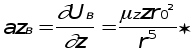
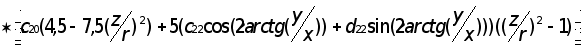
2) Возмущающее ускорение, вызванное сопротивлением атмоВнсферы.
При движении в атмосфере на КА действует сила аэродинамичеВнского ускорения Rx, направленная против вектора скорости КА отВнноВнсительно атмосферы:
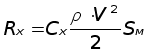
где Cx= 2 - коэффициент аэродинамического сопротивления.
Sм = 2,5 м2 - площадь миделевого сечения - проекция КА на плосВнкость, перВнпендикулярную направлению скорости полета.
V - скорость КА.
r - плотность атмосферы в рассматриваемой точке орбиты.
Так как исследуемая орбита - круговая с высотой Н = 574 км, буВндем считать, что плотность атмосферы одинакова во всех точках орВнбиты и равна плотности атмосферы на высоте 574 км. Из табВнлицы стандартной атмосферы находим плотность наиболее близВнкую к выВнсоте Н = 574 км. Для высоты Н = 580 км r = 5,098ТС10-13 кг/м3.
Сила аэродинамического ускорения создает возмущающее касаВнтельное ускорение aa:
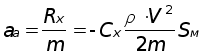
Найдем проекции аэродинамического ускорения на оси абсолютВнной системы координат axa, aya, aza:
aa направлено против скорости КА, следовательно единичный векВнтор направления имеет вид
ea = [Vx/|V|, Vy|V|, Vz/|V|], |V| = Ц(Vx2+Vy2+Vz2)
Таким образом,
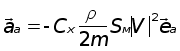
Значит
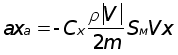 ,
, 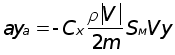 ,
, 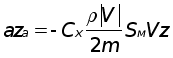
3) Возмущающее ускорение, вызванное давлением солнечного света.
Давление солнечного света учитывается как добавок к постоянВнной тяготения Солнца - Dmc. Эта величина вычисляется следующим обВнразом:
Dmc = pSмA2/m
где = 4,64ТС10-6 Н/м2 - давление солнечного света на расстоянии в одну астрономиВнческую единицу А.
A = 1,496ТС1011 м - 1 астрономическая единица.
m - масса КА.
Sм= 8 м2 - площадь миделевого сечения - проекция КА на плосВнкость, перВнпендикулярную направления солнечных лучей.
Таким образом,
Dmc= 1,39154ТС1015 м3/c2.
4) Возмущающее ускорение, возникающее из-за влияния Солнца.
Уравнение движения КА в абсолютной системе координат OXYZ относительно Земли при воздействии Солнца:
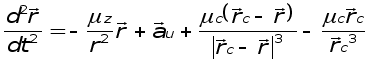
где mz - постоянная тяготения Земли.
mc- постоянная тяготения Солнца.
r - радиус-вектор от Земли до КА.
rc- радиус-вектор от Земли до Солнца.
Таким образом, возмущающее ускорение, возникающее из-за влияния Солнца:
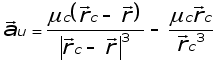 .
.
Здесь первое слагаемое есть ускорение, которое полуВнчил бы КА, если он был непритягиваюВнщим, а Земля отсутствовала.
Второе слагаемое есть ускорение, которое сообщает Солнце Земле, как непритягиваюВнщему телу.
Следовательно, возмущающее ускорение, которое получает КА при движении относительно Земли - это разность двух слагаемых.
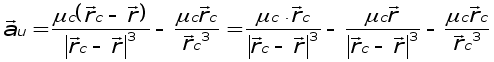
Так как rc>>r, то в первом слагаемом можно пренебречь r. СледоВнваВнтельно

| rc - r| = Ц((xc-x)2+(yc-y)2+(zc-z)2)
где xc, yc, zc- проекции радиуса-вектора Солнца на оси абсолютВнной сисВнтемы координат.
Моделирование движения Солнца проводилось следующим обВнраВнзом: за некоторый промежуток времени t Солнце относительно Земли сместится на угол J = Jн+ wct,
где Jн= W + (90 - D) - начальное положение Солнца в эклиптичеВнской системе коорВндинат.
W = 28,1В° - долгота восходящего узла первого витка КА.
D = 30В° - угол между восходящим узлом орбиты КА и терминатоВнром.
wc - угловая скорость Солнца относительно Земли.
wc = 2/T = 2p/365,2422ТС24ТС3600 = 1,991ТС10-7 рад/c = 1,14ТС10-5 В°/c
Таким образом, в эклиптической системе координат проекции составляют:
xce = rccosJ
yce = rcsinJ
zce = 0
rc = 1,496ТС1011 м (1 астрономическая единица) - расстояние от Земли до Солнца
Плоскость эклиптики наклонена к плоскости экватора на угол e= 23,45В°, проекцииrc на оси абсолютной системы координат можно найти как
xc = xce = rccosJ
yce = ycecose = rccosJcose
zce = rcsinJsine
Таким образом, проекции возмущающего ускорения на оси абсоВнлютной системы координат:
axc = - mcx/(Ц((xc-x)2+(yc-y)2+(zc-z)2))3
ayc = - mcy/(Ц((xc-x)2+(yc-y)2+(zc-z)2))3
azc = - mcz/(Ц((xc-x)2+(yc-y)2+(zc-z)2))3
С учетом солнечного давления
axc = - (mc-Dmc)x/(Ц((xc-x)2+(yc-y)2+(zc-z)2))3
ayc = - (mc-Dmc)y/(Ц((xc-x)2+(yc-y)2+(zc-z)2))3
azc = - (mc-Dmc)z/(Ц((xc-x)2+(yc-y)2+(zc-z)2))3
5) Возмущающее ускорение, возникающее из-за влияния Луны.
Уравнение движения КА в абсолютной системе координат OXYZ относительно Земли при воздействии Луны:
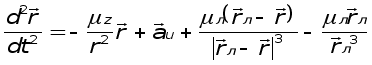
где mл = 4,902ТС106 м3/c2- постоянная тяготения Луны.
rл - радиус-вектор от Земли до Луны.
Таким образом, возмущающее ускорение, возникающее из-за влияния Луны:
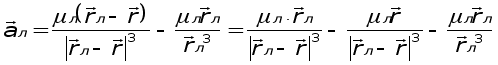
Так как rл>>r, то в первом слагаемом можно пренебречь r. СледоВнваВнтельно
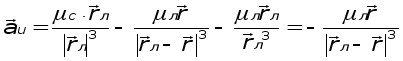
|rл- r| = Ц((xл-x)2+(yл-y)2+(zл-z)2)
где xл, yл, zл- проекции радиуса-вектора Луны на оси абсолютной системы координат.
Движение Луны учитывается следующим образом: положение Луны в каждый момент времени рассчитывается в соответствии с данными астрономического ежегодника. Все данные заносятся в массив, и далее этот массив считается программой моделирования движения КА. В первом приближении принимается:
- орбита Луны - круговая.
- угол наклона плоскости орбиты Луны к плоскости эклиптики i = 5,15В°.
- период обращения линии пересечения плоскостей лунной орВнбиты и эклиптики (по ходу часовой стрелки, если смотреть с северВнного полюса) = 18,6 года.
Угол между плоскостями экватора Земли и орбиты Луны можно найти по формуле
cos(hл) = cos(e)cos(i) - sin(e)sin(i)cos(Wл)
где Wл - долгота восходящего узла лунной орбиты, отсчитываВнется от направления на точку весеннего равноденствия.
e- угол между плоскостями эклиптики и экватора Земли.
Величина hл колеблется с периодом 18,6 лет между минимумом при hл = e - i = 18В°18’ и максимумом приhл = e + i = 28В°36’ при W= 0.
Долгота восходящего узла лунной орбиты Wл изменяется с течеВннием времени t на величину Wл= tТС360/18,6ТС365,2422ТС24ТС3600.
Положение Луны на орбите во время t определяется углом
J л= tТС360/27,32ТС24ТС3600.
По формулам перехода найдем проекции вектора положения Луны на оси абсолютной системы координат:
xл = rл(cosJлcosWл- coshлsinJлsinWл)
yл = rл(cosJлsinWл+ coshлsinJлcosWл)
zл = rлsinhлsinJл
rл= 3,844ТС108 м - среднее расстояние от Земли до Луны
Таким образом, проекции возмущающего ускорения на оси абсоВнлютной системы координат:
axл= - mлx/(Ц((xл!-x)2+(yл-y)2+(zл-z)2))3
ayл= - mлy/(Ц((xл!-x)2+(yл-y)2+(zл-z)2))3
azл= - mлz/(Ц((xл!-x)2+(yл-y)2+(zл-z)2))3
Уравнения возмущенного движения при действ
Вместе с этим смотрят:
Астрология-этап развития астрономии
Бесконечные воды вселенной
Биографии астрономов
Биографии астрономов_2
Затменно-переменные звёзды и возможности их наблюдений любителями астрономии