Единичная подгруппа и вся группа называются несобственными подгруппами, а все остальные подгруппы называются собственными.
В основном нас будут интересовать собственные подгруппы групп.
1.2. ТЕОРЕМЫ О ПОДГРУППАХ
Для каждого подмножества множества Sn, которое является подгруппой, должны выполняться все требования определения группы. Но проверять все эти требования не нужно, так как справедлива следующая теорема о подгруппах.
Теорема: подмножество Н группы Sn, которое содержит по меньшей мере одну перестановку, является подгруппой группы Sn тогда и только тогда, когда:
вместе с каждыми двумя элементами  в него входит их произведение
в него входит их произведение 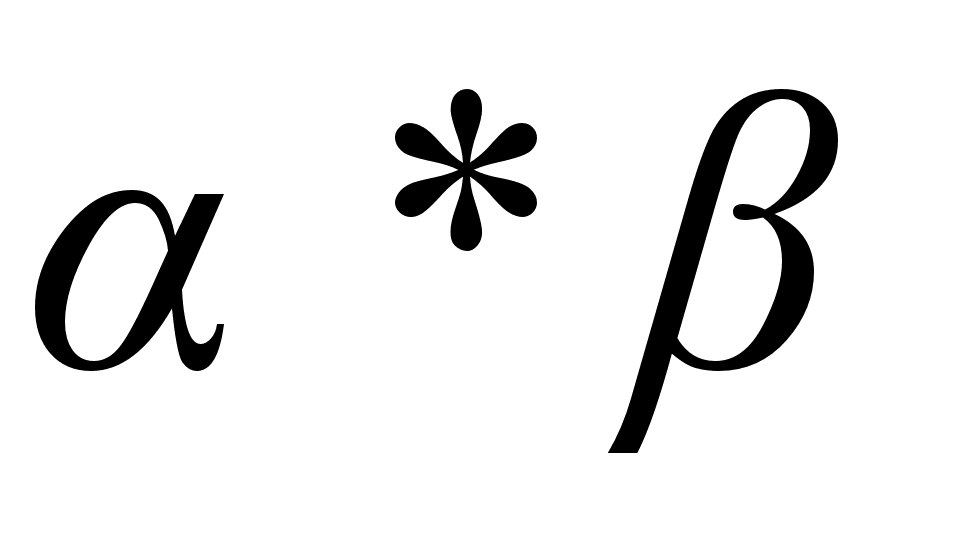 ;
;
если 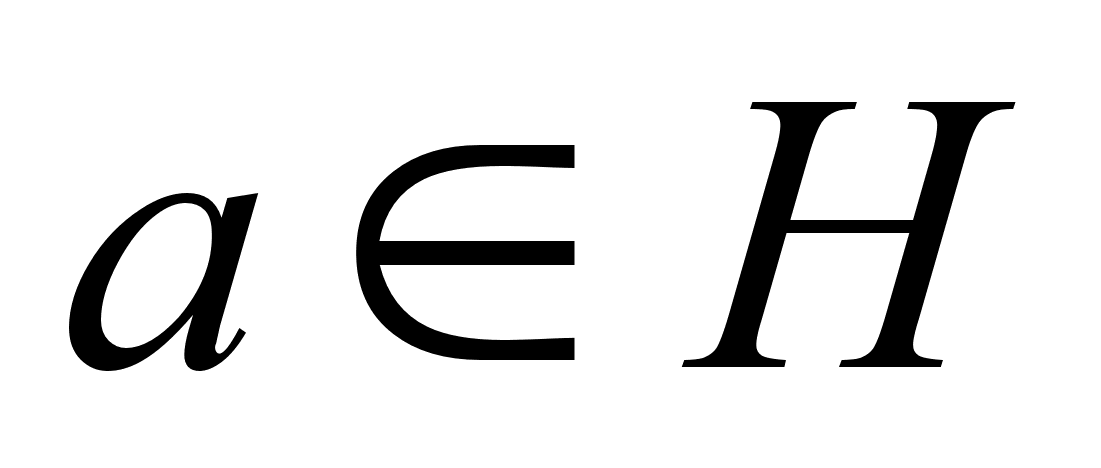 , то
, то 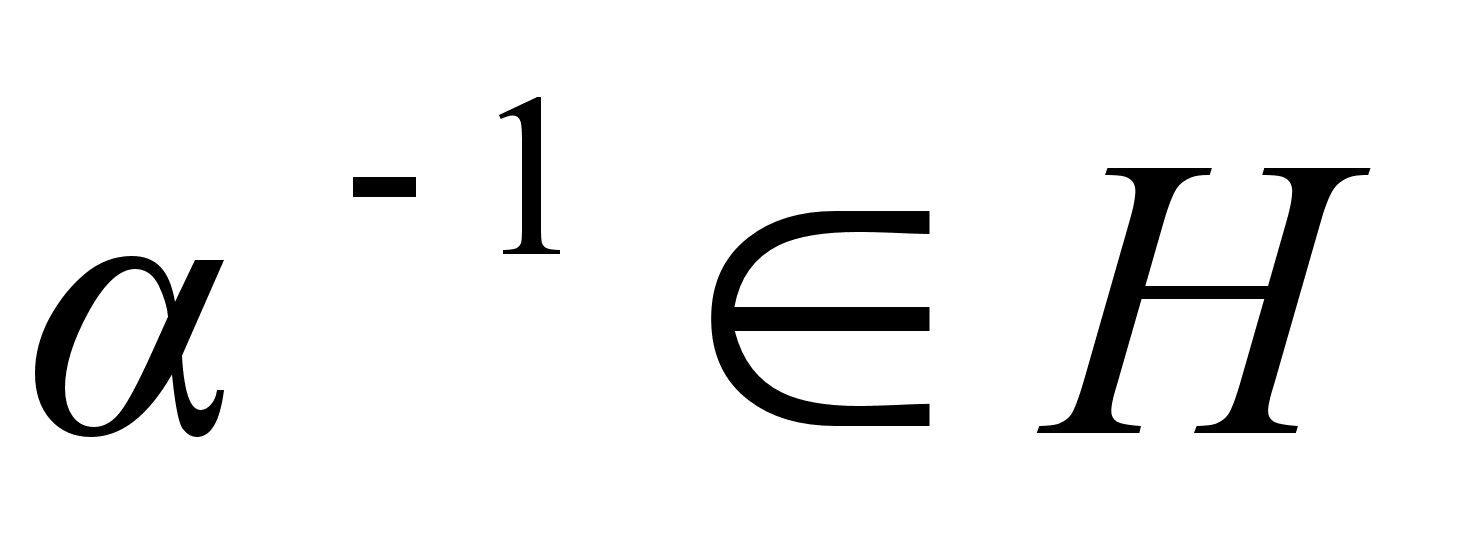 .
.
Доказательство.
Необходимость.
Действительно, если Н тАУ подгруппа группы Sn, то она замкнута относительно действия упражнения перестановок, которые принадлежат Н, то есть выполняется условие 1). Каждый элемент из Н имеет обратный, следовательно, выполняется условие 2).
Достаточность.
Пусть для множества Н перестановок выполняются условия 1) и 2). Проверим, имеет ли множество Н все свойства группы. Условие 1) означает, что множество Н замкнуто относительно действия умножения своих элементов следовательно, выполняются первое требование определения группы. Ассоциативность действия умножения перестановок Н имеет место, так как умножение произвольных перестановок (в частности, и тех, которые принадлежат Н) имеет такое свойство. Тождественная перестановка также должна принадлежать множеству Н. Действительно, Н содержит хоть одну перестановку, например 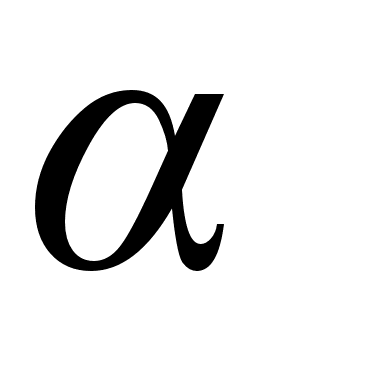 , а тогда Н принадлежит по условию 2) и перестановка
, а тогда Н принадлежит по условию 2) и перестановка 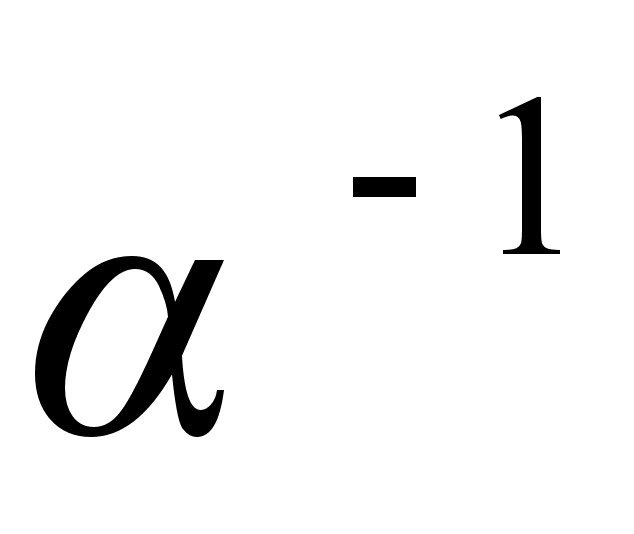 . Поэтому по условию 1) Н принадлежит перестановка
. Поэтому по условию 1) Н принадлежит перестановка 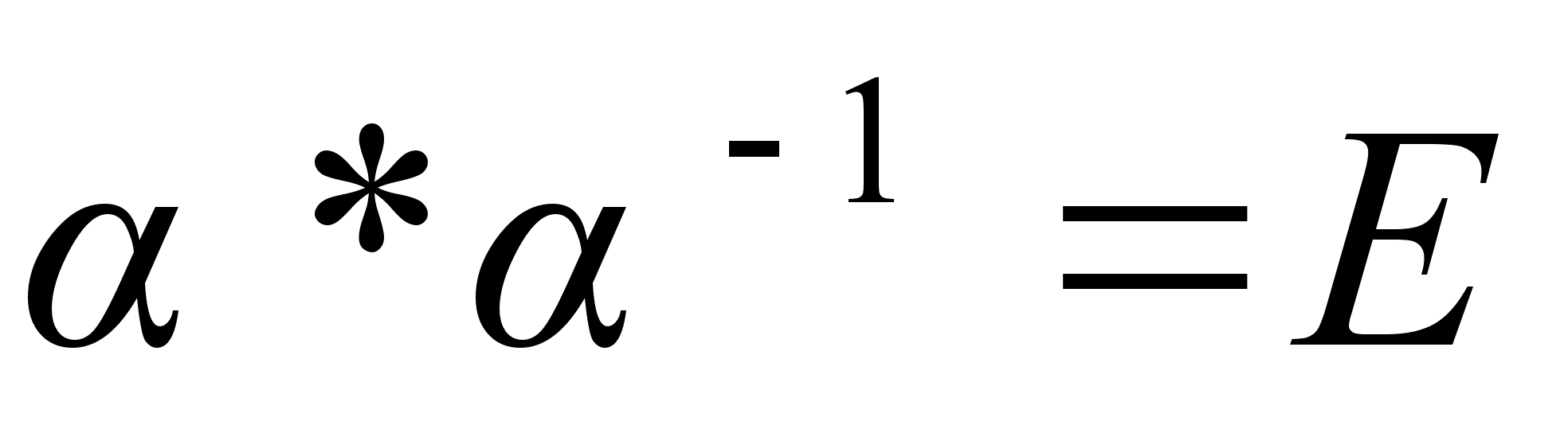 . Наконец, условие 2) показывает, что каждый элемент из Н имеет обратный, который также принадлежит Н. Следовательно, Н является подгруппой группы Sn.
. Наконец, условие 2) показывает, что каждый элемент из Н имеет обратный, который также принадлежит Н. Следовательно, Н является подгруппой группы Sn.
Теорема доказана.
Пример 1.
Пусть Н тАУ множество перестановок  ,
, 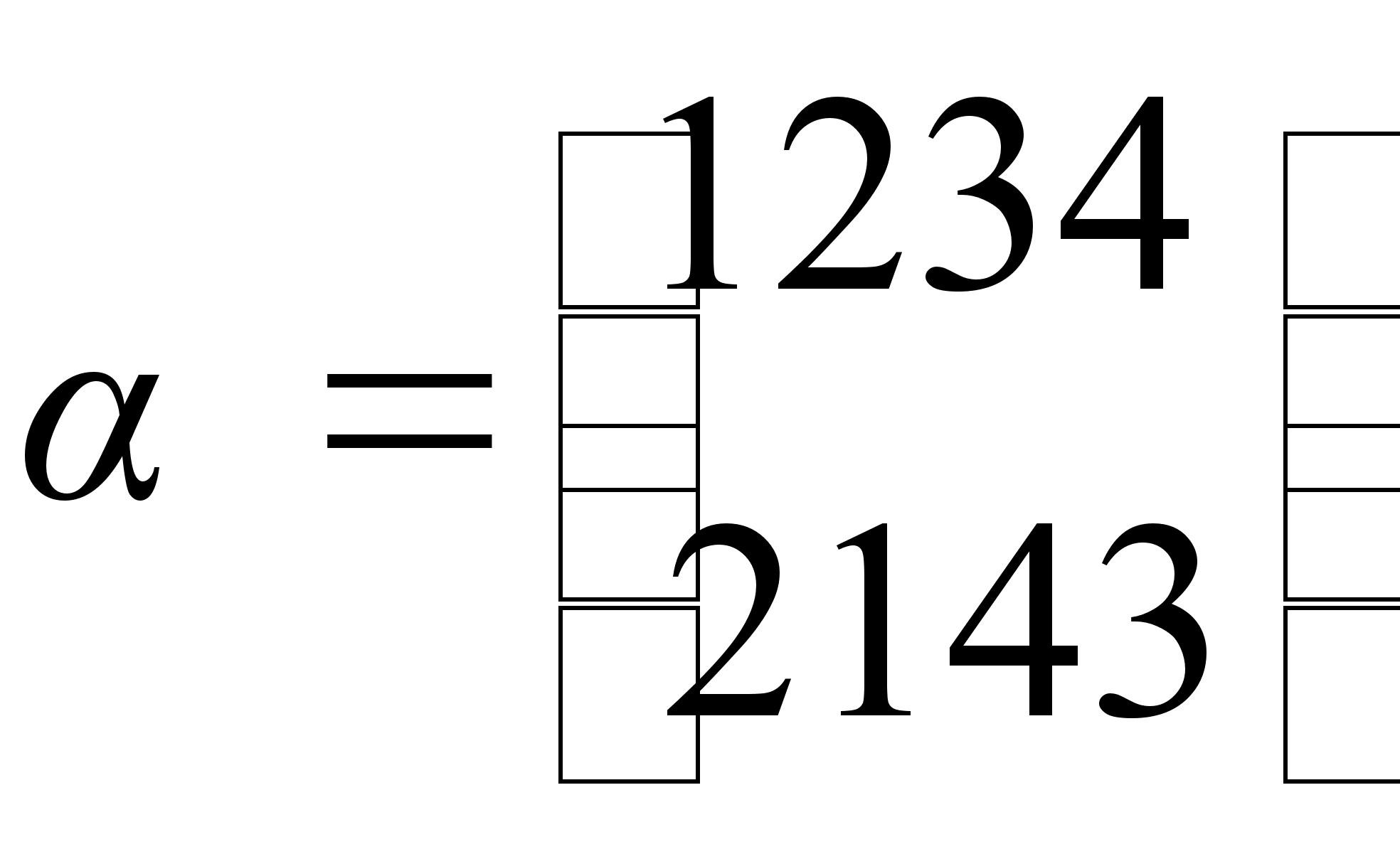 ,
,  ,
,  .
.
Проверим, является ли Н подгруппой группы S4.
Имеем: 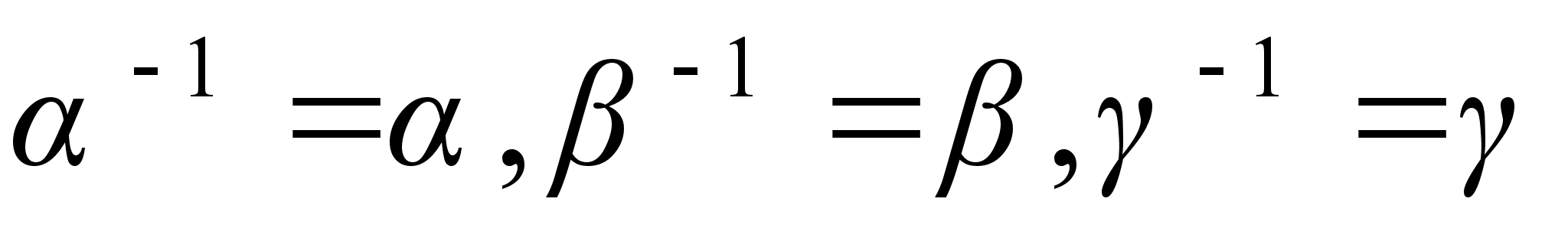 , следовательно, для множества Н выполняется условие 2) только что доказанной теоремы. Проверим выполнение условия 1) теоремы.
, следовательно, для множества Н выполняется условие 2) только что доказанной теоремы. Проверим выполнение условия 1) теоремы.


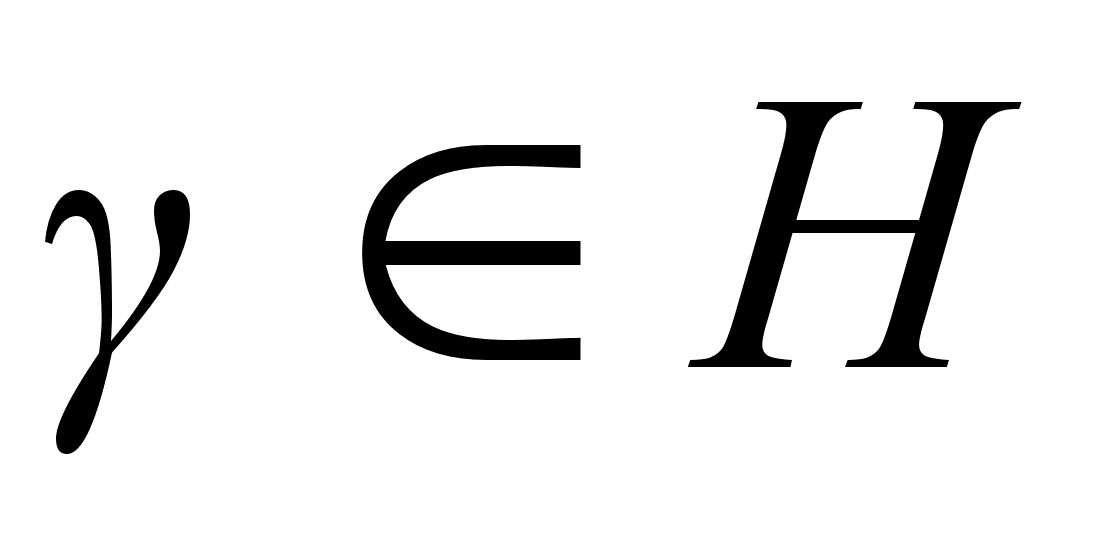

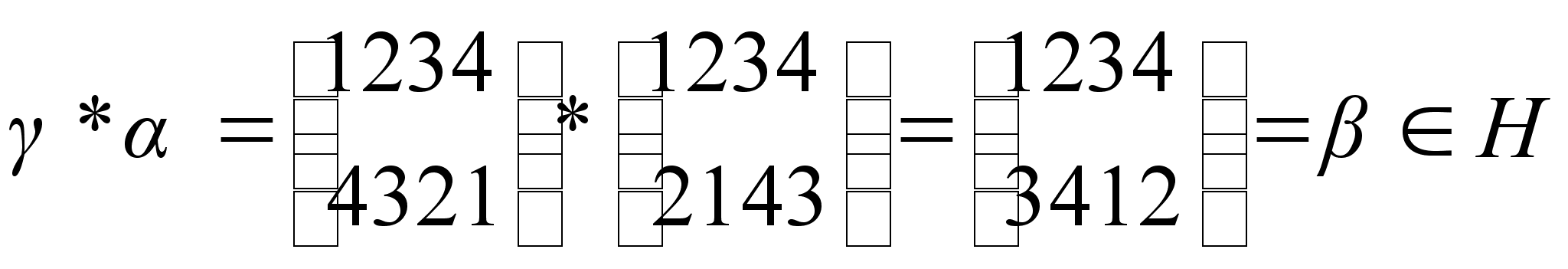





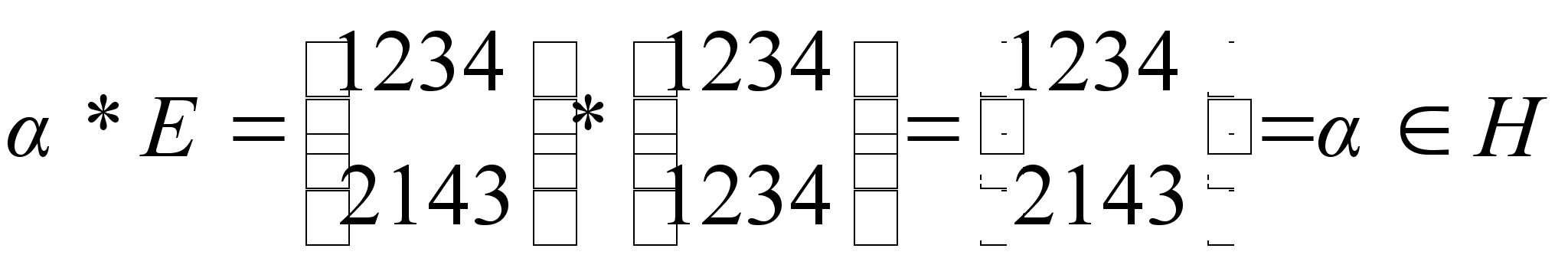


Следовательно, произведение каждых двух элементов множества Н является элементов того же множества, то есть для Н выполняется и условие 1) упомянутой выше теоремы.
Таким образом, подмножество Н является подгруппой группы S4.
Пример 2.
Пусть Т тАУ множество перестановок  ,
, 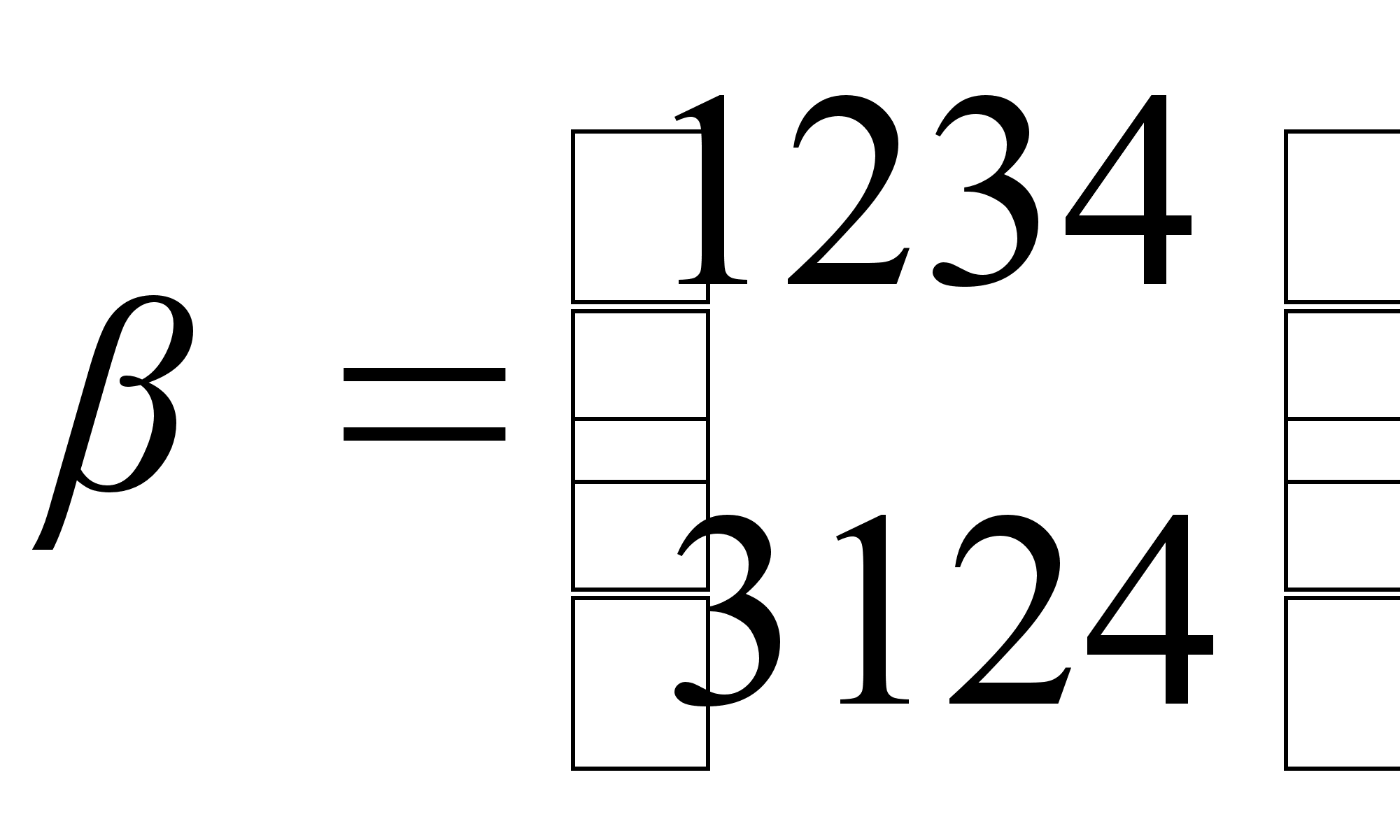 ,
, 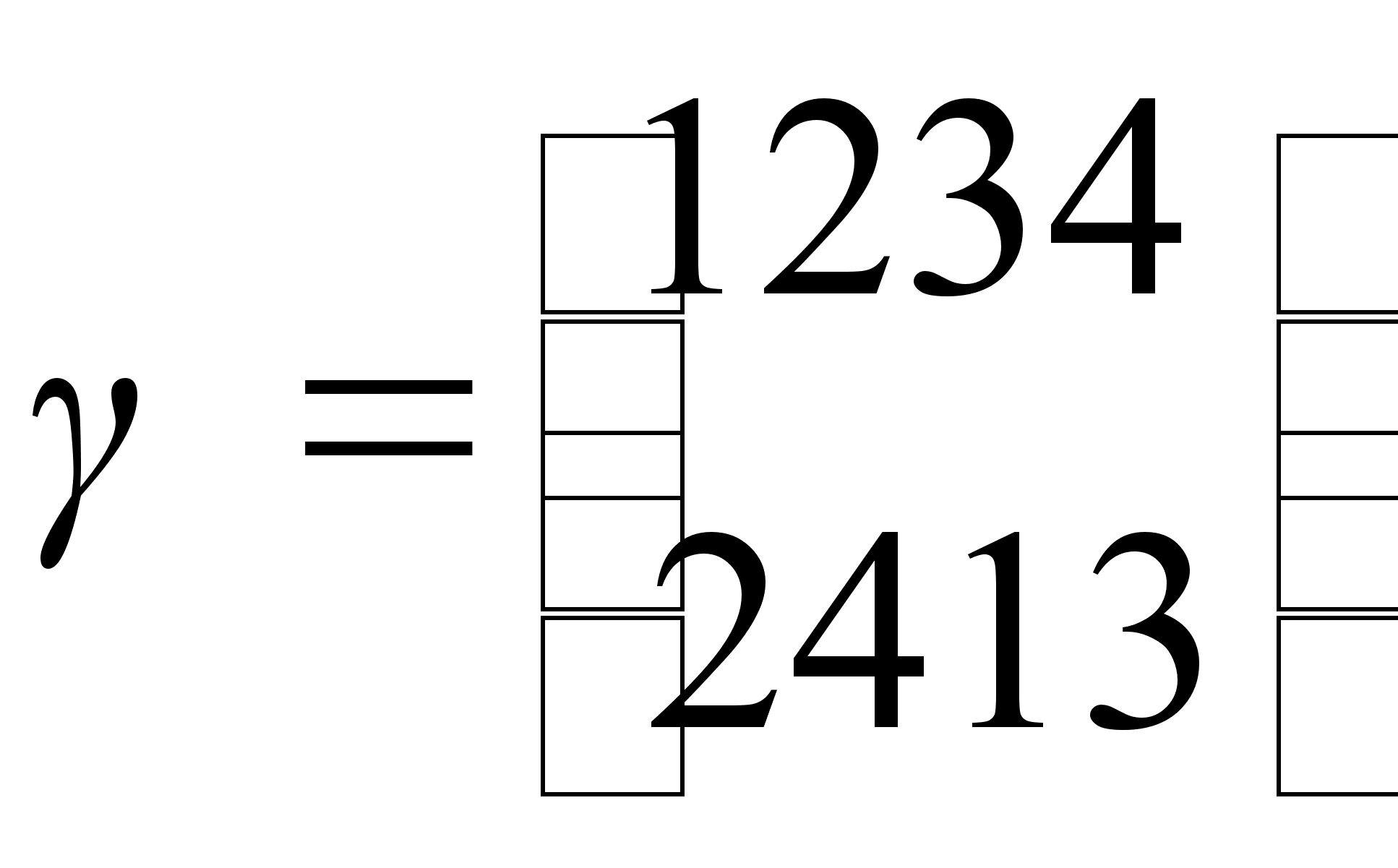 ,
,  .
.
Проверим, является ли Т подгруппой группы S4.
Оказывается, что множество Т не является подгруппой группы S4, так как для него не выполняется ни одно из условий 1), 2) теоремы о подгруппах. Действительно, 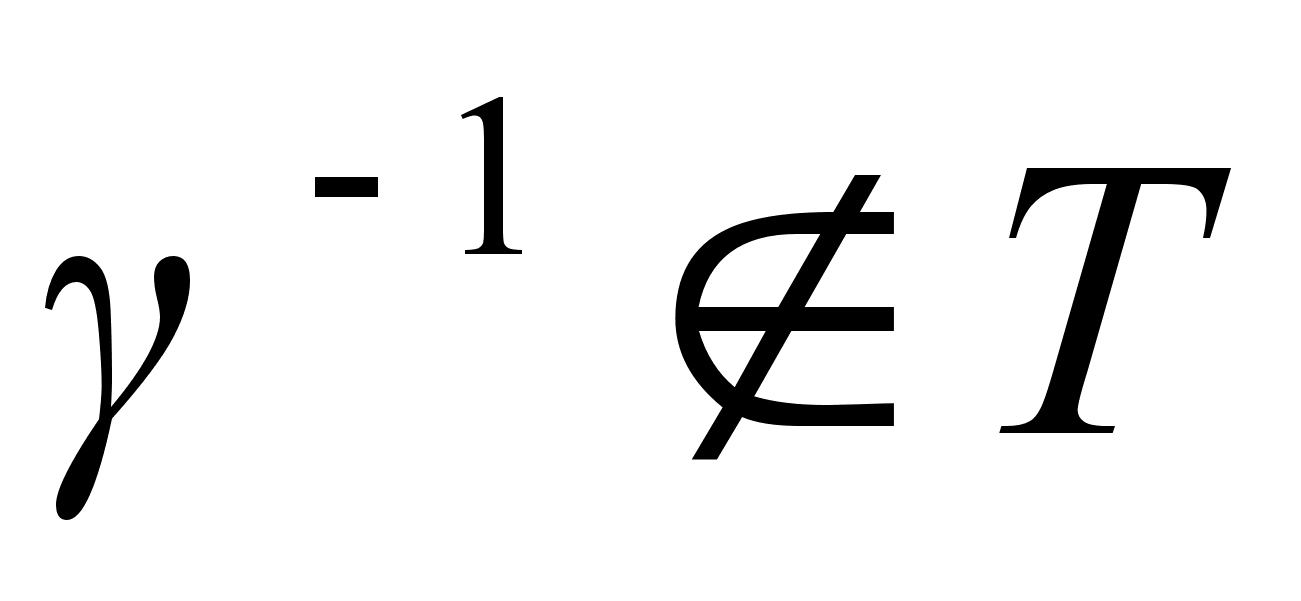 , так как
, так как  ,
, 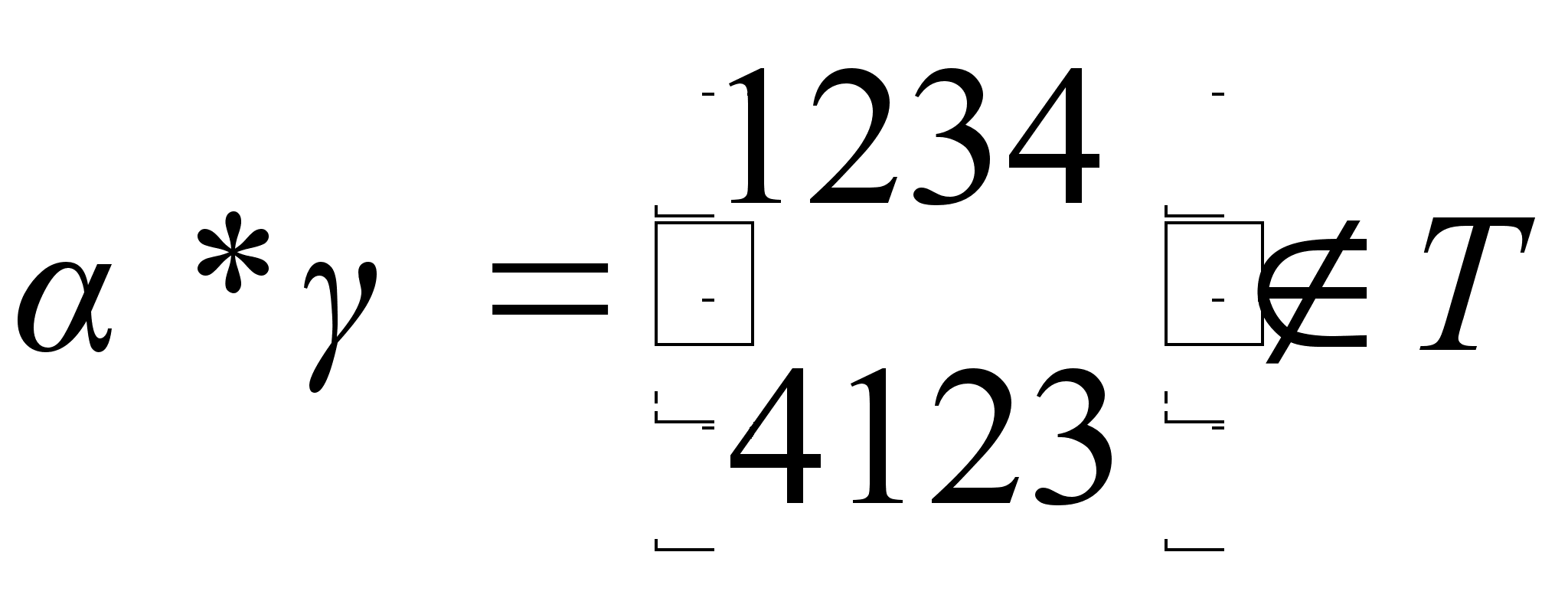 .
.
Следует отметить, что сформулированная выше теорема справедлива для бесконечных групп. В случае конечных групп проверка условия 2) является излишней, то есть для конечных групп справедлива следующая теорема о подгруппах.
Теорема: пусть 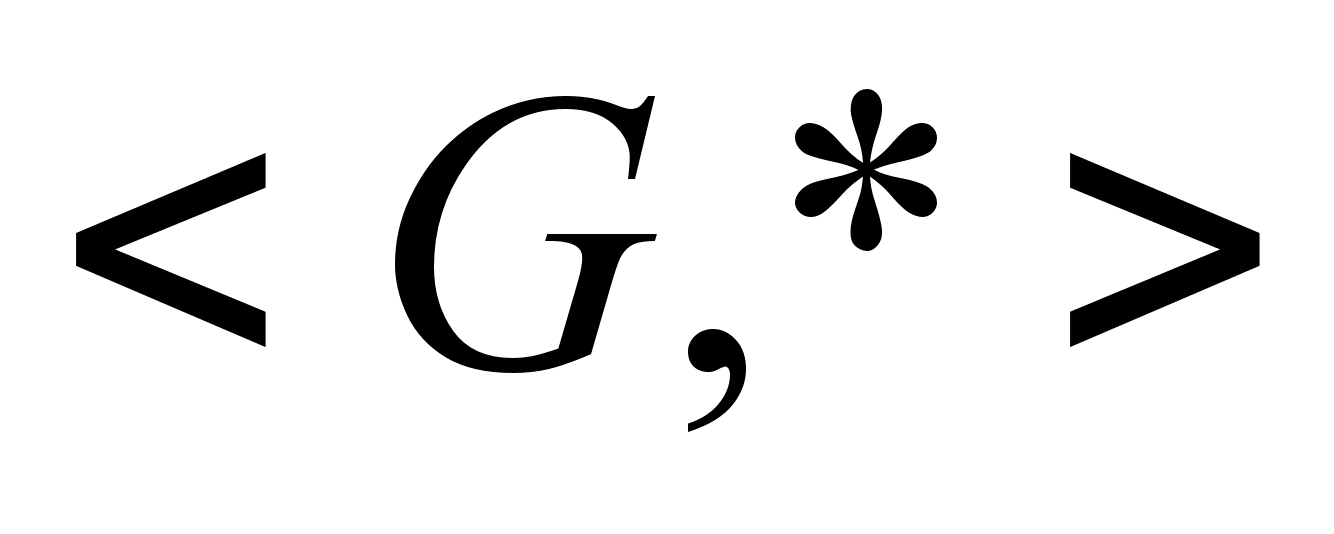 - группа, Н - ее конечное подмножество и оно замкнуто относительно умножения. Тогда Н тАУ подгруппа группы G.
- группа, Н - ее конечное подмножество и оно замкнуто относительно умножения. Тогда Н тАУ подгруппа группы G.
Доказательство.
Докажем замкнутость Н относительно существования обратного элемента.
Возьмем произвольный элемент  . Если
. Если 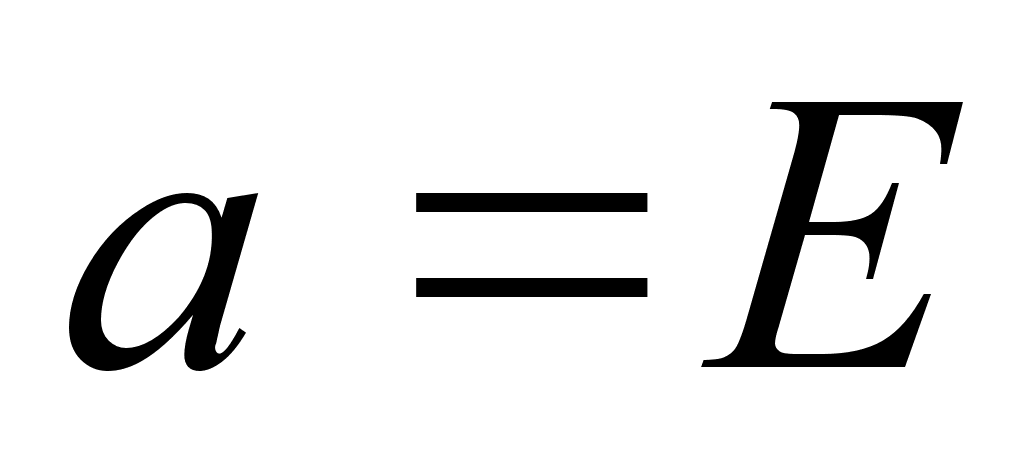 , то
, то 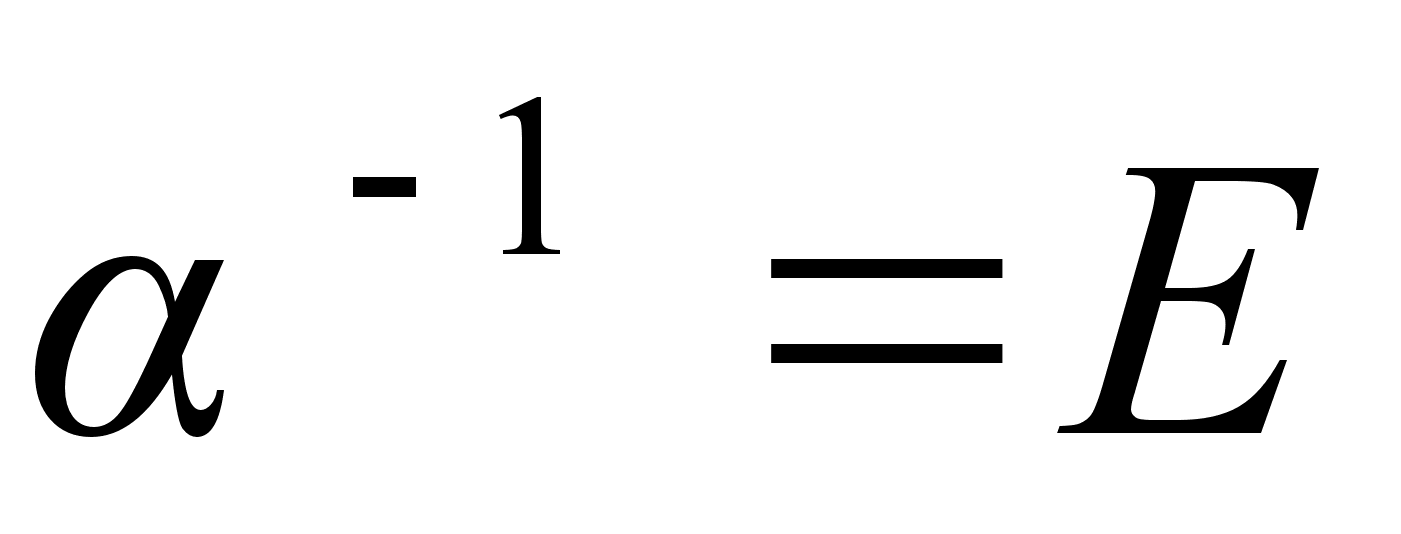 и
и 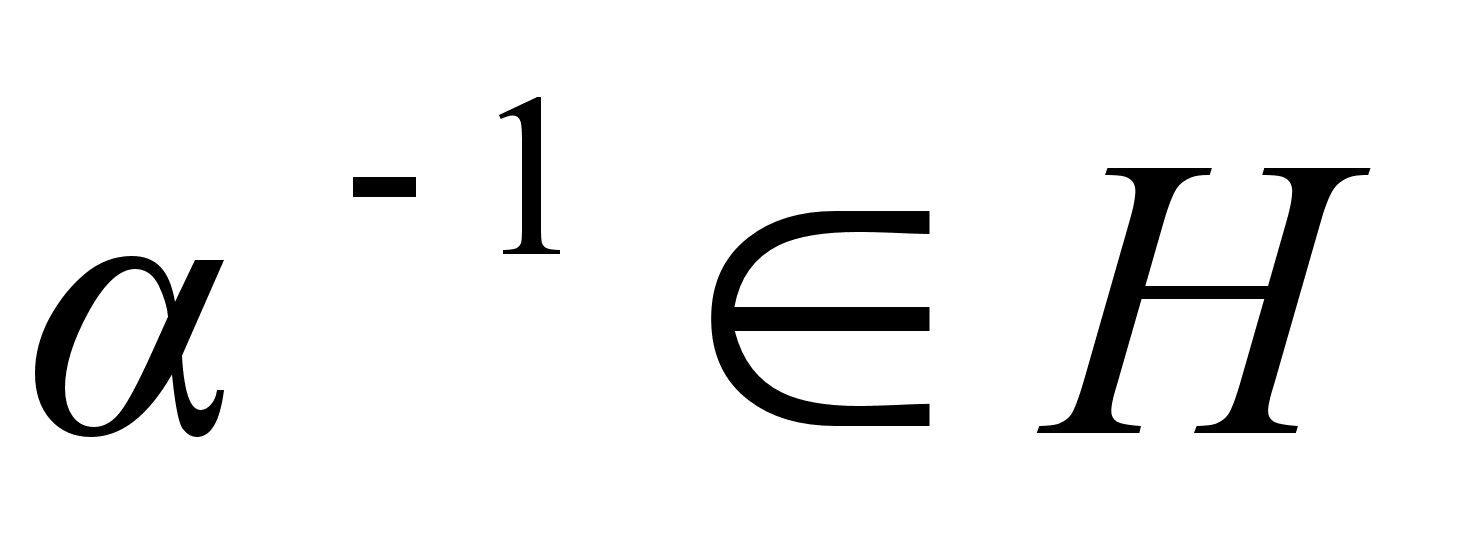 .
.
Пусть 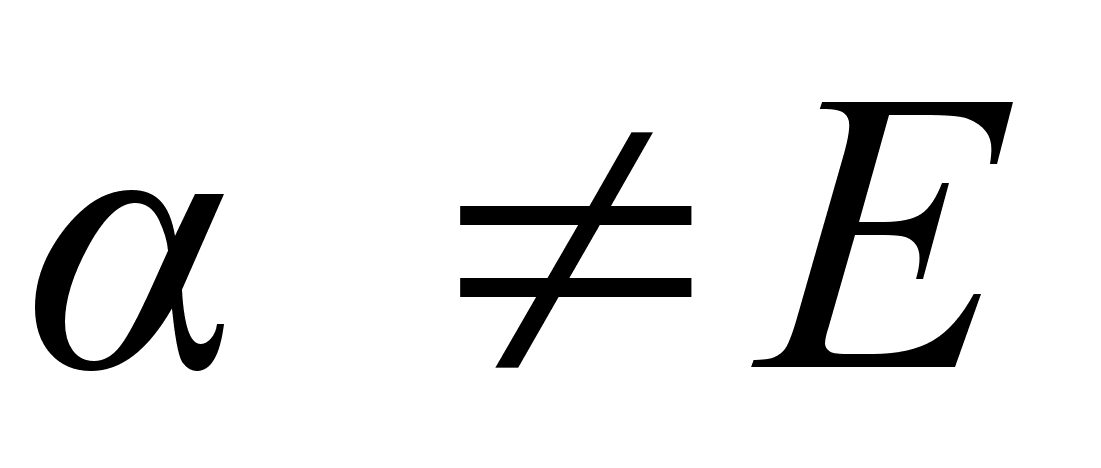 . Рассмотрим степени элемента
. Рассмотрим степени элемента 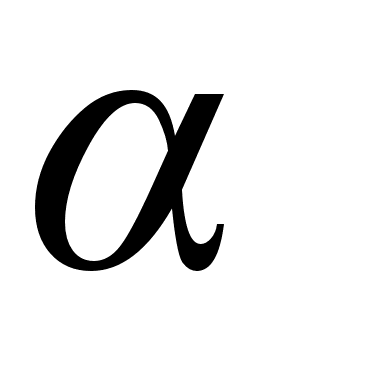 :
: 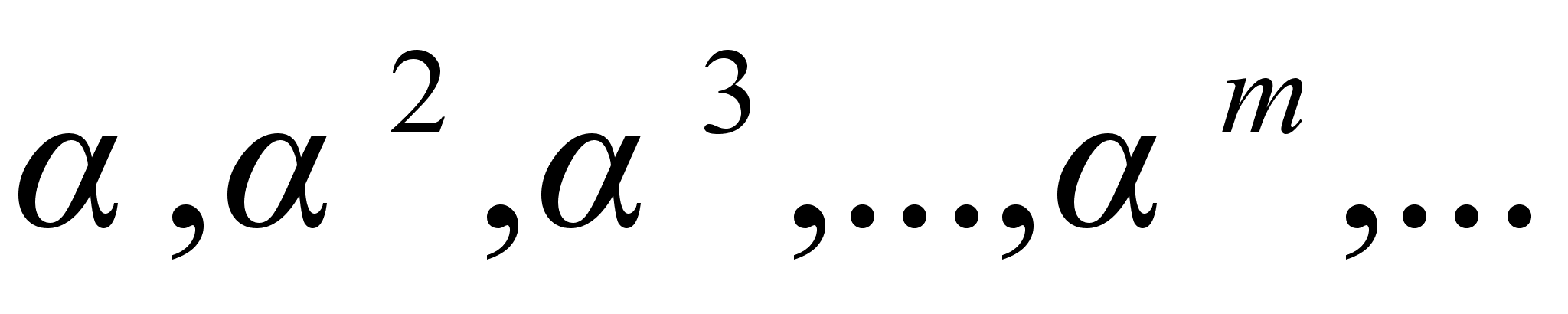 - все эти числа принадлежат Н (так как Н замкнуто относительно умножения по условию). Так как множество Н конечно, то все эти числа различны быть не могут.
- все эти числа принадлежат Н (так как Н замкнуто относительно умножения по условию). Так как множество Н конечно, то все эти числа различны быть не могут.
Значит, существуют 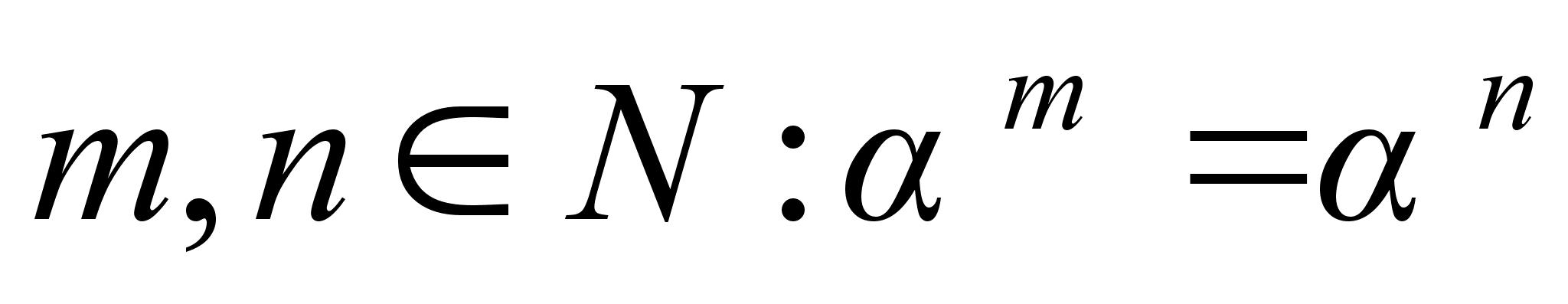 . Пусть
. Пусть 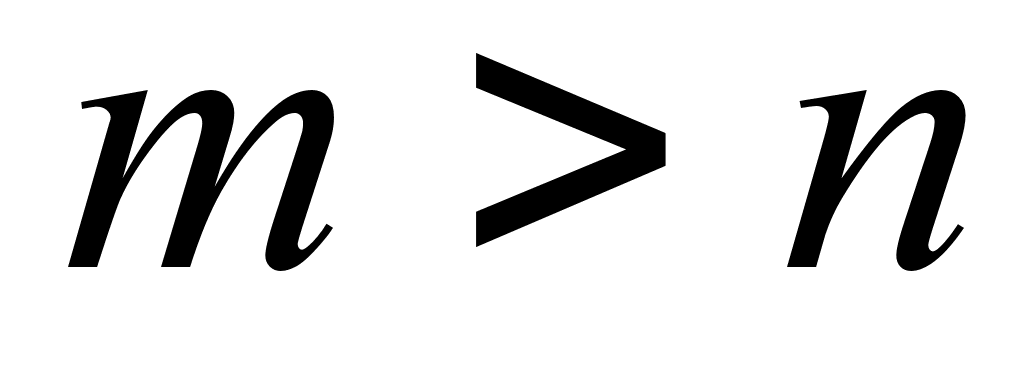 (в случае
(в случае  доказательство проводится аналогично). Тогда
доказательство проводится аналогично). Тогда 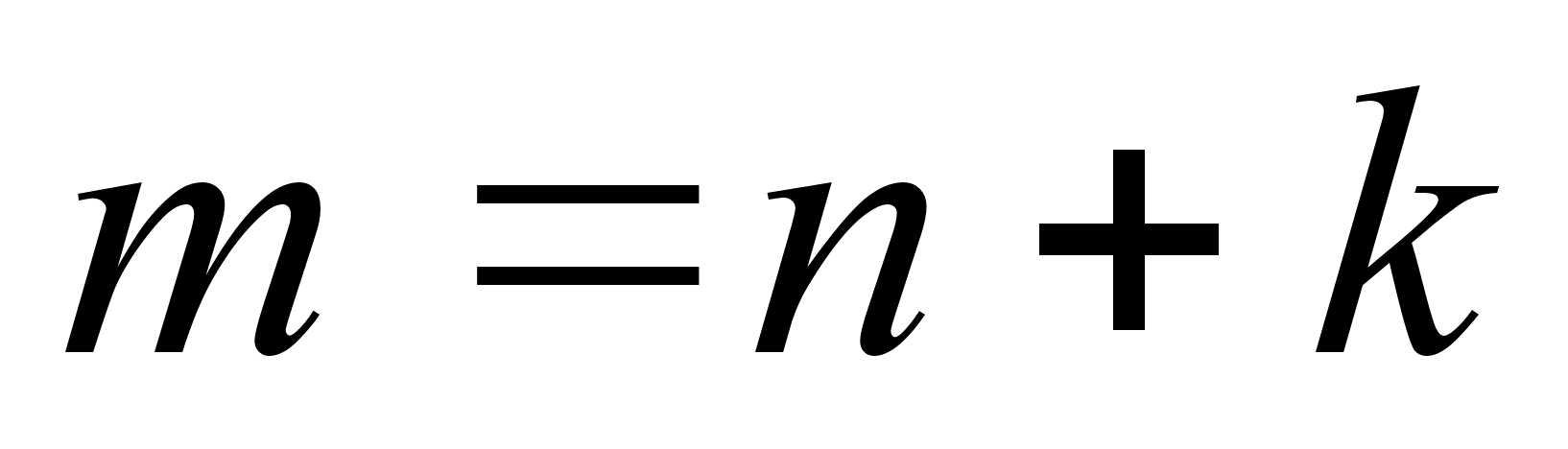 и
и 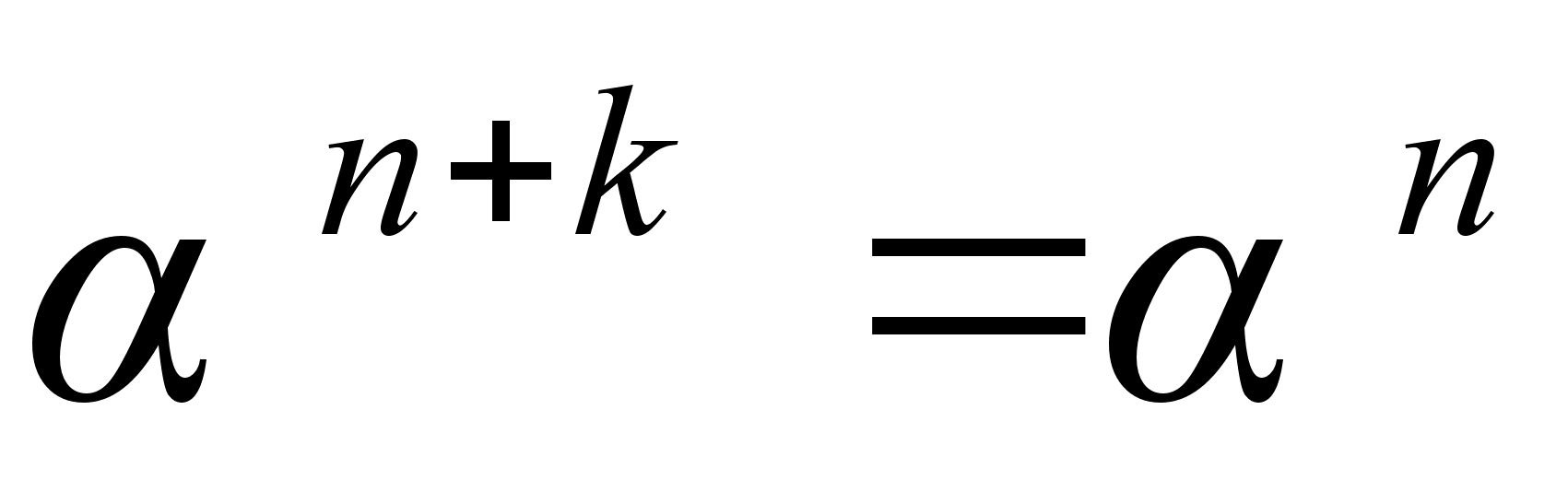 ,
, 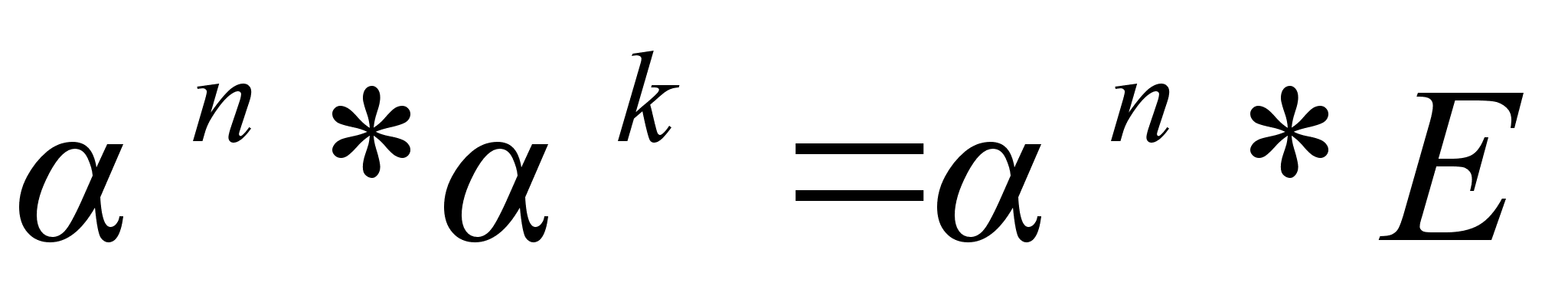 ,
,  ,
,  .
.
Следовательно, 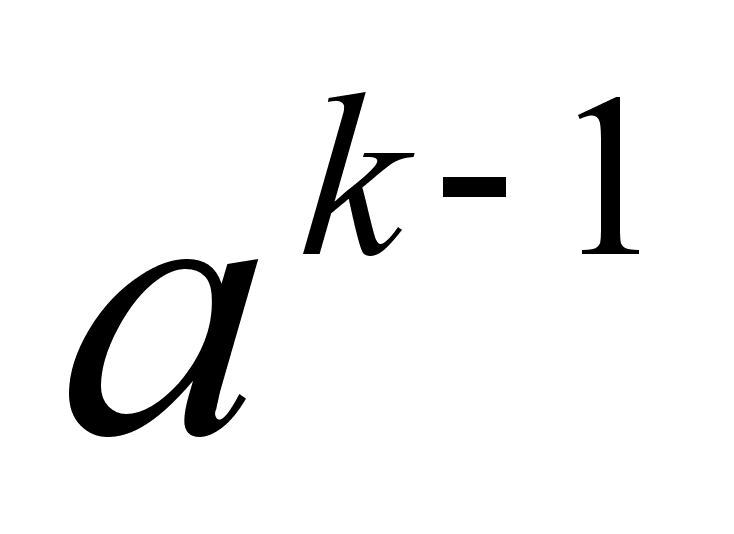 - обратный для
- обратный для  , то есть
, то есть 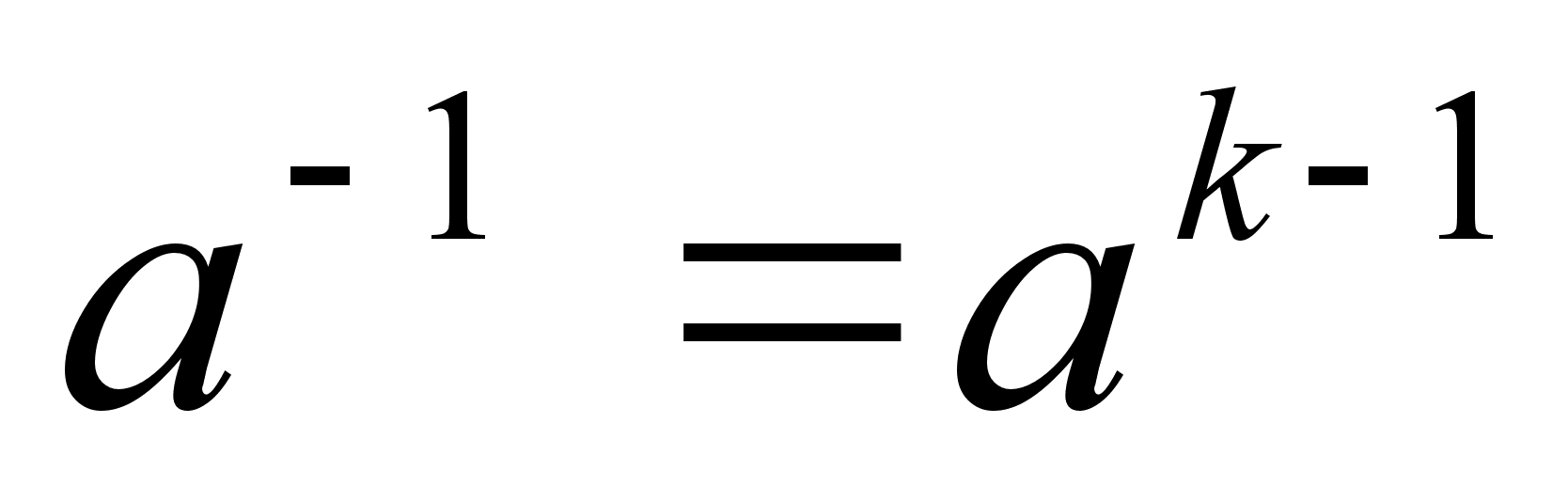 . Но
. Но 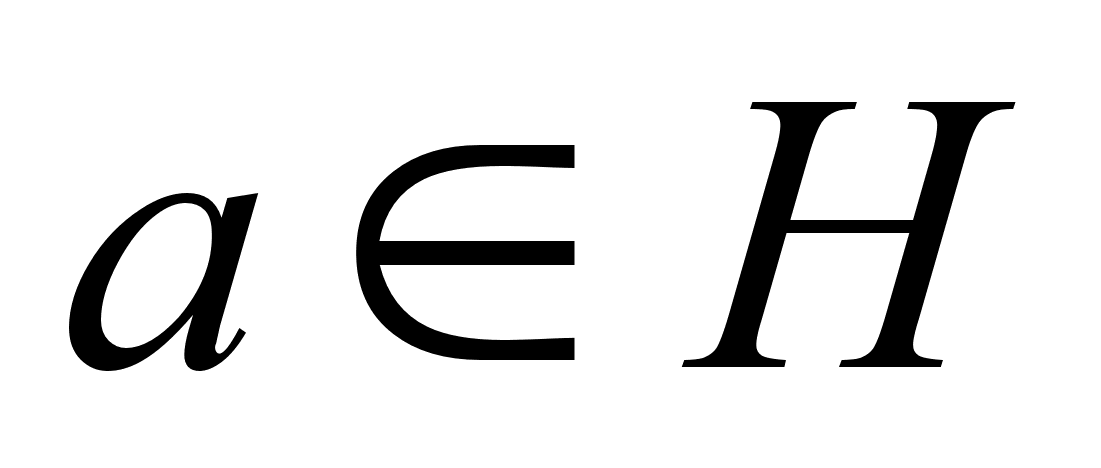 . Следовательно,
. Следовательно, 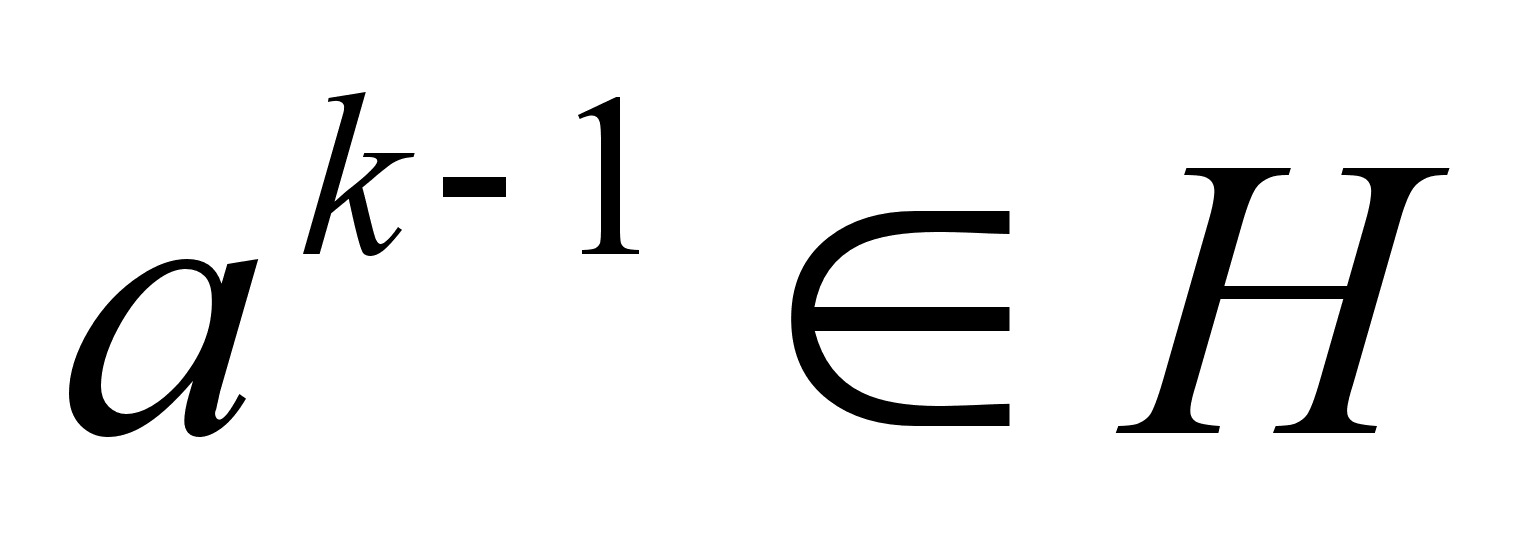 , то есть
, то есть 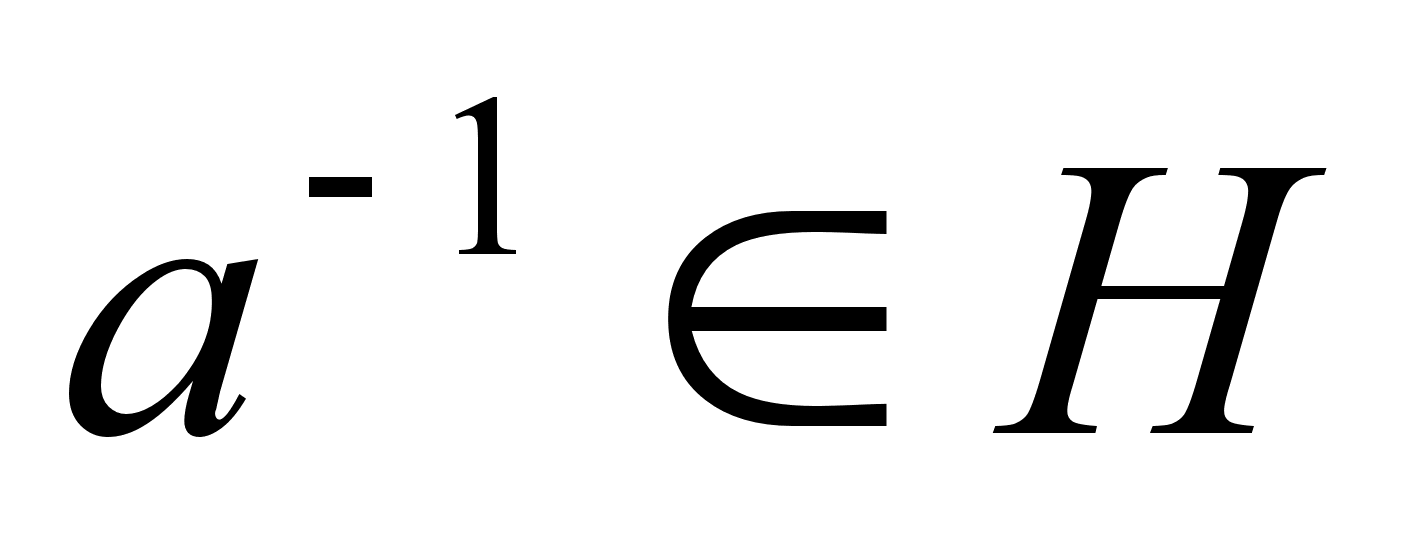 . Таким образом, для произвольного элемента
. Таким образом, для произвольного элемента 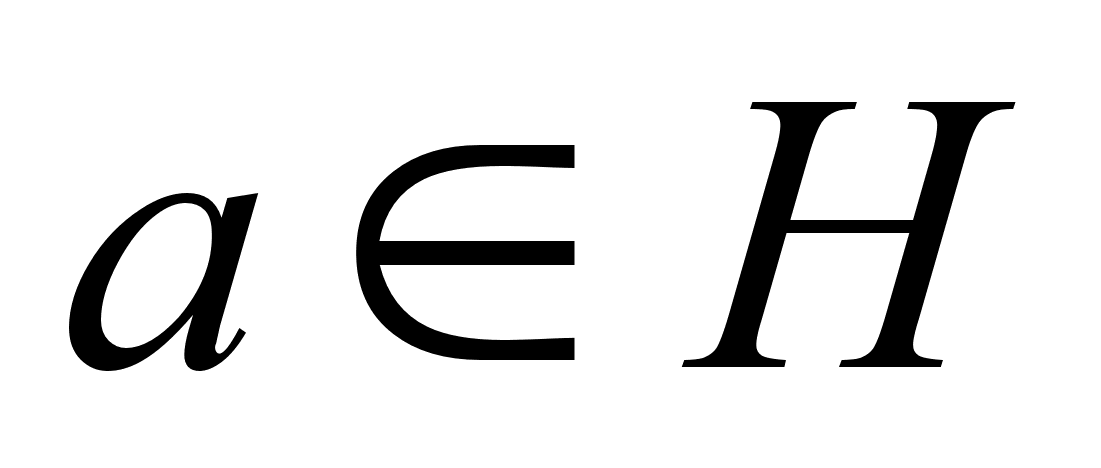 получили, что
получили, что 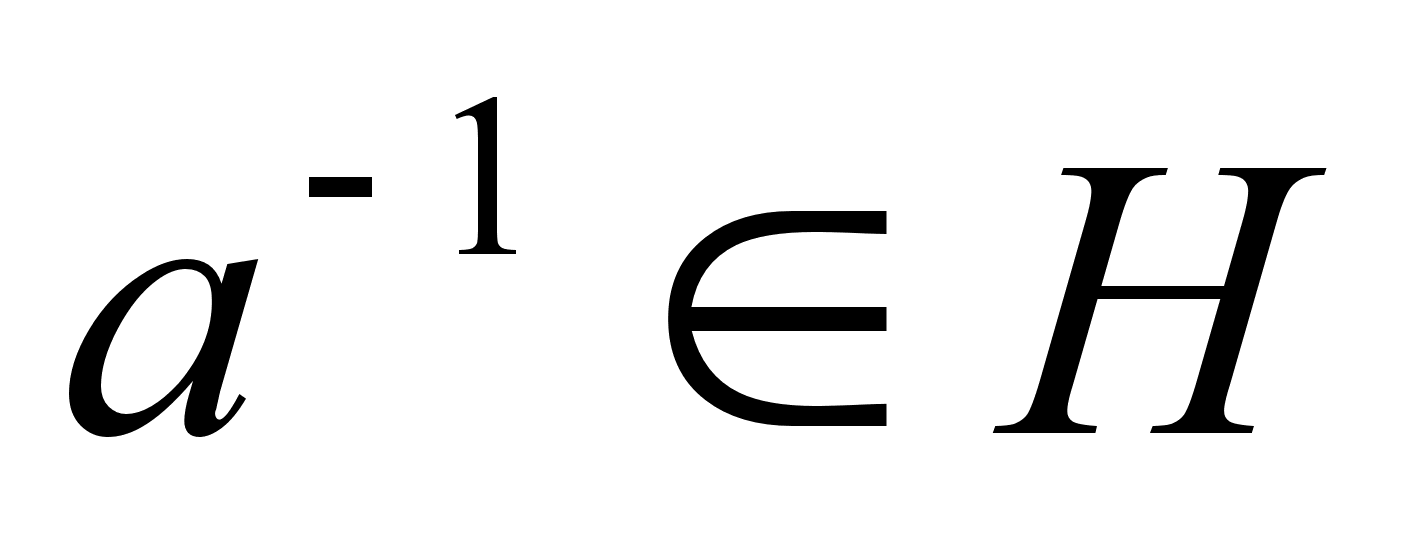 . Значит, Н тАУ подгруппа группы G.
. Значит, Н тАУ подгруппа группы G.
Теорема доказана.
Нам известно, что симметрическая группа Sn является конечной. Поэтому для того чтобы подмножество Н группы Sn являлось подгруппой группы Sn, достаточно чтобы произведение произвольных двух элементов из Н также принадлежало Н.
1.3. ЗНАКОПЕРЕМЕННАЯ ГРУППА
Особенный интерес представляет множество An всех четный перестановок на множестве из n символов. Ясно, что это подмножество симметрической группы Sn. Утверждается, что An является подгруппой группы Sn. Чтобы доказать это, проверим, что An удовлетворяет двум условиям, характеризующим подгруппу:
замкнутость.
Если р1 и р2 тАУ перестановки из An, представимые в виде произведений n1 и n2 транспозиций соответственно, то их произведение 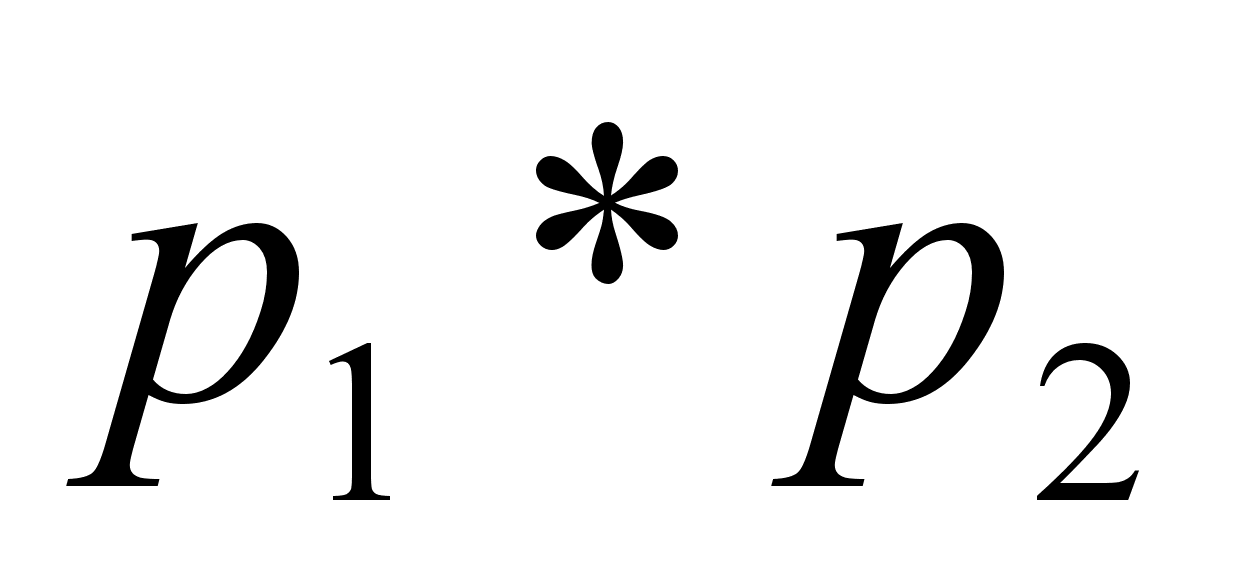 можно записать с помощью
можно записать с помощью 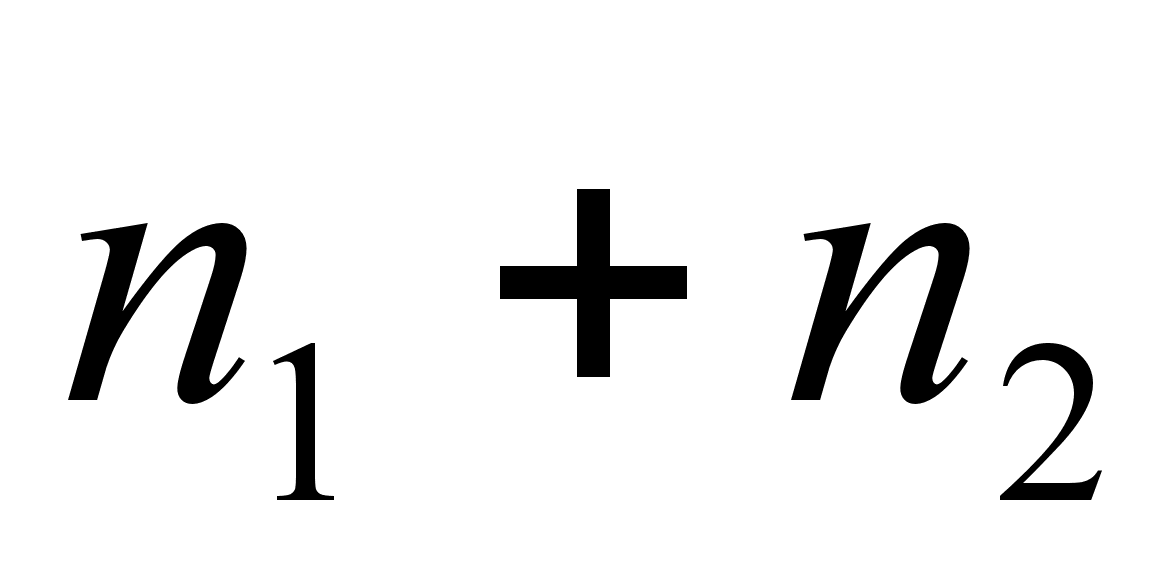 транспозиций. Если n1 и n2 тАУ четные числа, то и n1+n2 четно, откуда можно заключить, что перестановка
транспозиций. Если n1 и n2 тАУ четные числа, то и n1+n2 четно, откуда можно заключить, что перестановка 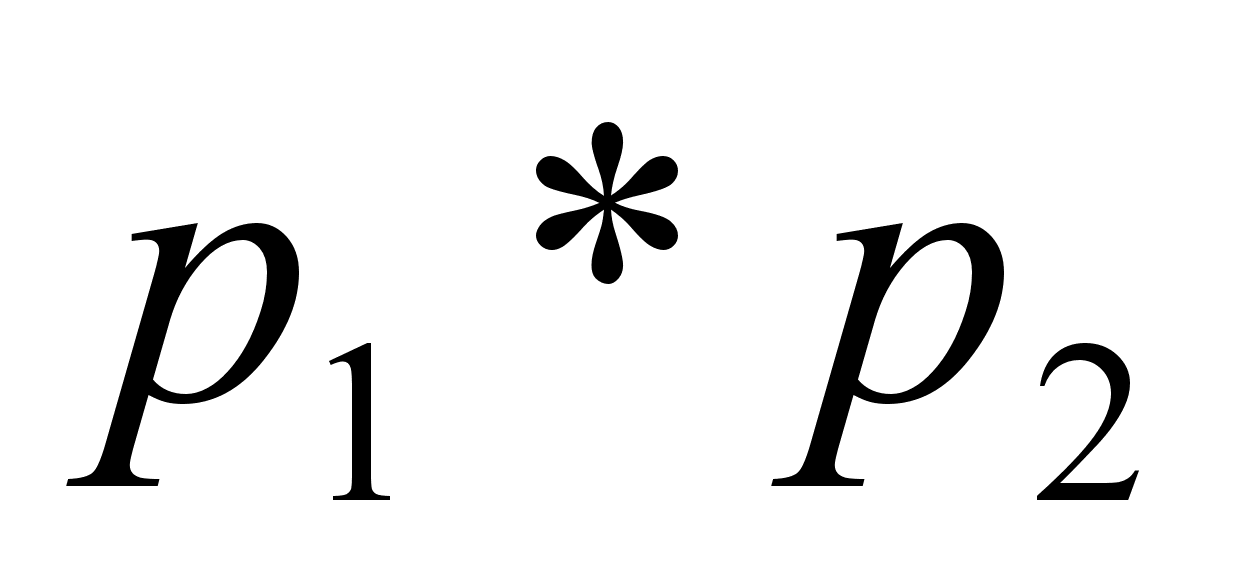 четная и, следовательно, эта перестановка принадлежит An.
четная и, следовательно, эта перестановка принадлежит An.
обратимость.
Перестановка р имеет обратную р-1 (в группе Sn); р*р-1=Е можно представить только с помощью четного числа транспозиций, поскольку Е тАУ четная перестановка. Значит, если р тАУ четная перестановка, то р-1 также должна быть четной, то есть у каждого элемента из группы An есть обратный в An.
Следовательно, для подмножества An выполняются два условия теоремы о подгруппах (причем, второе условие можно было бы и не проверять, так как Sn тАУ конечная группа). Поэтому An является подгруппой симметрической группы Sn. Подгруппа An группы Sn называется знакопеременной группой.
Теорема: порядок группы An равен  .
.
Доказательство.
Пусть а тАУ транспозиция из симметрической группы 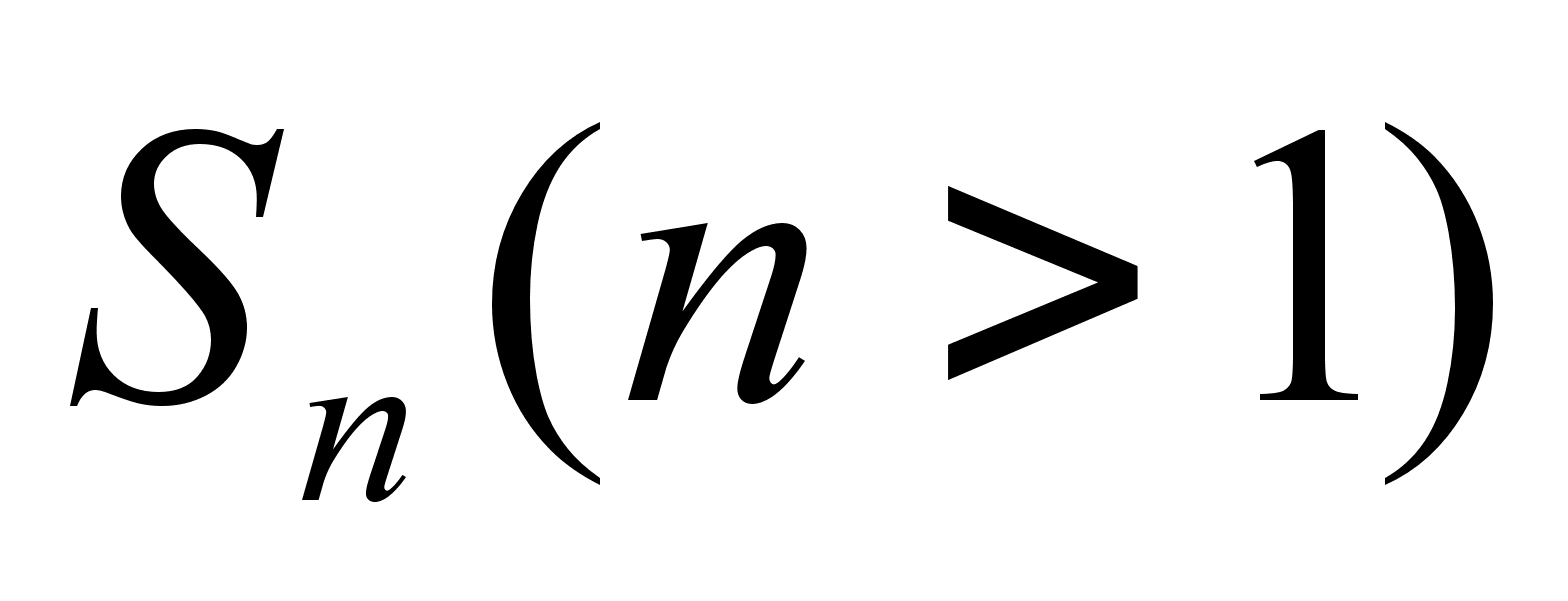 , пусть а=(12)=(12)(3)(4)тАж(n). Умножим каждый элемент группы Sn слева на а=(12). В результате снова получим множество всех элементов из Sn и ни один из них не повторяется дважды. Но произведение любой четной перестановки из Sn и элемента (12) является нечетной перестановкой, а произведение нечетной перестановки и элемента (12) является четной перестановкой. Множество нечетных перестановок и множество четных при этом умножении взаимно однозначно отображаются одно на другое. Это возможно лишь при том условии, что количество четных и нечетных перестановок одинаково. Следовательно, порядок группы An равен
, пусть а=(12)=(12)(3)(4)тАж(n). Умножим каждый элемент группы Sn слева на а=(12). В результате снова получим множество всех элементов из Sn и ни один из них не повторяется дважды. Но произведение любой четной перестановки из Sn и элемента (12) является нечетной перестановкой, а произведение нечетной перестановки и элемента (12) является четной перестановкой. Множество нечетных перестановок и множество четных при этом умножении взаимно однозначно отображаются одно на другое. Это возможно лишь при том условии, что количество четных и нечетных перестановок одинаково. Следовательно, порядок группы An равен 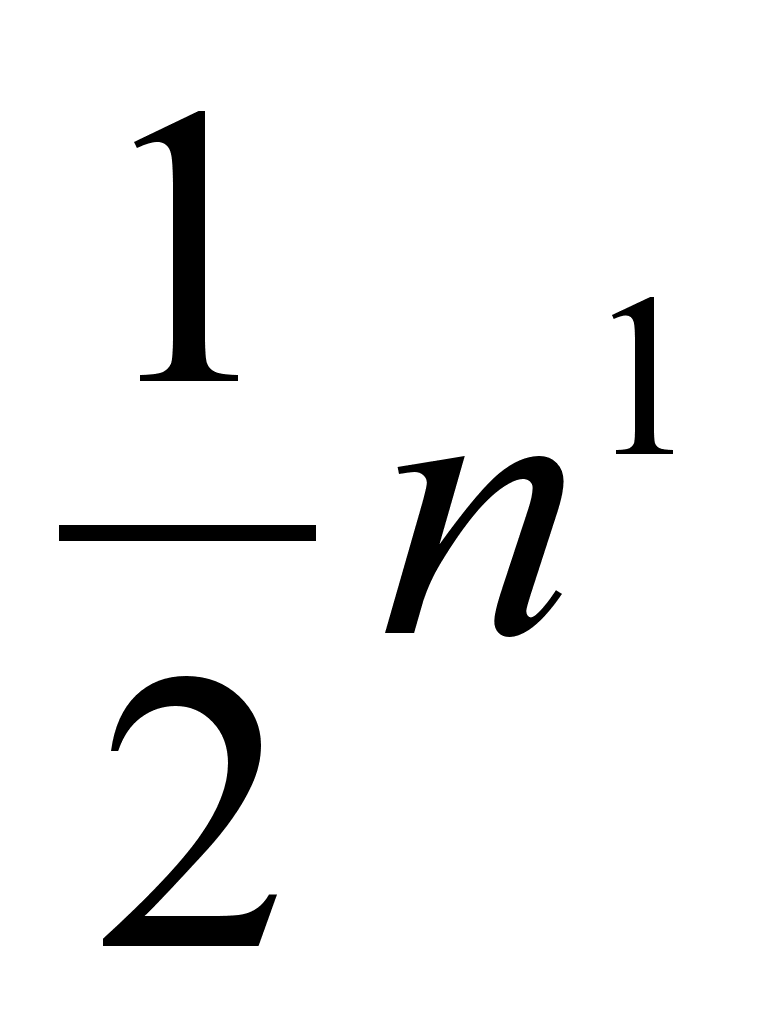 .
.
Теорема доказана.
Эта группа играет очень важную роль в теории групп перестановок.
1.4. ТЕОРЕМА ЛАГРАНЖА
Пусть Н и G тАУ группы перестановок, причём Н является подгруппой G. В теории групп существует теорема, доказанная Лагранжем, устанавливающая связь между порядками групп Н и G. Эта теорема очень часто применяется в теории групп.
Теорема Лагранжа: если Н тАУ подгруппа группы G, то ее порядок является делителем порядка G.
Доказательство.
Пусть Е, а1, а2, тАж, аn-1 тАУ все перестановки, содержащиеся в группе G,  - все перестановки из Н (то есть
- все перестановки из Н (то есть 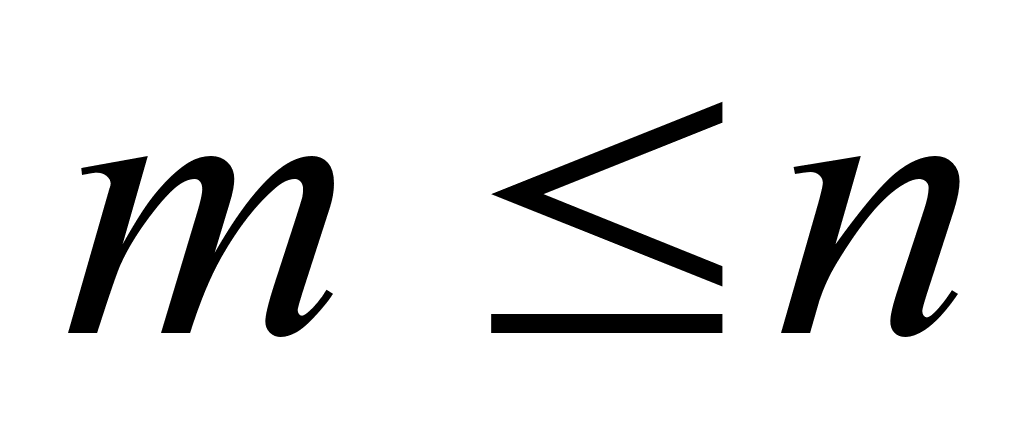 ). Если Н=G, то утверждение теоремы справедливо, поэтому предположим, что Н
). Если Н=G, то утверждение теоремы справедливо, поэтому предположим, что Н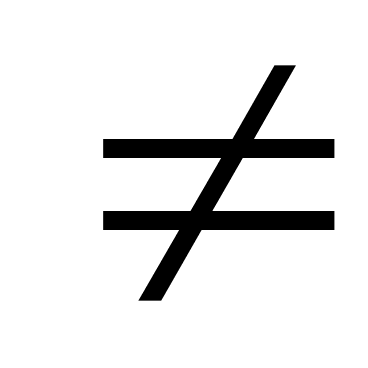 G (Н тАУ собственная подгруппа G). В силу этого предложения существует перестановка
G (Н тАУ собственная подгруппа G). В силу этого предложения существует перестановка 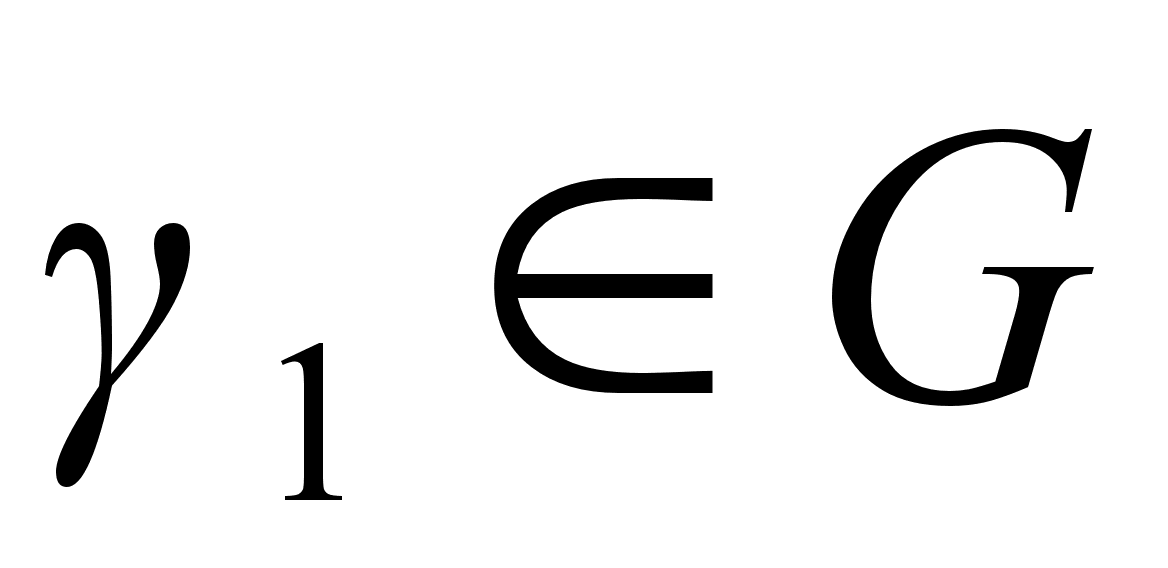 такая, что
такая, что 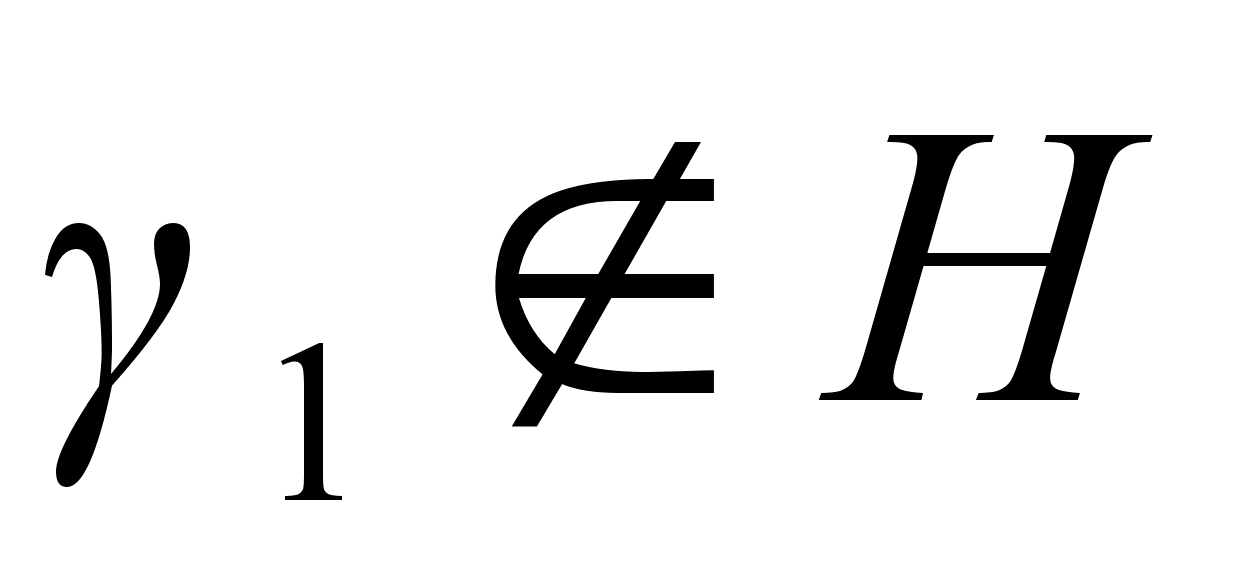 . Рассмотрим ряд перестановок.
. Рассмотрим ряд перестановок.
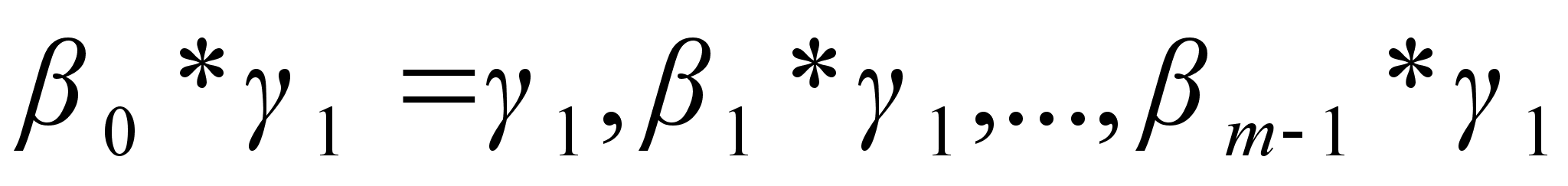 (1)
(1)
Все перестановки ряда (1) различны: если бы для каких-то i, j имело место равенство 
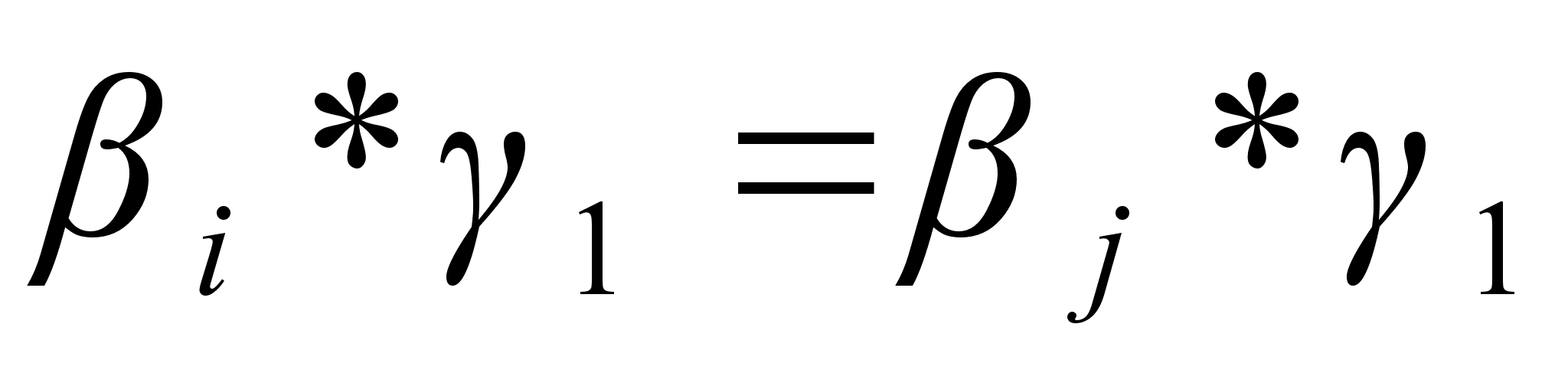 , то, умножив его правую и левую части на
, то, умножив его правую и левую части на 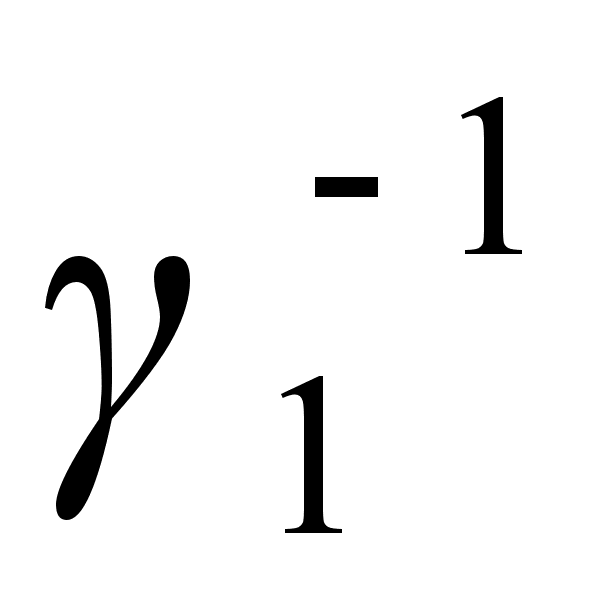 , мы получили бы равенство
, мы получили бы равенство 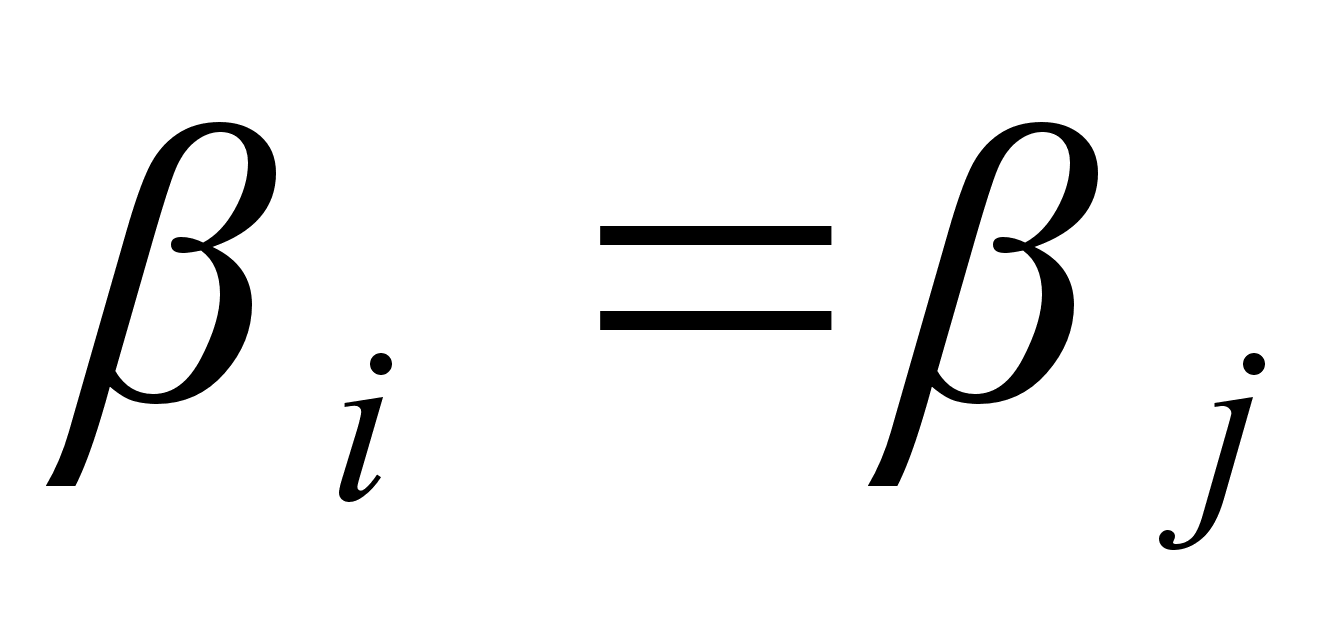 . Кроме того, ни одна из них не содержится в подгруппе Н: если бы для какого-то номера i имело место включение
. Кроме того, ни одна из них не содержится в подгруппе Н: если бы для какого-то номера i имело место включение 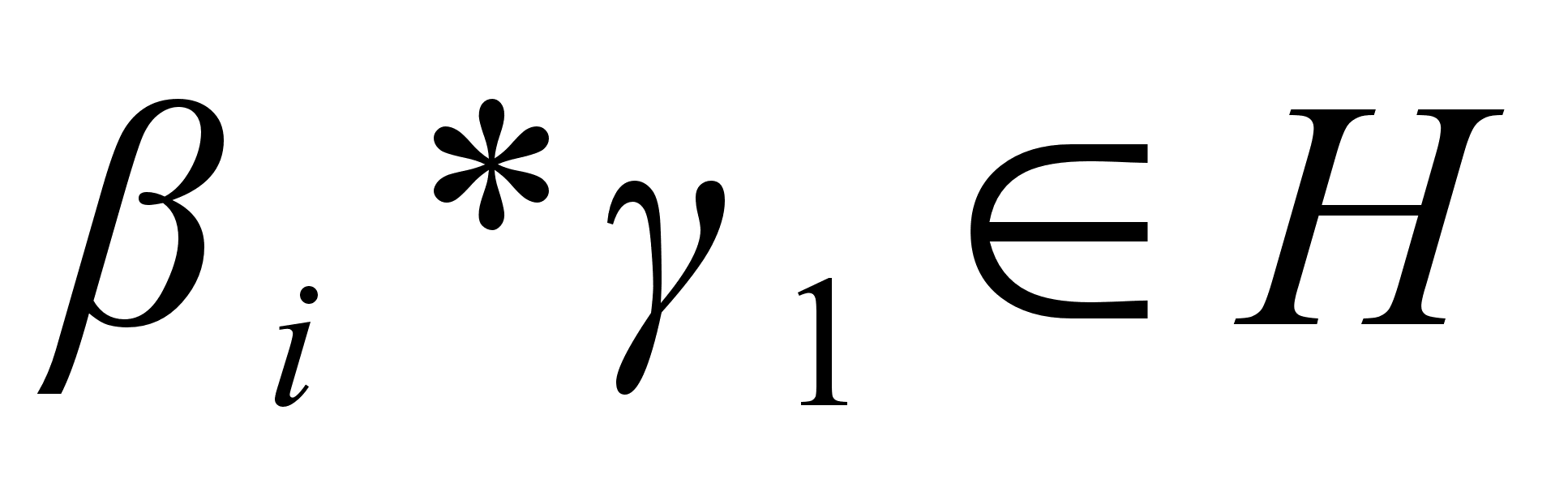 , то это означало бы, что
, то это означало бы, что  для какого-то j. Из этого равенства имеем
для какого-то j. Из этого равенства имеем 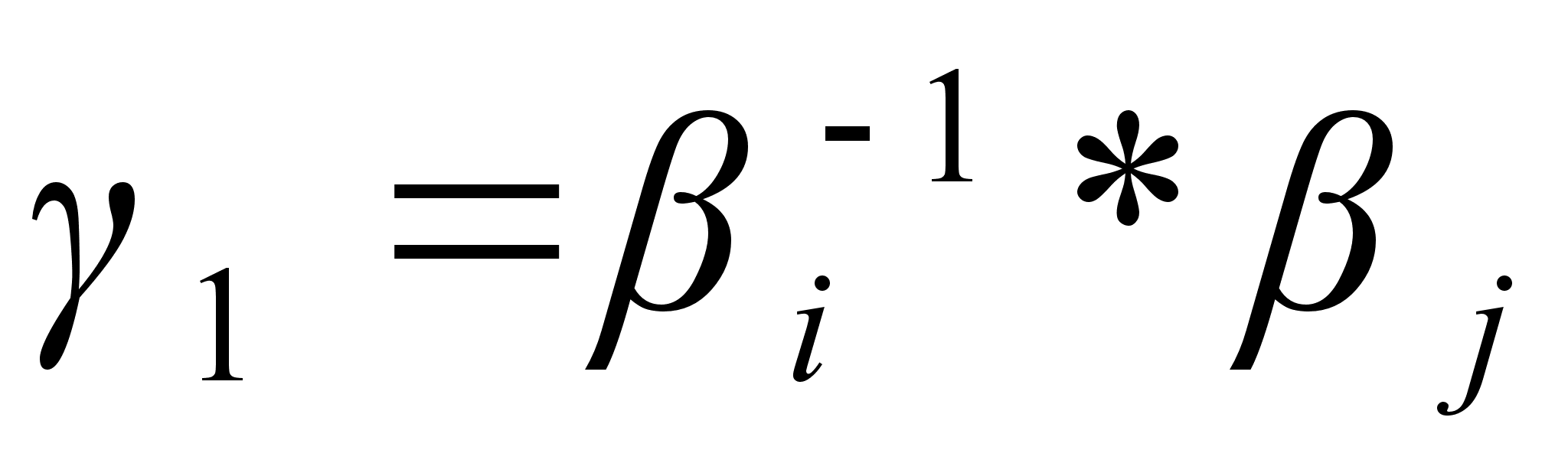 , а так как Н тАУ группа перестановок, то
, а так как Н тАУ группа перестановок, то  , что противоречит выбору этой перестановки.
, что противоречит выбору этой перестановки.
Если перестановками группы Н и ряда (1) исчерпаны все перестановки из G, то |G|=2|H|, и все доказано. В противном случае найдется такая перестановка 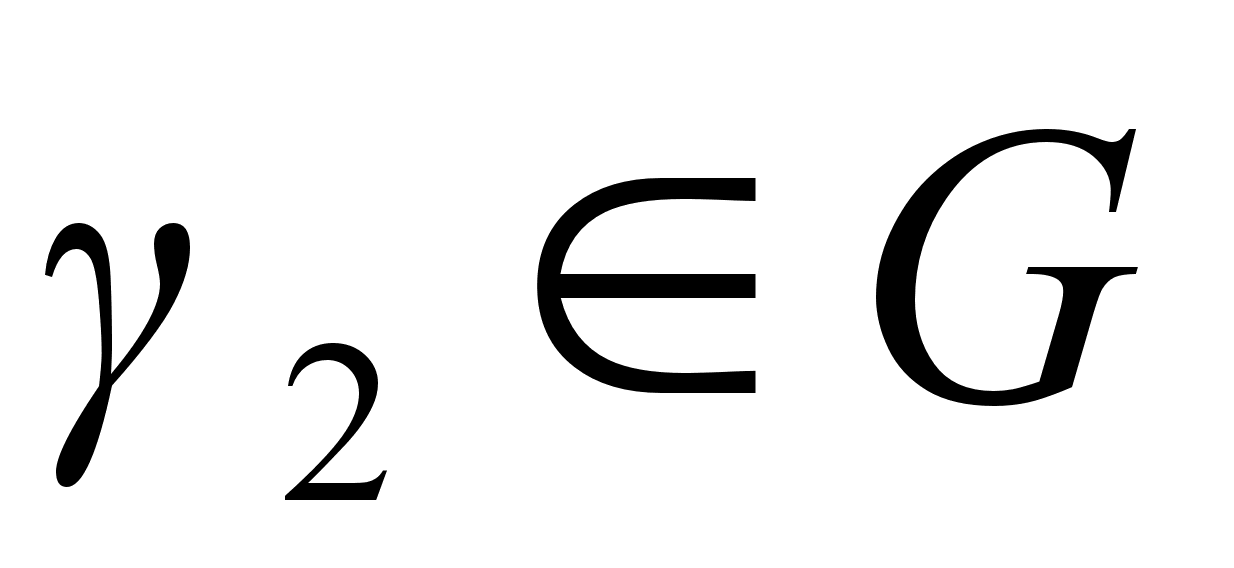 , что
, что 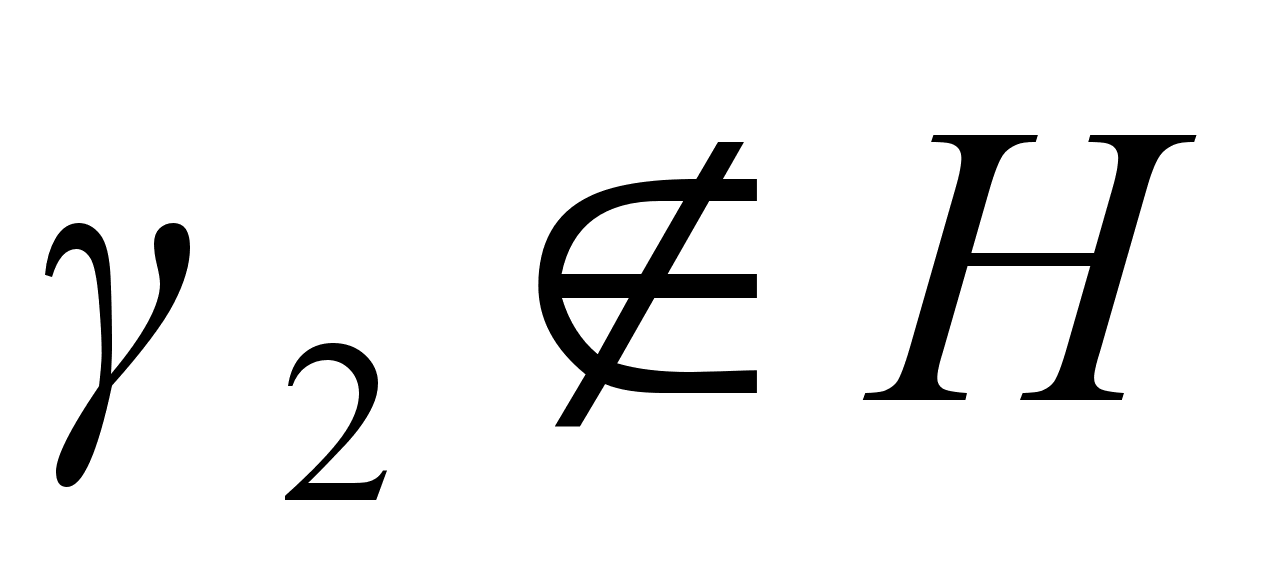 и
и 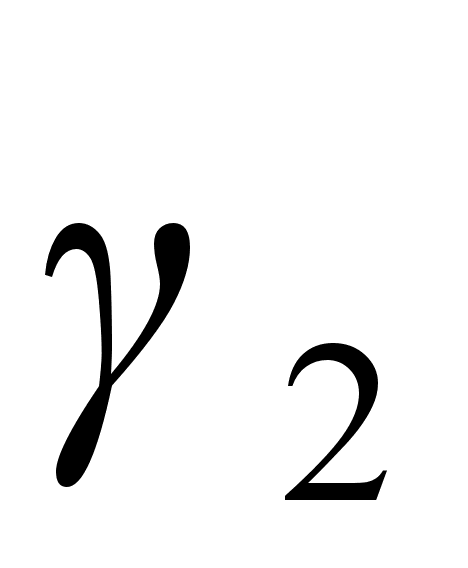 не содержится в ряде (1). Определим для нее ряд перестановок.
не содержится в ряде (1). Определим для нее ряд перестановок.
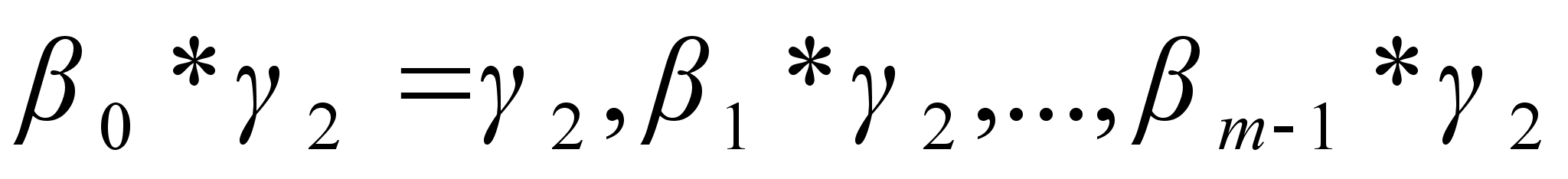 (2)
(2)
Аналогично проверяется, что:
все перестановки ряда (2) различны;
они не содержатся в Н;
ни одна из них не встречается среди перестановок ряда (1).
Если перестановками из подгруппы Н и рядов (1) и (2) исчерпываются все элементы группы G, то |G|=3|H|, и все доказано.
В противном случае продолжаем процесс выбора перестановок  и построения рядов вида (1) и (2) дальше. Так как группа G конечная, то на каком-то, например, на k-м шаге все перестановки из G будут исчерпаны. Иными словами, все их можно расположить в такую таблицу:
и построения рядов вида (1) и (2) дальше. Так как группа G конечная, то на каком-то, например, на k-м шаге все перестановки из G будут исчерпаны. Иными словами, все их можно расположить в такую таблицу:
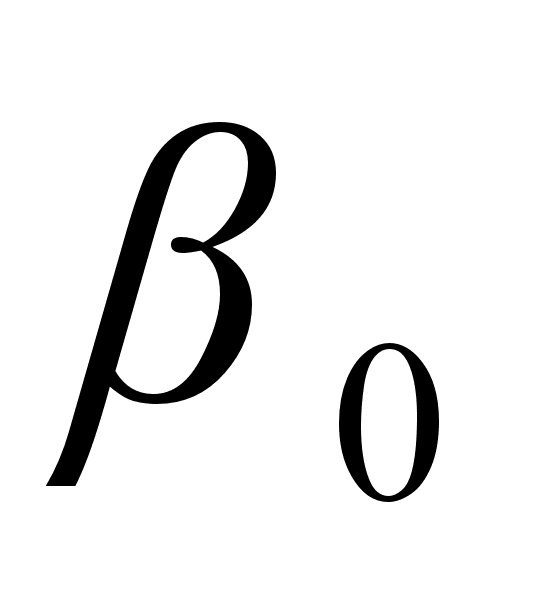 , ,
| 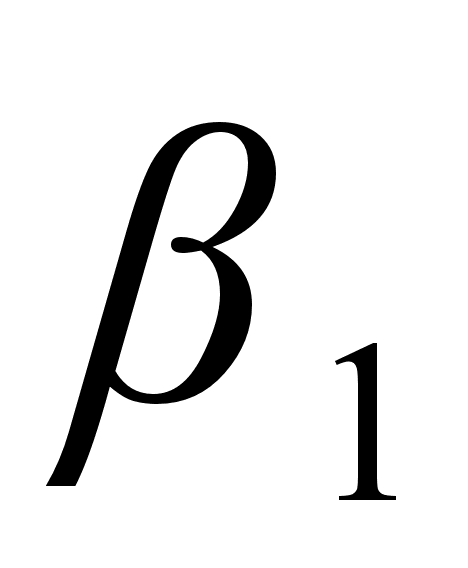 , ,
| 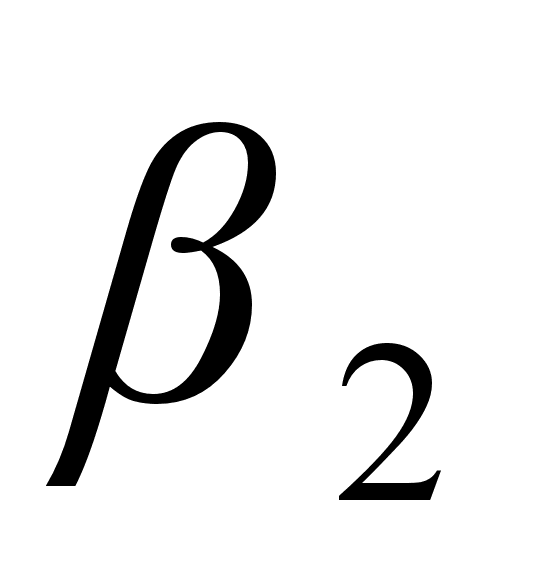 , ,
| .., | 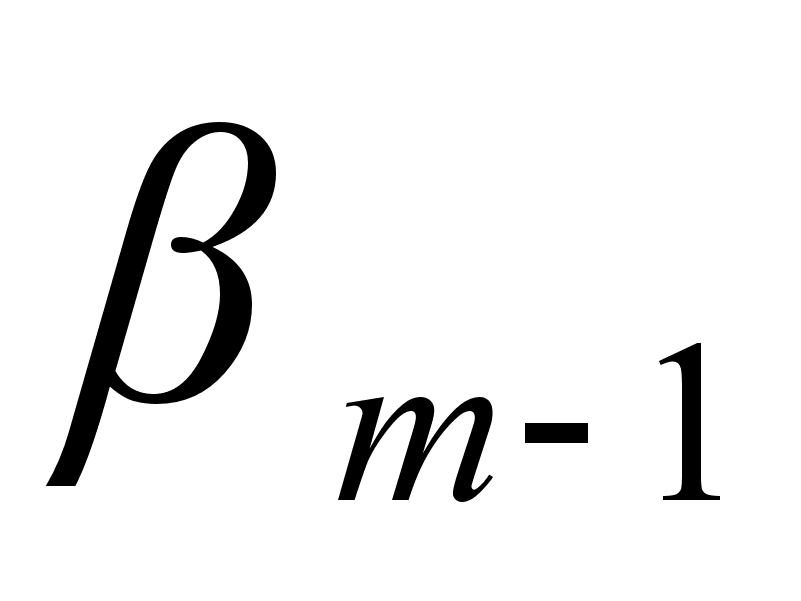 , ,
|
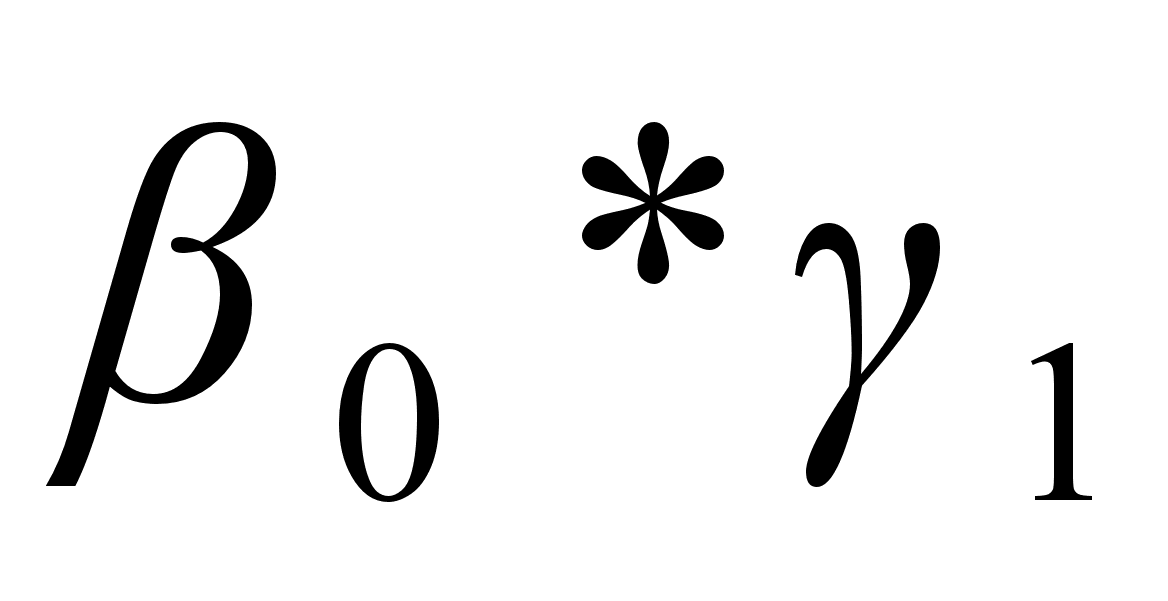 , ,
|  , ,
|  , ,
| .., | 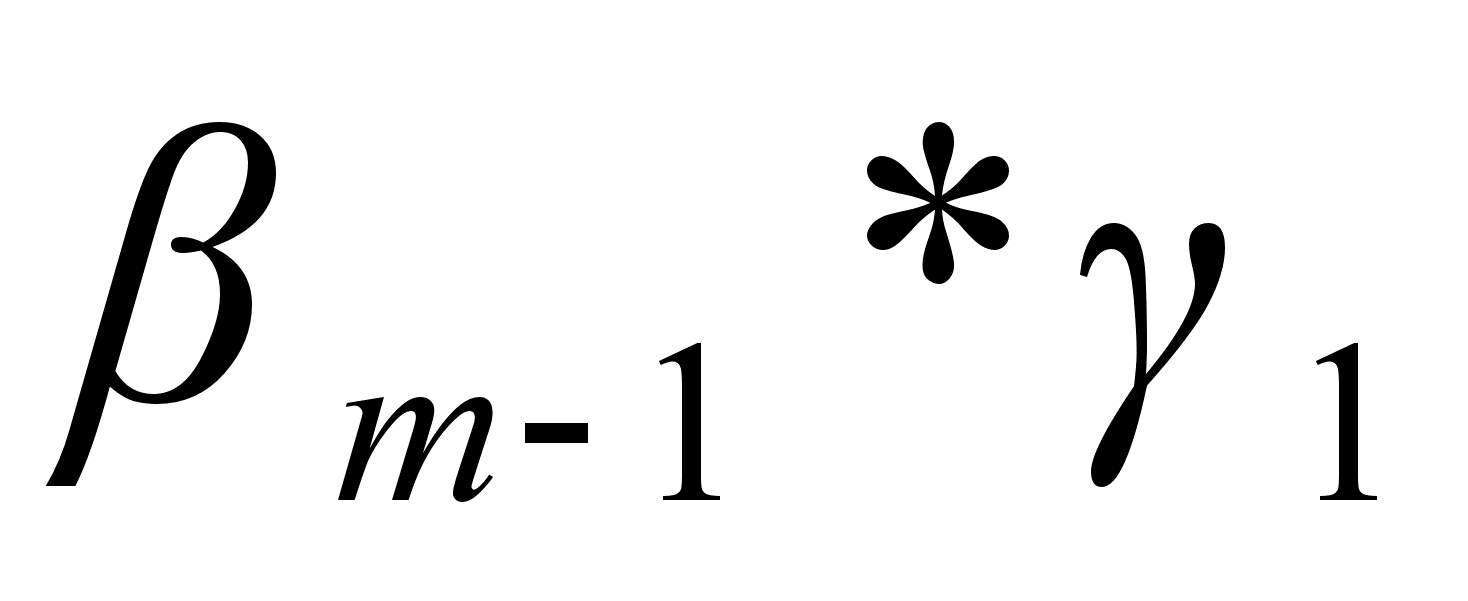 , ,
|
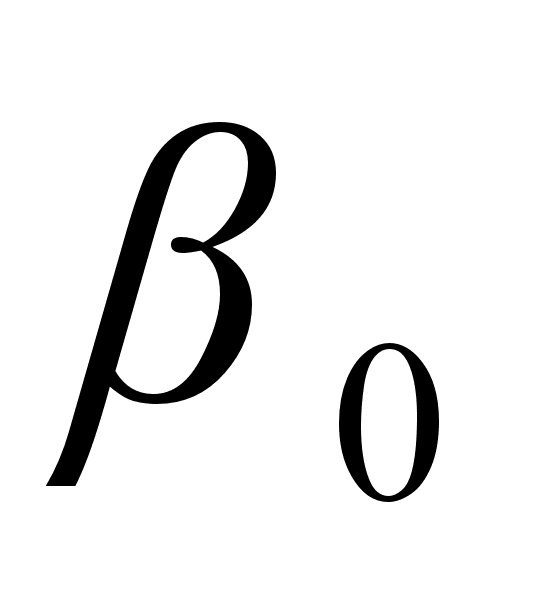 * *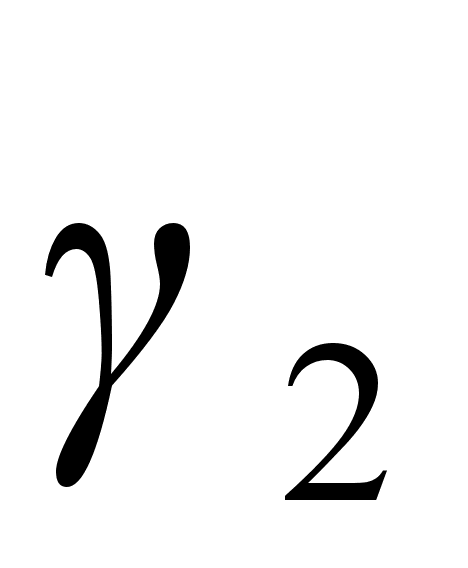 , ,
| 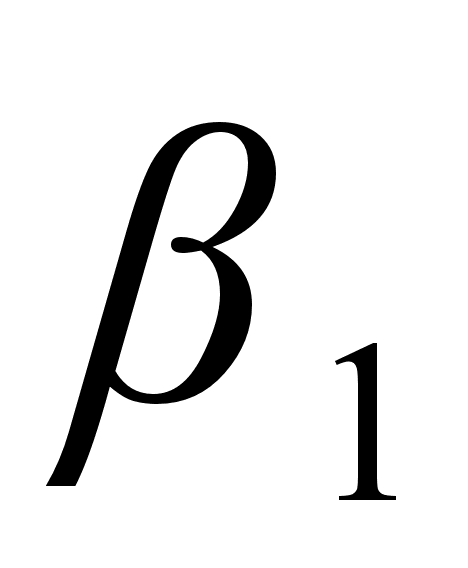 * *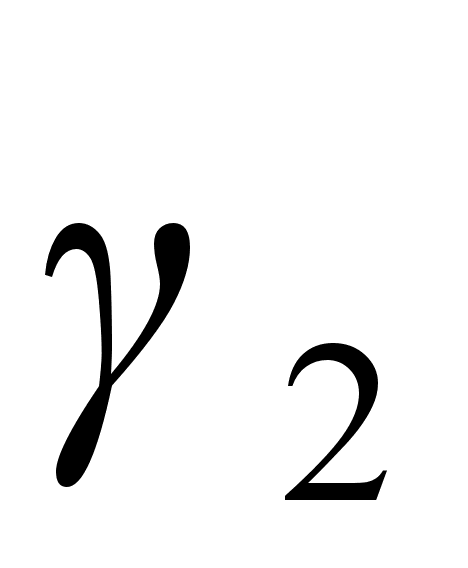 , ,
| 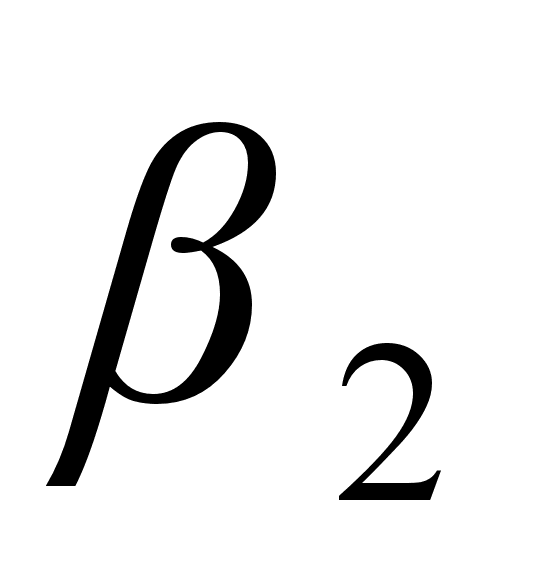 * *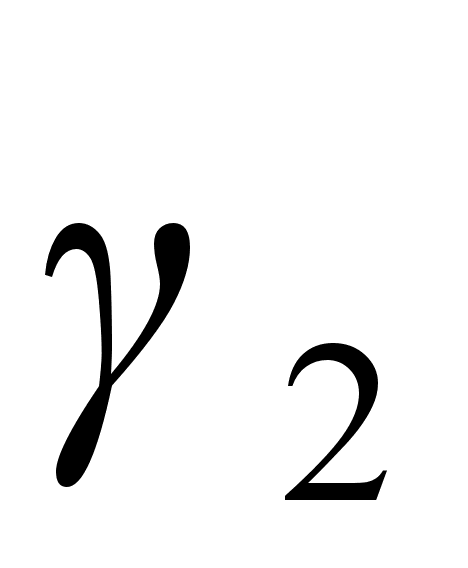 , ,
| .., | 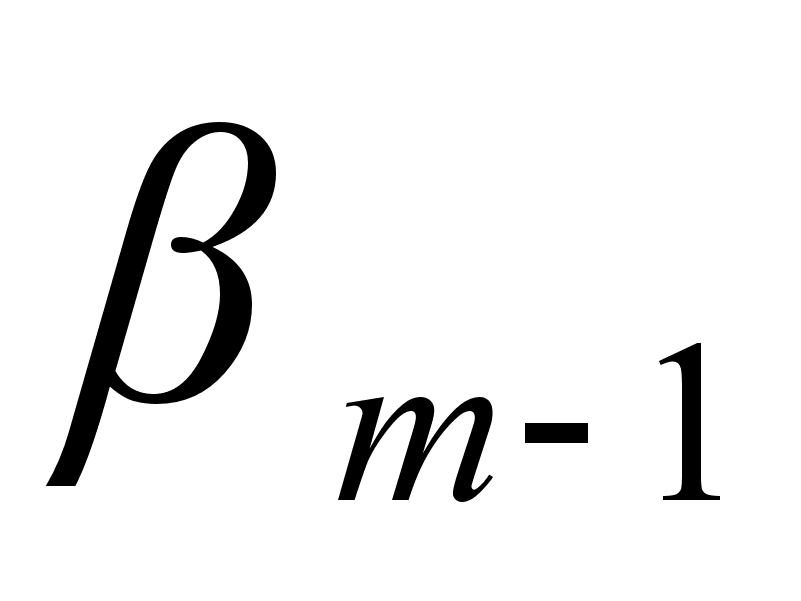 * *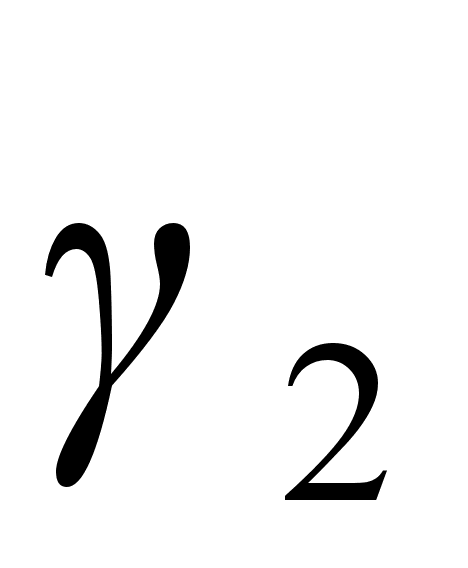 , (3) , (3)
|
.., | .., | .., | .., | .., |
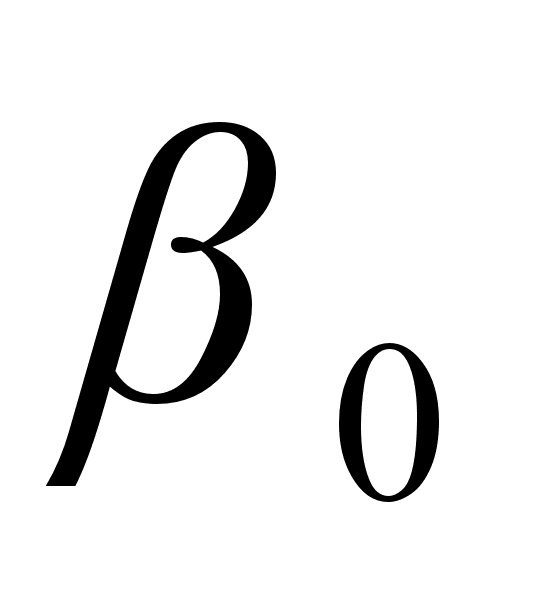 * *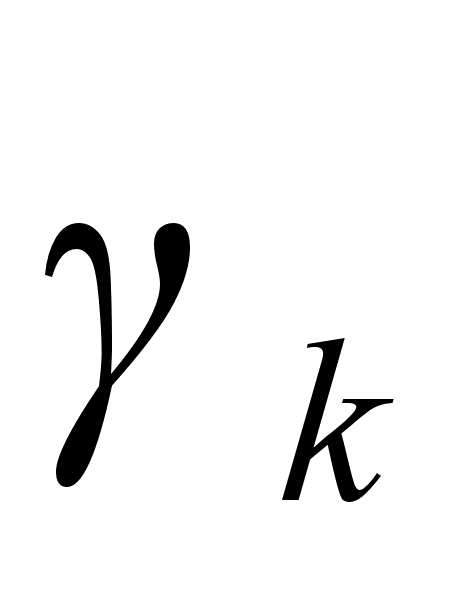 , ,
| 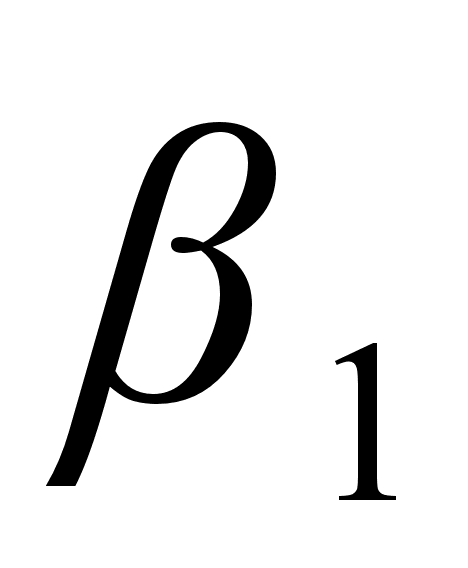 * *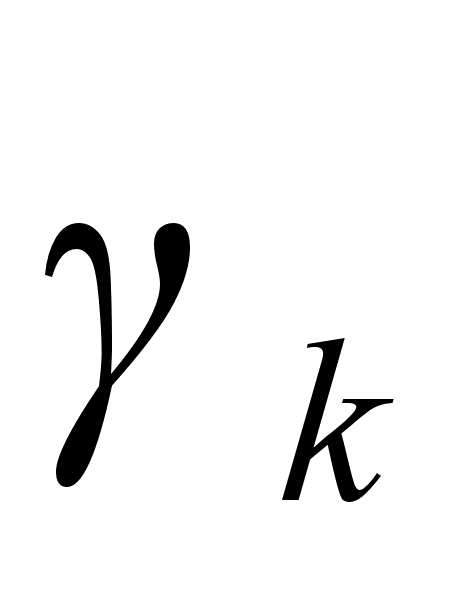 , ,
| 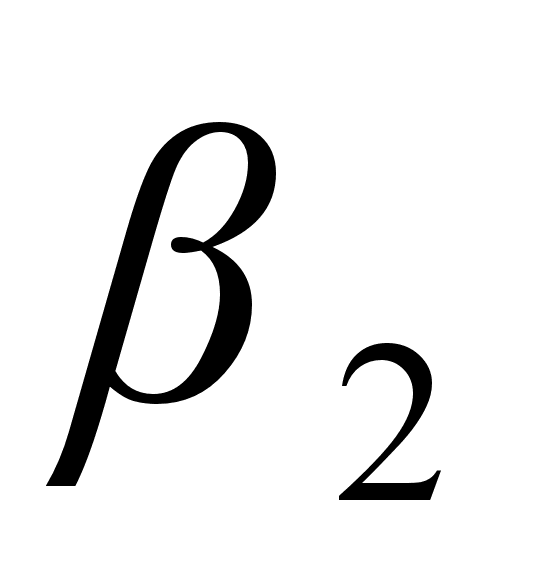 * *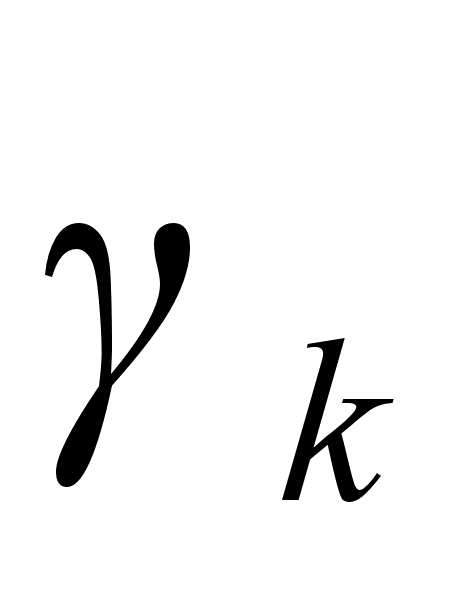 , ,
| .., | 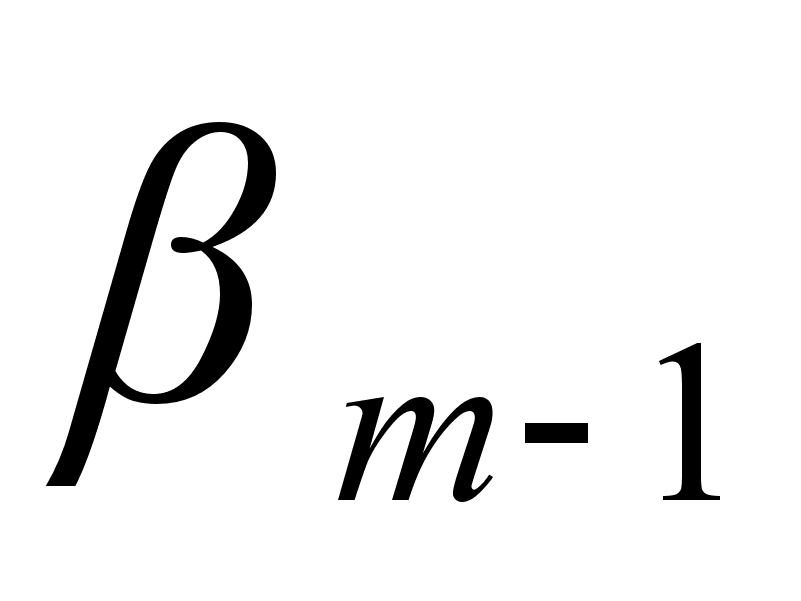 * *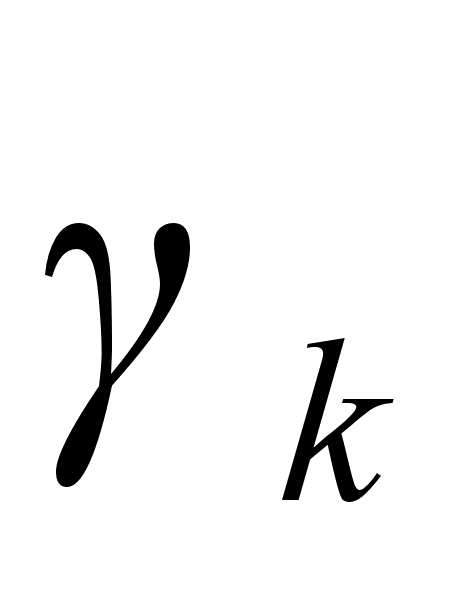 , ,
|
при этом все перестановки в каждой из строк этой таблицы различны и любые 2 строки не имеют общих элементов. Поскольку общее число элементов в таблице равно n (порядок группы G), а число элементов в каждой строке равно m (порядок группы Н), то имеем равенство 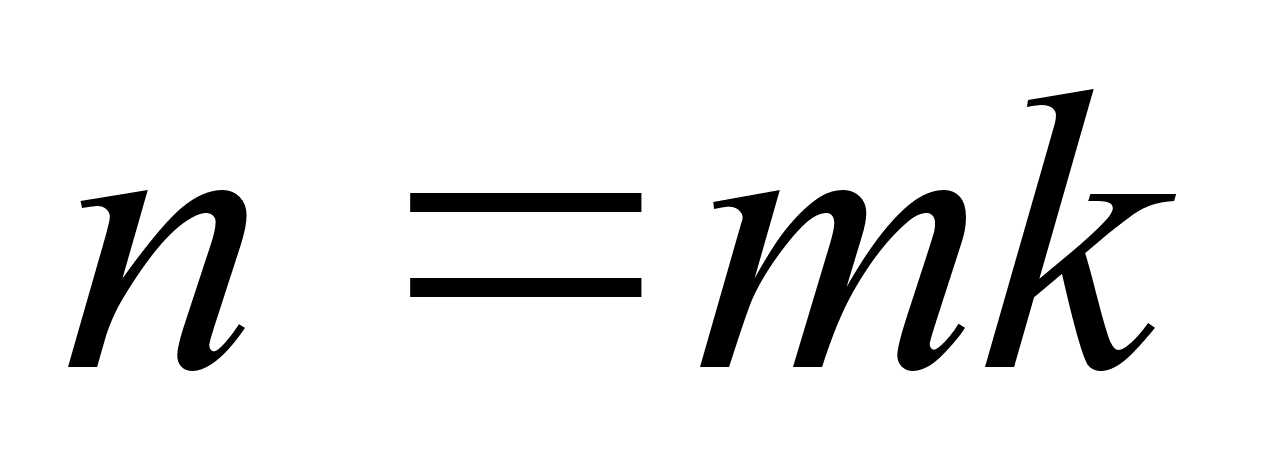 , то есть m является делителем n.
, то есть m является делителем n.
Теорема доказана.
Число k называют индексом подгруппы Н в группе G и обозначают [G:H]. Из доказательства теоремы Лагранжа мы получаем, что имеет место равенство |G|=|H|[G:H].
Так как порядок циклической подгруппы, порожденной перестановкой  , совпадает с порядком перестановки
, совпадает с порядком перестановки  , то из теоремы Лагранжа получаем, что порядок любой перестановки из G тАУ делитель |G|.
, то из теоремы Лагранжа получаем, что порядок любой перестановки из G тАУ делитель |G|.
Теорема Лагранжа позволяет существенно упростить решение задачи описания всех подгрупп данной группы. Например, собственные подгруппы из симметрической группы S3 могут состоять из двух и трех перестановок (делители числа 3!=6), поэтому не нужно непосредственно проверять являются ли подгруппами группы S3 подмножество, состоящее из 4 или 5 перестановок. А ведь эта проверка длинная, так как есть  подмножество из S3, состоящие из 4 или 5 элементов. Таким образом, даже на одном этом примере видно, насколько существенным может быть применение теоремы Лагранжа.
подмножество из S3, состоящие из 4 или 5 элементов. Таким образом, даже на одном этом примере видно, насколько существенным может быть применение теоремы Лагранжа.
1.5. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ЛАГРАНЖА
Сформулируем некоторые непосредственные следствия из теоремы Лагранжа о порядках подгрупп.
Теорема: если порядок группы G есть простое число, то:
группа G не имеет собственных подгрупп;
группа G является циклической.
Доказательство.
Утверждение 1) следует непосредственно из теоремы Лагранжа и определения простого числа.
Для доказательства утверждения 2) обозначим через  любой отличный от Е элемент группы G простого порядка.
любой отличный от Е элемент группы G простого порядка.
Если порядок  равен n, то
равен n, то 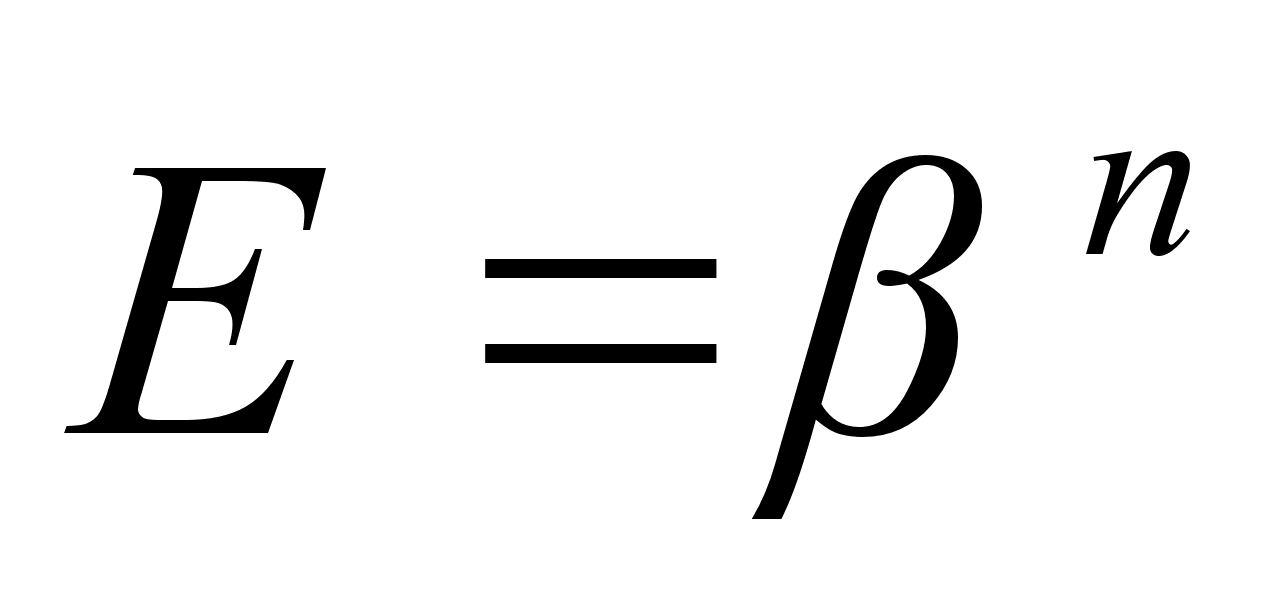 и n>1. Множество
и n>1. Множество 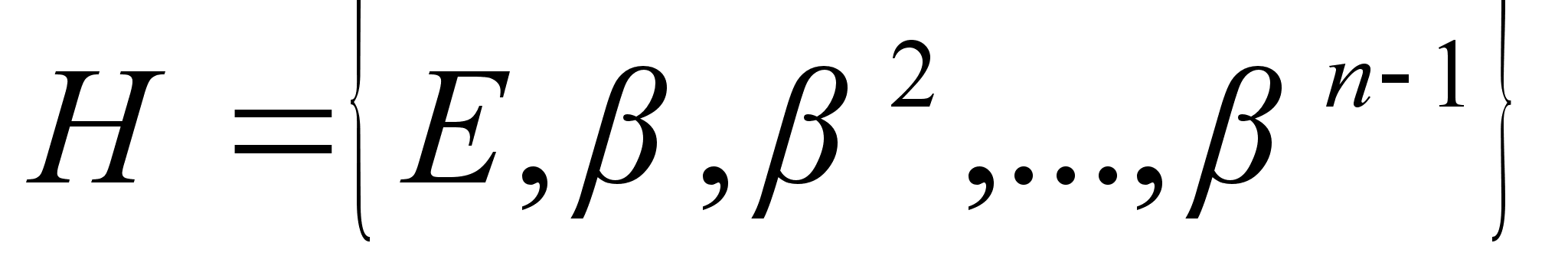 , n-1>0, составляет циклическую группу n-го порядка в группе G, так что Н тАУ подгруппа данной группы G простого порядка. По теореме Лагранжа порядок n этой подгруппы является делителем числа р. Так как
, n-1>0, составляет циклическую группу n-го порядка в группе G, так что Н тАУ подгруппа данной группы G простого порядка. По теореме Лагранжа порядок n этой подгруппы является делителем числа р. Так как  , то n=p. Но Н тАУ подгруппа группы G. Следовательно, Н совпадает с группой G. Это доказывает утверждение 2).
, то n=p. Но Н тАУ подгруппа группы G. Следовательно, Н совпадает с группой G. Это доказывает утверждение 2).
Теорема доказана.
Из теоремы Лагранжа следует только то, что если в группе G есть подгруппа Н, то порядок группы G кратен порядку группы Н. Но для нас остается открытым вопрос, верно ли обратное утверждение: если порядок группы G равен g, а h тАУ делитель числа g, то обязательно ли группа G имеет подгруппу порядка h? Для доказательства того факта, что это обратное утверждение не верно можно использовать знакопеременную группу А4. Эта группа имеет порядок 12, но в ней нет подгрупп порядка 6. Таким образом, утверждение, обратное к теореме Лагранжа, не верно.
Однако некоторое достаточное условие для того, чтобы группа G порядка g имела подгруппу порядка h, где h тАУ делитель числа g, указывается в следующей теореме Силова.
Теорема Силова: пусть G тАУ группа порядка g и h тАУ делитель числа g; если h=pn, где р тАУ простое число, а n тАУ положительное целое число, то G содержит подгруппу порядка h.
Теорема Силова существенно облегчает процесс нахождения подгрупп некоторой группы. Так, например, порядок группы А4 равен 12; простыми делителями числа 12 являются 2 и 3. По теореме Силова мы можем утверждать, что знакопеременная группа А4 содержит подгруппы порядка 2, 3 и 4=22, но мы все равно ничего не можем сказать о подгруппе порядка 6.
Исходя из всего выше описанного, можно сделать вывод о том, что теорема Лагранжа и непосредственные следствия из этой теоремы играют важную роль в теории групп. Они очень часто применяются как в самой теории групп, так и во всех ее приложениях.
1.6. ЗАДАЧИ
1. Описать все подгруппы симметрической группы S3.
Решение.
Порядок группы S3 равен 3!=6. из теоремы Лагранжа следует, что собственные подгруппы из S3 могут состоять из двух или трех перестановок. Следовательно, подмножества S3, состоящие из четырех или пяти перестановок, подгрупп не образуют.
1) Опишем сначала подгруппы, которые состоят из двух перестановок. Если Н тАУ такая подгруппа, то в нее входит элемент Е и еще какой-то другой элемент  , то есть
, то есть 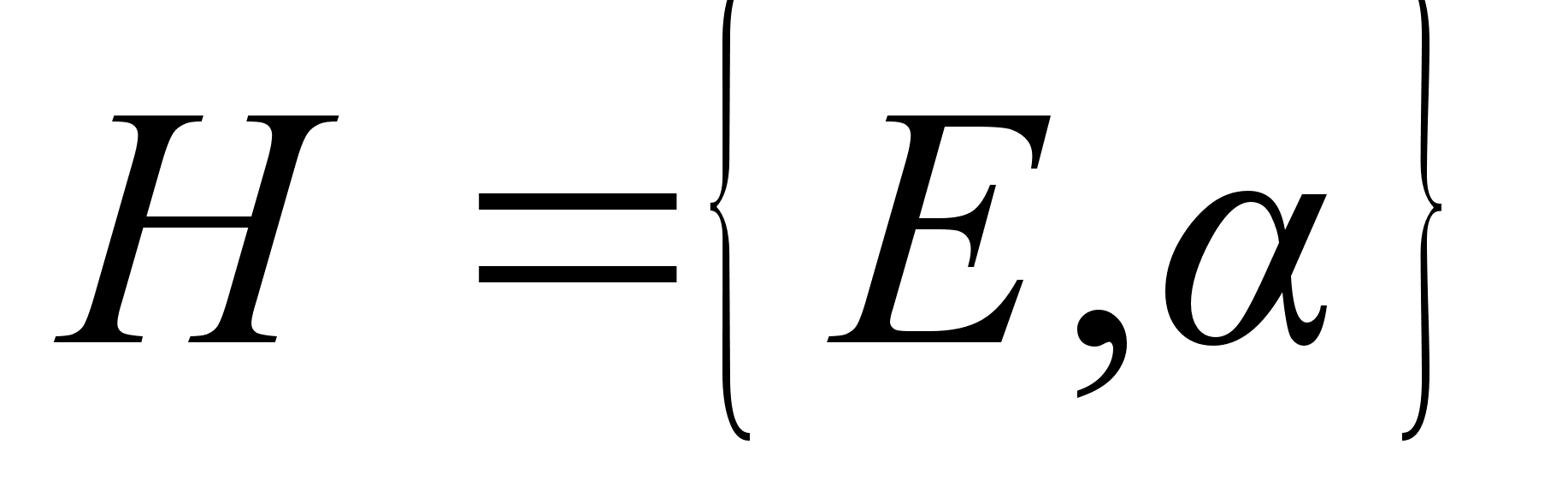 .
.
Элемент обратный к 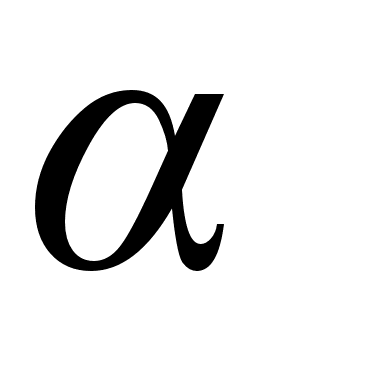 не может совпадать с Е, поэтому
не может совпадать с Е, поэтому 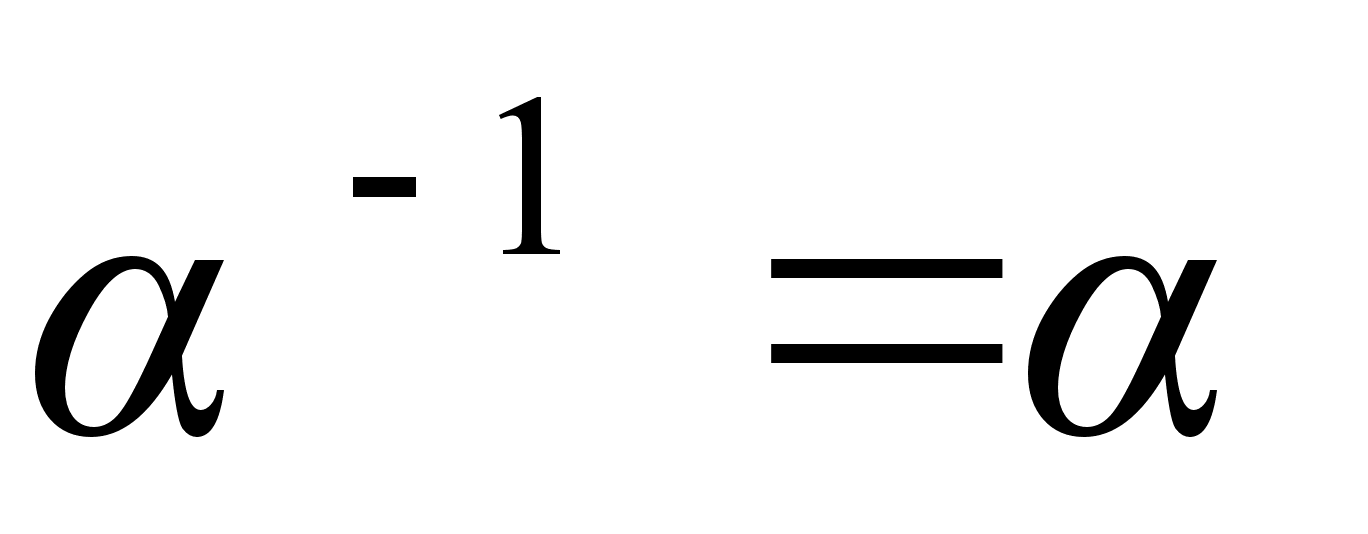 . Последнее равенство можно записать так:
. Последнее равенство можно записать так: 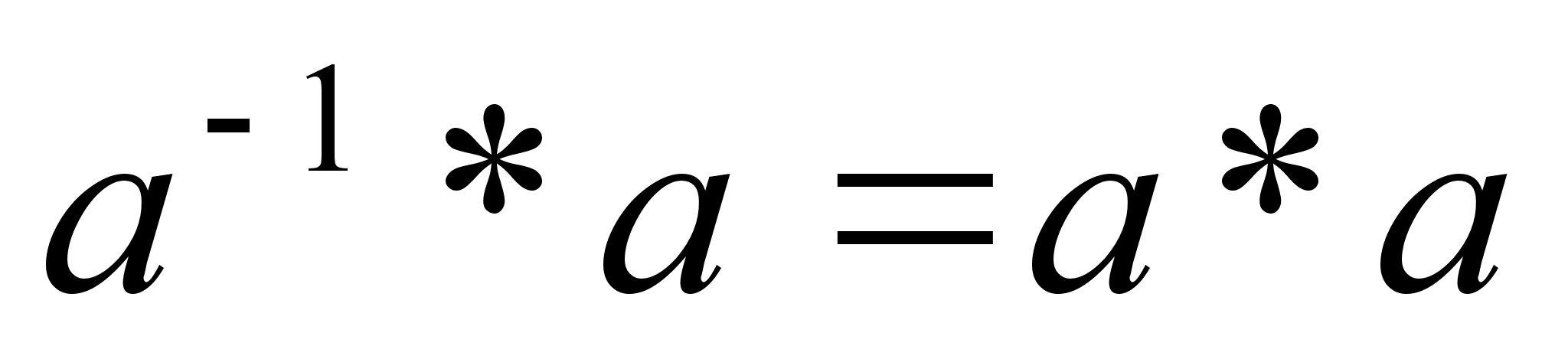 , то есть Е=
, то есть Е= . Следовательно, а тАУ перестановка второго порядка, то есть цикл длины 2.
. Следовательно, а тАУ перестановка второго порядка, то есть цикл длины 2.
Таким образом, существует не больше трех подгрупп второго порядка группы S3. эти подгруппы легко находятся с помощью таблицы Кэли. Это будут такие подмножества: 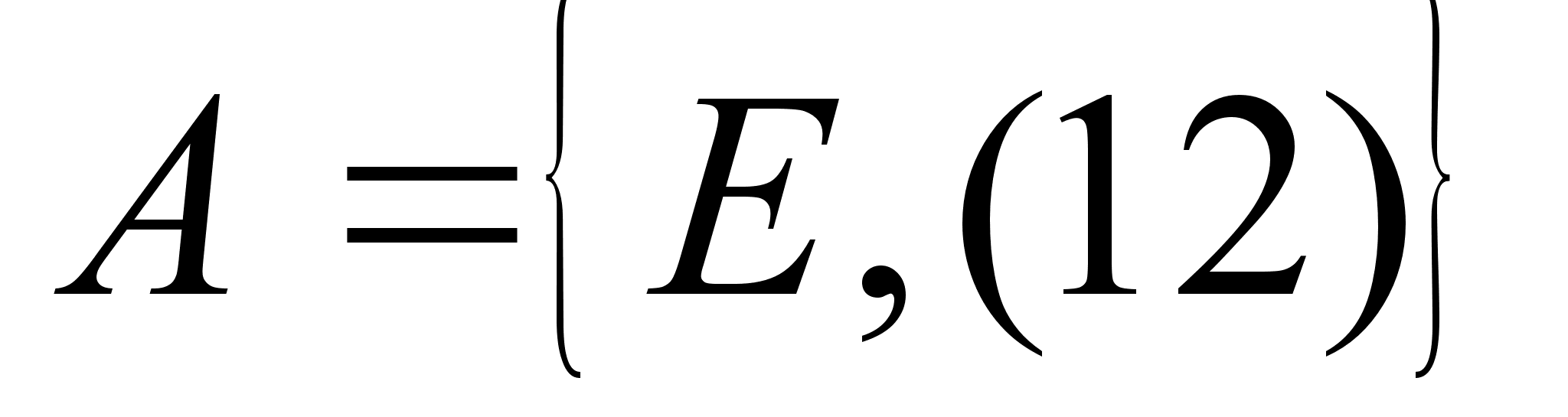 ,
, 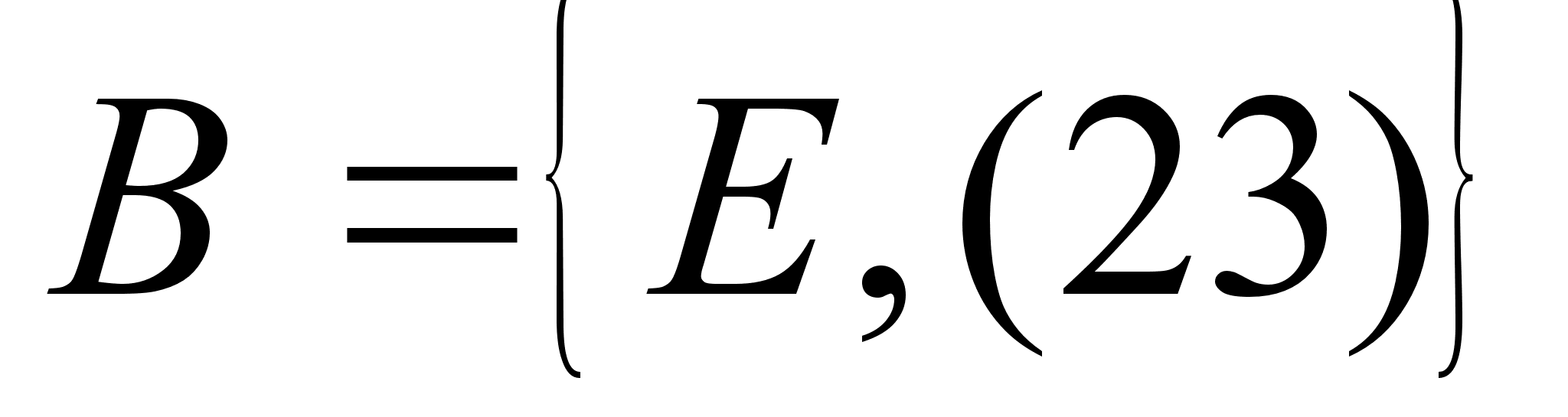 ,
, 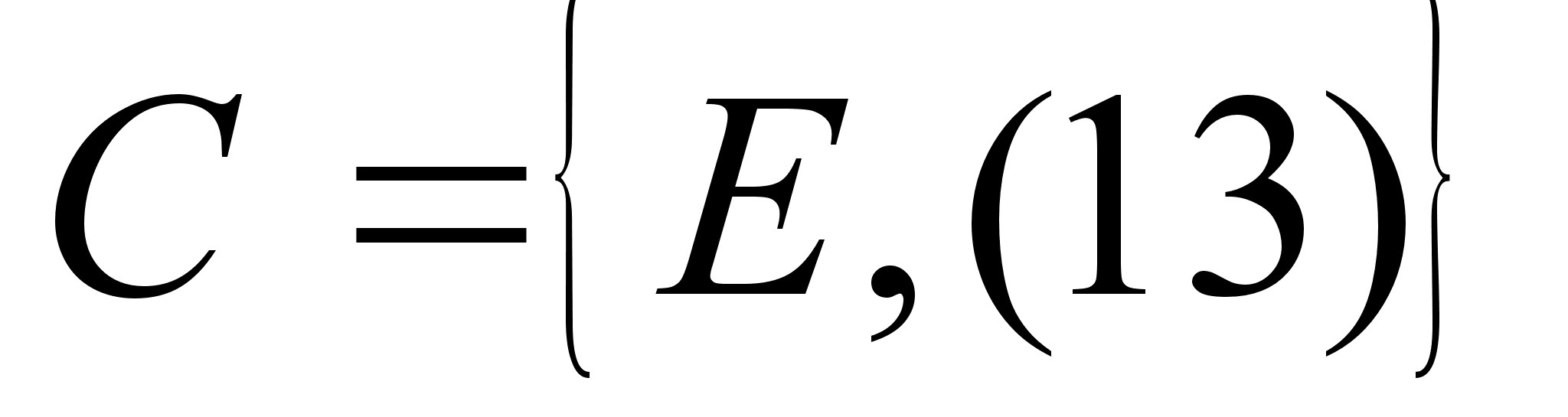 . Легко убедиться, что подмножества А, В и С действительно являются подгруппами группы S3, так как для каждого из них выполняется условие теоремы о подгруппах для конечных групп.
. Легко убедиться, что подмножества А, В и С действительно являются подгруппами группы S3, так как для каждого из них выполняется условие теоремы о подгруппах для конечных групп.
Для подмножества А:



Для подмножества В:


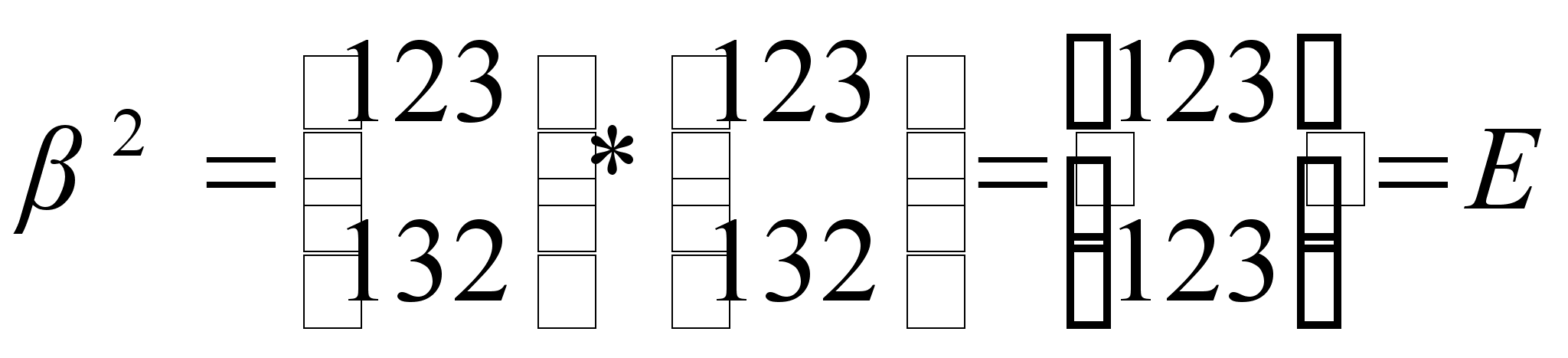
Для подмножества С:
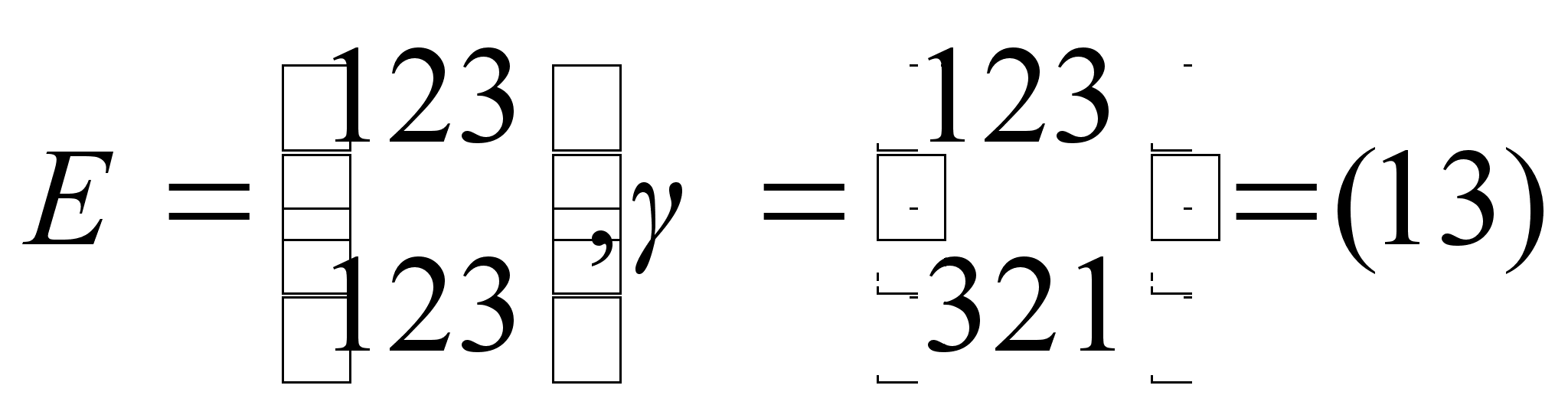
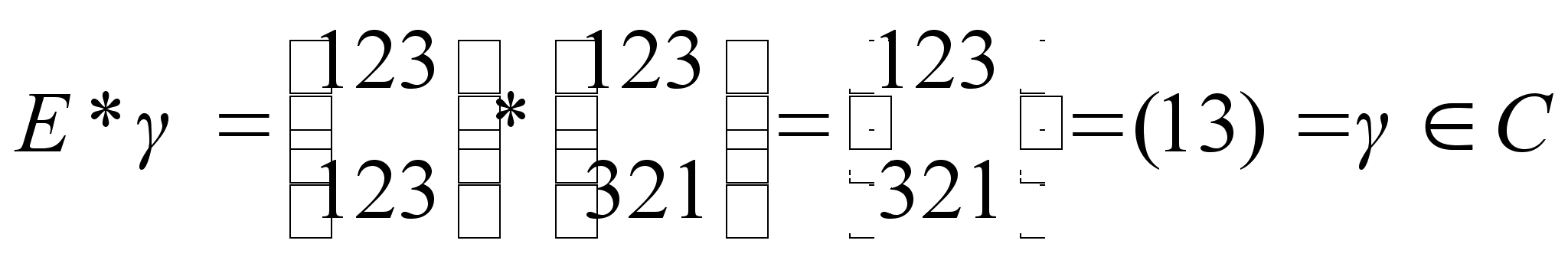

2) Теперь опишем подгруппы, которые состоят из трех перестановок. Если  - такая подгруппа, то перестановки
- такая подгруппа, то перестановки  и
и  должны иметь порядок 3. действительно, если одна из них, например
должны иметь порядок 3. действительно, если одна из них, например  , имеет порядок 2, то
, имеет порядок 2, то  =
= -1. Пусть
-1. Пусть 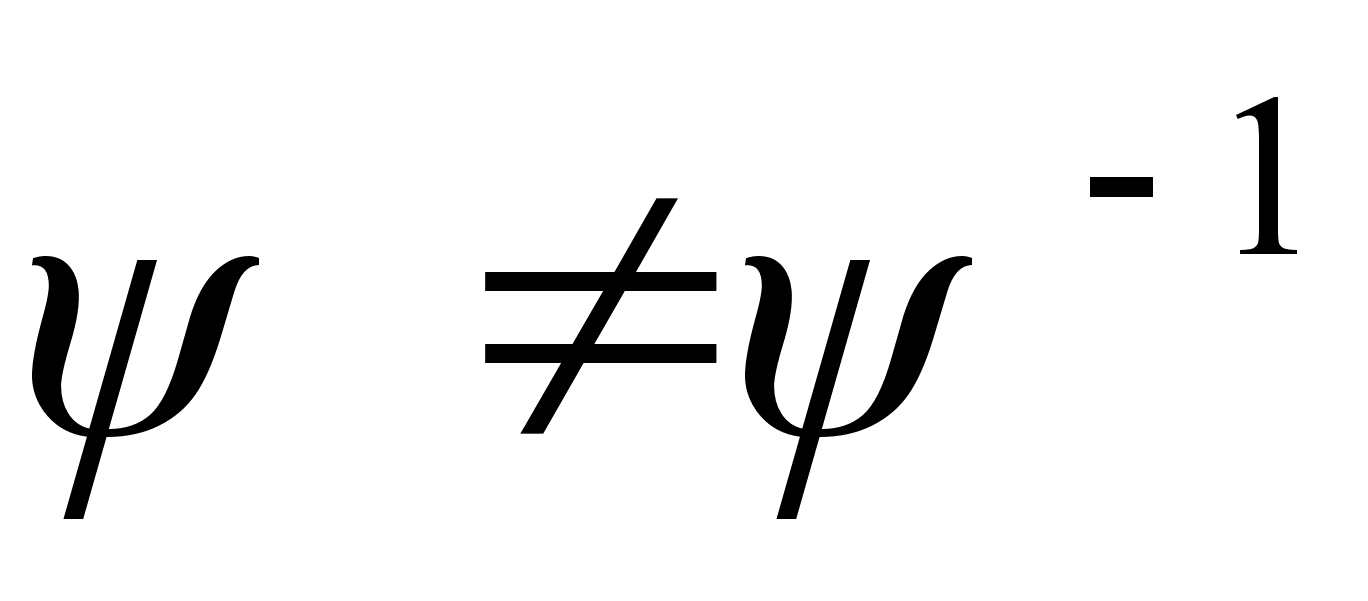 , тогда
, тогда  и
и 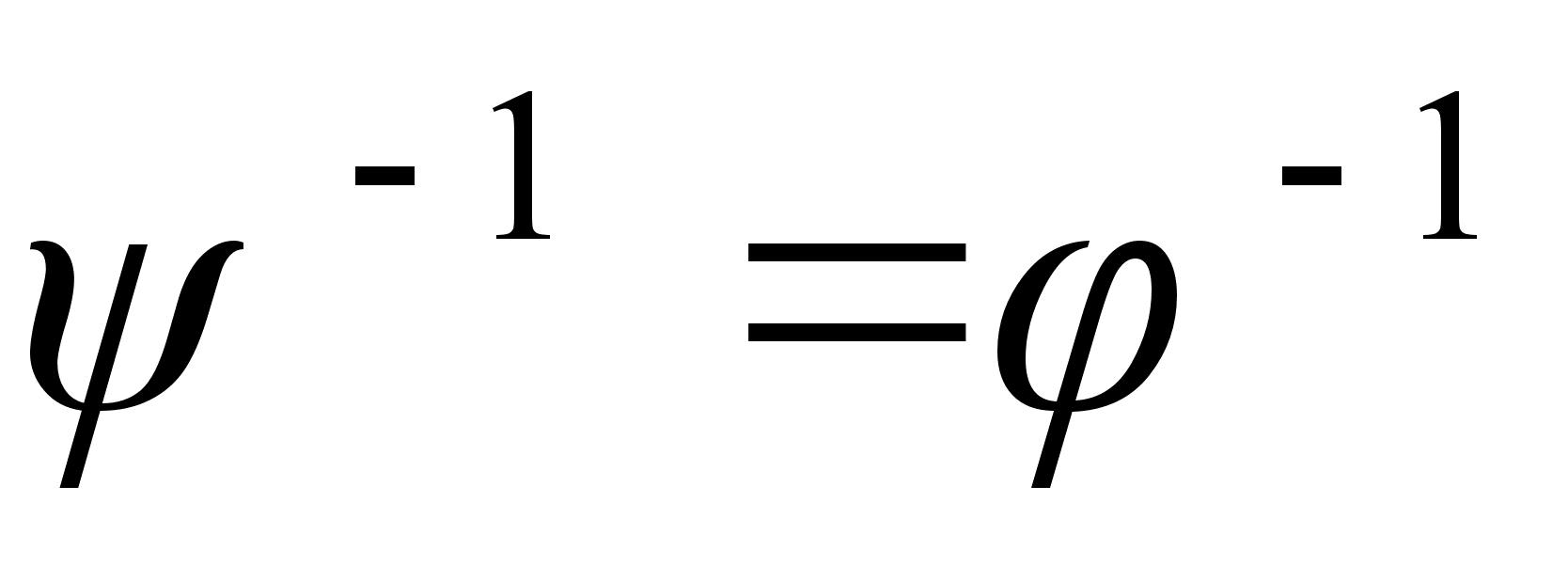 . Тогда
. Тогда  Следовательно, получили противоречие, так как у нас
Следовательно, получили противоречие, так как у нас  и
и 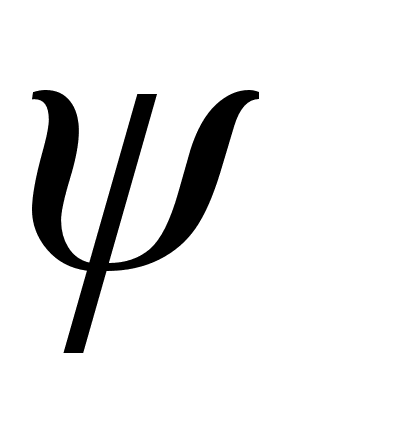 различны. Значит,
различны. Значит, 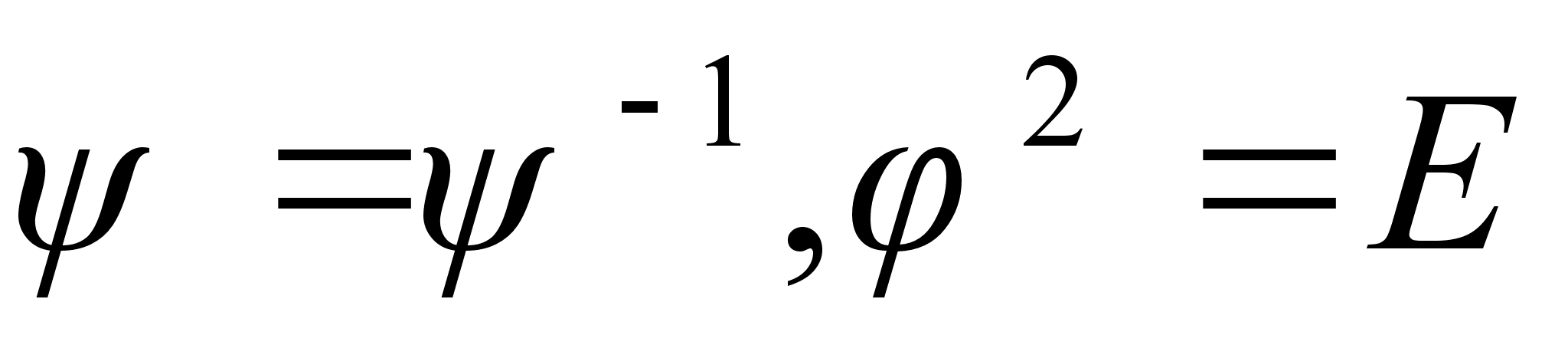 , то есть перестановка
, то есть перестановка 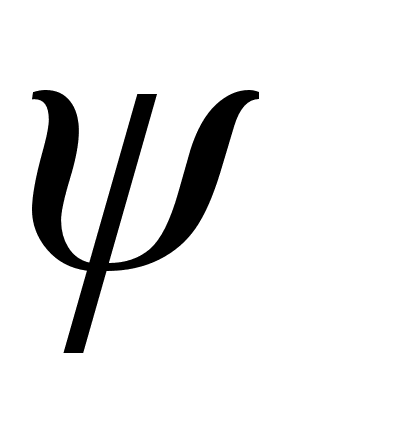 тоже будет иметь порядок 2. но легко проверить непосредственно, что произведение любых двух перестановок второго порядка является перестановка третьего порядка. Например,
тоже будет иметь порядок 2. но легко проверить непосредственно, что произведение любых двух перестановок второго порядка является перестановка третьего порядка. Например,  .
.
Следовательно, произведение  *
*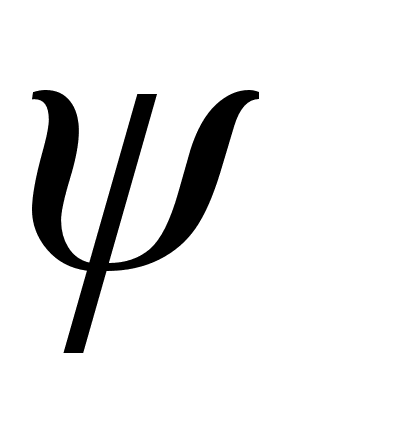 не принадлежит G и G тогда не является подгруппой.
не принадлежит G и G тогда не является подгруппой.
Таким образом, перестановки  и
и 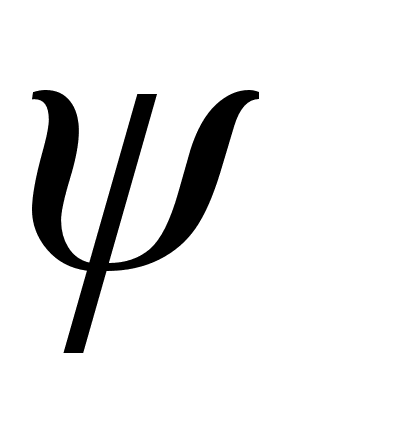 должны иметь порядок 3, то есть
должны иметь порядок 3, то есть  , где
, где  ,
,


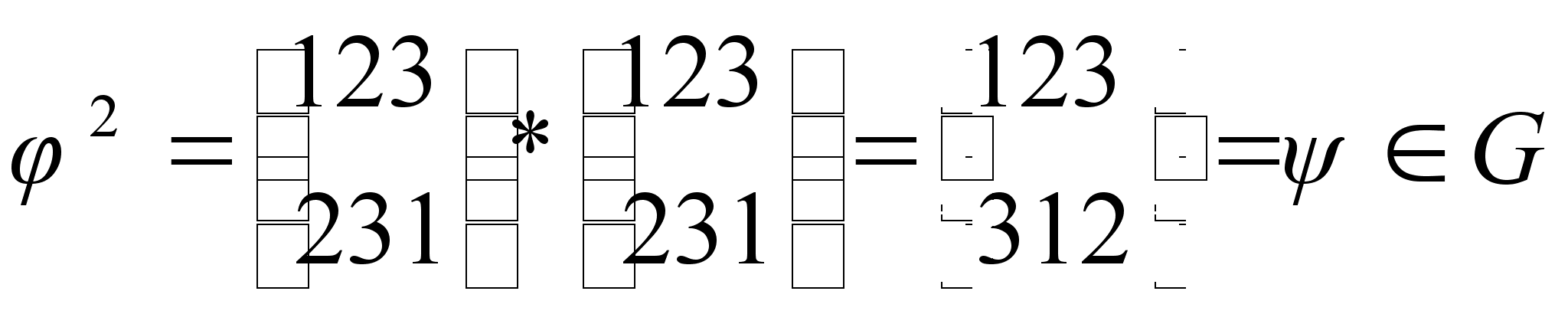


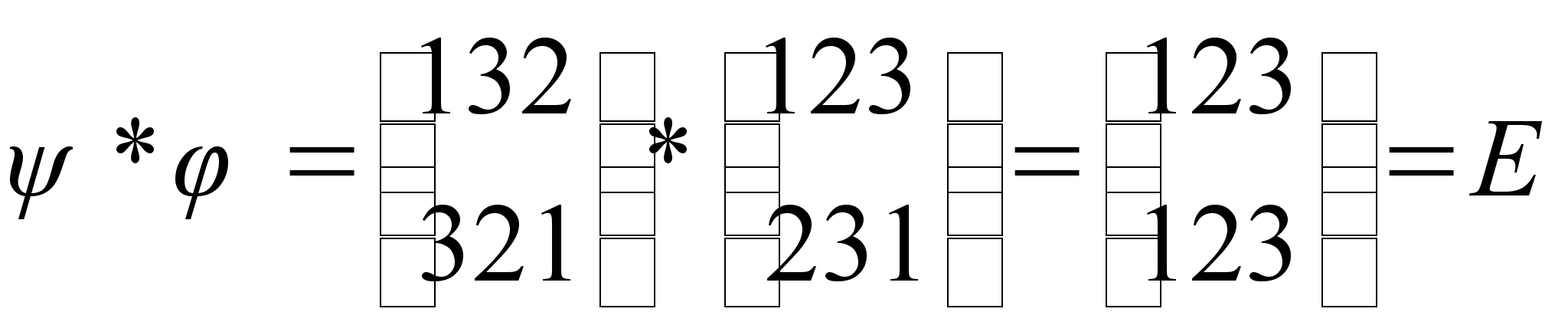
Как видим, произведение каждых двух элементов множества G является элементом из G, следовательно, выполняется условие теоремы о подгруппах для конечных групп. Значит, подмножество G множества S3 является подгруппой группы S3.
Таким образом, группа S3 имеет шесть разных подгрупп:
1. 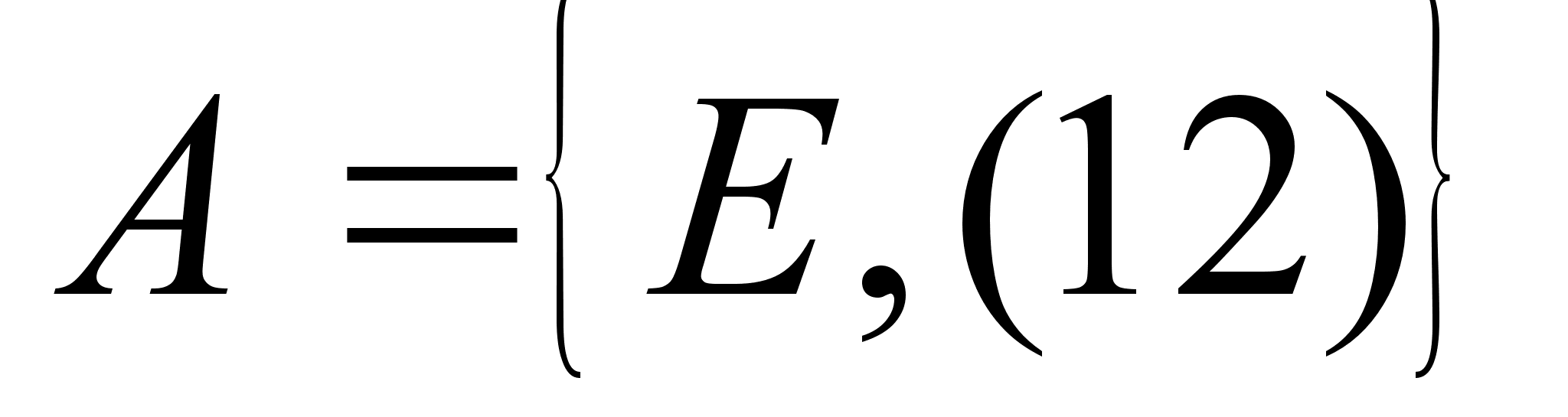
2. 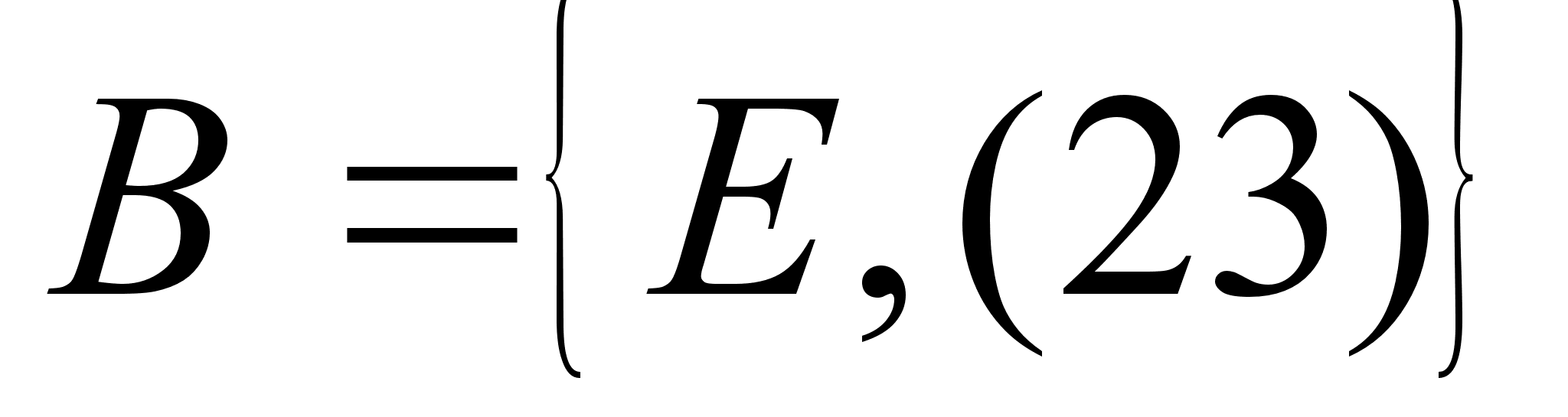
3. 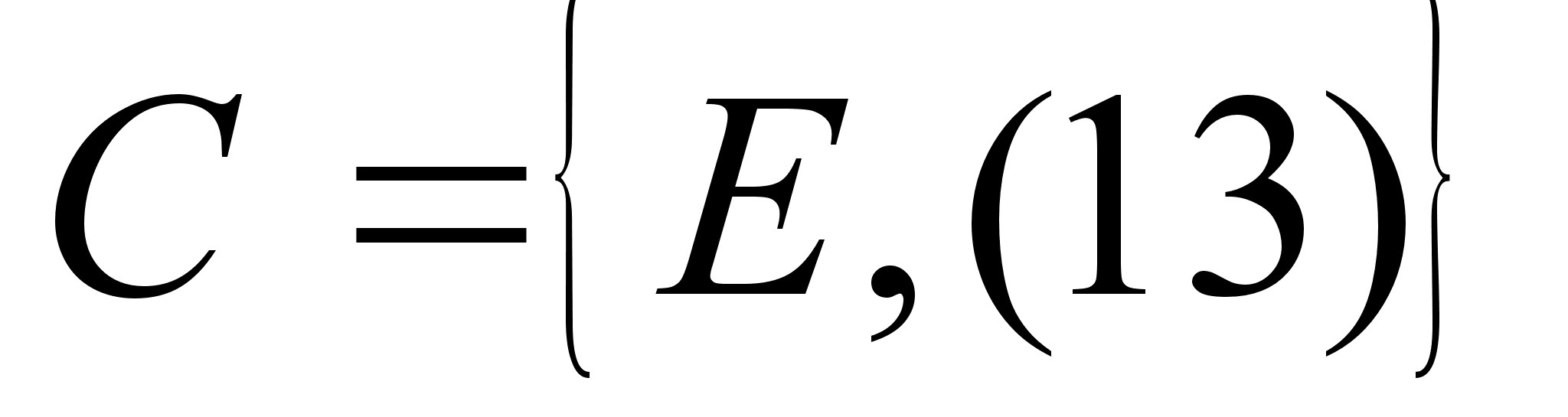
4. 
5. 
6. 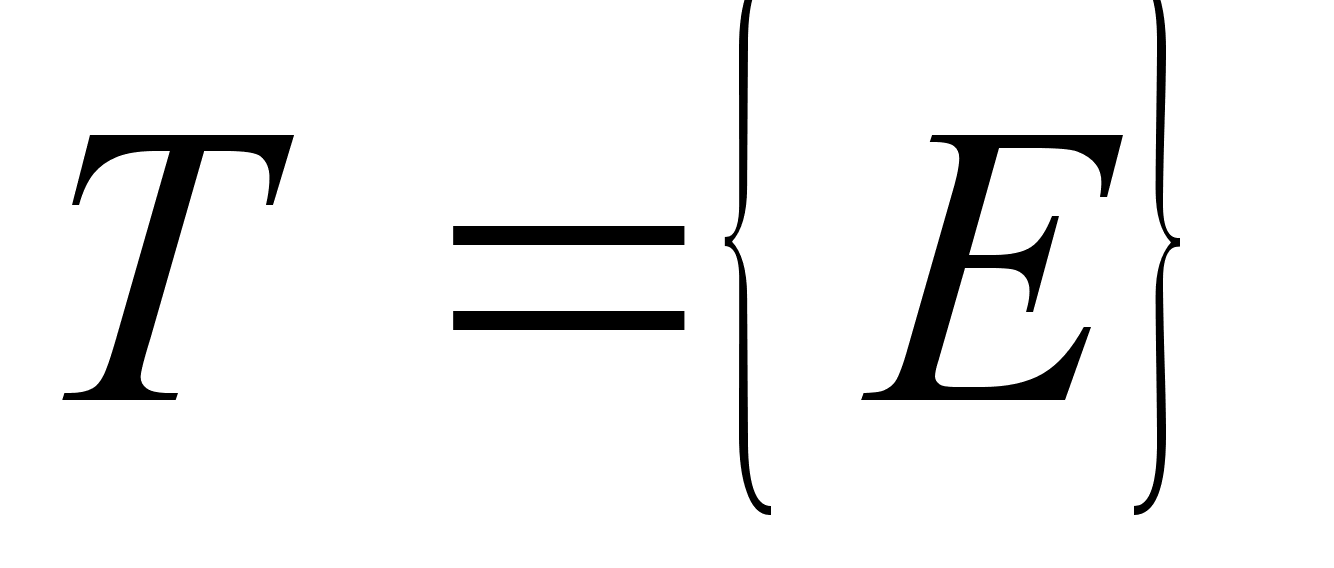
Результат только что рассмотренной задачи наталкивает нас на предположение о том, что если группа имеет порядок n, то она имеет и n различных подгрупп. Чтобы подтвердить или опровергнуть это предположение рассмотрим следующую задачу.
2. Опишите все подгруппы симметрической группы S4.
Решение: порядок группы S4 равен 4!=12. По теореме Лагранжа, собственные подгруппы из S4 могут состоять из 2, 3, 4, 6, 8, 12 перестановок. По теореме Силова можно лишь утверждать, что группа S4 содержит подгруппы порядка 2, 3, 4=22, 8=23, но ничего не можем сказать о подгруппах порядка 6 и 12. надо будет доказать существование или отсутствие подгрупп порядка 6 и 12.
1) Опишем подгруппы, состоящие из двух перестановок.
1. 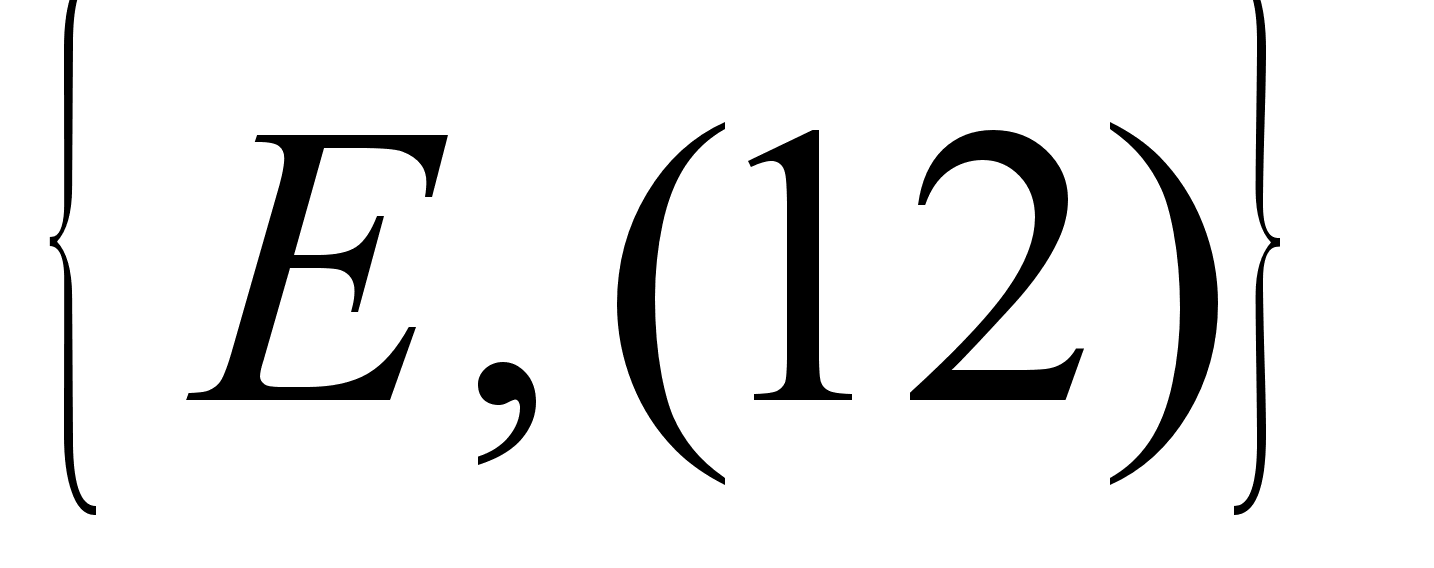
2. 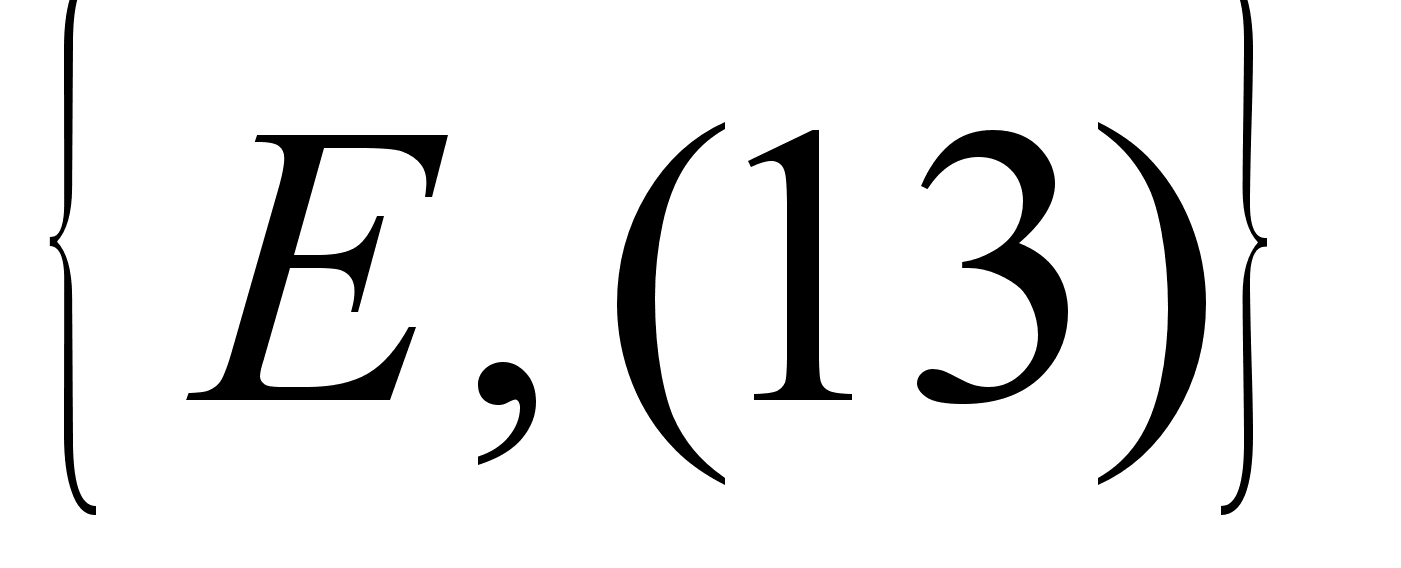
3. 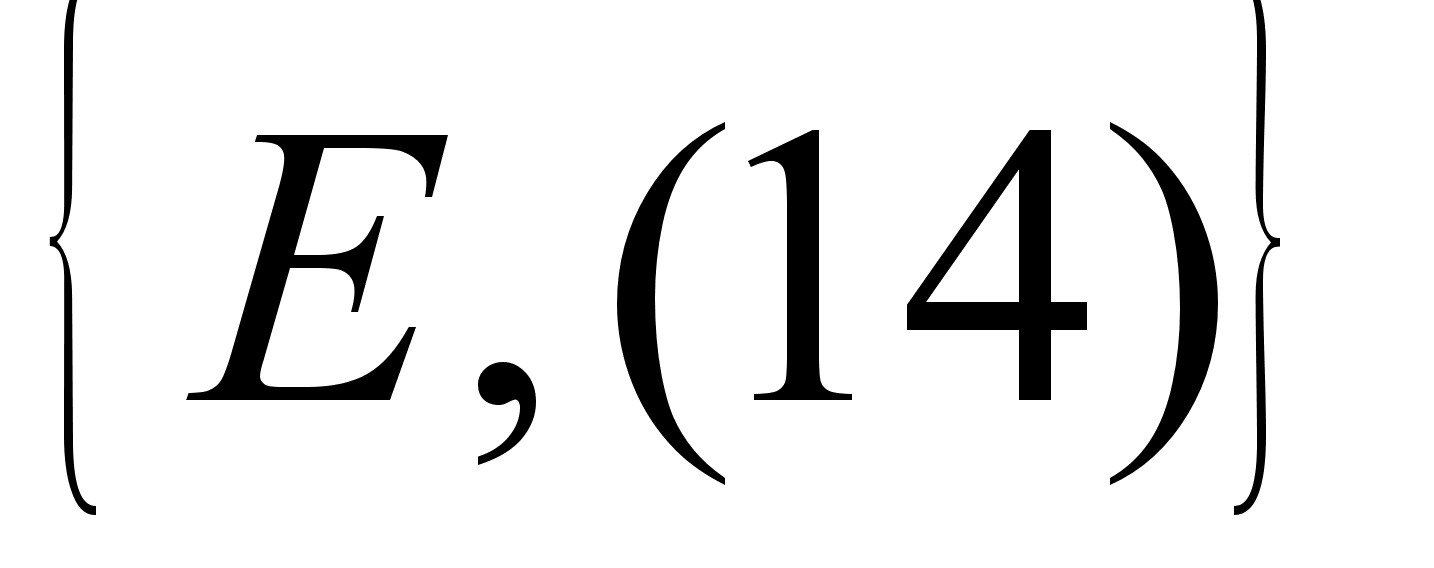
4. 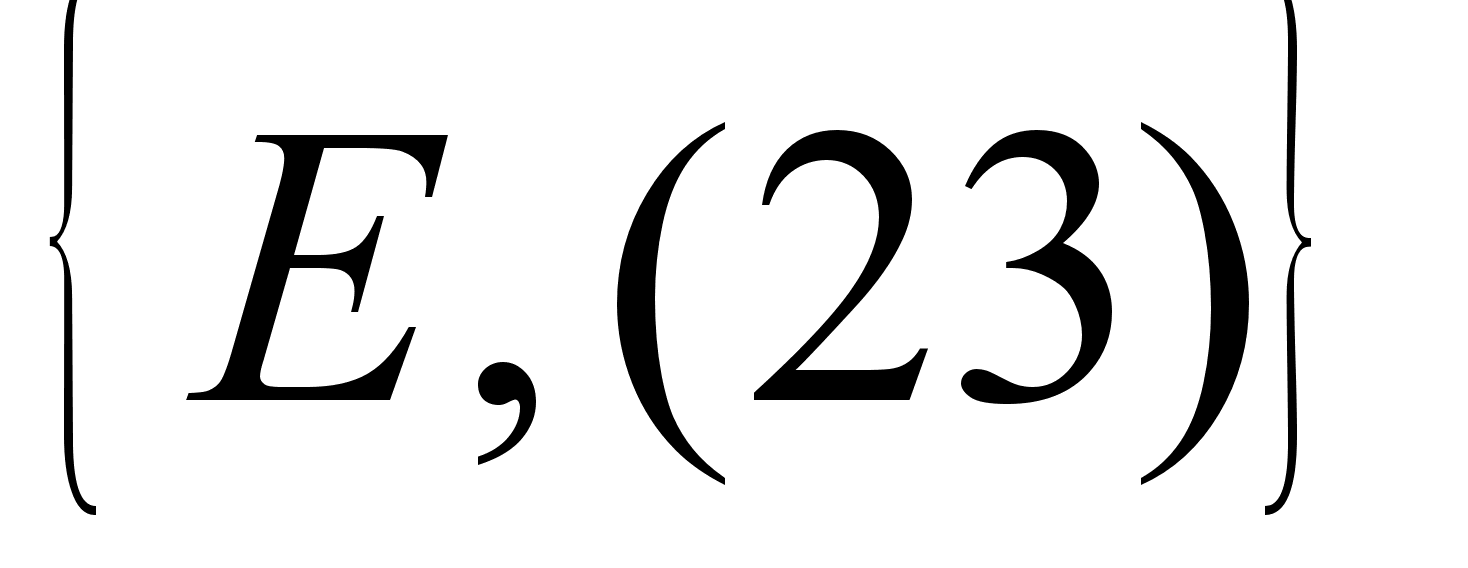
5. 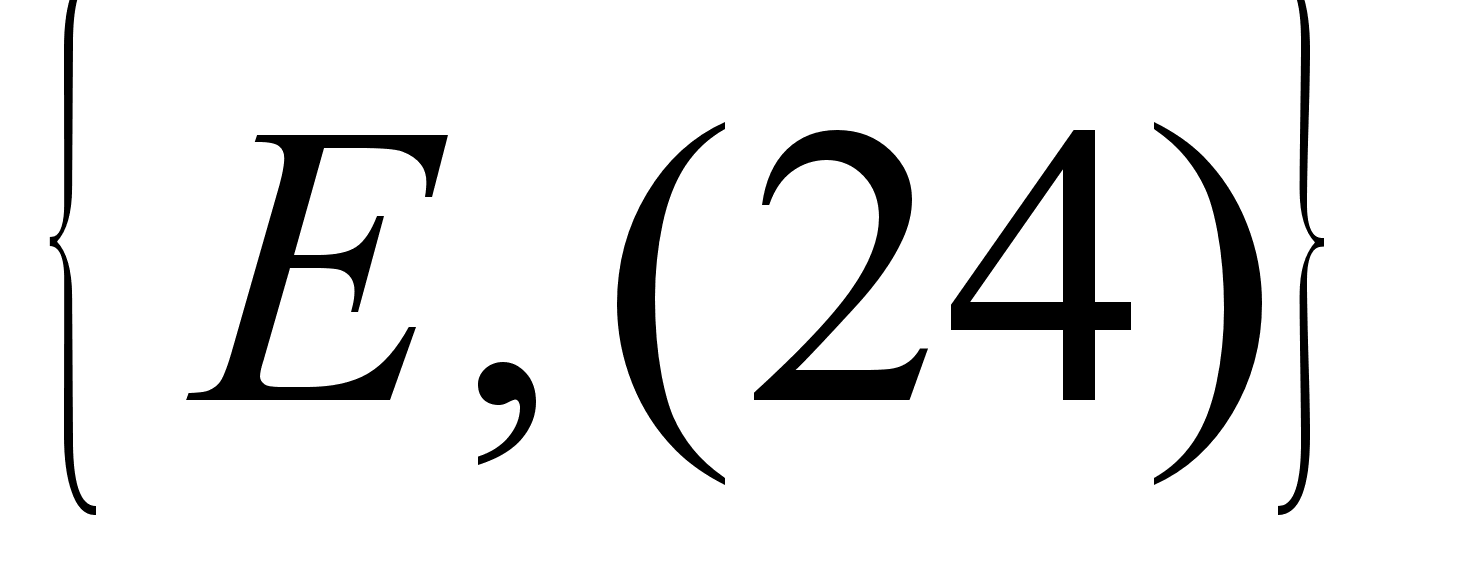
6. 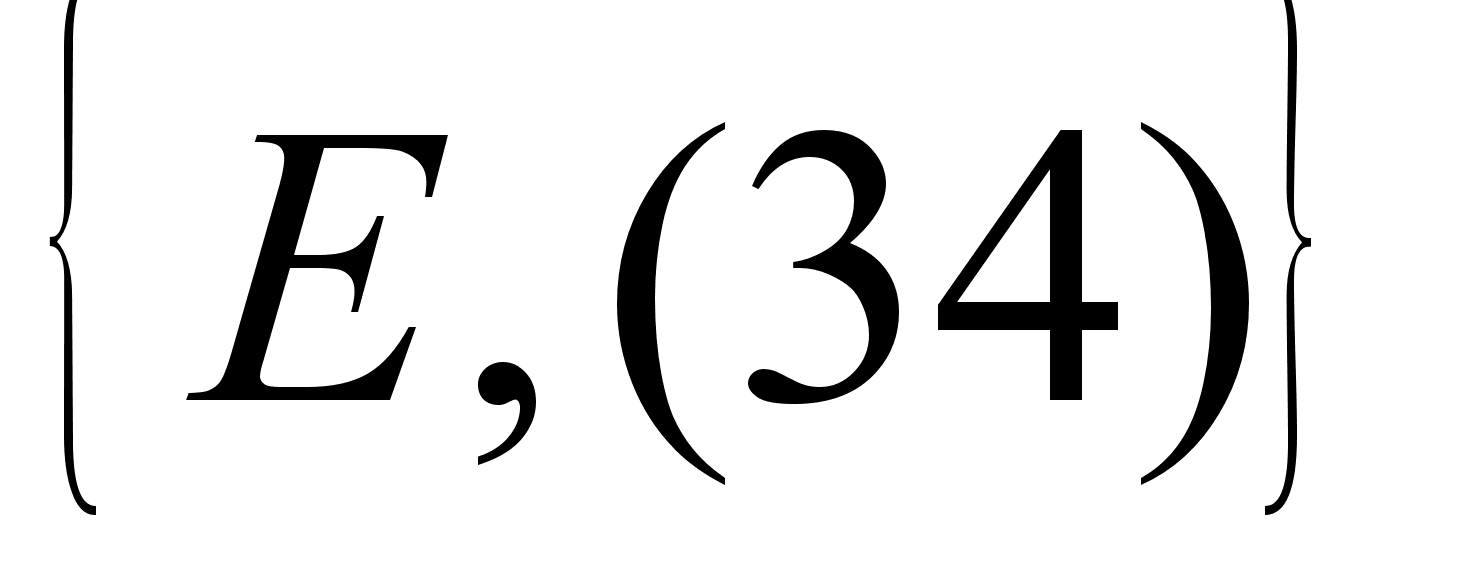
7. 
8. 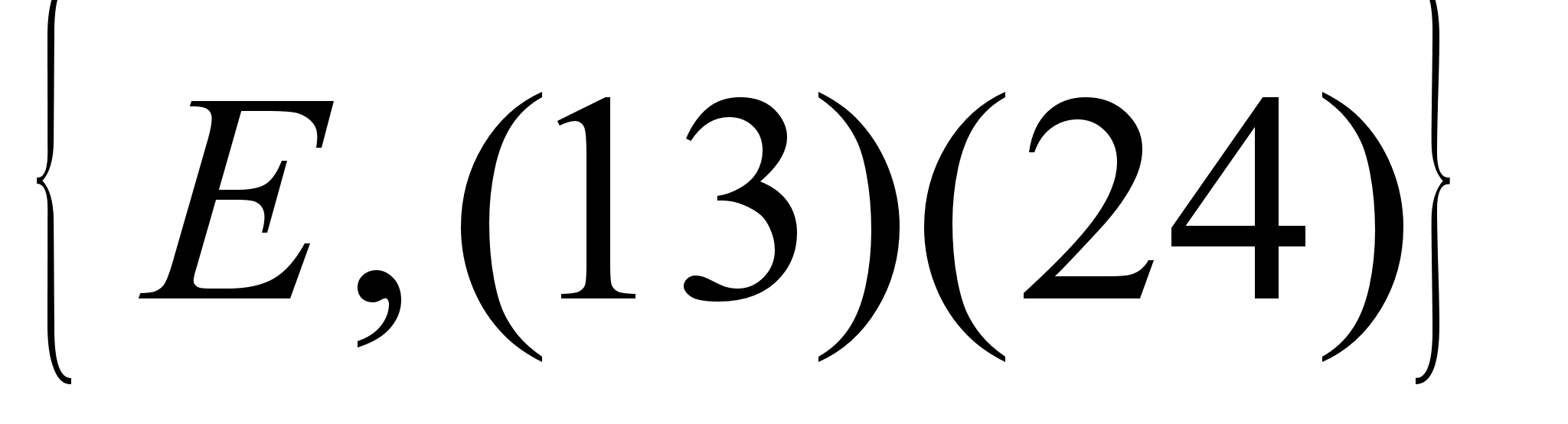
9. 
2) Опишем подгруппы, состоящие из трех перестановок.
10. 
11. 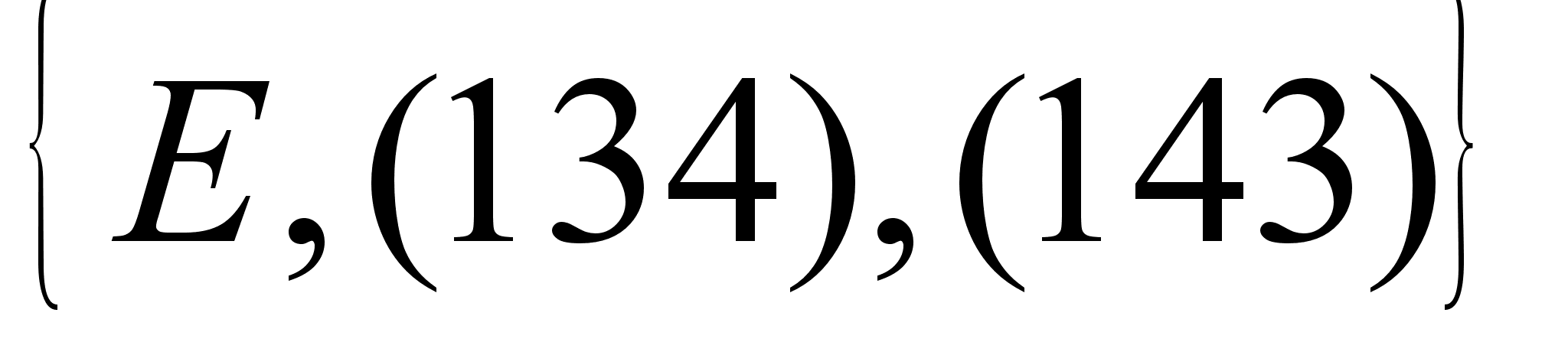
12. 
13. 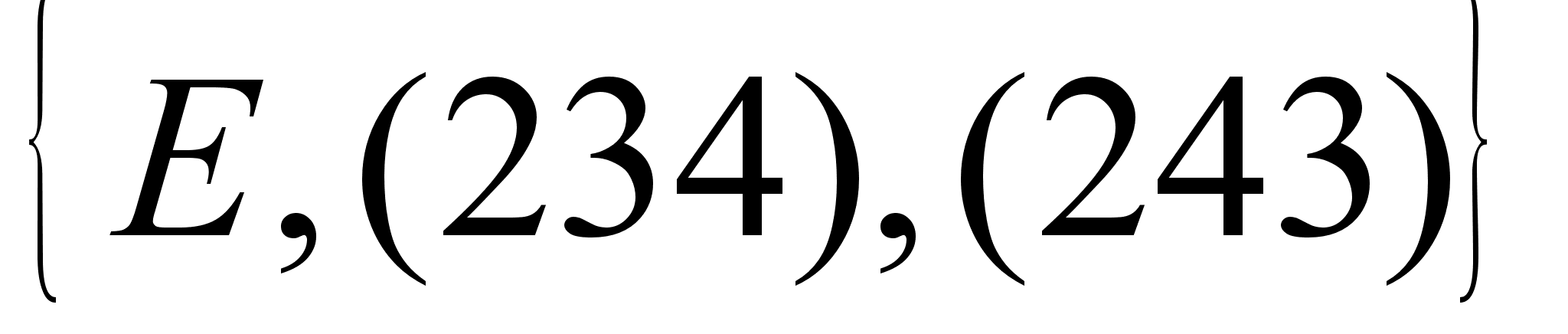
3) Опишем подгруппы, состоящие из четырех перестановок.
14. 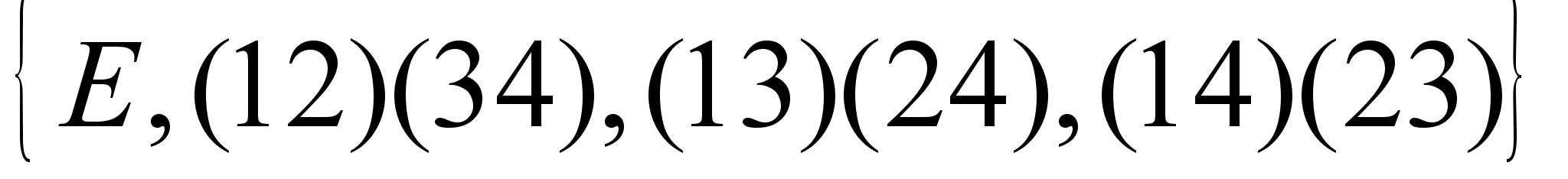
15. 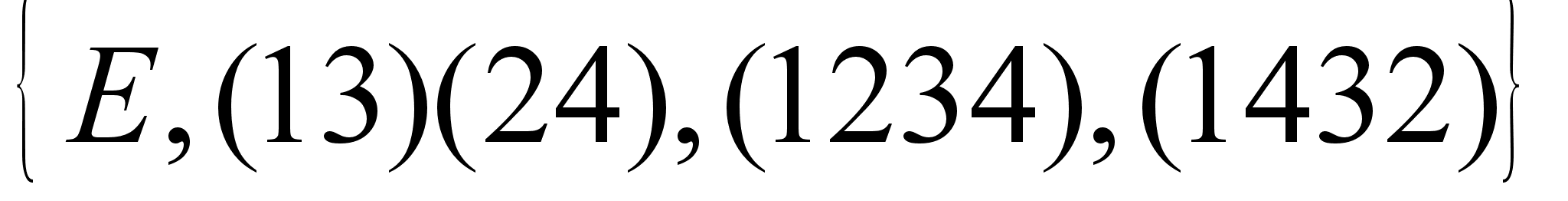
16. 
17. 
18. 
19. 
20. 
4) Опишем подгруппы, состоящие из шести перестановок.
21. 
22. 
23. 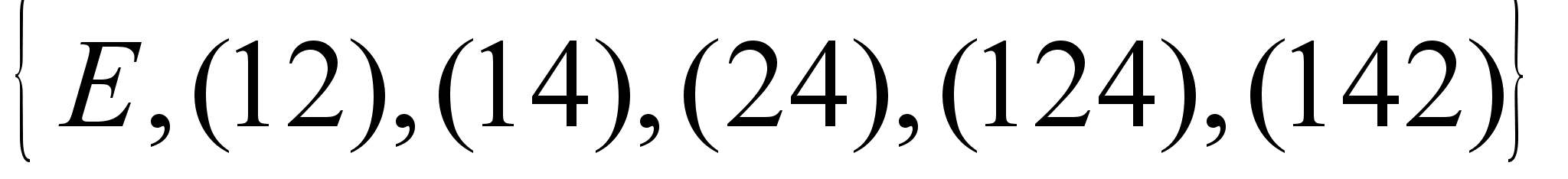
24. 
5) Опишем подгруппы, состоящие из восьми перестановок.
25. 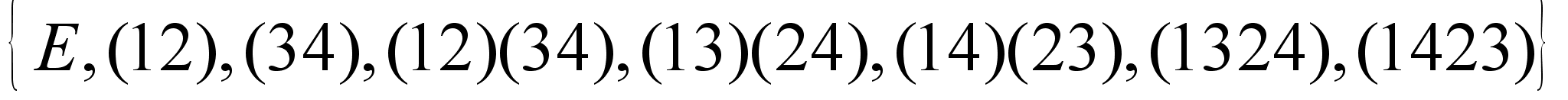
26. 
27. 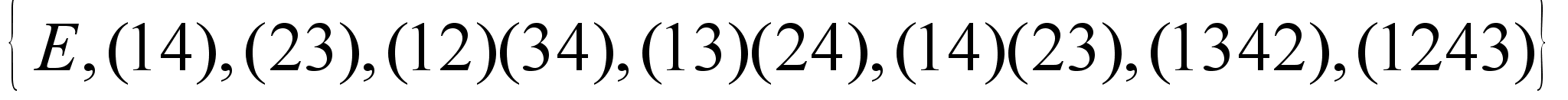
6) Опишем подгруппы, состоящие из двенадцати перестановок.
28. 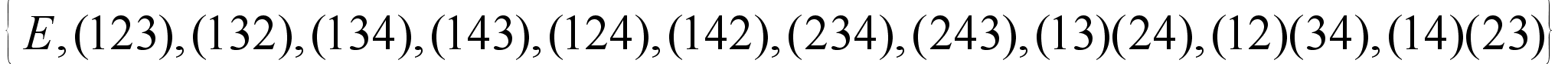
7) Опишем несобственные подгруппы группы S4.
29. 
30.  .
.
Все описанные выше подмножества действительно являются подгруппами, так как для каждого из них выполняется условие теоремы о подгруппах для конечных групп. Кроме того, в группе S4 имеются подгруппы 6-го и 12-го порядка.
Следовательно, симметрическая группа S4 имеет 30 разных подгрупп, а порядок группы S4 равен 24. поэтому, сформулированное нами предложение о том, что количество подгрупп некоторой группы равно порядку этой группы, оказалось не верным.
3. Доказать, что подмножество 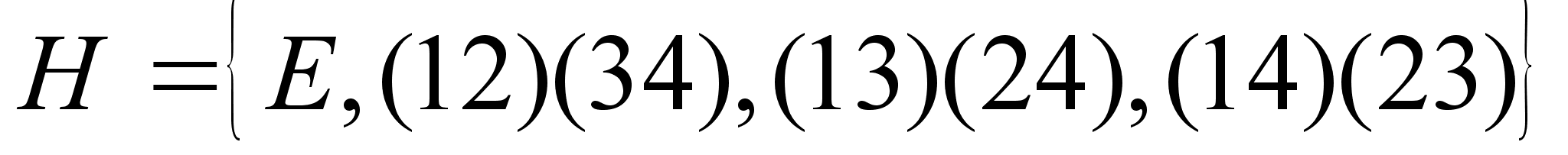 группы S4 является коммуникативной подгруппой. Составить таблицу умножения подгруппы Н.
группы S4 является коммуникативной подгруппой. Составить таблицу умножения подгруппы Н.
Решение.
Коммуникативной подгруппой называется подгруппы с коммуникативной операцией.
Операция на множестве Н называется коммуникативной, если для любых двух элементов h1 и h2 из Н выполняется условие: h1*h2=h2*h1.
Перестановки  и
и  коммутируют, если
коммутируют, если  .
.
Пусть  ,
, 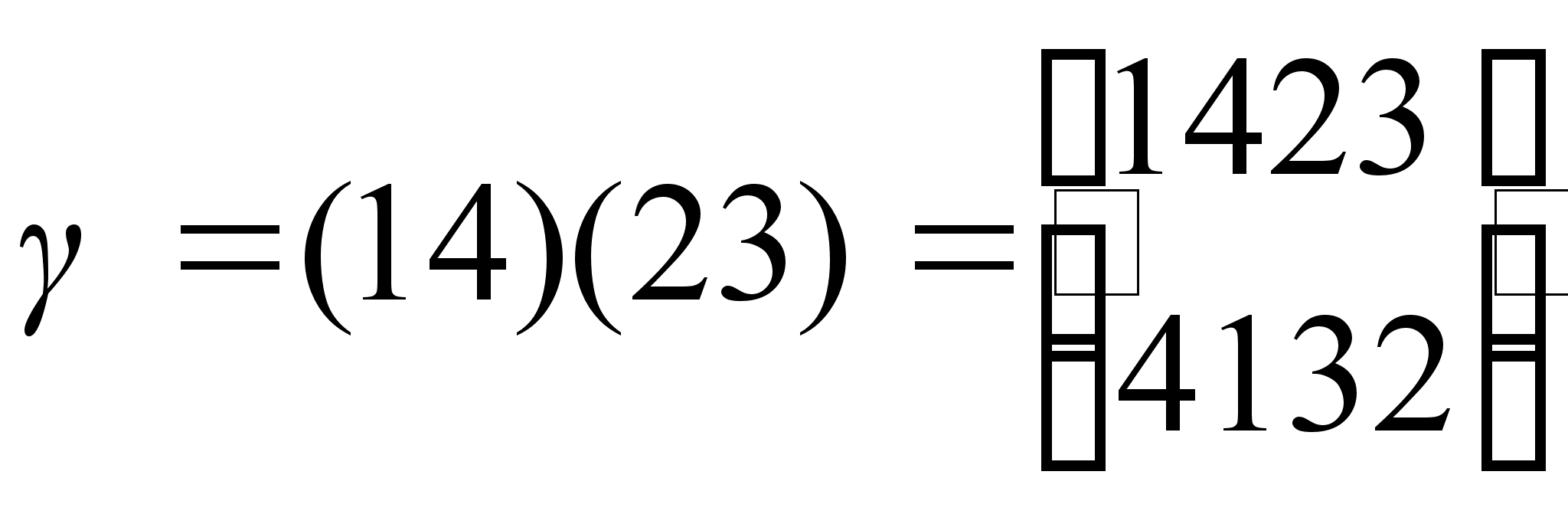 .
.
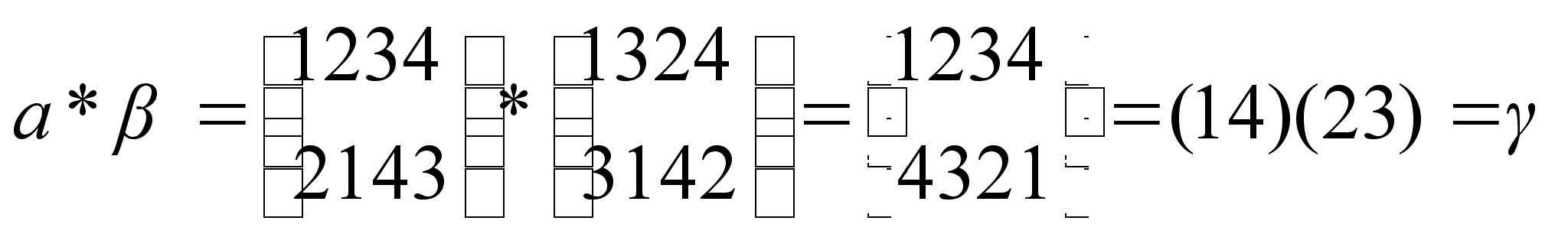

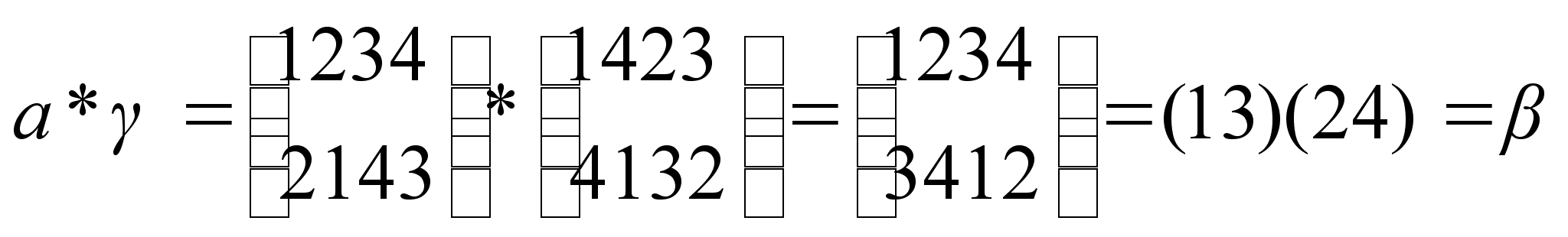
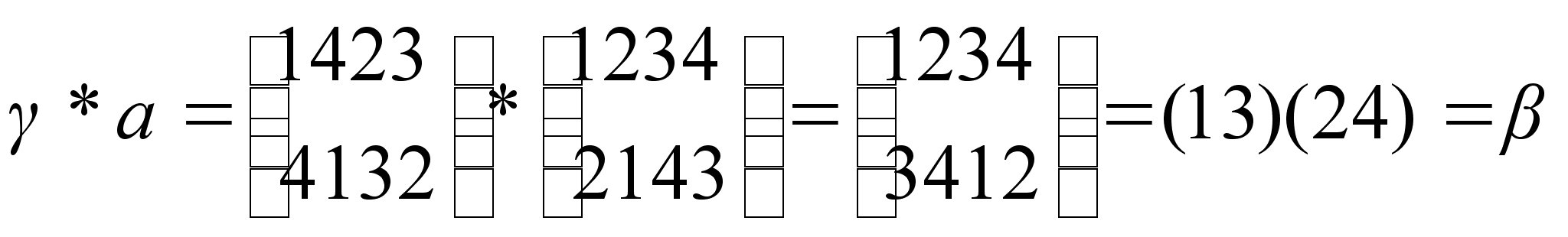
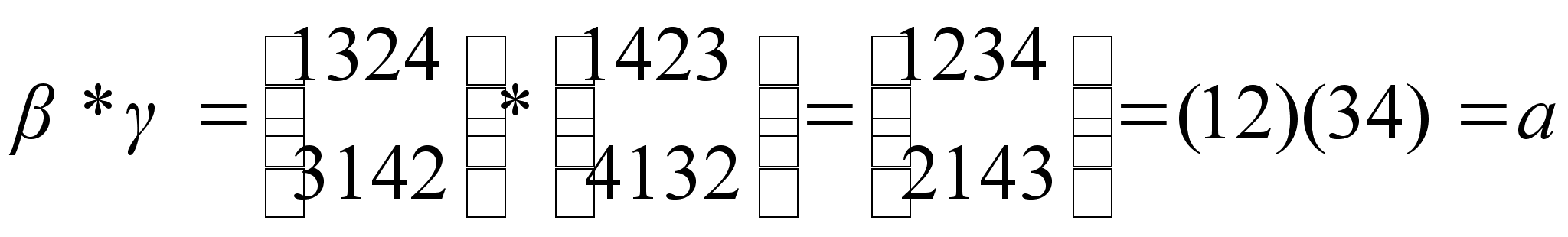
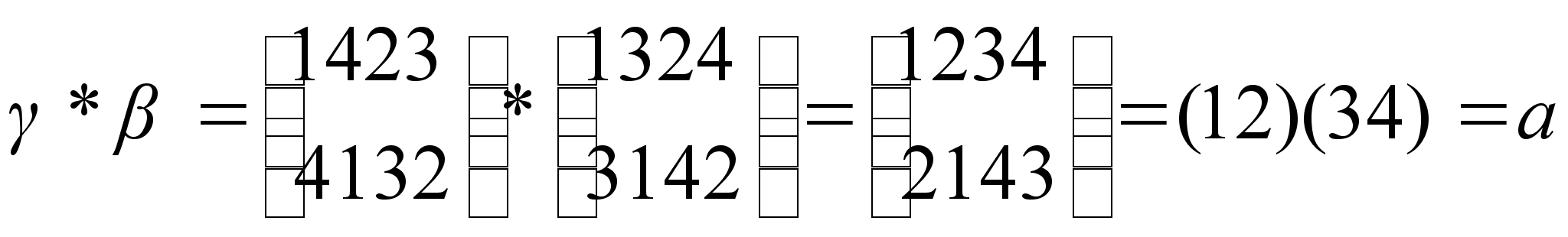

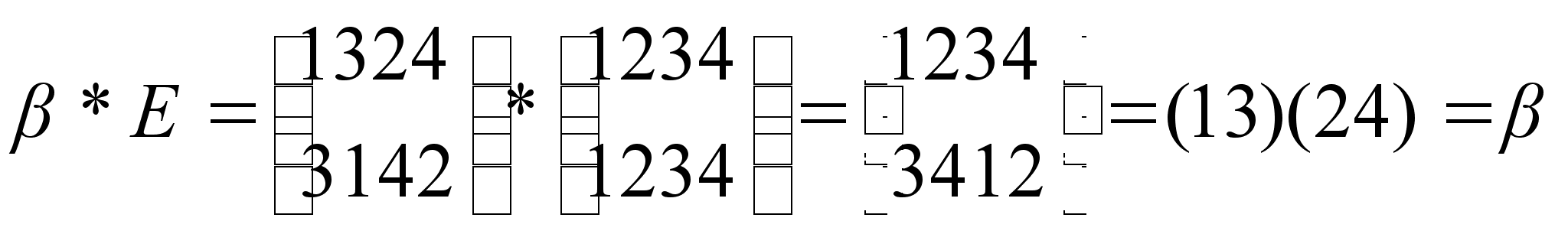

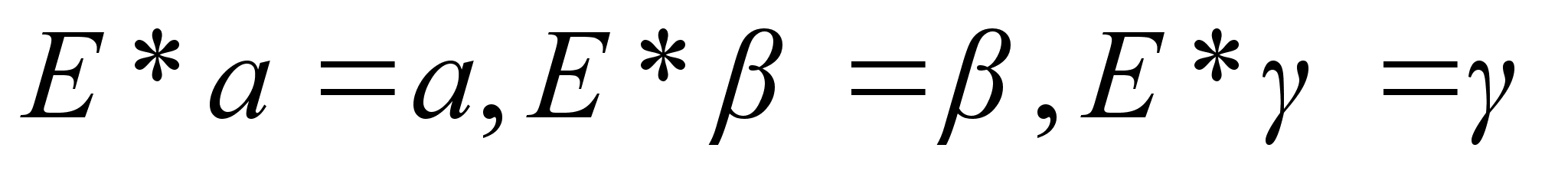

 "Инкарнация" кватернионов
"Инкарнация" кватернионов
* Алгебры и их применение
*-Алгебры и их применение
10 способов решения квадратных уравнений
Cпособы преобразования комплексного чертежа, применение при изображении предметов