Лекции по матану (III семестр) переходящие в шпоры

1 Двойной интеграл

Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией Г, являющейся замкнутой непрерывной кривой. z = l(P) = f(x,y), P= (x,y) Î D тАУ произвольные ф-ции определенные и ограниченные на D. Диаметром области D наз. наибольшее расстояние между граничными точками. Область D разбивается на n частых областей D1тАжDn конечным числом произв. кривых. Если S тАУ площадь D, то DSi тАУ площадь каждой частной области. Наибольший из диаметров областей обозн l. В каждой частной области Di возьмем произв. точку Pi (xi , Di) Î Di, наз. промежуточной. Если диаметр разбиения D l à 0 , то число n областей Di à ¥. Вычислим зн-ие ф-ции в промежуточных точках и составим сумму:I = 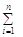f(xi, Di)DSi (1), наз. интегральной суммой ф-ции. Ф-ция f(x,y) наз. интегрируемой в области D если существует конечный предел интегральной суммы.

Двойным интегралом ф-ии f(x,y) по области D наз. предел интегральной суммы при l à 0. Обозн:

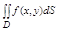или

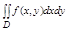
2 Понятие числового

ряда и его суммы

Пусть задана бесконечная последовательность чисел u1, u2, u3тАж

Выражение u1+ u2+ u3тАж+ un (1) называется числовым рядом, а числа его составляющие- членами ряда.

Сумма конечно числа n первых членов ряда называется n-ной частичной суммой ряда: Sn = u1+.+un

Если сущ. конечный предел: , то его называют суммой ряда и говорят, что ряд сходится, если такого предела не существует, то говорят что ряд расходится и суммы не имеет.

№ 2

1 Условие существования

двойного интеграла

Необходимое, но недостаточное:

Ф-ция f(x,y) интегрируема на замкнутой области D, ограничена на D.

1 достаточный признак существования: если ф-ция f(x,y) непрерывна на замкнутой, огр. области D, то она интегрируема на D.

2 достаточный признак существования: если ф-ция f(x,y) ограничена в замкнутой области D с какой-то границей и непрерывна в ней за исключением отдельных точек и гладки=х прямых в конечном числе где она может иметь разрыв, то она интегрируема на D.

2 Геометрический и

арифметический ряды

Ряд состоящий из членов бесконечной геометрической прогрессии наз. геометрическим: или

а+ а×q +тАж+a×q^n-1

a ¹ 0 первый член q тАУ знаменатель. Сумма ряда: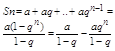

следовательно конечный предел последовательности частных сумм ряда зависит от величины q

Возможны случаи:

1 |q|<1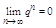

т. е. ряд схд-ся и его сумма 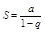2 |q|>1 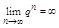и предел суммы так же равен бесконечности

т. е. ряд расходится.

3 при q = 1 получается ряд: а+а+тАж+атАж Sn = n×a 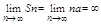ряд расходится

4 при q¹1 ряд имеет вид: а-а+а тАж (-1)^n-1a Sn=0 при n четном, Sn=a при n нечетном предела частных суммы не существует. ряд расходится.

Рассмотрим ряд из бесконечных членов арифметической прогрессии: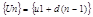 u тАУ первый член, d тАУ разность. Сумма ряда

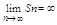при любых u1 и d одновременно ¹ 0 и ряд всегда расходится.

№3

1 Основные св-ва 2ного интеграла

1. Двойной интеграл по области D = площади этой области.

2. Если область G содержится в Д, а ф-ция ограничена и интегрируема в Д, то она интегрируема и в G.

3. Аддитивное св-во. Если область Д при помощи кривой г разбивают на 2 области Д1 и Д2, не имеющих общих внутренних точек, то: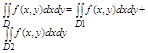

4. константы выносятся за знак интеграла, а сумму в ф-ции можно представить в виде суммы интегралов:

5. Если ф-ции f и g интегрируемы в Д, то их произведение также интегрируемо в Д. Если g(x,y) ¹ 0 то и f/g интегрируема в Д.

6. Если f(x,y) и g(x,y) интегрируемы в Д и всюду в этой области f(x,y) <= g(x,y), то:

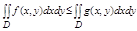
В частности: g(x,y) >=0 то и

7. Оценка абсолютной величины интеграла: если f(x,y) интегрируема в Д, то и |f(x,y)| интегрир. в Д причем

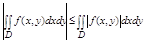
обратное утверждение неверно, итз интегрируемости |f| не следует интегрируемость f.

8. Теорема о среднем значении.

Если ф-ция f(x,y) интегр. в Д., то в этой области найдется такая точка (x, h) Î Д, что:

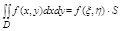(2), где S тАУ площадь фигуры Д. Значение f(x, h) опред по ф-ле (2) наз. средним значением ф-ции f по области Д.

2 С-ва сходящихся рядов

Пусть даны два ряда: u1+u2+тАжun =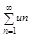(1) и v1+v2+тАжvn = (2)

Произведением ряда (1) на число l Î R наз ряд: lu1+lu2+тАжlun =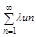(3)

Суммой рядов (1) и (2) наз ряд:

(u1+v1)+(u2+v2)+тАж(un+vn) = 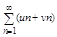(для разности там только - появица)

Т1 Об общем множителе

Если ряд (1) сходится и его сумма = S, то для любого числа l ряд 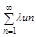=l ×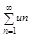 тоже сходится и его сумма SтАЩ = S×l Если ряд (1) расходится и l ¹ 0, то и ряд 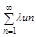тоже расходится. Т. е. общий множитель не влияет на расходимости ряда.

Т2 Если ряды (1) и (2) сходятся, а их суммы = соотв S и SтАЩ, то и ряд: 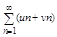тоже сходится и если s его сумма, то s = S+SтАЩ. Т. е. сходящиеся ряды можно почленно складывать и вычитать. Если ряд (1) сходится, а ряд (2) расходится, то их сумма(или разность) тоже расходится. А вот если оба ряда расходятся. то ихняя сумма (или разность)может как расходится (если un=vn) так и сходиться (если un=¹vn)

Для ряда (1) ряд 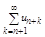называется n тАУ ным остатком ряда. Если нный остаток ряда сходится, то его сумму будем обозначать: r_n =

Т3 Если ряд сходится, то и любой его остаток сходится, если какой либо остаток ряда сходится, то сходится и сам ряд. Причем полная сумма = частичная сумма ряда Sn + r_n

Изменение, а также отбрасывание или добавление конечного числа членов не влияет на сходимость (расходимость) ряда.

№4

1 Сведение

2ного интеграла к повторному

Пусть у1(х), у2(х) непрерывны на отрезке [a, b], у1(х)<= у2(х) на всем отрезке.

D={x,y}: a<=x<=b; y1(x)<=y<=y2(x)

Отрезок [a,b] тАУ проекция Д на ось ох. Для такой области людбая прямая, параллельная оу и проходящая через внутреннюю точку области Д пересекает границу области не более чем в 2 точках. Такая область наз. правильной в направлении оси оу.

Если фция f(x,y) задана на Д и при каждом х Î [a,b] непрерывна на у , на отрезке, [y1(x),y2(x)], то фц-ия F(x) = , наз. интегралом, зависящим от параметра I, а интеграл : , наз повторным интегралом от ф-ции f(x,y) на области Д. Итак, повторный интеграл вычисляется путем последовательного вычисления обычных определенных интегралов сначала по одной., а затем по другой переменной.

2 Необходимый

признак сходимости рядов

Если ряд сходится, то предел его общего члена равен нулю: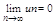

Док-во: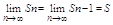

Sn=u1+u2+тАж+un

Sn-1\u1+u2+тАж+un-1

un=Sn-Sn-1, поэтому:

Сей признак является только необходимым, но не является достаточным., т. е. если предел общегоь члена и равен нулю совершенно необязательно чтобы ряд при этом сходился. Следовательно, вот сие условие при его невыполнении является зато достаточным условием расходимости ряда.

№5

1 Замена переменных в двойном интеграле.

Общий случай криволинейных координат

Пусть существует ф-ция f(x,y) интегр на области Д, можно прямолинейные координаты x, y с помощью формул преобразования перейти к криволинейным: x = x(u,v), y=y(u,v), где эти ф-ции непрерывные вместе с частными производными первого порядка, устанавливают взаимно однозначное и в обе стороны непрерывное соответствие между точками плоской области Д и области ДтАЩ и определитель преобразования, наз. Якобианом не обращается в 0: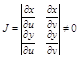если это выполняется можно пользоваться ф-лой:

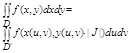
2 Интегральный признак

сходимости ряда. Ряд Дирихле

Т1 Пущай дан рядт 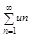(1), члены которого неотрицательны, и не возрастают: u1>=u2>=u3тАж>=un

Если существует ф-ция f(x) неотрицательная, непрерывная и не возрастающая на [1,+¥] такая, что f(n) = Un, " n Î N, то для сходимости ряда (1) необходимо унд достаточно, чтобы сходился несобственный интеграл:, а для расходимости достаточно и необходимо чтобы сей интеграл наоборот расходился (ВАУ!).

Применим сей признак для исследования ряда Дирихле: Вот он: , a Î R Сей ряд называют обобщенным гармоническим рядом, при a >0 общий член оного un=1/n^a à0 и убывает поэтому можно воспользоваться интегральным признаком, функцией здеся будет ф-ция f(x)=1/x^a (x>=1)сия ф-ция удовлетворяет условиям теоремы 1 поэтому сходимость (расходимости) ряда Дирихле равнозначна сходимости расходимости интеграла: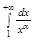

Возможны три случая:

1 a >1,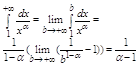

Интеграл а потому и ряд сходится.

2 0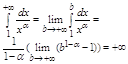

Интеграл и ряд расходится

3 a=1,

Интеграл и ряд расходится

№ 6

1 Двойной интеграл

в полярных координатах

Переход к полярным координатам частный случай замены переменных.

Луч, проходящий из произв точки О имеет на плоскости полярные координаты A(r, j) где r = |ОA| расстояние от О до А полярный радиус. j = угол между векторами ОА и ОР тАУ полярный угол отсчитываемой от полярной оси против часовой стрелки. всегда 0<=r<=+¥, 0<=j <=2p .

Зависимость между прямоугольными и полярными координатами: x = r×cosj , y = r×sinj .

Якобиан преобразования будет равен:

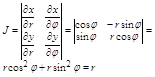И формула при переходе примет вид:

2 Признаки сравнения

Т(Признаки сравнения)

Пущай и ряды с неотрицательными членами и для любого n выполняется нер-во:

un<=vn (1)тогда

1 Если ряд vn сходится, то сходится и ряд un

2 если ряд un расходится, то расходится и ряд vn. Т. е. говоря простыми русскими словами для простых русских людей (ну для дураков вроде тебя): Из сходимости ряда с большими членами следует сходимость ряда с меньшими, а из расходимости ряда с меньшими членами следует расходимости ряда с большими и не наоборот!!!

Причем можно требовать, чтобы неравенство (1) выполнялось не для всех номеров n, а начиная с некоторого n0, т. е. для некоторых номеров меньших n0 неравенство (1) может и не выполняться. При применении сего признака сравнения удобно в качестве ряда сравнения брать ряд Дирихле или геометрический ряд, с которыми и так уже все ясно.

Т3 Засекреченная

Если сущ вышеописанные неотр. ряды, то если сущ предел:

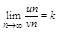(0

№7

1 Вычисление

площади плоской области

с помощью 2ного интеграла

Если Д правильная в направлении оу a<=x<=b, y1(x)<=y<=y2(x), то

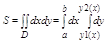
Если Д огр линиями в полярных координатах, то

2 Признаки Даламбера и Коши

Т(Признак Далембера)

Пущай для ряда un с положит членами существует предел:

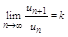, то

1 Если k<1, то ряд сходится

2 Если k>1 ряд расходится

Т(Признак Коши)

Пусть для того же самого ряда (т. е. положительного) существует предел: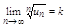, тогда

1 Если k<1, то ряд сходится

2 Если k>1 ряд расходится

А вот если эти все пределы по Коши и дедушке Даламберу равны 1, то о сходимости или расходимости ряда ничего сказать низзя. Вот низзя и все тут. Вот.

№8

1 Вычисление объема

с помощью 2ного интеграла

Рассматривая в пространстве тело Р, огр снизу плоскостью оху, сверху z = f(x,y), кот проектируется в Д, сбоку границей области Д, называемое криволинейным цилиндром. Объем этого тела вычисляют по формуле: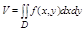

если f(x,y)<=0 в Д тор тело находится под плоскостью оху. Его объем равен объему цилиндрического тела. огр сверху ф-цией:

z = |f(x,y)|>=0.

тогда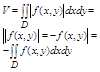

если в Д ф-ция меняет знак, то область разбивается на 2. Область Д1, f(x,y)>=0; Д2, f(x,y)<=0, тогда:

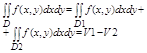
2 Знакочередующиеся ряды. Признак Лейбница.

Ряд называется знакочередующимся если каждая пара соседних членов имеет разные знаки (один ♀, другой ♂), если считать каждый член сего ряда положительным то его можно записать в виде: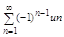

Т (Признак Лейбница)

Если для знакочередующегося ряды выполняются условия:

1) u1>=u2>=u3тАж>=un>=un+1тАж

2)

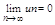
то ряд сходится, а его сумма и остаток rn удовлетворяют неравенствам: 0<=S<=un и |r_n|<=un+1

Ряд удовлетворяющий условиям теоремы наз. рядом Лейбница.

Если условие чередования знаков выполняется не с первого члена, а с какого-нибудь исчо, то при существовании равного 0 предела ряд будет также сходится.

№9

1 Вычисление

площади поверхности

с помощью двойного интеграла.

Пусть дана кривая поверхность Р, заданная ур-ями z = f(x,y) и имеющая границу Г, проецирующуюся на плоскость оху в область Д. Если в этой области ф-ция f×(x,y) непрерывна и имеет непрерывные частные производные: тогда площадь поверхности Р вычисляется:

для ф-ций вида x = m (y,z) или y = j(x,z) там будут тока букыв в частных производных менятца ну и dxdy.

2 Знакопеременные ряды.

Абсолютная и условная

сходимость рядов.

Ряд называют знакопеременным, если его членами являются действительные числа, а знаки его членов могут меняться как кому в голову взбредет. Пусть дан ряд:

u1+u2тАж+un=(1), где un тАУ может быть как положительным, так и отрицательным. Рассмотрим ряд состоящий из абсолютных значений этого ряда:

|u1|+|u2|тАж+|un|=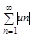(2),

Если сходится ряд (2), то ряд (1) называют абсолютно сходящимся, а вот если ряд (1) сходится, а ряд (2) расходится. то ряд (1) наз сходящимся условно.

Т. Признак абсолютной сходимости:

Если знакочередующийся ряд сходится условно. то он и просто так сходится, при этом:

<=

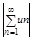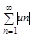
Доквы:

т. к. 0<=|un|+un<=2|un|, то по признаку сравнения сходится ряд |un|+un, тогда сходится ряд: (|un|+un)-|un|=un. Далее, т. к. по св-ву абсолютной величины |Sn|=|u1+u2+тАж+un|<=|un| " n Î N, то переходя к пределу получим:

<=

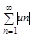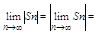
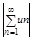
Т2 Если ряд (1) абсолютно сходится, то и любой ряд составленный из тех же членов, но в любом другом порядке тоже абсолютно сходится и его сумма равна сумме ряда un тАУ Sn. А вот с условно сходящимися рядами все гораздо запущенней.

Т(Римана)

Если знакопеременный ряд с действительными членами сходится условно, то каким бы ни было дейст. число S можно так переставить члены ряда, что его сумма станет равна S, т. е. сумма неабсолютно сходящегося ряда зависит от порядка слагаемых

№10

1 Вычисление массы,

координат центра масс,

моментов инерции плоской

материальной пластины с

помощью 2ного интеграла.

Масса плоской пластины вычисляется по ф-ле:

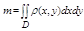, где r(х, у) тАУ поверхностная плотность.

Координаты центра масс выч по ф-ле:

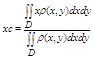
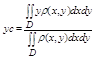
если пластина однородная, т. е. r(х, у) тАУ const, то ф-лы упрощаются:

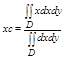
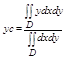
Статические моменты плоскостей фигуры Д относит осей оу и ох

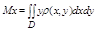
Момент инерции плоской пластины относительно осей ох, оу, начала координат:

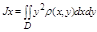
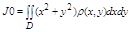
J0=Jx+Jy

если пластина однородная, то ро вышвыривается на фиг и считается равной 1.

2 Сходимость функциональных последовательностей и рядов

Функциональной последовательностью заданной на множестве Е, наз. последовательность ф-ций {fn(x)} (1)определенных на Е и принимающих числовые действительные значения.

Пусть задана поледовательность числовых ф-ций {un(x)} Формальнг написанную сумму: 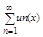(2) называют функциональным рядом на множестве Е, а ф-цию un(x) тАУ его членами. Аналогично случаю числовых рядов сумма: Sn(x) = u1(x)+u2(x)+тАж+un(x) называется частичной суммой ряда n порядка, а ряд: un+1? un+2тАж - его n-ным остатком. при каждом фиксированном х = х0 Î Е получим из (1) числовую последовательность {fn(x0)}, а из (2) тАУ числовой ряд, которые могут сходится или расходится. если кто-нибудь из оных сходится, то сходится и функциональная посл (1) в т х0, и сия точка наз. точкой сходимости.

Если посл(1) сход на м-ж Е, то ф-ция f, определенная при " x Î E f(x) = 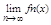назывется пределом посл (1), если ряд(2) сходится на м-ж Е, то ф-ция S(x) определенная при " x Î Е равенством

S(x)=

называется суммой ряда (2).

Остаток ряда сходится только когда на этом же м-ж сходится сам ряд., если обозначить сумму остатка ряда через r_n(ч), то S(x) = Sn(x)+r_n(x)

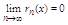Если ряд (2) сходится абсолютно, то он наз абсолютно сходящимся на м-ж Е. Множество всех точек сходимости функционального ряда наз областью сходимости. Для определения области сходимости можно использовать признак Даламбера и Коши. С ихнею помашшю ф-ц ряд исследуется на абсолютную сходимость Например, если существует

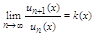и

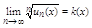, то ряд (2) абсолютно сходится при k(x)<1 и расходится при k(x)>1.

№11

1 Тройные интегралы

Пусть на некоторой ограниченной замкнутой области V трехмерного пространства задана ограниченная ф-ция f (x,y,z). Разобьем область V на n произвольных частичных областей, не имеющих общих внутренних точек, с объемами DV1тАж DVn В каждой частичной области возбмем произв. точку М с кооорд Mi(xi,hi,ci) составим сумму: 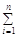f(xi,hi,ci)×DVi, кот наз интегральной суммой для ф-ции f(x,y,z). Обозначим за l максимальный диаметр частичной области. Если интегральная сумма при l à 0 имеет конечный предел, то сей предел и называется тройным интегралом от ф-ции f(x,y,z) по области V И обозначается:

2 Равномерная

сходимость функциональных

последовательностей и рядов.

Признак Вейерштрасса.

Ф-циональную последовательность {fn)x)} x Î E наз. равномерно сходящейся ф-цией f на м-ж Е, если для Î e >0, сущ номер N, такой, что для " т х Î E и " n >N выполняется ¹-во: |fn(x)-f(x)|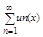

наз. равномерно сходящимся рядом, если на м-ж Е равномерно сходится последовательность его частичной суммы. , т. ен. равномерная сходимость ряда означает:Sn(x) à f(x) Не всякий сходящийся ряд является равномерно сходящимся, но всякий равномерно сходящийся тАУ есть сходящийся (не, вот это наверное лет 500 выдумывали.)

Т. (Признак Вейерштрасса равномерной сходимости ряда)

Если числовой ряд: (7),

где a >=0 сходится и для " x Î E и " n = 1,2тАж если выполняется нер-во |un(x)|<=an(8), ряд 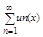(9) наз абсолютно и равномерно сходящимся на м-ж Е.

Док-вы:

Абсолютная сходимость в каждой т. х следует из неравенства (8) и сходимости ряда (7). Пусть S(x) тАУ сумма ряда (9), а Sn(x) тАУ его частичная сумма.

Зафиксируем произвольное e >0 В силу сходимости ряда (7) сущ. номера N, " n >N и вып. нерво

Следовательно: |S(x)-Sn(x)| =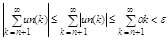

Это означает, что Sn(x) à S(x) что означает равномерную сходимость ряда.

№12

1 Замена переменных

в тройном интеграле.

Если ограниченная замкнутая область пространства V = f(x,y,z) взаимно однозначно отображается на область VтАЩ пространства = (u,v,w) Если непрерывно дифференцируемы функции: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) и существует якобиан

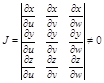
то справедлива формула:

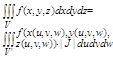
При переходе к цилиндрическим координатам, с вязанными с x,y,z формулами: x=rcosj, y=rsinj, z=z (0<=r<=+¥, 0<=j <= 2p, -¥<=z<=+¥)

Якобиан преобразования:

И поэтому в цилиндрических координатах переход осуществляется так:

При переходе к сферическим координатам: r? j q, связанными с z,y,z формулами x=rsinq×cosj,

y=r sinqsinj, z=rcosq.

(0<=r<=+¥, 0<=j <= 2p,

0<=q <=2p)

Якобиан преобразования:

Т. е. |J|=r²×sinq.

Итак, в сферических координатах сие будет:

2 Свойства равномерно

сходящихся рядов

Т1 Если ф-ция un(x), где х Î Е непрерывна в т. х0 Î E и ряд 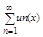(1) равномерно сходится на Е, то его сумма S(x) = 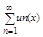также непрерывна в т. х0.

Т2 (Об поюленном интегрировании ряда)

Пусть сущ. ф-ция un(x) Î R и непрерывная на отр. [a,b] и ряд 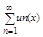(3) равномерно сходится на этом отрезке, тогда какова бы ни была т. х0 Î [a, b] 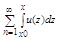(4) тоже равномерно сходится на [a,b]. В частности: при x0 = a, х = b: т. е. ряд (3) можно почленно интегрировать.

Т3 (о почленном дифференцировании ряда)

Пусть сущ. ф-ция un(x) Î R и непрерывная на отр. [a,b] и ряд её производных 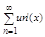(6) равномерно сходящийся на отр [a,b] тогда, если ряд 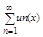сходится хотя бы в одной точке x0 Î [a,b] то он сходится равномерно на всем отрезке [a,b], его сумма S(x) = 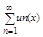является непрерывно дифференцируемой ф-цией и

SтАЩ(x)= 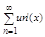(9)

В силу ф-л ы (8) последнее равенство можно записать:

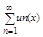()тАЩ =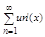

So ряд (7) можно почленно дифференцировать

№13

1 Приложения

тройных интегралов

Объем тела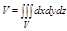

Масса тела: 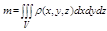, где r(М) = r(x,y,z) - плотность.

Моменты инерции тела относительно осей координат:

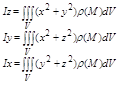
Момент инерции относительно начала координат:

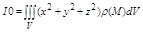
Координаты центра масс:

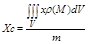
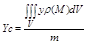
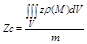m тАУ масса.

Интегралы, стоящие в числителях выражают статические моменты тела: Myz, Mxz, Mxy относит коорд плоскостей oyz, oxz, oxy. Если тело однородное: r(М) = const, то из формул она убирается и оне упрощаются как в 2ных интегралах.

2 Степенные ряды. Теорема Абеля

Степенным рядом наз функциональный ряд вида: a₀+a₁x+a₂x²+тАж + a_nxⁿ = 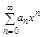(1) x Î R членами которого являются степенные ф-ции. Числа an Î R, наз коэффициентами ряда(1). Степенным рядом наз также ряд:

a₀+a₁(x-x0)+a₂(x-x0)²тАж + a_n(x-x0)ⁿ = 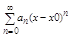(2)

Степенной ряд (1) сходится абсолютно по крайней мере в т. х = 0, а ряд (2) в т х = х0, т .е в этих случаях все лены кроме 1 равны 0. Ряд (2) сводится к ряду (1) по ф-ле у = х-х0.

Т Абеля

1Если степенной ряд (1) сходится в т. х0 ¹ 0, то он сходится абсолютно при любом х, для которого |x|<|x0|.

2Если степеннгой ряд (1) расходится в т. х0, то он расходится в любой т. х, для которой |x|>|x0|

№14

1 Определение криволинейных

интегралов 1 и 2 рода

Криволинейный интеграл по длине дуги (1 рода)

Пусть ф-ция f(x,y) определена и непрерывна в точках дуги АВ гладкой кривой К. Произвольно разобъем дугу на n элементарных дуг точками t0.tn пусть Dlk длина k частной дуги. Возьмем на каждой элементарной дуге произвольную точку N(xk,hk) и умножив сию точку на соотв. длину дуги составим три интегральную суммы:

d1 =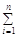 f(xk,hk)×Dlk

d2 =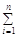 Р(xk,hk)×Dхk

d3 =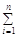 Q(xk,hk)×Dyk,

где Dхk = x_k-x_k-1, Dyk = y_k-y_k-1

Криволинейным интегралом 1 рода по длине дуги будет называться предел интегральной суммы d1 при условии, что max(Dlk) à 0

Если предел интегральной суммы d2 или d3 при l à 0, то этот предел наз. криволинейным интегралом 2 рода, функции P(x,y) или Q(x,y) по кривой l = AB и обозначается:

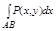или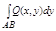

сумму: 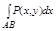+ 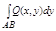принято называть общим криволинейным интегралом 2 рода и обозначать символом:

в этом случае ф-ции f(x,y), P(x,y), Q(x,y) тАУ называются интегрируемыми вдоль кривой l = AB. Сама кривая l наз контуром или путем интегрирования А тАУ начальной, В тАУ конечной точками интегрирования, dl тАУ дифференциал длины дуги, поэтому криволинейный интеграл 1 рода наз. криволинейным интегралом по дуге кривой, а второго рода тАУ по функции.

Из определения криволинейных интегралов следует, что интегралы 1 рода не зависят от того в каком направлении от А и В или от В и А пробегается кривая l. Криволинейный интеграл 1 рода по АВ:

, для криволинейных интегралов 2 рода изменение направления пробегания кривой ведет к изменению знака:

В случае, когда l тАУ замкнутая кривая т. е. т. В совпадает с т. А, то из двух возможных направлений обхода замкнутого контура l называют положительным то направление, при котором область лежащая внутри контура остается слева по отношению к ??? совершающей обход, т. е. направление движения против часовой стрелки. Противоположное направление обхода наз тАУ отрицательным. Криволинейный интеграл АВ по замкнутому контуру l пробегаемому в положит направлении будем обозначать символом:

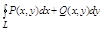
Для пространственной кривой аналогично вводятся 1 интеграл 1 рода:

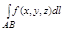и три интеграла 2 рода:

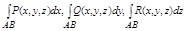
сумму трех последних интегралов наз. общим криволинейным интегралом 2 рода.

2 Радиус сходимости и интервал сходимости степенного ряда.

Рассмотрим степенной ряд:

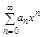(1) Число (конечное или бесконечное) R>=0 наз радиусом сходимости ряда (1) если для любого х такого, что |x|R ряд расходится Интервал на числовой оси состоящий из т. х для которых |x|

Т1 Для всякого степенного ряда (1) существует радиус сходимости R 0<=R<=+¥ при этом, если |x|

Если вместо х взять у = х-х0, то получится: интервал сходимости: |x-x0

Т2 Если для степенного ряда (1) существует предел (конечный или бесконечный): 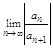, то радиус сходимости будет равен этому пределу.

Док-вы: Рассмотрим ряд из абсолютных величин и по Даламберу исследуем его на сходимость:

(5)

1)Рассмотрим случай, когда 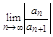конечен и отличен от 0. Обозначив его через R запишем (5) в виде 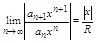При числовом значении х степенной ряд становится числовым рядом, поэтому по Даламберу ряд (1) сходится если |x|/R<1, т. е. |x|

2)Пусть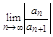 = ¥ тогда из(5) следует, что для любого х Î R Итак ряд (1) сходится при любом х причем абсолютно.

3) Пусть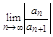 =0 тогда из (5) следует, что 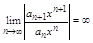и ряд расходится для любого х. Он сходится только при х = 0 В этом сл-е R = 0.

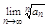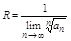Т3 Если существует предел конечный или бесконечный , то (10)

№15

1 условия

существования и вычисления

криволинейных интегралов.

Кривая L наз. гладкой, если ф-ции j(t), y(t) из определяющих её параметрических уравнений:

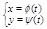(1)

имеет на отрезке [a,b] непрерывные производные: jтАЩ(t), yтАЩ(t).Точки кривой L наз особыми точками, если они соответствуют значению параметра t Î [a,b] для которых (jтАЩ(t))²+(yтАЩ(t))² = 0 т. е. обе производные обращаются в 0. Те точки для которых сие условие не выполняется наз. обычными (ВАУ!).

Если кривая L=AB задана ф-лами (1), является гладкой и нет имеет обычных точек, а ф-ции f(x,y), P(x,y), Q(x,y) непрерывны вдоль этой кривой, то криволинейные интегралы всех видов существуют (можно даже ихние формулы нарисовать для наглядности) и могут быть вычислены по следующим формулам сводящим эти интегралы к обычным:

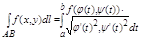
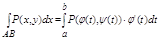
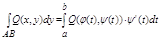
Отседова жа вытекаает штаа:

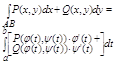
В частности, если кривая АВ задана уравнением y = y(x), a<=x<=b , где у(х) непрерывно дифференцируемая ф-ция, то принимая х за параметр t получим:

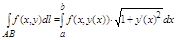
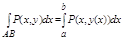
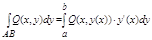
ну и сумма там тожжа упростица.

ну и наоборот тожжа так будит, если х = х(у)

Если АВ задана в криволинейных координатах a <= j <= b где ф-ция r(j) непрерывно дифференцируема на отрезке [a, b] то имеет место частный случай, где в качестве параметра выступает полярный угол j. x = r(j)×cos(j),

y= r(j)×sin(j).

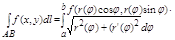
и у второго рода так же.

Прямая L наз кусочно-гладкой, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую. В этом случает криволинейные интегралы по этой кривое определяются как сумма криволинейных интегралов по гладким кривым составляющим сию кусочно-гладкую кривую. все выше сказанное справедливо и для пространственной кривой (с буквой зю).

2 Свойства степенных рядов

Т1 Если степенной ряд 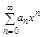(1) имеет радиус сходимости R>0, то на любом отрезке действительной оси вида |x|<=r, 0

Для ряда 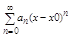отрезком равномерной сходимости будет отрезок |x-x0|<=r или ([x0-r,x0+r])

Т2 На любом отрезке |x-x0|<=r сумма степенного ряда является непрерывной ф-цией.

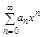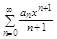Т3 Радиусы сходимости R, R1, R2 соответственно рядов× (5), (6), 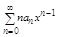(7) равны: R1=R2=R3. Итак ряды (6) и (7) полученные с помощью формального интегрирования и дифференцирования имеют те же радиусы сходимости, что и исходный ряд.

Пусть ф-ция f(x) является суммой степенного ряда 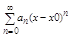(9)

Т4 Дифференцирование степенного ряда

Если ф-ция f(x) на интервале (x0-R, x0+R) является суммой ряда (9), то она дифференцируема на этом интервале и её производная fтАЩ(x) находится дифференцированием ряда (9):

fтАЩ(x)= 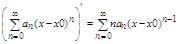При этом радиус сходимости полученного ряда = R

Т5 О интегрировании степенного ряда

Степенной ряд (9) можно почленно интегрировать на любом отрезке целиком принадлежащем интервалу сходимости при этом полученный степенной ряд имеет тот же радиус сходимости что и исходный ряд.

Последовательное применение Т4 приводит к утверждению, что ф-ция f имеет на интервале сходимости производные всех порядков, которые могут быть найдены из ряда (9) почленным дифференцированием. При интегрировании и дифференцировании степенного ряда внутри интервала сходимости радиус сходимости R не меняется, однако на концах интервала может изменяться.

№16

1 Свойства

криволинейных интегралов

Св-ва криволинейных интегралов 1 рода:

1.Константа выносится за знак интеграла, а интеграл суммы можно представить в виде суммы интегралов:

2. Если дуга АВ состоит из двух дуг Ас и Св не имеющих общих внутренних точек и если для ф-ции f(x,y) сущ криволинейный интеграл по АВ, то для для сей ф-ции сущ криволинейные интегралы по АС и по ВС причем:

3.

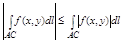
4.Ф-ла среднего значения

если ф-ция f(x,y) непрерывна вдоль кривой АВ, то на этой кривой найдется точка М, такая, что:

, где l тАУ длина кривой

Криволинейный интеграл 2 рода обладает всеми свойствами интегралов 1 рода, и исчо при изменении направления прохождения кривой он меняет знак. .И вапще все сказанное выше справедливо и для пространственной кривой (этта та которая с буквой зю)

2 Разложение ф-ций в степенные ряды. Ряды Тейлора и Маклорена.

Пусть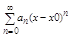(1) сходится при |x-x0|(2) В этом случае говорят, что ф-ция f(x) разложена в степенной ряд. (1) .

Т1 Если ф-ция f распространяется в некоторой окрестности т. х0 f(x)= 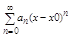, то

и справедлива формула: (15) Если в некоторой окрестности заданной точки ф-ция распадается в степенной ряд, то это разложение единственно.

Пусть дествит. ф-ция f определена в некоторой окрестности т. х0 и имеет в этой точке производные всех порядков, тогда ряд: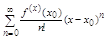(6) наз рядом Тейлора ф-ции f в т, х0

При х0=0 ряд Тейлора принимает вид:

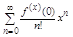(6тАЩ) и называется ряд Маклорена.

Ряд Тейлора может:

1 Расходится всюду, кроме х=х0

2 Сходится, но не к исходной ф-ции f(x), а к какой-нибудь другой.

3 Сходится к исходной ф-ции f(x)

Бесконечная дифференцируемость ф-ции f(x) в какой-то т. х0 является необходимым условием разложимости ф-ции в ряд Тейлора, но не является достаточным. Для введения дополнительных условий треб. ф-ла Тейлора.

Т2 Если ф-ция f(x) (n+1) раз дифференцируема на интервале (x0-h, x0+h) h>0, то для всех x Î (x0-h, x0+h) имеет место ф-ла Тейлора:

где остаток r_n(x) можно записать:

(8)

(9) Формула (8) наз остаточным членом ф-лы Тейлора в интегральной форме. Ф-ла (9) тАУ формулой Лагранжа.

Преобразуя ф-лу Тейлора при х0 = 0 получаем ф-лу Маклорена.

Т3 Если ф-ция f(x) имеет в окрестности т х0 производные любого порядка и все они ограниченны одним и тем же числом С, т е " x Î U(x0) |f⁽ⁿ⁾(x)|<=C, то ряд Тейлора этой ф-ции сходится в ф-ции f(x) для всех х из этой окрестности.

№17

1 Формула Грина

Сия очень полезная в сельском хозяйстве формула устанавливает связь между криволинейными и двойными интегралами.

Пусть имеется некоторая правильная замкнутая область Д, ограниченная контуром L и пущая ф-ции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными: в данной области. тогда имеет место ф-ла:

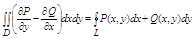
И вот вся эта фигулина и есть формула Грина.

Контур L определяющий область д может быть задан показательными уравнениями х = х1(у), х=х2(у) с<=y<=d x1(y)<=x2(y) или

y = y1(x), y=y2(x) a<=x<=b y1(x)<=y2(x).

Рассмотрим область Д ограниченную неравенствами: a<=x<=b и y1(x)<=y2(x). и преобразуем двойной интеграл 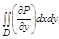к криволинейным для чего сведем его к повторному и ф-ле Невтона-Лыебница выполним интегрирование по у и получим:

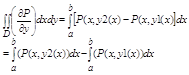каждый из 2 определенны

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Cпособы преобразования комплексного чертежа, применение при изображении предметов