Методы обучения математике в 10 -11 класах
РОЗДРЖЛ 2
Використання методiв навчання при вивченнi деяких змiстових лiнiй курсу алгебри i початкiв аналiзу. „Елементарнi функцii”, “Похiдна та ii застосування”
Вз1. ПОЯСНЮВАЛЬНО-РЖЛЮСТРАТИВНИЙ МЕТОД
Пояснювально-iлюстративний метод можна використовувати на будь-якому уроцi, а не лише при поясненнi нового, складного матерiалу. Цей метод сприяi розвитку просторового уявлення i через наочнiсть покращуi розумiння матерiалу. Розглянемо застосування методу при вивченнi понять “Парнi та непарнi функцii”.
Розглянемо функцii, область визначення яких симетрична вiдносно початку координат.
Означення. Функцiя 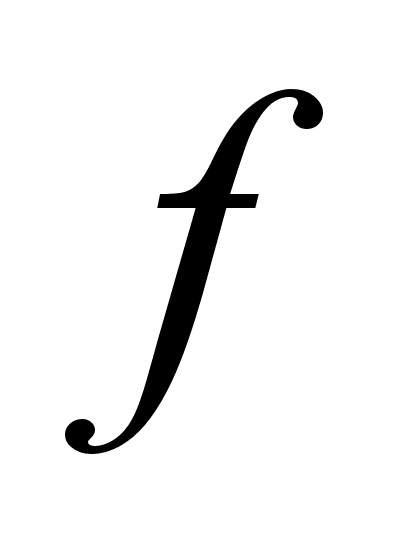 називаiться парною, якщо для довiльного
називаiться парною, якщо для довiльного 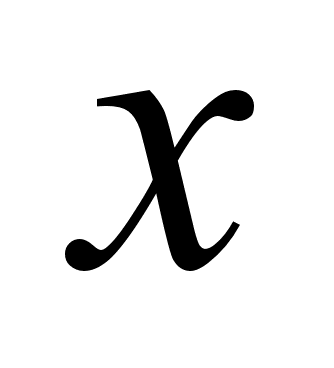 з ii областi визначення
з ii областi визначення 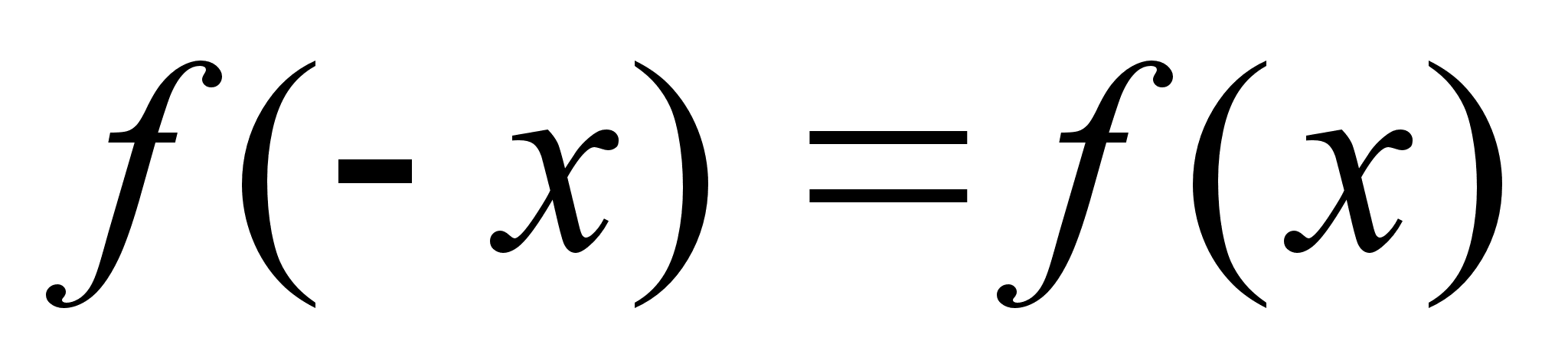 .
.
Вчитель пояснюi, що для довiльних значень х , додатних чи вiд’iмних, знак самоi функцii не змiнюiться.
Означення. Функцiя 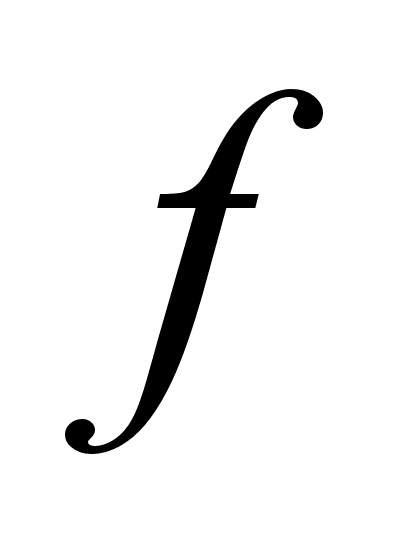 називаiться непарною, якщо для довiльного
називаiться непарною, якщо для довiльного 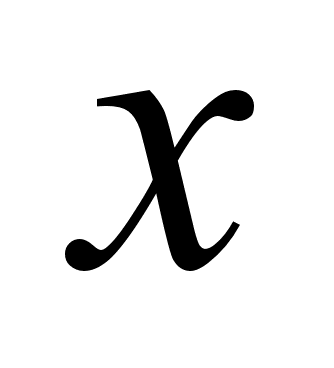 з ii областi визначення
з ii областi визначення 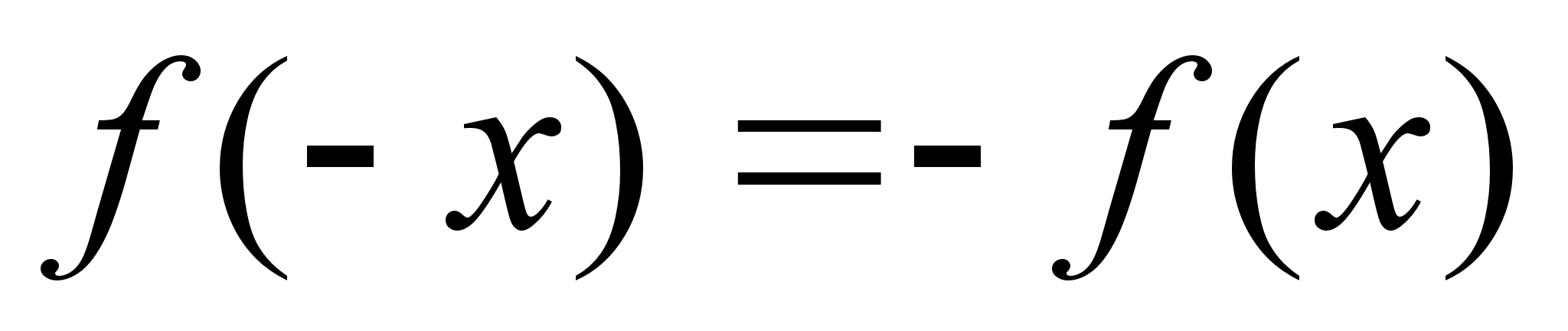 .
.
Тобто для довiльних значень х , знак функцii залежить вiд знаку аргументу.
Д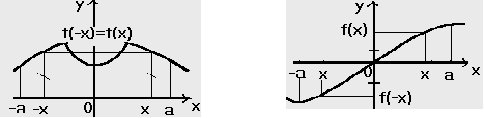
ля закрiплення розумiння понять, на дошцi малюються вiдповiднi малюнки, чи демонструються готовi намальованi на плакатi.
Мал. 1 Мал. 2
Пiсля цього наводять приклад парних та непарних функцiй.
 - парнi
- парнi  тАУ непарнi.
тАУ непарнi.
Дiйсно, область визначення кожноi з них симетрична вiдносно початку координат, та виконуються рiвностi: f(-x) = f(-x)2n= f(x)2n= f(x) тАУ парнiсть, та для g(-x)=g(-x)2n+1= тАУg(x)2n+1= тАУg(x) тАУ непарнiсть.
Г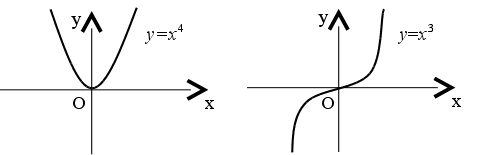 рафiки цих функцiй варто продемонструвати на плакатi чи намалювати на дошцi. Розглянемо функцii у=х4 та у=х3.
рафiки цих функцiй варто продемонструвати на плакатi чи намалювати на дошцi. Розглянемо функцii у=х4 та у=х3.
Мал. 3 Мал. 4
Пiсля побудови графiкiв функцiй потрiбно акцентувати увагу учнiв на те, що вiтки графiка парноi функцii симетричнi вiдносно осi ординат, а вiтки графiка непарноi функцii симетричнi вiдносно початку координат. Це варто довести до учнiв як властивостi парноi та непарноi функцii, що допоможе iм при побудовi графiкiв.
При поясненнi нового, дещо складнiшого матерiалу варто користуватись наочнiстю, це найкраще вiдображаi саму суть теми, всi процеси, пов’язанi з утворенням певних понять. Розглянемо використання наочностi та iлюстрацiй при вивченнi теми “Похiдна та ii застосування” при дослiдженнi функцiй на екстремуми.
Учнi вже вивчили i знають геометричний змiст похiдноi, ознаки зростання i спадання функцii, тому просто варто пригадати це на початку урока.
Геометричний змiст похiдноi: Похiдна функцii f(x) в точцi х0 дорiвнюi тангенсу кута нахилу дотичноi до кривоi з додатним напрямом осi ОХ у точцi з абсцисою х0.
Тому, коли f(x)0, то учням потрiбно пояснити, що  - тангенс кута нахилу дотичноi до кривоi з додатнiм напрямком осi ОХ бiльший нуля, тобто
- тангенс кута нахилу дотичноi до кривоi з додатнiм напрямком осi ОХ бiльший нуля, тобто 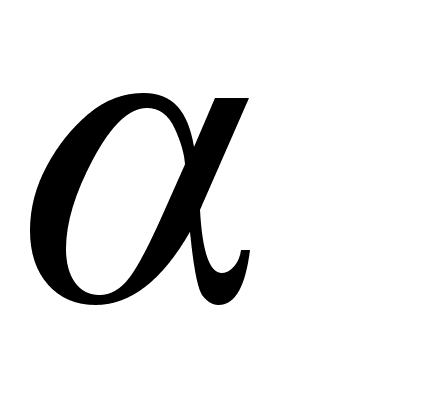 (0;
(0; 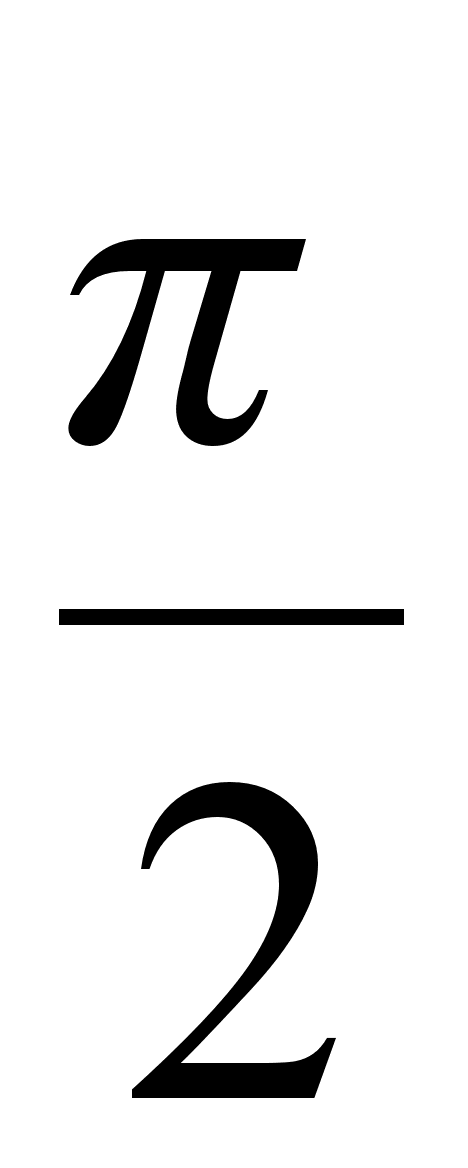 ). Продемонструiмо це на малюнку (мал. 5).
). Продемонструiмо це на малюнку (мал. 5).
З малюнку видно, що на промiжку а; дотична може займати положення, при якому кут 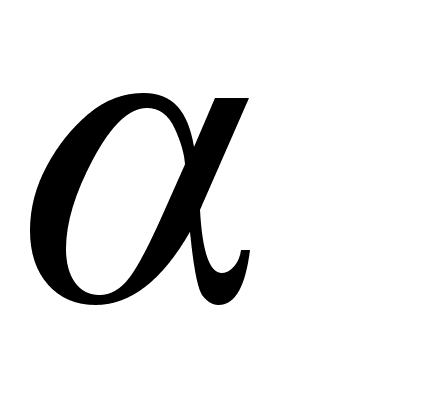 (0;
(0; 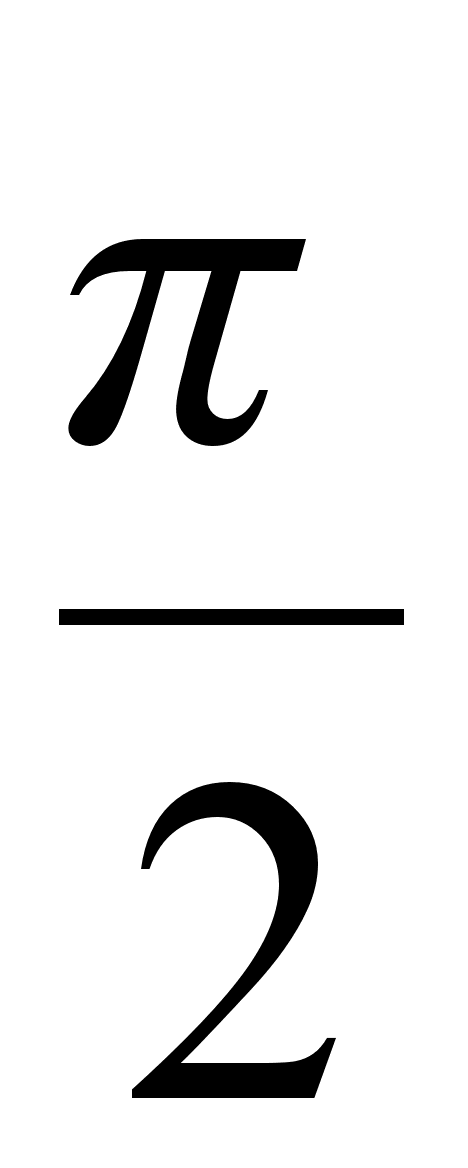 ) i функцiя на цьому промiжку зростаi.
) i функцiя на цьому промiжку зростаi.
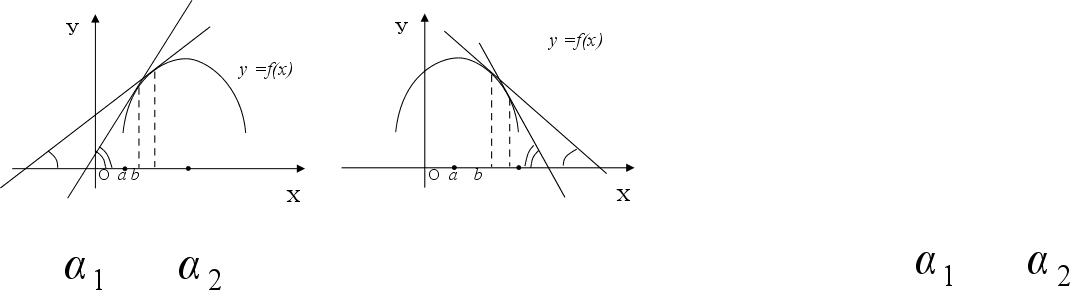
Мал. 5 Мал. 6
Якщо ж f(x)0, то tg(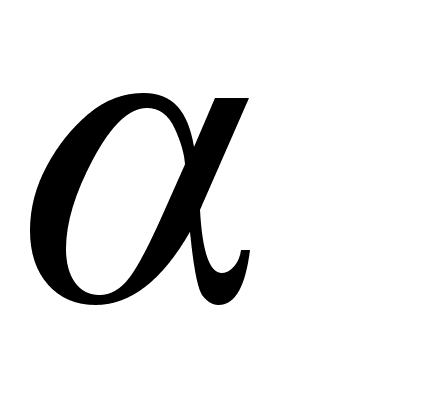 )0,
)0, 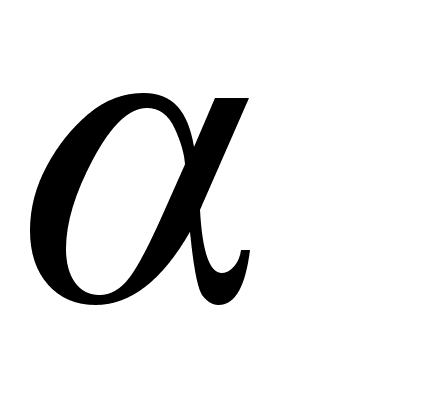 (0; тАУ
(0; тАУ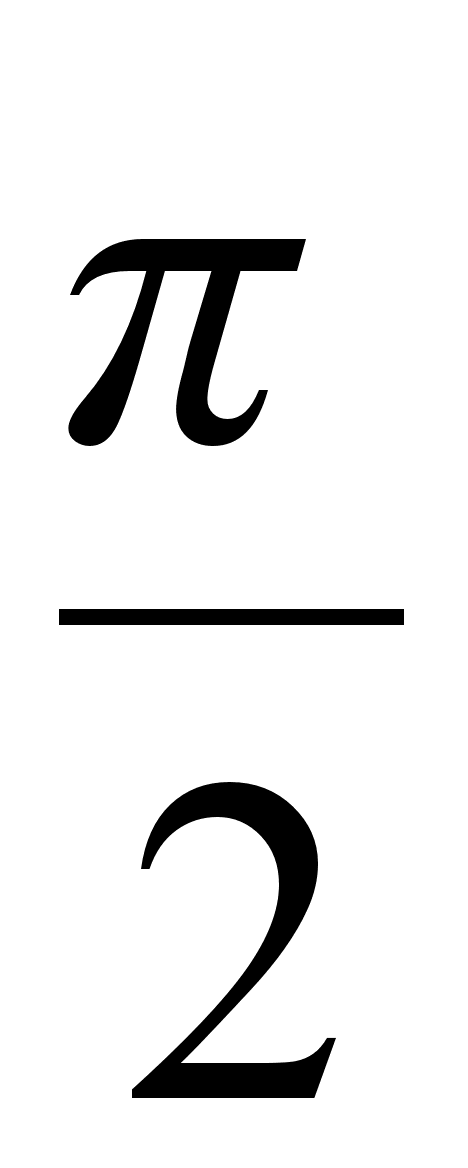 ) , значить функцiя спадаi. Показуiмо це на малюнку (мал. 6).
) , значить функцiя спадаi. Показуiмо це на малюнку (мал. 6).
В першому випадку функцiя f(x) i зростаючою на промiжку а; , в другому - спадною. Потрiбно спитати учнiв, а яким же чином веде себе функцiя, коли f(x) при переходi через деяку точку х0 змiнюi свiй знак.
Це буваi лише тодi, коли в точцi х0 функцiя приймаi своi найбiльше або найменше значення. Якщо похiдна змiнюi свiй знак з “+” на “-” (спочатку функцiя зростала, а при переходi через точку х0 почала спадати), то х0- i точкою максимуму, значення функцii в цiй точцi i максимумом функцii. РЖнакше, якщо при переходi через точку х0 похiдна змiнила свiй знак з “-” на “+”, то х0 - i точкою мiнiмума, а значення функцii в цiй точцi тАУ мiнiмумом функцii. Цi точки називають екстремальними точками функцii.
Внутрiшнi точки областi визначення функцii, в яких ii похiдна дорiвнюi нулю або не iснуi називають критичними точками цiii функцii.
Формулюiться необхiдна умова екстремуму.
Якщо функцiя  у внутрiшнiй точцi
у внутрiшнiй точцi  промiжку
промiжку 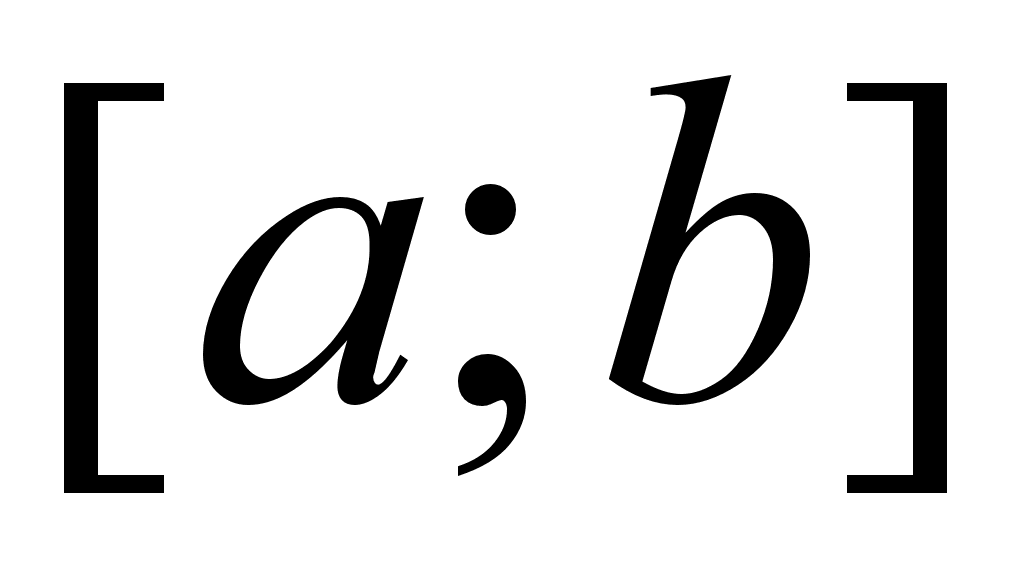 маi екстремум, то в цiй точцi похiдна
маi екстремум, то в цiй точцi похiдна 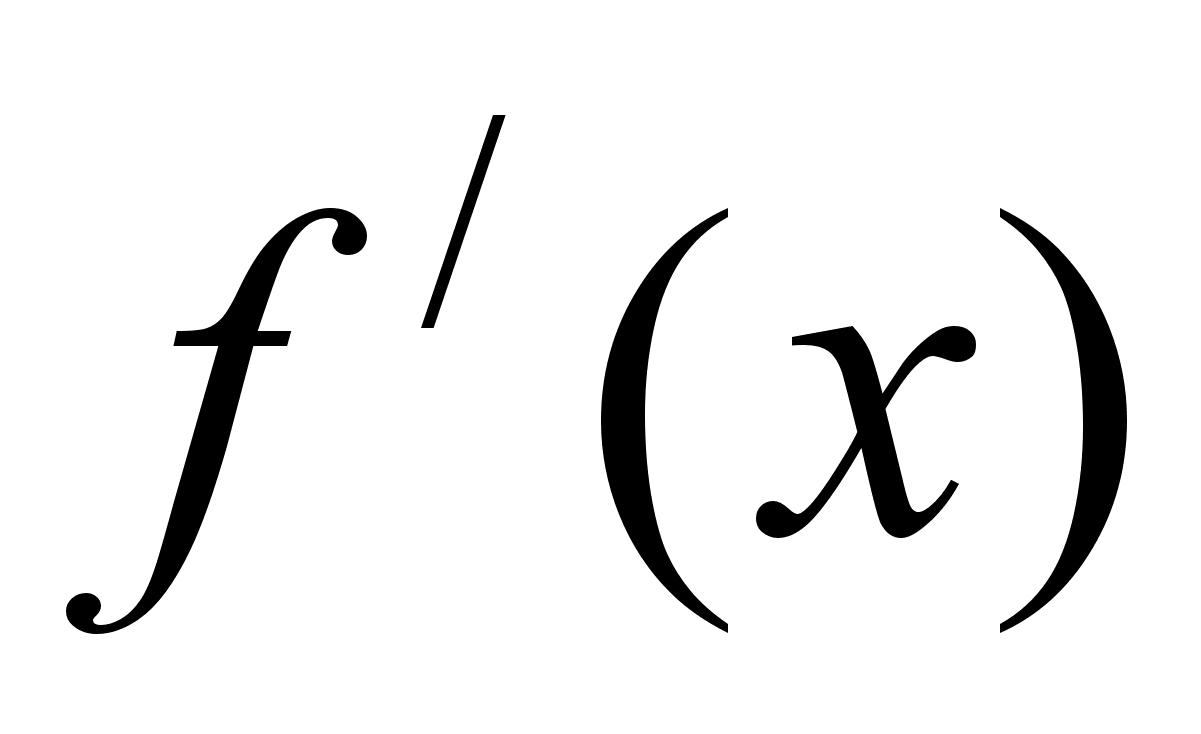 , якщо вона iснуi , дорiвнюi нулю f/ (х0)=0.
, якщо вона iснуi , дорiвнюi нулю f/ (х0)=0.
Доведемо методом вiд супротивного. Нехай в точцi  , яка i екстремальною для
, яка i екстремальною для  , iснуi похiдна
, iснуi похiдна 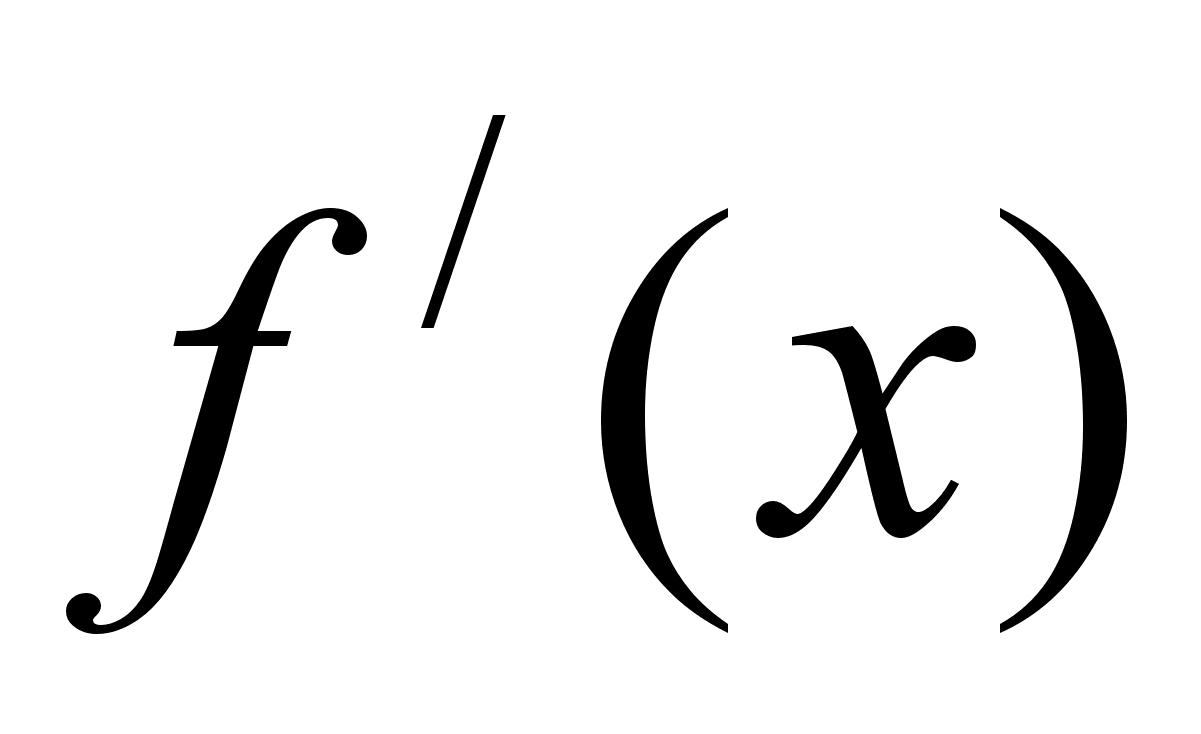 i
i  . Припустимо, що
. Припустимо, що 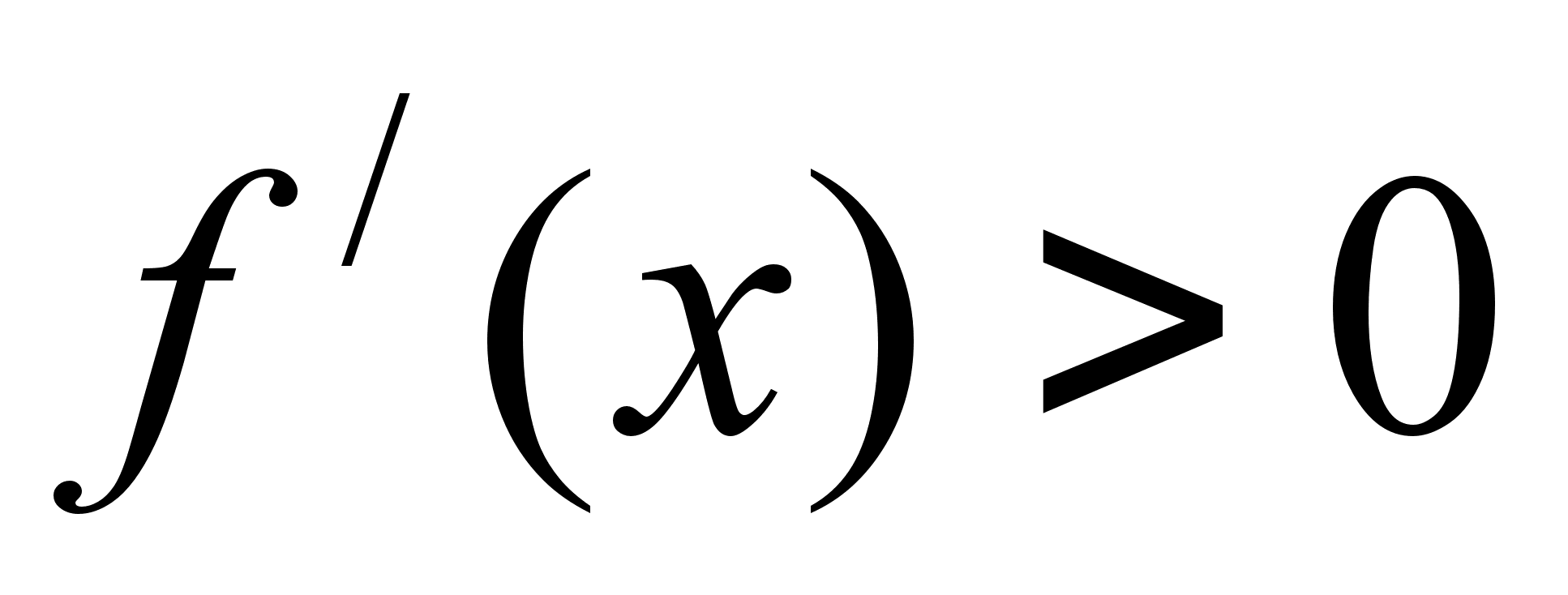 , значить функцiя
, значить функцiя  в точцi
в точцi  зростаi. Отже
зростаi. Отже  не i екстремальною точкою. Якщо
не i екстремальною точкою. Якщо 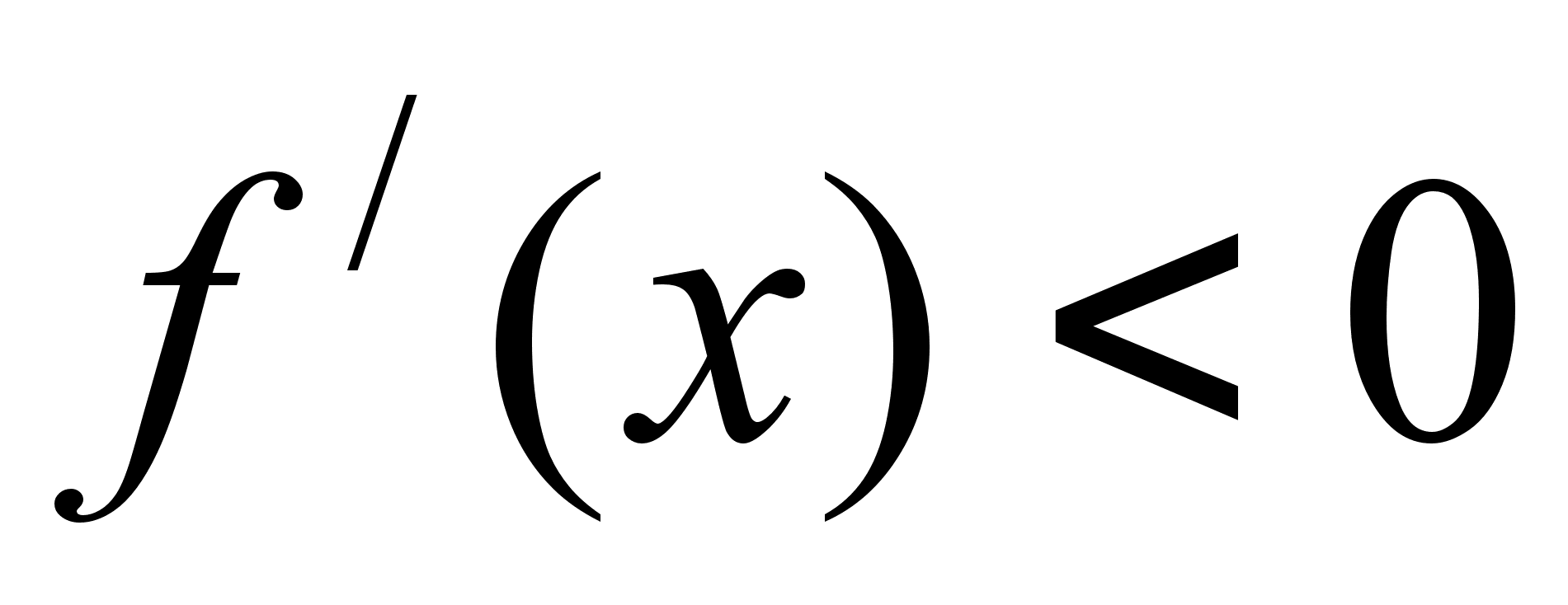 , то функцiя
, то функцiя  в точцi
в точцi  спадаi. Отже прийшли до суперечностi. Тобто теорему доведено.
спадаi. Отже прийшли до суперечностi. Тобто теорему доведено.
А ле з того, що похiдна функцii
ле з того, що похiдна функцii  в точцi
в точцi  рiвна нулю, не обов’язково слiдуi , що
рiвна нулю, не обов’язково слiдуi , що  i точкою екстремуму.
i точкою екстремуму.
Наприклад, похiдна функцii 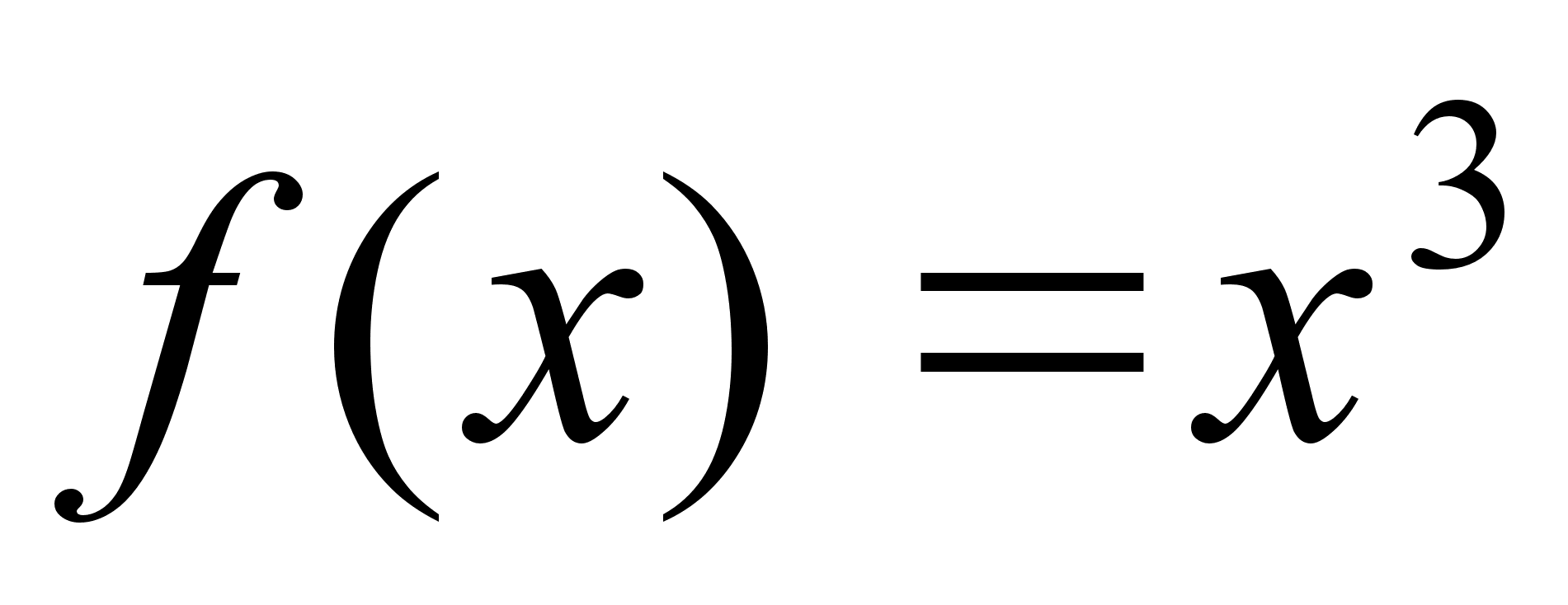 рiвна нулю в точцi
рiвна нулю в точцi 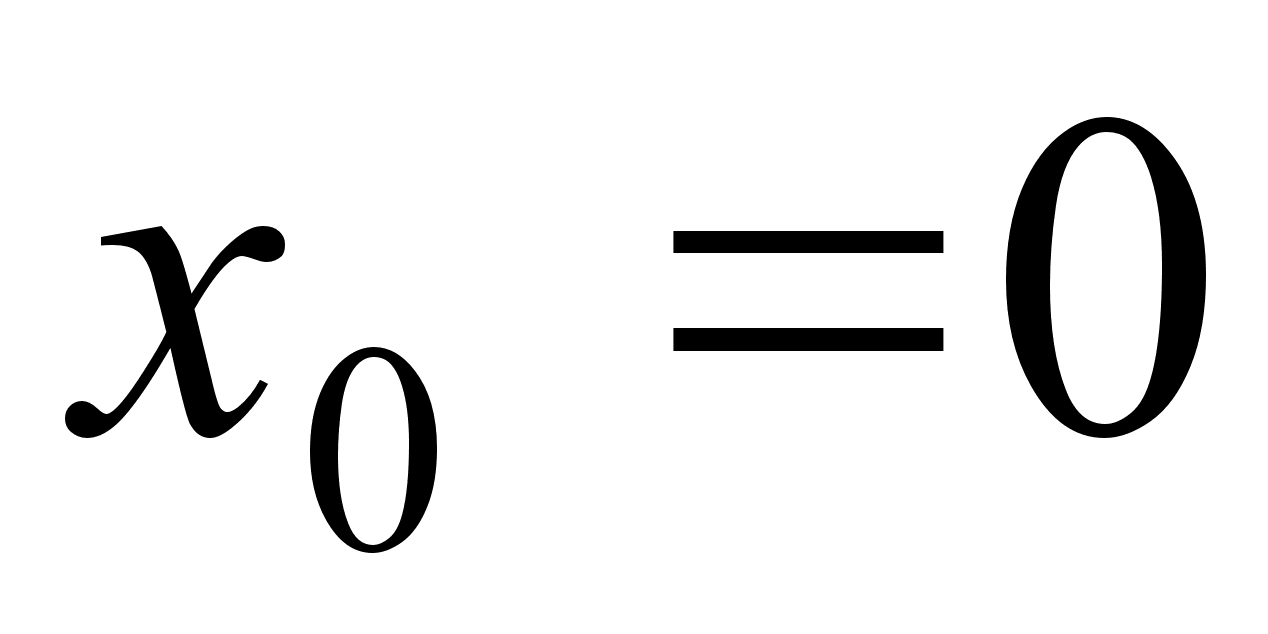 , але функцiя екстремуму в цiй точцi не маi.
, але функцiя екстремуму в цiй точцi не маi.
Внутрiшня точка  промiжку
промiжку 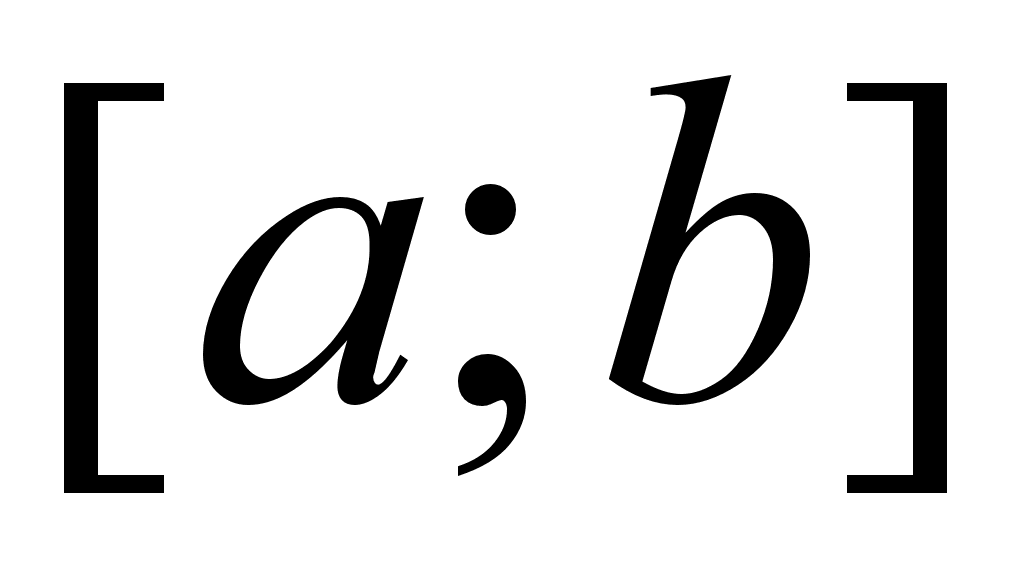 називаiться стацiонарною точкою функцii
називаiться стацiонарною точкою функцii  , якщо в цiй точцi
, якщо в цiй точцi 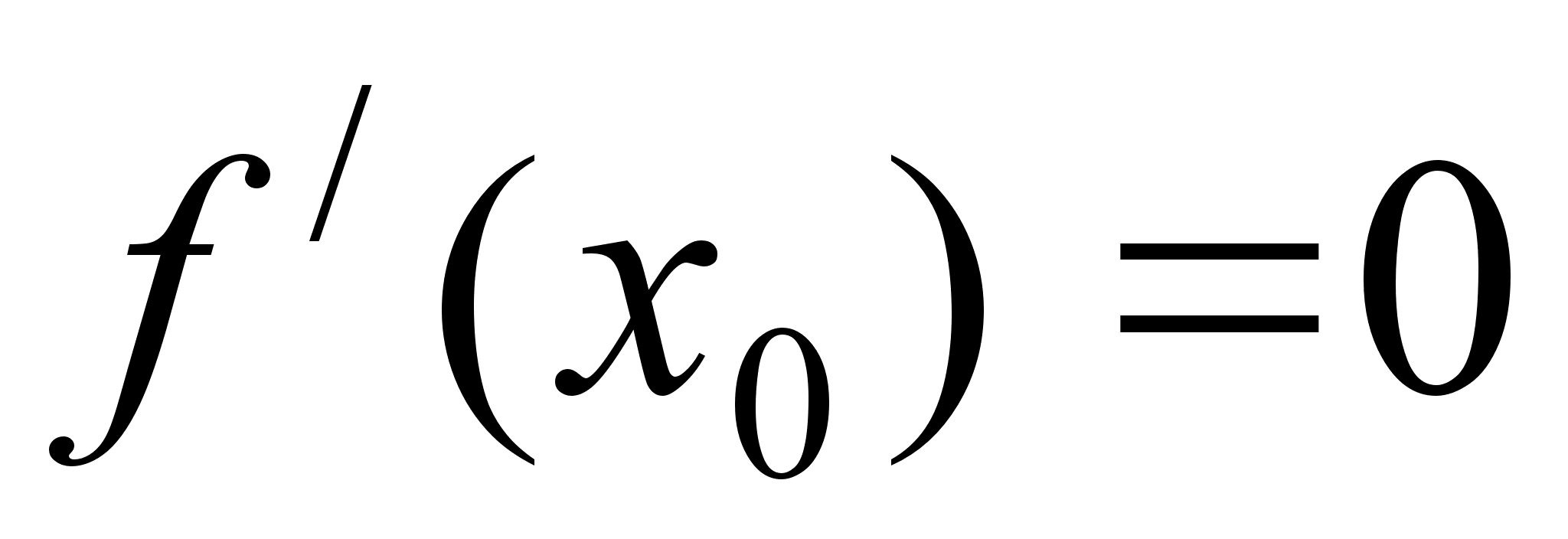 .
.
Розглянемо критичнi точки, похiдна в яких не iснуi. Наприклад точка 0 для функцii  не i критичною, бо не внутрiшня точка областi визначення функцii.
не i критичною, бо не внутрiшня точка областi визначення функцii.
Приклад. Розглянемо функцiю  , ця функцiя не маi похiдноi в точцi 0. Значить точка 0 тАУ критична, та ще й функцiя в точцi 0 маi мiнiмальне значення (0 - точка мiнiмуму). Далi розглядаються ознаки максимуму i мiнiмуму функцii.
, ця функцiя не маi похiдноi в точцi 0. Значить точка 0 тАУ критична, та ще й функцiя в точцi 0 маi мiнiмальне значення (0 - точка мiнiмуму). Далi розглядаються ознаки максимуму i мiнiмуму функцii.
Вз2. РЕПРОДУКТИВНИЙ МЕТОД
Розглянемо застосування цього методу при вивченнi теми “Застосування похiдноi до дослiдження функцii”.
Так як репродуктивний метод використовують найчастiше для закрiплення вивченого теоретичного матерiалу, то вчителю можна користуватися цим методом не лише по закiнченню пояснення новоi теми, а навiть i пiсля кожноi порцii викладеноi iнформацii.
Учням пояснюють, як дослiджуiться деяка функцiя, показують схему дослiдження, а в кiнцi дослiдження будують графiк. Це робить вчитель на дошцi, дослiджуючи функцiю f1(x), заносячи результати кожного кроку дослiдження до таблицi.
Потiм учням пропонуiться дослiдити деяку функцiю самостiйно i побудувати ii графiк. Учнi, або один учень бiля дошки, самостiйно, або з допомогою вчителя, виконують такi самi дослiдження для функцii f2(x), а данi дослiджень заносять до тiii ж таблицi на дошцi, але в другий, порожнiй стовпець.
| Властивiсть функцii |
|
| |
| 1. | Область визначення Область значень | (-; -1)(-1;1)(1;) (-; ) | (-;0)(0;) (-; |
| 2. | Парнiсть | Непарна: f(-x)= тАУ f(x) | Нi парна, |
| 3. | Перiодичнiсть | Неперiодична | Неперiодична |
| 4. | Точки перетину графiка з вiссю OX з вiссю OY | (0;0) (0;0) | х = 2 |
| 5. | Промiжки зростання: | (-; (-1;0)(0;1)(1; | (0;4) (-;0)(4;) |
| 6. | Точки: |
|
|
| 7. |
|
|
нема |
Потiм учнi самостiйно будують графiк другоi функцii (мал. 9*).
Пiсля пояснення вчителем теоретичного матерiалу i наведення декiлькох прикладiв дослiдження функцii учнi вже самi дослiджують i будують графiки функцiй.

Мал. 9 Мал. 9*
Вз3. ПРОБЛЕМНИЙ ВИКЛАД
При вивченнi теми “Застосування похiдноi в фiзицi та технiцi” урок починаiться з пригадування того, яким чином визначаiться швидкiсть руху в курсi фiзики. Розглянемо випадок, коли матерiальна точка рухаiться по координатнiй прямiй, i задано закон руху цiii точки, тобто координата х цiii точки i вiдома функцiя  часу
часу 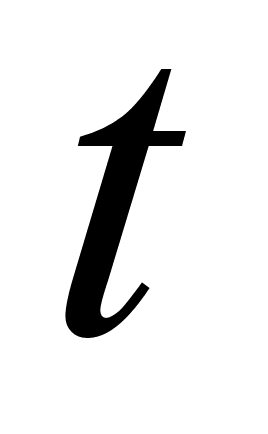 . За момент часу вiд
. За момент часу вiд 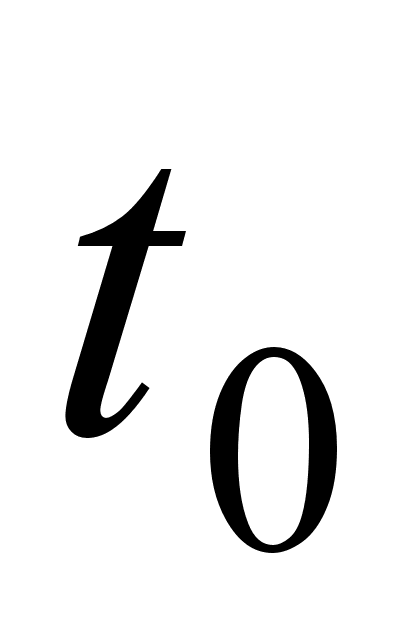 до
до 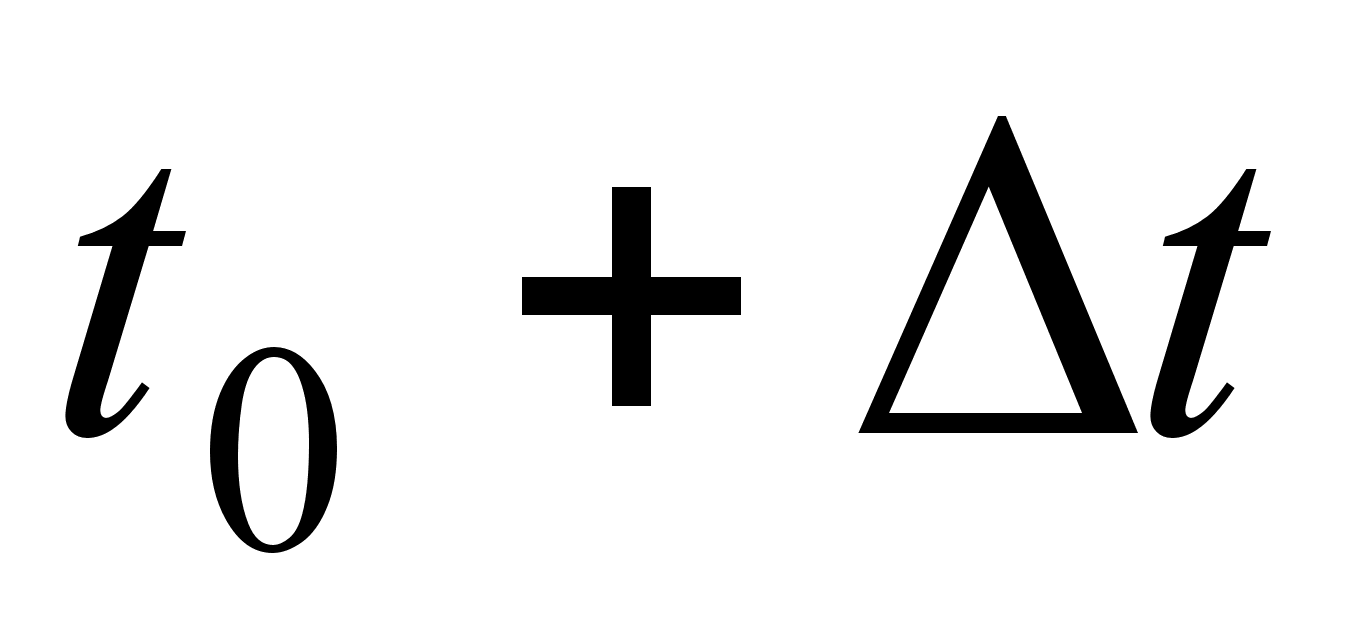 перемiщення точки можемо записати як
перемiщення точки можемо записати як 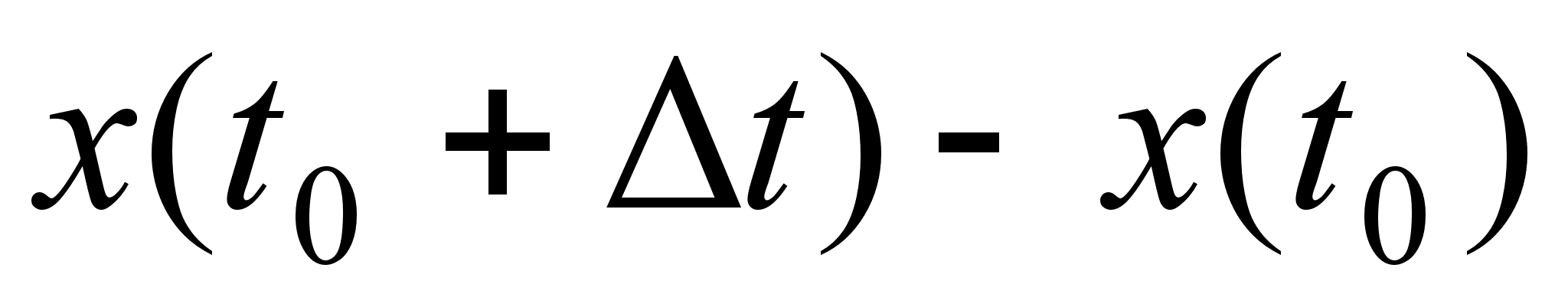 = =
= = , а середня швидкiсть руху точки
, а середня швидкiсть руху точки 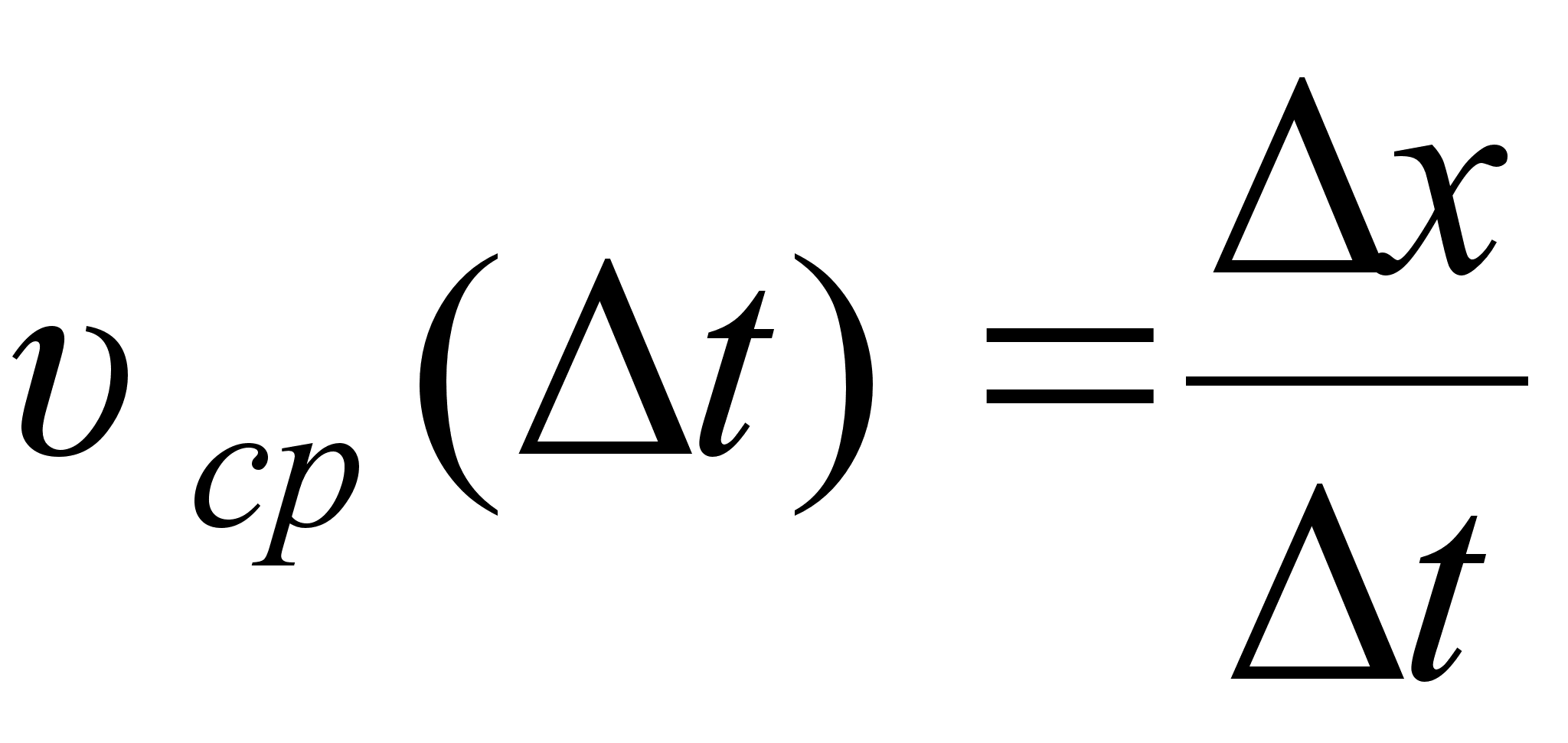 .
.
При  значення середньоi швидкостi прямуi до конкретного значення, яке називають миттiвою швидкiстю
значення середньоi швидкостi прямуi до конкретного значення, яке називають миттiвою швидкiстю 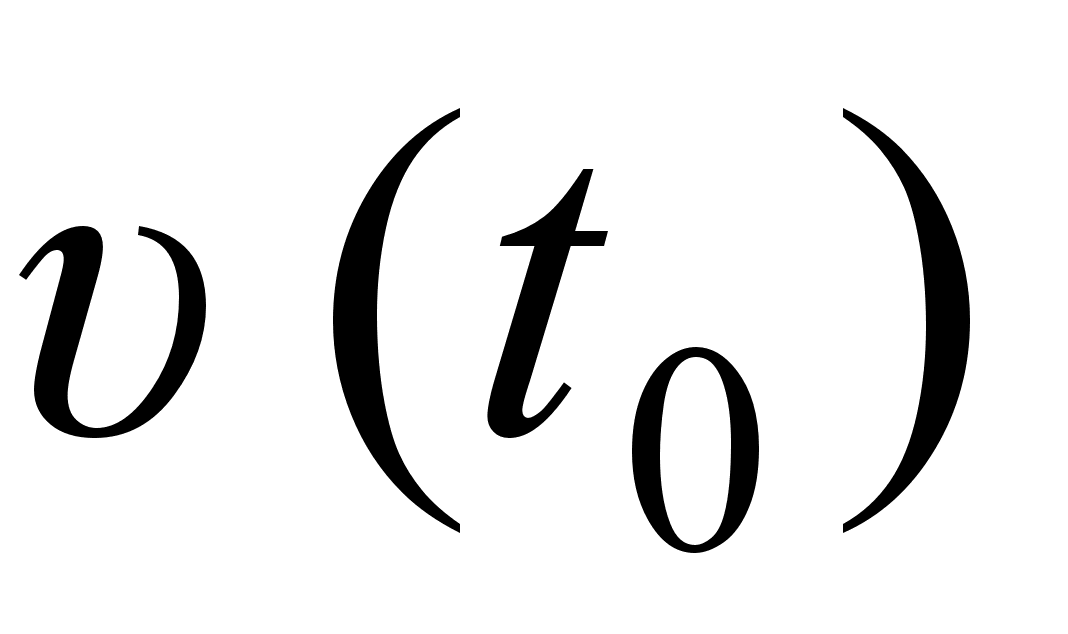 матерiальноi точки в момент часу
матерiальноi точки в момент часу 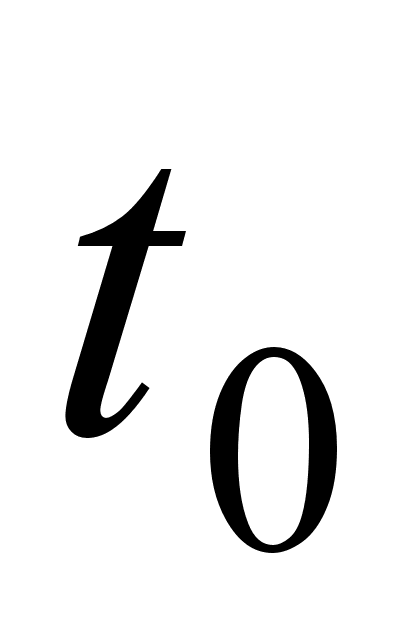 . Тобто
. Тобто 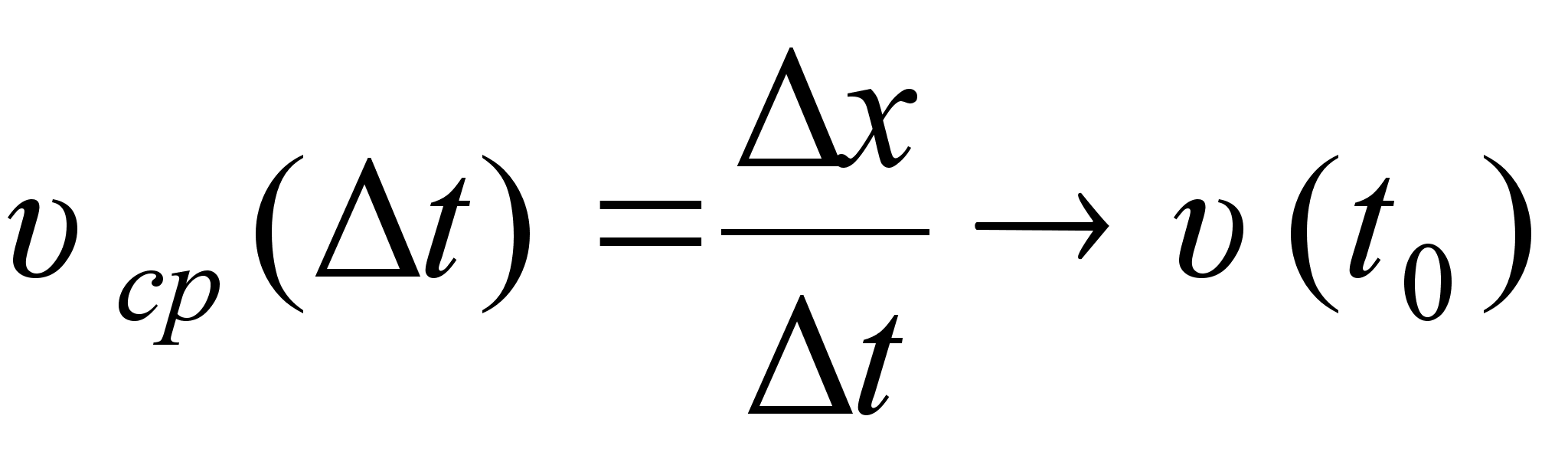 при
при  .
.
За означенням похiдноi  при
при  .
.
Вважають, що миттiва швидкiсть  визначена тiльки для диференцiйованоi функцii
визначена тiльки для диференцiйованоi функцii  , тому
, тому 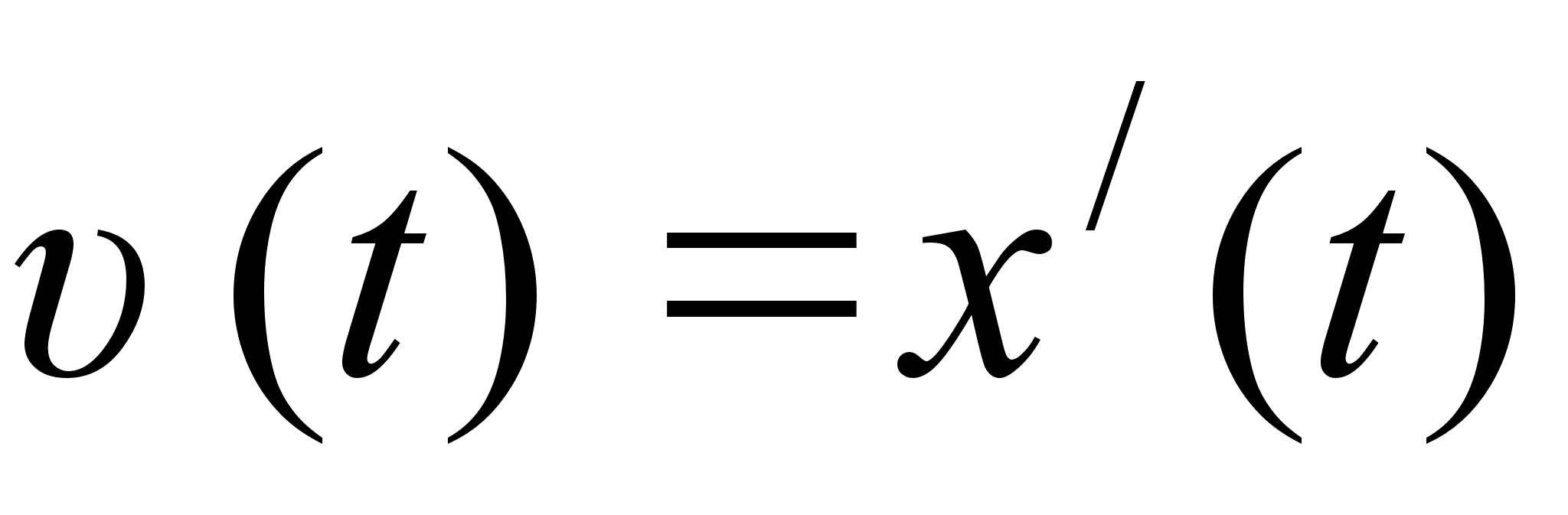 .
.
Скорочено це говорять наступним чином: похiдна вiд координати за часом i швидкiсть. Це механiчний змiст похiдноi. Миттiва швидкiсть може приймати довiльнi значення.
Аналогiчно кажуть про змiну швидкостi: похiдна вiд швидкостi за часом i прискорення.  .
.
Тепер розглядаються приклади.
Приклад 1. Розглянемо вiльне падiння матерiальноi точки.
З фiзики вiдомо, що при вертикальному падiннi рух тiла задаiться формулою 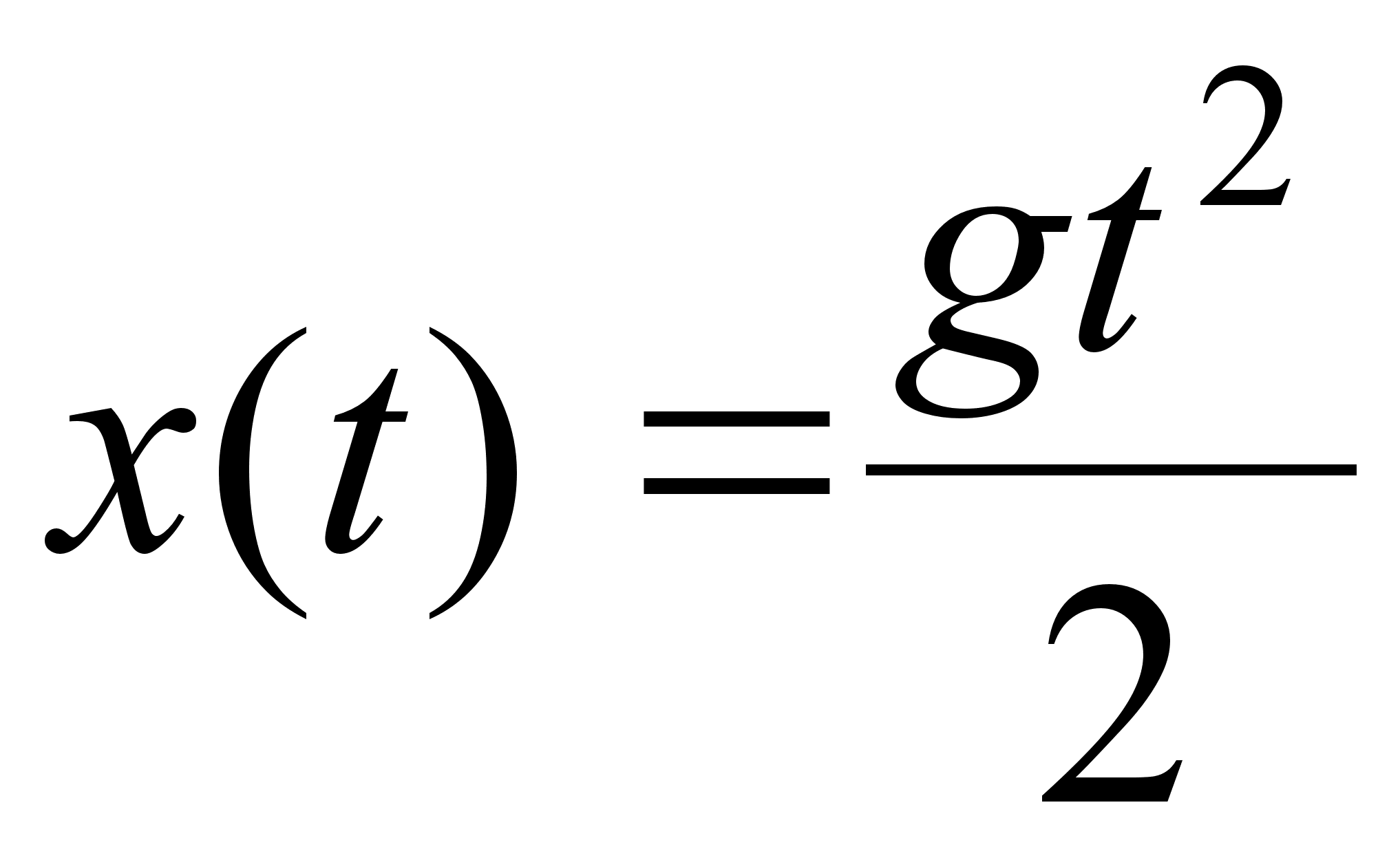 . Вiдшукаiмо швидкiсть падiння точки в момент часу
. Вiдшукаiмо швидкiсть падiння точки в момент часу 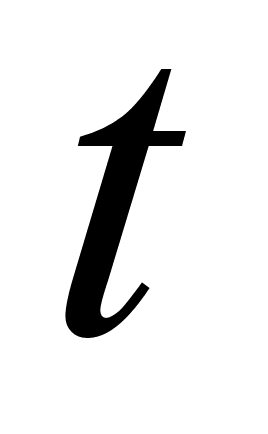 :
: 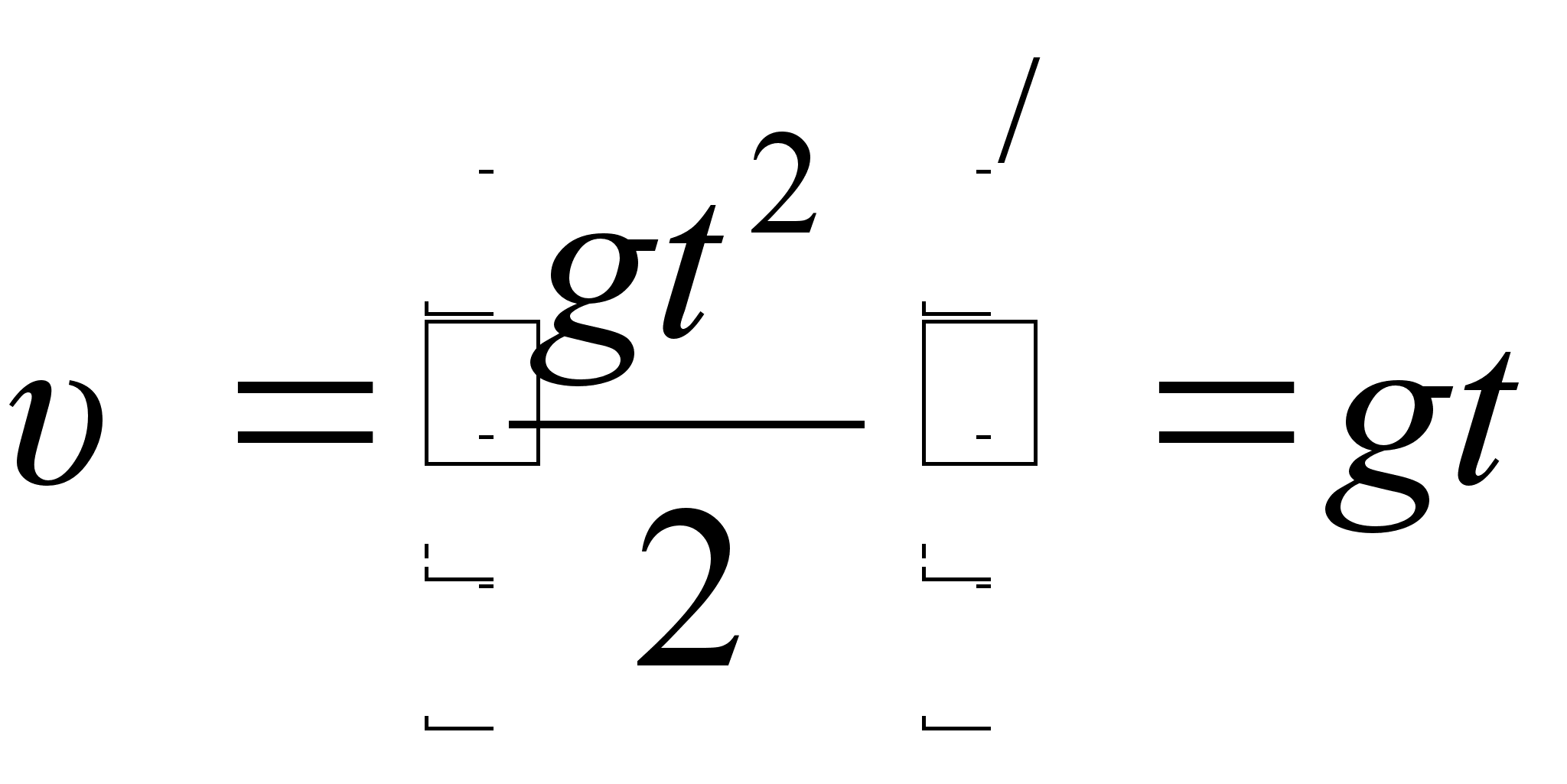 . Вiдшукаiмо прискорення падiння точки:
. Вiдшукаiмо прискорення падiння точки:  , прискорення i величина постiйна.
, прискорення i величина постiйна.
Приклад 2.Нехай залежнiсть координати точки, що рухаiться по прямiй, вiд часу виражена формулою: 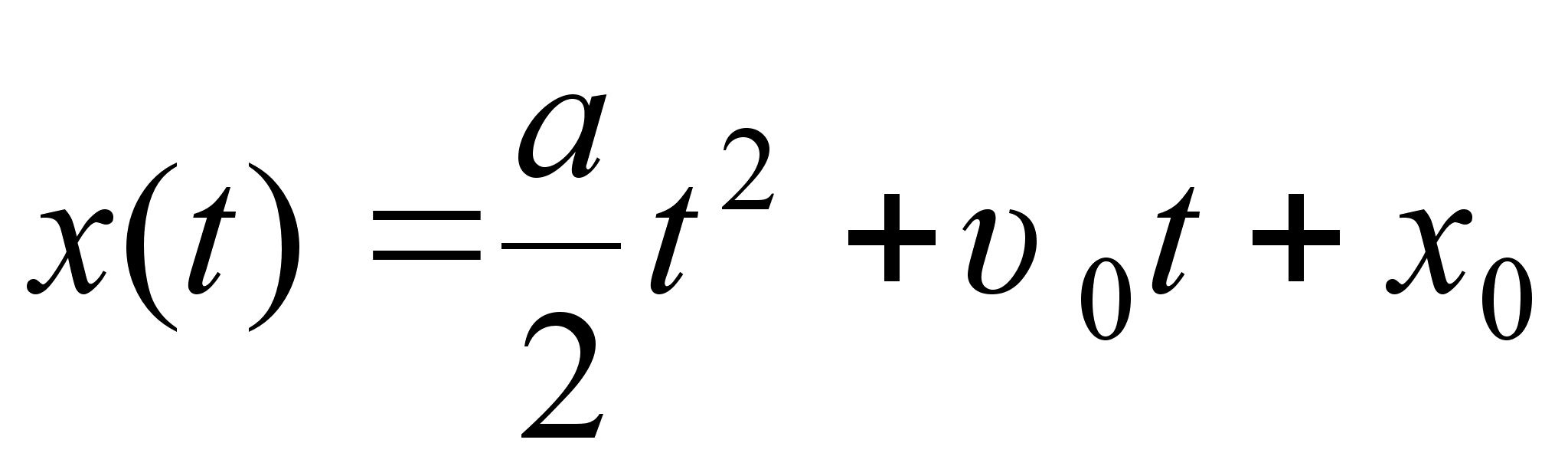 , де
, де 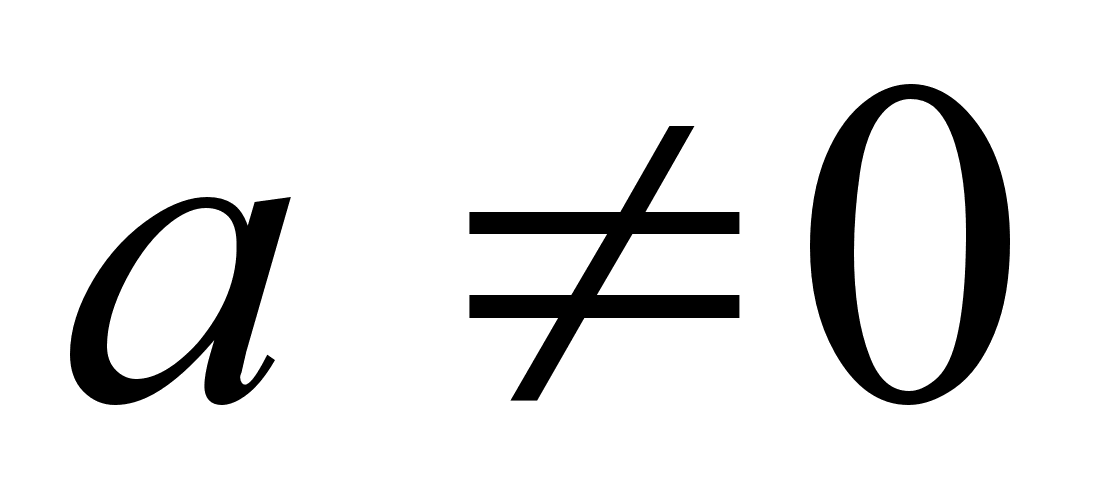 ,
, 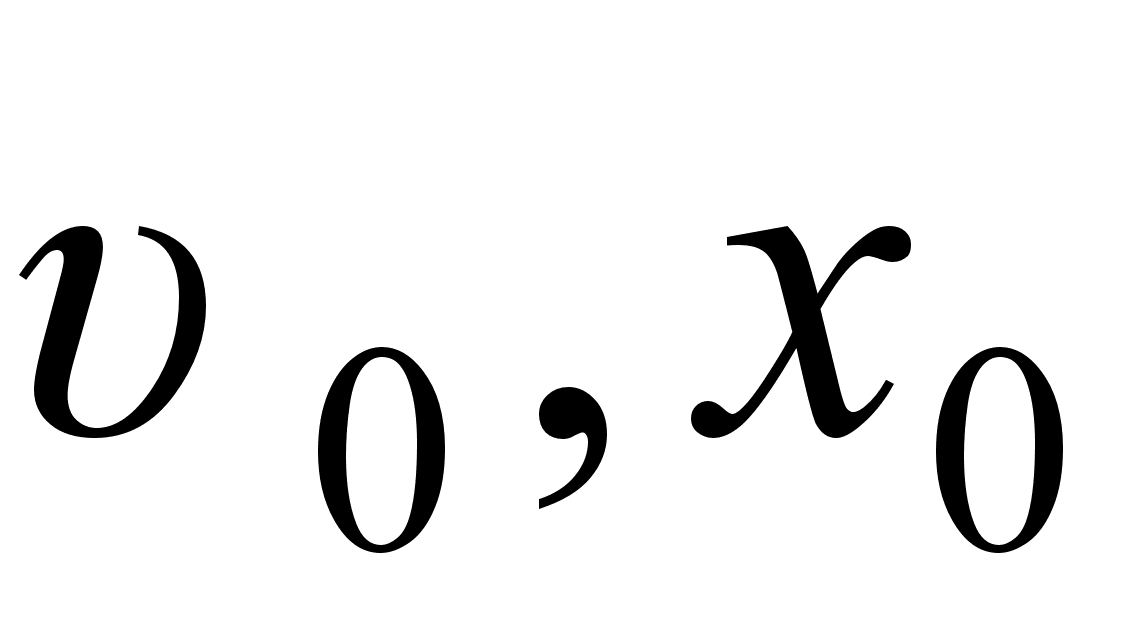 - константи. Вiдшукаiмо швидкiсть i прискорення руху.
- константи. Вiдшукаiмо швидкiсть i прискорення руху.
Швидкiсть руху буде: 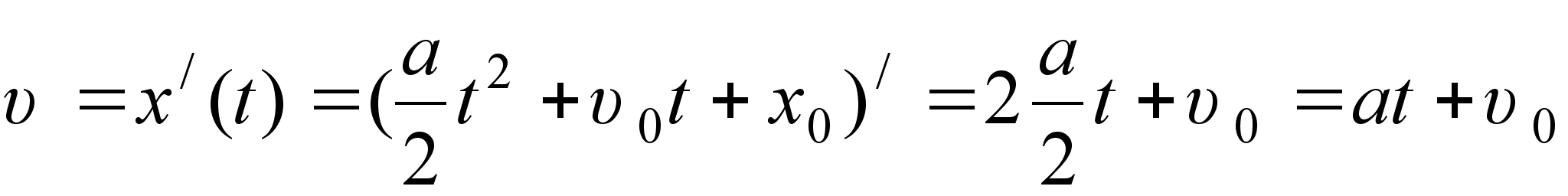 .
.
Так як нам вiдома швидкiсть руху як функцiя часу, то можемо знайти прискорення цього руху:  . Бачимо що а тАУ константа, i при а > 0 тАУ це буде прискорений рух, а при а < 0 тАУ рух сповiльнений.
. Бачимо що а тАУ константа, i при а > 0 тАУ це буде прискорений рух, а при а < 0 тАУ рух сповiльнений.
Приклад 3. Судно В знаходиться на сходi вiд судна А на вiдстанi
75 км i пливе на захiд зi швидкiстю 12 км/год. Судно А пливе на пiвдень зi швидкiстю 4 км/год. Чи буде в деякий момент часу вiдстань мiж ними мiнiмальною?
Розв’язання
Перш за все необхiдно намалювати малюнок.
З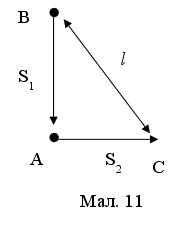 малюнку видно, що 2 судна В i А рухаються перпендикулярно один одному, тому вiдстань мiж ними можемо записати, за теоремою Пiфагора,
малюнку видно, що 2 судна В i А рухаються перпендикулярно один одному, тому вiдстань мiж ними можемо записати, за теоремою Пiфагора, 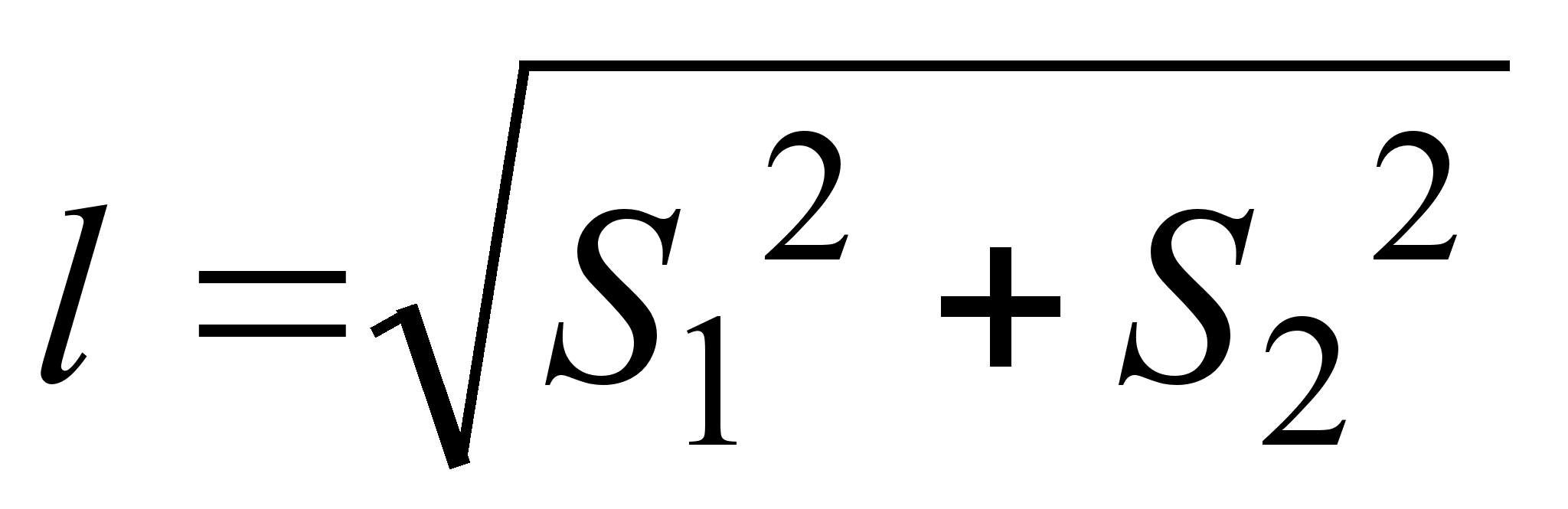 . А вiдстанi ми можемо записати за вiдомими швидкостями:
. А вiдстанi ми можемо записати за вiдомими швидкостями: 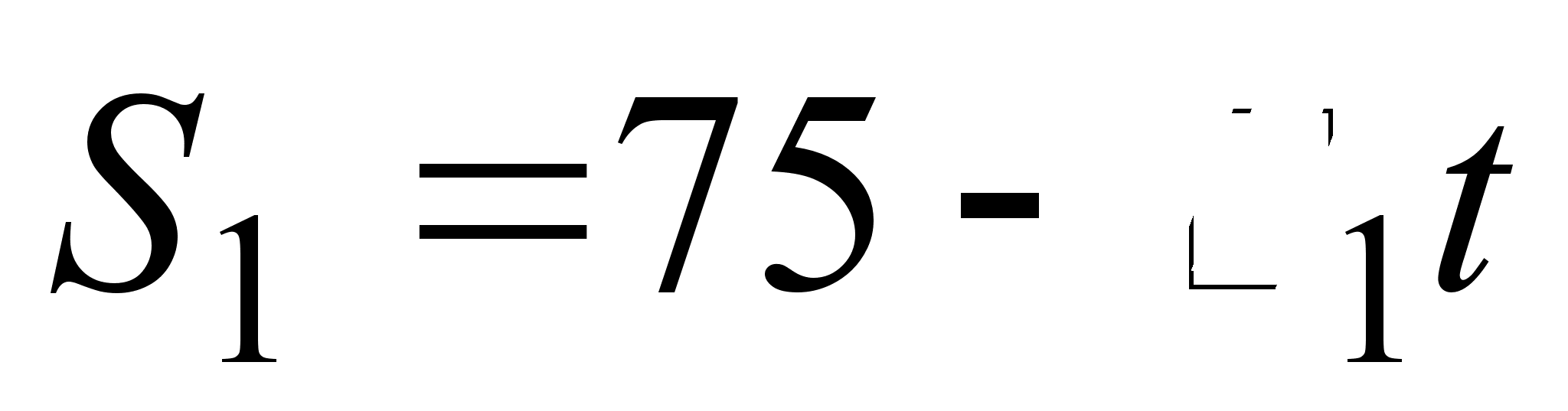 ,
,  .
.
Тому  . Ми отримали функцiю, яка характеризуi змiну вiдстанi мiж суднами в залежностi вiд часу. Дослiдимо цю функцiю на мiнiмум.
. Ми отримали функцiю, яка характеризуi змiну вiдстанi мiж суднами в залежностi вiд часу. Дослiдимо цю функцiю на мiнiмум.
Знайдемо похiдну  . Вiдшукаiмо критичнi точки, промiжки зростання та спадання функцii на цих промiжках та знайдемо точку екстремуму:
. Вiдшукаiмо критичнi точки, промiжки зростання та спадання функцii на цих промiжках та знайдемо точку екстремуму:
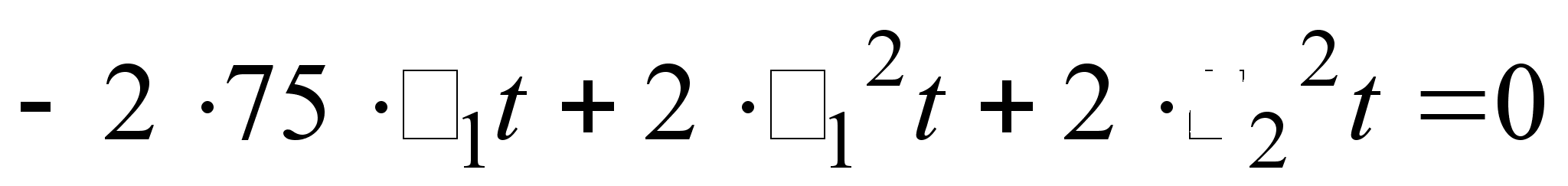 ;
;
 ;
;
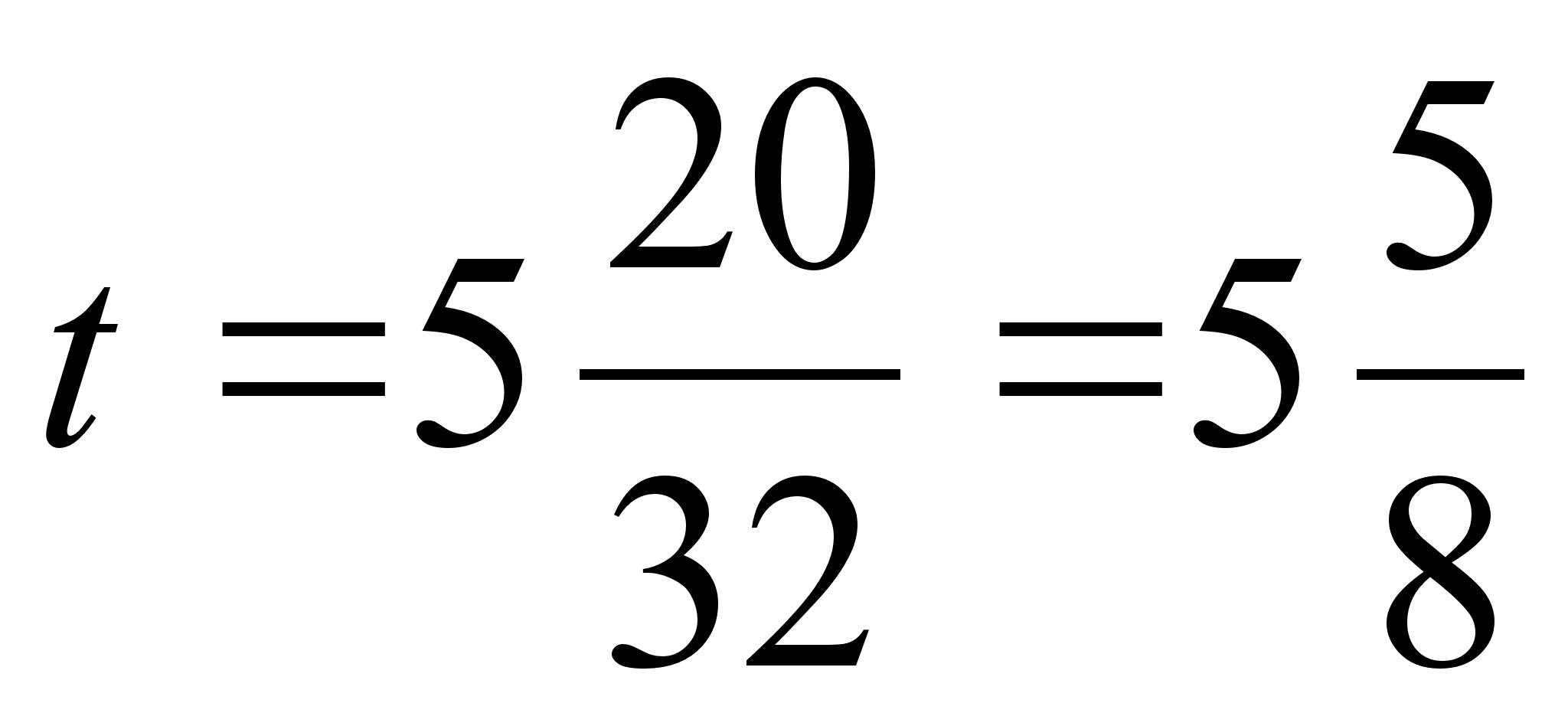 .
.
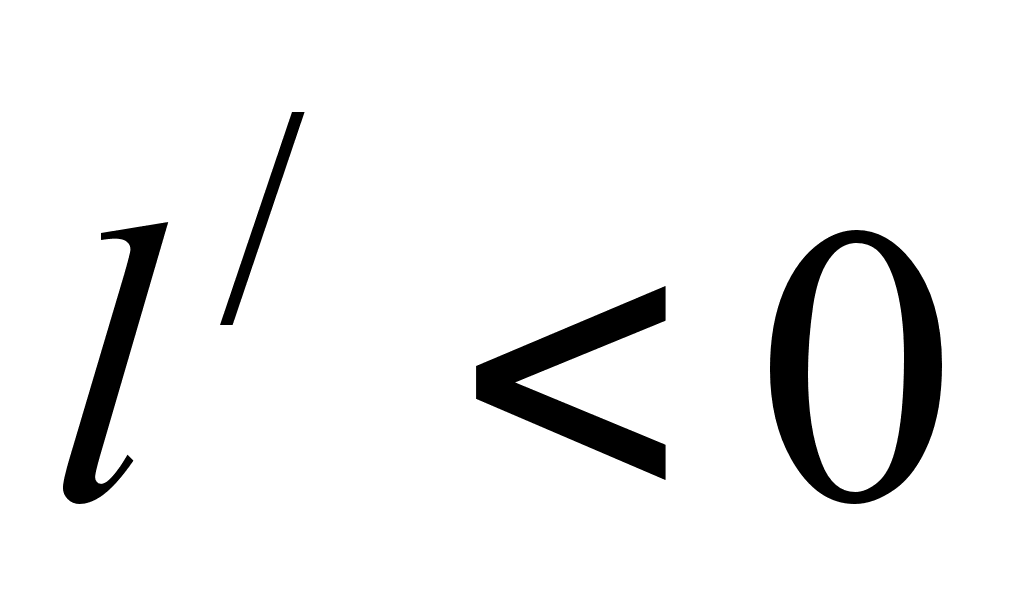 на промiжку (-;
на промiжку (-;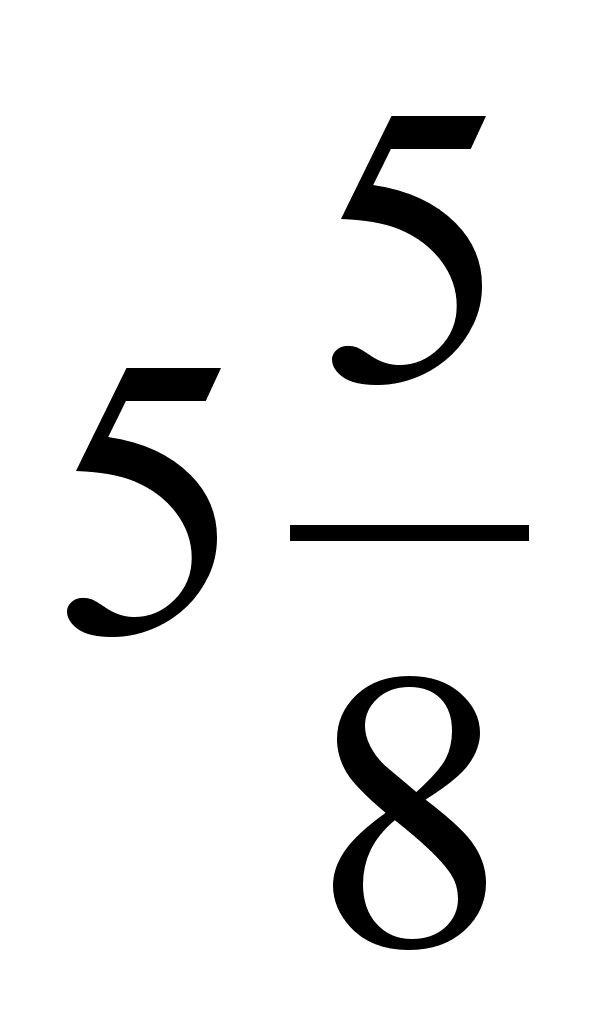 ),
),  на промiжку (
на промiжку (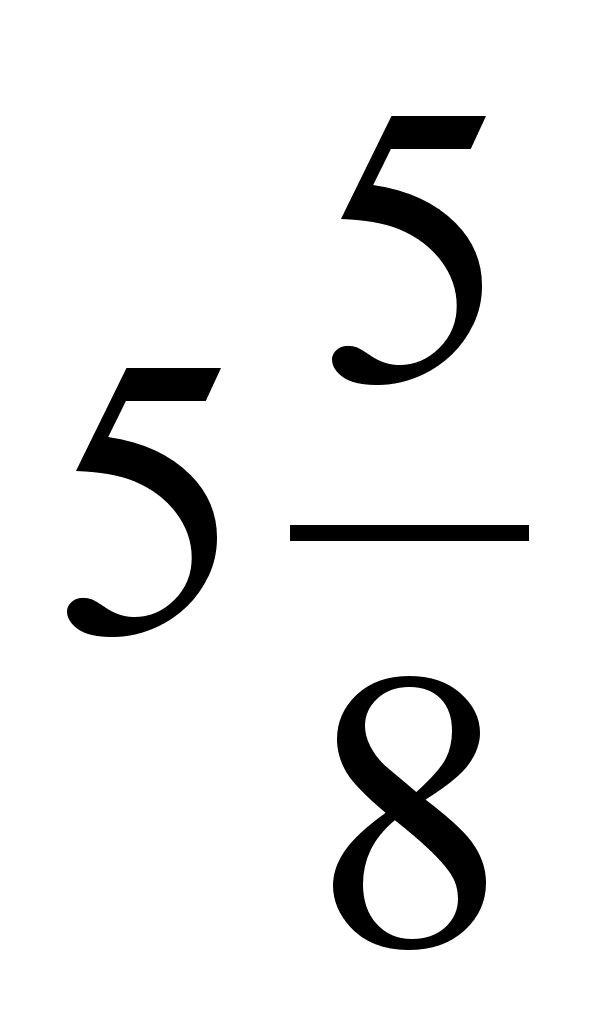 ;), тобто
;), тобто
tm=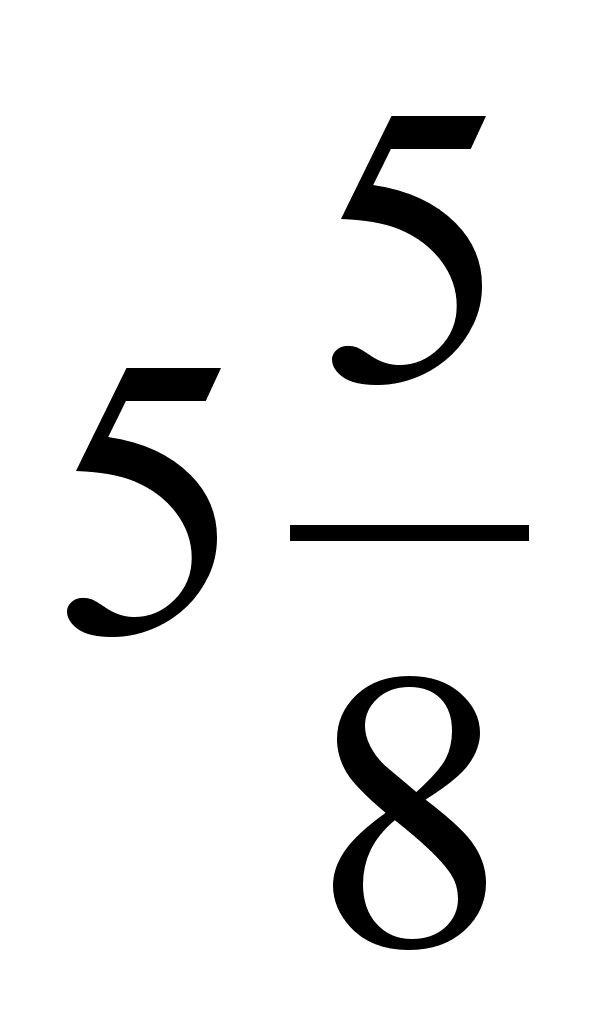 - точка мiнiмуму функцii l.
- точка мiнiмуму функцii l.
В момент часу tm=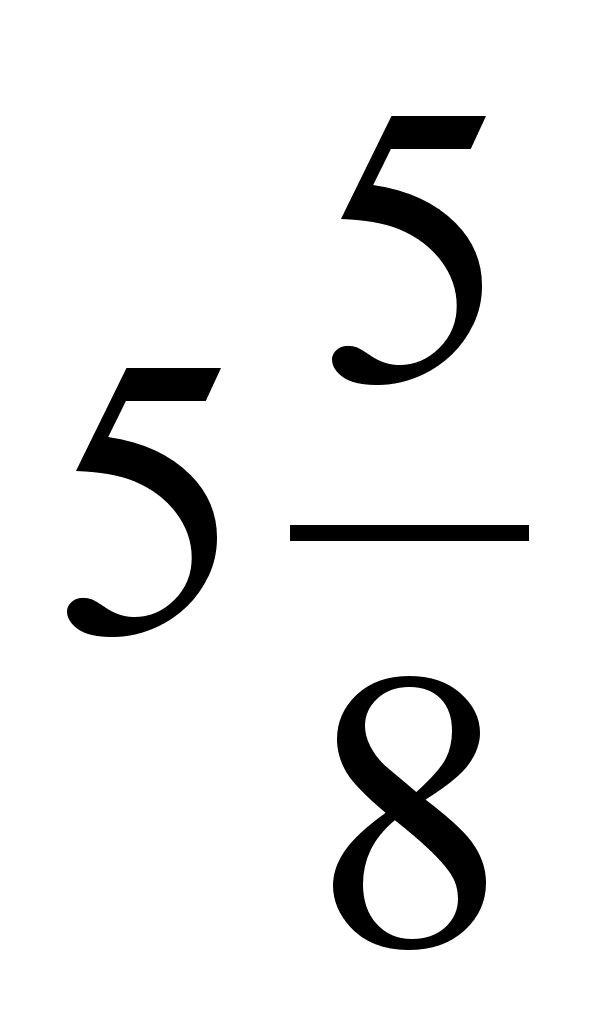 вiдстань мiж суднами буде мiнiмальною.
вiдстань мiж суднами буде мiнiмальною.
В сильному класi, для розширення кругозору учнiв, та розширення можливостей застосування похiдноi можна розглянути задачi геометричного та бiологiчного типу, при вивченнi теми “Найбiльше та найменше значення функцii”.
Приклад 1. Для будiвництва будинку прямокутноi форми зображеного на планi темним прямокутником з площею 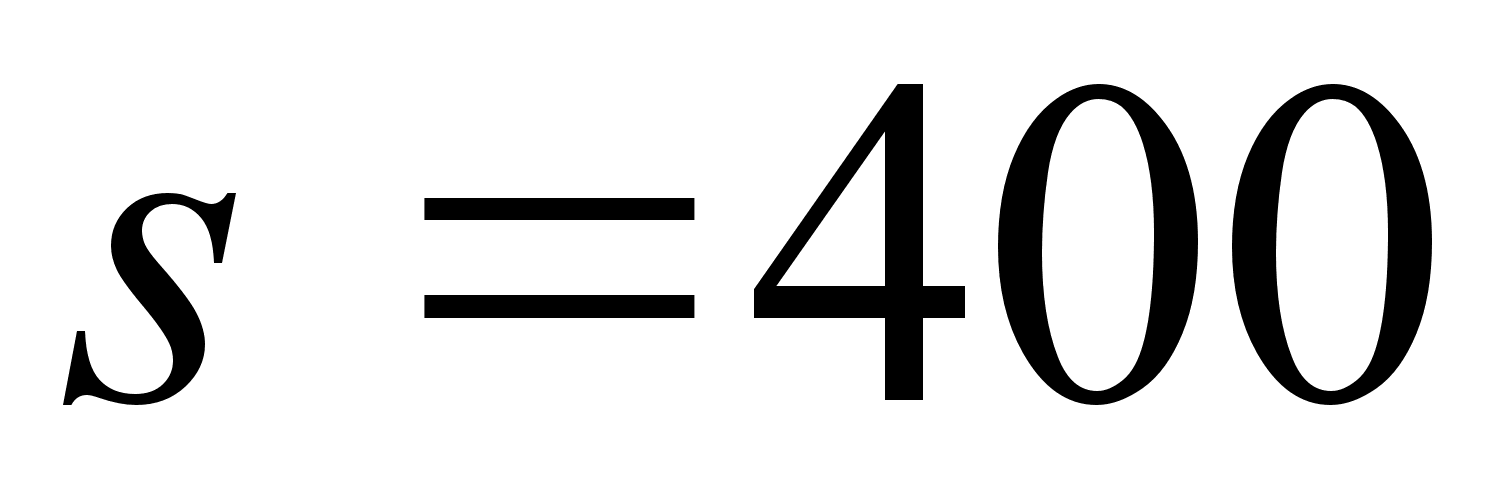 м2 вiдведено дiлянку прямокутноi форми, межi якоi повиннi знаходитись вiд будинку на вiдстанi 36 i 16 метрiв. Якi розмiри потрiбно надати будинку, щоб площа дiлянки ABCD була найменшою ?
м2 вiдведено дiлянку прямокутноi форми, межi якоi повиннi знаходитись вiд будинку на вiдстанi 36 i 16 метрiв. Якi розмiри потрiбно надати будинку, щоб площа дiлянки ABCD була найменшою ?
Розв’язання
П означимо розмiри будинку через
означимо розмiри будинку через  i
i 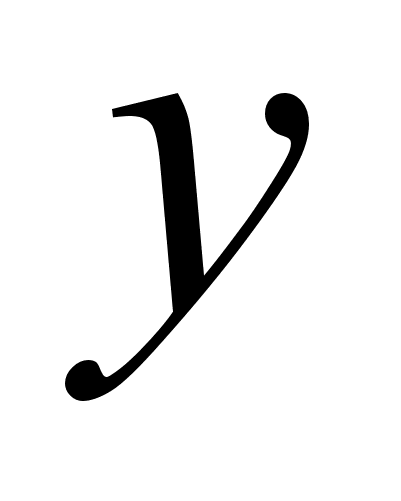 .
.
Площа будинку 400 м2, тобто  м2.
м2.
Враховуючи вiдстанi вiд будинку до межi отримаiмо довжини меж: AD= i AB=
i AB=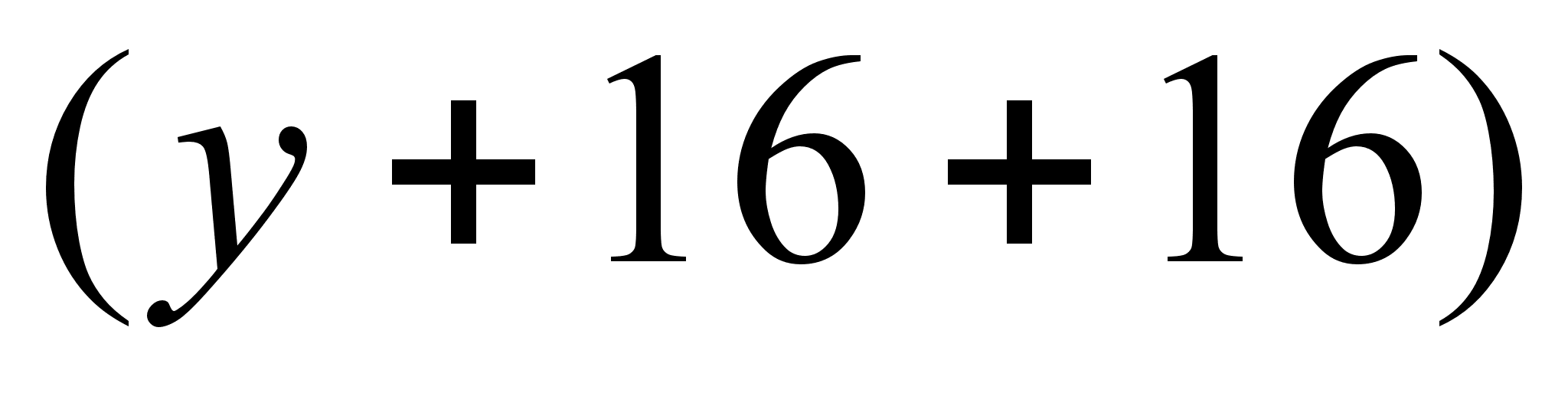 м.
м.
Запишемо площу дiлянки як функцiю сторони х: 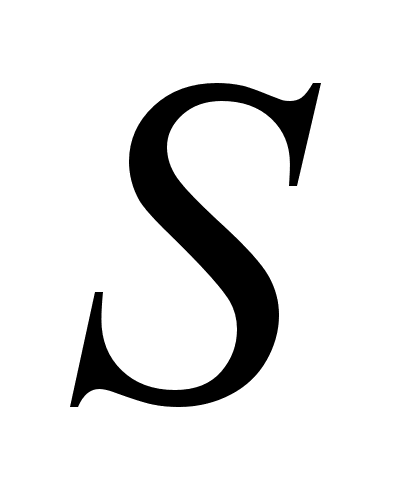 (х) =
(х) = .
.
Для знаходження мiнiмальноi площi дiлянки скористаiмося властивiстю похiдноi для дослiдження цiльовоi функцii на мiнiмум.
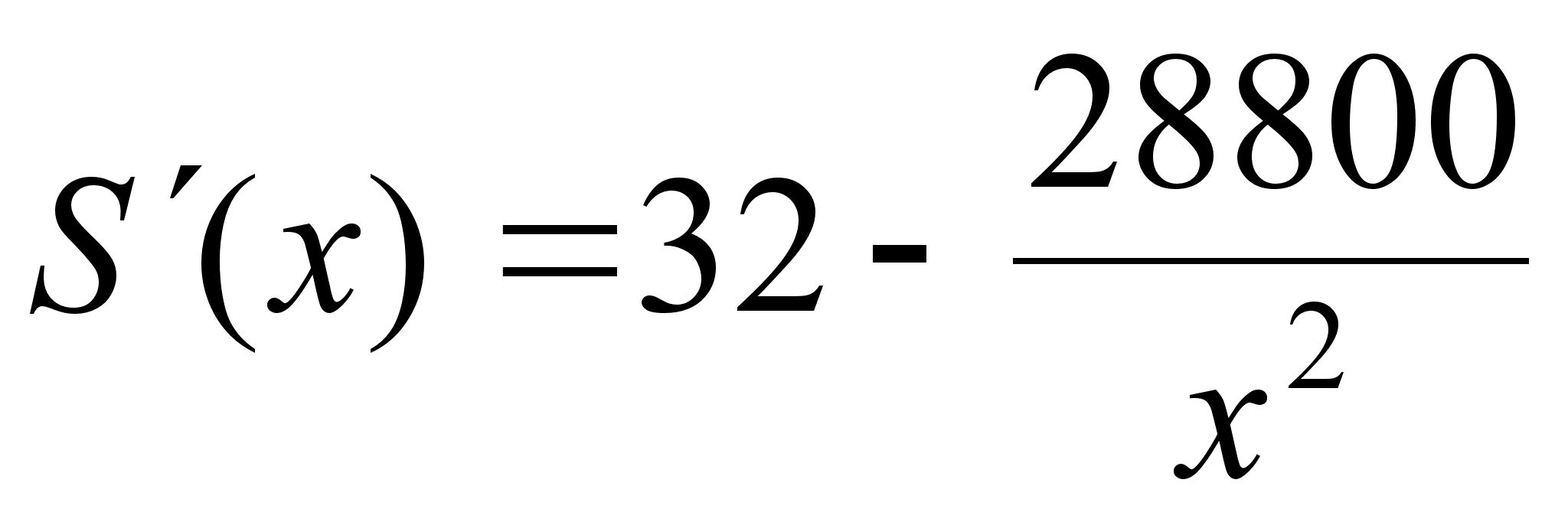 . Прирiвняiмо до нуля i отримаiмо значення:
. Прирiвняiмо до нуля i отримаiмо значення:  . Беремо додатне значення змiнноi х,
. Беремо додатне значення змiнноi х, 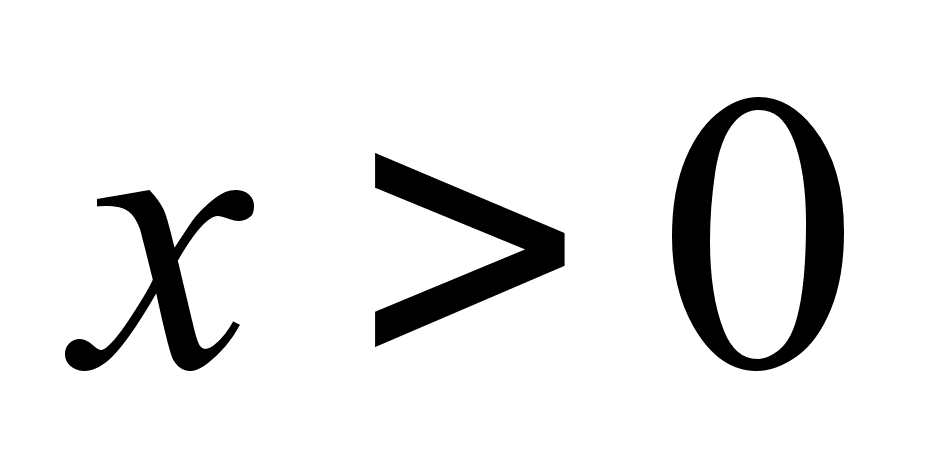 - бо сторона.
- бо сторона.
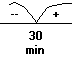
Дослiдимо знак похiдноi на промiжках:
Похiдна змiнюi знак з “тАУ“ на “+”, тобто  буде точкою мiнiмуму. А значення функцii в цiй точцi
буде точкою мiнiмуму. А значення функцii в цiй точцi  .
.
Вiдповiдь: 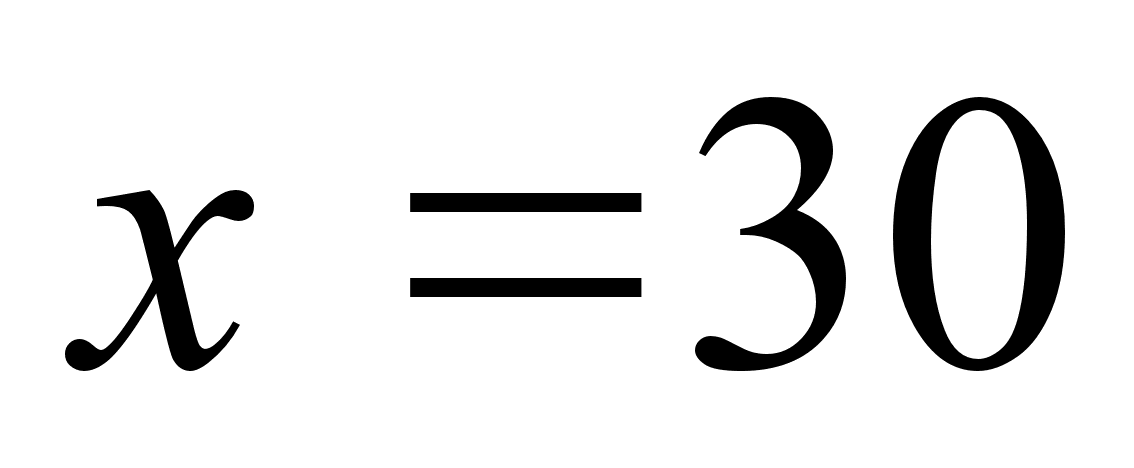 ,
, 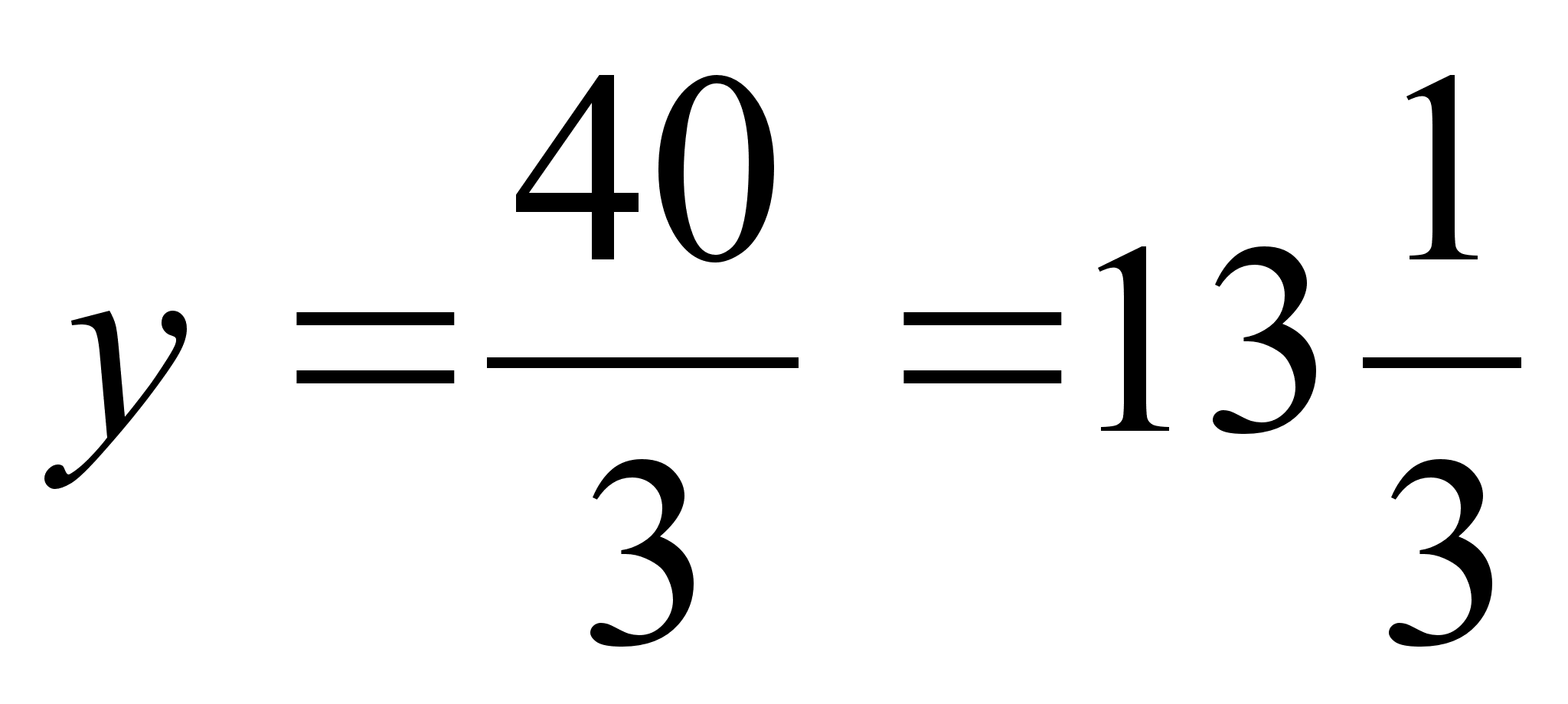 .
.
Приклад 2. Швидкiсть зростання популяцii x задана формулою y=0,001x(100-x) (час t виражено в днях). При якiй чисельностi популяцii ця швидкiсть максимальна ? Скiльки особин повинна мiстити рiвноважна популяцiя, щоб швидкiсть зростання ii спала до нуля?
Розв’язання
В цьому прикладi y тАУ це функцiя, яку необхiдно дослiдити на максимум. Тому знайдемо першу похiдну: y=0,1-0,002x. Знайдемо критичнi точки, прирiвнявши ii до нуля: x=50. Ця точка i точкою максимуму функцii. Тобто при чисельностi 50 особин, швидкiсть зростання популяцii буде максимальною.
Тепер необхiдно перевiрити, чи i таке число особин, при якому швидкiсть зростання популяцii спадаi до нуля. Прирiвнюiмо швидкiсть до нуля 0,001x(100-x)=0, i отримаiмо значення шуканоi чисельностi х=0 або х=100, нуль вiдкидаiмо, бо не задовольняi умову. Тому при чисельностi в 100 особин, швидкiсть зростання популяцii буде рiвна нулю.
Вз4. ЧАСТКОВО-ПОШУКОВИЙ МЕТОД
Цей метод вимагаi майже самостiйноi роботи учнiв, а вчитель лише спрямовуi мислення учнiв до певних висновкiв.
Цим методом краще користуватись, коли необхiдно закрiпити пройдений матерiал чи певну тему, або для перевiрки пiдготовленостi учнiв до вивчення певноi теми.
Розглянемо використання методу на прикладi вивчення перiодичностi функцii.
Варто наступним чином розпочати урок.
Вчитель повинен показати, якi процеси iснують в математицi чи фiзицi i як вони можуть повторюватись. Це може бути обертання Мiсяця навколо Землi, коливання маятника в годиннику, повторення значень функцii через певний крок та iнше.
С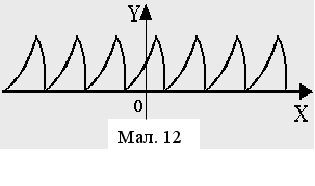 початку можна намалювати схематично графiк i показати учням, що через певний крок значення функцii i однаковими, i немаi значення в якому напрямку ми будемо рухатись по осi OX.
початку можна намалювати схематично графiк i показати учням, що через певний крок значення функцii i однаковими, i немаi значення в якому напрямку ми будемо рухатись по осi OX.
П отiм можна намалювати учням графiк вже вiдомоi iм функцii
отiм можна намалювати учням графiк вже вiдомоi iм функцii  .
.
Учнi помiчають, що значення функцii повторюються через 2П.
Вчитель звертаi увагу на те, що функцiя маi те саме значення i в точцi  , i в точцi
, i в точцi 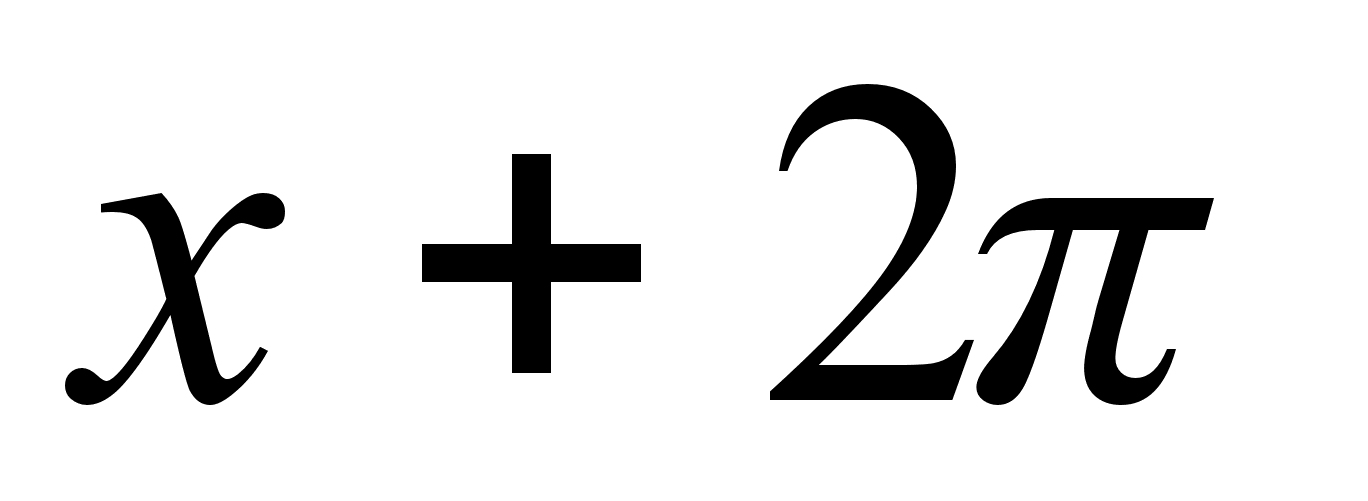 , i в точцi
, i в точцi 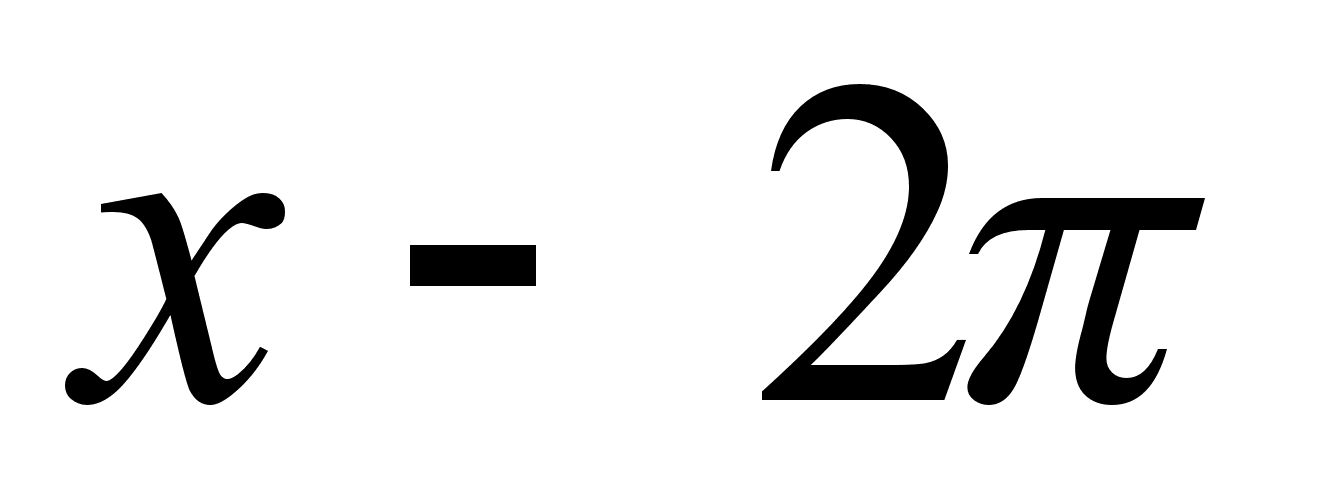 ,
,  ,
, 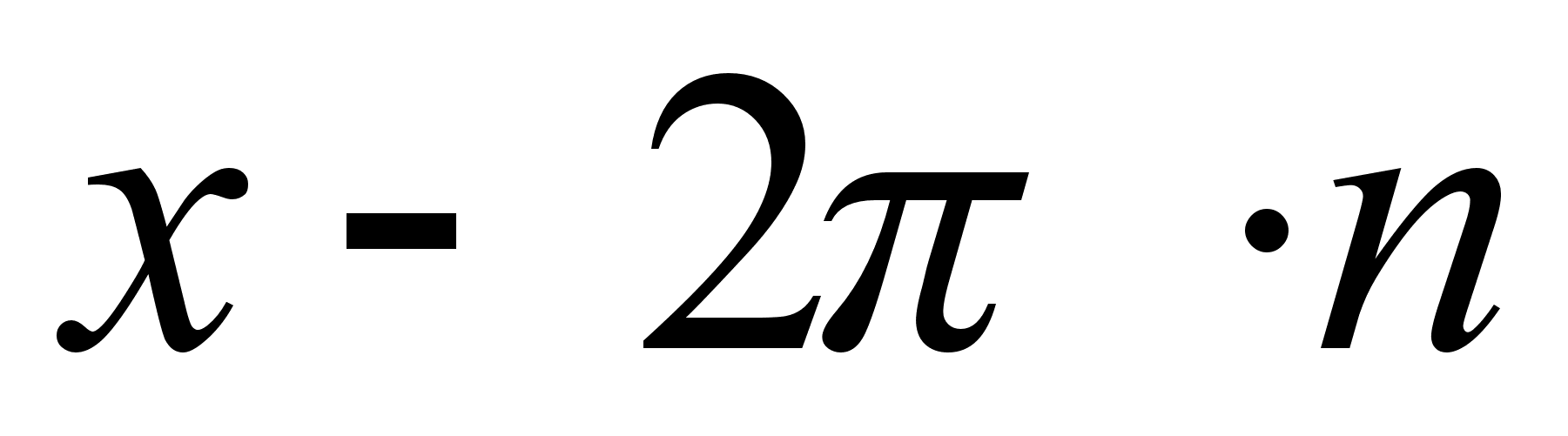 i мiнiмальне число, яке додаiться до значення аргументу, називаiться перiодом, позначають його буквою Т.
i мiнiмальне число, яке додаiться до значення аргументу, називаiться перiодом, позначають його буквою Т.
Учнi повиннi спробувати вже сформулювати означення перiодичноi функцii, хоча вчитель може допомагати.
Означення. Функцiя 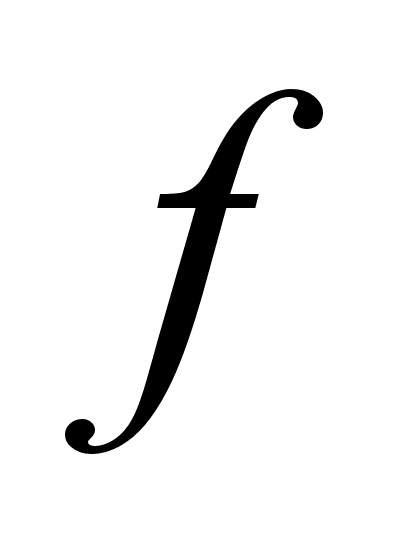 називаiться перiодичною з перiодом Т
називаiться перiодичною з перiодом Т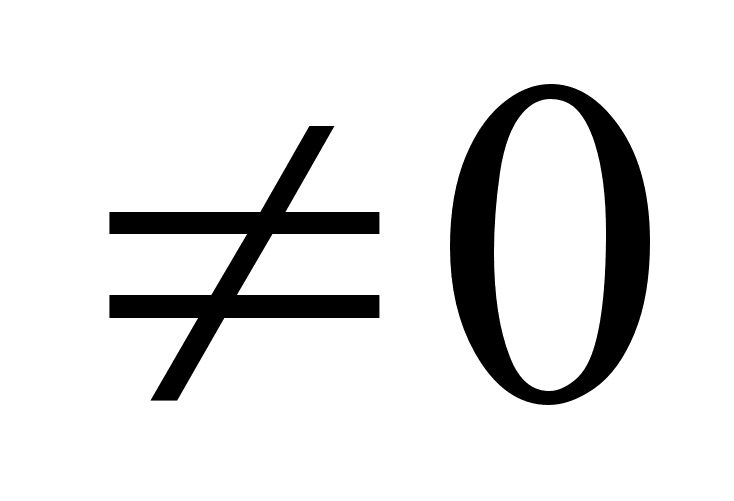 , якщо для довiльного
, якщо для довiльного 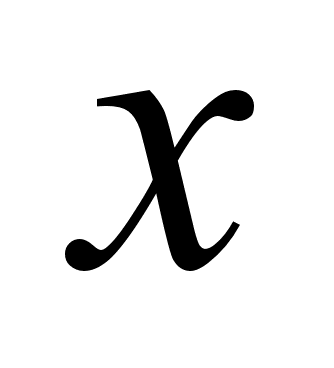 з областi визначення значення функцii в точках x, x+Т, x-Т рiвнi. Тобто
з областi визначення значення функцii в точках x, x+Т, x-Т рiвнi. Тобто  .
.
Потiм переходять до розв’язування прикладiв.
Вз5. ДОСЛРЖДНИЦЬКИЙ МЕТОД
Цим методом користуються вже на певному етапi навчання учнiв, коли учнi вже здатнi логiчно мислити, робити самостiйнi висновки. Також це корисно для розвитку логiчного мислення. Користування цим методом покращуi працездатнiсть учнiв i викликаi в них зацiкавленiсть, розвиваi самостiйнiсть в дослiдженнi певних закономiрностей чи властивостей певних об’iктiв.
Розглянемо цей метод на прикладi дослiдження функцii з використанням похiдноi.
Приклад1. Дослiдити функцiю i побудувати ii графiк:  .
.
Розв’язування
1) Область визначення функцii - множина дiйсних чисел, бо функцiя i многочленом.
2) Функцiя не i нi парною нi непарною, бо  i область визначення функцii симетрична вiдносно початку координат.
i область визначення функцii симетрична вiдносно початку координат.
3) Маi точку перетину з вiссю 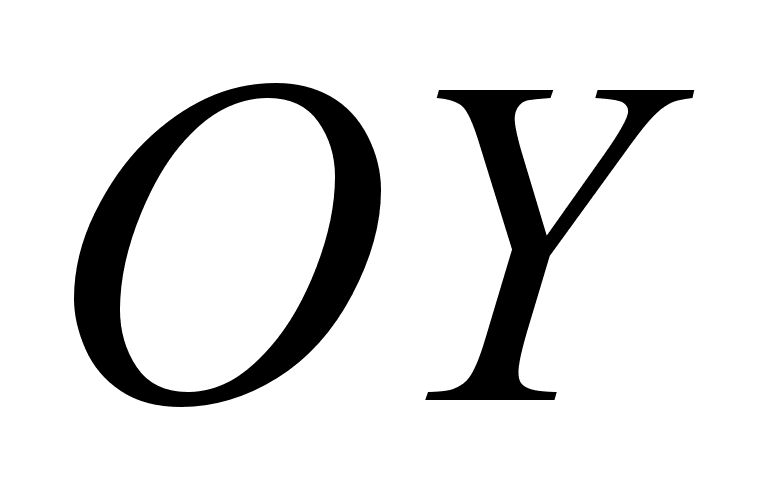 : при
: при 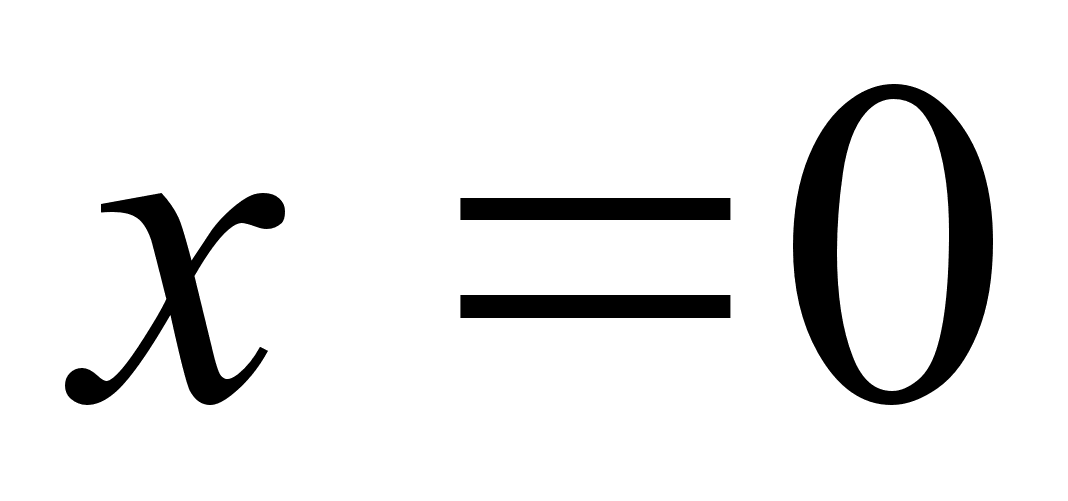
 , тобто точка з координатами
, тобто точка з координатами  .
.
4) Маi точки перетину з вiссю 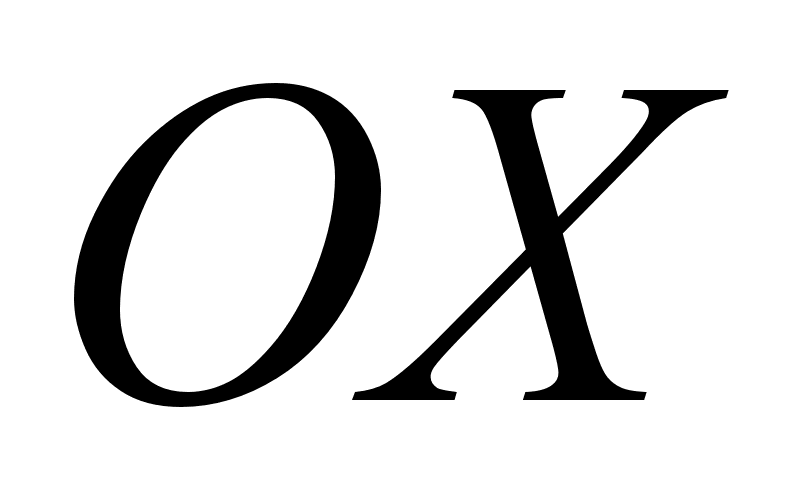 :
: 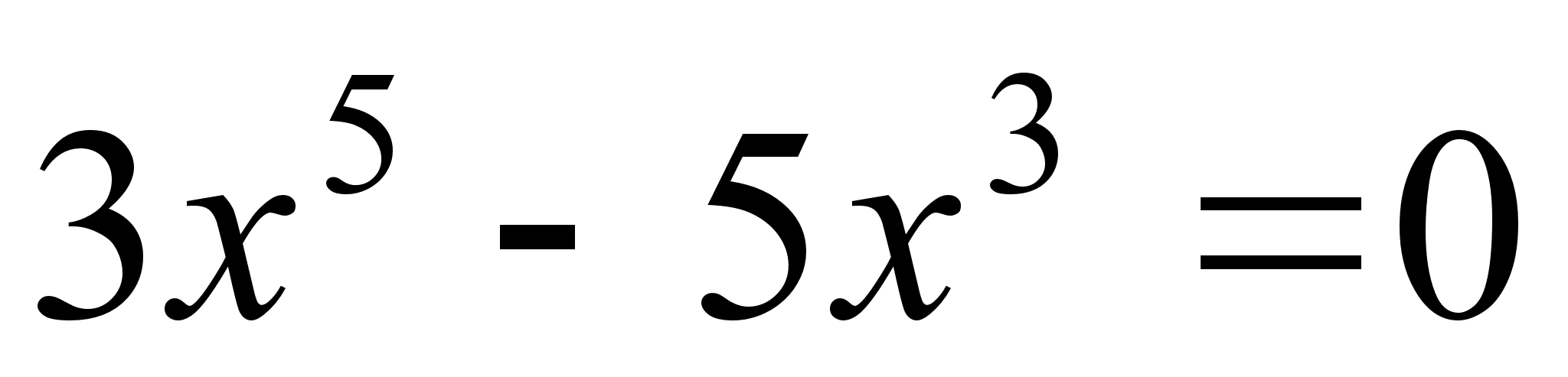 ;
; ;
;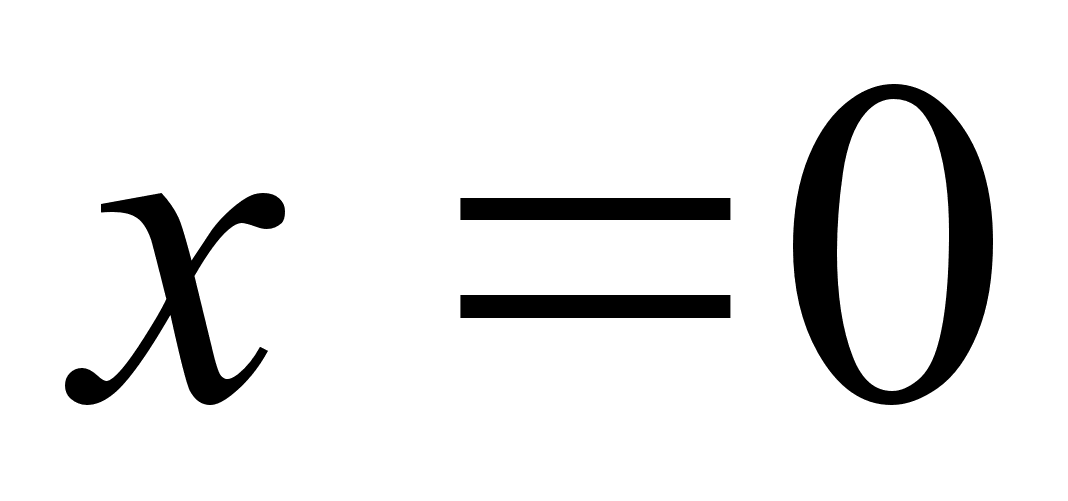 або
або 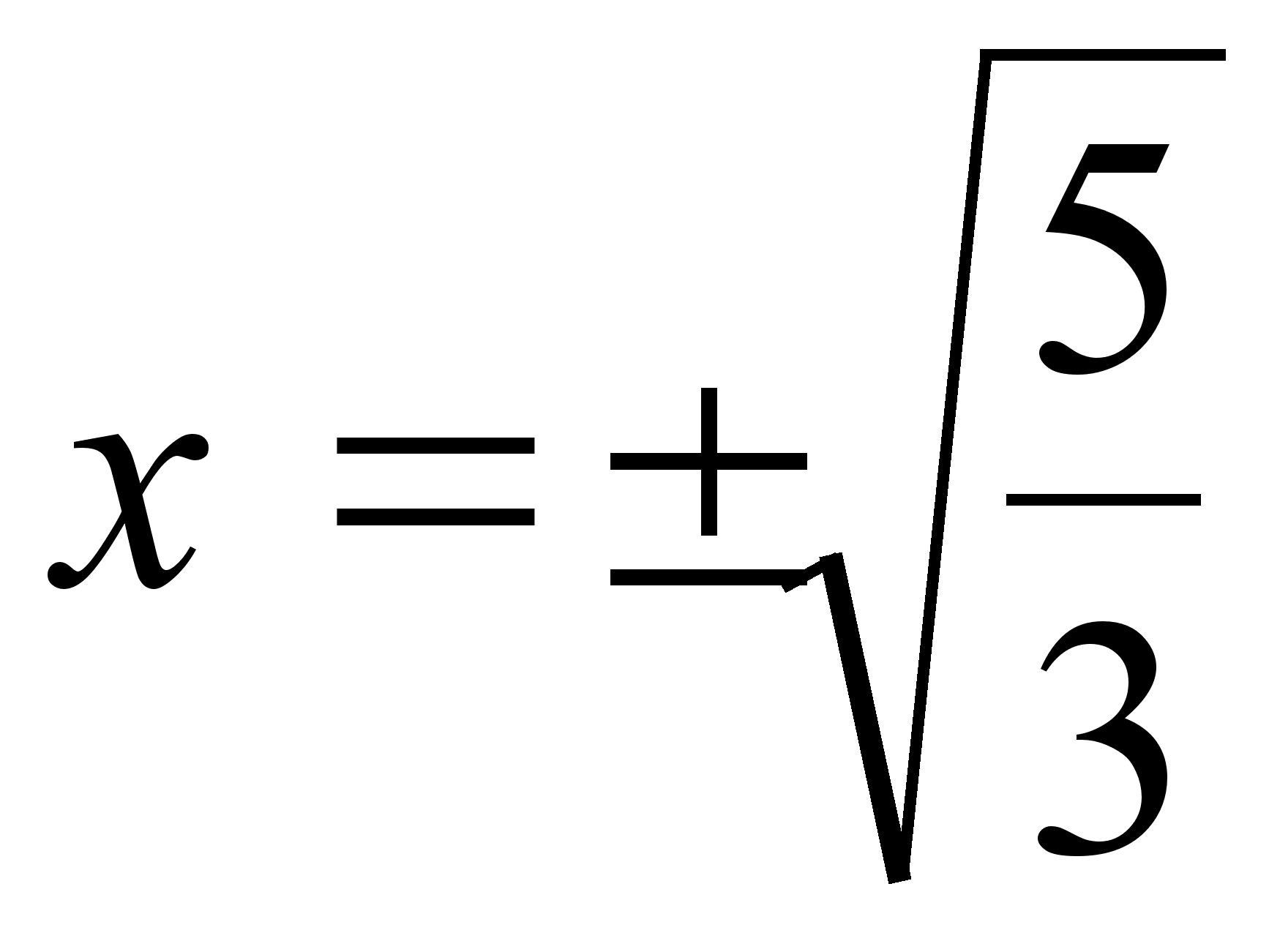 . Тобто точки з координатами
. Тобто точки з координатами  ,
,  .
.
5) Знаходимо максимуми i мiнiмуми функцii.
Знайдемо критичнi точки. Для цього знайдемо першу похiдну функцii:  .
.
Прирiвнявши похiдну до нуля отримаiмо три критичнi точки:
х= -1, х= 0, х= 1.
Знайдемо серед них точки максимуму i мiнiмуму.
При переходi через точку х= -1 похiдна змiнюi знак з “+” на “-” тАУ точка максимума, а при переходi через точку х=1, похiдна змiнюi знак з “-” на “+” тАУ точка мiнiмума. А при переходi через точку х=0 тАУ не мiняi знаку.
6) Дослiдимо функцiю на точки перегину:
 .
.
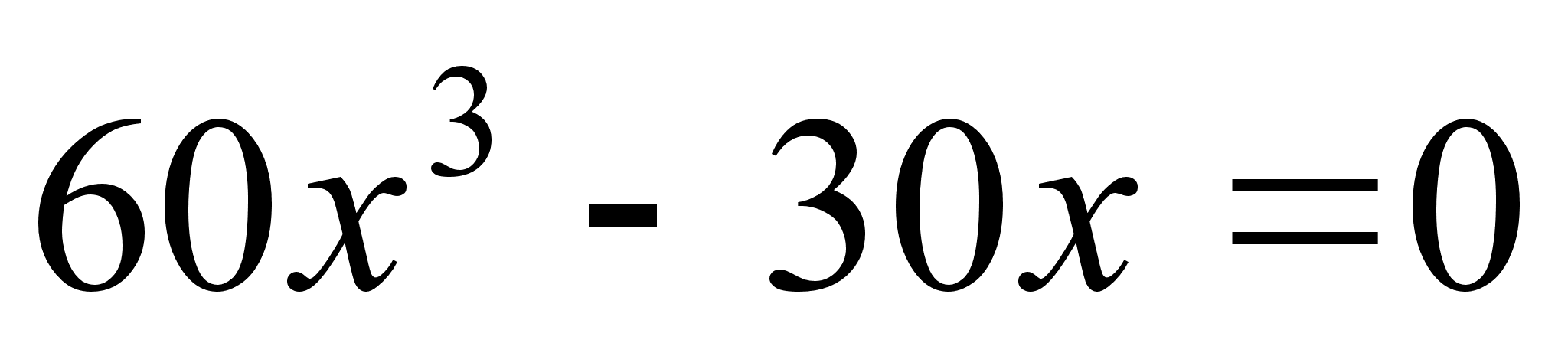 ;
;
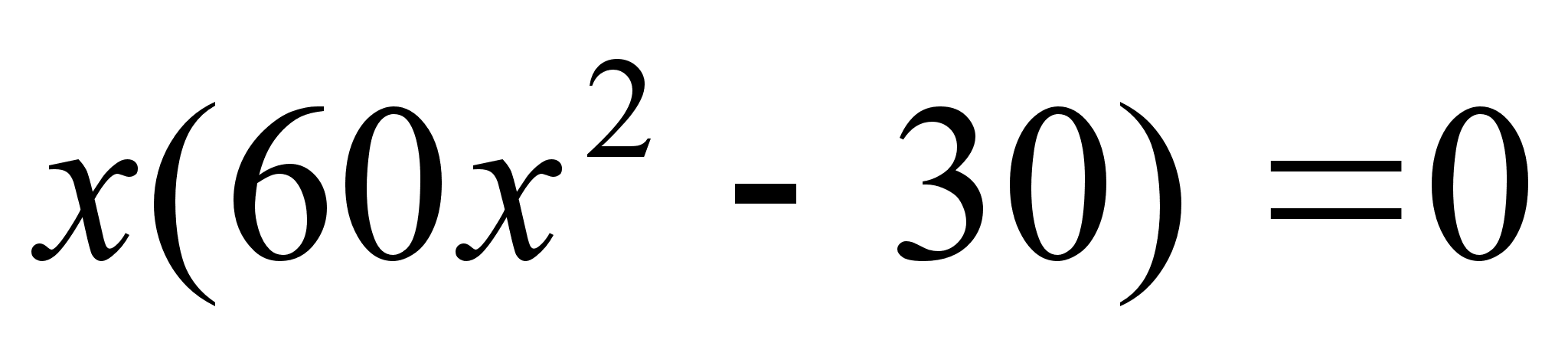 ;
;
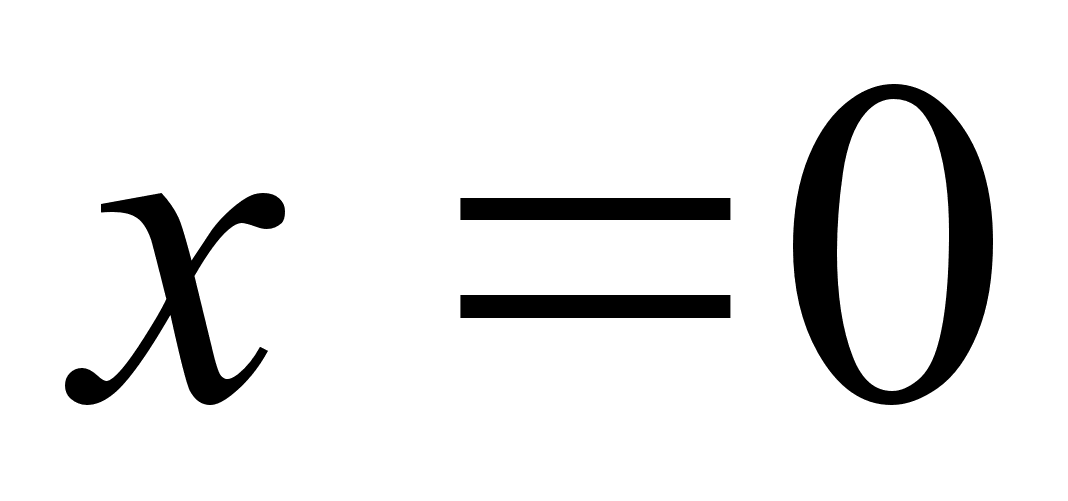 або
або 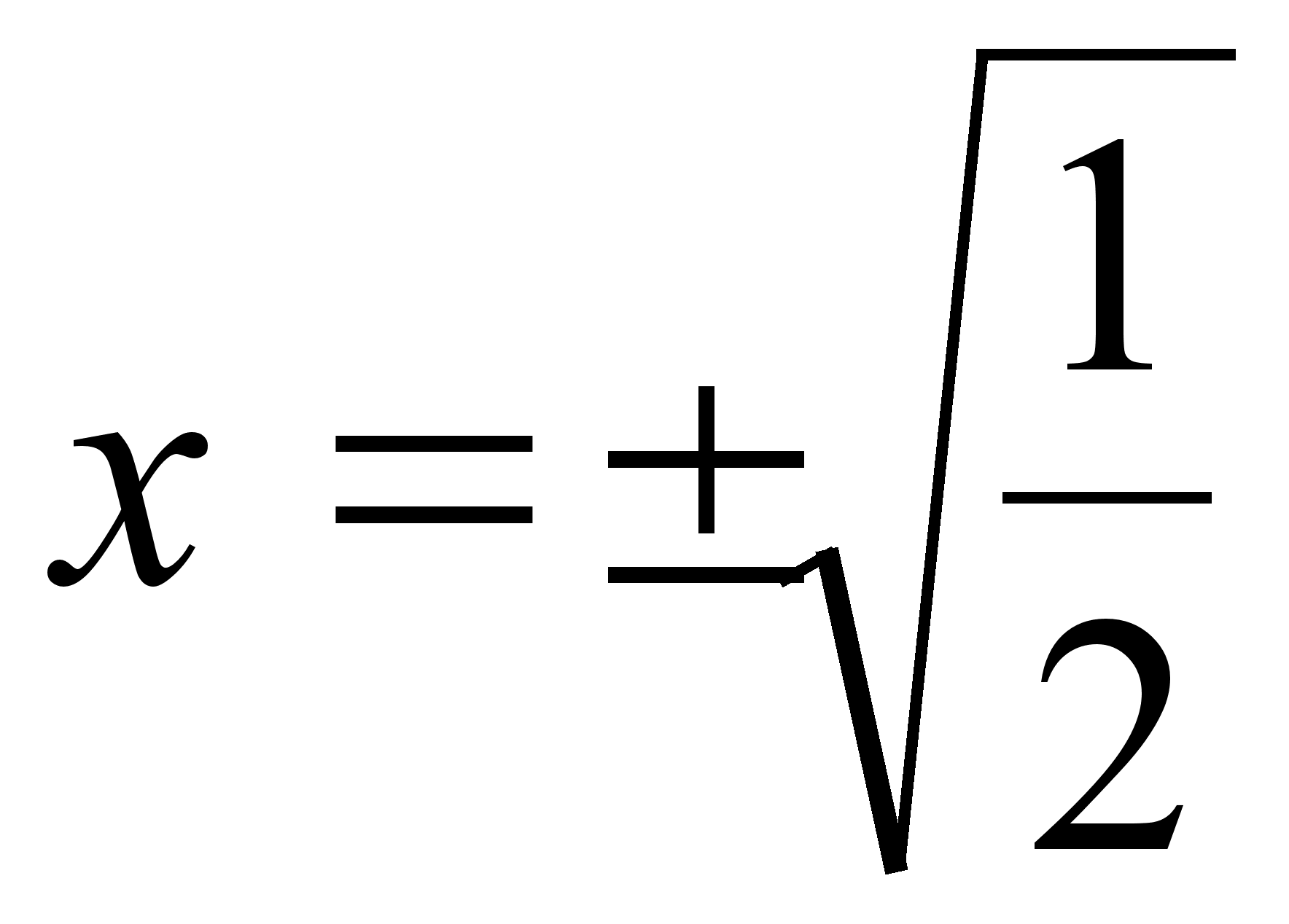 - отримали точки пiдозрiлi на точки перегину.
- отримали точки пiдозрiлi на точки перегину.
Учнi складають таблицю:
| X | (- | -1 | (-1;0) | 0 | (0;1) | 1 | (1; |
| + | 0 | тАУ | 0 | тАУ | 0 | + |
| Зростаi | 2 | спадаi | 0 | спадаi | -2 | зростаi |
| MAX | MIN |
З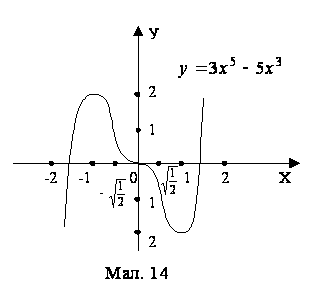 таблицi видно, що функцiя маi максимум в точцi
таблицi видно, що функцiя маi максимум в точцi 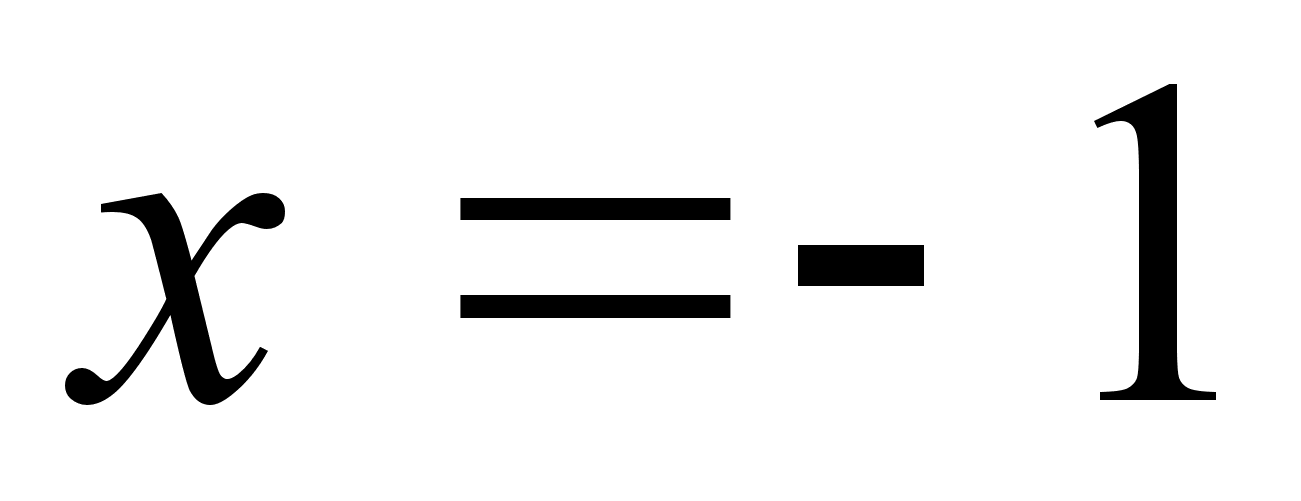 i мiнiмум в точцi
i мiнiмум в точцi  .
.
Будуiмо сам графiк використовуючи отриманi данi з таблицi. Спочатку учнi вiдмiчають на графiку точки максимуму i мiнiмуму, точки перетину з осями, а потiм будують графiк даноi функцii.
Приклад2.За даним рiвнянням руху авто  знайти його швидкiсть (при t = 2 сек.) ; момент часу, коли авто почало рухатись в зворотному напрямку та вiдстань, на яку воно вiдiйшло вiд деякого пункту (початок руху) до розвороту.
знайти його швидкiсть (при t = 2 сек.) ; момент часу, коли авто почало рухатись в зворотному напрямку та вiдстань, на яку воно вiдiйшло вiд деякого пункту (початок руху) до розвороту.
Розв’язання
Бажано спочатку намалювати графiк руху авто, це спростить розв’язування задачi, та дасть можливiсть зрозумiти, яким чином рухалось авто.
З умови задачi видно, що  .
.
Знаходимо точки перетину графiка функцii  з вiссю ОХ: t3 - 4t = 0;
з вiссю ОХ: t3 - 4t = 0;
t = 0, t = В± 2. (t = -2 не розглядаiмо, бо час t >0).
Знаходимо точки екстремуму функцii: 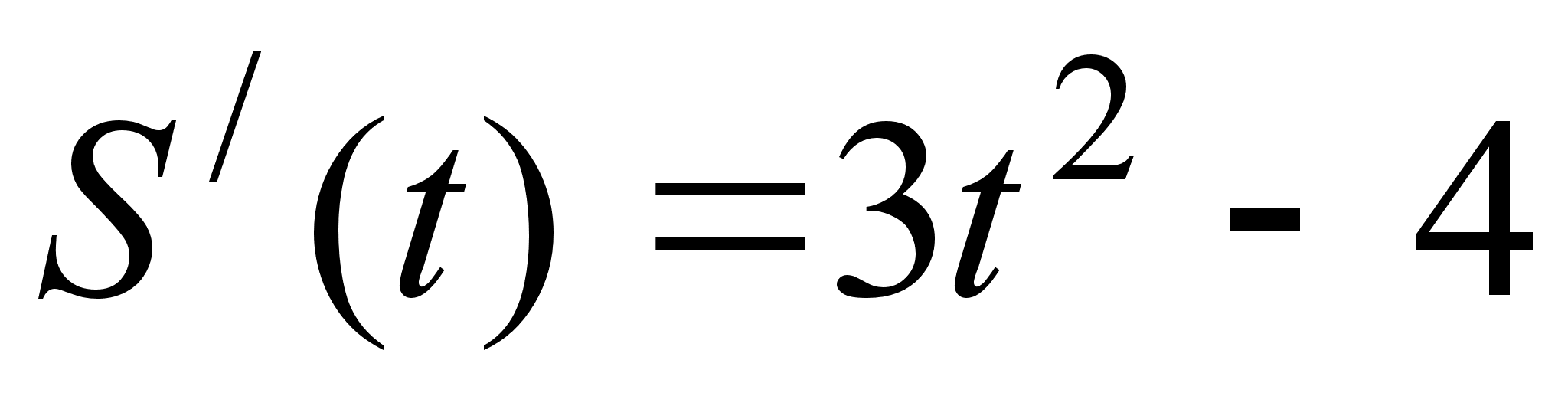 ; 3t 2 тАУ 4 = 0; t =
; 3t 2 тАУ 4 = 0; t =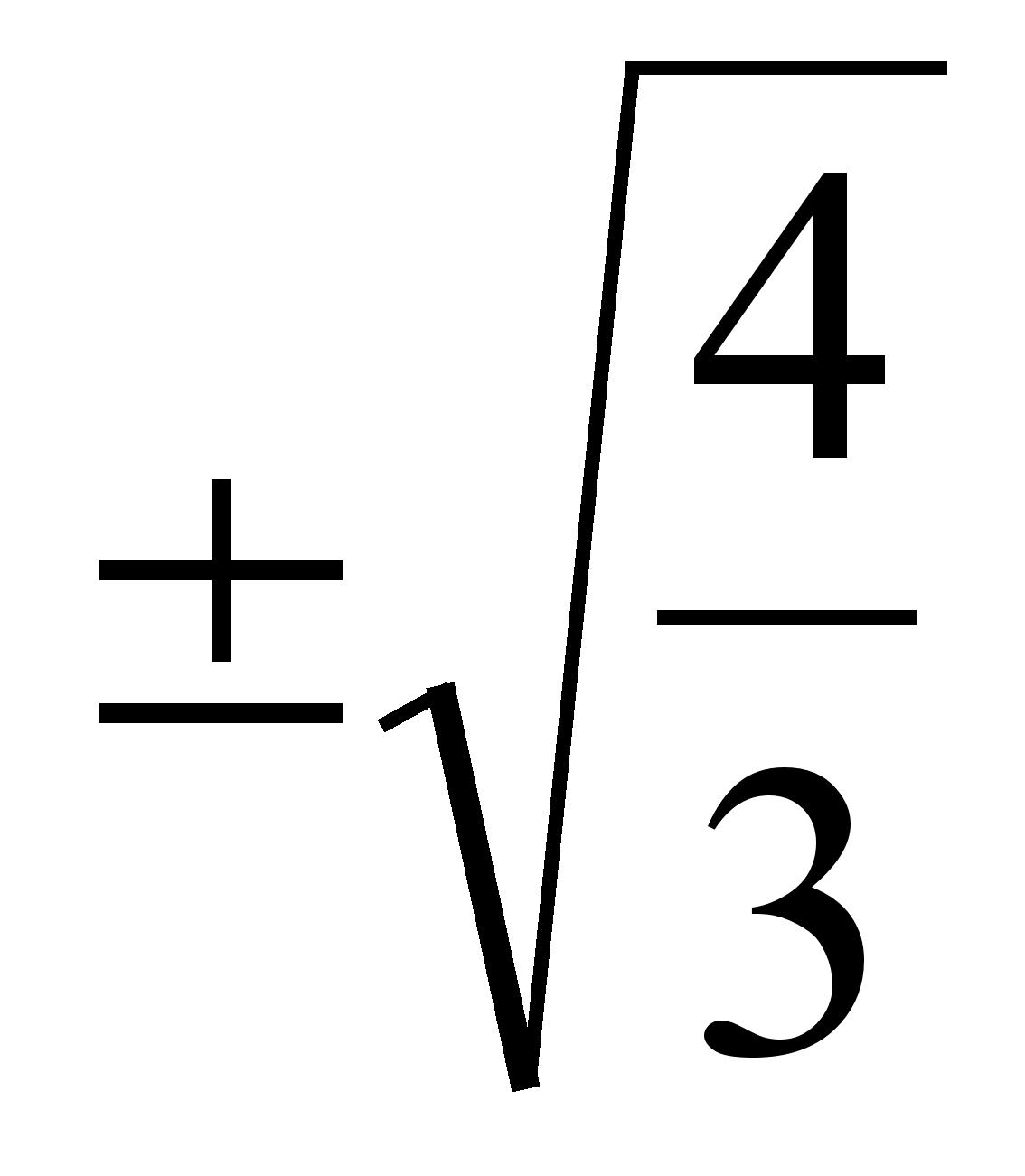 .
.
Значення 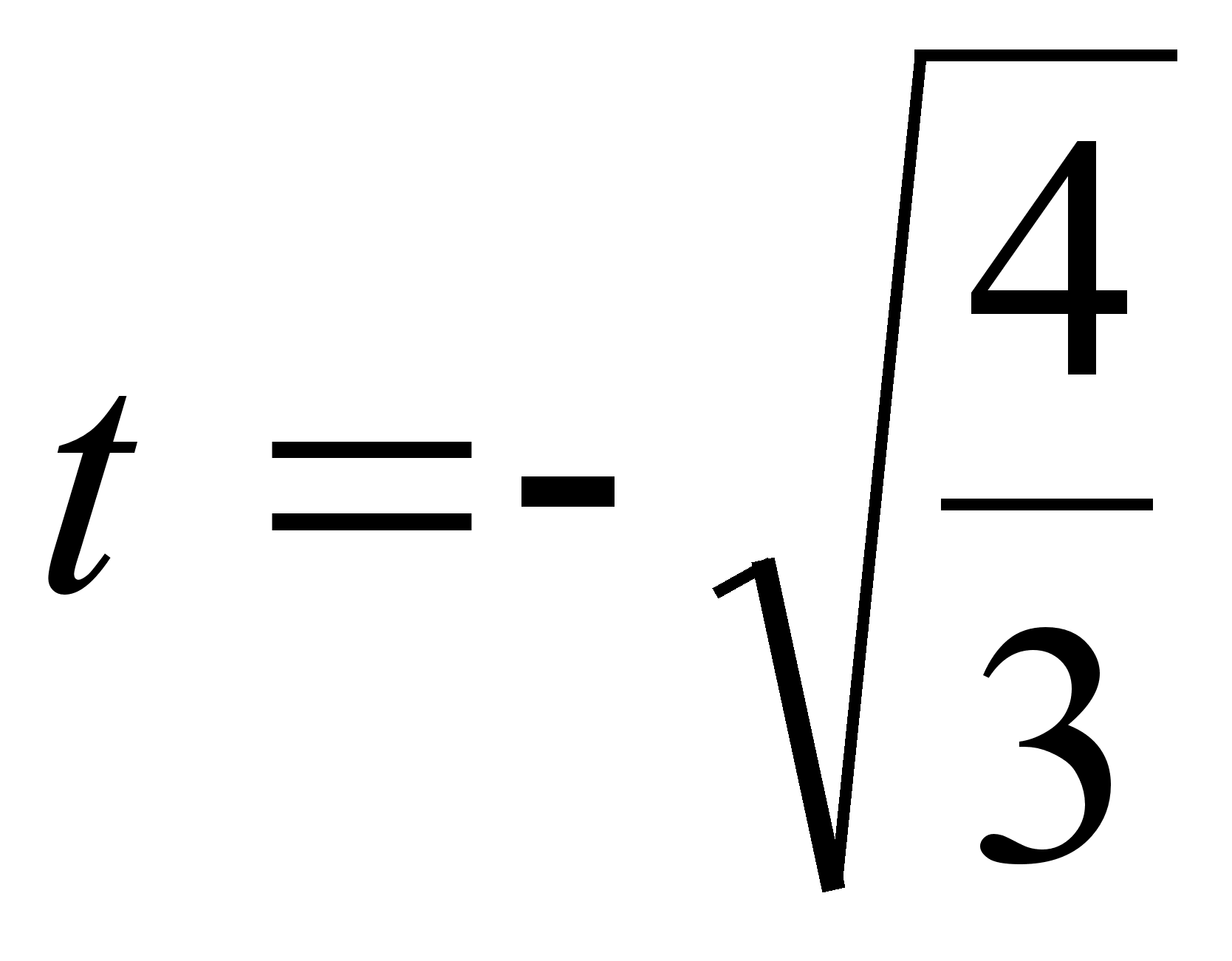 - не задовольняi умовi
- не задовольняi умовi  . Перевiримо як змiнюi знак похiдна при переходi через точку
. Перевiримо як змiнюi знак похiдна при переходi через точку 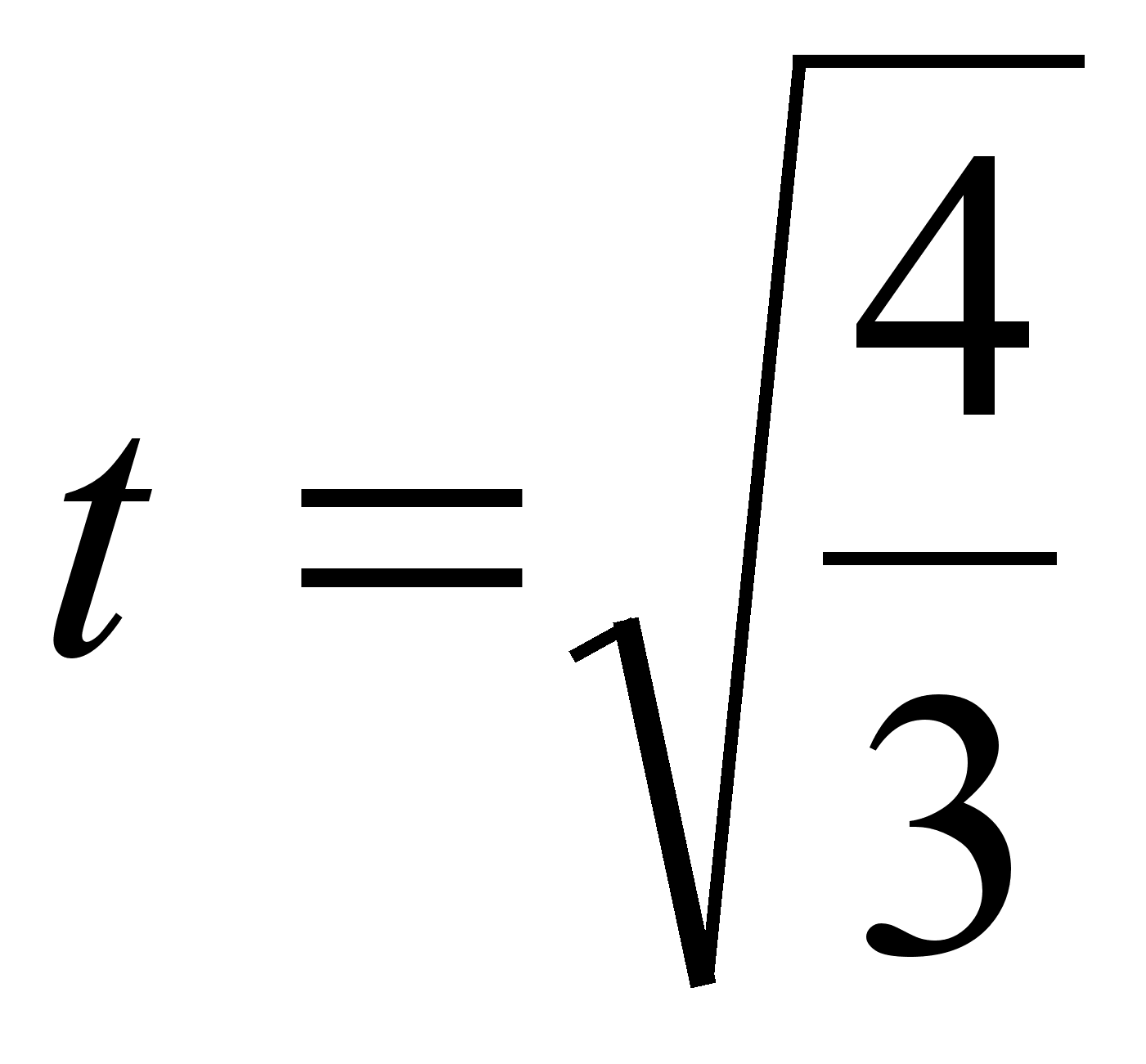 .
.
При переходi через цю точку, похiдна змiнюi свiй знак з “тАУ” на “+”, тобто це точка мiнiмуму.
М алюiмо малюнок.
алюiмо малюнок.
З малюнку видно, що в момент часу t =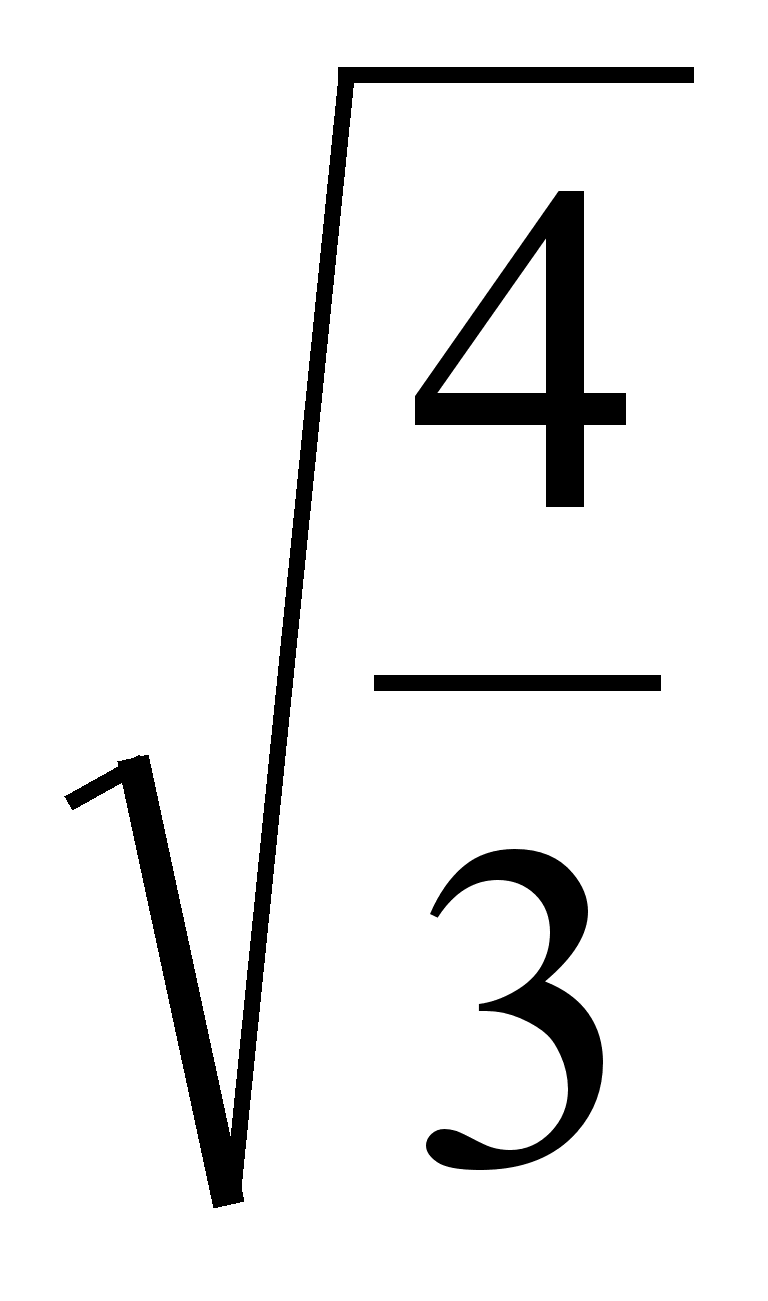 авто знаходилось на максимальнiй вiдстанi вiд деякого пункту (хоч i рухалося в зворотному напрямку).
авто знаходилось на максимальнiй вiдстанi вiд деякого пункту (хоч i рухалося в зворотному напрямку).
Тому в момент часу t =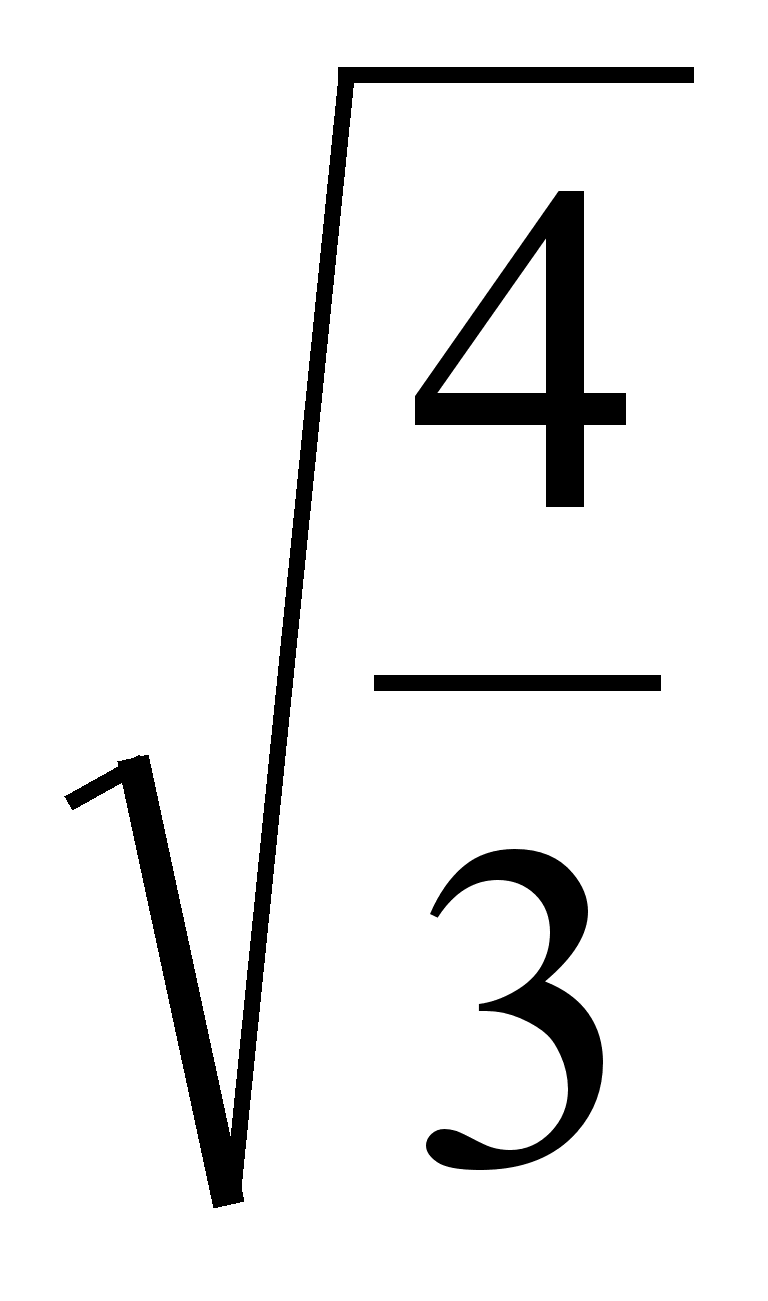 авто змiнило напрям руху.
авто змiнило напрям руху.
Вiдстань в цей момент була: 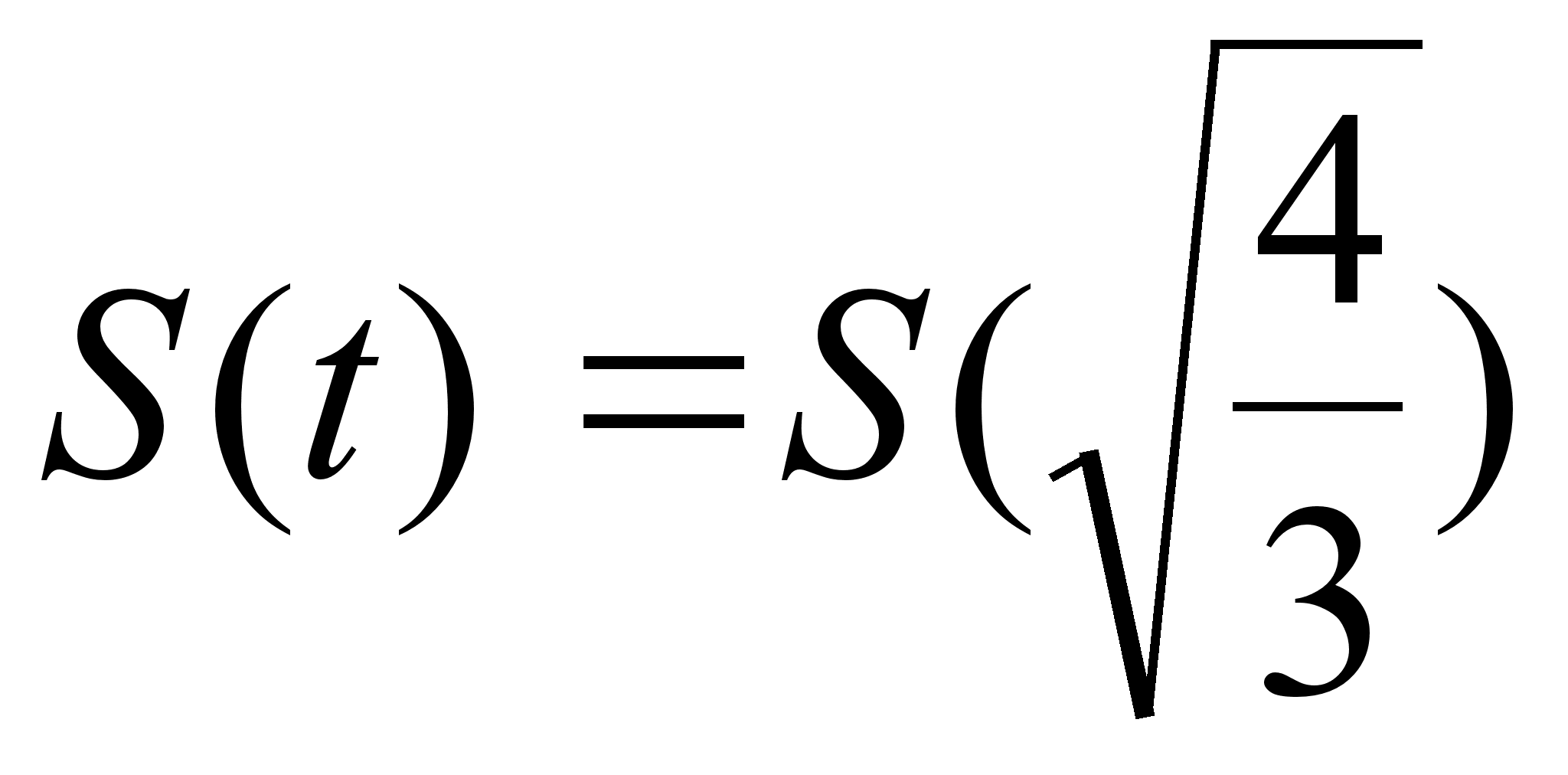 =
= .
.
(стоiть модуль, бо вiдстань повинна бути додатна).
Похiдна вiд вiдстанi це i швидкiсть, яку ми вже знайшли: 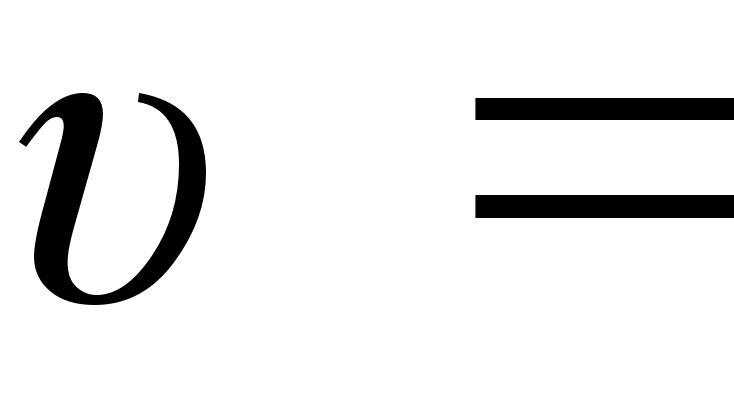
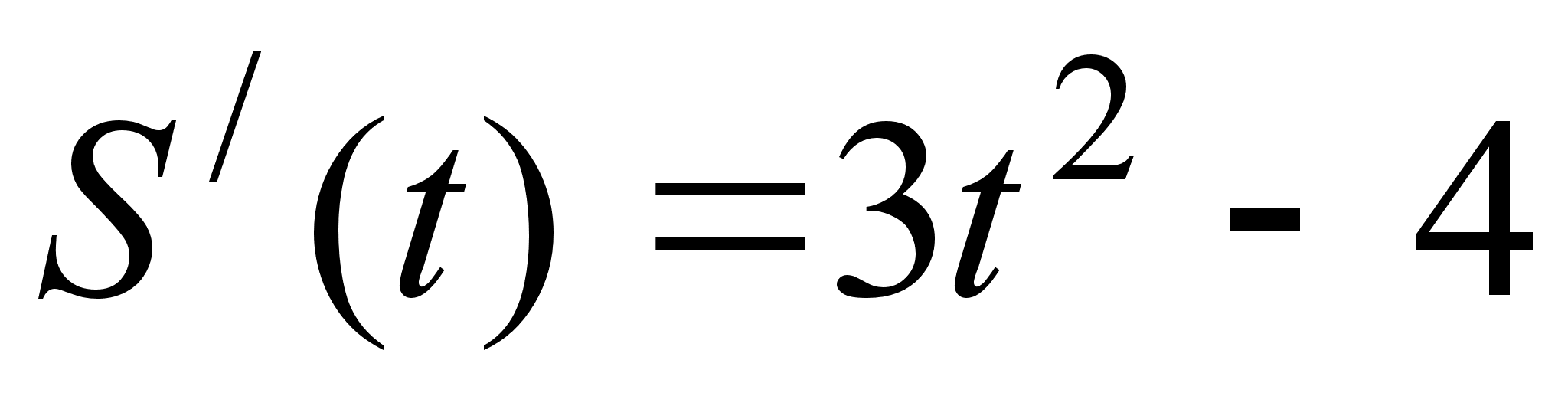 , тому через 2 секунди пiсля початку руху авто мало швидкiсть
, тому через 2 секунди пiсля початку руху авто мало швидкiсть 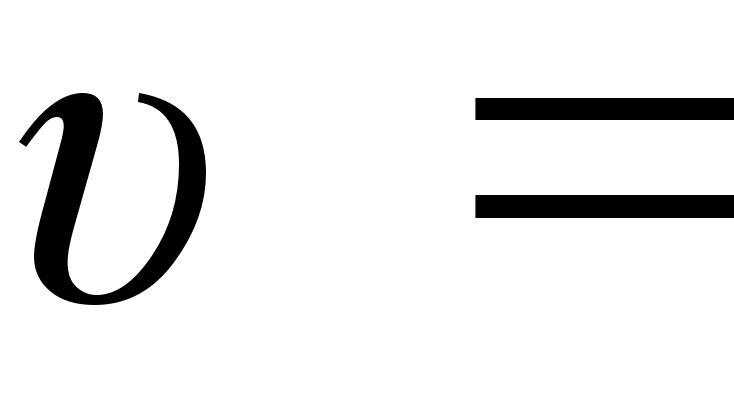
 м/с.
м/с.
Вз6 . МЕТОД ДОЦРЖЛЬНИХ ЗАДАЧ
В багатьох випадках , в певних темах цей метод застосовуiться не дуже часто, але при продовженнi деякоi теми, чи при вивченнi теми з розв’язання практичних задач краще скористатися ним, тодi в учнiв при вивченнi теми буде повнiше розумiння вивченого матерiалу. Як вже було вище сказано, суть методу в тому, що розгляд новоi теми розпочинаiться з наведення деяких прикладiв, що можуть допомогти учням краще орiiнтуватися в тому, про що йде мова в данiй темi, або протягом уроку посилатися на деякi з них.
Розглянемо його використання на прикладi вивчення теми “Функцii та iх графiки”.
Вчитель на початку уроку, але вже пiсля означення поняття функцii, може наводити приклади, будувати з учнями графiки, а потiм на основi графiкiв вивести певнi закономiрностi iх побудови i запропонувати учням використовувати цi закономiрностi при подальшому розв’язуваннi прикладiв.
П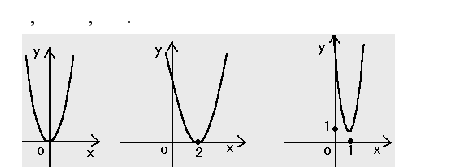 обудуiмо графiки таких елементарних функцiй:
обудуiмо графiки таких елементарних функцiй:
Мал. 16 Мал. 17 Мал.18
Учнi помiчають, що другий графiк (Мал. 17.) зсунутий на 2 одиницi вправо, а в формулi стоiть знак мiнус перед цiiю цифрою. Третiй графiк (Мал. 18.) вiдрiзняiться вiд другого тим, що не тiльки зсунутий по осi OX, а й по осi OY тАУ на 1, але тут вже спостерiгаiться вiдповiднiсть знаку.
Пiсля розглядання цих прикладiв учнi можуть сформулювати основнi правила побудови графiкiв не тiльки степеневих функцiй, а i графiкiв довiльних функцiй.
Запишемо загальний вигляд функцii: 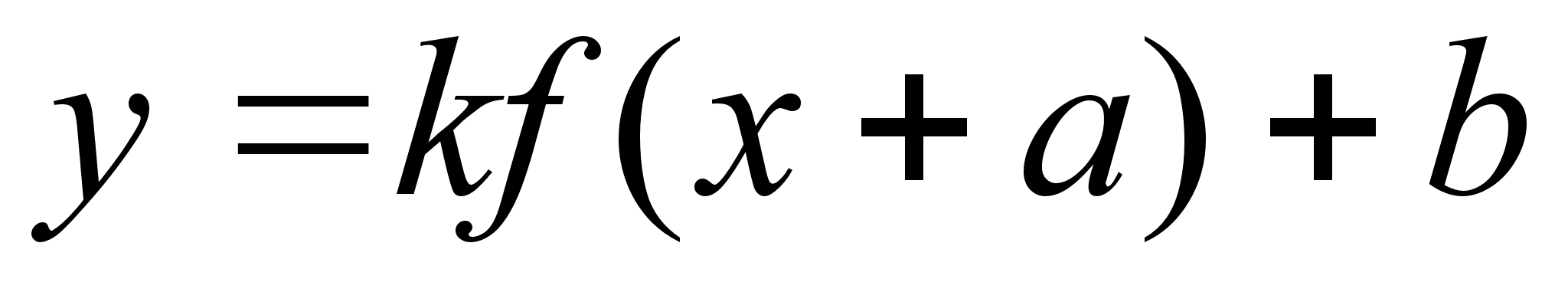 (
( ,
,  ).
).
Для побудови графiку довiльноi степеневоi функцii необхiдно:
побудувати графiк функцii
 ;
;зсунути його на a значень влiво (напрямок обирають протилежно до знаку a), при
 - влiво, при
- влiво, при  - вправо;
- вправо;зсунути на значень вгору (вiдповiднiсть зi знаком), при
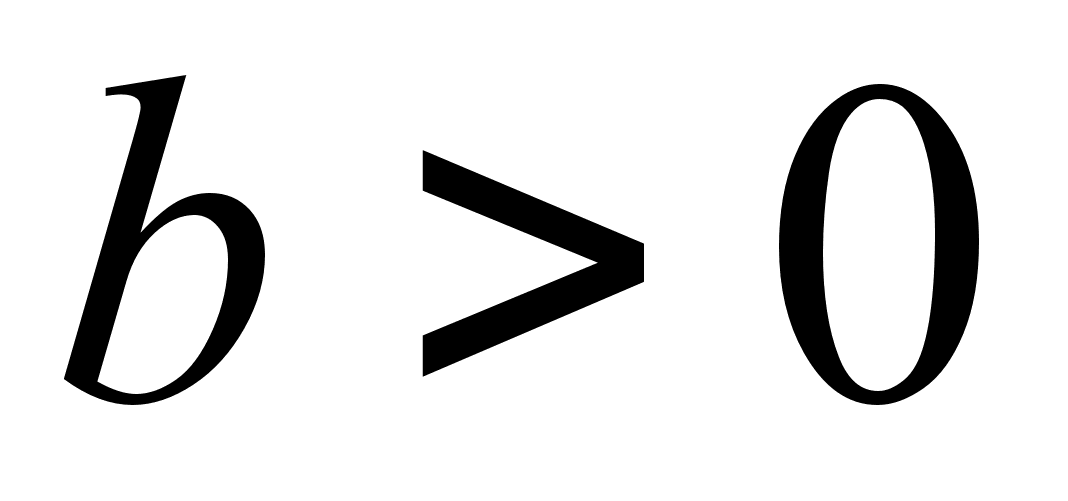 - вгору, при
- вгору, при 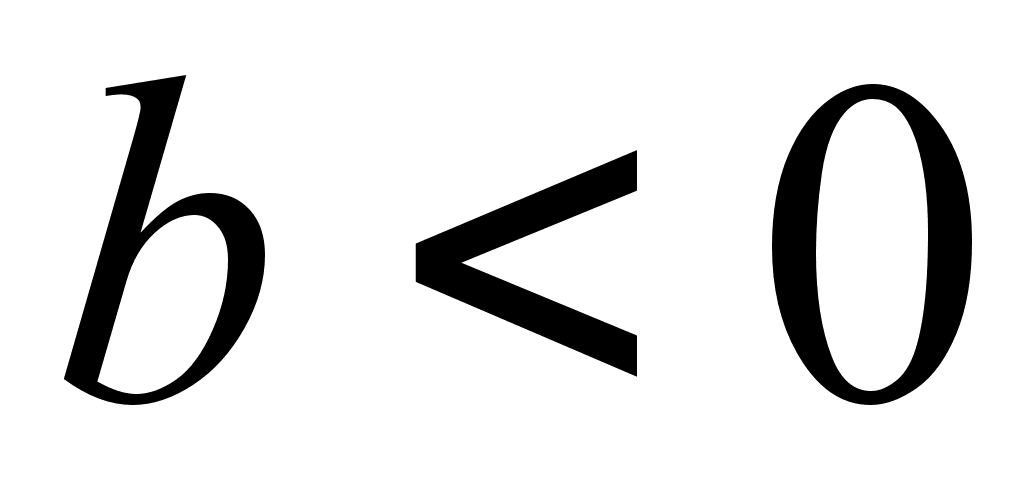 - вниз;
- вниз;стиснути в k разiв до осi
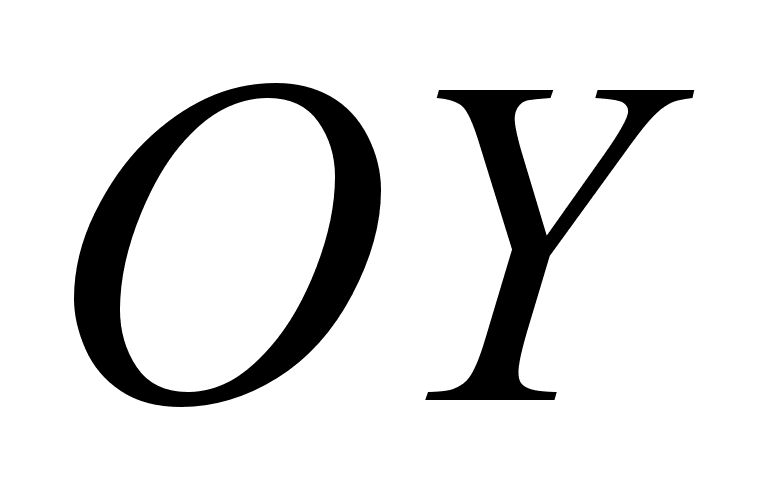 . (кожне значення функцii стаi в k раз бiльше).
. (кожне значення функцii стаi в k раз бiльше).
Доцiльно пiсля цього дати учням побудувати графiк деякоi функцii за точками., а коли вони його побудують, то показати простiший спосiб побудови графiка, за допомогою змiщення деякого вiдомого графiку по осям координат та стиснення його в 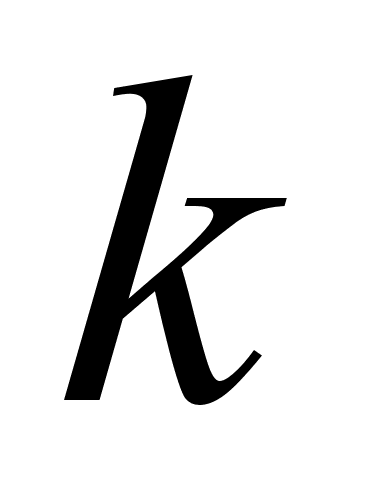 разiв.
разiв.
Так само i для тригонометричних функцiй. Тригонометричнi функцii викликають в учнiв бiльший iнтерес при побудовi, особливо при розгляданнi додавання та множення графiкiв.
Вз7. АБСТРАКТНО-ДЕДУКТИВНИЙ РЖ КОНКРЕТНО-РЖНДУКТИВНИЙ МЕТОДИ
Конкретно-iндуктивний метод i природним розширенням i удосконаленням методу доцiльних задач. За словами К.Ф.Лебединцева, цей метод краще пiдходить для застосування в шкiльному навчаннi. Метод чимось нагадуi проблемний виклад - вчитель пропонуючи розв’язати певний приклад, ставить перед класом невелику проблемну ситуацiю, а розв’язуючи цей приклад робить висновок чи даi означення.
При використаннi абстрактно-дедуктивного методу, вчитель повiдомляi тему уроку, даi означення, формулюi теореми, а вже пiсля викладу теорii переходить до практичних завдань. Учнi починають розв’язувати приклади, доводити твердження на основi вивчених означень чи властивостей певних об’iктiв, тим самим засвоюючи новий матерiал.
Розглянемо застосування абстрактно-дедуктивного методу на прикладi вивчення теми: “Застосування похiдноi до дослiдження функцiй”.
Вивчення починаiться з пригадування геометричного змiсту похiдноi, лише потiм можна перейти до вивчення новоi теми.
Геометричний змiст: Похiдна функцii f(x) в точцi х0 дорiвнюi тангенсу кута нахилу дотичноi до кривоi з додатним напрямом осi ОХ у точцi з абсцисою х0.
Тангенс кута нахилу дотичноi називають кутовим коефiцiiнтом 
Функцiя може зростати чи спадати на деякому промiжку (можна намалювати малюнок).





Означення. Функцiя f(x) тАУ називаiться зростаючою на промiжку  , якщо для довiльного x(а; b) , що x1 x2 виконуiться нерiвнiсть
, якщо для довiльного x(а; b) , що x1 x2 виконуiться нерiвнiсть
f (x1) f (x2).
Означення. Функцiя f(x) тАУ називаiться спадною на промiжку  , якщо для довiльного x(а; b) , що x1 x2 виконуiться нерiвнiсть
, якщо для довiльного x(а; b) , що x1 x2 виконуiться нерiвнiсть
f (x1) f (x2).
Далi в звичайних класах формулюються ознаки зростання та спадання функцii. При доведеннi ознак використовуiться формула Лагранжа, тому в класах з поглибленим вивченням математики можна спочатку довести теорему Лагранжа.
Теорема Лагранжа. Якщо функцiя f(x) неперервна i диференцiйовна на а; b, та iснуi точка с(а, b), то f(а)-f(b)=f /(с)(b-а).
Доведення
Р озглянемо функцiю f(x) що визначена на промiжку а, b та вiзьмемо точку с, що с(а, b).
озглянемо функцiю f(x) що визначена на промiжку а, b та вiзьмемо точку с, що с(а, b).
Дотична до графiка функцii f (x) утворюi кут з додатнiм напрямком осi ОХ.
Кут - подiбний куту ВАD.
ΔВАD тАУ прямокутний, тому 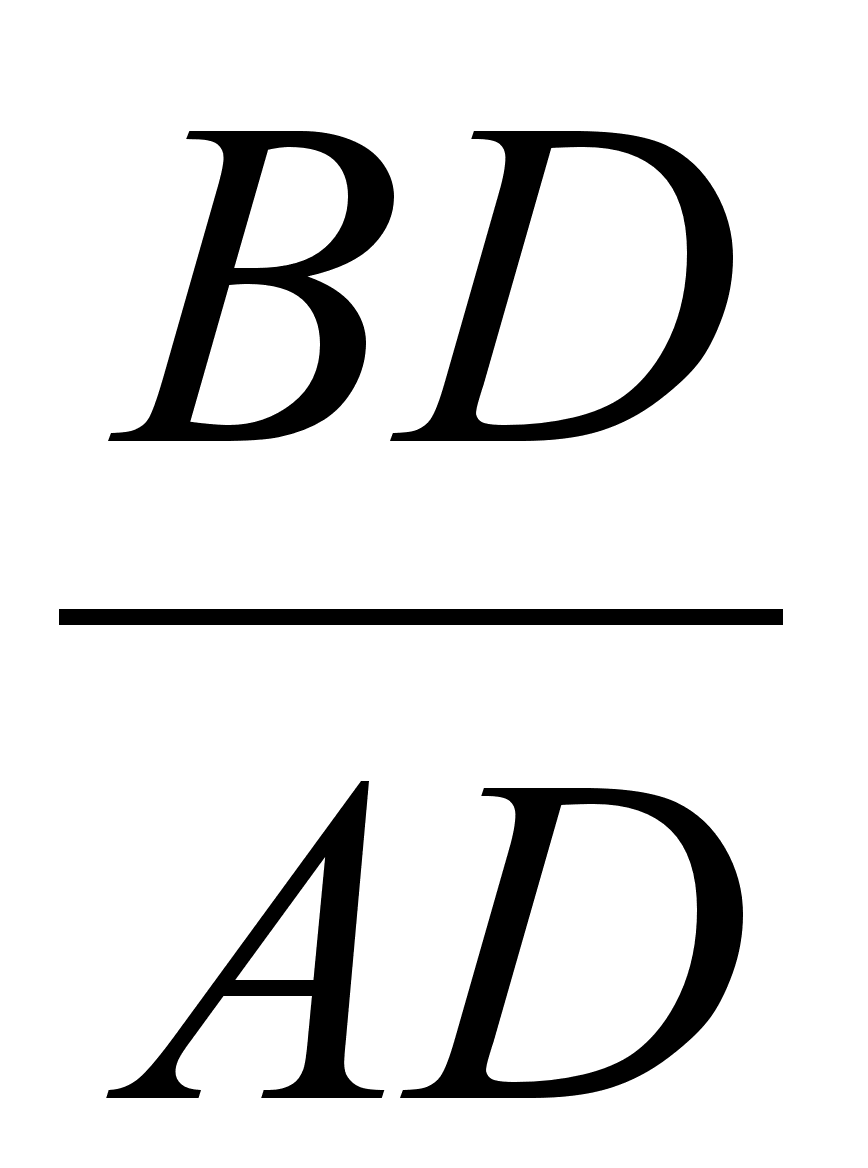 =tg()=f /(x).
=tg()=f /(x).
Так як ВD=f(b)-f(а), аАD=b-а, тому
f /(c)= - формула Лагранжа.
- формула Лагранжа.
Далi розглядаються ознаки зростання та спадання функцii.
Ознака зростання функцii:
Якщо функцiя f(x) неперервна i диференцiйовна в кожнiй точцi iнтервалу (x1; x2) i f /(x) 0 на цьому iнтервалi, то функцiя зростаi.
Ознака спадання функцii:
Якщо функцiя f(x) неперервна i диференцiйовна в кожнiй точцi iнтервалу (x1; x2) i f /(x) 0 на цьому iнтервалi, то функцiя спадаi.
Доведення цих ознак можна провести в класах з математичним нахилом.
При доведеннi використовуiться теорема Лагранжа.
Розв’язуiться приклад.
Приклад.
Як веде себе функцiя f(x)=x2-8x+12 на промiжках (-; 4)(4; +).
Д ослiдження. Знайдемо похiдну, критичнi точки та дослiдимо функцiю на кожному з отриманих промiжкiв: f /(x)=2x-8; тобто x=4 i це i критична точка. На промiжку (-; 4) похiдна маi вiд’iмний знак, тому функцiя спадаi, а на промiжку (4; +) похiдна маi додатнiй знак, тому функцiя на цьому промiжку зростаi.
ослiдження. Знайдемо похiдну, критичнi точки та дослiдимо функцiю на кожному з отриманих промiжкiв: f /(x)=2x-8; тобто x=4 i це i критична точка. На промiжку (-; 4) похiдна маi вiд’iмний знак, тому функцiя спадаi, а на промiжку (4; +) похiдна маi додатнiй знак, тому функцiя на цьому промiжку зростаi.
Ми отримали точку х=4, переходячи через яку похiдна змiнюi знак , тобто в цiй точцi дотична паралельна осi ОХ, а це може бути лише в найвищiй або в найнижчiй точцi. Таку точку називають точкою екстремуму. Похiдна функцii в цiй точцi дорiвнюi нулю, тобто кутовий коефiцiiнт рiвний нулю.
Точки максимумiв та мiнiмумiв функцii називають тАУ екстремальними точками.
Означення. Внутрiшнi точки областi визначення функцii в яких похiдна рiвна нулю або не iснуi тАУ називаються критичними точками.
Формулюiться Н еобхiдна умова iснування екстремуму функцii в точцi. (Терема Ферма)
Якщо функцiя f(x) - неперервна i диференцiйовна на (а, b) i в точцi x0 маi екстремум, то похiдна функцii в цiй точцi рiвна нулю.
Переходимо до розв’язування прикладiв.
Дослiдити на екстремуми функцiю:
f(x)=2х3-9х2+12х-8.
f /(x)=6х2-18х+12;
f /(x)=0;
6х2-18х+12=0;
х2-3х+12=0;
х1=1; х2=2.
Н аносимо критичнi точки на координатну вiсь i перевiряiмо знак на кожному з отриманих промiжкiв.
аносимо критичнi точки на координатну вiсь i перевiряiмо знак на кожному з отриманих промiжкiв.
f/(1)=-3; - максимум функцii
f/(2)= -4. тАУ мiнiмум функцii.
Вз8. ПРОГРАМОВАНЕ НАВЧАННЯ
Програмоване навчання використовуiться дуже часто, особливо цей метод використовують для написання самостiйних робот, контрольних, пiд час складання iспитiв. Використовують для контролю знань i iнодi для проведення урокiв, щоб пiдвищити увагу та зацiкавленiсть учнiв, коли вчитель спецiально заготовлюi програмованi завдання до тiii теми, яку важче розумiють учнi. Таким чином цей метод може покращувати рiвень знань учнiв.
Розглянемо деякi приклади завдань, що використовуються на вступних iспитах, на шкiльному випускному iспитi, та на контрольних роботах.
Визначити парнiсть (непарнiсть) функцii:
1) 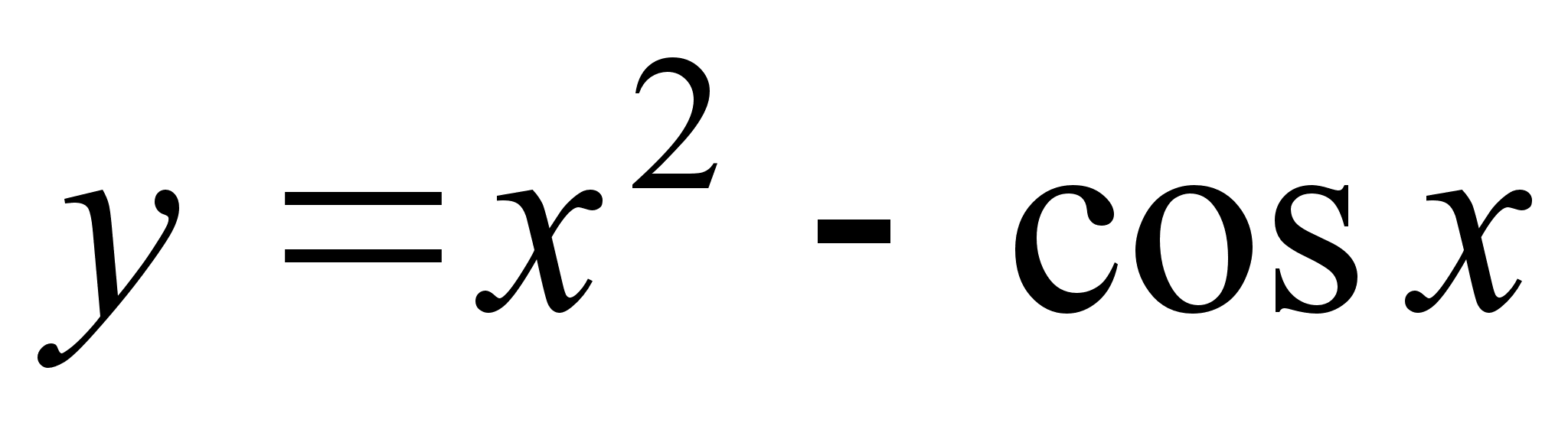
а) парна, б) непарна, в) iнша вiдповiдь.
(вiрно тАУ парна, бо  - парна функцiя,
- парна функцiя, - парна ).
- парна ).
2) 
а) парна, б) непарна, в) iнша вiдповiдь.
(вiрно тАУ iнша вiдповiдь, бо синус непарна функцiя, а косинус - парна).
Знайти область визначення функцii:
1)  ;
;
а)  , б)
, б)  , в) iнша вiдповiдь.
, в) iнша вiдповiдь.
Розв’язання. ОДЗ: 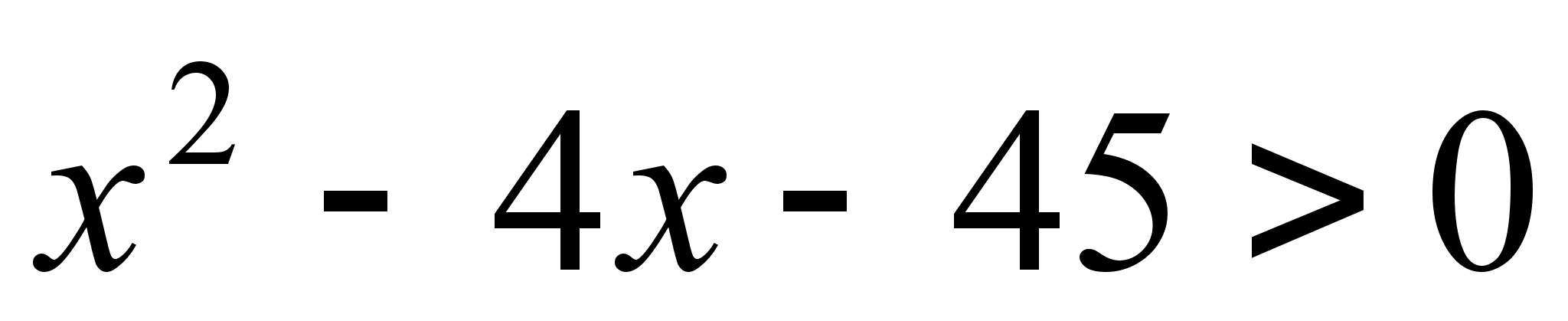 .
. 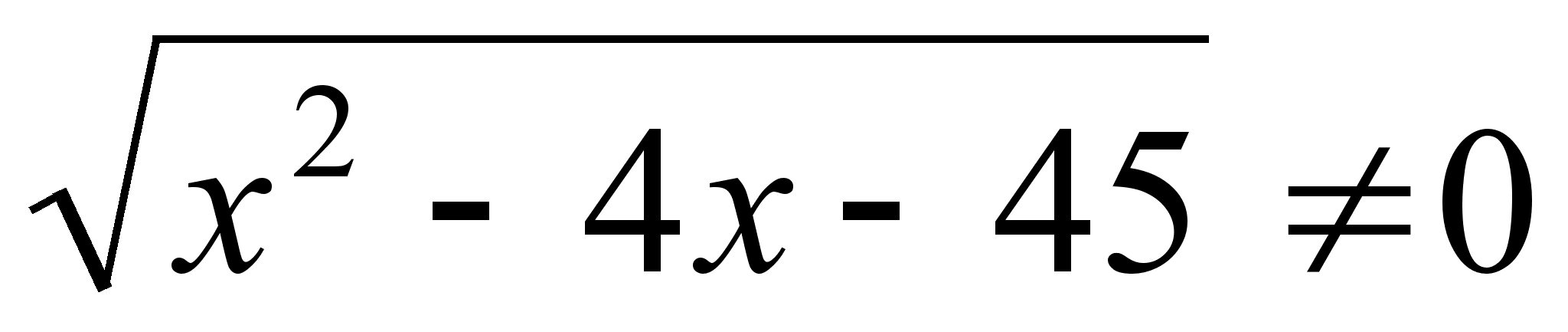 ,
, ,
, . Розглянемо отриманi промiжки, i виберемо з них тi, що задовольняють ОДЗ. Тобто
. Розглянемо отриманi промiжки, i виберемо з них тi, що задовольняють ОДЗ. Тобто 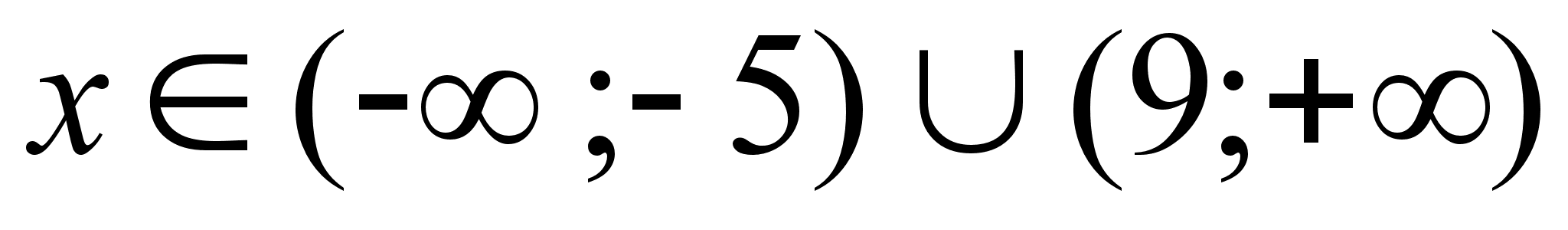 .
.
(вiрно -  ).
).
2) 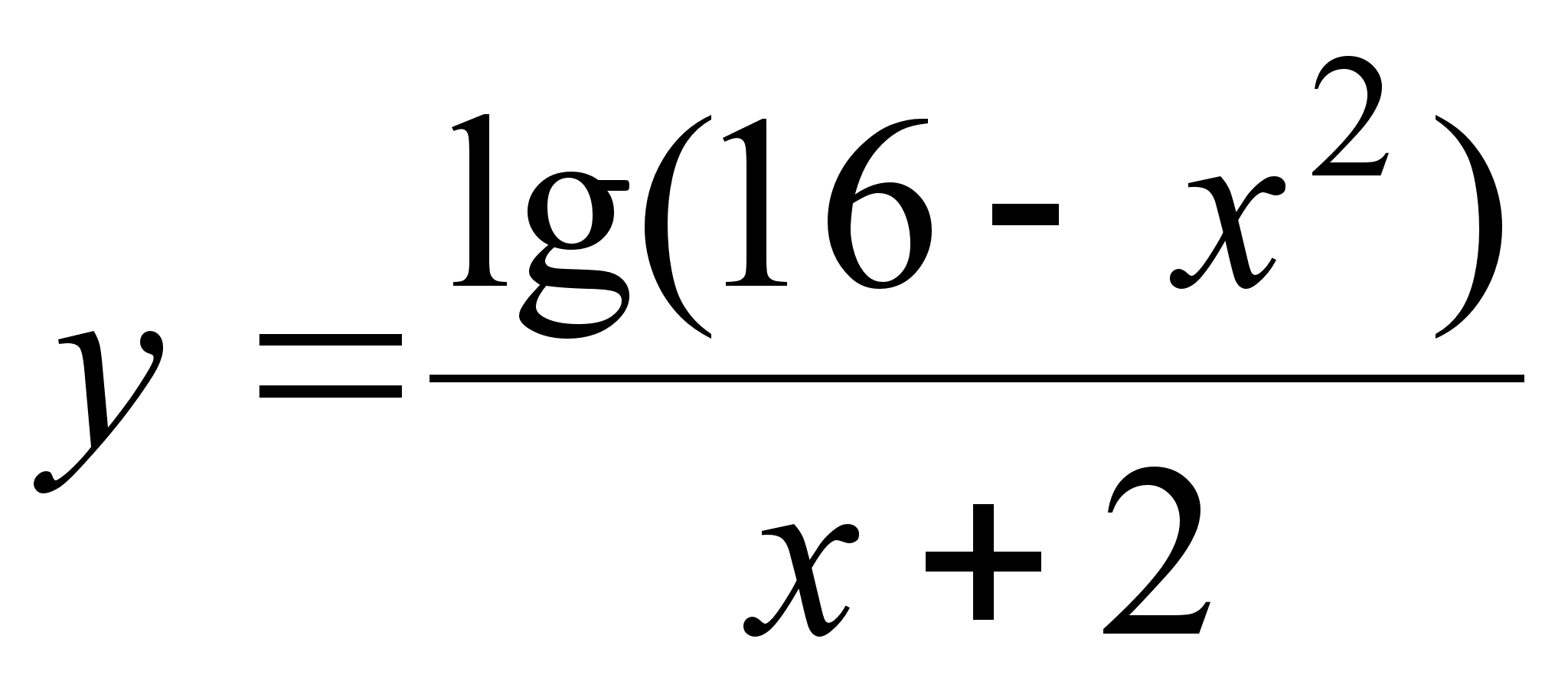 ;
;
а)  , б)
, б)  , в) iнша вiдповiдь.
, в) iнша вiдповiдь.
Розв’язання. Пiдлогарифмiчний вираз завжди додатнiй, а знаменник не рiвний нулю.
 ,
,
 ,
,
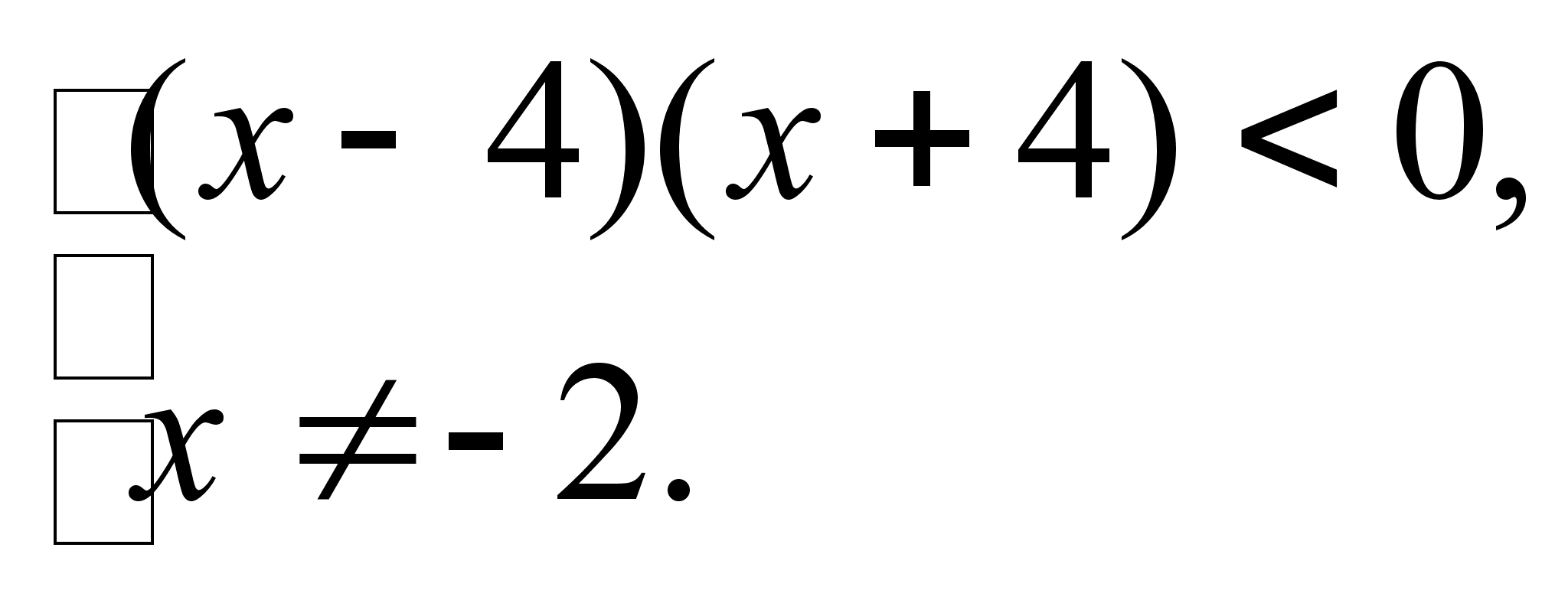
Нанесемо значення  "Инкарнация" кватернионов
"Инкарнация" кватернионов
10 способов решения квадратных уравнений
Cпособы преобразования комплексного чертежа, применение при изображении предметов
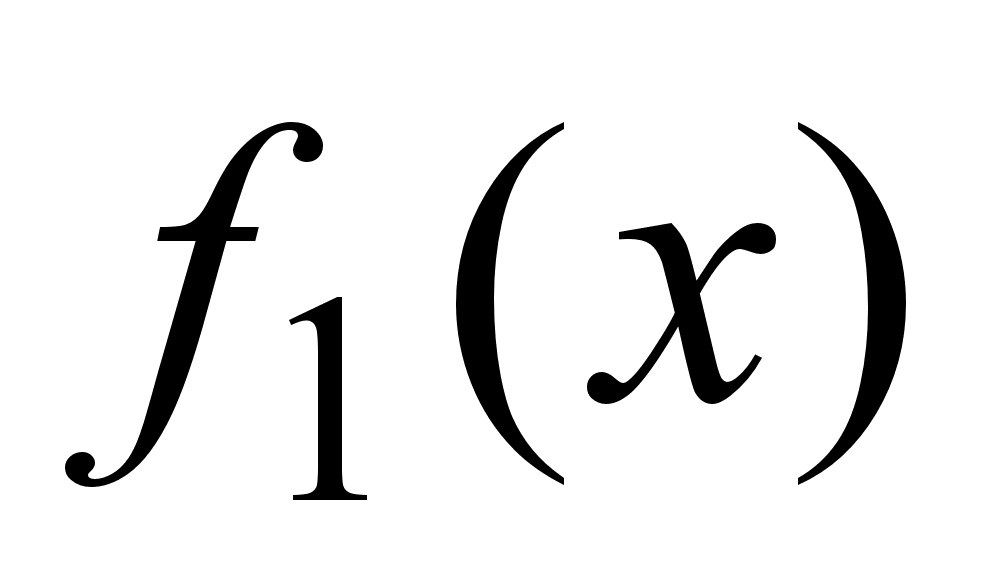 =
=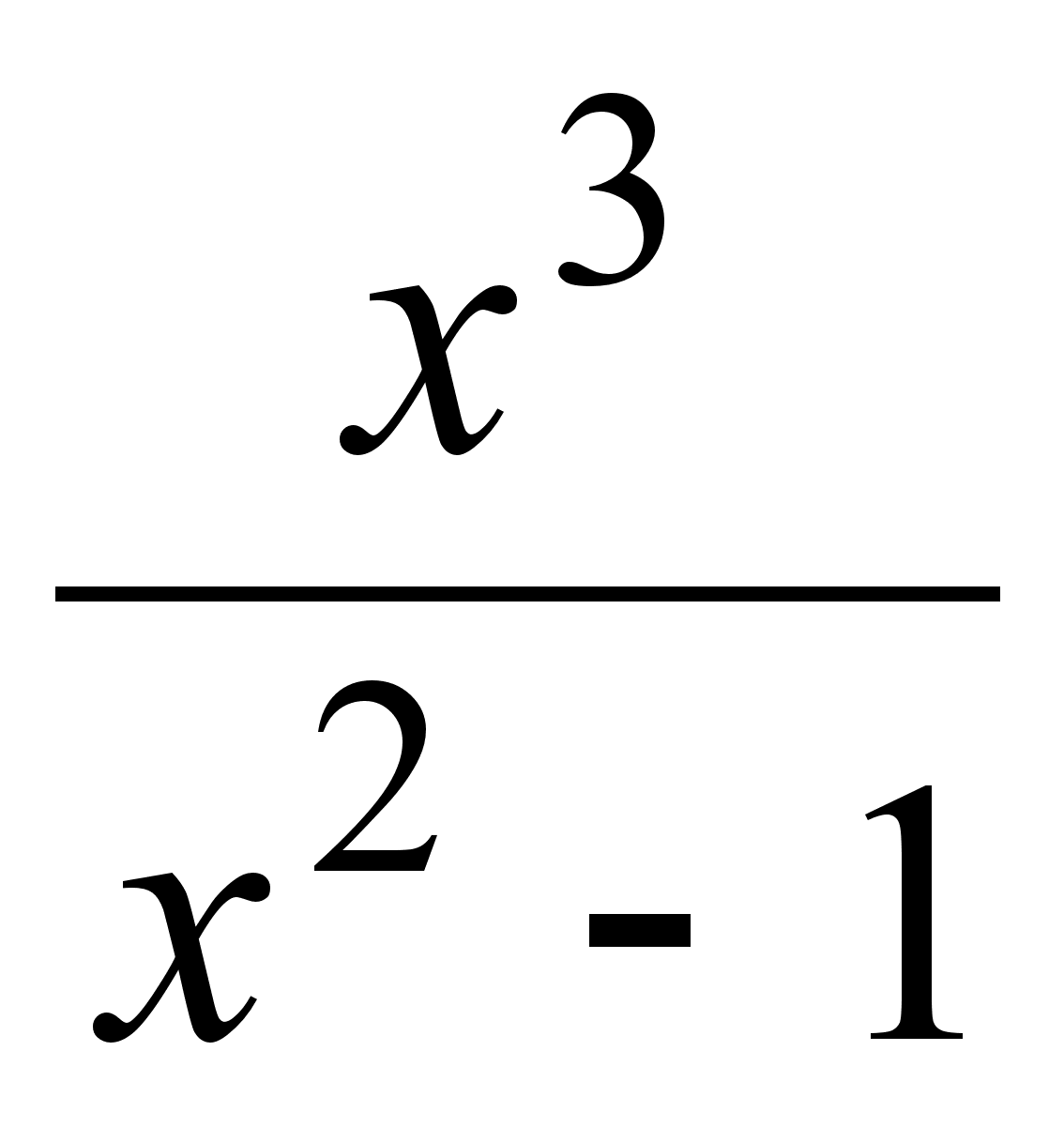
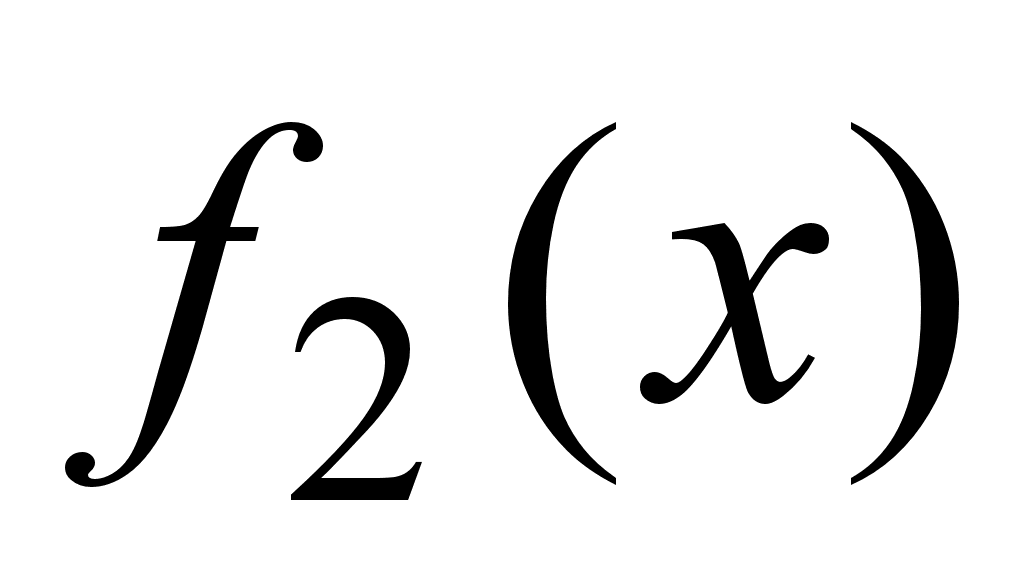 =
=
 )
)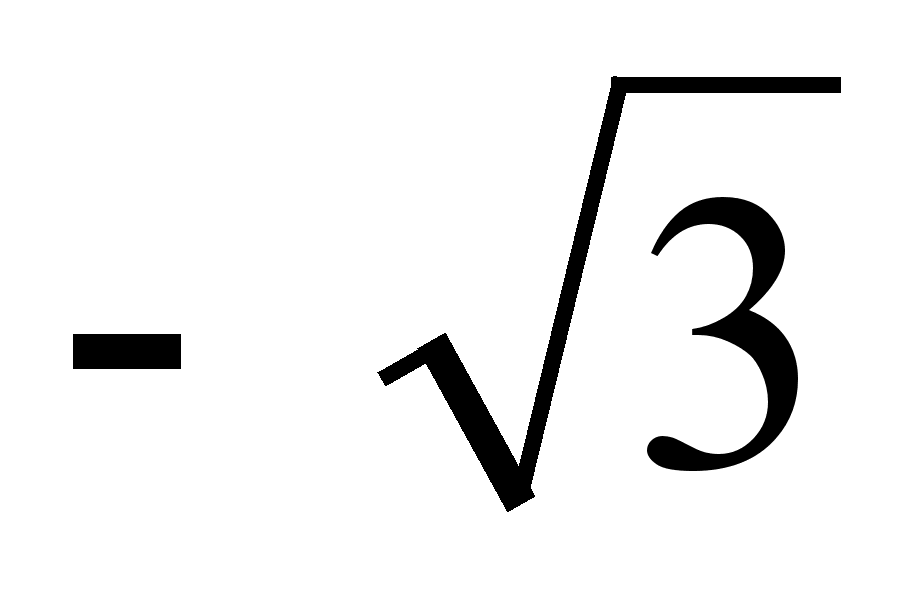 )
)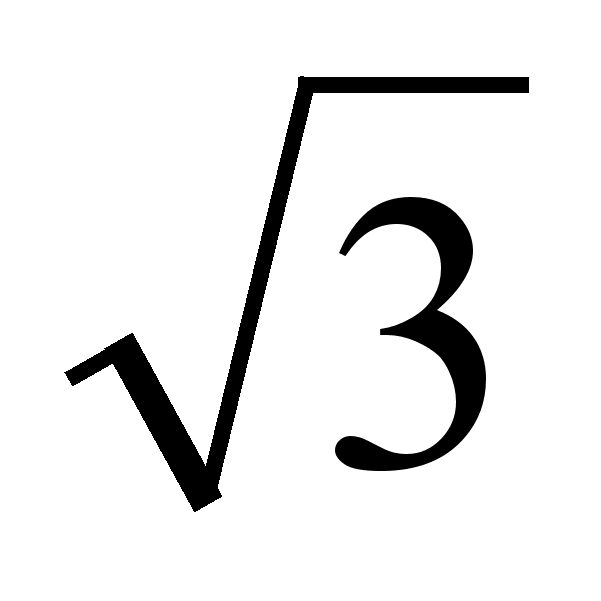 ;
; )
)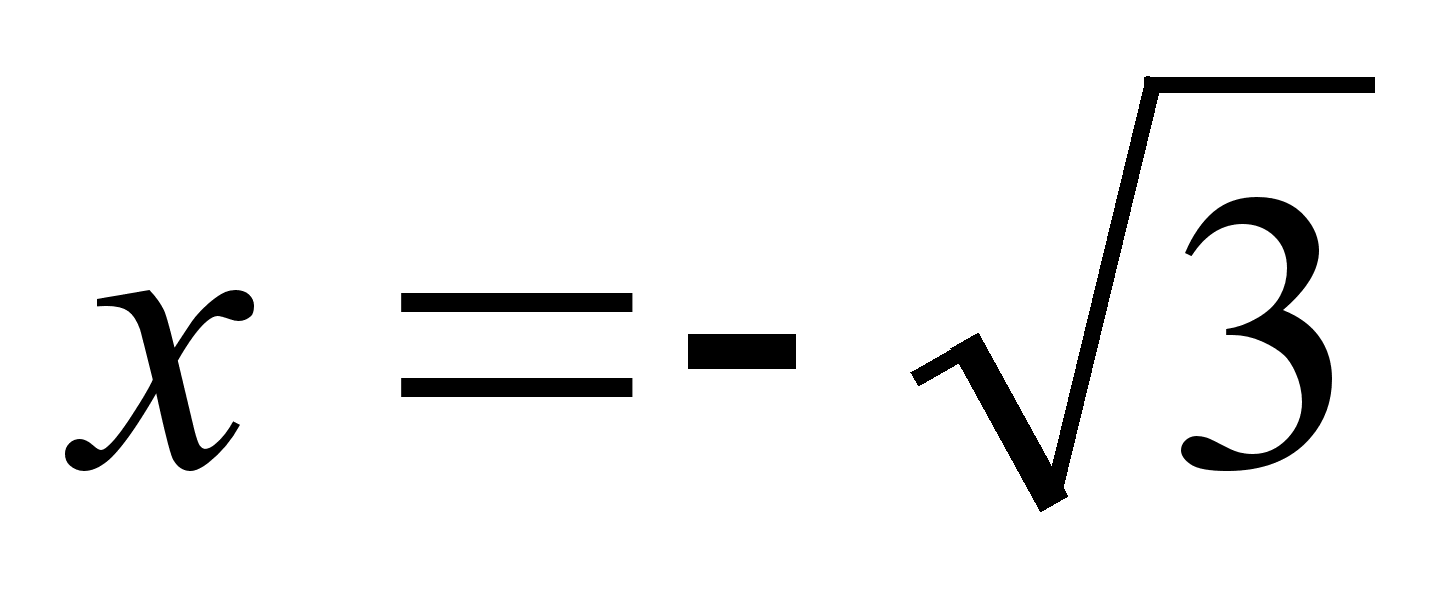 , для х
, для х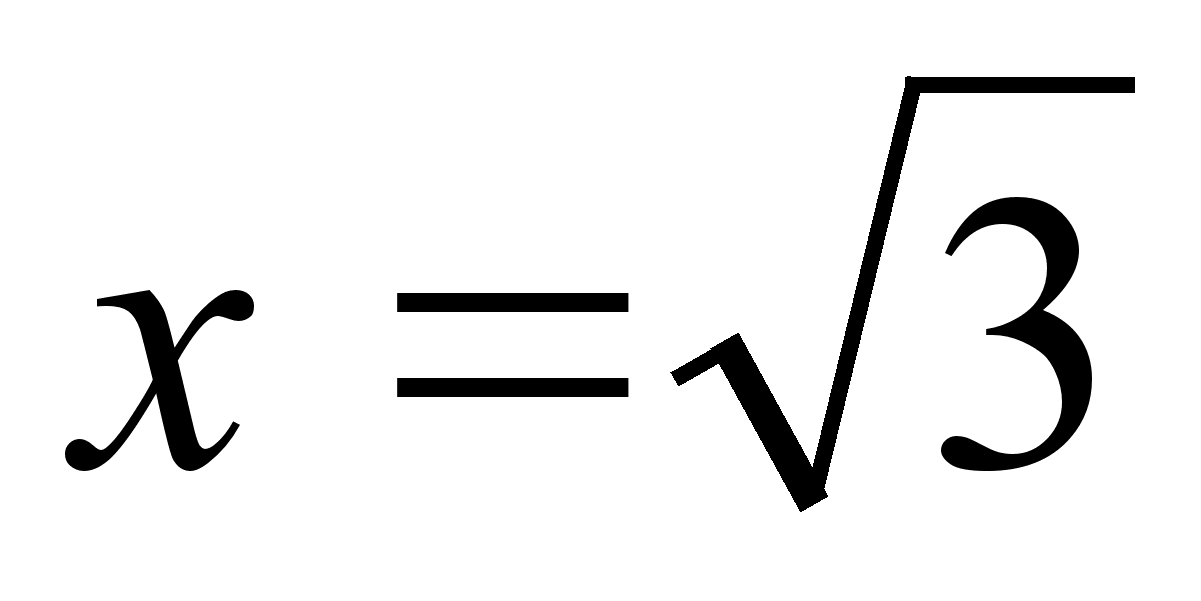 , для х
, для х
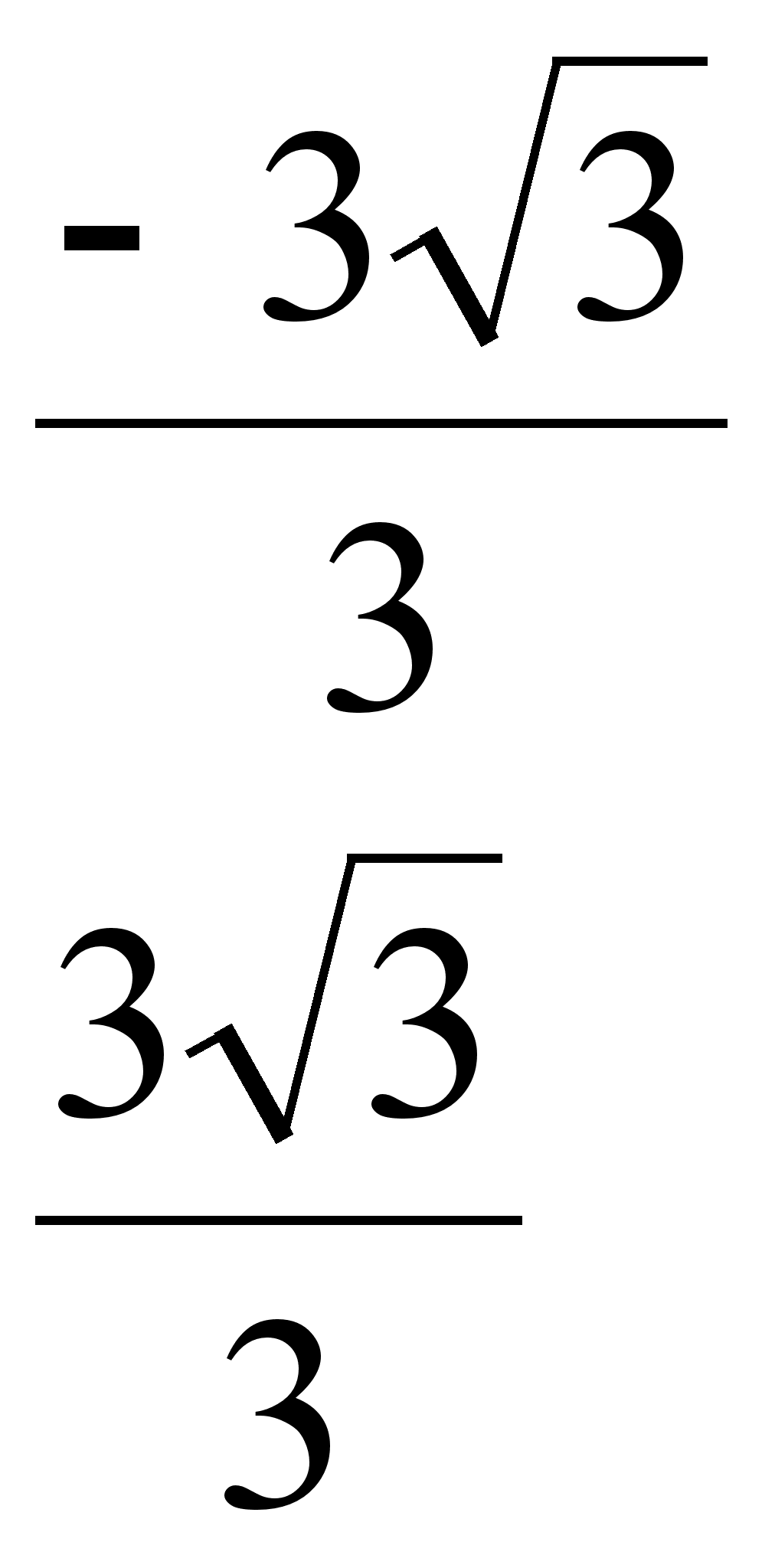
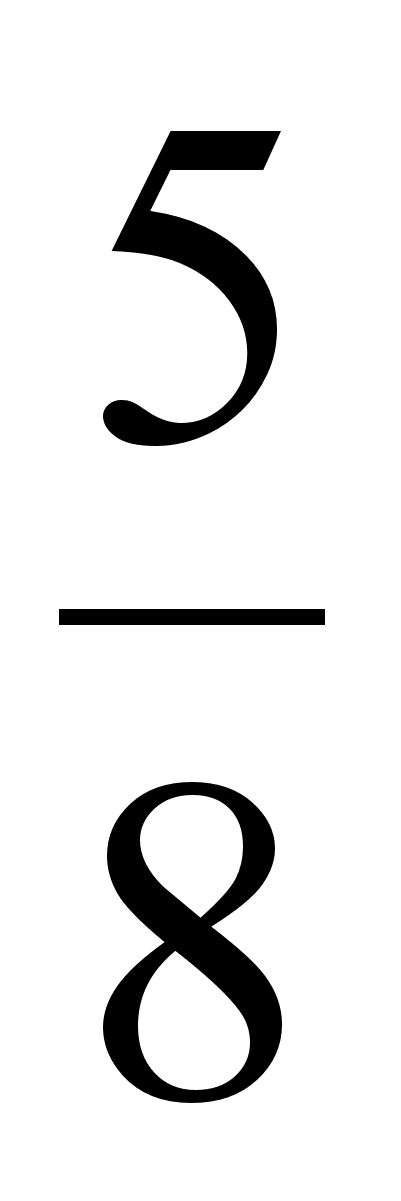
 ;-1)
;-1)