Некоторые дополнительные вычислительные методы
Министерство образования и науки РФ
ГОУ ВПО тАЬУГТУ-УПИтАЭ
Курсовая работа
по тАЬВычислительной математикетАЭ
на тему: тАЬНекоторые дополнительные вычислительные методытАЭ
Семестр № 3
Преподаватель Кочнев В.П.
Студент гр. № р-23021д Логиновских М.А.
Номер зачетной книжки 17309013
Екатеринбург
2004
_____________________________________________________________________________
Домашнее задание по ________________________________ № ________________
№ записи в книге регистрации __________________ дата регистрации ___________200_г.
Преподаватель _________________________________________
Студент _________________________________________ группа № ________________
Деканат ФДО _______________
СОДЕРЖАНИЕ
1. Решение систем линейных уравнений тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 3
а) Схема Халецкого тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.... 3
б) Метод Зейделя и условия сходимости тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 5
2. Методы решения нелинейных уравнений тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 6
а) Метод хорд тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 7
б) Метод Ньютона (метод касательных) тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 8
в) Метод итерации тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 9
3. Интерполирование и экстраполирование тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 11
а) Интерполирование с помощью многочленов тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 11
б) Интерполяционный многочлен Лагранжа тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 12
в) Интерполяционные многочлены Стирлинга и Бесселя тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 13
г) Тригонометрическое интерполирование тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАжтАжтАж.. 15
д) Интерполяция сплайнами тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАжтАжтАж.. 15
4. Численное дифференцирование и интегрирование тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАжтАж. 16
а) Постановка задачи численного интегрирования тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.. 16
б) Составные квадратурные формулы тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАж 17
5. Приближенное вычисление обыкновенных дифференциальных уравнений тАжтАжтАжтАж. 18
а) Метод Рунге-Кутта тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 18
б) Экстраполяционные методы Адамса тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 20
в) Метод Милна тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 20
г) Краевые задачи для обыкновенных дифференциальных уравнений тАжтАжтАжтАжтАжтАж.. 21
6. Приближенные методы решения дифференциальных уравнений с частными производными тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 21
а) Классификация дифференциальных уравнений второго порядка тАжтАжтАжтАжтАжтАжтАжтАж 22
б) Постановка краевых задач тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 23
в) Метод конечных разностей (метод сеток) тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж. 24
г) Разностные схемы для решения уравнения теплопроводности тАжтАжтАжтАжтАжтАжтАжтАжтАж 25
д) Разностные схемы для решения уравнения колебания струны тАжтАжтАжтАжтАжтАжтАжтАжтАж 26
7. Список литературы тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж 27
1. Решение систем линейных уравнений
Системы линейных уравнений (СЛУ) имеют в вычислениях очень большое значение, так как к ним может быть приведено приближенное решение широкого круга задач. Так, основными источниками возникновения СЛУ являются теория электрических цепей, уравнения балансов и сохранения в механике, гидравлике и т.д. Существует несколько способов решения таких систем, которые в основном делятся на два типа: 1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы, 2) итерационные методы, позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов. Заметим, что даже результаты точных методов являются приближенными из-за неизбежных округлений. Для итерационных процессов также добавляется погрешность метода.
Пример системы линейных уравнений: 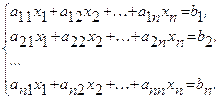
Или в матричном виде: 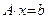 ,
,
где  матрица коэффициентов системы;
матрица коэффициентов системы;
 - вектор неизвестных;
- вектор неизвестных; 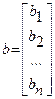 - вектор свободных членов.
- вектор свободных членов.
Схема Халецкого
Запишем систему линейных уравнений в матричном виде: 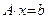 ,
,
где A=[aij] тАУ квадратная матрица порядка n и
 ,
, 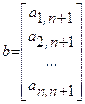 - векторы-столбцы.
- векторы-столбцы.
Представим матрицу A в виде произведения нижней треугольной матрицы B=[bij] и верхней треугольной матрицы C=[cij] с единичной диагональю 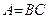 , где
, где
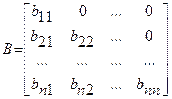 и
и 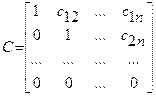 .
.
Тогда элементы bij и cij определяются по формулам
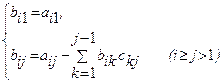 и
и 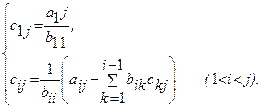
Отсюда искомый вектор x может быть вычислен из уравнений 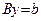 и
и  .
.
Так как матрицы B и C тАУ треугольные, то системы легко решаются:
 и
и 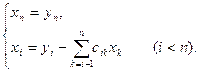
Из этих двух формул видно, что числа yi выгодно вычислять вместе с коэффициентами cij. Этот метод получил название схемы Халецкого. В схеме применяется обычный контроль с помощью сумм. Если матрица A тАУ симметрическая aij=aji, то 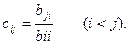
Пример. Решить систему 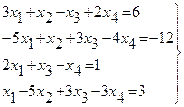
Решение.
В первый раздел таблицы впишем матрицу коэффициентов системы, ее свободные члены и контрольные суммы. Далее так как 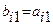
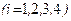 , то первый столбец из раздела 1 переносится в первый столбец раздела II. Чтобы получить первую строку раздела II, делим все элементы первой строки раздела I на элемент
, то первый столбец из раздела 1 переносится в первый столбец раздела II. Чтобы получить первую строку раздела II, делим все элементы первой строки раздела I на элемент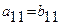 , в нашем случае на 3.
, в нашем случае на 3.
Имеем: 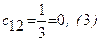 ;
; 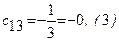 ;
; 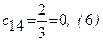 ;
; 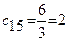 ;
; 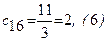 .
.
Переходим к заполнению второго столбца раздела II, начиная со второй строки. Пользуясь формулами, определяем 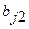 :
: 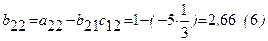 ;
; 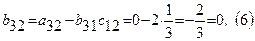 ;
; 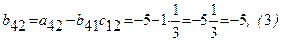 .
.
Далее определяя по формулам, заполняем вторую сетку для раздела II:
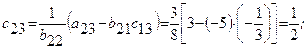
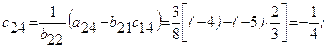
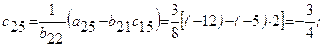
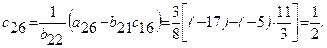
Затем переходим к третьему столбцу, вычисляя его элементы  и
и 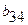 по формулам и т.д., пока не будет заполнена вся таблица раздела II. Таким образом, заполнение раздела II происходит способом тАЬелочкитАЭ: столбец - строка, столбец - строка и т.д.
по формулам и т.д., пока не будет заполнена вся таблица раздела II. Таким образом, заполнение раздела II происходит способом тАЬелочкитАЭ: столбец - строка, столбец - строка и т.д.
В разделе Ш, пользуясь формулами, определяем 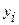 и
и 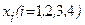 .
.
Текущий контроль осуществляется с помощью столбца ∑, над которым производятся те же действия, что и над столбцом свободных членов.
| 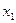
| 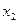
| 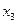
| 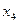
| | 
| 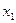
| 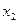
| 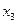
| 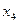
| | 
|
| I | 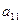
| 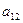
| 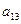
| 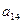
| 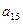
| 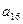
| 3 | 1 | -1 | 2 | 6 | 11 |
| I | 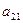
| 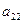
| 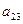
| 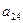
| 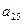
| 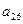
| -5 | 1 | 3 | -4 | -12 | -17 |
| I | 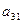
| 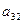
| 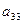
| 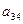
| 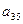
| 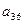
| 2 | 0 | 1 | 1 | 1 | 3 |
| I | 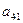
| 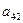
| 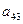
| 
| 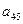
| 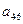
| 1 | -5 | 3 | 3 | 3 | -1 |
| II | 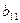
| 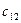
| 
| 
| 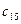
| 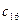
| 3 | 0.333333 | -0.333333 | 2 | 2 | 3.666667 |
| II | 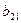
| 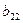
| 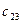
| 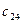
| 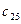
| 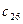
| -5 | 2.666667 | -0.25 | 0.25 | -0.75 | 0.5 |
| II | 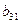
| 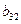
| 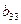
| 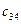
| 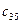
| 
| 2 | -0.666667 | 2 | -1.25 | -1.75 | -2 |
| II | 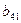
| 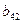
| 
| 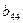
| 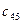
| 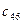
| 1 | -5.333333 | 6 | 2.5 | 3 | 4 |
| III | | | | | 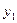
| 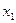
| | | | | 2 | 1 |
| III | | | | | 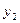
| 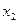
| | | | | -0.75 | -1 |
| III | | | | | 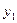
| 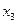
| | | | | -1.75 | 2 |
| III | | | | | 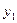
| 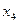
| | | | | 3 | 3 |
Метод Зейделя и условия сходимости
Этот метод представляет собой модификацию метода простой итерации. Его смысл заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1)-е приближения x1, x2, .., xi-1. Пусть дана приведенная линейная система 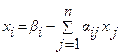 (i = 1, 2, тАжn). Выберем произвольно начальные приближения корней
(i = 1, 2, тАжn). Выберем произвольно начальные приближения корней 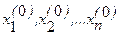 , стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным x1, x2, x3, .., xn. Предположим, что k-е приближение
, стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным x1, x2, x3, .., xn. Предположим, что k-е приближение  корней известно, тогда в соответствии с идеей метода будем строить (k+1)тАУе приближение по следующим формулам:
корней известно, тогда в соответствии с идеей метода будем строить (k+1)тАУе приближение по следующим формулам: 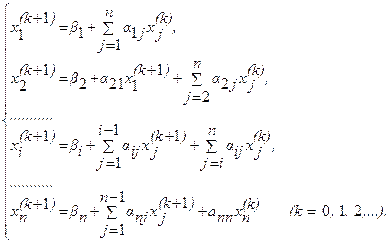
Обычно процесс Зейделя сходится быстрее, чем метод простой итерации. Бывает, что процесс Зейделя сходится, когда простая итерация расходится и т.п. Правда, бывает и наоборот. Во всяком случае, достаточные условия сходимости для метода простой итерации достаточны и для сходимости метода Зейделя. То есть процесс итерации сходится, если выполнено одно из условий
1) 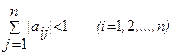 или 2)
или 2) 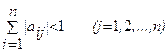 .
.
Пример. Методом Зейделя решить систему уравнений 
Решение. Приведем эту систему к виду, удобному для итерации, 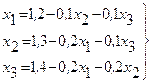
В качестве нулевых приближений корней возьмем: 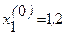 ;
; 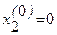 ;
; 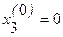 .
.
Применяя процесс Зейделя, последовательно получим:
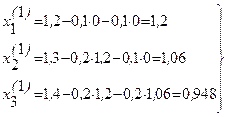
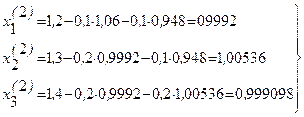 и т.д.
и т.д.
Результаты вычислений с точностью до четырех знаков помещены в таблице:
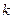
| 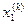
| 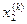
| 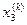
|
| 0 | 1,2000 | 0,0000 | 0,0000 |
| 1 | 1,2000 | 1 ,0600 | 0,9480 |
| 2 | 0,9992 | 1,0054 | 0,9991 |
| 3 | 0,9996 | 1.0001 | 1,0001 |
| 4 | 1 ,0000 | 1,0000 | 1,0000 |
| 5 | 1 ,0000 | 1,0000 | 1,0000 |
Точные значения корней: 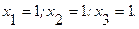 .
.
2. Методы решения нелинейных уравнений
Как известно, далеко не всякое уравнение f(x)=0 можно решить точно, т.е. не всегда можно найти число 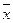 такое что f(
такое что f(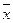 )≡0. В первую очередь это относится к трансцендентным уравнениям. Кроме того, даже для алгебраических уравнений степени выше четвертой не существуют формулы, выражающей их решения через коэффициенты уравнения при помощи арифметических операций и извлечение корней. Для уравнений третьей и четвертой степени формулы для отыскания корней существуют, но они настолько сложны, что практически не применяются. Поэтому большое значение имеет приближенное вычисление корней уравнения f(x)=0. Для этого существует множество методов некоторые, из которых мы рассмотрим.
)≡0. В первую очередь это относится к трансцендентным уравнениям. Кроме того, даже для алгебраических уравнений степени выше четвертой не существуют формулы, выражающей их решения через коэффициенты уравнения при помощи арифметических операций и извлечение корней. Для уравнений третьей и четвертой степени формулы для отыскания корней существуют, но они настолько сложны, что практически не применяются. Поэтому большое значение имеет приближенное вычисление корней уравнения f(x)=0. Для этого существует множество методов некоторые, из которых мы рассмотрим.
Метод хорд
Пусть дано уравнение f(x)=0, где функция f(x) определена и непрерывна на интервале
[a, b] и f(a)f(b)<0. Пусть для определенности f(a)<0 и f(b)>0. Разделим отрезок [a, b] в отношении - f(a):f(b). Это даст нам приближенное значение корня x1 = a + h1, где
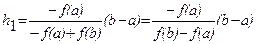 .
.
Далее этот прием применяем к одному из отрезков [a, x1] или [x1, b], на концах которого функция f(x) имеет противоположные знаки. Аналогично находим второе приближение x2 и т.д. Геометрически этот способ эквивалентен замене кривой y = f(x) хордой, проходящей через точки А[a, f(a)] и B[b, f(b)].

f(b)