Об алгебраических уравнениях высших степеней

Министерство общего и профессионального образования РФ

Кубанский государственный технологический университет

Кафедра общей математики

ОБ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЯХ ВЫСШИХ СТЕПЕНЕЙ

Белокопытов А.Ю., Морозов В.О.

группа 20-КТ-61

Краснодар, 2001

Уравнения! Можно утверждать наверняка, что не найдется ни одного человека, который бы не был знаком с ними. Дети сызмала начинают решать Влзадачи с иксомВ». Дальше тАУ больше. Правда, для многих знакомство с уравнениями и заканчивается школьными делами. Известный немецкий математик Курант писал: ВлНа протяжении двух с лишним тысячелетий обладание некоторыми, не слишком поверхностными, знаниями в области математики входило необходимой составной частью в интеллектуальный инвентарь каждого образованного человекаВ». И среди этих знаний было умение решать уравнения.

Уже в древности люди осознали, как важно научиться решать алгебраические уравнения вида

a₀xⁿ + a₁x^{n тАУ 1} + тАж + a_n = 0

тАУ ведь к ним сводятся очень многие и очень разнообразные вопросы практики и естествознания (конечно, здесь можно сразу предполагать, что а₀ ¹ 0, так как иначе степень уравнения на самом деле не , а меньше). Многим, разумеется, приходила в голову заманчивая мысль найти для любой степени формулы, которые выражали бы корни уравнения через его коэффициенты, т.е., решали бы уравнение в радикалах. Однако Влмрачное средневековьеВ» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи тАУ в течение целых семи столетий требуемых формул никто не нашел! Только в XVI веке итальянским математикам удалось продвинуться дальше тАУ найти формулы для = 3 и 4. История их открытий и даже авторство найденных формул достаточно темны по сей день, и мы не будем здесь выяснять сложные отношения между Ферро, Кардано, Тартальей и Феррари, а изложим лучше математическую суть дела.

Рассмотрим сначала уравнение

a₀x³ + a₁x² + a₂x + a₃ = 0.

Легко проверить, что если мы положим 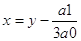, где y тАУ новое неизвестное, то дело сведется к решению уравнения

y³ + py + q = 0,

где p, q тАУ новые коэффициенты. Счастливая догадка итальянцев состояла в том, чтобы искать y в виде суммы y = u + v, где u, v тАУ д в а новых неизвестных. Для них наше уравнение перепишется тАУ после небольшой перегруппировки слагаемых тАУ так:

u³ + v³ + (3uv + )(u + v) + q = 0.

Так как неизвестных теперь два, на них можно наложить еще какое-нибудь условие тАУ лучше всего

3uv + = 0,

тогда исходное уравнение примет совсем простой вид

u³ + v³ + q = 0.

Это означает, что сумма кубов u³, v³ должна равняться тАУ q, а их произведение . Следовательно, сами u³, v³ должны быть конями квадратного уравнения

t² + qtтАУ p³/27 = 0,

а для него формула уже известна. В итоге получается формула

причем из девяти пар значений входящих в нее кубических радикалов надо брать только пары, дающие в произведении тАУp/3, как вытекает из нашего рассуждения. Исторически за этой формулой закрепилось название формулы Кардано, хотя вопрос о ее авторстве так до конца и не выяснен.

Для = 4 формулу открыл Феррари, она выглядит сложнее, но тоже использует только четыре арифметических действия и извлечение радикалов. Вот набросок вывода формулы Феррари. Прежде всего, подобно предыдущему, положим 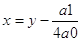, тогда дело сведется к решению уравнения вида

y⁴ + py² + qy + r = 0.

Дополнив y⁴ до (y² + z)², т.е. прибавив и вычтя в левой части 2zy² + z², где z тАУ вспомогательное неизвестное, получим

(y² + z)² тАУ [(2z тАУ ) y² тАУ qy + (z² тАУ r)] = 0.

Подберем теперь z так, чтобы квадратный трехчлен в квадратных скобках оказался полным квадратом; для этого нужно, чтобы его дискриминант равнялся нулю, т.е. чтобы было

q² тАУ 4(2z тАУ p) (z² тАУ r) = 0.

Можем ли мы решить это уравнение относительно z? Да, можем, так как оно кубическое. Пусть z₀тАУ какой-нибудь его корень (даваемый формулой Кардано) тогда исходное уравнение перепишется в виде

[(y² + z₀) тАУ (тАж)] * [(y² + z₀) + (тАж)] = 0,

где многоточия означают многочлен не более чем первой степени от y, оба раза один и тот же.

;

;

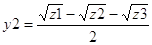
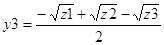При этом знаки перед радикалами 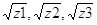выбирают так, чтобы выполнялось равенство .

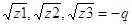В 1770-71 гг. знаменитый французский математик Лагранж (1736-1819) публикует в Мемуарах Берлинской Академии свой мемуар ВлМысли над решением алгебраических уравненийВ», в котором делает критический пересмотр всех решений уравнений 3-й и 4-й степеней, данных его предшественниками, и замечает, что все они в сущности основаны на следующем принципе. Пусть x₁, x_2, тАж, x_nбудут корни заданного уравнения, и пусть j (x₁, x_2, тАж, x_n) будет их рациональная функция, принимающая при всевозможных ! перестановках между корнями v значений. Тогда эта функция удовлетворяет уравнению степени v с рациональными коэффициентами. Согласно точке зрения Лагранжа, задача заключается в том, чтобы подобрать функцию j (x₁, x_2, тАж, x_n) таким образом, чтобы v было меньше . И вот оказалось, что при п>4 невозможно.

Эти исследования Лагранжа дали для последующих алгебраистов весьма удобный аппарат. Кроме того, они указали путь, по которому следовало искать доказательства невозможности общего решения уравнений в радикалах.

Дальнейшим этапом в выяснении проблемы решения уравнений в радикалах послужили работы Руффини (P. Ruffini, 1765-1822) и Абеля (N.-H. Abel, 1802 - 1829). Руффини (1799) предложил доказательство неразрешимости в радикалах уравнений 5-й степени, коэффициенты которого являются независимыми переменными. Однако его доказательство окончилось неудачей.

Нужен был принципиально новый подход. На этот раз он не заставил себя долго ждать тАУ уже в 1824 году молодой (и в возрасте 27 лет умерший) норвежский математик Нильс Генрик Абель, опираясь на идеи Лагранжа, связанные с перестановками корней уравнения, доказал, что требуемых формул, которые решали бы в радикалах уравнение общего вида, при ³5 действительно не существует. Теорема Абеля дала отрицательный ответ только для уравнений общего вида, т.е. с буквенными коэффициентами a₀, a₁, тАж, a_n, но, разумеется, многие конкретные уравнения сколь угодно высокой степени вполне могут решаться в радикалах (пример: уравнение x⁹⁰ + 5x⁴⁵ + 7 = 0). Поэтому сразу же встал вопрос о полном решении задачи тАУ нахождении критерия разрешимости уравнений в радикалах, т.е. необходимого и достаточного условия, которое по коэффициентам a₀, a₁, тАж, a_n любого заданного уравнения позволяло бы судить, решается уравнение в радикалах или нет.

Вопрос о разрешимости уравнений в радикалах был окончательно разобран, во всяком случае принципиально, в работах Галуа (Evariste Galois, 1811-1832). Личность Галуа представляет собой совершенно исключительное в истории науки явление. Жизнь Галуа, умершего всего на 21 году, протекала крайне бурно. Дважды провалившись на вступительных экзаменах в знаменитую Политехническую школу, Галуа поступил в Подготовительную школу (преобразованную из Высшей нормальной школы во время реакционного правления Карла IX), откуда вскоре после июльского переворота был уволен за печатное выступление против школы. После этого Галуа открыл Влпубличный курсВ» по алгебре, но политическая жизнь страны быстро вовлекла его в свой водоворот. Имея репутацию ярого республиканца и активного врага Луи-Филиппа, он два раза сидел в тюрьме за политические выступления и в мае 1832 года был убит на дуэли, причины которой остаются до сих пор загадочными.

За свою короткую жизнь Галуа успел создать теорию, которая до сих пор стоит в фокусе математической мысли. Рассматривая численные уравнения, он установил понятие их группы, т.е. совокупности таких подстановок между их корнями, которые не нарушают рациональных соотношений между ними. Эта группа определяет для каждого уравнения алгебраическую структура его корней. В частности, уравнение разрешимо в радикалах тогда и только тогда, если его группа принадлежит к числу так называемых разрешимых групп. Таким образом вопрос о разрешимости каждого данного уравнения в радикалах может быть решен при помощи конечного числа действий.

Обратимся теперь к исходному объекту исследования тАУ уравнению

a₀xⁿ + a₁x^{n тАУ 1} + тАж + a_n = 0,

где a₀, a₁, тАж, a_n - заданные числа. Еще Гаусс в конце XVIII века доказал Влосновную теорему алгебрыВ», гласящую, что при любых a₀, a₁, тАж, a_n данное уравнение имеет в поле комплексных чисел п корней, точнее, стоящий в его левой части многочлен f(x) может быть разложен на линейные множители

f(x) = a₀(x - a₁)тАж(x - a_n),

где a₁ тАж a_nтАУ некоторые комплексные числа (называемые корнями уравнения). Задача состоит в том, чтобы узнать, существуют ли формулы, выражающие корни a₁, тАж, a_n через коэффициенты a₀, a₁, тАж, a_n с помощью четырех арифметических действий и извлечения радикалов? Прежде всего, сразу можно считать, что все числа a₁, тАж, a_n различны, иначе мы поделили бы многочлен f на наибольший общий делитель этого f и его производной fтАЩ, что дало бы нам новый многочлен с теми же самыми корнями, но уже без повторений.

Ключевой идеей, поистине прозрением Галуа, явилась мысль связать с каждым алгебраическим уравнением группу всех автоморфизмов его Влполя корнейВ» Q(a₁, тАж, a_n), которые оставляют неподвижным Влполе коэффициентовВ» Q(a₀, a₁, тАж, a_n). Понятно, что это действительно группа, так как если j, y - два таких автоморфизма, то автоморфизмы jy и j ^-1 тоже оставляют числа a₀, a₁, тАж, a_n неподвижными.

Как действует любой такой автоморфизм j на корни нашего уравнения? Если a - корень, т.е.

a₀aⁿ + a₁a^{n тАУ 1} + тАж + a_n = 0,

то, применив j к обеим частям, получим

a₀(a^j)ⁿ + a₁(a^j)^{n тАУ 1} + тАж + a_n = 0,

т.е. a^j тАУ корень того же уравнения! Другими словами, автоморфизм j просто переставляет корни a₁, тАж, a_nмежду собой, определяя тем самым некоторую перестановку

a₁ тАж a_n

a₁ тАж a_in

легко сообразить, что произведению автоморфизмов будет отвечать произведение соответствующих перестановок, так что все получающиеся при этом перестанвоки сами составляют группу. Она называется группой симметрий или группой Галуа уравнения f=0 и обозначается Gal(f). Понятно, что Gal(f) тАУ подгруппа группы S_n всех перестановок п символов. Оказывается, свойствами группы Галуа и определяется ответ на вопрос о разрешимости данного уравнения в радикалах.

Вот этот знаменитый

Критерий Галуа. Уравнение f=0 тогда и только тогда разрешимо в радикалах, когда его группа Gal(f) обладает полициклической матрёшкой.

Прежде всего, может возникнуть недоумение: ВлКак можно манипулировать перестановками корней, когда сами корни неизвестны? А если корни будут найдены, то никакие перестановки уже не понадобятся. В чем здесь достижение?В»

Оказывается, что группу Gal(f) действительно можно вычислить, не зная корней уравнения f = 0, а пользуясь лишь, так сказать, соображениями симметрии.

Рассмотрим уравнение

x⁴ тАУ x² + 1 = 0.

Конечно, без всякого критерия Галуа видно, что оно биквадратное и легко решается в радикалах, но наша цель сейчас в другом продемонстрировать на этом простеньком примере, как, не пользуясь знанием корней уравнения, найти его группу Галуа. Сейчас мы убедимся, что это вполне возможно. Прежде всего заметим, что многочлен

f = x⁴ тАУ x² + 1,

стоящий в левой части, не разлагается на множители меньшей степени с рациональными коэффициентами. Для выяснения этого имеется несложный общей прием, на котором мы не будем останавливаться.

Пусть a какой-нибудь корень нашего уравнения. Понятно, что тогда -a, 1/a, -1/a - тоже корни, причем все они попарно различны. Занумеруем их, пусть

a₁ = a, a₂ = - a, a₃ = 1/a, a₄ = -1/a

Очевидно,

Q (a₁, a₂, a₃, a₄ )= Q (a)

Какие перестановки войдут в группу Gal(f)? Разумеется, далеко не все 24 перестановки четырех символов. В самом деле, если при каком-то автоморфизме поля Q (a) число a переходит в a₁, т.е. остается на месте, то легко понять, числа a₂, a₃, a₄ тоже останутся на месте. Другими словами, получится единичная перестановка е. Далее, если a перейдет в a₂, то по той же причине получится перестановка