Основные понятия дифференциального исчисления и история их развития (Бакалавр)

Министерство общего и профессионального образования

Астраханский Государственный Педагогический Университет

Бакалаврская работа

Студентки IV курса физикотАУматематического факультета

Ночевной Светланы Павловны

Кафедра:

Математического анализа

Тема:

Основные понятия дифференциального исчисления и история их развития

Научный руководитель

ст. преподаватель

Пономарёва Н.Г.

Астрахань

1998 г.

План.

1. Основные понятия дифференциального исчисления функций одной переменной.

   1. Определение производной и её геометрический смысл.

   2. Дифференциальные функции. Определение дифференциала.

   3. Инвариантность формы первого дифференциала.

   4. Дифференциал суммы, произведения и частного.

   5. Геометрическая интерпретация дифференциала.

2. Основные понятия интегрального исчисления функций одной переменной.

   1. Первообразная функция и неопределённый интеграл.

   2. Геометрический смысл неопределённого интеграла.

   3. Основные свойства неопределённого интеграла.

   4. Метод непосредственного интегрирования.

   5. Метод замены переменной (способ подстановки).

   6. Интегрирование по частям.

   7. Определённый интеграл как предел интегральной суммы.

   8. Основные свойства определённого интеграла.

   9. Геометрический смысл определённого интеграла.

   10. Теорема НьютонатАУЛейбница.

   11. Формула НьютонатАУЛейбница.

   12. Замены переменных в определённых интегралах.

   13. Интегрирование по частям.

3. Исторические сведения о возникновении и развитии основных понятий.

   1. Происхождение понятия определённого интеграла и инфинитезимальные методы Архимеда.

   2. От Архимеда к Кеплеру и Кавальери.

   3. Теорема Паскаля.

   4. ВлО глубокой геометрииВ» Лейбница.

   5. ВлМетод флюксийВ» Ньютона.

   6. Дифференциальные методы.

Цель работы: ВлИзучить основные понятия дифференциального и интегрального исчислений и ознакомиться с историей их развитияВ».

1.Основные понятия дифференциального исчисления функций одной переменной.

1.1.Определение производной и её геометрический смысл.

Пусть функция y = f(х) определена в окрестности точки х_о. возьмём точку х₁ этой окрестности, отличную от х_о.

Определение. Разность х₁ тАУ х₀, которую обозначают символом х, будем называть приращением независимой переменной.

Определение. Подобным образом соответствующая разность

у₁ тАУ у₀ = f(х₁) тАУ f(х₀), обозначается символом у и называется приращением зависимой переменной, или приращением функции.

Получаются следующие соотношения:

х₁ = х₀ + х,

у₁ = у₀ + у,

у₀ + у = f(х₀ + х)

Так как у₀ = f(х₀),

то у = f(х₀ + х) тАУ f(х₀).

у f(х₀+х)тАУ f(х₀)

хх

Определение. Частное будем называть разностным отношением.

Выражение f(х₀+х)тАУ f(х₀)

х

(принимая что х₀ имеет определённое постоянное значение) можно считать функцией приращения х.

Определение. Если предел этого выражения при х, стремящемся к нулю, существует, то его мы будем называть производной функции у = f(х) по х в точке х₀

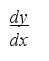
И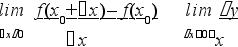так, = = f’(х₀) = у’_х = у’=

Пример. у=х² . Вычислите производную для х=2.

Имеем: f(х+х) = (х+х)² ,

Поэтому у = (х+х)² тАУ х² = 2хх+(х)²

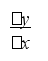
Отсюда = 2х+х

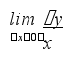
Переходя к пределу получим: = 2х + = 2х.

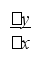
Д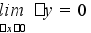ля того, чтобы отношение имело предел, необходимо, чтобы , то есть, чтобы функция рис.1

была непрерывной в точке х⁰.

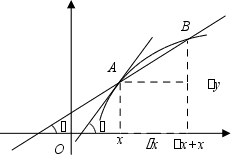
Рассмотрим график функции у = f(х) (рис.1)

Легко заметить, что отношение равно тангенсу угла , образованного положительным направлением секущей, проходящей через точки А и В (соответствующие точкам х и х+х), с положительным направлением оси Ох, то есть, от А к В если теперь приращение х будет стремиться к нулю, точка В будет стремиться к А, то угол  будет стремиться к , образованному положительным направлением касательной с положительным направлением оси Ох, а tg будет стремиться к tg.

П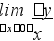оэтому = tg  (положительным направлением касательной считаем то направление, в котором х возрастает).

Таким образом, можно утверждать следующее:

Производная в данной точке х равна тангенсу угла, образованного положительным направлением касательной в соответствующей точке (х,f(х)) нашей кривой с положительным направлением оси Ох.

1.2 Дифференциальные функции. Определение дифференциала.

Определение. Функция у = f(х) называется дифференцированной в точке х, если её приращение у в этой точке можно представить в виде

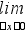у = f’(х)х+(х)х,

где  (х) = 0

К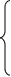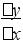ак видно из из определения, необходимым условием дифференцируемости является существование производной. Оказывается что это условие также и достаточно. В самом деле пусть существуют у’ = f’(х)

П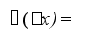оложим тАУ f’(х), х 0

0. , х = 0

При таком определении  имеет для всех х

у = f’(х)х +(х)х .

О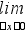стаётся, следовательно, установить непрерывность (х) при х = 0, то есть, равенство  (х) = (0) = 0, но, очевидно,

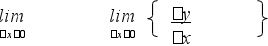 (х) = тАУ f’(х) = f’(х) тАУ f’(х) = 0,

что и требовалось.

Таким образом, для функции одной переменной дифференцируемость и существование производной тАФ понятия равносильные.

О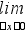пределение. Если функция у = f’(х) дифференцируема, то есть, если у = f’(х)х + ^.х,  = 0,

то главную линейную часть f’(х)х, её приращения будем обозначать d_ху, d_хf(х) и называть дифференциалом переменной у по переменной х в точке х.

Написав для симметрии d_хх вместо х, получим следующую формулу:

d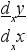_ху = f’(х)d_хх,

откуда = f’(х).

Заметим ещё, что дифференциалы d_ху и d_хх являются функциями переменной х, причём функция d_хх принимает постоянное значение х.

1.3 Инвариантность формы первого дифференциала.

В случае, когда переменная у = f(х) была функцией независимой переменной х, мы имеем, по определению,

у = f’(х)х или d_хх = f’(х)d_хх (1)

Рассмотрим теперь случай, когда х является в свою очередь функцией другой переменной,

х = х(t).

Теорема. Если функции х = (t) и у = (t) дифференцируемы в соответствующих точках t = tВн₁ и х = х₁ = (t₁), то дифференциал сложной функции у = f((t)) = (t) может быть представлен в виде

d_tу = f’(х₁) d_tх.

Доказательство: Согласно определению дифференциала имеем

d_tх = ’(t₁) d_tt (1¹)

d_tу = ’(t₁) d_tt (2)

Но на основании теоремы о производной сложной функции мы видим, что

’(t₁) = f’(х₁) ’(t₁)

Подставив это выражение в формулу (2), получим:

d_tу = f’(х₁) ’(t₁) d_tt,

отсюда в силу формулы (1¹)

d_tу = f’(х₁) d_tх (3)

Сравнив формулу (1) с формулой (3), мы заметим что их можно записать символически в виде

dу = f’(х) dх (4)

Формулу (1) или (3) мы получаем из формулы (4), написав вместо d, соответственно d_х или d_t.

Символы dх и dу не являются совершенными, однако во многих случаях, когда возможность ошибиться будет исключена, мы будем ими пользоваться вместо символов d_хх и d_ху или, соответственно, d_tх и d_tу.

Значение формулы (4)становится ясным, если обратить внимание на то, что при отыскании производной приходится пользоваться двумя формулами для определения производной у по х. А именно, когда переменная у зависит непосредственно от х, то

у’_х = f’(х);

когда же зависимость переменной у от х даётся при помощи некоторой (промежуточной) функции и, то

у’_х = f’(и)и’_х.

При отыскании же дифференциалов получим в обоих случаях одинаковые формулы:

d_ху = f’(х) d_хх, d_ху = f’(и) d_хи

или

dу = f’(х) dх, dу =f’(и) dи.

1.4 Дифференциал суммы, произведения и частного.

Из теорем о производных суммы, произведения и частного можно получить аналогичные формулы для дифференциалов суммы, произведения и частного. Пусть и и  тАФ функции от х:

и = f(х),  = (х),

имеющие непрерывные частные производные.

Если положить у = и + ,

то у’_х = и’_х + ’_х,

откуда у’_хdх = и’_х dх + ’_хdх,

следовательно dу = dи + d,

то есть d(и + ) = dи + d.

Аналогично dси = сdи,

где с тАУ постоянное число;

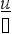
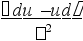d(и) = иd + dи,

d ( ) = .

Замечание. На практике часто бывает выгоднее оперировать дифференциалами, а потом делением на дифференциал независимой переменной переходить к производной.

1.5 Геометрическая интерпретация дифференциала.

Дифференциал можно геометрически представить следующим образом:

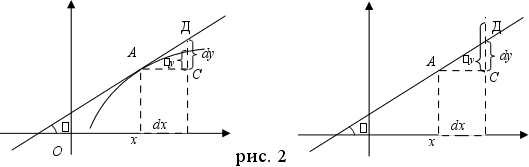
Из рис. 2 видно, что dу = f’(х)dх = tg ^.dх = СД.

Таким образом, если у тАУ приращение ординаты кривой, то dу тАУ приращение ординаты касательной.

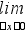
Д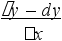ифференциал dу, вообще говоря, отличается от у, но их разность очень мала по сравнению dх для очень малых dх, так как

=  (х) = 0

На практике, когда речь идёт только о приближённых значениях, можно для малых приращений dх считать

у = dу = f’(х)dх.

2.Основные понятия интегрального исчисления функций одной переменной.

2.1.Первообразная функция и неопределённый интеграл.

Основной задачей дифференциального исчисления является нахождение производной f’(х) или дифференциала f’(х)dх данной функции f(х).

В интегральном исчислении решается обратная задача:

Дана функция f(х); требуется найти такую функцию F(х), производная которой f(х)dх в области определения функции f(х), то есть, в этой области функции f(х) и F(х) связаны соотношением F’(х) = f(х) или dF(х)= F’(х)dх = f(х)dх.

Определение. Функция F(х) называется первообразной функцией для данной функции f(х), если для любого х из области определения f(х) выполняется равенство F’(х) = f(х) или dF(х) = f(х)dх.

Примеры. 1)Пусть f(х) = cos х.

Решение: Тогда F(х) = sin х, так как F’(х) = cos х = f(х) или dF(х) = cos хdх = f(х)dх

2) Пусть f(х) = х².

Решение: Тогда F(х) = , так как F’(х) = х² = f(х) или dF(х) = х²dх = f(х)dх.

Известно, что если две функции f(х) и (х) отличаются друг от друга на постоянную величину, то производные или дифференциалы этих функций равны, то есть, если f(х) = (х) + С, то f’(х) = ’(х) или f’(х)dх = ’(х)dх.

Известно также, что и наоборот, если две функции f(х) и (х) имеют одну и ту же производную или один и тот же дифференциал, то они отличаются друг от друга на постоянную величину, то есть, если

f’(х) = ’(х) или dхf(х) = d(х), то

f(х) = (х) + С.

Замечание. Действительно, если производная f’(х) обращается в нуль для любых значений х в (а,в), то в этом интервале f(х) = С.

В самом деле, если х₁ (а,в) и х₂ (а,в), то в силу теоремы Лагранжа, имеем f(х₂) тАУ f(х₁) = (х₂тАУх₁) f’(х₀), где х₁х₀х₂ . Но, так как f’(х₀) = 0, то f(х₂) тАУ f(х₁) = 0.

Отсюда непосредственно следует что, если в формуле у = F(х) + С мы будем придавать постоянной С все возможные значения, то получим все возможные первообразные функции для функции f(х).

Определение. Множество F(х) +С всех первообразных функций для функции f(х), где С принимают все возможные числовые значения, называется неопределённым интегралом от функции f(х) и обозначается символом

f(х)dх

Таким образом, по определению,

f(х)dх = F(х) + С, (А)

где F’(х) = f(х) или dF(х) = f(х)dх и С тАУ произвольная постоянная. В формуле (А) f(х) называется подынтегральной функцией, f(х)dх тАУ подынтегральным выражением, а символ тАУ знаком неопределённого интеграла.

Неопределённым интегралом называют не только множество всех первообразных, но и любую функцию этого множества.

Определение. Нахождение первообразной по данной функции f(х) называется интегрированием

2.2.Геометрический смысл неопределённого интеграла.

Пусть задан неопределённый интеграл F(х) + С для функции f(х) в некотором интервале. При фиксированном значении С = С₁ получим конкретную функцию у₁ = F(х) + С₁, для которой можно построить график; его называют интегральной кривой. Изменив значение С и положив С = С₂, получим другую первообразную функцию С соответствующей новой интегральной кривой.

А
налогично можно построить график любой первообразной функции. Следовательно, выражение у = F(х) + С можно рассматривать как уравнение семейства интегральных кривых неопределённого интеграла F(х) + С. Величина С является параметром этого семейства тАУ каждому конкретному значению С соответствует единственная интегральная кривая в семействе. Интегральную кривую, соответствующую значению параметра С₂, можно получить из интегральной кривой, соответствующей значению параметра С₁, параллельным сдвигом в направлении оси Оу на величину /С₂ тАУ С₁/. На рис. 3 изображён неопределённый интеграл х² + С от функции f(х) = 2х, то есть, семейства парабол.

2.3.Основные свойства неопределённого интеграла.

1. Производная неопределённого интеграла равна подынтегральной функции, то есть,

[ f(х)dх ]’= f(х) .

Доказательство. Согласно определению неопределённого интеграла,

f(х)dх = F(х) + С, (V)

где F’(х) = f(х)

Дифференцируя обучение части равенства (V), имеем

[ f(х)dх ]’ = [F(х) + С ]’,

откуда

[ f(х)dх ]’ = F’(х) + С¹ = F’(х) = f(х) .

2. Дифференциал неопределённого интеграла равен подынтегральному выражению, то есть

d f(х)dх = f(х)dх

Доказательство. Согласно определению неопределённого интеграла,

f(х)dх = F(х) + С

d f(х)dх = d(F(х) + С) = dF(х) = dС = F’(х)dх = f(х)dх

3. Неопределённый интеграл от дифференциала некоторой функции F(х) равен самой функции с точностью до произвольной постоянной С, то есть

dF(х) = F(х) + С, (v)

Доказательство. Продифференцировав оба равенства (v), будем иметь

d dF(х) = dF(х) (по свойству 2)

d(F(х) + С) = dF(х)

следовательно, функции dF(х) и dF(х) отличаются друг от друга на постоянную величину, то есть

dF(х) = F(х) + С

4. Постоянный множитель можно выносить за знак неопределённого интеграла, то есть

а f(х)dх = а f(х)dх (а 0)

Доказательство. Продифференцируем обучение части равенства. Тогда получим

d а f(х)dх = а f(х)dх (по свойству 2)

и d [ a f(х)dx ] = ad f(х)dх =а f(х)dх

(в силу свойства дифференциала)

Таким образом, дифференциалы функций

аf(х)dх и аf(х)dх равны, а потому эти функции отличаются друг от друга на постоянную величину, то есть, аf(х)dх = = аf(х)dх * dх + С. Но постоянную С можно считать включённой в состав неопределённого интеграла, следовательно,

аf(х)dх = аf(х)dх.

5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций, например:

[f₁(х) + f₂(х) тАУ f₃(х)]dх = f₁(х)dх + f₃(х)dх тАУ f₃(х)dх (v)

Доказательство: Продифференцируем обе части равенства.

Дифференцирование любой части равенства даёт:

d [f₁(х) + f₂(х) тАУ f₃(х)]dх = [f₁(х) + f₂(х) тАУ f₃(х)]dх

В результате дифференцирования правой части равенства (v), получается дифференциал алгебраической суммы нескольких функций, который как известно равен алгебраической сумме дифференциалов слагаемых функций. Следовательно,

d[ f₁(х)dх + f₂(х)dх тАУ f₃(х)dх] =

= df₁(х)dх + f₂(х)dх тАУ f₃(х)dх

Применяя свойство 1, в правой части последнего равенства получаем

f₁(х)dх + f₂(х)dх тАУ f₃(х)dх = [ f₁(х) + f₂(х) тАУ f₃(х)]dх

Итак, после дифференцирования обеих частей равенства (v) получены тождественные результаты, следовательно, справедлива формула (v) (см. доказательство свойства 3).

2.4. Метод непосредственного интегрирования.

Определение. Непосредственным интегрированием называется интегрирование заключающееся в прямом применении формул таблицы основных интегралов. Чтобы найти неопределённый интеграл от какойтАУнибудь функции f(х), нужно прежде всего отыскать в таблице интегралов формулу в левой части которой стоит интеграл такого же вида, как данный, и записать ответ в соответствии с правой частью этой формулы.

Примеры.

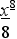1. х⁷dх

Решение. х⁷dх = + С

2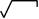. 2³х²dх

Р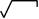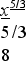ешение. Имеем 2 ³х²dх = 2х^2/3dх

Применяя формулы, получаем 2х^2/3dх = 2 х^2/3dх = 2 + С.

Т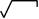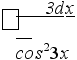аким образом, 2х^2/3dх = х ³х² + С.

3)

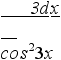
Р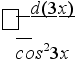ешение. Согласно известному свойству дифференциала, 3dх = d(3х), а потому

=

Применяя формулу, получаем tg3х + С

В тех случаях, когда под знаком интеграла стоит алгебраическая сумма обычно разлагают данный интеграл на сумму нескольких интегралов, из которых каждый можно найти по соответствующей формуле.

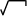
3. (2х³ + 9х² тАУ 5 х + 4/ х )dх

Решение. (2х³ + 9х² тАУ 5 х + 4/ х )dх =

= 2 х³dх + 9 х²dх тАУ 5 х^1/2 + 4 dх/ х =

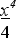
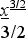
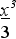
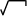= 2 + 9 тАУ 5 + 4 * 2 х + С =

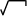
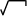= х⁴ / 2 + 3х³ тАУ 10/3 хх + 8 х + С.

2.5. Метод замены переменной (способ подстановки).

Наиболее общим приёмом интегрирования функций является способ подстановки, который применяется тогда, когда искомый интеграл f(х)dх не является табличным, но путём но путём ряда элементарных преобразований он может быть сведён к табличному.

Метод подстановки основан на применении следующей формулы:

f(х)dх = f[(t)]’(t)dt, (1)

где х = (t) тАУ дифференцируемая функция от t, производная которой ’(t) сохраняет знак для рассматриваемых значений переменных.

Сущность применения этой формулы состоит в том, что в данном интеграле f(х)dх переменная х заменяется переменной t по формуле х = (t) и, следовательно, dх произведением ’(t)dt.

Справедливость формулы (1) будет доказана если после дифференцирования обеих её частей получатся одинаковые выражения. Продифференцировав левую часть формулы, имеем

d [ f(х)dх ] = f(х)dх = f [(t)] ’(t)dt

Продифференцировав правую часть формулы, имеем

df [(t)] ’(t)dt = f [ (t) ] ’(t)dt

Таким образом, формула (1) справедлива. Часто употребляется обратная замена переменной, то есть, подстановка t = (t), dt = ’(t)dх.

Примеры.

1. (2х + 3)⁴dх.

Данный интеграл можно свести к табличному интегралу (V). Подстановка выбирается из простого соображения: в подынтегральном выражении табличного интеграла (V) в основании степени и под знаком дифференциала стоит одно и тоже выражение и.

Следовательно, в данном случае нужно применить подстановку и = 2х + 3, отсюда имеем dи = 2dх и dх = dи/2, а потому

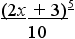(2х + 3)⁴dх = и⁴(dи/2) = 1/2 и⁴dи =

= 1/2 * и⁵/5 + С = + С.

2.6 Интегрирование по частям.

Допустим, что u, v тАУ функции переменной х, непрерывные и имеющие производные в интервале (а,в). имеем тогда

(uv)’ = uv’ + vu’

так что uv’ = (uv)’ тАУ vu’

Беря неопределённые интегралы от обоих частей и учитывая, что uv’dх = uv тАУ vu’dх, (1)

Если оба интеграла существуют.

Пользуясь дифференциалами предыдущую формулу можно написать в следующем виде:

udv = uv тАУ vdu. (2)

Формула (2) даёт возможность вычисления интеграла udv свести к вычислению интеграла vdu , который, быть может, берётся легче. Этот метод называется интегрированием по частям.

Примеры.

1) J = хе^хdх.

Положим и = х, dи = dх, dv = е^хdх,

v = е^хdх = е^х

Следовательно,

J = хе^х тАУ е^хdх = хе^х тАУ е^х + С.

2) ln хdх .

Положим, u = ln х, dи = dх/х

dv = dх v = dх = х.

Следовательно,

J = х ln х тАУ dх = х ln х тАУ х + С.

2.7. Определённый интеграл как предел интегральной суммы.

Пусть интервал [а,в], на котором задана функция у = f(х), разбит точками деления х₁х₂ тАж х_{п тАУ 1}на п частичных интервалов ₁ = [х₀,х₁], ₂ = [х₁,х₂], тАж,  = [х_птАУ1,х_п], где а =х₀ , в = х_п, причём в каждом частичном интервале _i выбрана какаятАУлибо точка _i:

х_iтАУ1_i х_i (i = 1, 2, тАж, п). Пусть, далее, х_i тАУ длина интервала _i, то есть,

х_i тАУ х_iтАУ1 = х_i (i = 1, 2, тАж, п),

а max х_i тАУ наибольшее из чисел х_i.

Требуется найти предел суммы

1. f(₁) х₁ + f(₂) х₂ + тАж + f(_п) х_п = f(_i) х_i,

когда длины х_i всех частичных интервалов _iстремятся к нулю (при этом с необходимостью число п этих интервалов будет стремиться к бесконечности). Другими словами, требуется найти предел этой суммы при max х_i 0, так как условие, что максимальная из длин частичных интервалов _iстремится к нулю, равносильно условию, что все х_i 0.

И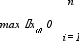так, требуется найти

lim f(х_i) х_i.

Определение. Сумму (1) называют интегральной суммой.

О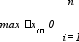пределение. Функция f(х) называется интегрируемой на интервале [а,в], если существует конечный предел

lim f(_i) х_i, (2)

не зависящий от того, каким образом интервал [а,в] делится на частичные интервалы и каким образом выбираются точки _iна этих частичных интервалах, лишь бы длина максимального из них стремилась к нулю. Этот предел называется определённым интегралом от функции f(х) на интервале [а,в] и обозначается символом

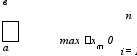f(х)dх = lim f(_i) х_i.

Для того чтобы не оставалось неясностей, сформулируем точно, как следует понимать предел (2).

Определение. Число J называется пределом интегральной суммы f(_i)х_i при max х_i 0, если для любого заданного  0 найдётся такое  0, что выполняется неравенство:

|f(_i)х_i тАУ J |

при любом выборе частных интервалов, ₁, ₂, тАж, _пи точек ₁, ₂, тАж, _п на этих интервалах, лишь бы только выполнялось требование max х_i 0, тоесть лишь бы длина наибольшего (а значит, и всех) из частичных интервалов была меньше .

Из определения определённого интеграла отнюдь не следует, что любая функция интегрируема на любом интервале. Можно подобрать такие функции, для которых определённый интеграл не существует, то есть для которых интегральная сумма не стремится к определённому пределу. Существование определённого интеграла от функции, заданной на интервале [а,в], обеспечивает непрерывность этой функции на [а,в], поэтому непрерывность функции на [а,в] является достаточным условием её интегрируемости на этом интервале, то есть

Теорема 1. Если функция f(х) непрерывна на замкнутом интервале [а,в], то она интегрируема на этом интервале, то есть имеет определённый интеграл

f(х)dх.

Иногда на практике приходится интегрировать и разрывные функции. Приведём несколько более широкое достаточное условие существования интеграла.

Теорема 2. Если на интервале [а,в] функция ограничена и имеет лишь конечное число точек разрыва, то она интегрируема на [а,в].

2.8. Основные свойства определённого интеграла.

Теорема 1. Пусть с тАУ промежуточная точка интервала [а,в] (а  с в). Тогда имеет место равенство

f(х)dх = f(х)dх + f(х)dх,

если все эти три интеграла существуют.

Доказательство: Разобьём [а,в] на п частичных интервалов [а,х₁], [х₁,х₂], тАж, [х_птАУ1, в] длиной соответственно х₁, х₂, тАж, х_п так, чтобы точка с была точкой деления. Пусть, наприме

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Cпособы преобразования комплексного чертежа, применение при изображении предметов