Расширения полей

В педагогических вузах введена программа единого курса алгебры и теории чисел. Главная цель этого курсатАФизучение основных алгебраических систем и воспитание алгебраической культуры, необходимой будущему учителю для глубокого понимания целей и задач как основного школьного курса математики, так и школьных факультативных курсов.

На наш взгляд, наиболее целесообразным является введение в школьное преподавание элементов современной абстрактной алгебры.

Начавшийся в ХХ веке процесс алгебраизации математики не прекращается, а это вызывает упорные попытки введения в школьное математическое образование основных алгебраических понятий.

Математическая глубина и необычайно широкая сфера применения полей сочетаются с простотой ее основных положений тАУ понятий полей, целый ряд важных теорем можно сформулировать и доказать, обладая начальными представлениями в области теории множеств. Поэтому теория полей как нельзя лучше подходит для того, чтобы показать школьникам образец современной математики.

Кроме того, изучение элементов теории поля полезно для школьников, способствует их интеллектуальному росту, проявляющемуся в развитии и обогащении различных сторон их мышления, качеств и черт личности, а также воспитанию у учащихся интереса к математике, к науке.

1. Простое алгебраическое расширение поля.

1.1.Простое расширение поля.

Пусть P[x]тАФ кольцо полиномов от xнад полем P, где P тАФ подполе поля F. Напомним, что элемент a поля Fназывается алгебВнраическим над полем P, если aявляется корнем какого-нибудь полинома положительной степени из P [x].

Определение. Пусть P < F и a0F. Простым расширением поля P с помощью элемента aназывается наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение Pс помощью a обознаВнчается через P (a), основное множество поля P (a) обоВнзначается через Р(a).

Пусть a0F, P [x] тАФ кольцо полиномов от x и

P[x]={f(a)*f0P[x]},

т. е. P[a] есть множество всех выражений вида a₀ + a₁a+..+ a_naⁿ, где а₀, a_1,..a_n0P и тАФ любое натуральВнное число.

Легко видеть, что алгебра +P[a], +, тАФ, ., 1, тАФ подкольцо поля P (a) тАФ является кольцом; это кольцо обозначается символом P [a].

Теорема 1.1. Пусть P[x]тАФ кольцо полиномов от х над P и P (a)тАФ простое расширение поля P. Пусть y тАФ отображение P[x] на P[a] такое, что y(f)=f(a) для любого f из P[x]. Тогда:

(а) для любого а из Р y (а) = а;

() y(x) = a

(с) y является гомоморфизмом кольца P [x] на кольцо P [a];

(d) Ker y ={f0P[x]*f(a)=0};

(е) фактор-кольцо P [x]/Кег y изоморфно кольцу P [a].

Доказательство. Утверждения (а) и (Ь) непосредственно следуют из определения y. Отображение y сохраняет главные операции кольца P [x], так как для любых f и g из P[x]

y(f + g)=f(a)+g(a), y(fg)= f(a)g(a), y(1)=1.

Далее, по условию, y есть отображение Р[х]на Р[a].СлеВндовательно, y является гомоморфизмом кольца P [x]на кольцо P [a].

Утверждение (d) непосредственно следует из определеВнния отображения y.

Поскольку y тАФ гомоморфизм кольца P [x]на P [a], то фактор-кольцо P[x]/Кег y изоморфно кольцу P [a].

Следствие 1.2. Пусть a тАФ трансцендентный элемент над полем P. Тогда кольцо полиномов P [x] изоморфно кольцу P [a].

Доказательство. В силу трансцендентности a над P Kery={0}. Поэтому P[x]/{0}– P [a].Кроме того, фактор-кольцо кольца P [x]по нулевому идеалу изоморфно P [x]. Следовательно, P [x]– P [a].

1.2.Минимальный полином алгебраического элемента.

Пусть P [x]тАФ кольцо полиномов над полем P.

Определение. Пусть a тАФ алгебраический элемент над полем P. Минимальным полиномом элемента a, над P называется нормированный полином из P[x] наименьшей степени, корнем которого является a. Степень минимального полинома называется степенью элемента a над P.

Легко видеть, что для всякого элемента a, алгебраического над P , существует минимальный полином.

Предложение 1.3. Если а тАФ алгебраический элемент над полем P, а g и j тАФ его минимальные полиномы над P, то g=j.

Доказательство. Степени минимальных полиномов gи j совпадают. Если g¹j, то элемент a (степени над P) будет корнем полинома g - j, степень которого меньше степени полинома j (меньше ), что невозможно. Следовательно, g=j.

Теорема 1.4. Пусть a тАФ алгебраический элемент степени над полем P (aóP) и g тАФ его минимальный полином над P. Тогда:

(а) полином g неприводим в кольце P [x];

() если f (a) = 0, где f0P[x], то g делит f

(с) фактор-кольцо P [x]/(g) изоморфно кольцу P [a];

(d) P [x]/(g) является полем;

(е) кольцо P [a] совпадает с полем P (a).

Доказательство. Допустим, что полином g приводим в кольце P [x], т. е. существуют в P[x] такие полиВнномы j и h, что

g = jh, 1£deg j, deg h

Тогда g(a) = j(a)h(a) = 0. Так как P (a) тАФ поле, то j( a) = О или h(a) = 0, что невозможно, поскольку, по условию, степень элемента a над Pравна п.

Предположим, что f 0 P[x]и f(a) = 0. По условию, g(a) = 0. Следовательно, f и g не могут быть взаимно проВнстыми. Поскольку полином gнеприводим, то gделит f.

Пусть j тАФ гомоморфизм кольца P [x]на кольцо P [a] (y(f)=f(a) для всякого f из P[x]), рассмотренный в теоВнреме 2.1. В силу (Ь) ядро гомоморфизма y состоит из кратВнных полинома g,т.е. Кег y = (g). Следовательно, фактор-кольцо P = P [x]/(g) изоморфно кольцу P [a].

Поскольку P[a]ÌP(a), то P [a] есть область целостВнности. Так как P @ P[a], то фактор-кольцо P также есть область целостности. Нам надо показать, что любой ненулевой элемент f из Pобратим в P. Пусть f тАФ элемент смежного класса f. Так как f ¹ 0, то f(a)¹0; поэтому полином gне делит полином f. Поскольку полином gнеприводим, отсюда следует, что полиномы f и g тАФ взаимно простые. Следовательно, в Р[x]существуют такие полиномы uи v, что uf + vg=1. Отсюда вытекает равенство uf = 1, показывающее, что элемент fобратим в кольце P. Итак, установлено, что фактор-кольцо Pявляется полем.

В силу (с) и (d) P [a] является полем и поэтому P(a)ÌP[a]. Кроме того, очевидно, P[a]ÌP(a). Значит, P[a] = P(a). Следовательно, кольцо P [a] совпадает с полем P (a).

1.3.Строение простого алгебраического расширения поля.

Теорема 1.5. Пусть a тАФ алгебраический над полем P элемент положительной степени . Тогда любой элемент поля P(a) однозначно представим в виде линейной комбиВннации элементов 1, a, .., a^n-1с коэффициентами из Р.

Доказательство. Пусть bтАФ любой элемент поля P (a). По теореме 1.4, P(a) = P[a]; следовательно, существует в P[x] полином f такой, что

(1) = f(a).

Пусть g тАФ минимальныйполином для a над P; в силу условия теоремы его степень равна п. По теореме о делении с остатком, существуют в P[x] полиномы hиrтакие, что

(2) f = gh + r, где r = 0 или der r < der g = n , т. е. r=c₀+c₁x +тАжc_n-1x^n-1(c_i0P). Полагая в (2) x = а и учитывая равенство (1), имеем

(3) = c₀+c₁a +тАжc_n-1a^n-1

Покажем, что элемент b однозначно представим в виде линейной комбинации элементов 1, a, .., a^n-1. Пусть

(4) = d₀+d₁a +тАжd_n-1a^n-1(d_i 0 P)

тАФлюбое такое представление. Рассмотрим полином j

j = (с₀ тАУ d₀) + (c₁ - d_i.)x + . . . + (с_n-1 тАУd_n-1)x^n-1

Случай, когда степень j меньше , невозможен, так как в силу (3) и (4) j(a) = 0 и степень j меньше степени g. Возможен лишь случай, когда j = 0, т. е. с₀ = d₀, . . . , с_n-1 = d_п-1.Следовательно, элемент b однозначно представим в виде линейной комбинации элементов 1, a,тАж,a^n-1.

1.4.Освобождение от алгебраической иррациональности в знаменателе дроби.

Задача об освобождении от алгебраической иррациональности в знаменателе дроби состоит в следующем. Пусть a тАФ алгебраический элемент степени n>1 над полем P; f и h тАФ полиномы из кольца полиноВнмов P [x]и h(a)¹0. Требуется представить элемент f(a)/h(a)P(a) в виде линейной комбинации степеней элеВнмента a,т. е. в виде j(a),

где jP[x].

Эта задача решается следующим образом. Пусть gтАФ минимальный полином для a над P. Так как, по теореме 1.4, полином неприводим над Pи h(a) ¹ 0, то gне делит hи, значит, полиномы hи g тАФ взаимно простые. Поэтому существуют в P[x]такие полиномы uи v, что

uh+vg=1 (1)

Поскольку g(a) = 0, из (1) следует, что

u(a)g(a) = 1, 1/h(a) = u(a).

Следовательно, f(a)/h(a) = f(a)u(a), причем f,u P[x] и f(a)u(a)P[a]. Итак, мы освободились от иррациональности в знаменателе дроби f(a)/h(a) .

Пример.

Освободиться от иррациональности в знаменателедроби

.

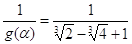Решение. В нашем случае a=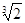. Минимальным многочленом этого числа является

p(x)=x³-2.

Многочлены (x) и g(x)=-x²+x+1 взаимно просты. Поэтому существуют такие многочлены j и y, что

j+gy=1.

Для отыскания j и y применим алгоритм Евклида к многочленам p и g:

-x³-2 -x²+x+1 -x²+x+1 2x-1

x³-x²-x -x-1 -x²+1/2x -1/2x+1/4

x²+x-2 1/2x+1

x²-x-1 1/2x-1/4

2x-1 5/4

Таким образом,

p=g(-x-1)+(2x-1),

g=(2x-1)(-1/2x+1/4)+5/4.

Откуда находим

(2x-1)=p+g(x+1),

5/4=g-(p+g(x+1))(-1/2x+1/4)

или

p1/5(2x-1)+g(4/5+1/5(2x²+x-1))=1,

p1/5(2x-1)+g(2/5x²+1/5x+3/5)=1.

Таким образом,

y(x)= (2/5x²+1/5x+3/5).

Тогда

y(a)=y()=.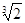

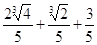Следовательно

.

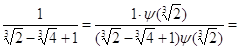
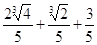2.Составное алгебраическое расширение поля.

2.1. Конечное расширение поля.

Пусть P тАФ подполе поля F. Тогда мы можем рассматривать F как векторное пространство над P, т. е. рассматривать векторное пространство +F, +, {w_l½l P},,

где w_l- операция умножения элементов из Fнаскаляр lP.

Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F : P].

Предложение 2.1. Если a тАФ алгебраический элемент степени над P, то [P (a):P]=.

Это предложение непосредственно следует из теоремы 1.5.

Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебраВническим над P.

Теорема 2.2. Любое конечное расширение F поля P является алгебраическим над P.

Доказательство. Пусть n-размерность F над P. Теорема, очевидно, верна, если n = 0. Предположим, что n>0. Любые n+1 элементов из Fлинейно зависимы над P. В частности, линейно зависима система элементов 1, a, .., aⁿ, т. е. существуют в Pтакие элементы с₀, с_1,тАж,c_nне все равные нулю, что с₀×1+ с_1a+тАж+c_n aⁿ= 0.

Следовательно, элемент a является алгебраическим над P.

Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями.

2.2. Составное алгебраическое расширение поля.

Расширение F поля Pназывается составным, если существует

возрастающая цепочка подполей Liполя F такая, что

P = L₀— L₁ —тАж— L_k= F и k>1.

Теорема 2.3. Пусть F тАФ конечное расширение поля L и L тАФ конечное расширение поля P. Тогда F является конечным расширением поля P и

(I) [F : P]= [F :L]@[L: P].

Доказательство. Пусть

(1) a₁,тАж,a_m тАФ базис поля Lнад P (как векторного пространства) и

(2) b₁,тАж,b_nтАФ базис поля F над L. Любой элемент d из F можно линейно выразить через базис:

(3) d = l₁b₁+..+l_nb_n (l_kL).

Коэффициенты 1_kможно линейно выразить через базис (1):

(4) l_k = p_1k a +тАж+ p_mk a_m (p_ikP).

Подставляя выражения для коэффициентов l_kв (3), получаем

d = å p_ik a_ib_k.

^{i{1,тАж,m}}

^{k{1,тАж,n}}

Таким образом, каждый элемент поля F представим в виде линейной комбинации элементов множества B, где

B = { a _ib_k½{1,.., m},k {l,.., n}}.

Отметим, что множество Bсостоит из nmэлементов.

Покажем, что Bесть базис F над полем P. Нам надо показать, что система элементов множества Bлинейно независима. Пусть

(5) åc_ika_ib_k = 0,

^I,k

где c_ik P. Так как система (2) линейно независима над L,то из (5) следуют равенства

(6) с_1ka ₁+..+с_mka_m = 0 (k = 1,.., n).

Поскольку элементы a ₁, .., a_mлинейно независимы над P,то из (6) следуют равенства

c_1k = 0,тАж,c_mk = 0 (k = 1, .., n),

показывающие, что все коэффициенты в (5) равны нулю. Таким образом, система элементов Bлинейно независима и является базисом F над P.

Итак установлено, что [F , P] = nm= [F:L]×[L: P].Следовательно, F является конечным расширением поля Pи имеет место формула (I).

Определение. Расширение F поля P называется составным алгебраическим, если существует возрастающая цепочка подполей поля P

P = L₀— L₁ —тАж— L_k= F и k>1 (1)

такая, что при i = 1,.., k поле L_i является простым алгебраическим расширением поля L_i-1.Число k назыВнвается длиной цепочки (1).

Следствие 2.4.Составное алгебраическое расширеВнние F поля P является конечным расширением поля P.

Доказательство легко проводится индукцией по длине цепочки (1) на основании теоремы 2.3.

Теорема 2.5. Пусть a₁,.., a_k тАФ алгебраические над полем P элементы поля F . Тогда поле P(a₁,.., a_k) является конечным расширением поля P.

Доказательство. Пусть

L₀ = P, L₁ = P [a₁], L ₂= P [a₁, a₂,],.., L_k = P [a₁ ,.., a_k].

Тогда L₁ = P [a₁] есть простое алгебраическое расширеВнние поля L₀; L₂ есть простое алгебраическое расширение поля L₁ , так как

L₂ = P [a₁,a₂] = (P [a₁])[a₂] = L₁[a₂] = L₁(a₂) и т. д.

Таким образом,

P = L₀—L₁ —тАж— L_k= F

где L_i = L_i-1(a_i) при i = 1, .., k, т. е. каждый член цепочки (2) является простым алгебраическим расширением предшествующего члена цепочки. Итак, поле Fявляется составным алгебраическим расширением поля P. Следовательно, в силу следствия 2.4 поле F является конечВнным расширением поля P .

Следствие 2.6. Составное алгебраическое расширеВнние поля является алгебраическим расширением этого поля.

2.3. Простота составного алгебраического расширения поля.

Теорема 2.7. Пусть числовое поле F есть составное алгебраическое расширение поля P . Тогда F является простым алгебраическим расширением поля P.

Доказательство. Пусть P —L — F , причем L = P(a), F = L(b)и, следовательно, F = P(a, b).

Пусть f и g тАФ минимальные полиномы над Pсоответственно для чисел a и и degf = m, degg = . Полиномы f и gнеприводимы над P и, следовательно, не имеют в поле Eкомплексных чисел кратных корней. Пусть

a = a₁ ,.., a_m тАФ корни полинома f в C и

= ₁ ,.., _nтАФ корни полинома gв C.

Рассмотрим конечное множество М:

M = {(a_i-a)/(b-b_k)½i0{1,тАж,m}, k0{2,тАж,n}}.

Поскольку P тАФ числовое множество (и, значит, бесконечВнное), то в Pсуществует число c, отличное от элементов множества М, c0P(М,cóМ. Пусть

(1) g = a + cb.

Тогда выполняются соотношения

(2) g ¹ a_i +cb_k = (i0{1,.., m}, k0{2, .., n}).

В самом деле, в случае равенства a +сb = a_i+сb_k было бы

с = (a_i-a)/(b-b_k) 0 M

что противоречило бы выбору числа c.

Пусть F₁ = P (g) и F₁ тАФ кольцо полиномов от x. Пусть h= f(g - cx) тАФ полином из F₁[x] (g, c0P(g) = F₁). Покажем, что x-b есть наибольший общий делитель полиномов hи gв кольце F₁[x].Так как g(b) = 0, то x-b делит gв E[x].Далее, в силу (1)

h(b) = f(g-cb) = f(a) = 0.

Поэтому x- делит полином h в E[x].Таким образом, x- есть общий делитель hи gв кольце E[x].

Докажем, что gи h в С не имеет корней, отличных от b. В самом деле, допустим, что b_k, k0{2 ,.., n},есть их общий корень. Тогда h(b_k) = f(g - сb_k) = 0. СлеВндовательно, найдется такой индекс i0{1 ,.., m},что g = a_i+cb_k(k>1), а это противоречит (2). На основании этого заключаем, что x-b есть наибольший общий делиВнтель gи h в E[x].Поскольку x - b тАФ нормированный полином, то отсюда следует, что x - b является наибольВншим общим делителем g и hв кольце F₁[x]. Поэтому

(x-b) 0 F₁[x] и b 0 F₁ = P(g).

Кроме того, a = g - cb 0 F₁. Таким образом,

F = P(a, b)Ì F₁, F₁ÌF.

Следовательно, F = P(g). Далее, так как g (как и всякий элемент из F) есть алгебраический элемент над P и F = P (g), то поле F =P (g)является искомым простым алгебраическим расширением поля P.

2.4. Поле алгебраических чисел.

В классе подполей поля комплексных чисел одним из наиболее важных является поле алгебраических чисел.

Определение. Алгебраическим числом называется комплексное число, являющееся корнем полинома полоВнжительной степени с рациональными коэффициентами.

Отметим, что алгебраическое число есть любое комплексное число, алгебраическое над полем Q. В частности, любое рациональное число является алгебраическим.

Теорема 2.8. Множество A всех алгебраических чисел замкнуто в кольце E = +С, +, тАФ, тАв, 1, комплексных чисел. Алгебра A = +А, +, тАФ, тАв, 1, является полем, подполем поля E.

Доказательство. Пусть aи тАФ любые элементы из А. По следствию 2.6, поле Q(a, )является алгебраическим над Q. Поэтому числа a+, -а, ab, 1 являются алгебраическими, т. е. принадлежат множеству A. Таким образом, множество А замкнуто относительно главных операций кольца E. Поэтому алгебра A тАФ подкольцо кольца E тАФ является кольцом.

Кроме того, если a тАФненулевой элемент из А, то a^-1 0 Q (a, )и поэтому а^-1принадлежит А. Следовательно, алгебра Aесть поле, подполе поля E.

Определение. Поле A = +А, +, тАФ, тАв, 1,назыВнвается полем алгебраических чисел.

Пример.

Показать, что число a=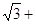 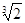является алгебраическим.

Решение. Из a=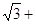 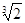следует a-.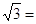

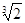Возведем обе части последнего равенства в третью степень:

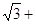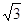a³-3a²9a-3=2

или

a³ +9a-2=3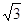(a²+1).

Теперь обе части равенства возводим во вторую степень:

a⁶+18a⁴+81a²-4a³-36a+4=27a⁴+54a²+27

или

a⁶-9a⁴-4a³+27a²-36a-23=0.

Таким образом a является корнем многочлена

f(x)=a⁶-9a⁴-4a³+27a²-36a-23=0

с рациональными коэффициентами. Это значит что a тАФ алгебраическое число.

2.5. Алгебраическая замкнутость поля алгебраических чисел.

Теорема 2.9. Поле алгебраических чисел алгебраически замкнуто.

Доказательство. Пусть A [x]тАФ кольцо полиномов от xнад полем Aалгебраических чисел. Пусть

f = а₀ + а₁x+.. + а_nхⁿ (а₀ ,тАж, а_n 0A)

тАФ любой полином положительной степени из A[x]. Нам надо доказать, что f имеет корень в А. Так как f0C[x] и поле E алгебраически замкнуто, то f имеет корень в E т. е. существует такое комплексное число с, что f(с) = 0. Пусть L= Q(а₀, .., а_n) и L (с) тАФпростое алгебраическое расширение поля Lс помощью с. Тогда Q —L — L (c) есть конечное алгебраическое расширение поля L. По теореме 2.2, Lесть конечное расширение поля Q. В силу теоремы 2.3 L (с)является конечным расширением поля Q. Отсюда, по теореме 2.2, следует, что поле L(с)является алгебраическим расширением поля Q и, значит, c0A. Таким образом, любой полином из A[x]положительной степени имеет в A корень, т. е. поле A алгебраически замкнуто.

3. Сепарабельные и несепарабельные расширения.

Пусть D тАФ поле.

Выясним, может ли неразложимый в D[x] многочлен обладать кратными корнями?

Для того чтобы f(x) обладал кратными корнями, многочлены f(x) и fN(x) должны иметь общий отличный от константы множитель, который можно вычислить уже в D[x]. Если многочлен f(x) неразложим, то ни с каким многочленом меньшей степени f(x) не может иметь непостоянных общих множителей, следовательно, должно иметь место равенство f '(x) = 0.

Положим

_{n n}

f(x) =3a_nxⁿfN(x) =3na_nx^n-1

^{0 1}

Так как fN(x) = О, в нуль должен обращаться каждый коэффициент:

a_n = 0 ( = l, 2, .., n).

В случае характеристики нуль отсюда следует, что a_n = 0 для всех n ¹ 0. Следовательно, непостоянный многочлен не может иметь кратных корней. В случае же характеристики p равенства na_n = 0 возможны и для n ¹ 0, но тогда обязаны выполняться сравнения

nº0(p).

Таким образом, чтобы многочлен f(x) обладал кратными корнями, все его слагаемые должны обращаться в нуль, за исключением тех a_nxⁿ, для которых nº0(p), т. е. f(x) должен иметь вид

f(x) = a₀+a_px^p+a_2px^2p+тАж

Обратно: если f(x) имеет такой вид, то fN(x)=0.

В этом случае мы можем записать:

f(x) = j(x^p).

Тем самым доказано утверждение: В случае характеристики нуль неразложимый в D [x] многочлен f (x) имеет только простые корни, в случае оке характеристики многочлен f(x) (если он отличен от константы) имеет кратные корни тогда и только тогда, когда его можно представить как многочлен j от x^p.

В последнем случае может оказаться, что j(x) в свою очередь является многочленом от x^p. Тогда f(x) является многочленом от x^p2. Пусть f(x) тАФ многочлен от x^pe

f(x) = y( x^pe),

но не является многочленом от x^pe+1. Разумеется, многочлен y(у) неразложим. Далее, y¢(у) ¹ 0, потому что иначе y(у) имел бы вид c(у^р) и, следовательно, f(x) представлялся бы в виде c(х^pе+1), что противоречит предположению. Следовательно, y(у) имеет только простые корни.

Разложим многочлен y(у) в некотором расширении основного поля на линейные множители: _m

y(y) = J(y-b_i).

¹

Тогда

_m

f(x) = J( x^pe -b_i)

¹

Пусть a_iтАФ какой-нибудь корень многочлена x^pe -_i. Тогда x_i^pe = _i,

x^pe -_i = x^pe тАУ a_i^pe = (x-a_i) ^pe.

Следовательно, a_i является р^е-кратным корнем многочлена x^pe -b_i и

_m

f(x) = J( x -a_i) р^е.

¹

Все корни многочлена f(x) имеют, таким образом, одну и ту же кратность р^е.

Степень m многочлена y называется редуцированной степенью многочлена f(x) (или корня a_i); число e называется показателем многочлена f (x) (или корня a_i) над полем D. Между степенью, редуцированной степенью и показателем имеет место соотношение

n = m р^е,

где m равно числу различных корней многочлена f(x).

Если q тАФ корень неразложимого в кольце D[x] многочлена, облаВндающего лишь простыми корнями, то q называется сепарабельным элементом над D или элементом первого рода над D¹). При этом неразложимый многочлен, все корни которого сепарабельны, назыВнвается сепарабельным. В противном случае алгебраический элеВнмент q и неразложимый многочлен f(x) называются несепарабельными или элементом (соответственно, многочленом) второго рода. Наконец, алгебраическое расширение S, все элементы которого сепарабельны над D, называется сепарабельным над D, а любое другое алгебраическое расширение называется несепарабельным.

В случае характеристики нуль согласно сказанному выше каждый неразложимый многочлен (а потому и каждое алгебраиВнческое расширение) является сепарабельным. Позднее мы увидим, что большинство наиболее важных и интересных расширений полей сепарабельны и что существуют целые классы полей, вообще не имеющих несепарабельных расширений (так называемые ВлсоверВншенные поляВ»). По этой причине в дальнейшем все связанное специально с несепарабельными расширениями набрано мелким шрифтом.

Рассмотрим теперь алгебраическое расширение S = D (q). Когда степень n уравнения f(x) = 0, определяющего это расширение, равна степени (S : D), редуцированная степень m оказывается равной числу изоморфизмов поля S в следующем смысле: рассмотВнрим лишь такие изоморфизмы S@S', при которых элементы подполя D остаются неподвижными и, следовательно, S перевоВндится в эквивалентное поле S' (изоморфизмы поля S над полем D) и при которых поле-образ S' лежит вместе с полем S внутри некоторого общего для них поля W. В этих условиях имеет место теорема:

При подходящем выборе поля W расширение S=D(q) имеет ровно m изоморфизмов над D и при любом выборе поля W поле S не может иметь более m таких изоморфизмов.

Доказательство. Каждый изоморфизм над D должен переВнводить элемент q в сопряженный с ним элемент q' из W. ВыбеВнрем W так, чтобы f(x) разлагался над W на линейные множители; тогда окажется, что элемент q имеет ровно m сопряженных элеВнментов q,q', .. При этом, как бы ни выбиралось поле W, элемент q не будет иметь в нем более m сопряженных. Заметим теперь, что каждый изоморфизм D(q)@D(q') над D полностью определяется заданием соответствия qВоq'. Действительно, если q переходит в q' и все элементы из D остаются на месте, то элемент

3a_kq^k (a_k0D)

должен переходить в

3a_kqN^k

а этим определяется изоморфизм.

В частности, если q тАФ сепарабельный элемент, то m = n и, следоВнвательно, число изоморфизмов над основным полем равно степени расширения.

Если имеется какое-то фиксированное поле, содержащее все рассматриваемые поля, в котором содержатся все корни каждого уравнения f(x) = 0 (как, например, в поле комплексных чисел), то в качестве W можно раз и навсегда взять это поле и поэтому отбросить добавление Влвнутри некоторого WВ» во всех предложеВнниях об изоморфизмах. Так всегда поступают в теории числовых полей. Позднее мы увидим, что и для абстрактных полей можно построить такое поле W.

Обобщением приведенной выше теоремы служит следующее утверждение:

Если расширение S получается из D последовательным присоединением m

алгебраических элементов a₁, .., a_m, причем каждое из a_i,- является корнем

неразложимого над D(a₁, .., a_i-1) уравнения редуцированной степени '_i, то

_m

расширение S имеет ровно Õn_i¢ изоморфизмов над D и ни в одном

¹

расширении нет большего числа таких изоморфизмов поля S.

Доказательство. Для m = 1 теорема уже была доказана выше. Предположим ее справедливой для расширения S₁ = D(a₁, .., a_m-1): в некотором подходящем расширении

_m-1

W₁ есть ровно Õ n_i¢ изоморфизмов поля S над D.

¹ _m-1

Пусть S₁ВоS₁тАФ один из этих Õ n_i¢ изоморфизмов. Утверждается, что в подходящим образом выбранном поле W он может быть продолжен до изоморфизма S = S₁ (a_m) @ S= S(a_m) не более чем n¢_m способами.

Элемент a_m удовлетворяет некоторому уравнению f₁(x) = 0 над S₁ с n¢_m разВнличными корнями. С помощью изоморфизма S₁ВоS₁многочлен f₁(x) перевоВндится в некоторый многочлен f₁(x). Но тогда f₁(x) в подходящем расширении имеет опять-таки n¢_m различных корней и не больше. Пусть a_mтАФ один из этих корней. В силу выбора элемента a_m изоморфизм S₁@S₁ продолжается до изоморфизма S (a_m) @ S (a_m) с a_mВоa_m одним и только одним способом: действительно, это продолжение задается формулой

åc_ka_m^k Воå c_ka_m^k

Так как выбор элемента a_m может быть осуществлен n'_m способами, существует n'_m продолжений такого сорта для выбранного изоморфизма å₁Воå₁

Так как в свою очередь этот изоморфизм может быть выбран

_m-1

Õ n'_i способами,

¹

то всего существует (в том поле W, в котором содержатся все корни всех рассматриваемых уравнений)

_{m-1 m}

Õ n'_i×n'_m = Õ n'_i

^{1 1}

изоморфизмов расширения S над полем D, что и требовалось доказать.

Если n_i тАФ полная (нередуцированная) степень элемента a_i над D (a₁,..,a_i-1), то n_i равно степени расширения D (a₁, .. , a_i) поля D(a₁, .. , a_i-1);

следовательно, степень (S : D) равна

_m

Õ n'_i .

¹

Если сравнить это число с числом изоморфизмов

_m

Õ n'_i .

¹

то получится следующее предложение:

Число изоморфизмов расширения S = D(a₁, .. , a_m) над D(в некотором подходящем расширении W) равно степени (S : D) тогда и только тогда, когда каждый элемент a_i сепарабелен над полем D(a₁, .. , a_i-1). Если же хотя бы один элемент a_i несепарабелен над соответствующим полем, то число изоморфизмов меньше степени расширения.

Из этой теоремы сразу получается несколько важных следствий. Прежде всего теорема утверждает, что свойство каждого элемента a_i быть сепарабельным над предыдущим полем есть свойство самого расширения S независимо от выбора порождающих элементов a_i. Так как произвольный элемент b поля может быть взят в качестве первого порождающего, элемент b оказывается сепарабельным, если все a_i являются таковыми. Итак:

Если к полю D последовательно присоединяются элементы a_i, .. ,a_n и каждый элемент a_i оказывается сепарабельным над полем, полученным присоедиВннением предыдущих элементов a_1, a₂ ,тАж,a_i-1 то расширение

S = D(a₁, .. ,a_n)

сепарабельно над D.

В частности, сумма, разность, произведение и частное сепарабедьных элементов сепарабельны.

Далее, если b сепарабелен над S, а поле S сепарабельно над D, то элеВнмент b сепарабелен над D. Это объясняется тем, что b удовлетворяет некотоВнрому уравнению с конечным числом коэффициентов a₁, .. ,a_m из S и, слеВндовательно, сепарабелен над D (a₁, .. ,a_m). Тем самым сепарабельно и расширение

D (a₁,.., a_m,b).

Наконец, имеет место следующее предложение: числа изоморфизмов конечного сепарабельного расширения S над полем D равно степени расширения (S : D).

4. Бесконечные расширения полей.

Каждое поле получается из своего простого подполя с помощью конечного или бесконечного расширения. В этой главе рассматриВнваются бесконечные расширения полей, сначала алгебраические, а затем тАФ трансцендентные.

4.1. Алгебраически замкнутые поля

Среди алгебраических расширений заданного поля важную роль играют, конечно, максимальные алгебраические расширения, т. е. такие, которые не допускают дальнейшего алгебраического расширения. Существование таких расширений будет доказано в настоящем параграфе.

Чтобы поле W было максимальным алгебраическим расширеВннием, необходимо следующее условие: каждый многочлен кольца W[x]полностью разлагается на линейные множители. Это условие является и достаточным. Действительно, если каждый многочлен в W[x]разлагается на линейные множиВнтели, то все простые многочлены в W[x]линейны и каждый элеВнмент любого алгебраического расширения W' поля W оказывается корнем некоторого линейного многочлена x тАФ aв W[x],т. е. совпадает с некоторым элементом aполя W.

Поэтому дадим следующее определение:

Поле W называется алгебраически замкнутым, если любой многочлен в W[x] разлагается на линейные множители.

Равнозначное с этим определение таково: поле W, алгебраически замкнуто, если каждый отличный от константы многочлен из W[x] обладает в W хоть одним корнем, т. е. хоть одним линейным множителем в W[x].

Действительно, если такое условие выполнено и произвольно взятый многочлен f(x) разлагается на неразложимые множители, то все они должны быть линейными.

ВлОсновная теорема алгебрыВ» утверждает, что поле комплексных чисел алгебраически замкнуто. Следующим примером алгебраически замкнутого поля может служить поле всех комплексных алгебраических чисел, т. е. множеВнство тех комплексных чисел, которые удовлетворяют какому-либо уравнению с рациональными коэффициентами. Комплексные корни уравнения с алгебраическими коэффициентами являются и в самом деле алгебраическими не только над полем алгебраических чисел, но и над полем рациональных чисел, т. е. сами являются алгебраВническими числами.

Здесь мы покажем, как построить алгебраически замкнутое расширение произвольно заданного поля P и притом чисто алгебраическим путем. Штейницу принадлежит следующая

Основная теорема. Для каждого поля P существует алгебраически замкнутое алгебраическое расширение W.Сточностью до эквивалентности это расширение определено однозначно: любые два алгебраически замкнут

Вместе с этим смотрят: