Цепные дроби
Содержание
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава I. ПРАВИЛЬНЫЕ КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
Вз1. Представление рациональных чисел цепными дробями
Вз2. Подходящие дроби. Их свойства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава II. БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
Вз1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями
1.1. Разложение действительного иррационального числа в правильную бесконечную цепную дробь . . . . . . . . . . . . . . . . . . . . .
1.2. Сходимость правильных бесконечных цепных дробей . . . . .
1.3. Единственность представления действительного иррационального числа правильной бесконечной цепной дробью
Вз2. Приближение действительного числа рациональными дробями с заданным ограничением для знаменателя
2.1. Оценка погрешности при замене действительного числа его подходящей дробью . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Приближение действительного числа подходящими дробями
2.3. Теорема Дирихле . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4. Подходящие дроби как наилучшие приближения
Вз3. Квадратические иррациональности и периодические цепные дроби. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Вз4. Представление действительных чисел цепными дробями общего вида . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Решение задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Используемая литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Введение
Целью моей курсовой работы является исследование теории цепных дробей. В ней я попытаюсь раскрыть свойства подходящих дробей, особенности разложения действительных чисел в неправильные дроби, погрешности, которые возникают в результате этого разложения, и применение теории цепных дробей для решения ряда алгебраических задач.
Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.
Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.
Глава I. Правильные конечные цепные дроби.
Вз1. Представление рациональных чисел цепными дробями.
Целое число, являющееся делителем каждого из целых чисел 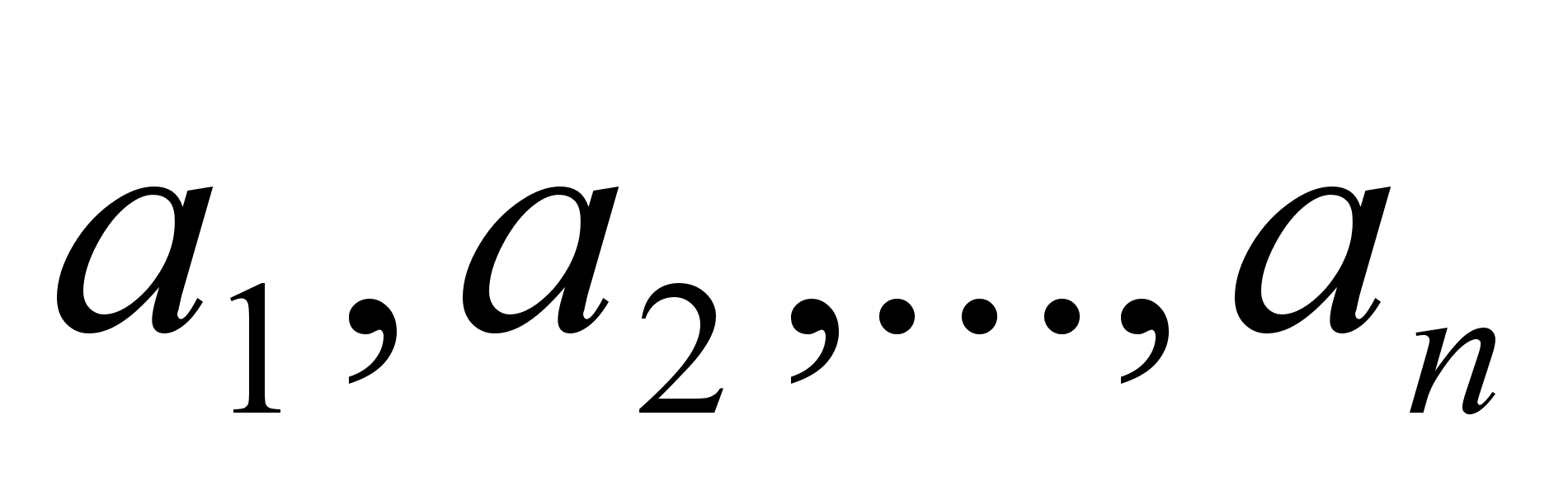 , называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
, называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
Пусть  - рациональное число, причем >0. Применяя к a и алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:
- рациональное число, причем >0. Применяя к a и алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:

где неполным частным последовательных делений 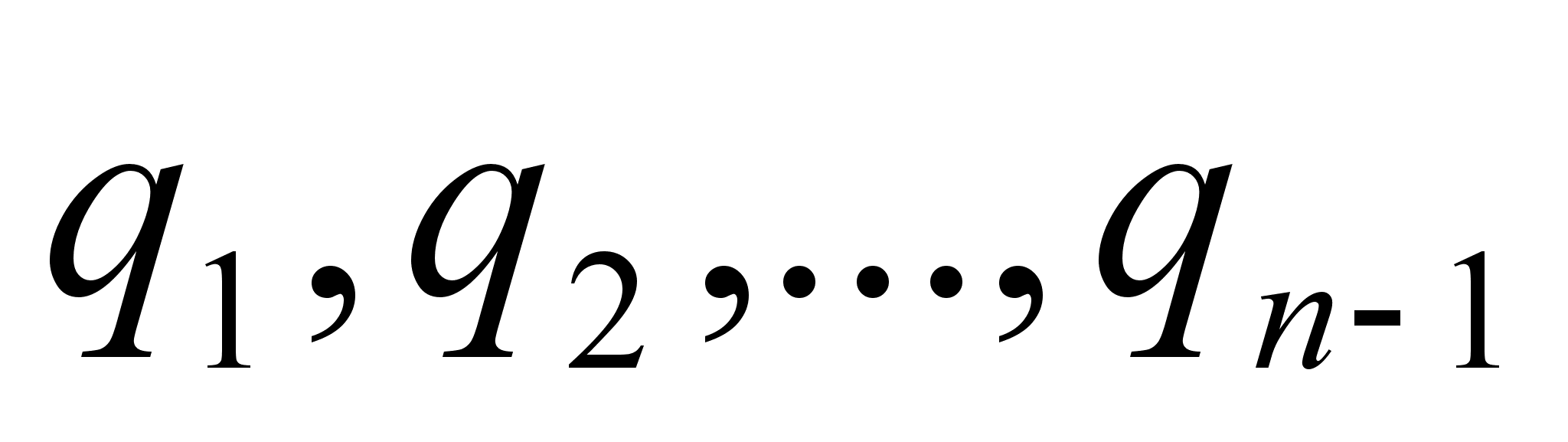 соответствуют остатки
соответствуют остатки 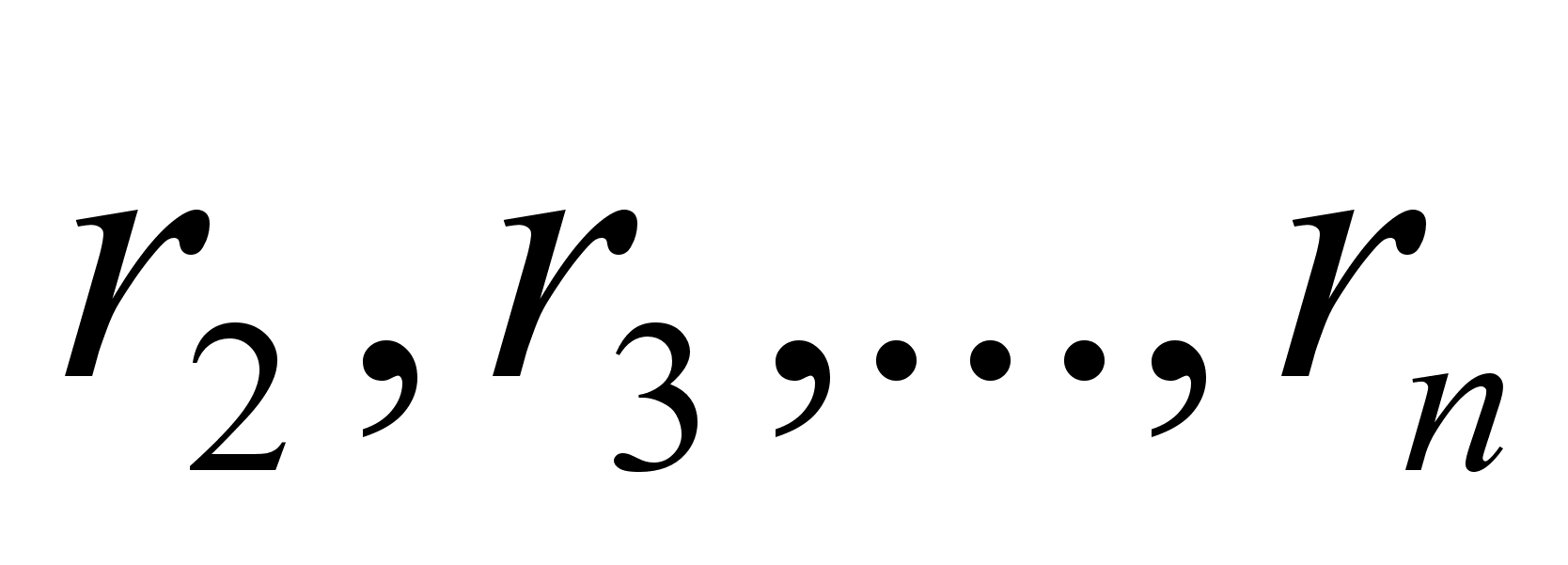 с условием b>
с условием b>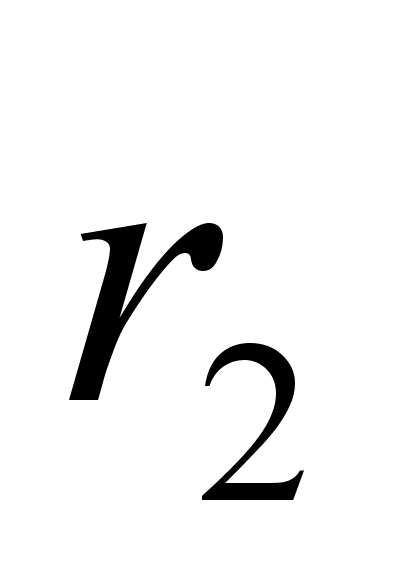 >
>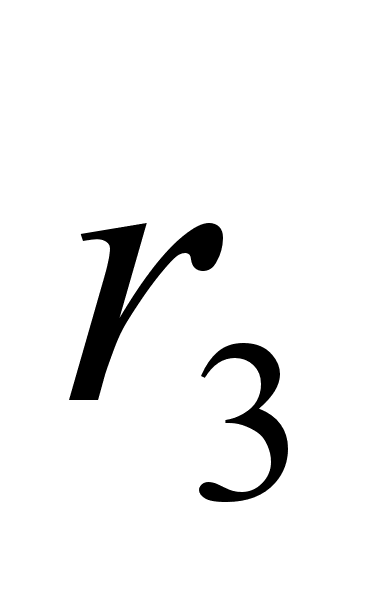 >тАж>
>тАж>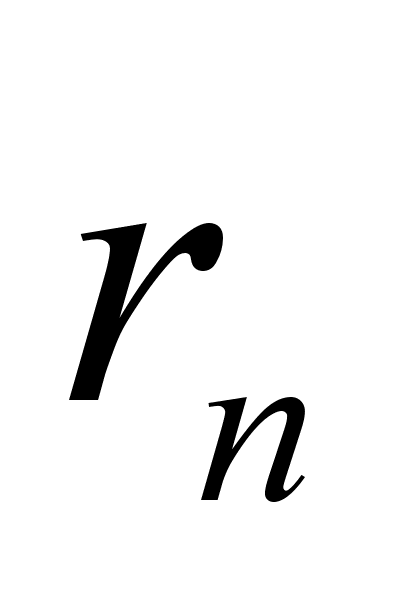 >0, а соответствует остаток 0.
>0, а соответствует остаток 0.
Системе равенств (1) соответствует равносильная система

из которой последовательной заменой каждой из дробей 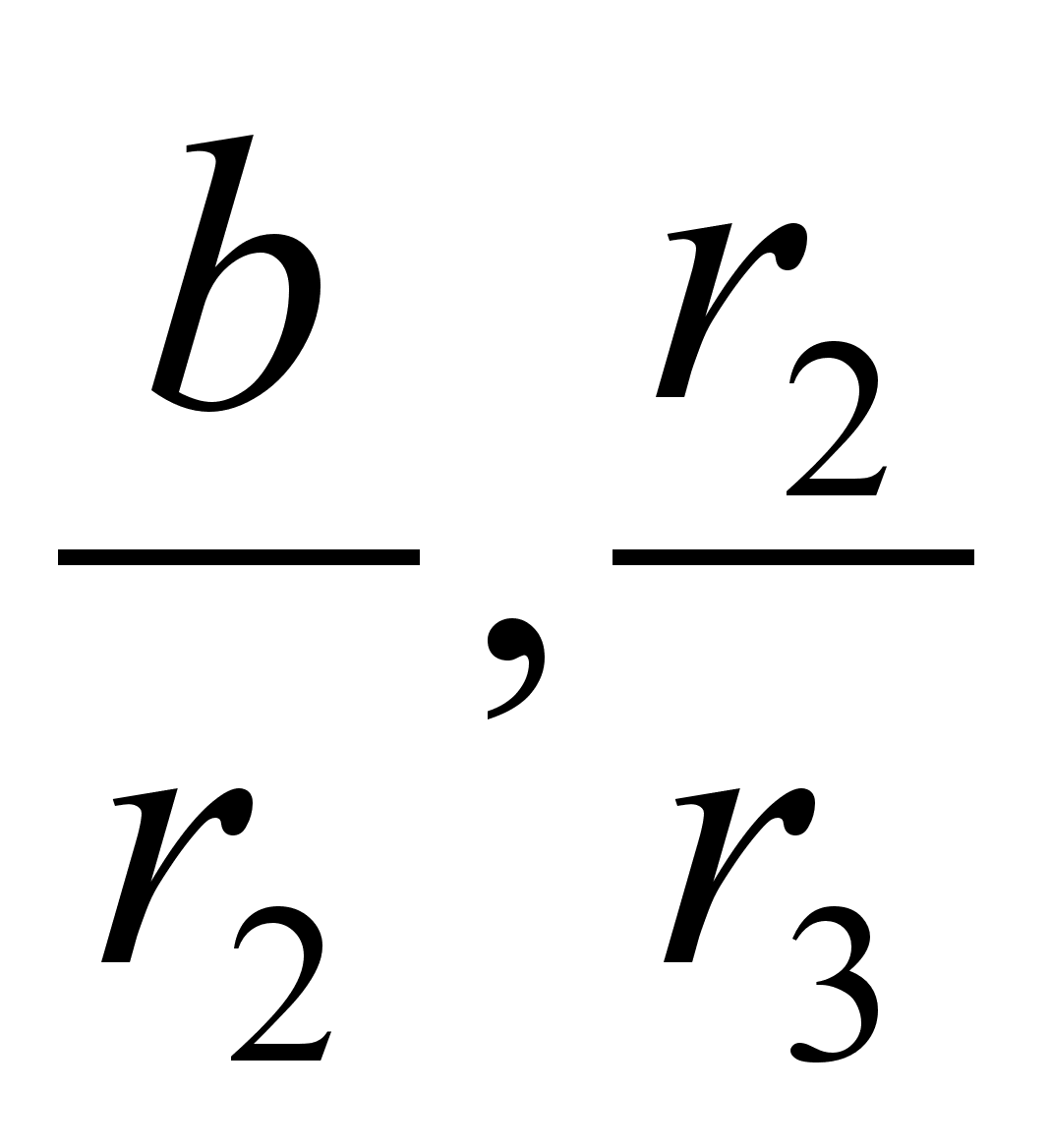 и т.д. ее соответствующим выражением из следующей строки получается представление дроби
и т.д. ее соответствующим выражением из следующей строки получается представление дроби  в виде:
в виде:



Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что 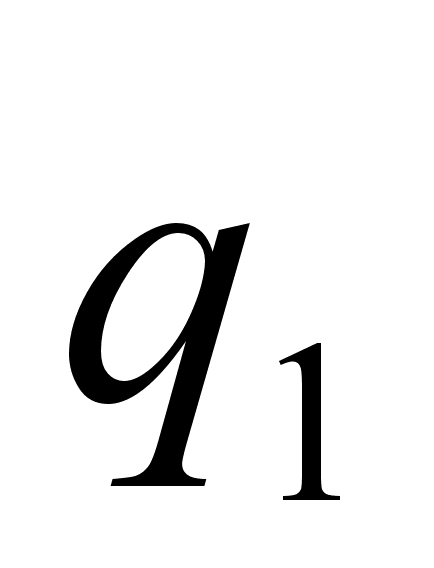 тАУ целое число, а
тАУ целое число, а 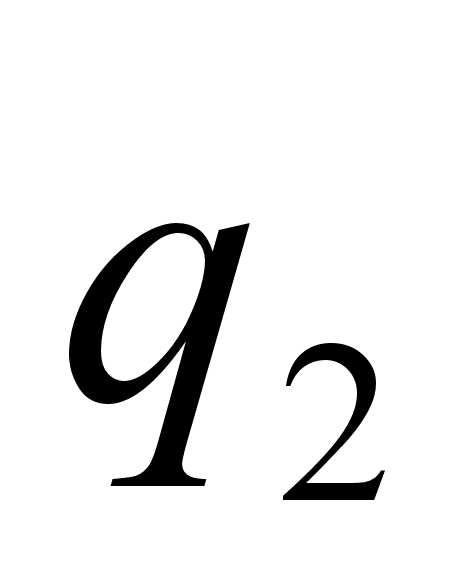 , тАж,
, тАж, 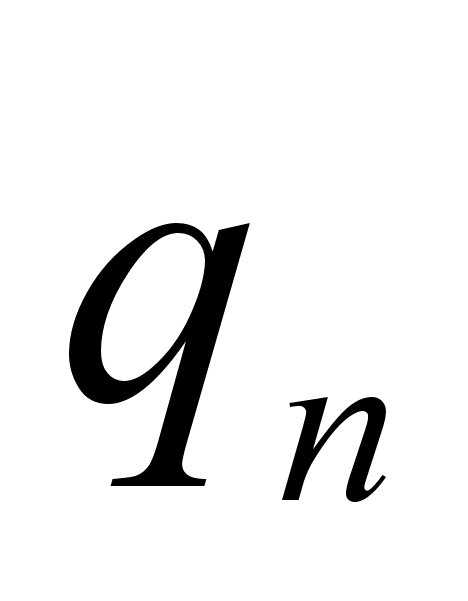 - натуральные числа.
- натуральные числа.
Имеются различные формы записи цепных дробей:



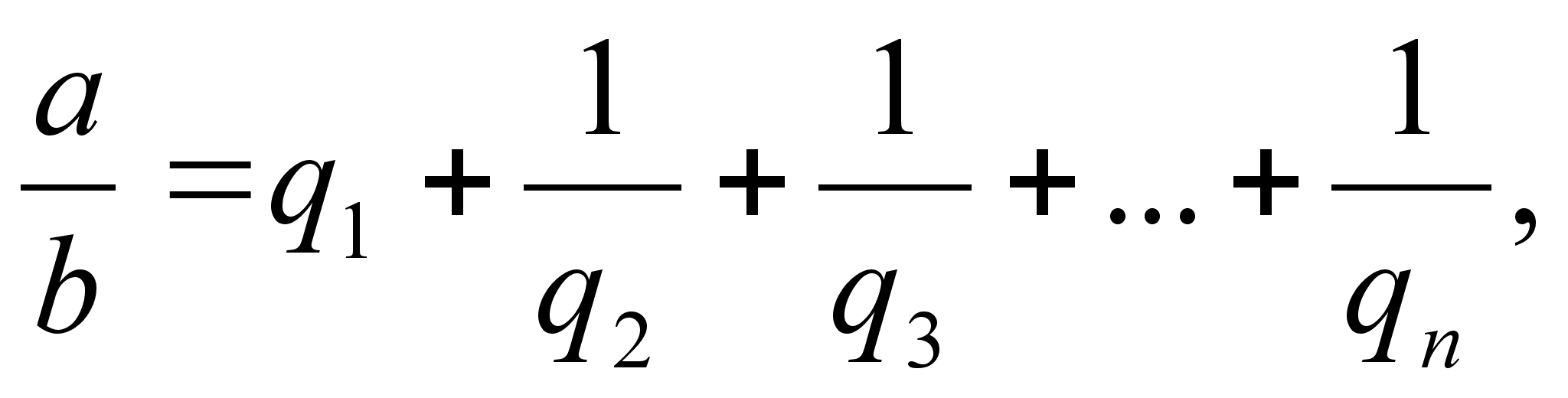
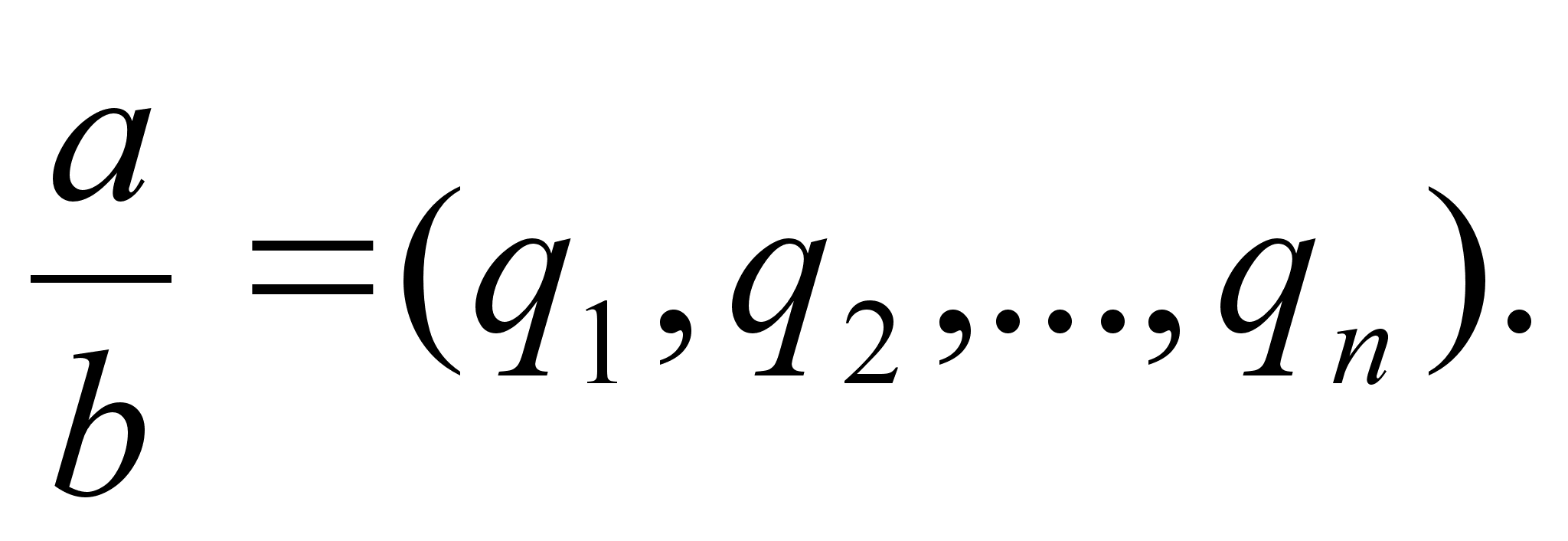
Согласно последнему обозначению имеем
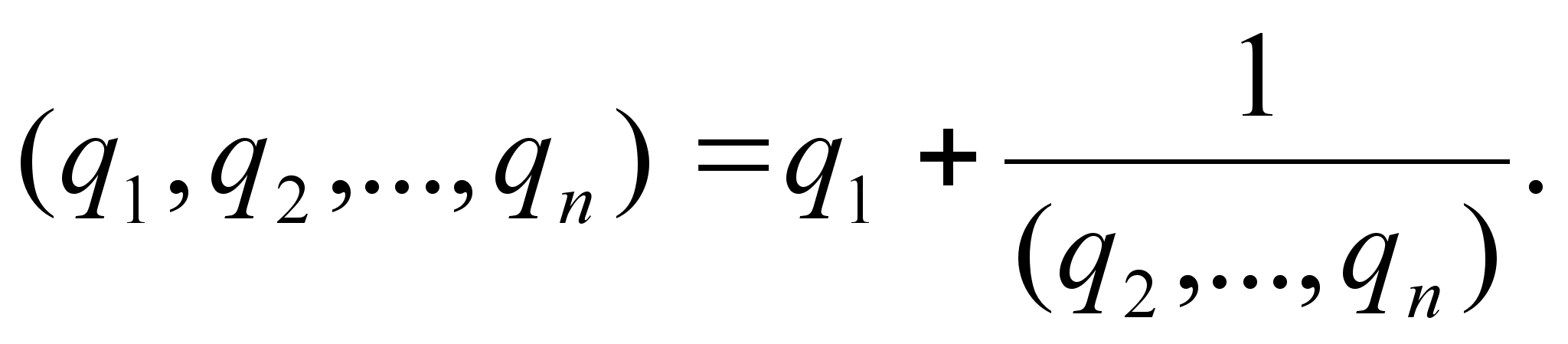
Числа 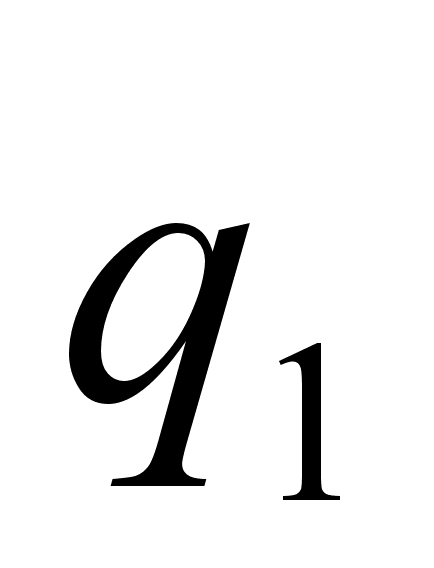 ,
, 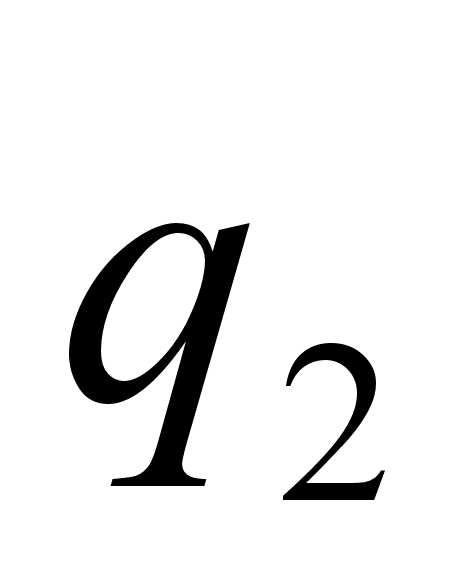 , тАж,
, тАж,  называются элементами цепной дроби.
называются элементами цепной дроби.
Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.
Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.
Разложение рационального числа  имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на является конечным.
имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на является конечным.
Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было 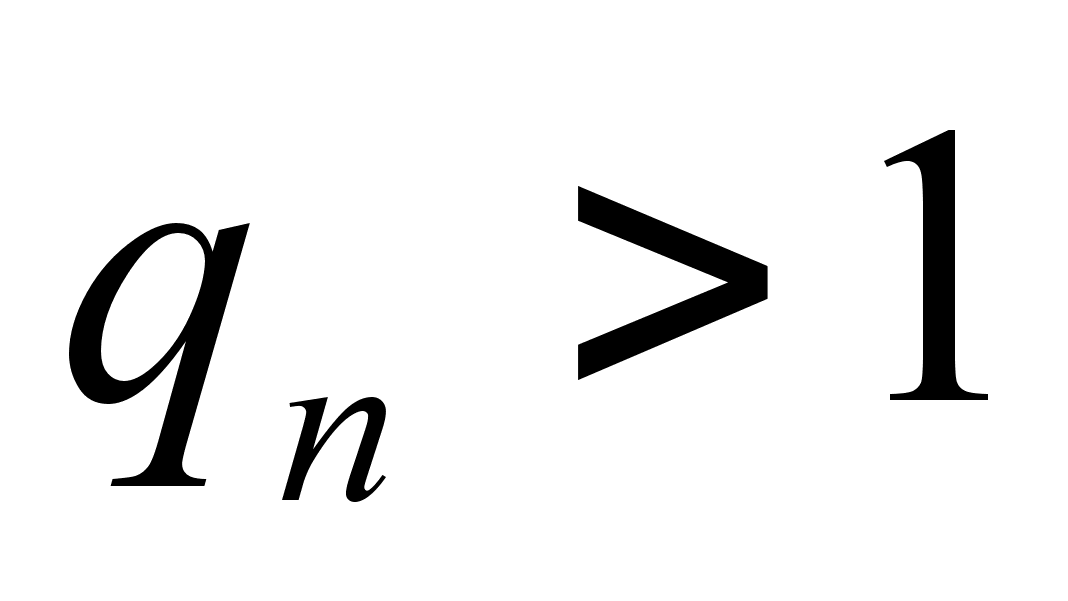 .
.
Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, но при условии, что 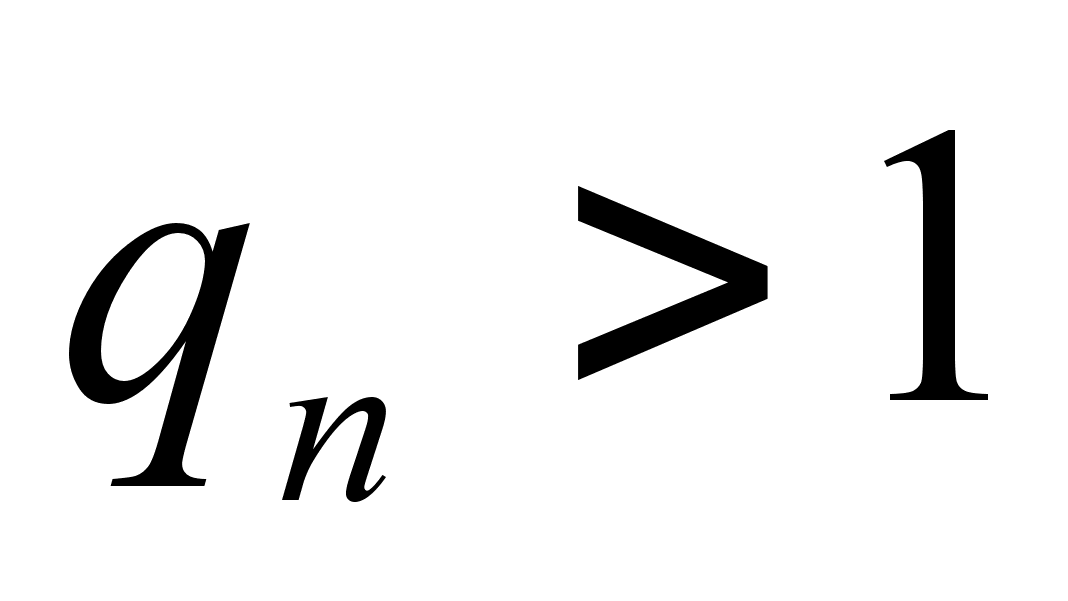 .
.
Доказательство: 1) Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при 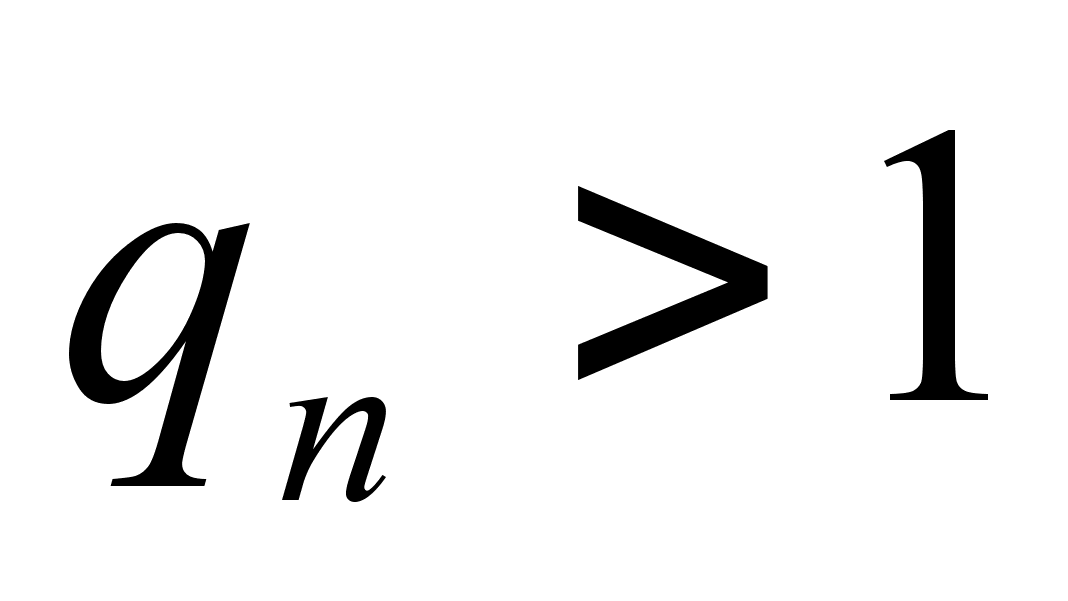 :
:
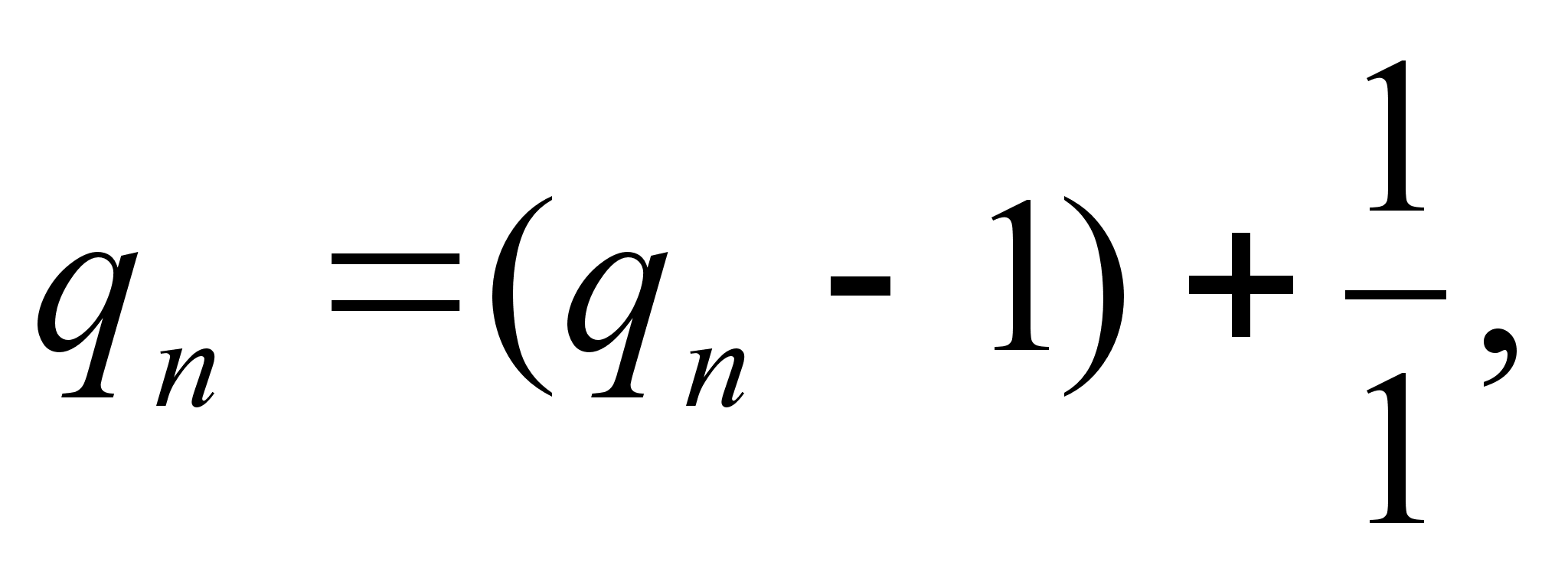
так что представление можно удлинить:
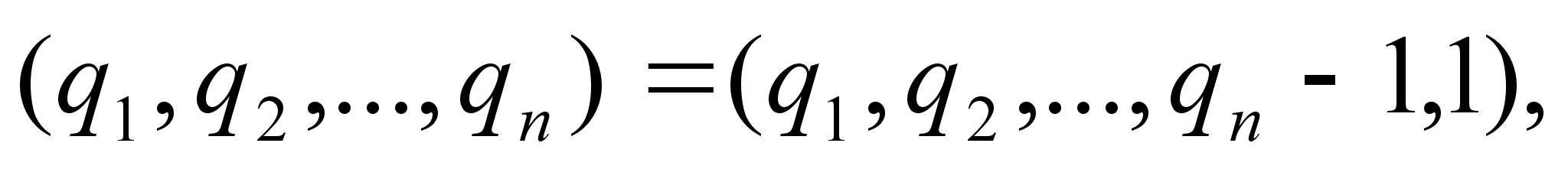
например, (2, 3, 1, 4, 2)=( 2, 3, 1, 4, 1, 1).
2) Принимая условие 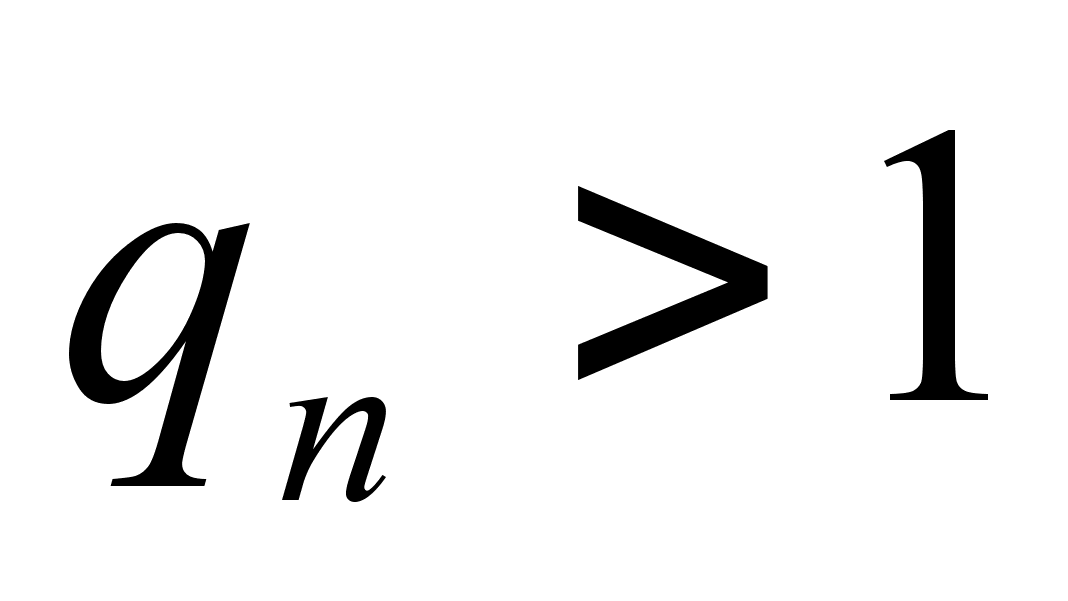 , можно утверждать, что целая часть цепной дроби
, можно утверждать, что целая часть цепной дроби 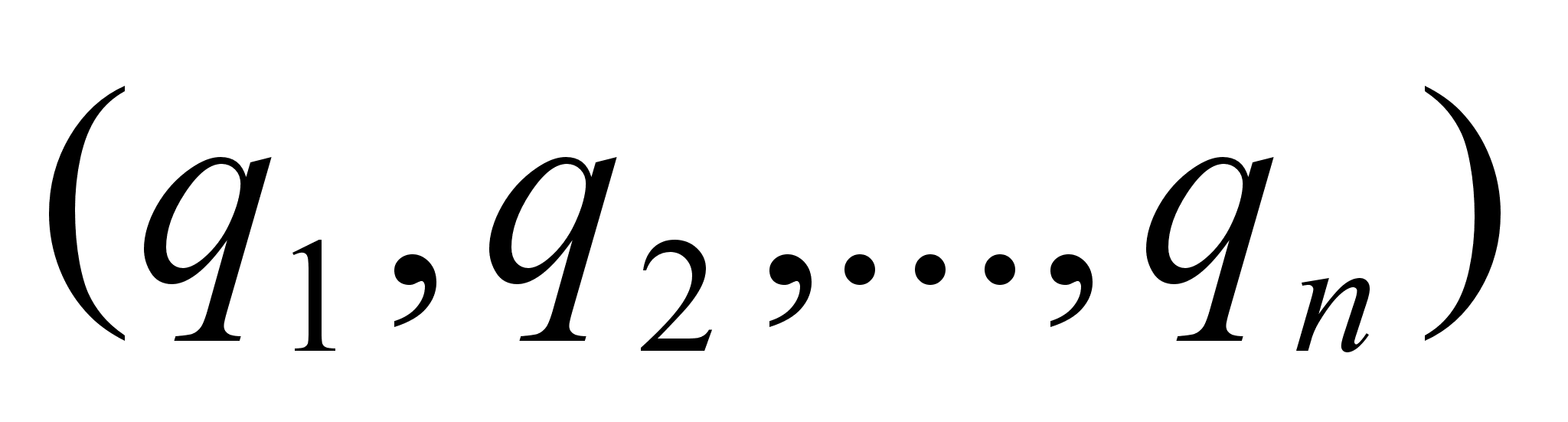 равна ее первому неполному частному
равна ее первому неполному частному 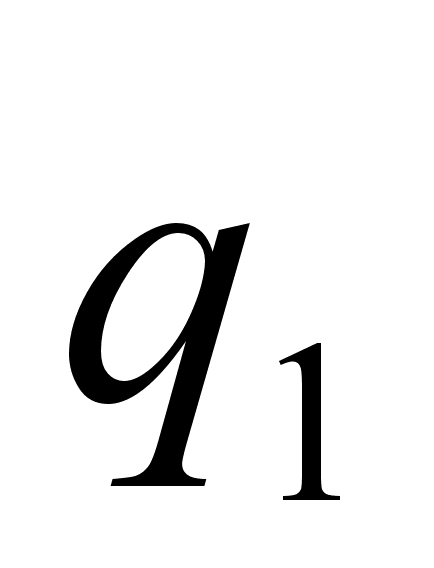 . В самом деле:
. В самом деле:
если n=1, то
если n=2, то 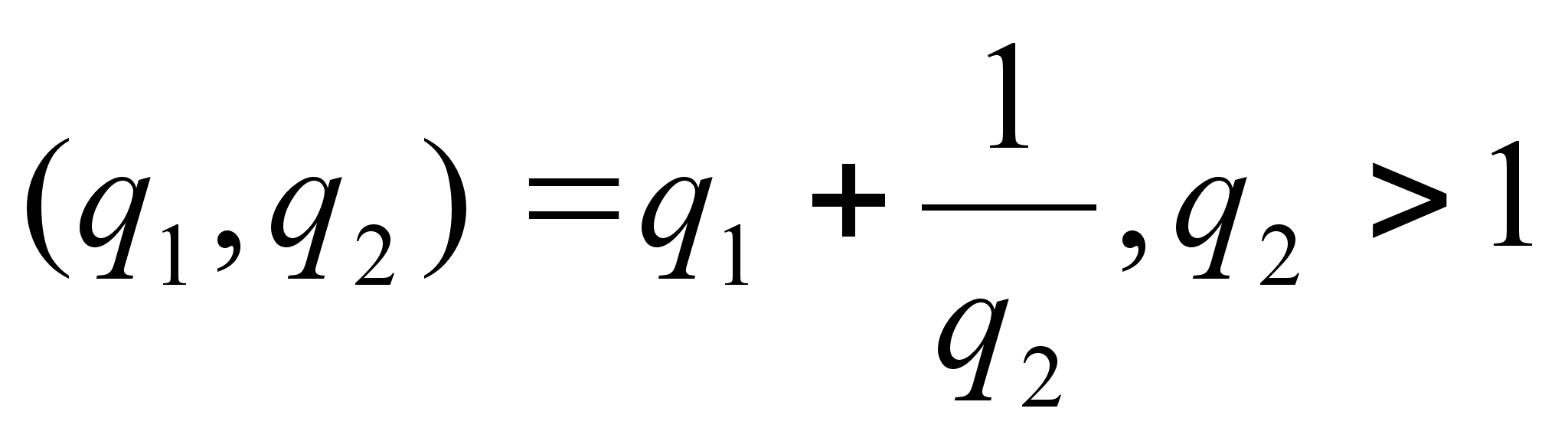 ; поэтому
; поэтому 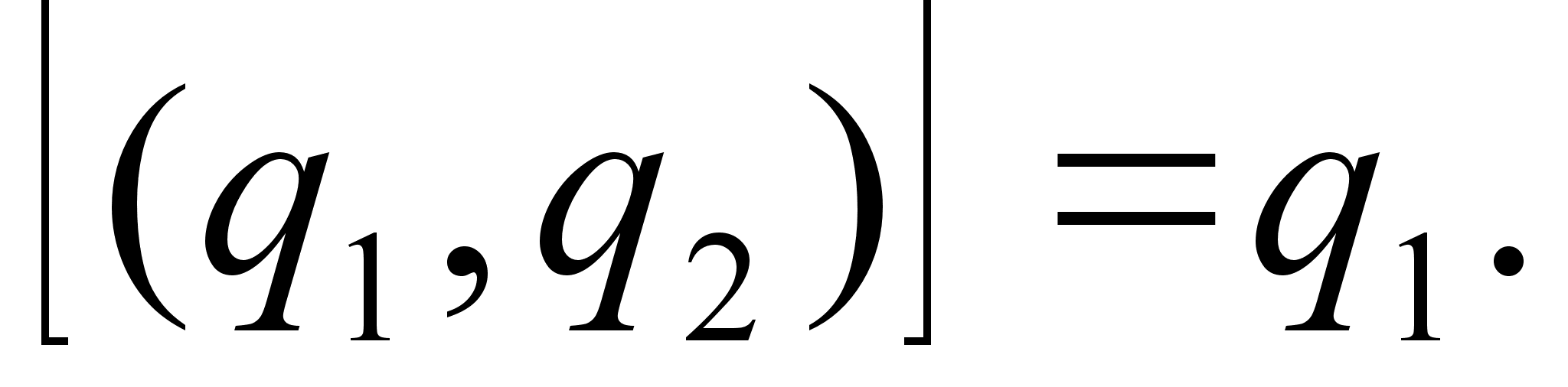
если n>2, то
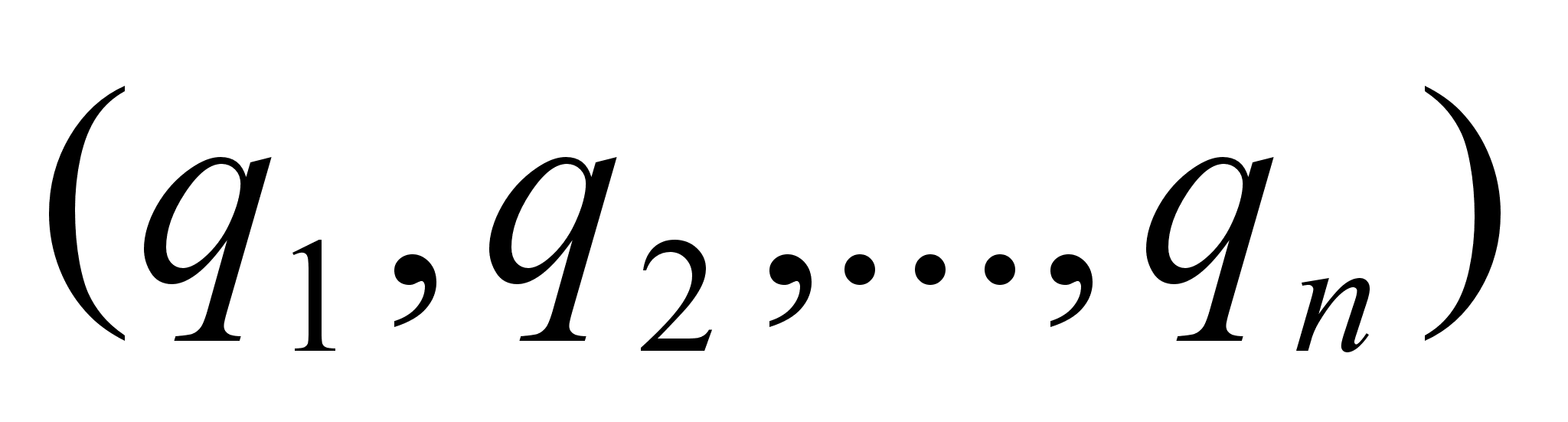 =
=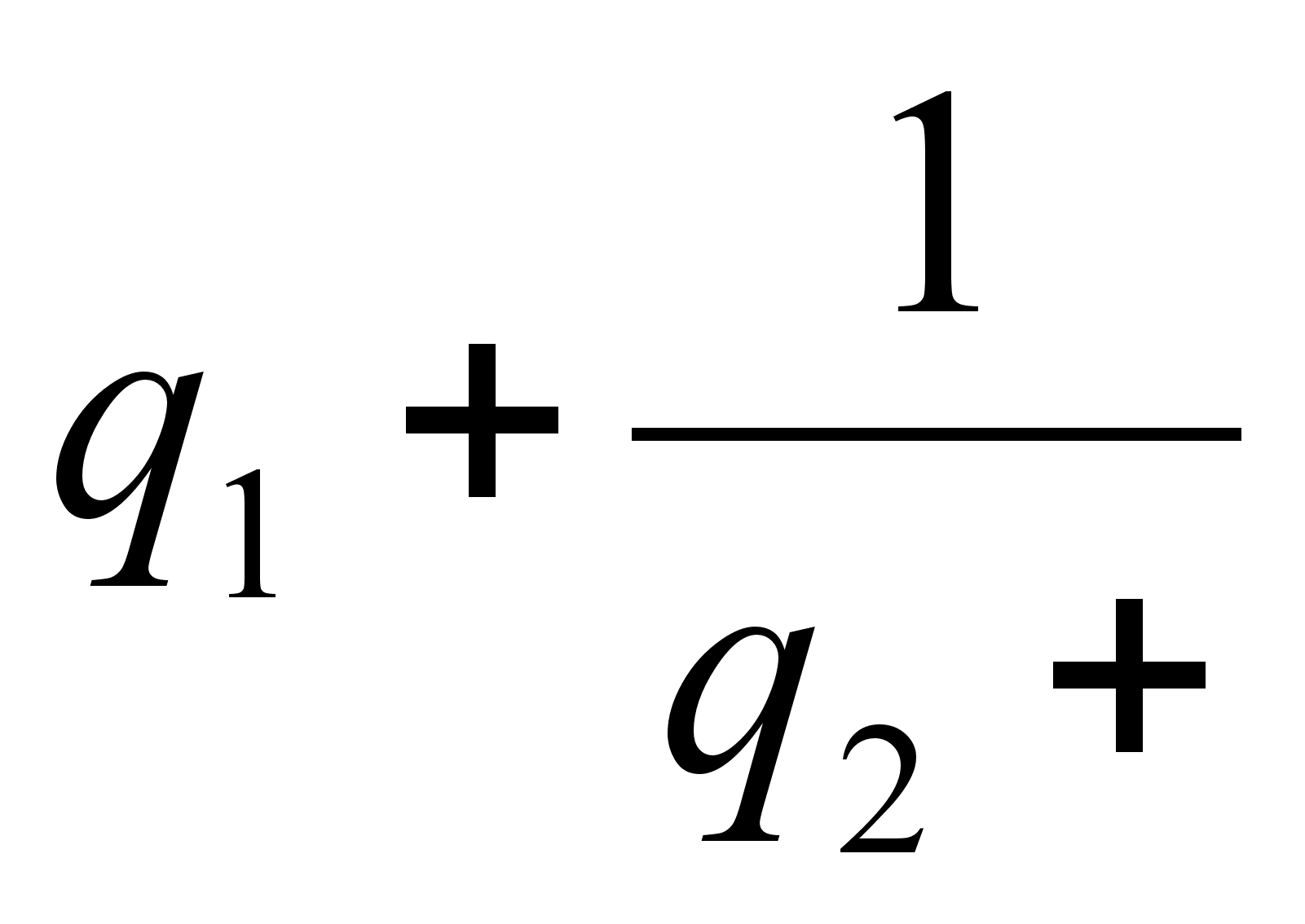

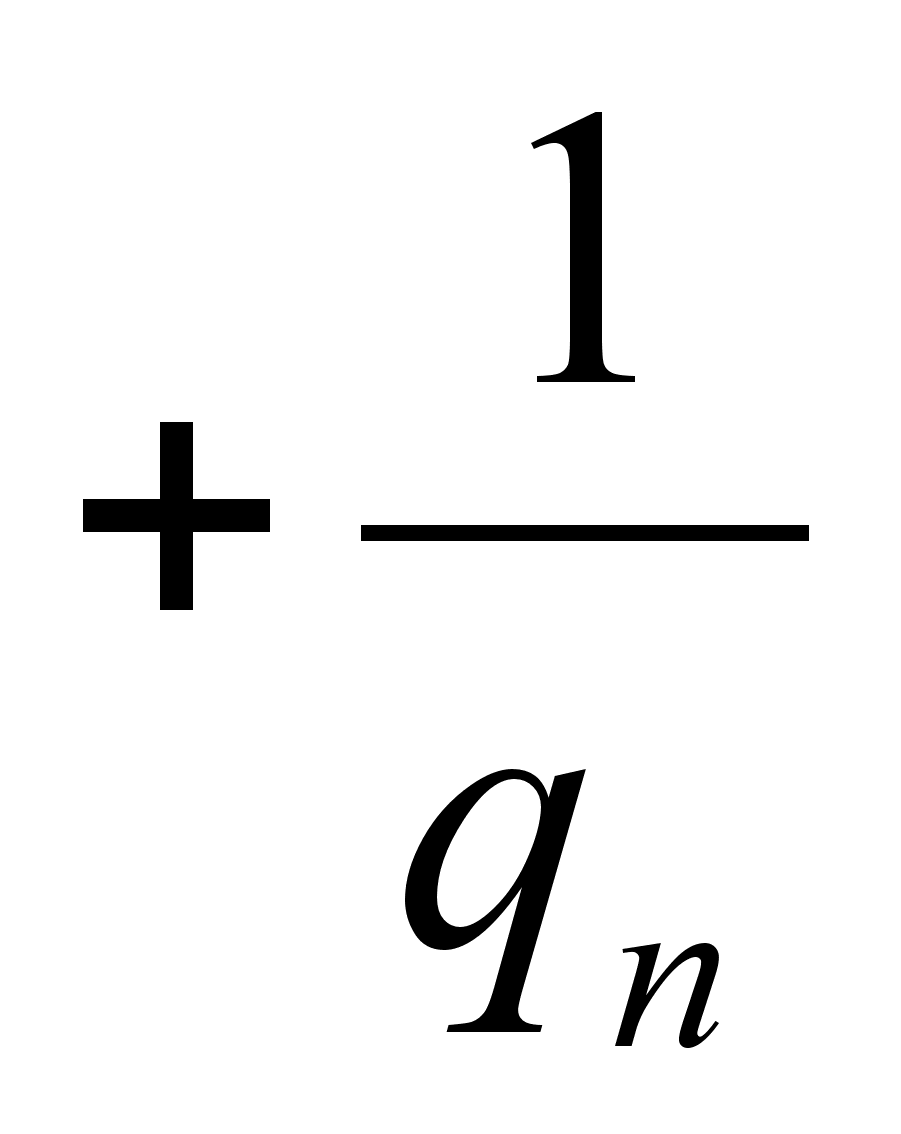 ,
,
где 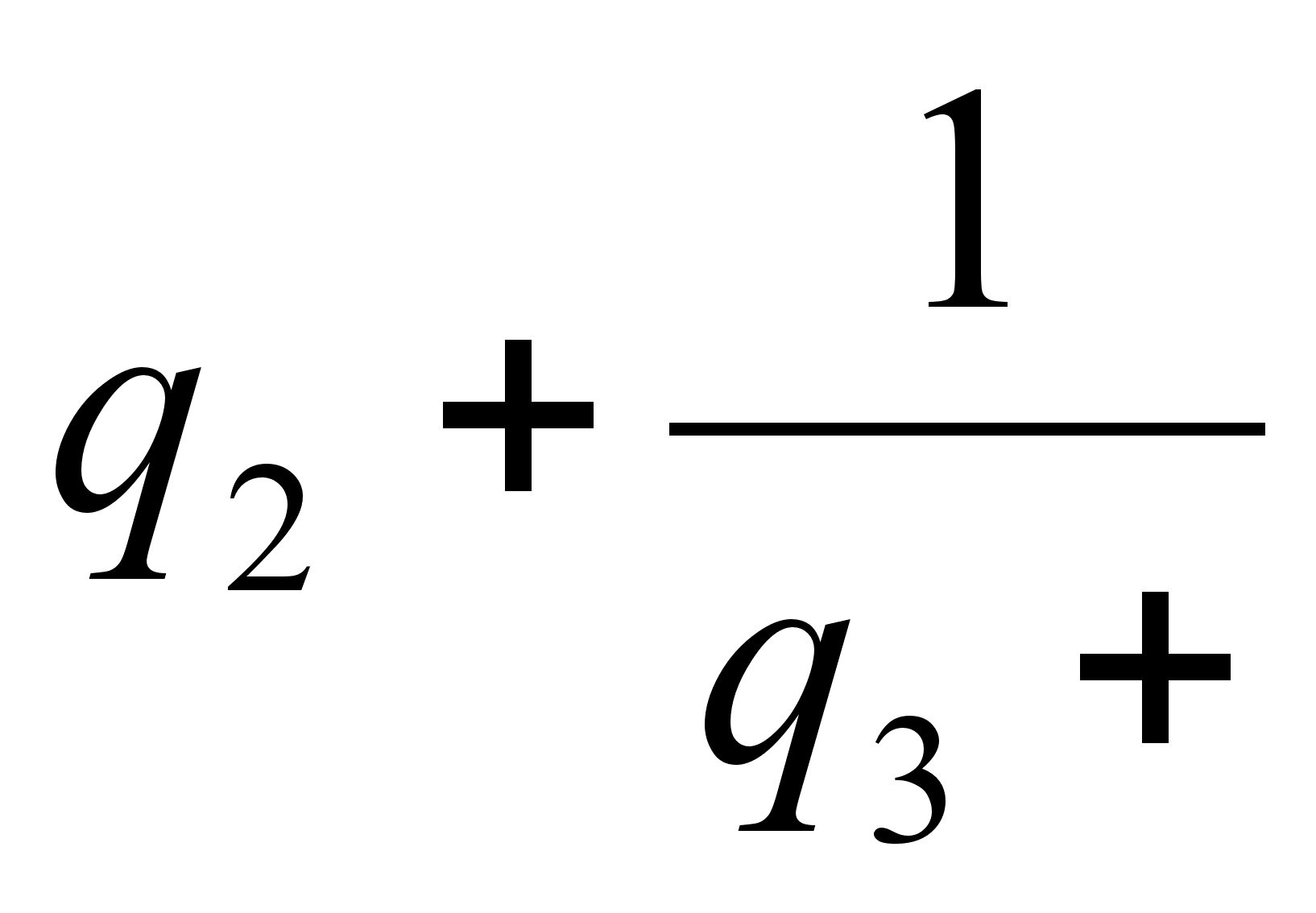 >1, т.к.
>1, т.к. 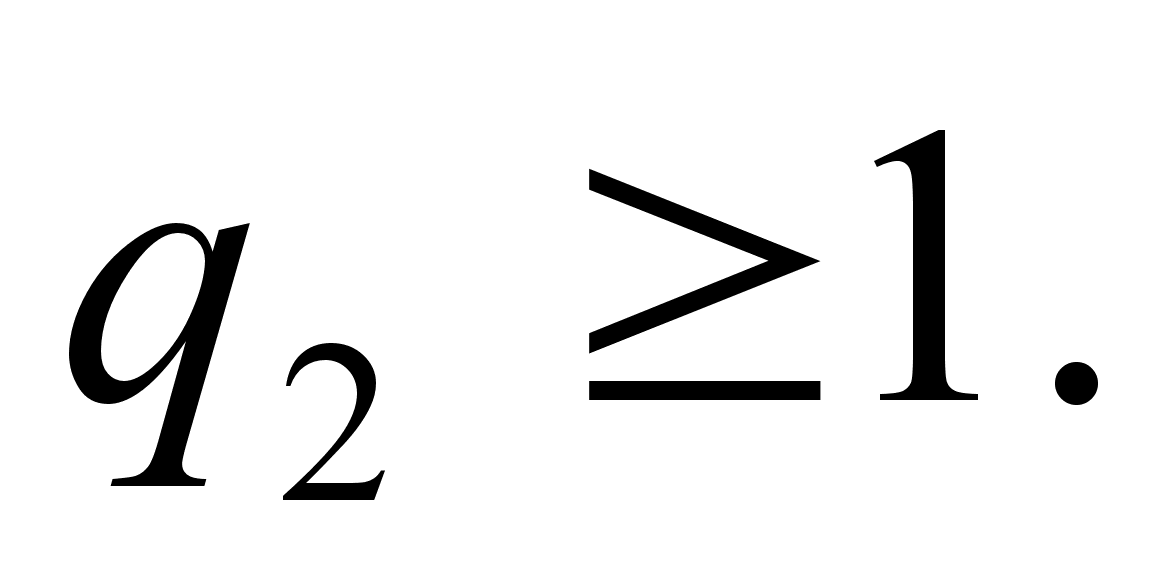

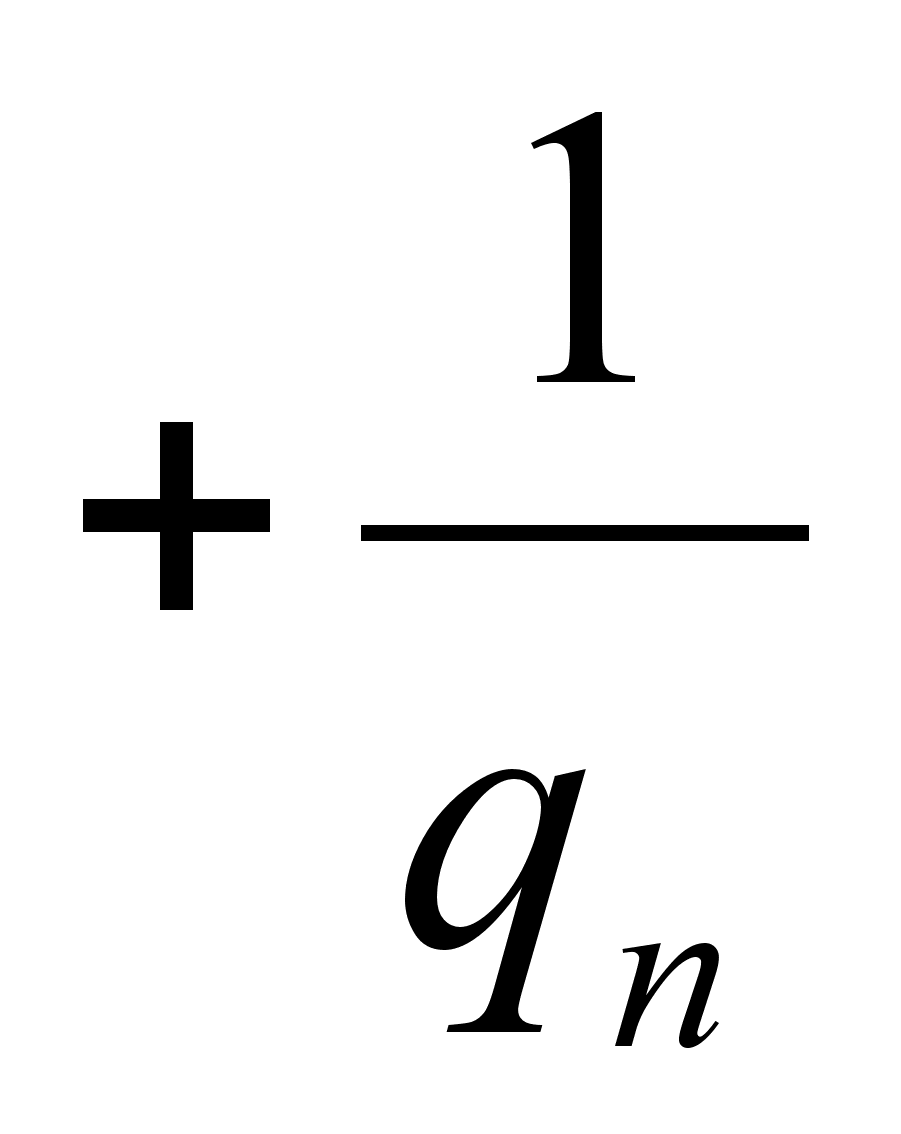
Поэтому и здесь 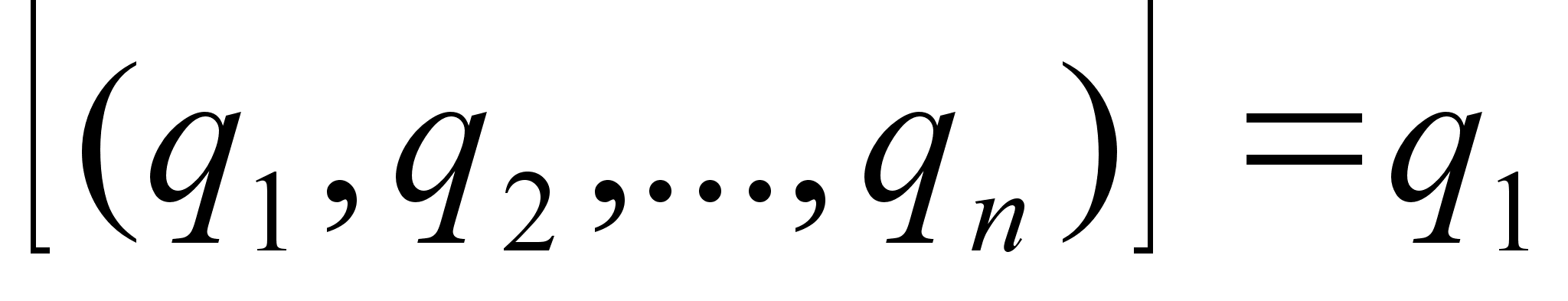 . Докажем то, что рациональное число
. Докажем то, что рациональное число  однозначно представляется цепной дробью
однозначно представляется цепной дробью 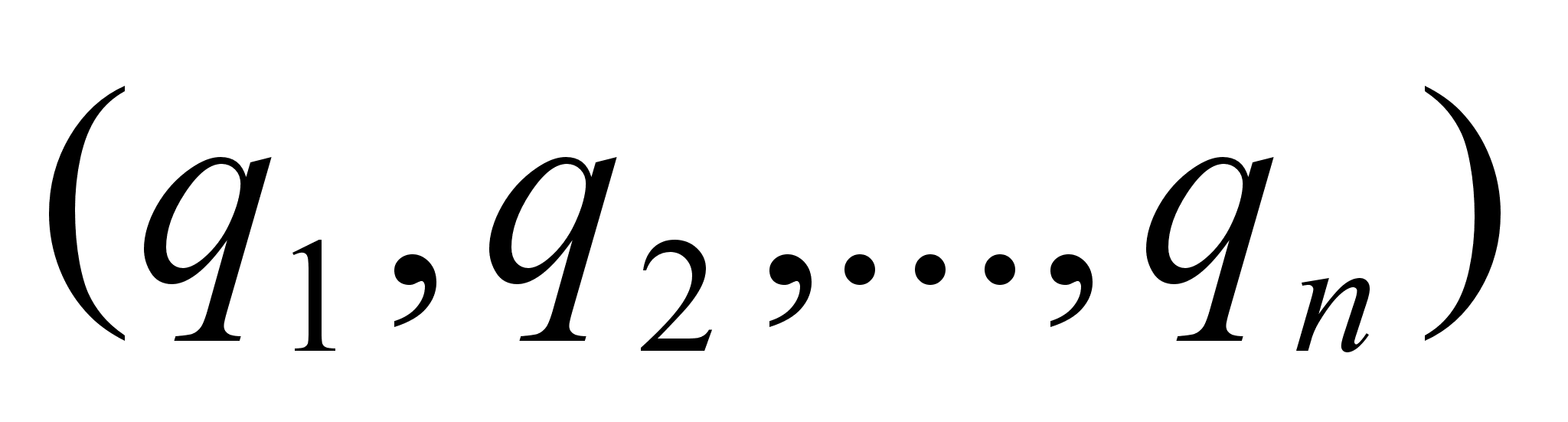 , если
, если 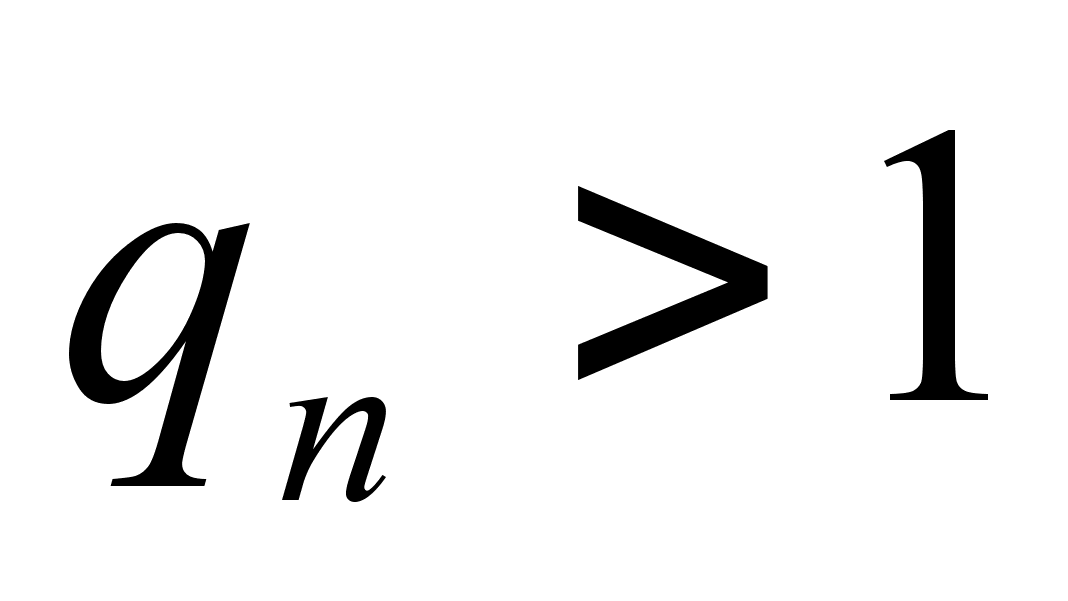 .
.
Пусть 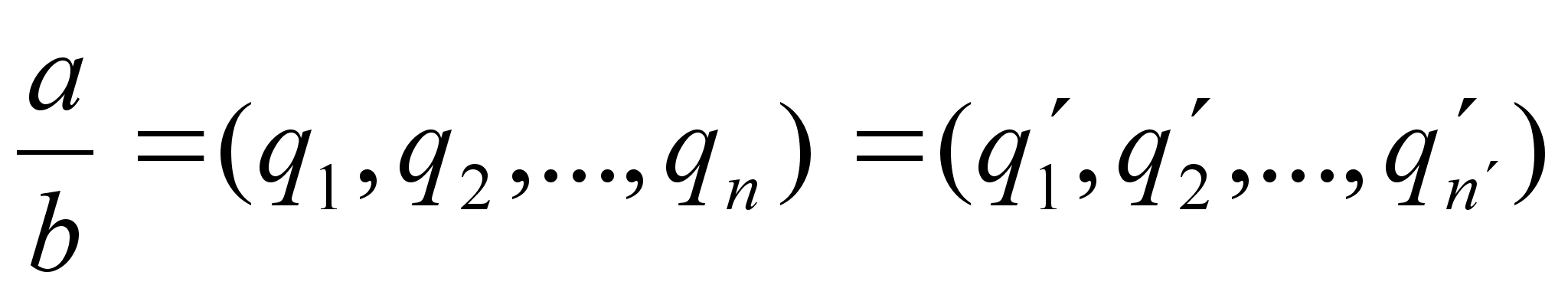 с условием
с условием 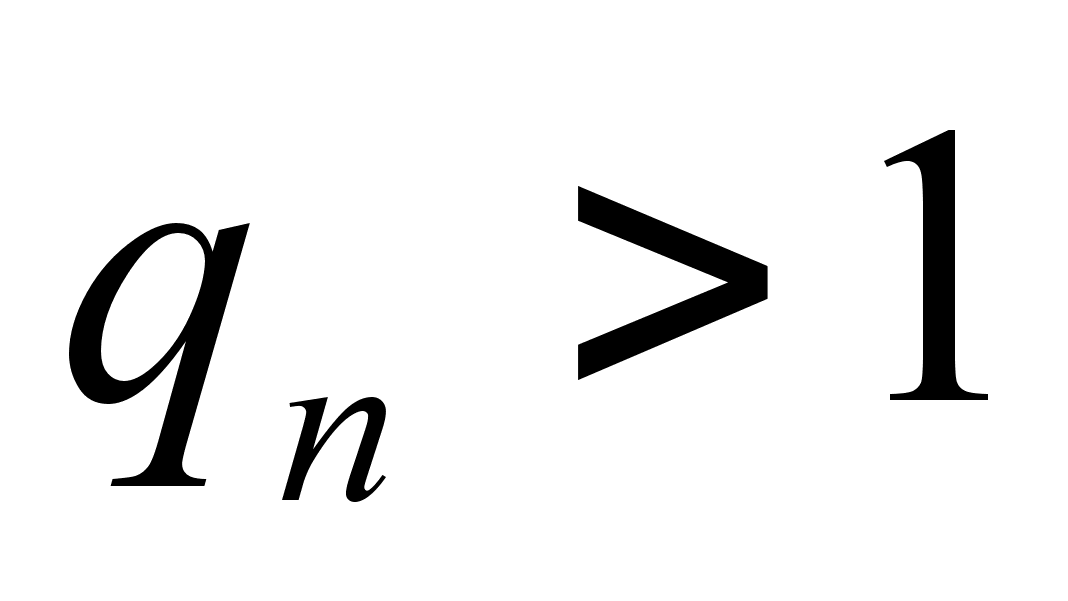 ,
,  . Тогда
. Тогда 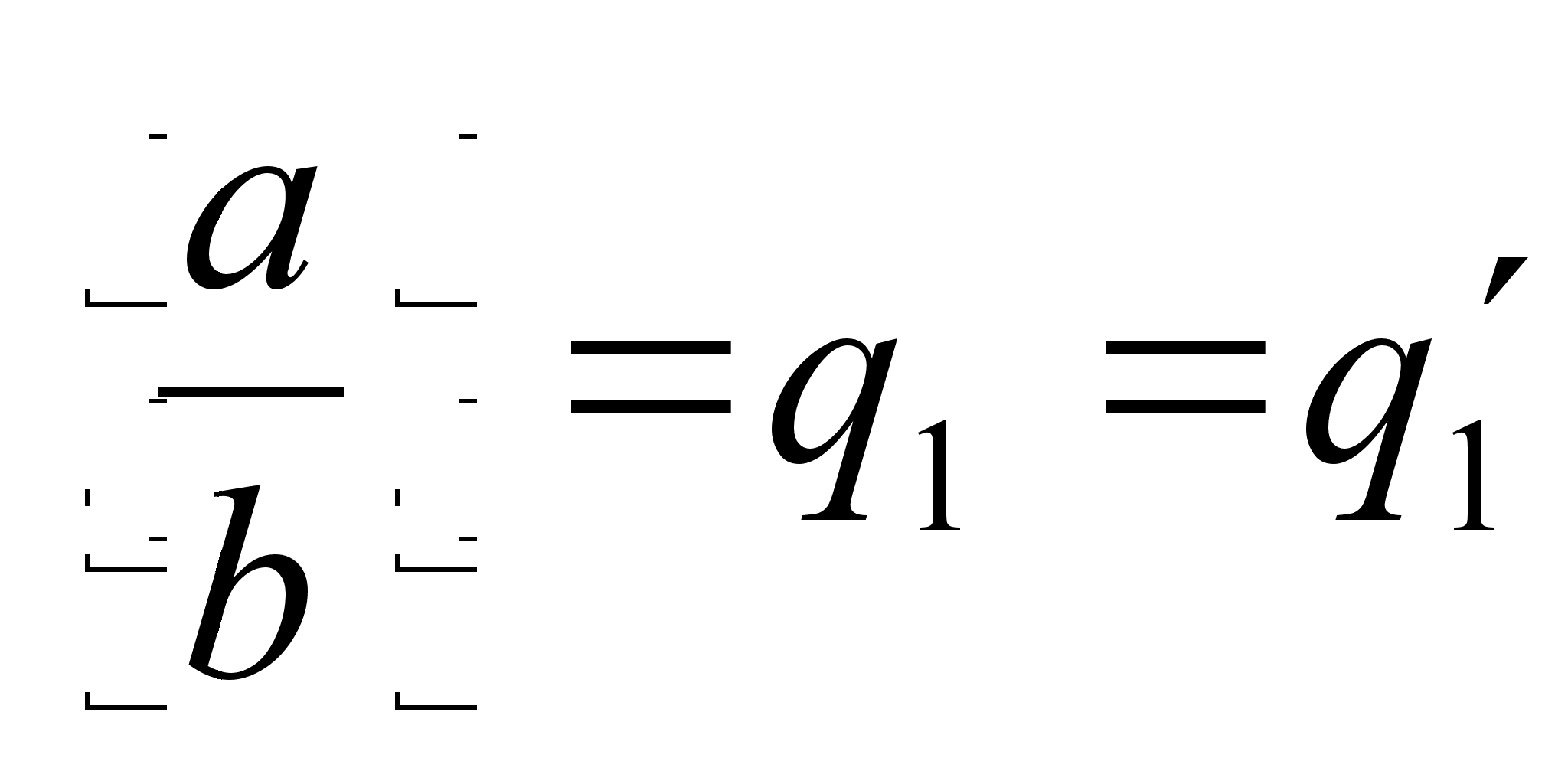 , так что
, так что 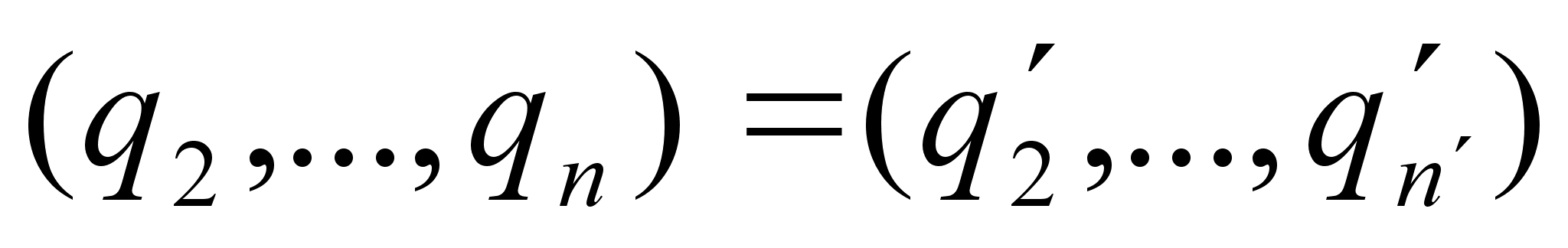 . Повторным сравнением целых частей получаем
. Повторным сравнением целых частей получаем 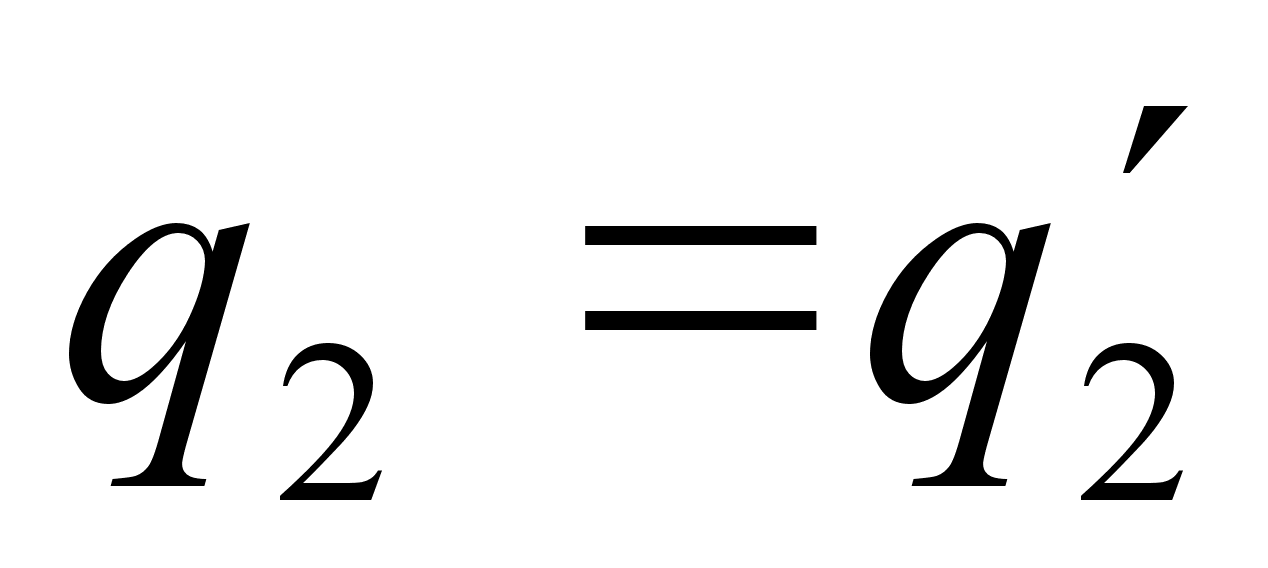 , а следовательно
, а следовательно 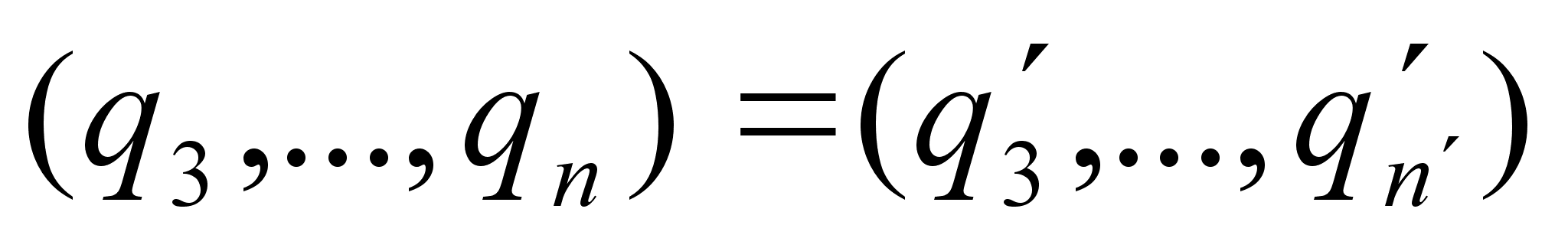 и так далее. Если
и так далее. Если 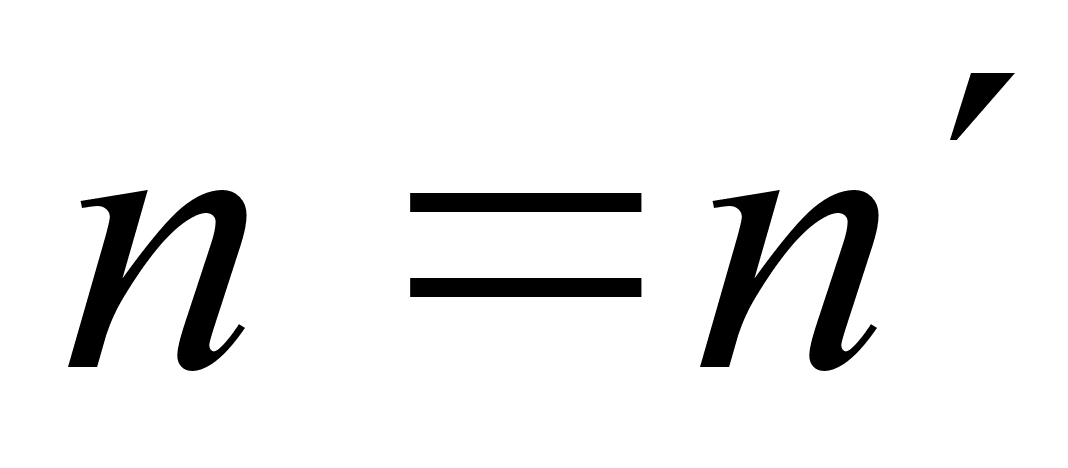 , то в продолжении указанного процесса получим также
, то в продолжении указанного процесса получим также 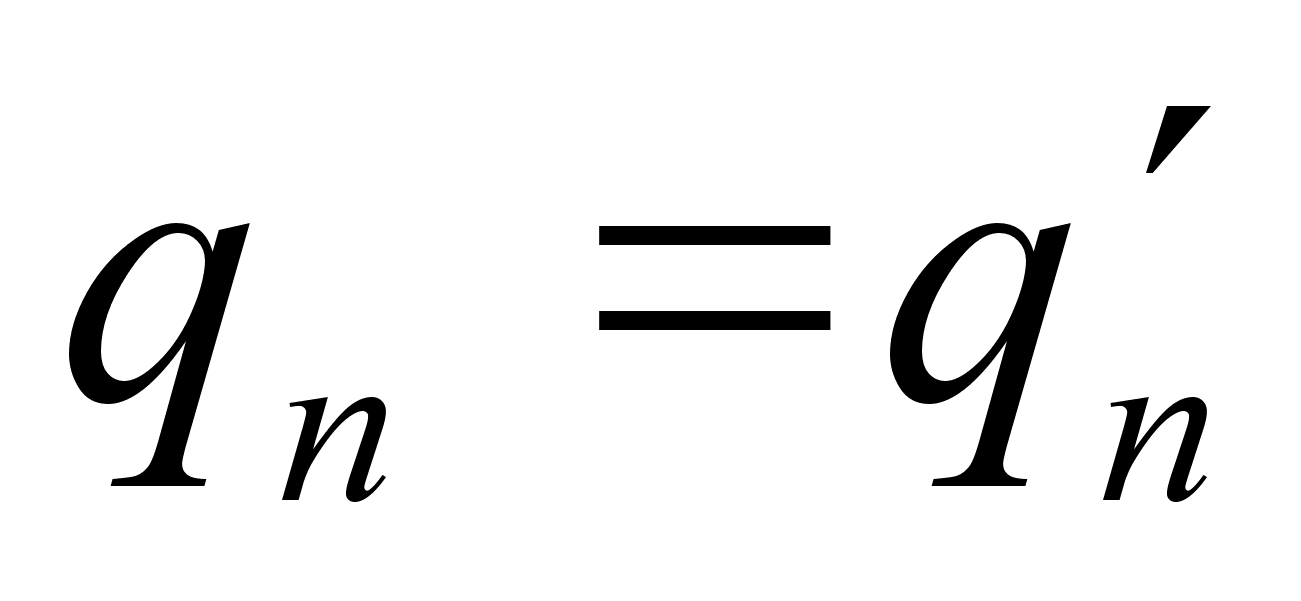 . Если же
. Если же 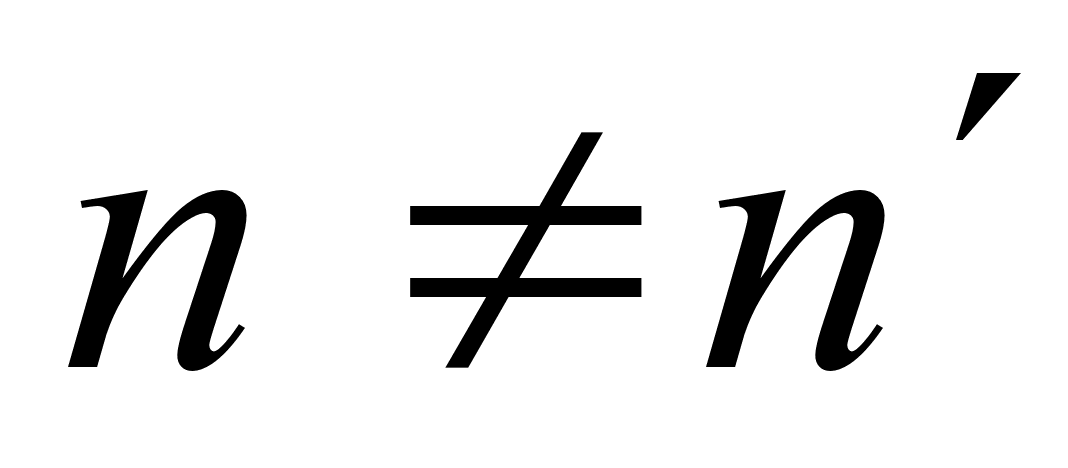 , например
, например 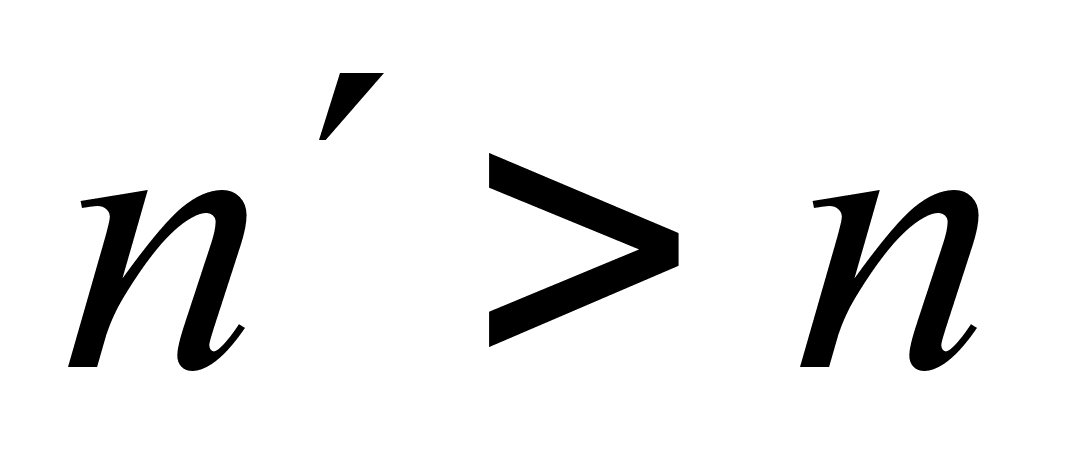 , то получим
, то получим 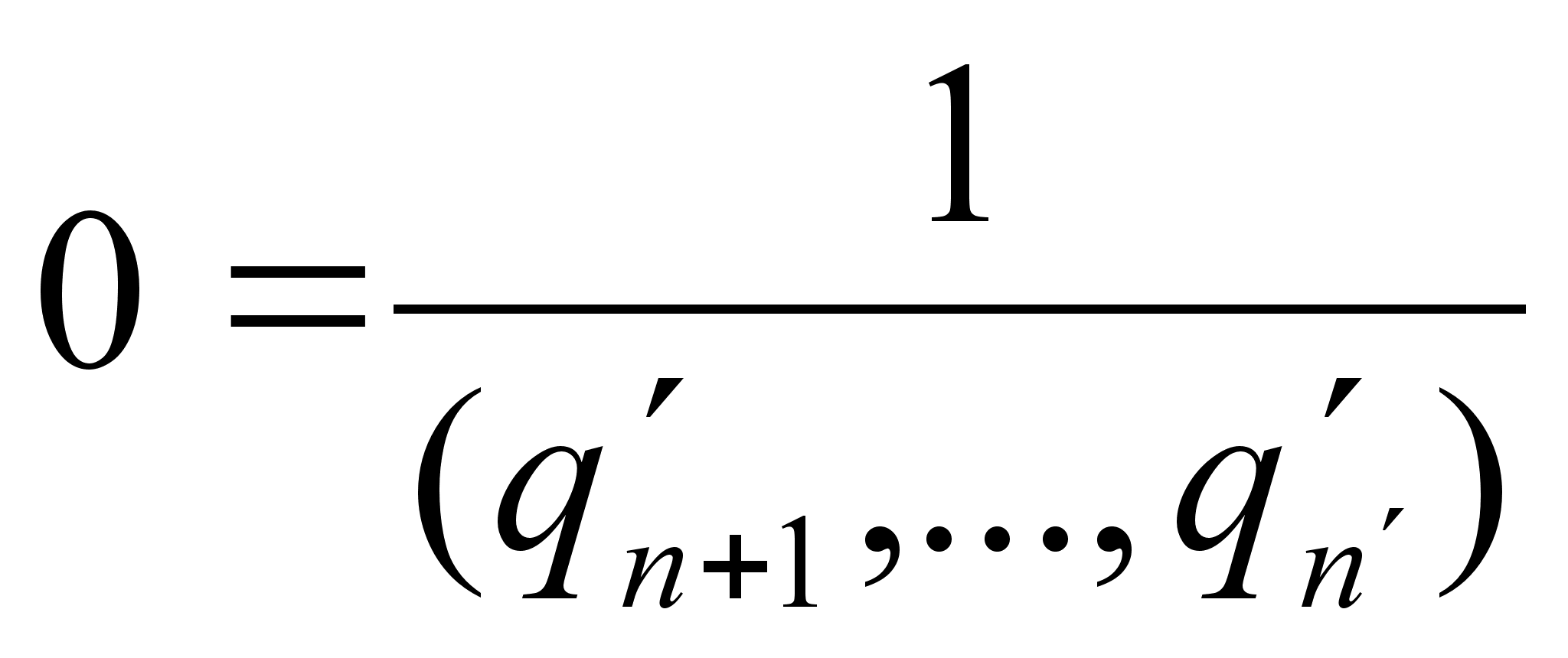 , что невозможно.
, что невозможно.
Теорема доказана.
Вместе с тем мы установили, что при соблюдении условия 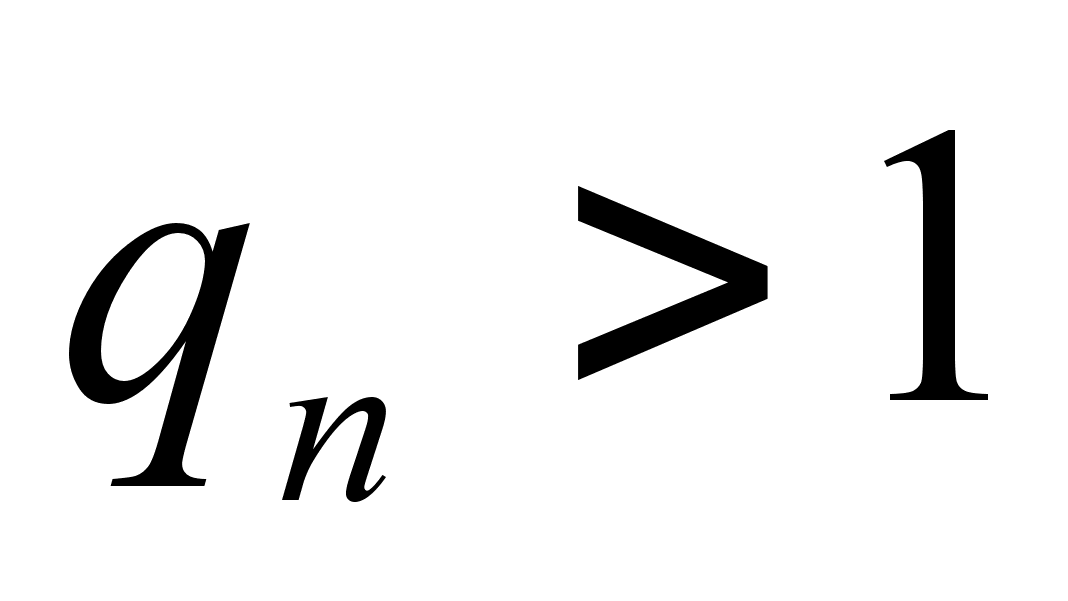 между рациональными числами и конечными цепными дробями существует взаимно однозначное соответствие.
между рациональными числами и конечными цепными дробями существует взаимно однозначное соответствие.
Замечания:
В случае разложения правильной положительной дроби первый элемент 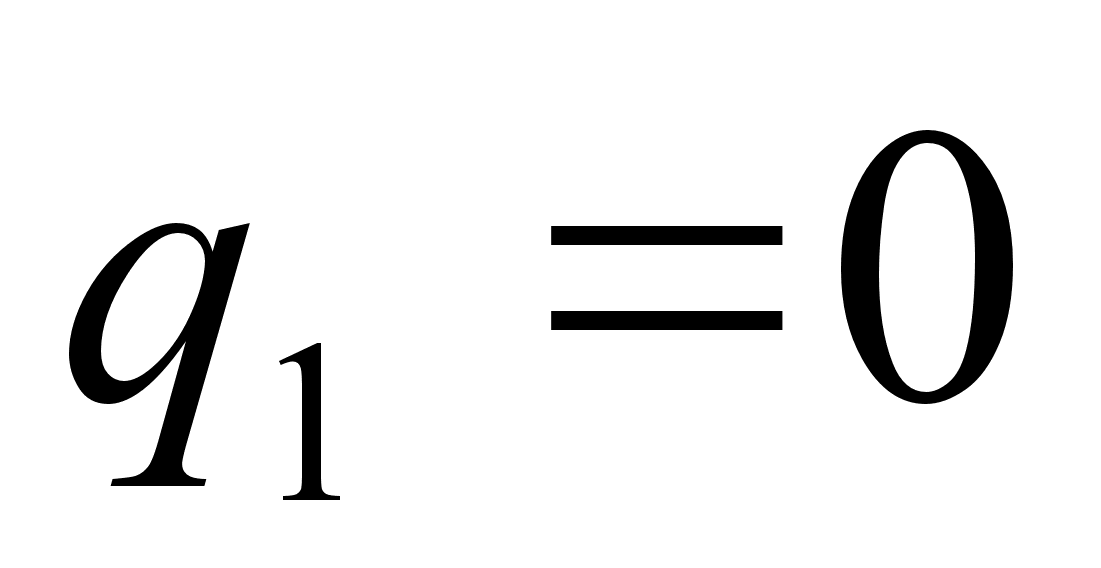 , например,
, например, 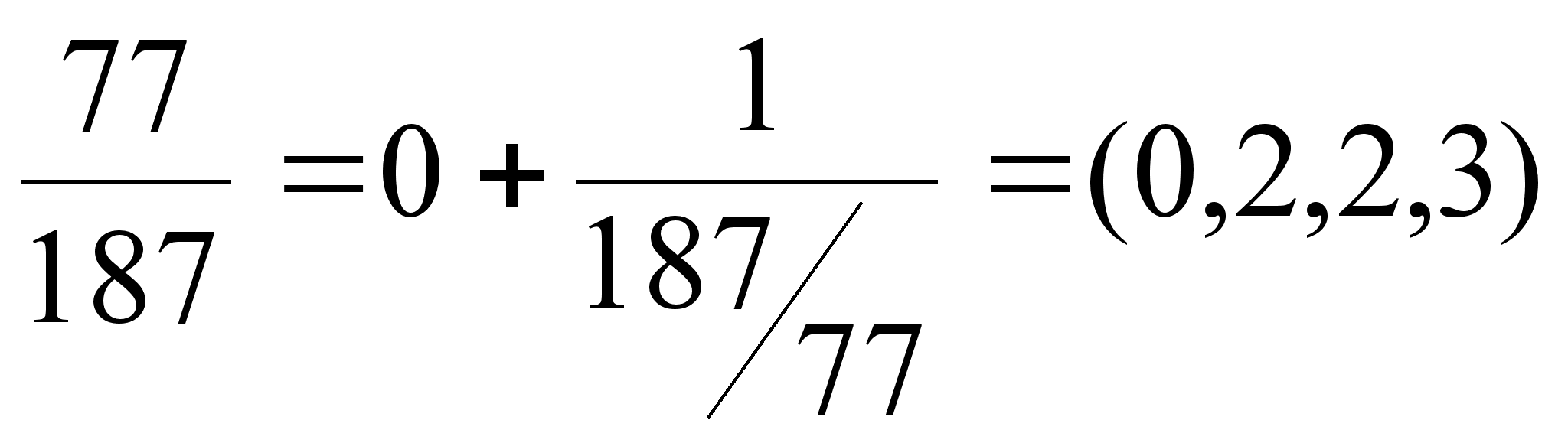 .
.
При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.
Пример: 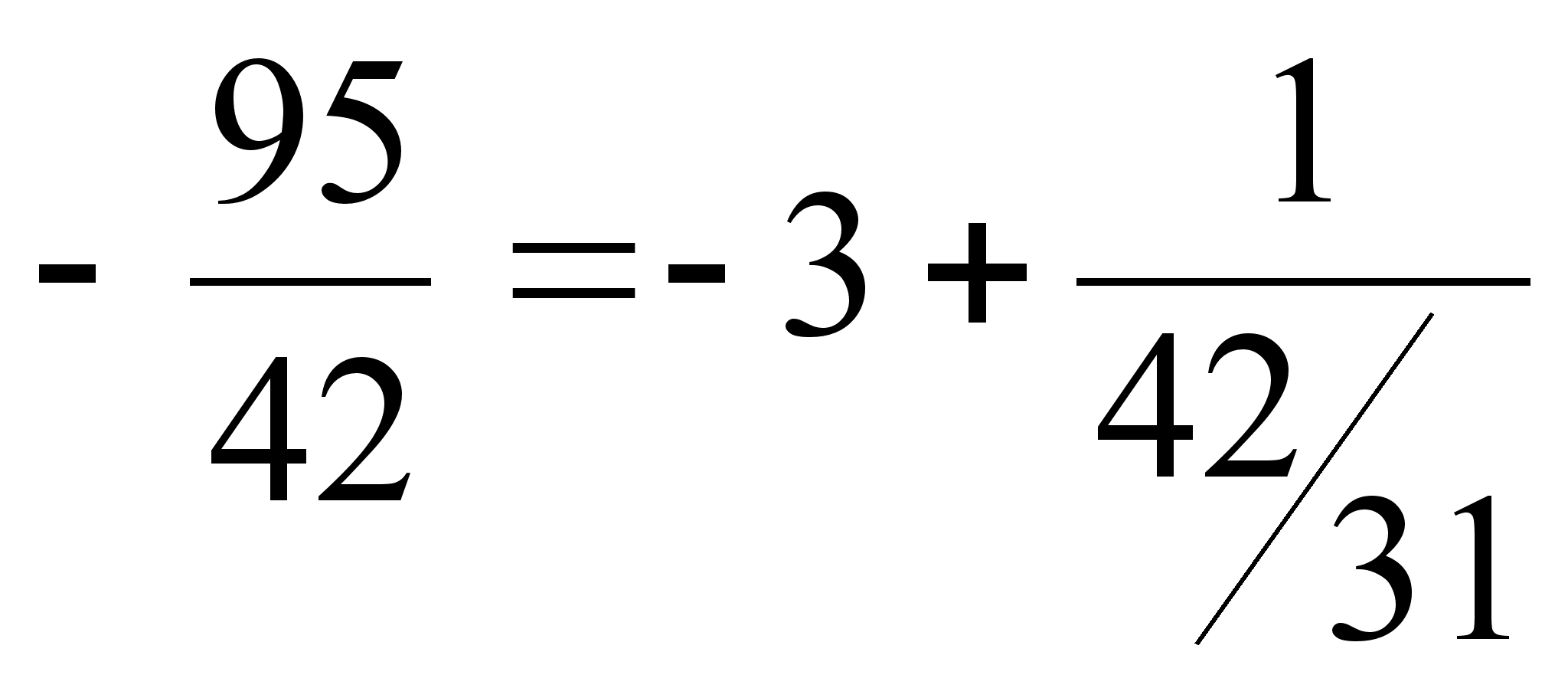 , а так как
, а так как  , то
, то 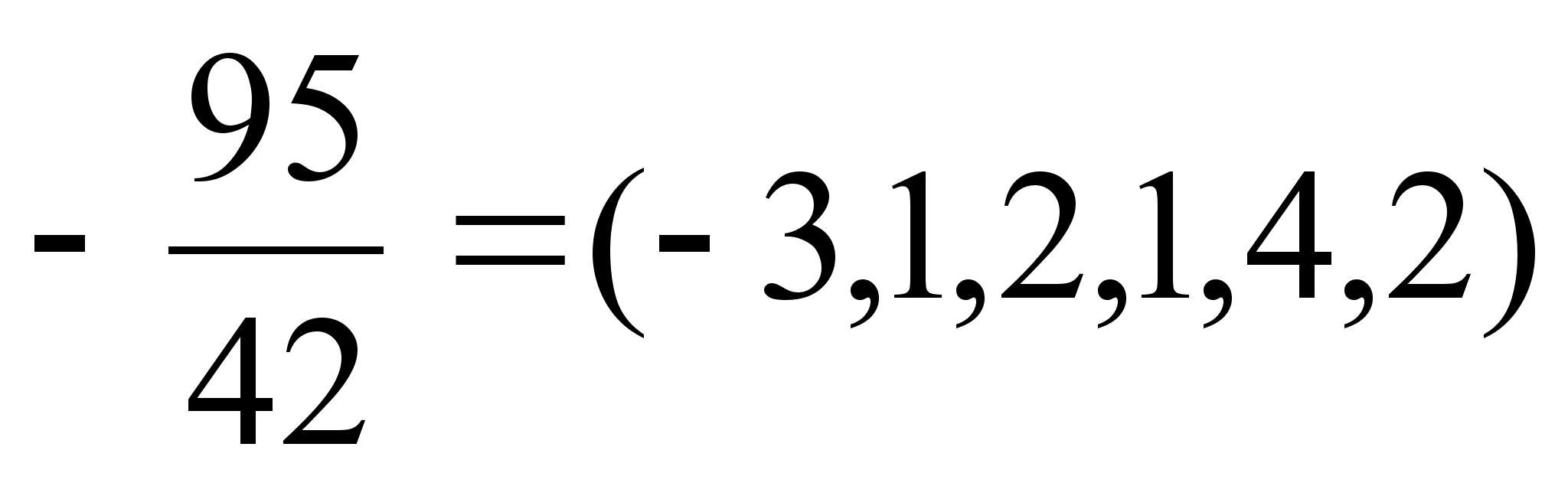 .
.
Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.
Пример: 5=(5); 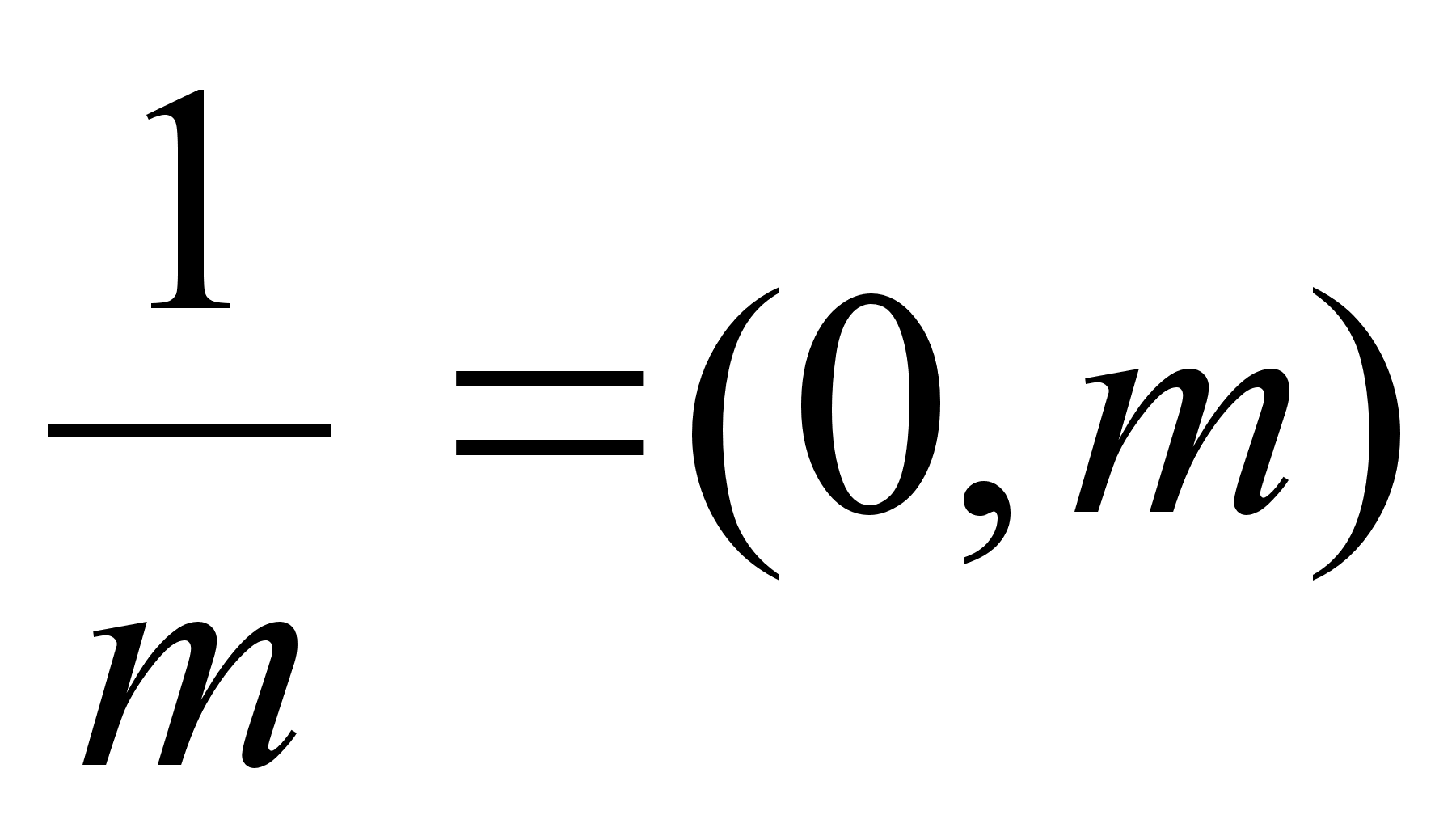 .
.
Вз2. Подходящие дроби. Их свойства.
Задаче разложения обыкновенной дроби в непрерывную дробь противостоит обратная задача тАУ обращения или свертывания цепной дроби 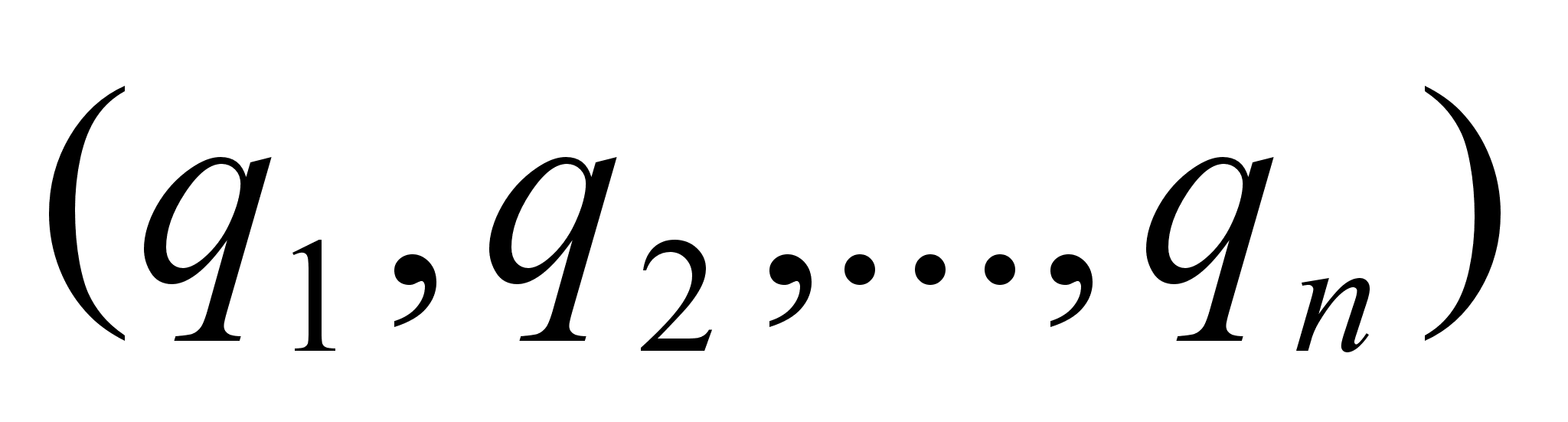 в простую дробь
в простую дробь  .
.
При этом основную роль играют дроби вида:
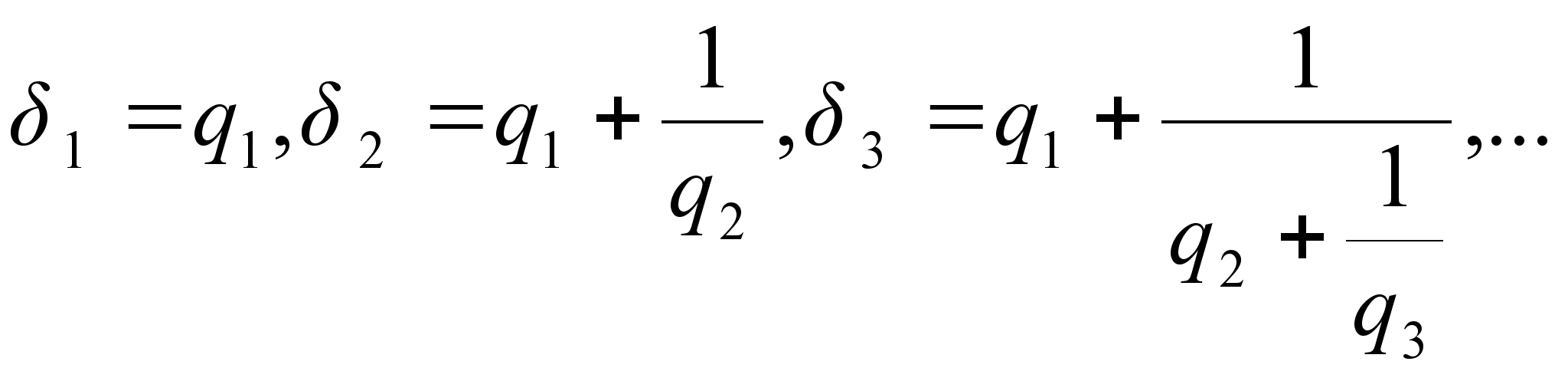 или
или
 которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа
которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа  .
.
Заметим, что  =
= =
= . Считается, что подходящая дробь
. Считается, что подходящая дробь 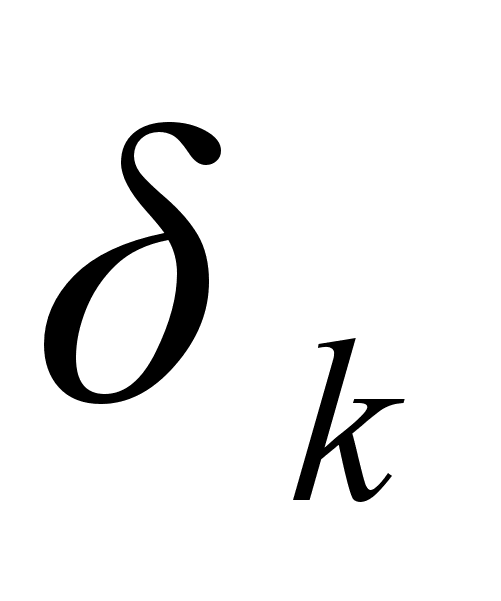 имеет порядок k.
имеет порядок k.
Прежде чем приступить к вычислению подходящих дробей заметим, что 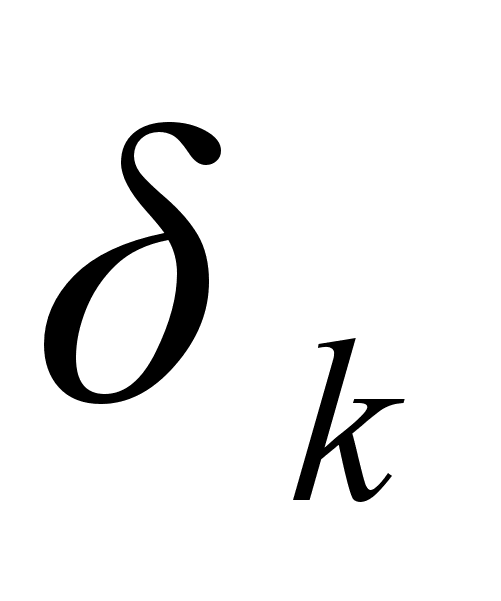 переходит в
переходит в  , если в первой заменить
, если в первой заменить 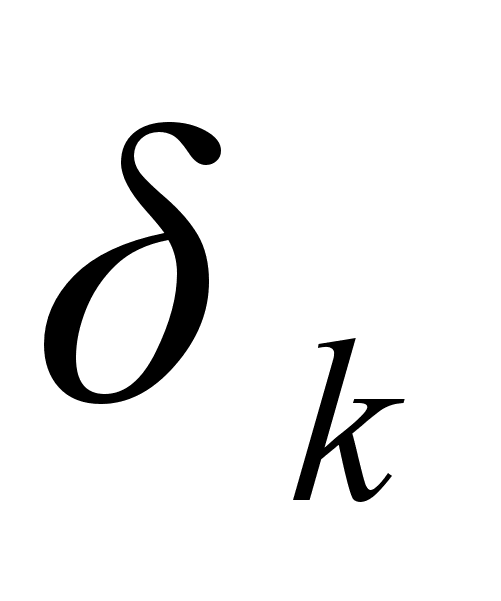 выражением
выражением 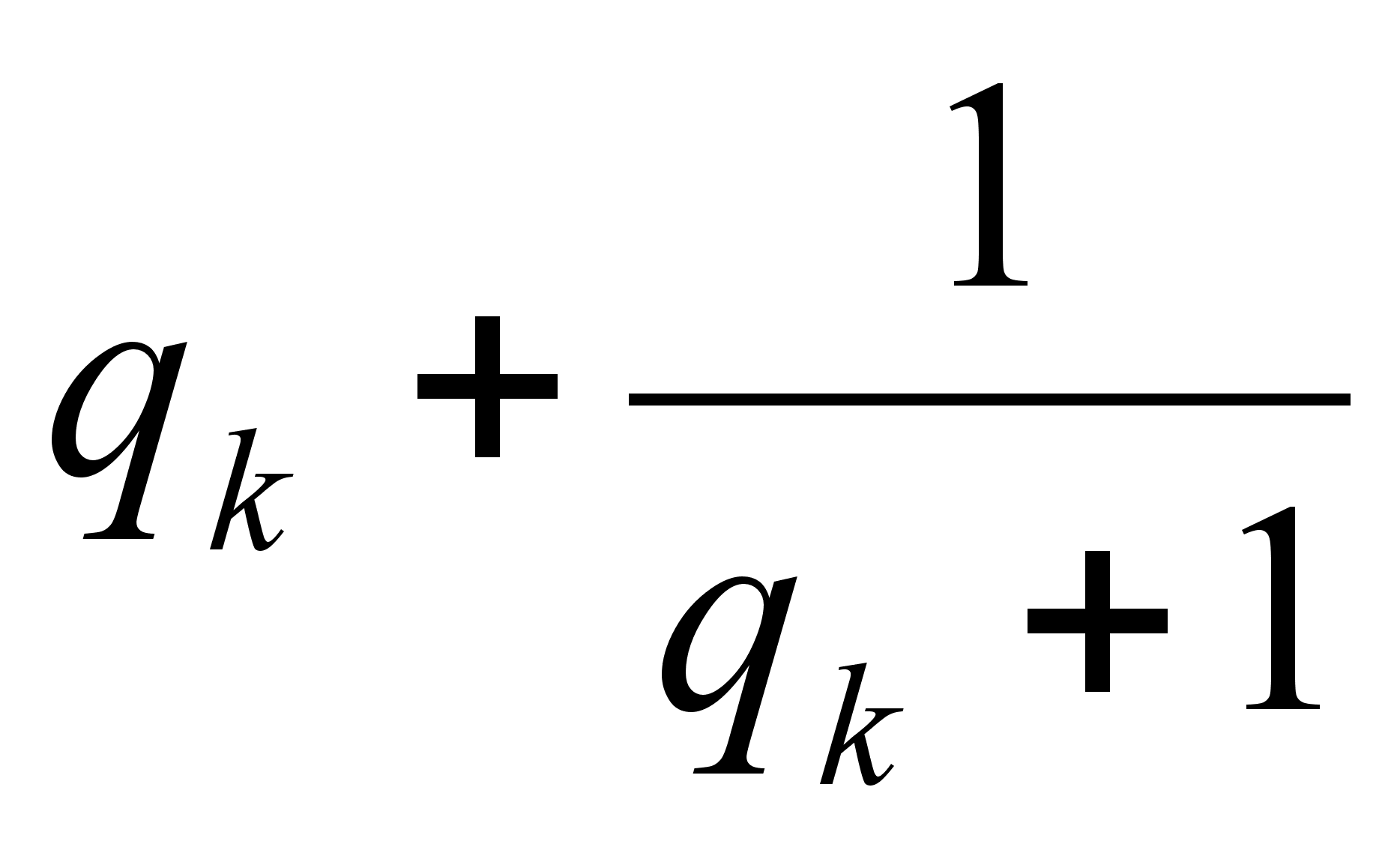 .
.
Имеем 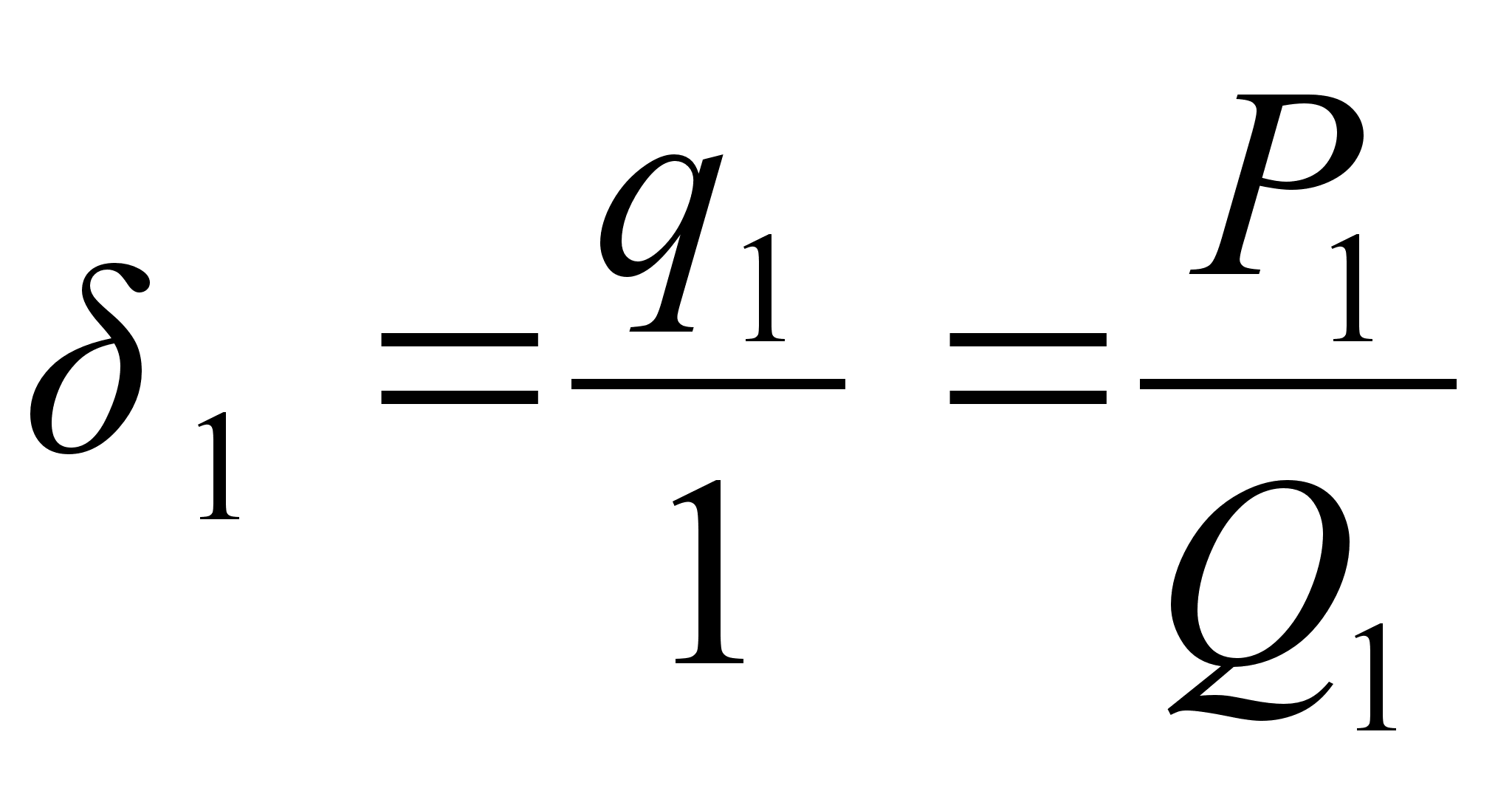 ,
,
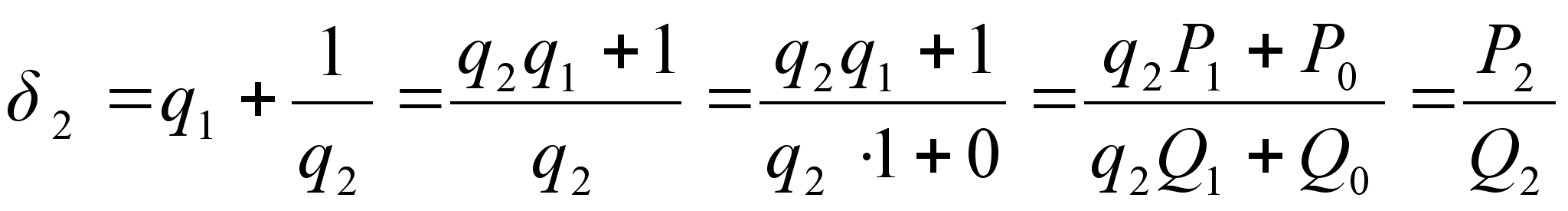 ,
,
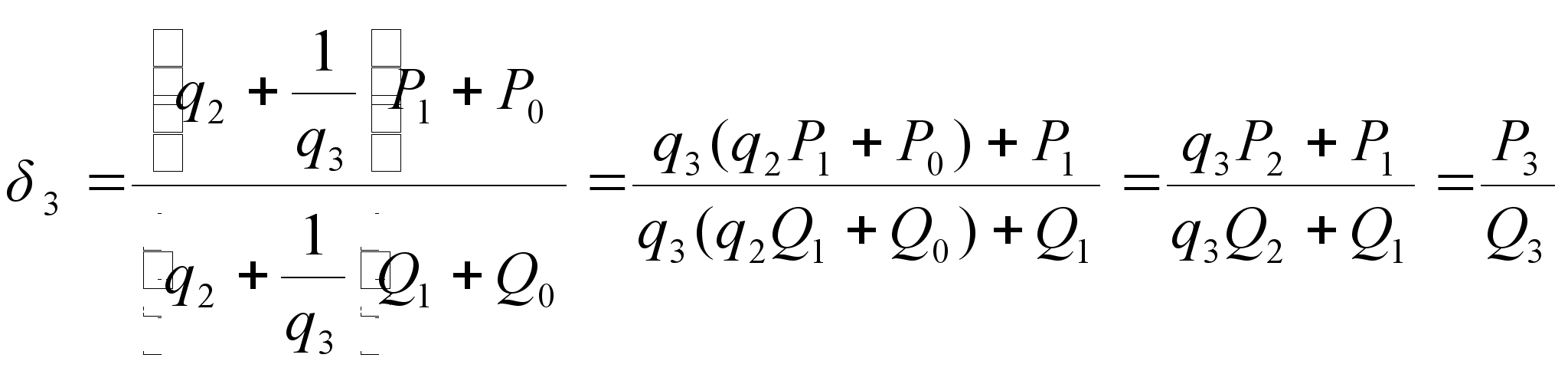 , тАж,
, тАж,
при этом принимается, что 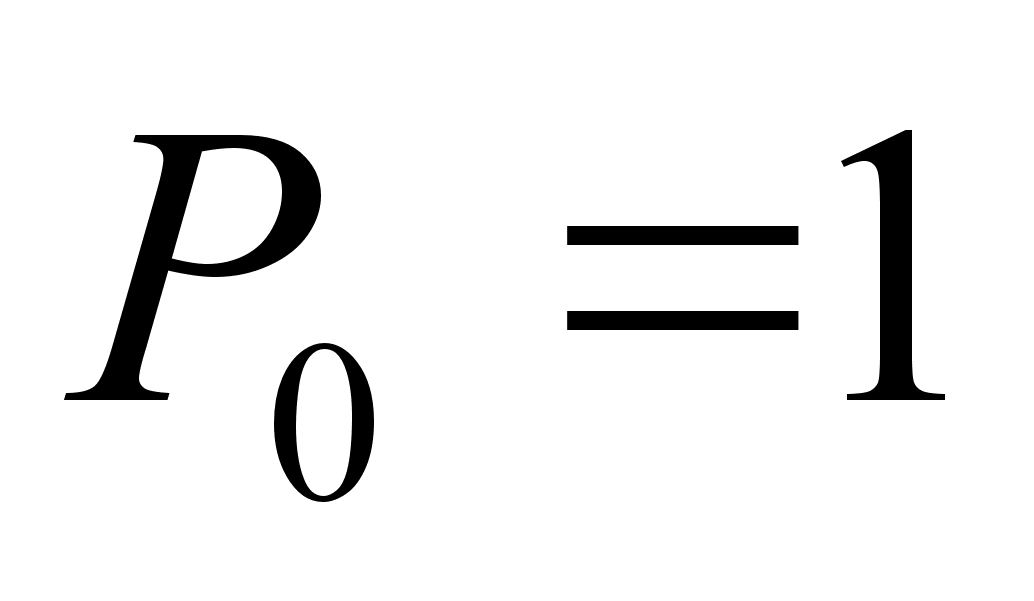 ,
, 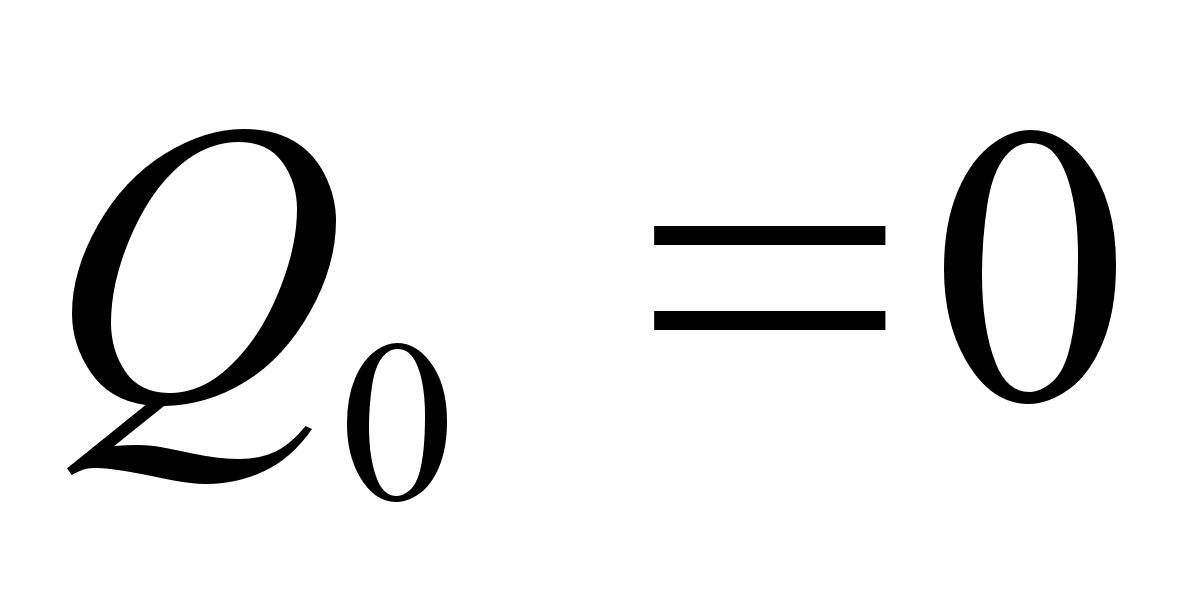 ,
, 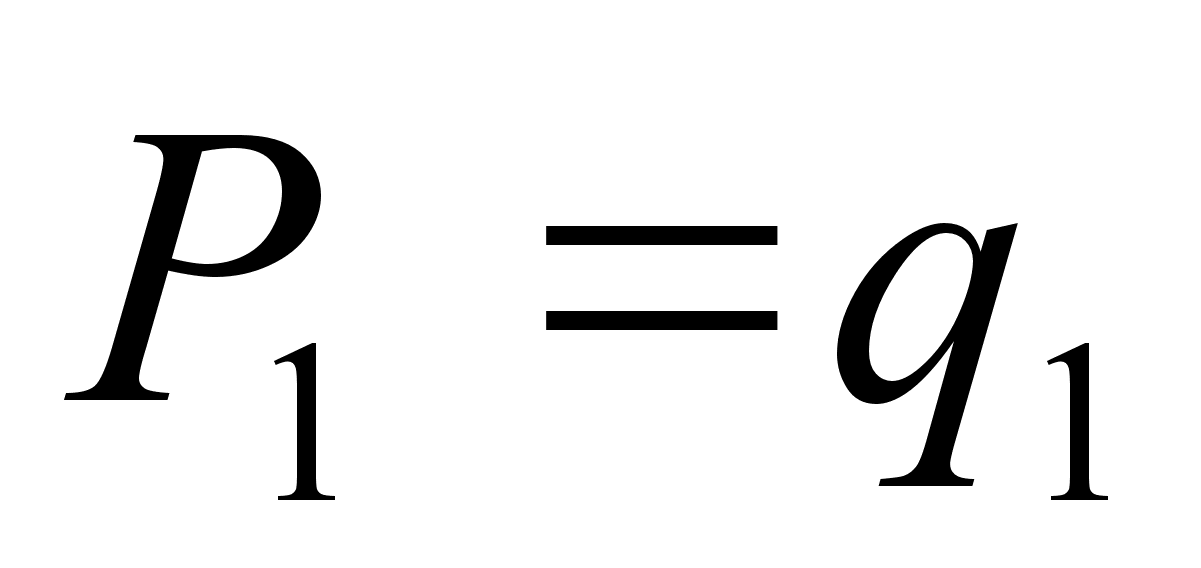 ,
, 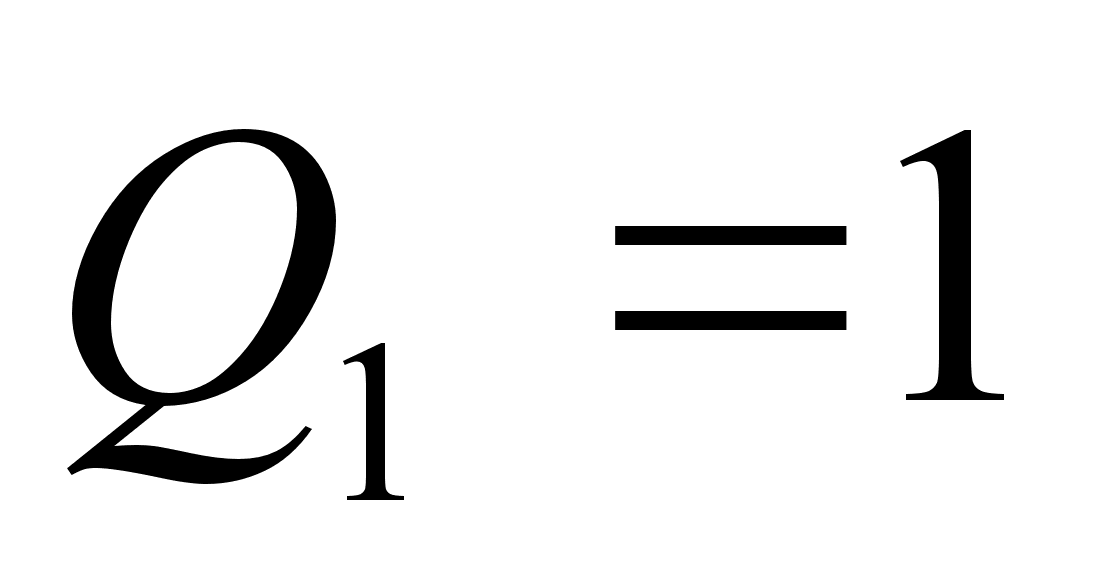 ,
, 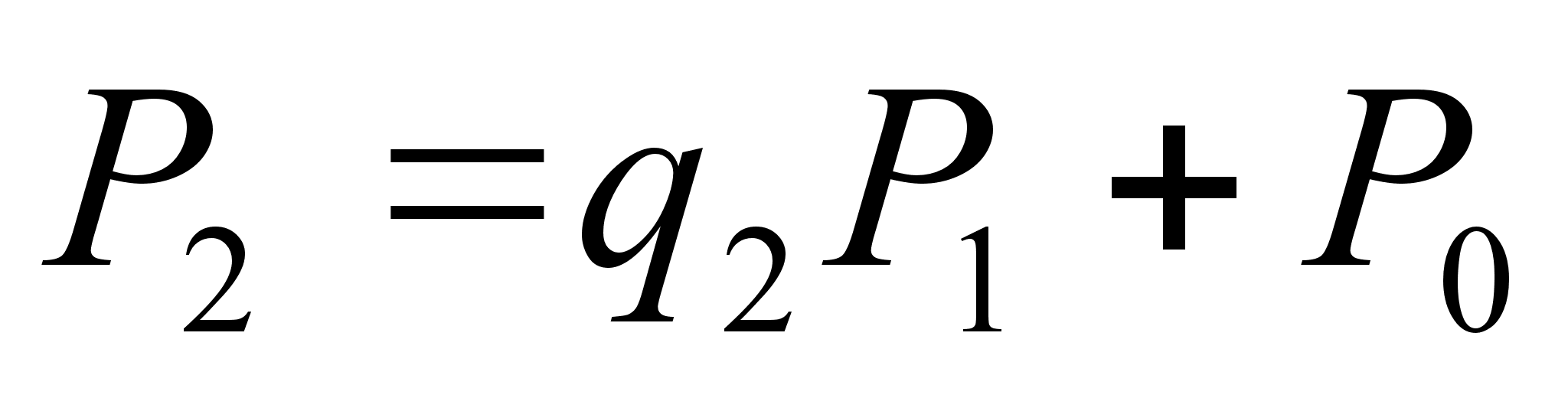 ,
, 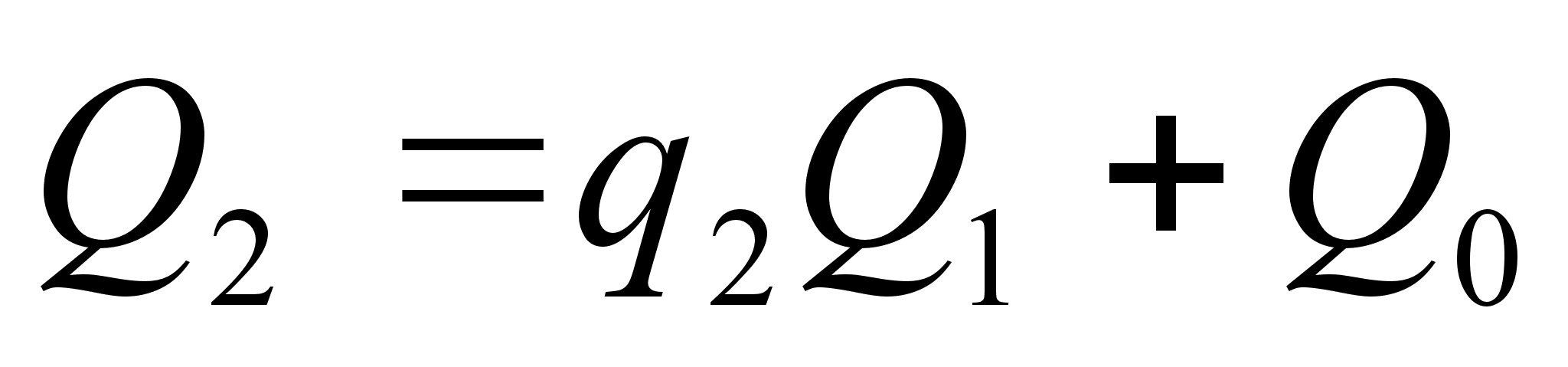 и так далее.
и так далее.
Закономерность, которую мы замечаем в построении формулы для 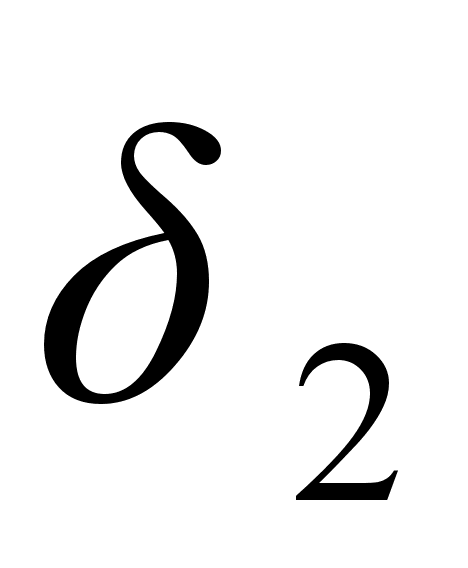 (ее числителя
(ее числителя 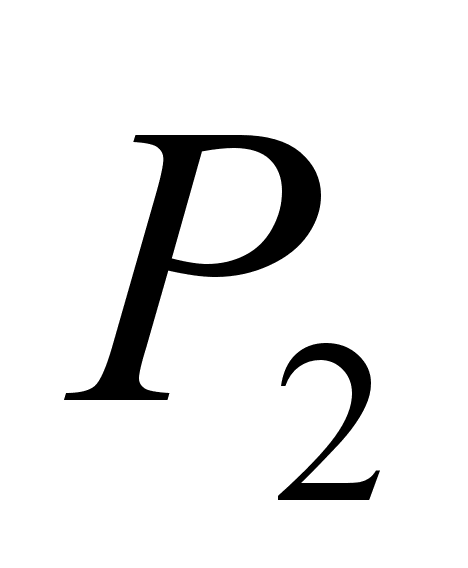 и знаменателя
и знаменателя 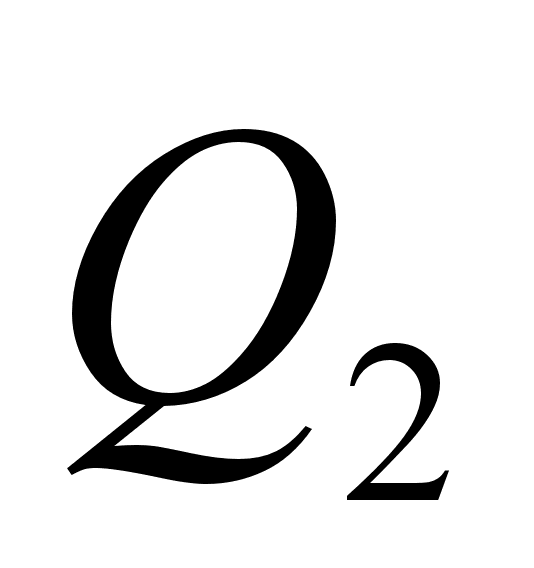 ), сохраняется при переходе к
), сохраняется при переходе к 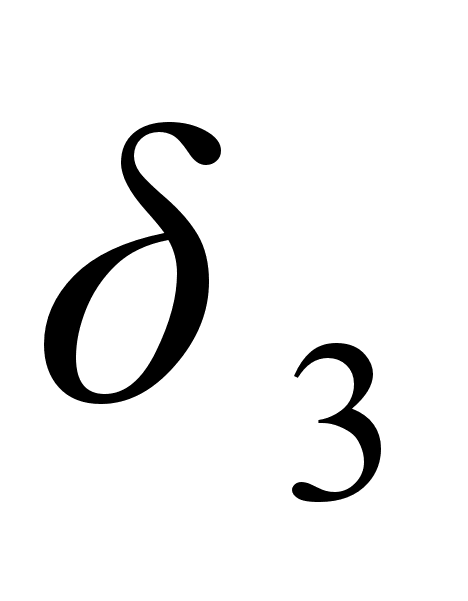 и сохранится также при переходе от k к (k+1).
и сохранится также при переходе от k к (k+1).
Поэтому, на основании принципа математической индукции, для любого k, где 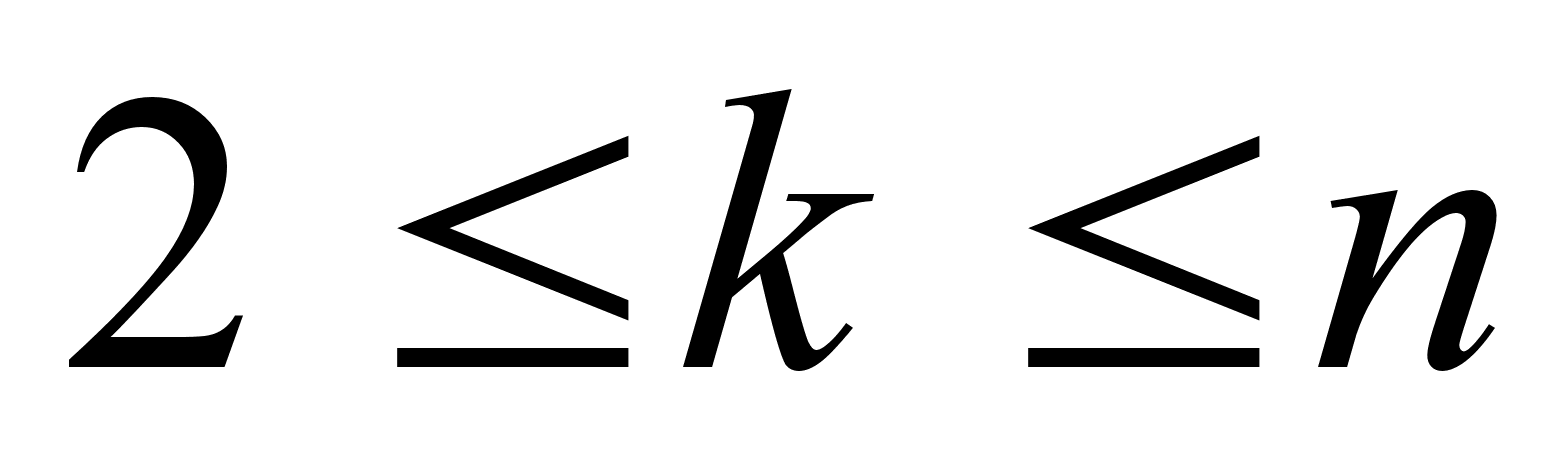 , имеем
, имеем
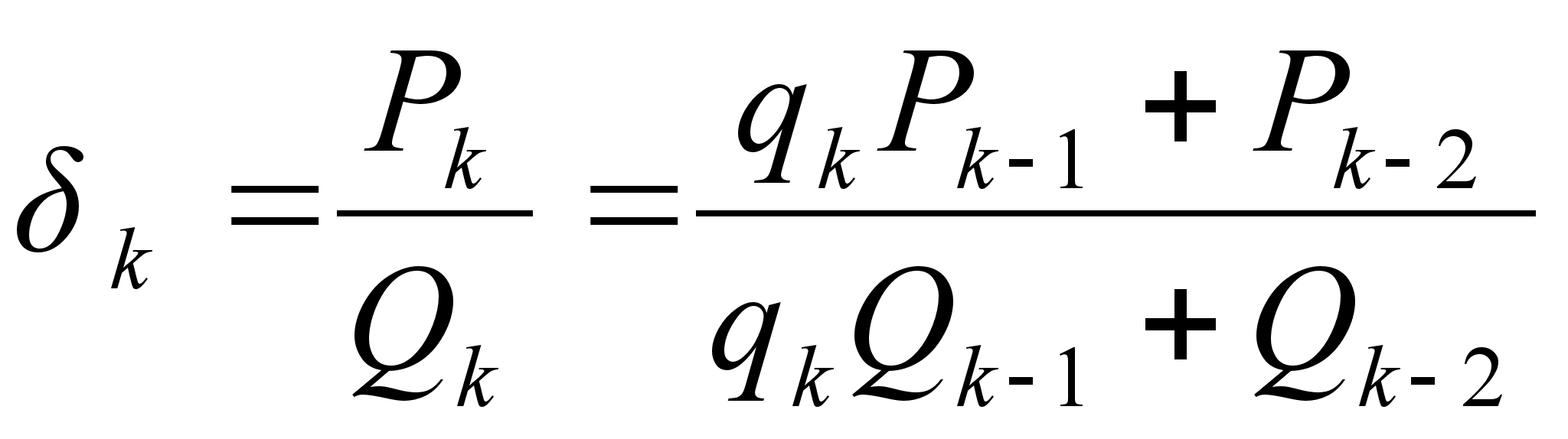 (1),
(1),
причем 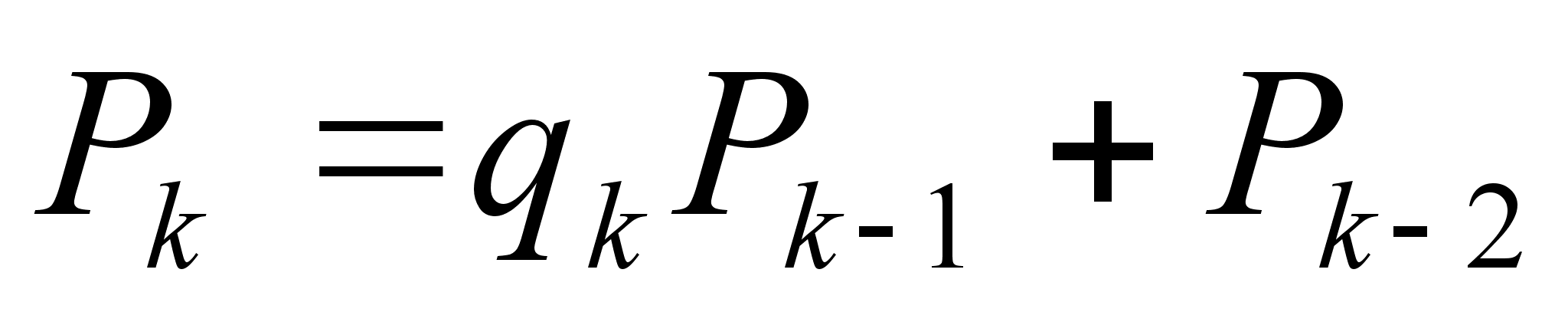 (2)
(2)
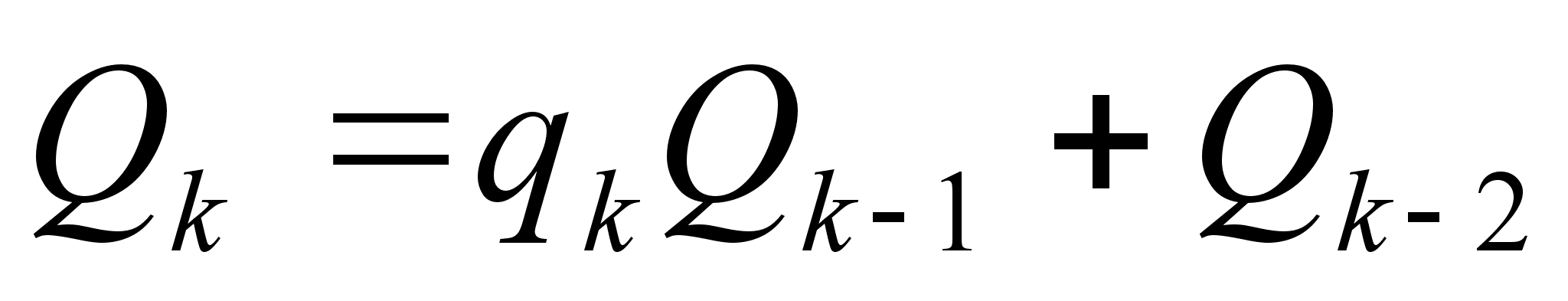 (3)
(3)
Далее, говоря о подходящих дробях 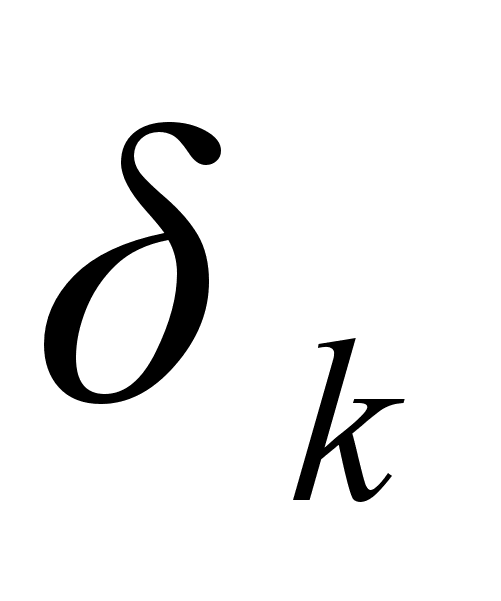 (в свернутом виде), мы будем иметь в виду их форму
(в свернутом виде), мы будем иметь в виду их форму 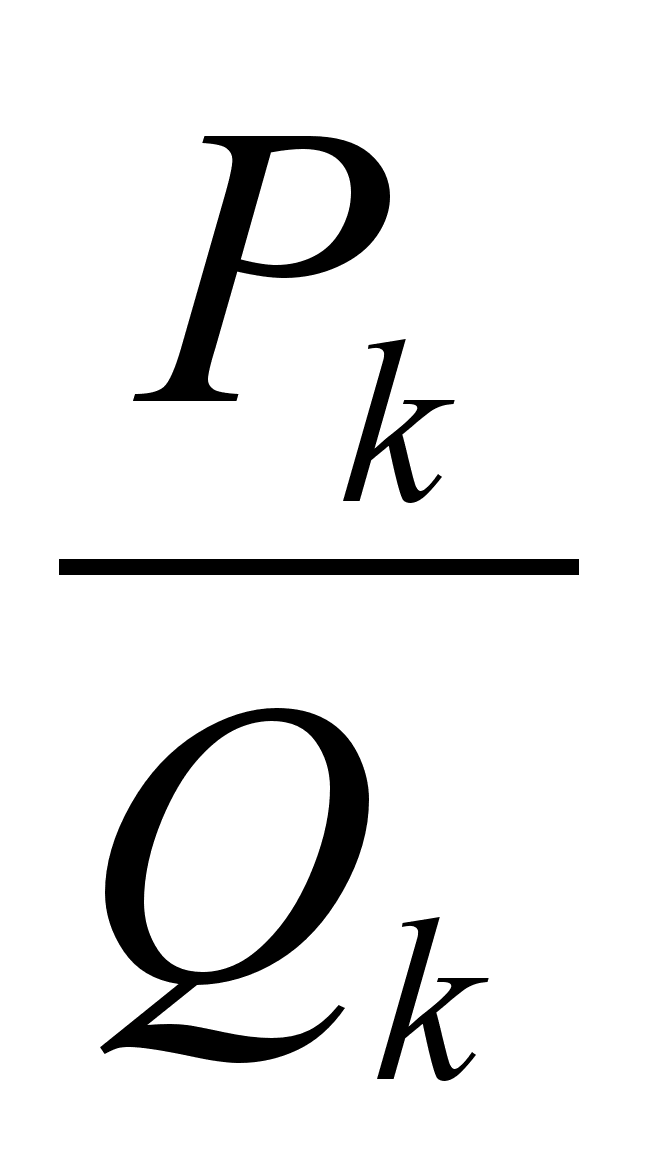 .
.
Соотношения (1) являются рекуррентными формулами для вычисления подходящих дробей, а также их числителей и знаменателей. Из формул для числителя и знаменателя сразу видно, что при увеличении k они возрастают. Последовательное вычисление числителей 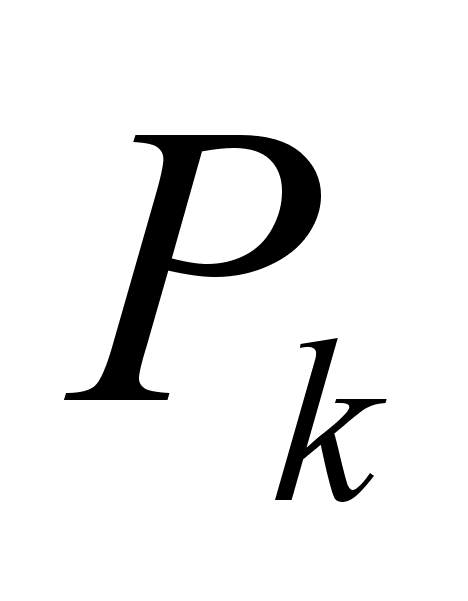 и знаменателей
и знаменателей  подходящих дробей по формулам (2) и (3) удобно располагать по схеме:
подходящих дробей по формулам (2) и (3) удобно располагать по схеме:
Пример: Найти подходящие дроби к цепной дроби (2, 2, 1, 3, 1, 1, 4, 3).
| 2 | 2 | 1 | 3 | 1 | 1 | 4 | 3 |
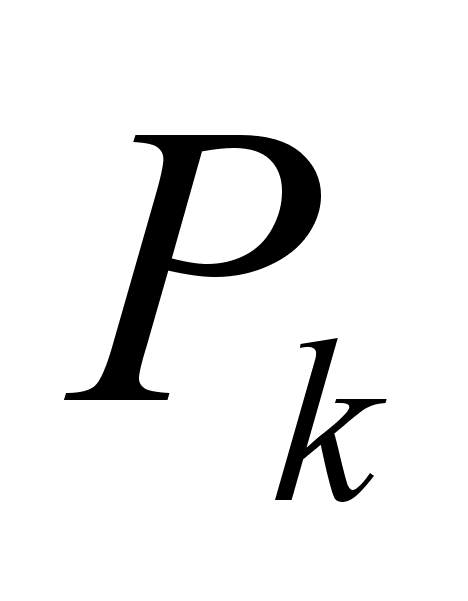
| 2 | 5 | 7 | 26 | 33 | 59 | 269 | 866 |

| 1 | 2 | 3 | 11 | 14 | 25 | 114 | 367 |
Подходящие дроби 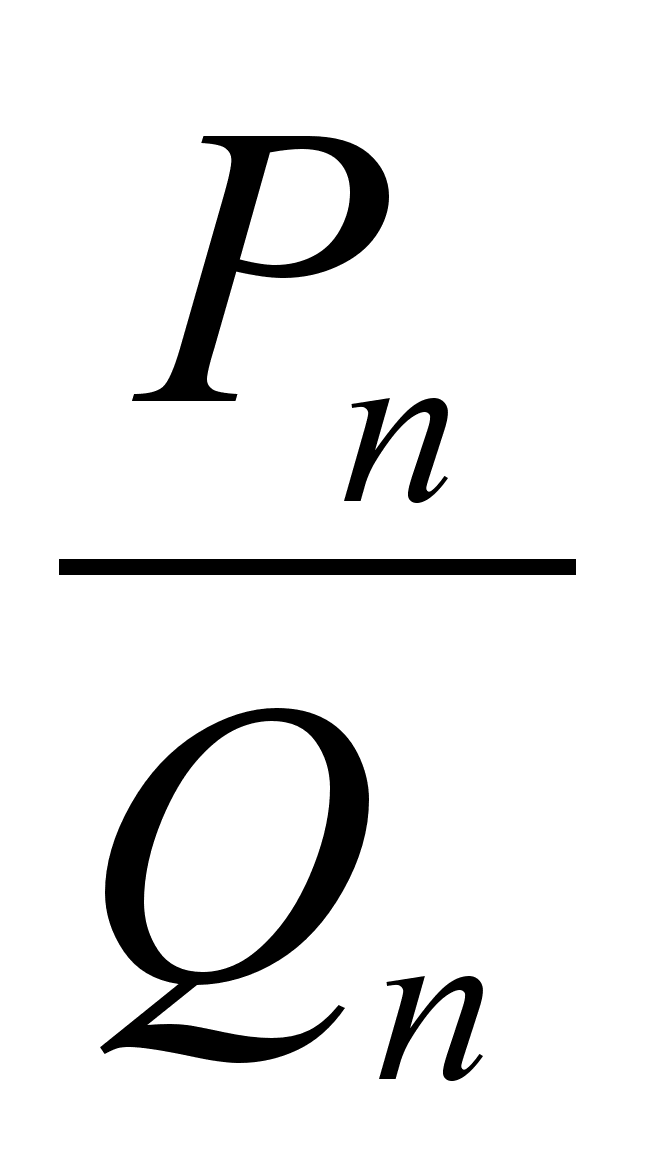 (
( ) равны соответственно
) равны соответственно  ;
; 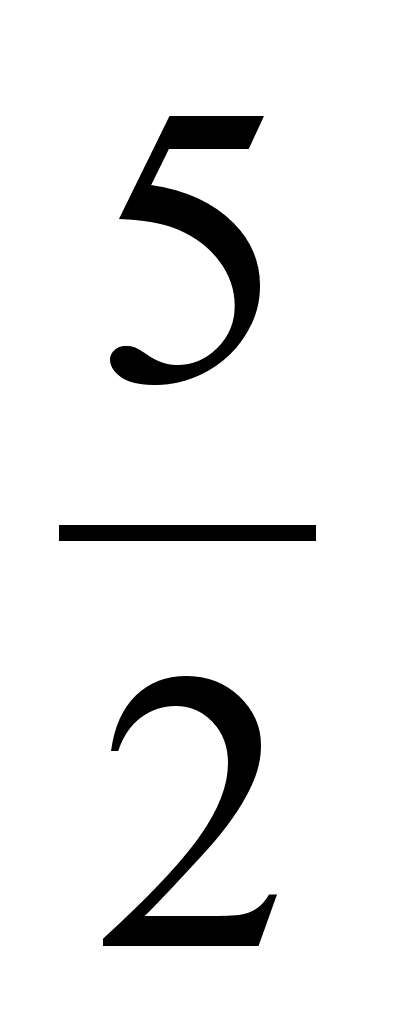 ;
;  ;
; 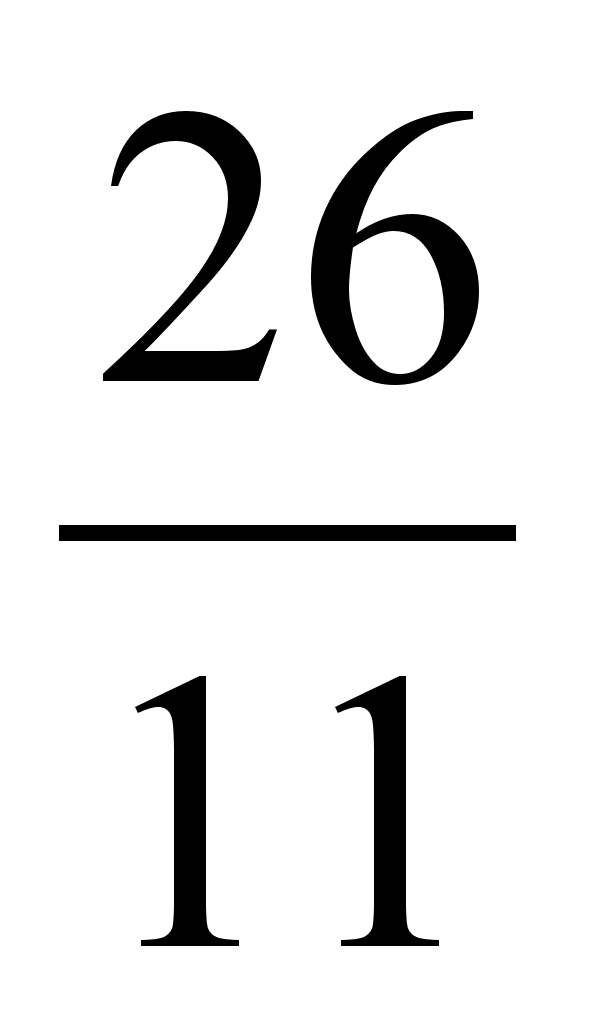 ;
; 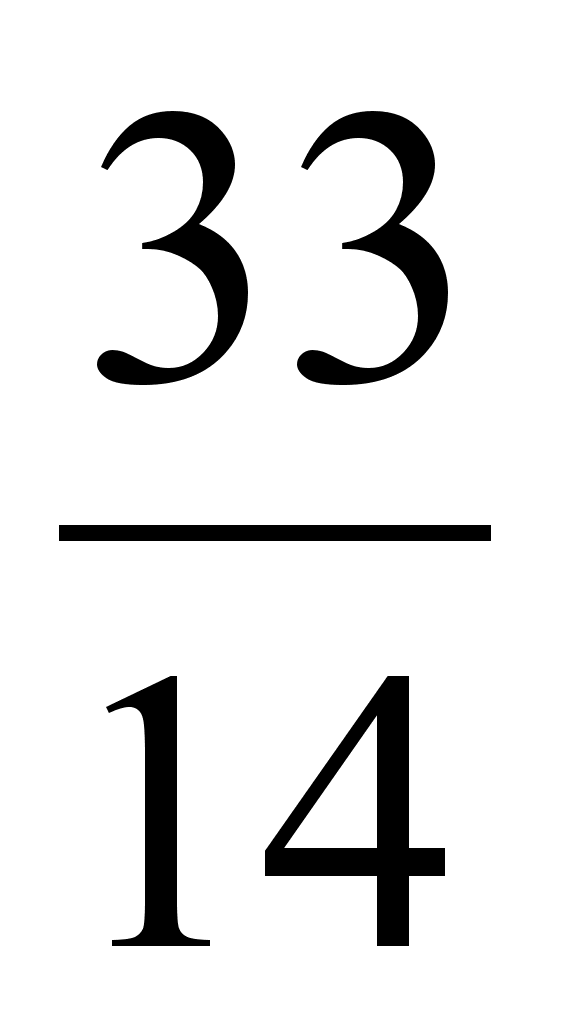 ;
; 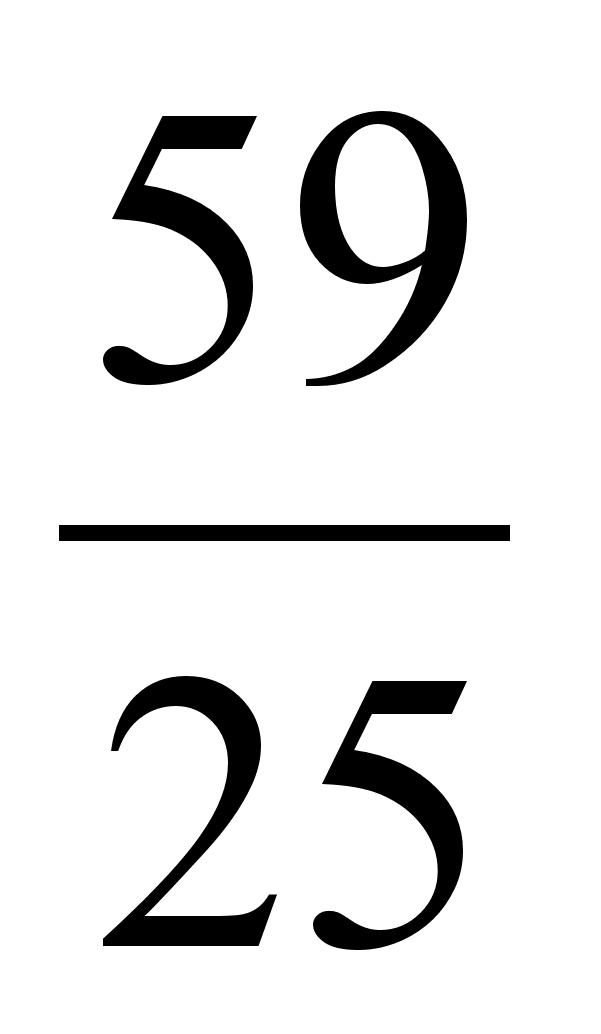 ;
; 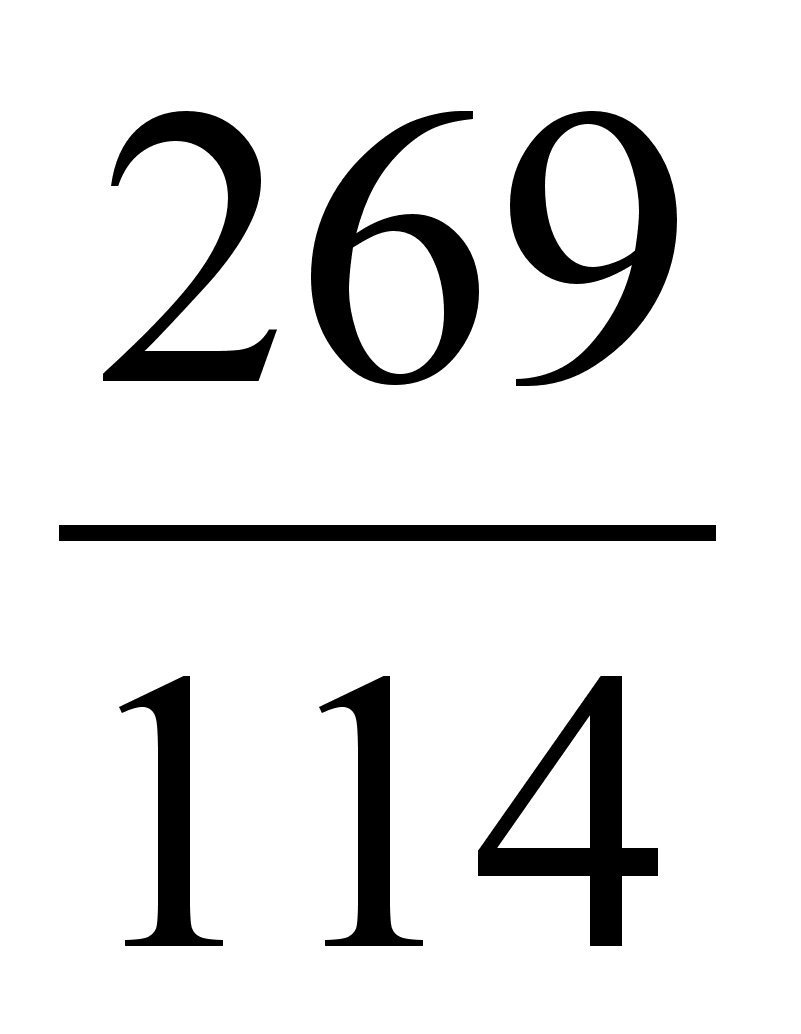 ;
; 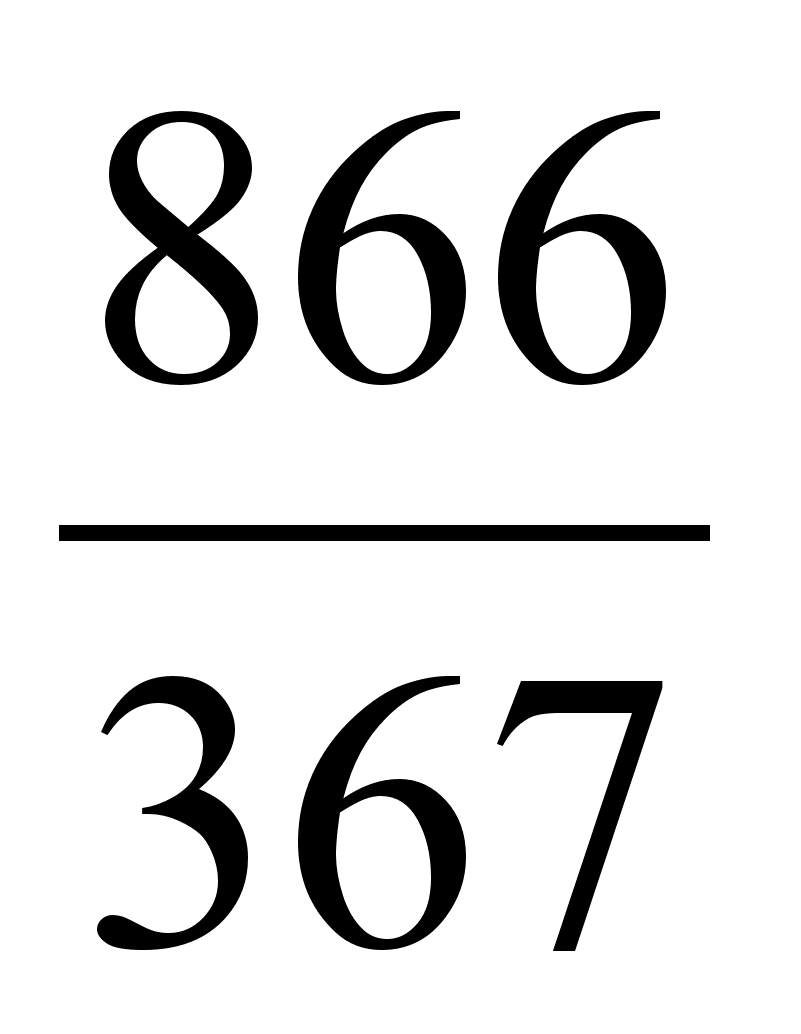 .
.
Практически нахождение неполных частных и подходящих дробей удобно объединить в одну краткую схему, которую приведем для 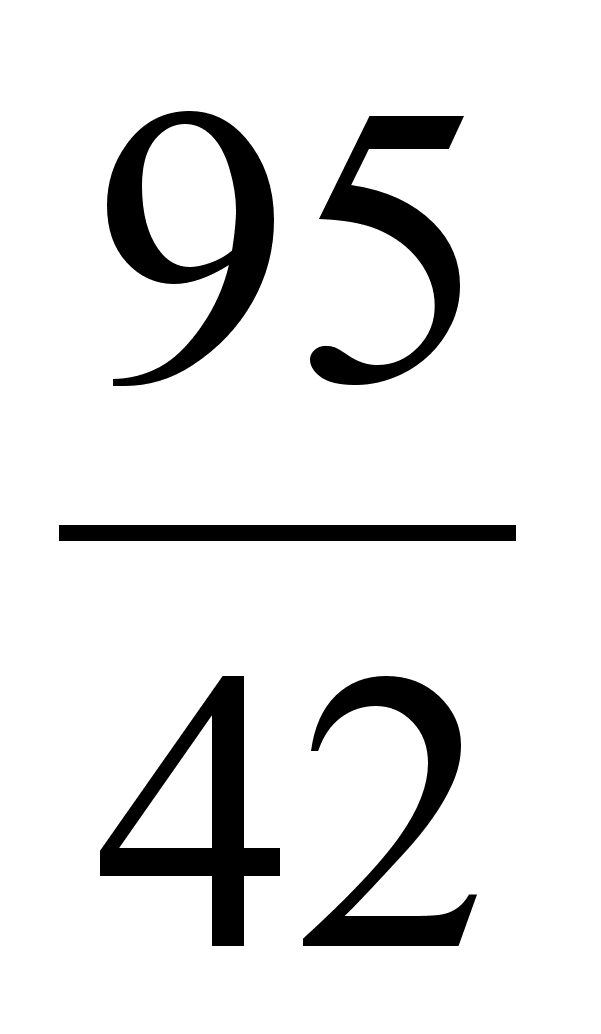 =(2, 3, 1, 4, 2)
=(2, 3, 1, 4, 2)
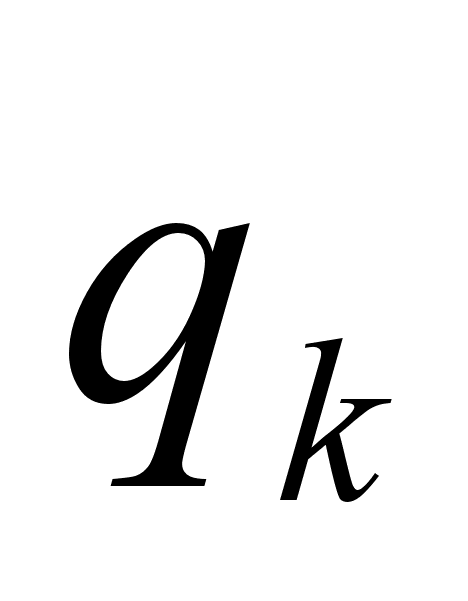
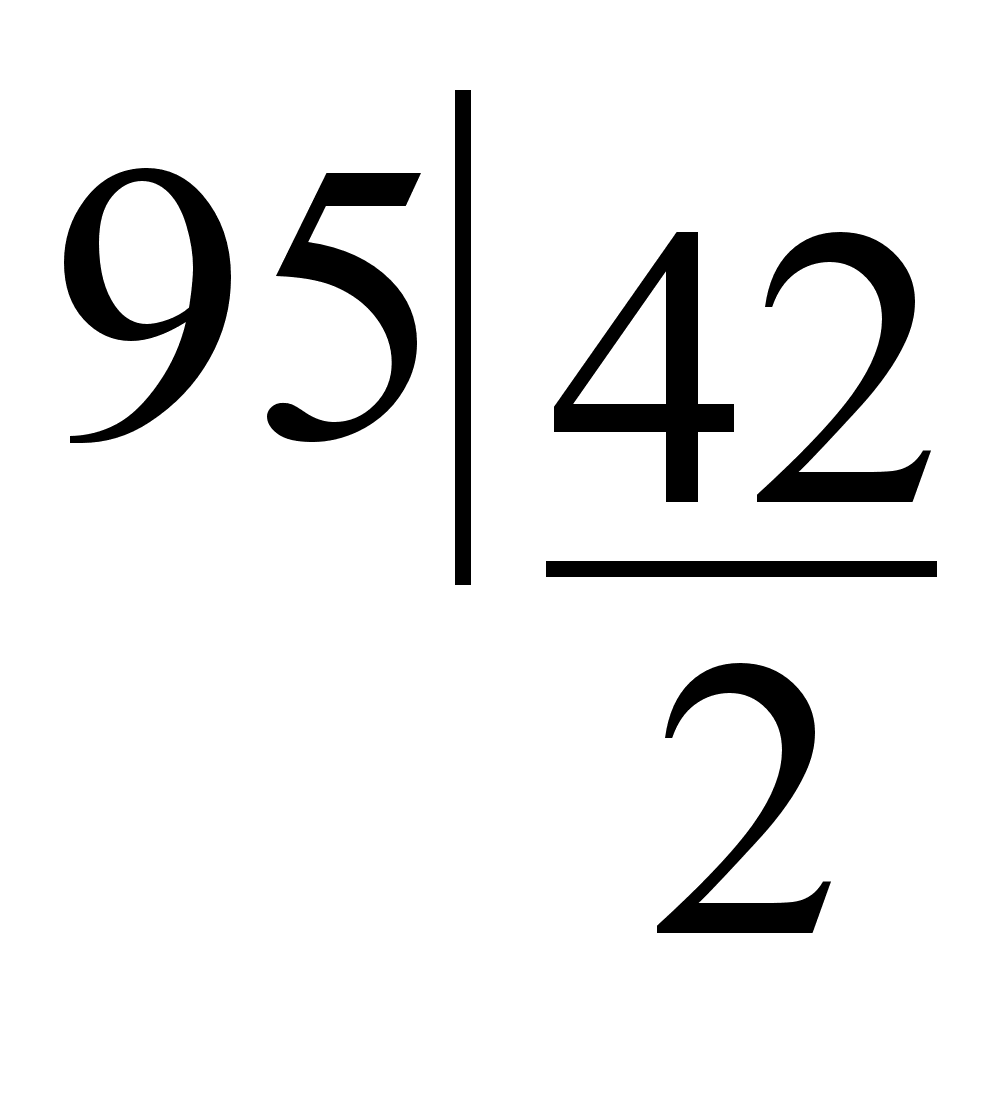
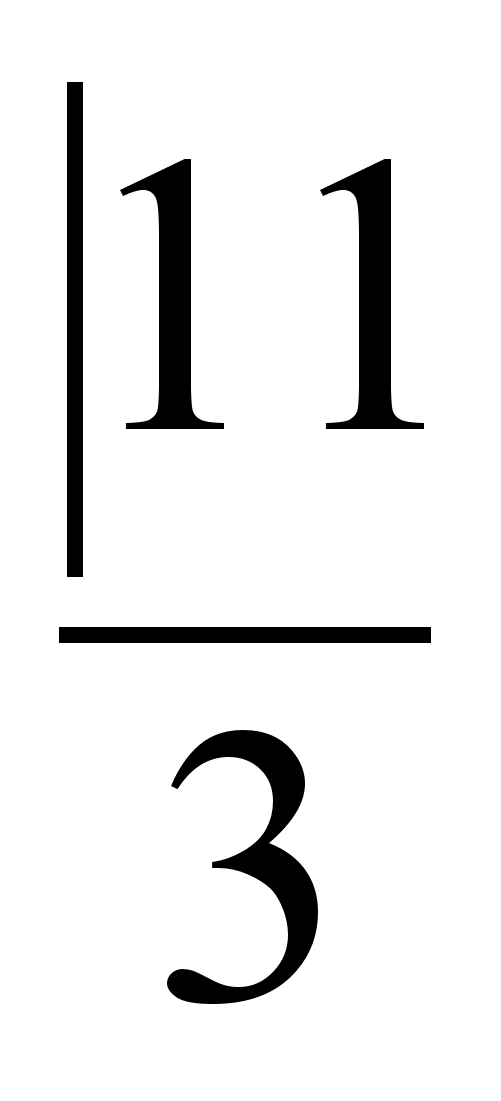
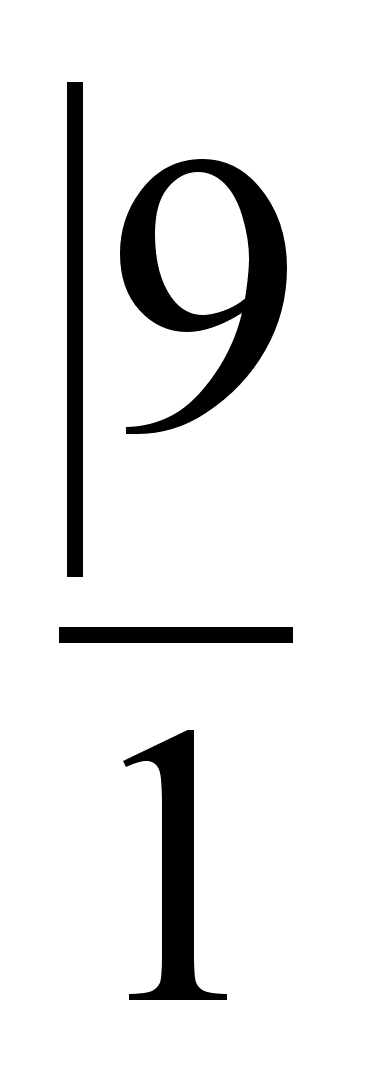

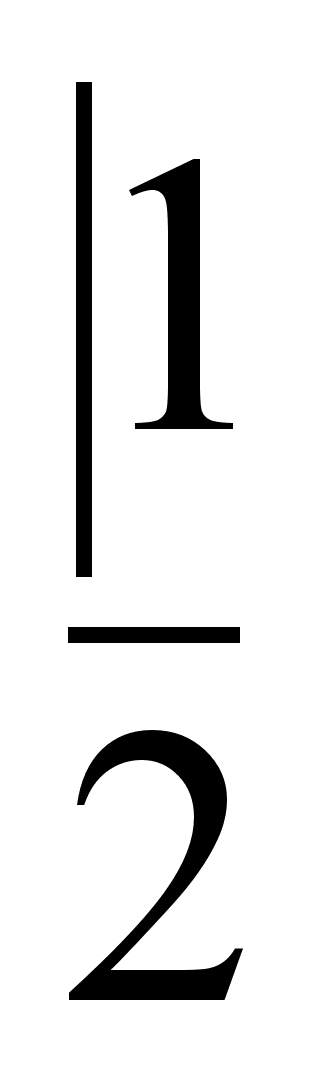
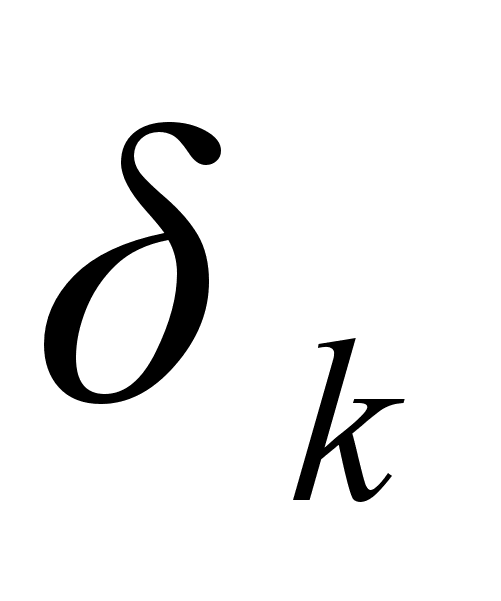
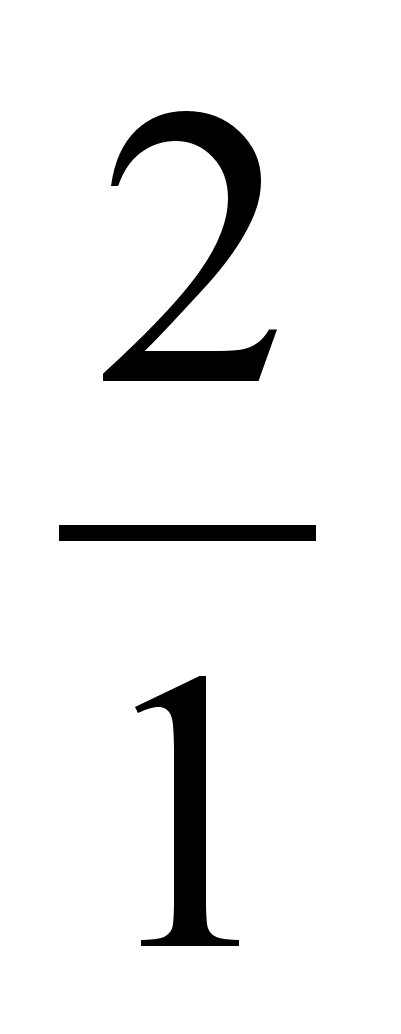

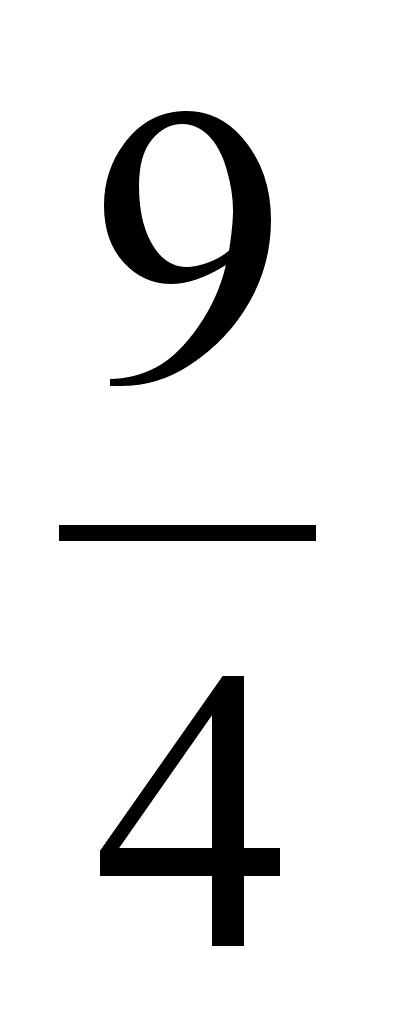
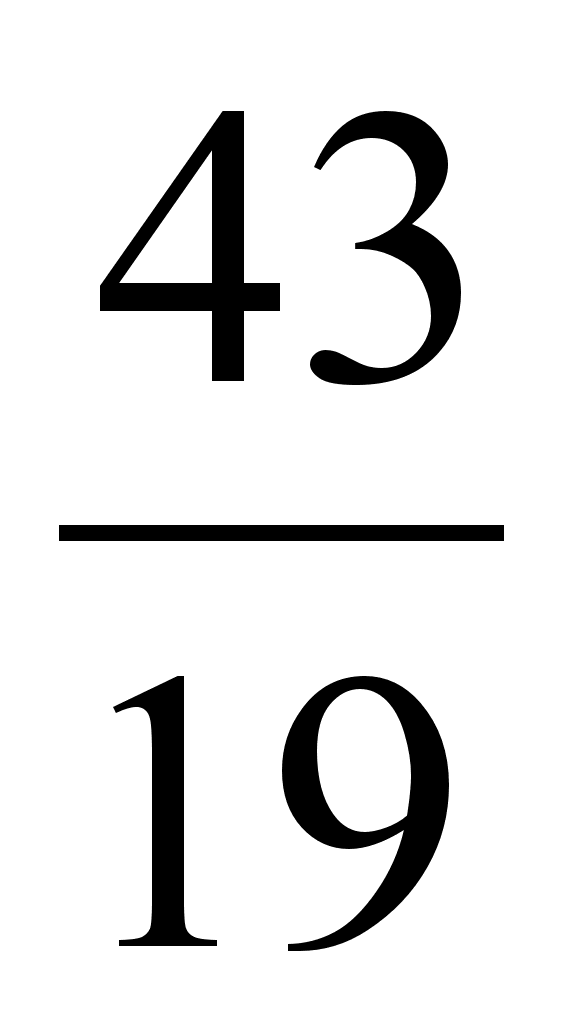
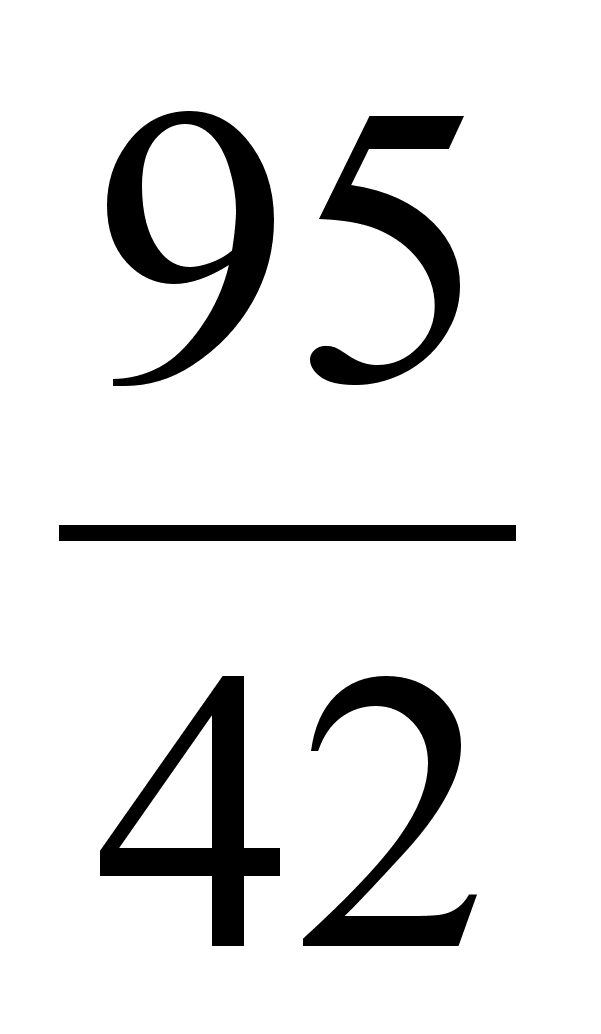 .
.
А сейчас рассмотрим ряд свойств подходящих дробей.
Теорема: При k=1, 2, тАж, выполняется равенство 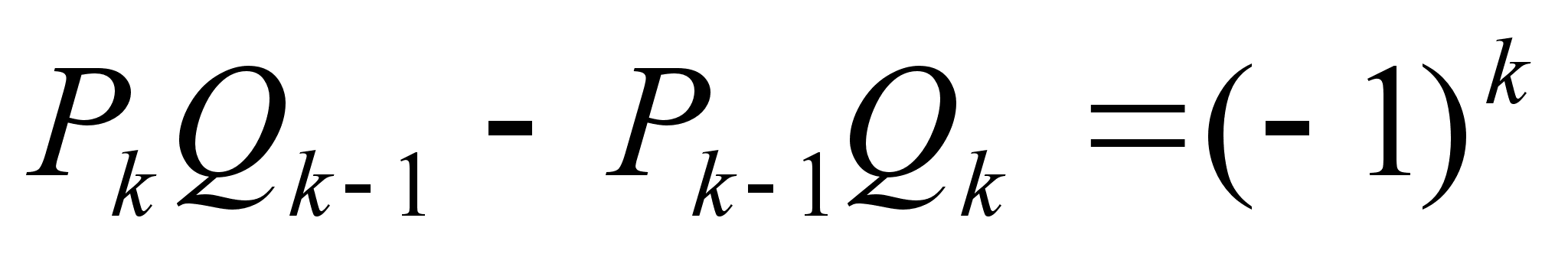
Доказательство: Проведем индукцию по k:
При k=1 равенство справедливо, так как 
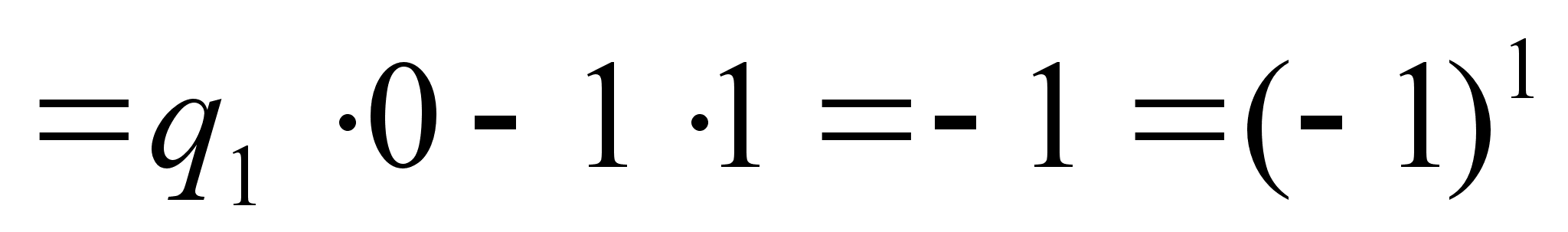 .
.
Пусть это равенство верно при некотором k=n (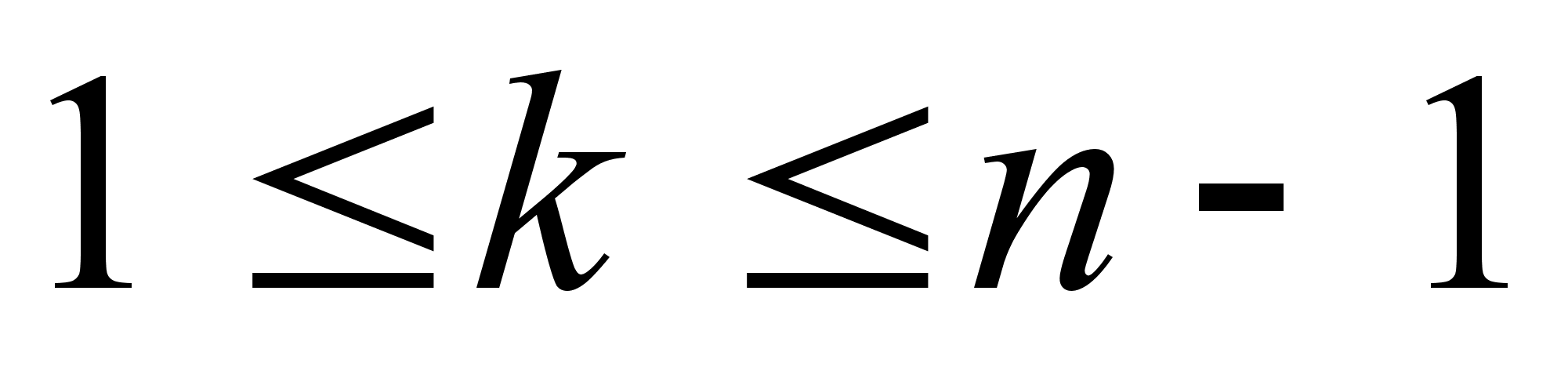 ).
).
Докажем справедливость равенства при k=n+1.
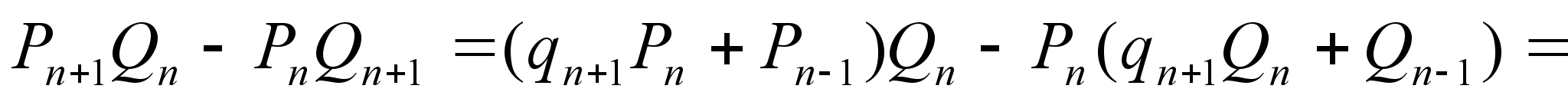
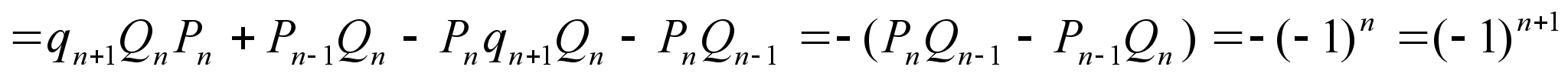
, то есть равенство верно при k=n+1.
Согласно принципу полной математической индукции равенство верно для всех k( ).
).
Теорема: Числитель и знаменатель любой подходящей дроби тАУ взаимно простые числа, то есть всякая kтАУподходящая дробь несократима.
Доказательство: Докажем это свойство методом от противного. По предыдущему свойству имеем 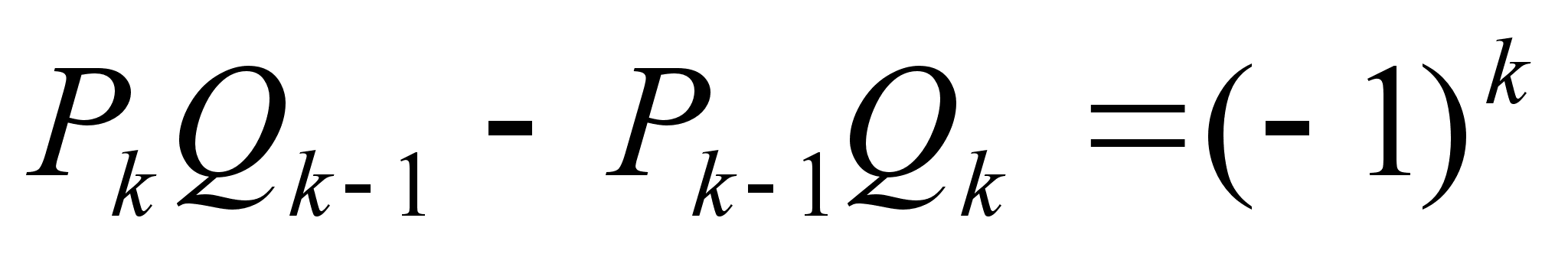 .
.
Пусть 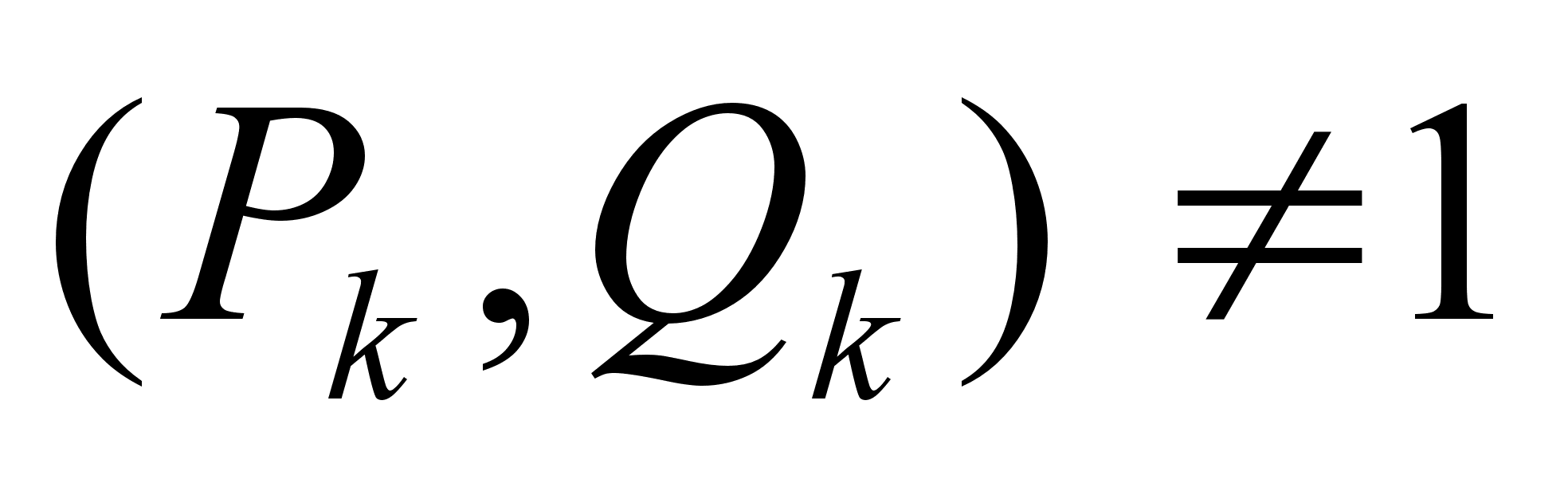 , то есть
, то есть  , тогда из равенства
, тогда из равенства 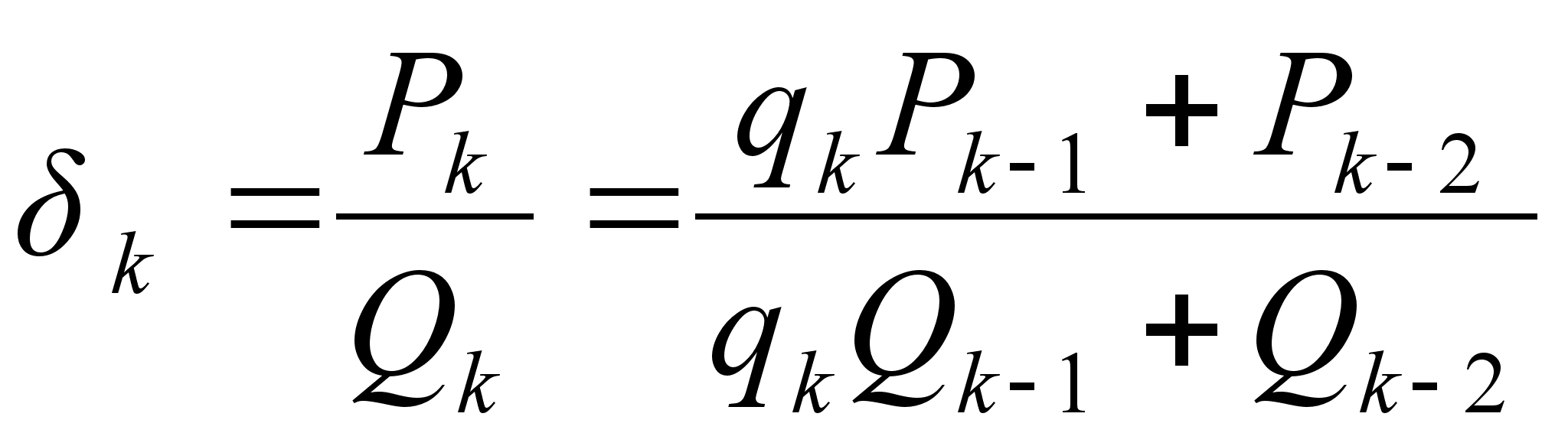 следует, что
следует, что 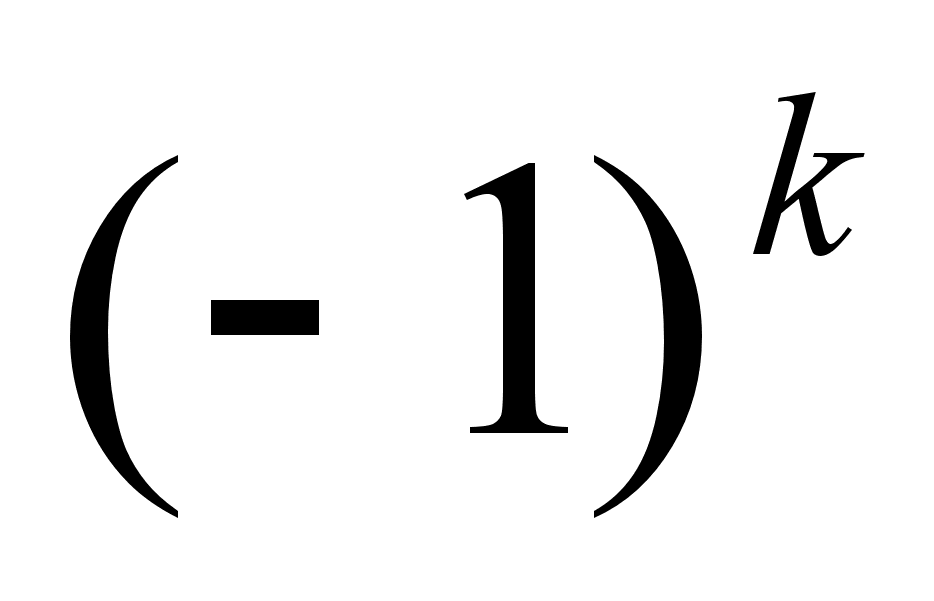 делится на
делится на 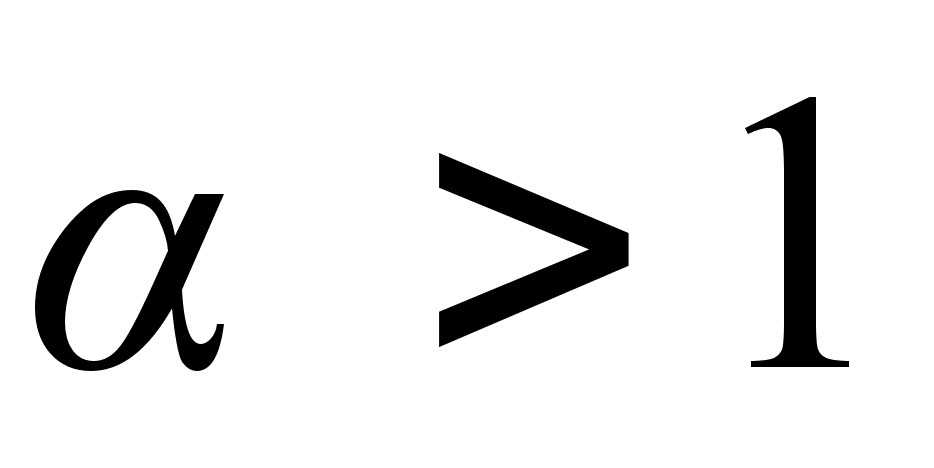 без остатка, что невозможно. Значит, наше допущение неверно, а верно то, что требовалось доказать, то есть
без остатка, что невозможно. Значит, наше допущение неверно, а верно то, что требовалось доказать, то есть  .
.
Теорема: При 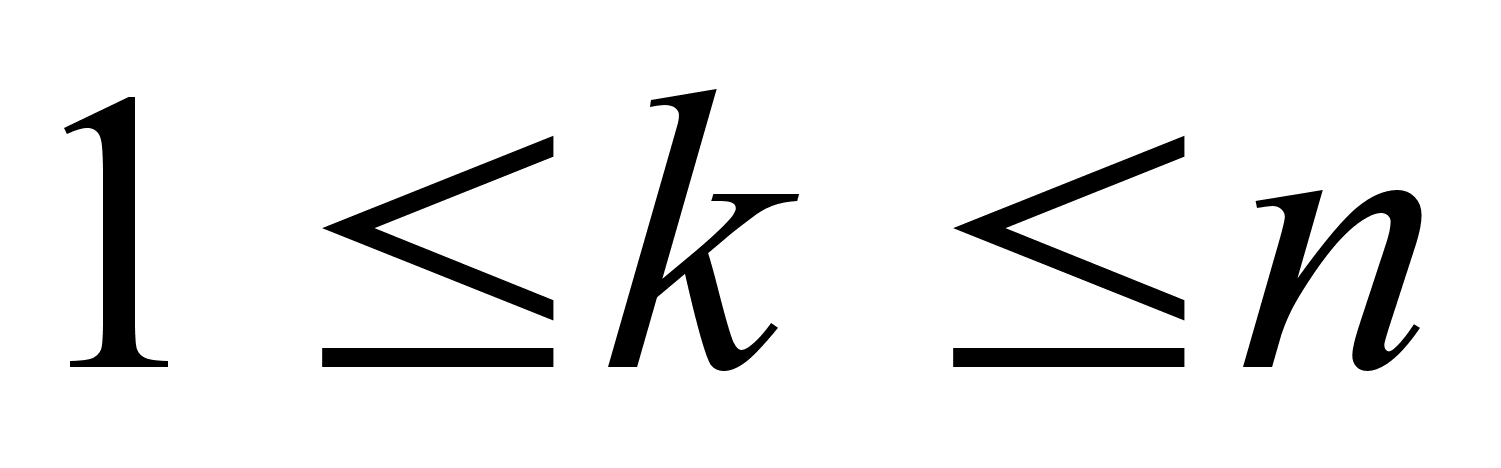
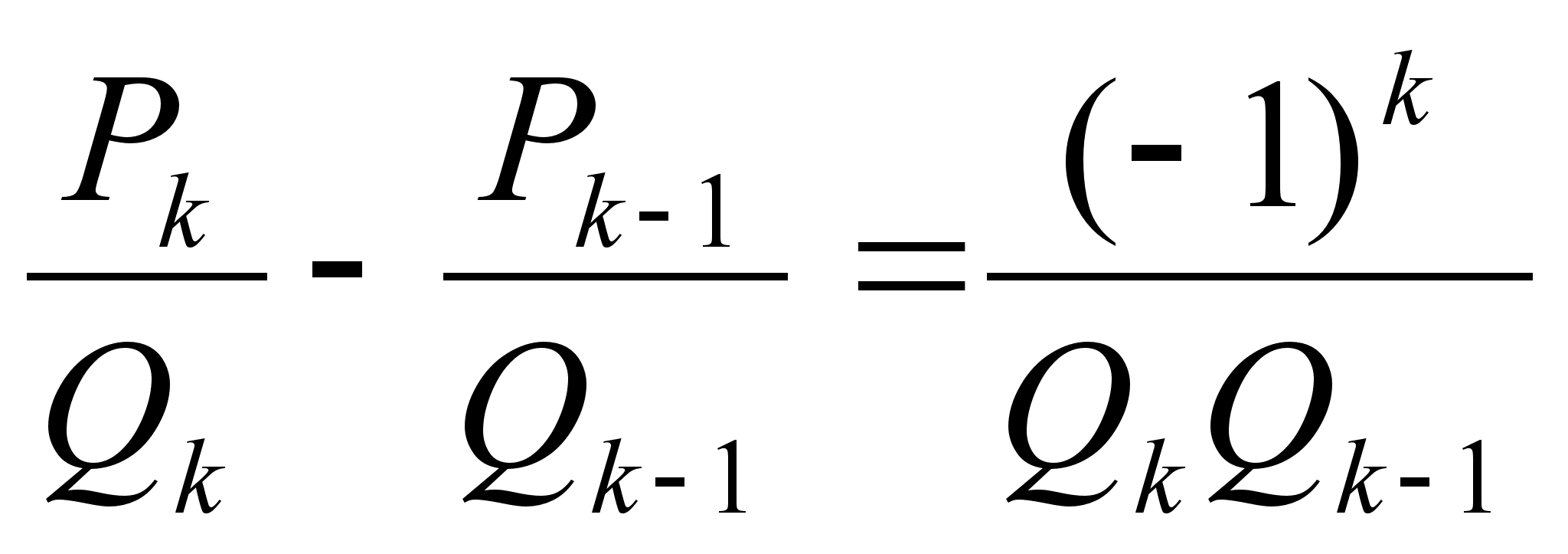 (
(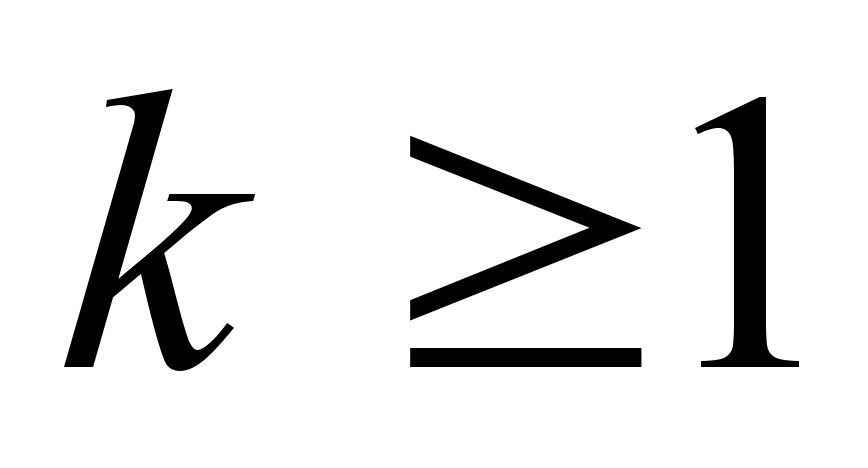 )
)
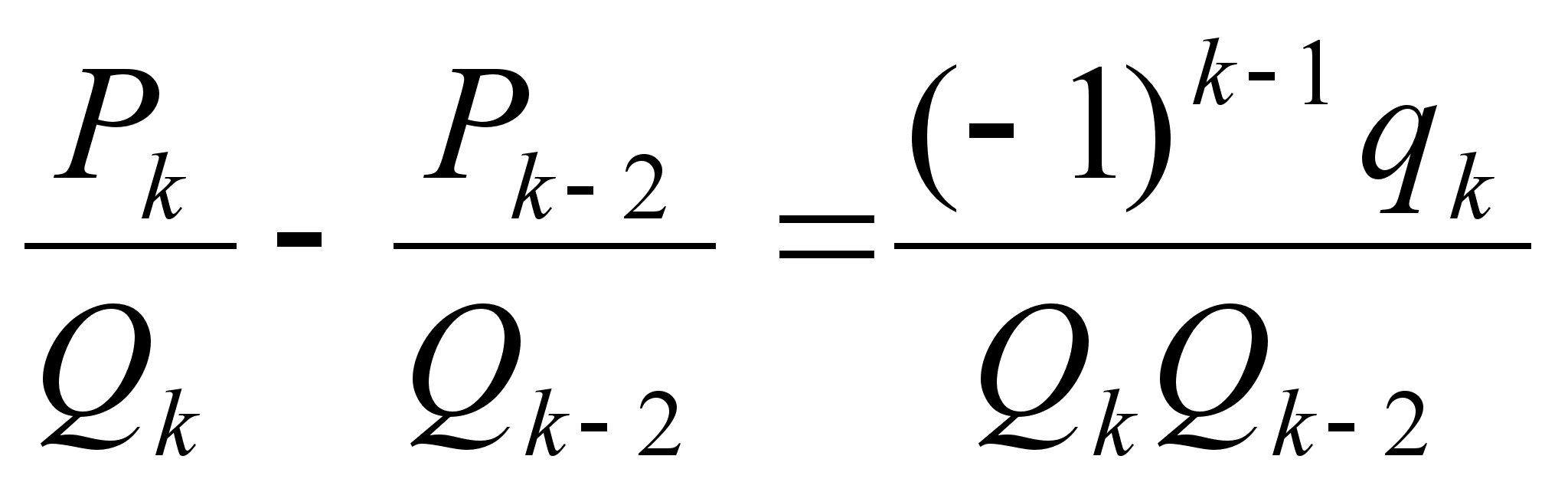 (
(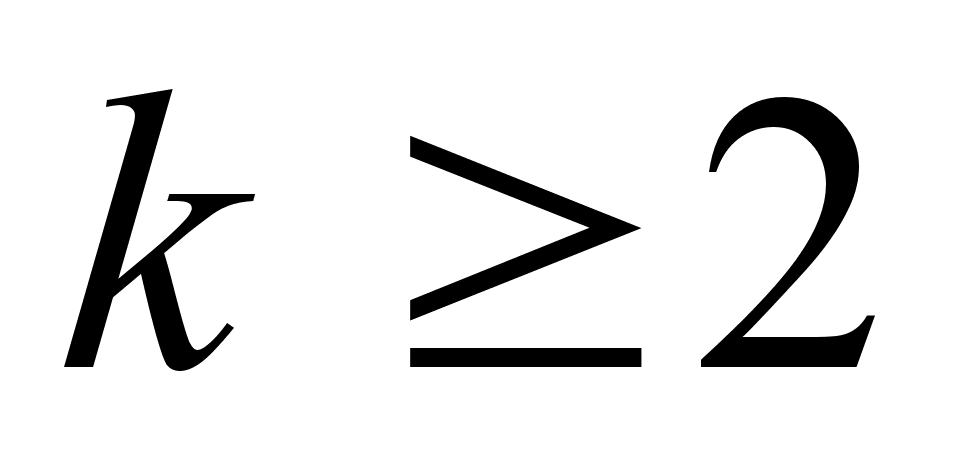 )
)
Доказательство: Первое соотношение можно получить из равенства 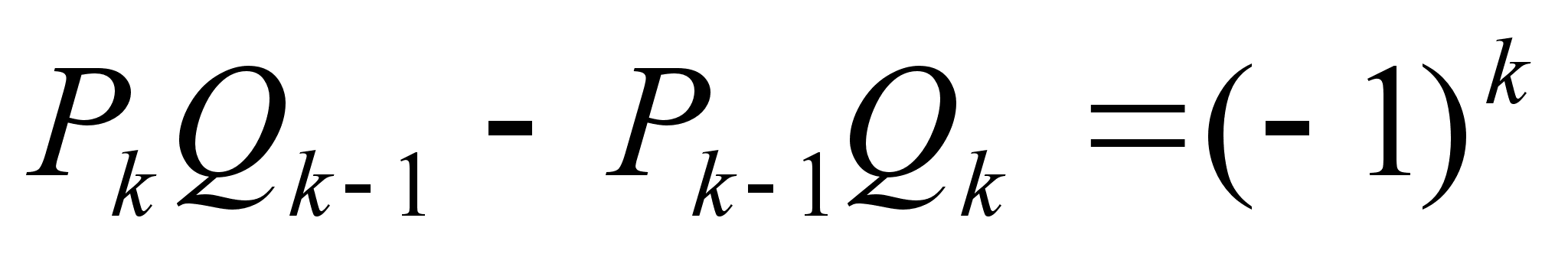 , доказанного выше, путем деления обеих частей на
, доказанного выше, путем деления обеих частей на 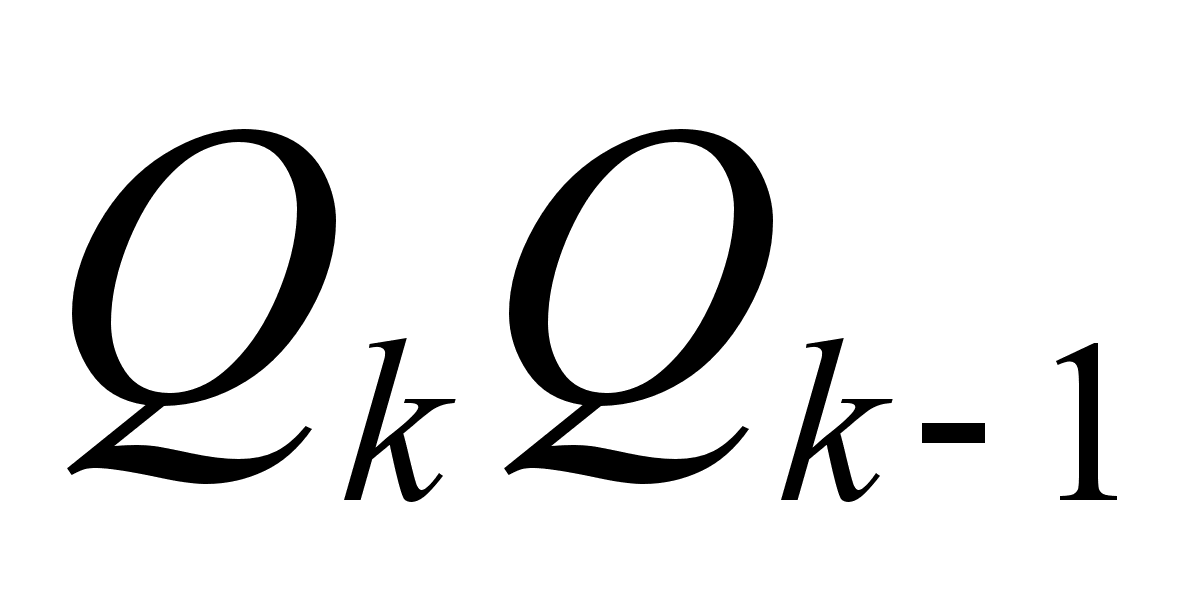 . Получаем
. Получаем 
 , что и требовалось доказать.
, что и требовалось доказать.
Докажем второе соотношение.
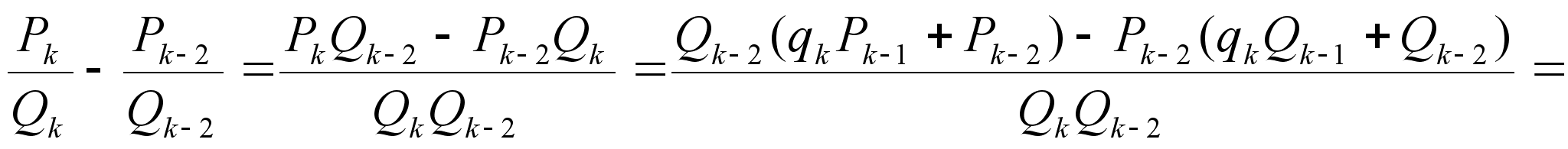
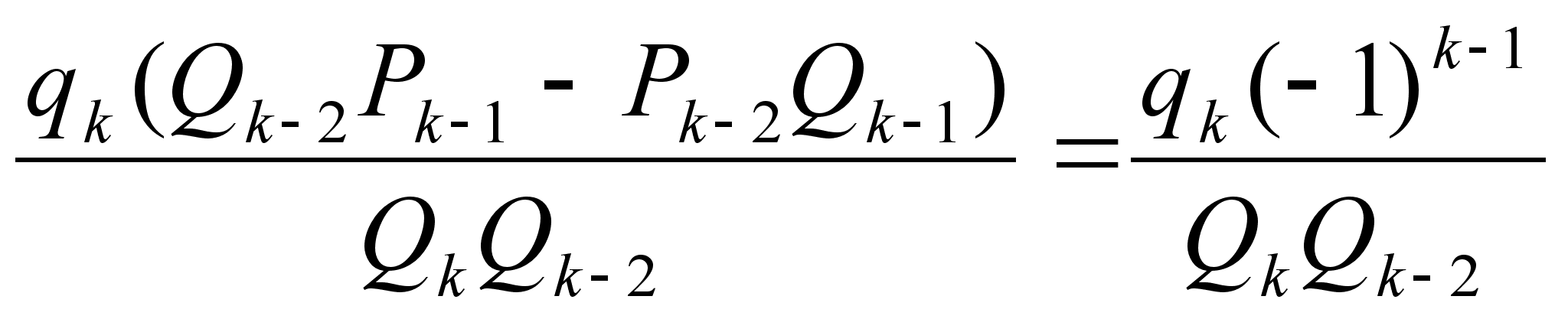 .
.
Теорема доказана полностью.
Теорема: Знаменатели подходящих дробей к цепной дроби, начиная с первого, образуют монотонно возрастающую последовательность, то есть 1=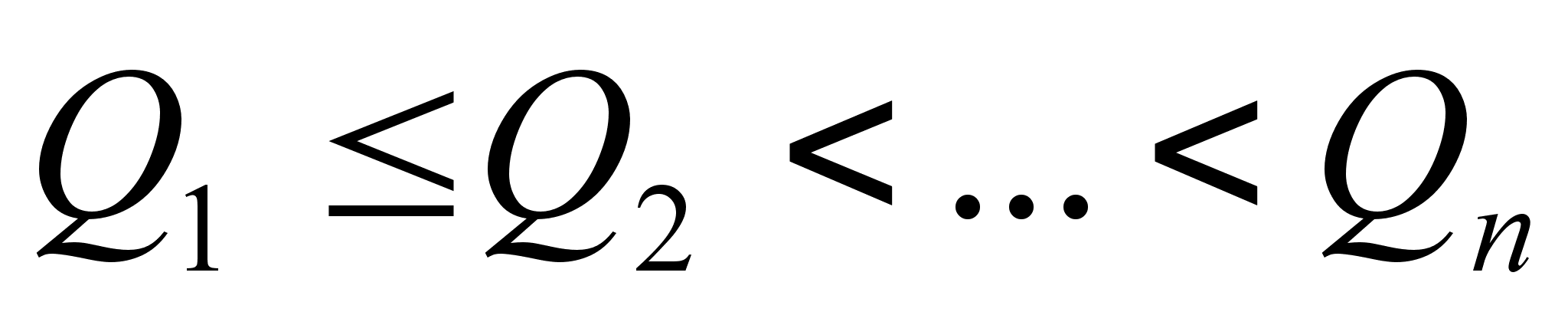 .
.
Доказательство: 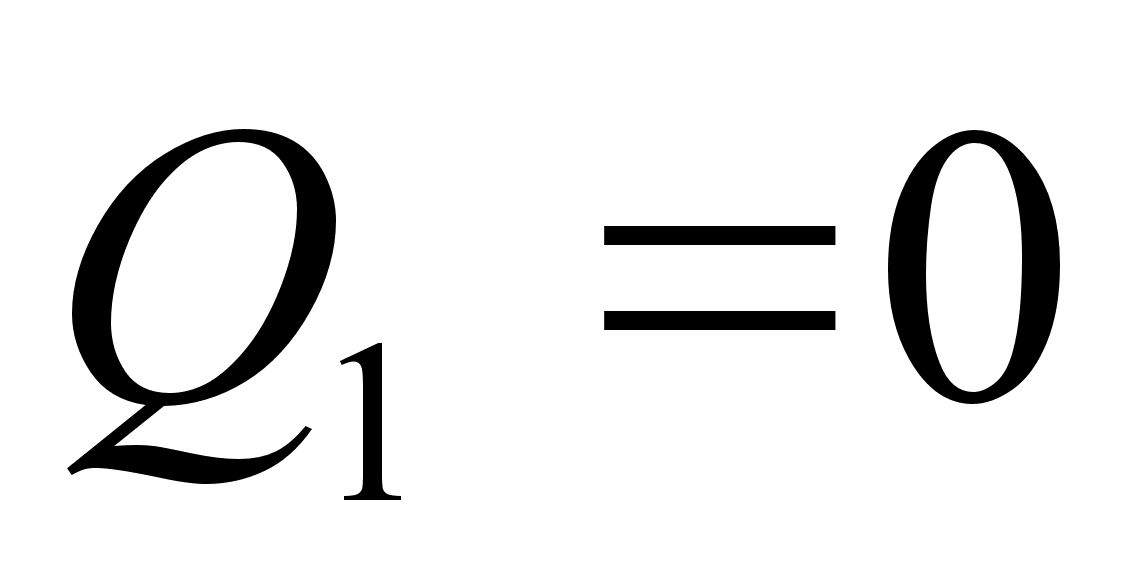 ,
,  , так что
, так что 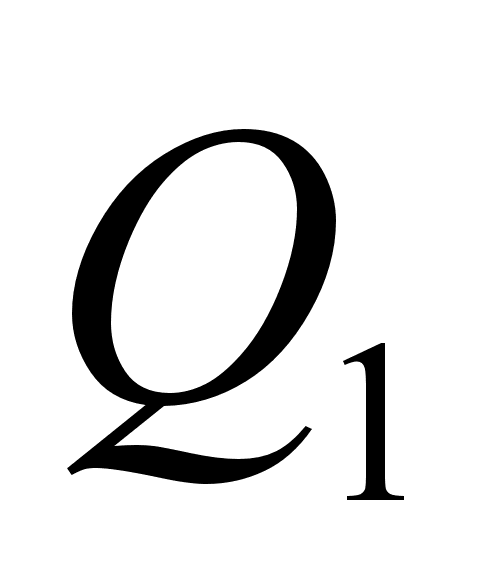 и
и 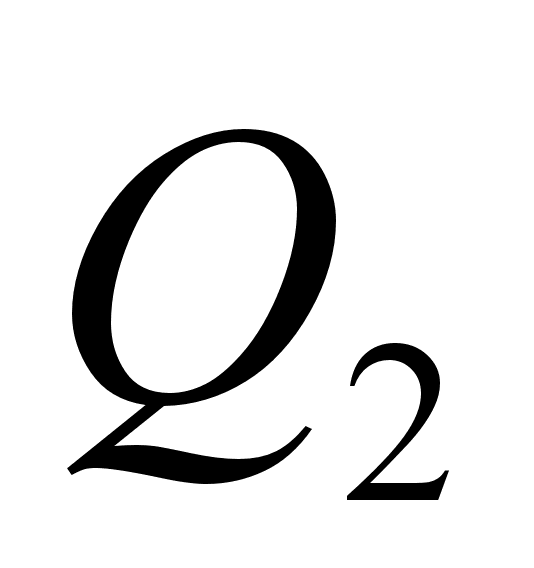 положительны.
положительны.
Соотношение 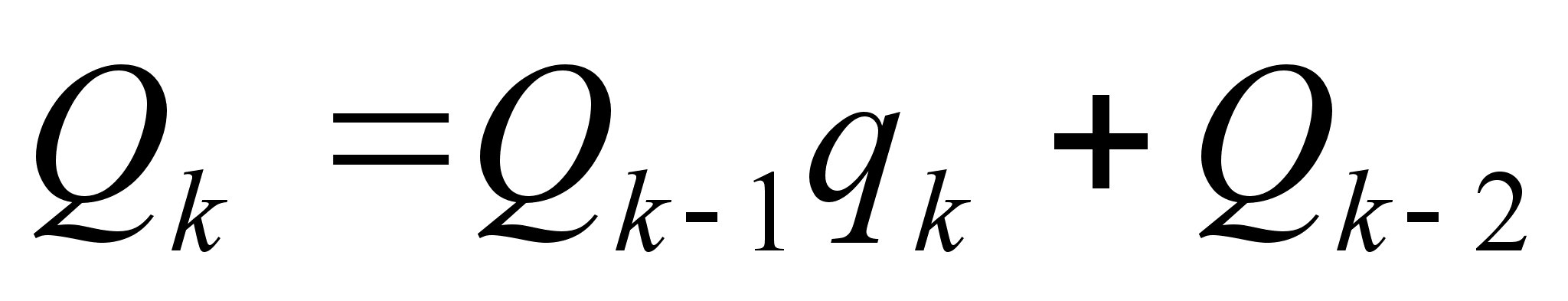 (
(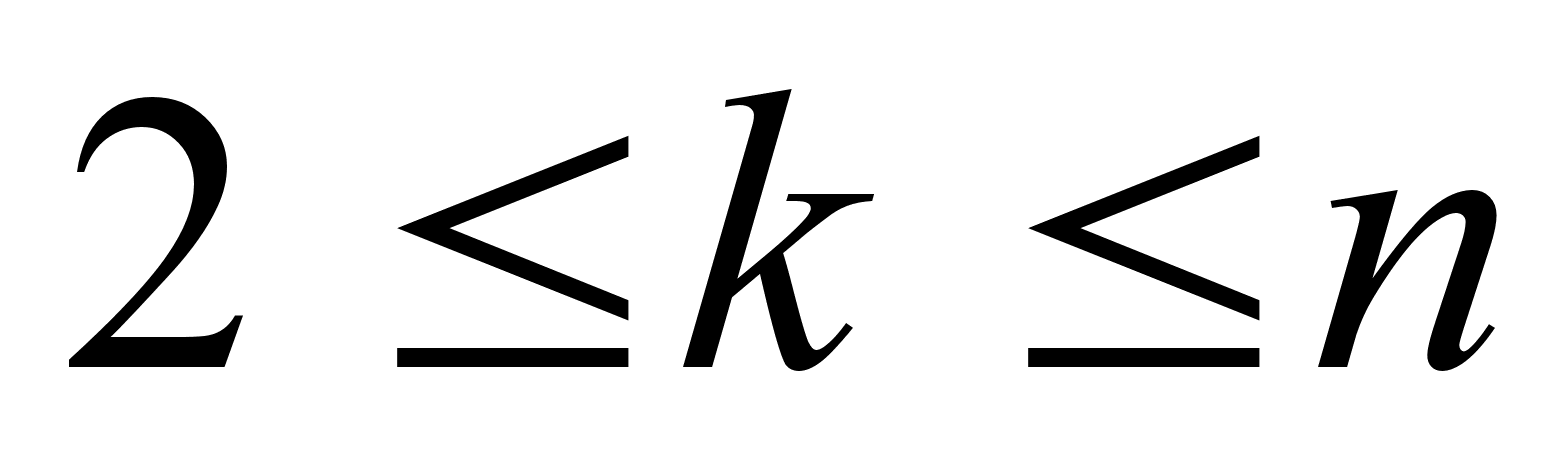 ) (*) показывает, что и все следующие знаменатели
) (*) показывает, что и все следующие знаменатели 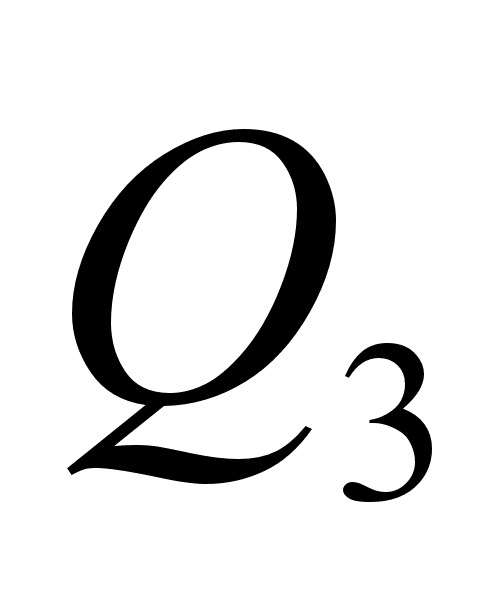 ,
, 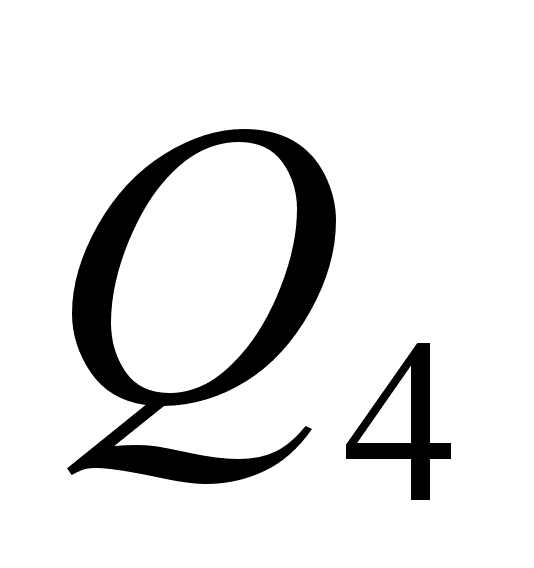 , тАж,
, тАж, 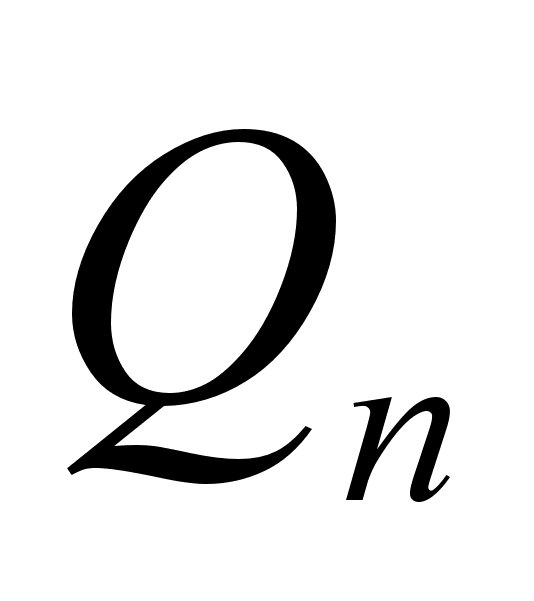 положительны. При
положительны. При 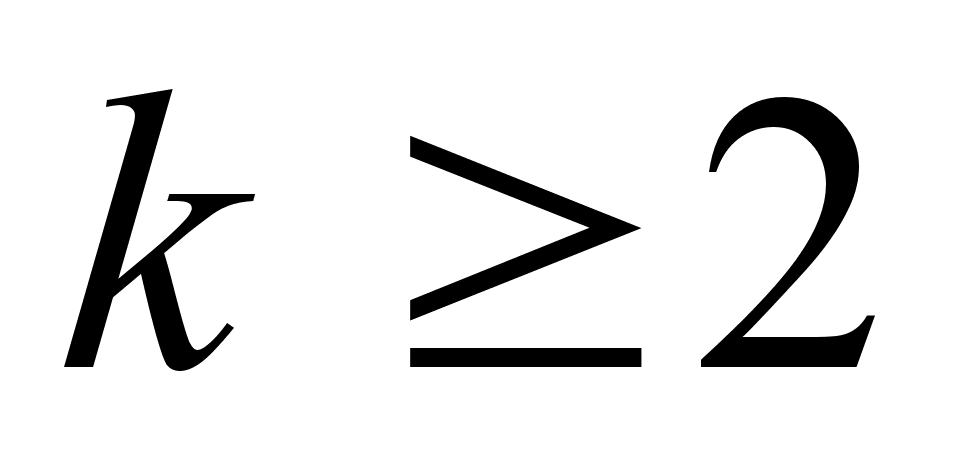 , поскольку тогда
, поскольку тогда 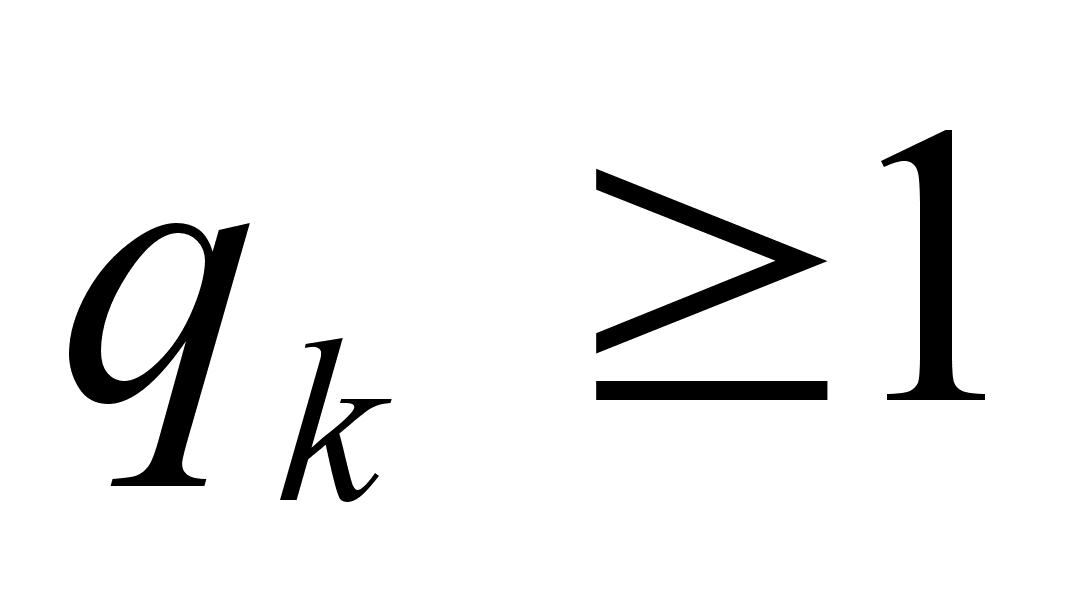 , из (*) получаем
, из (*) получаем
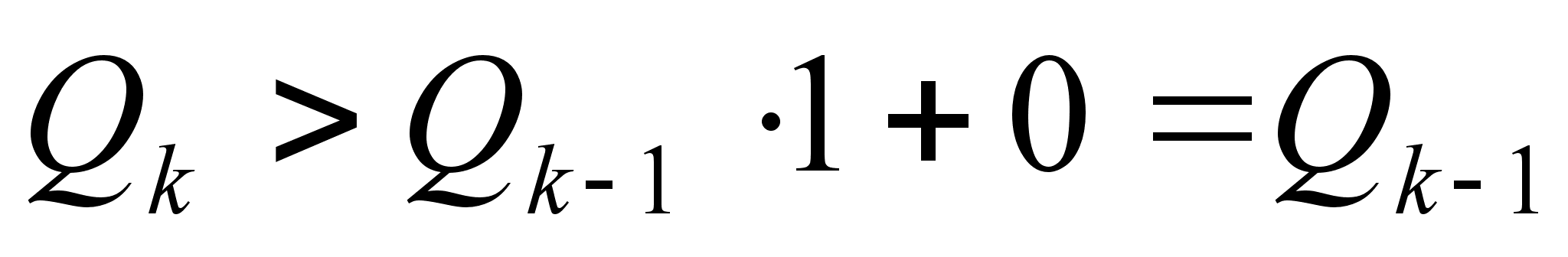 , что и требовалось доказать.
, что и требовалось доказать.
Теорема: Нечетные подходящие дроби образуют возрастающую, а четные подходящие дроби тАУ убывающую последовательность:
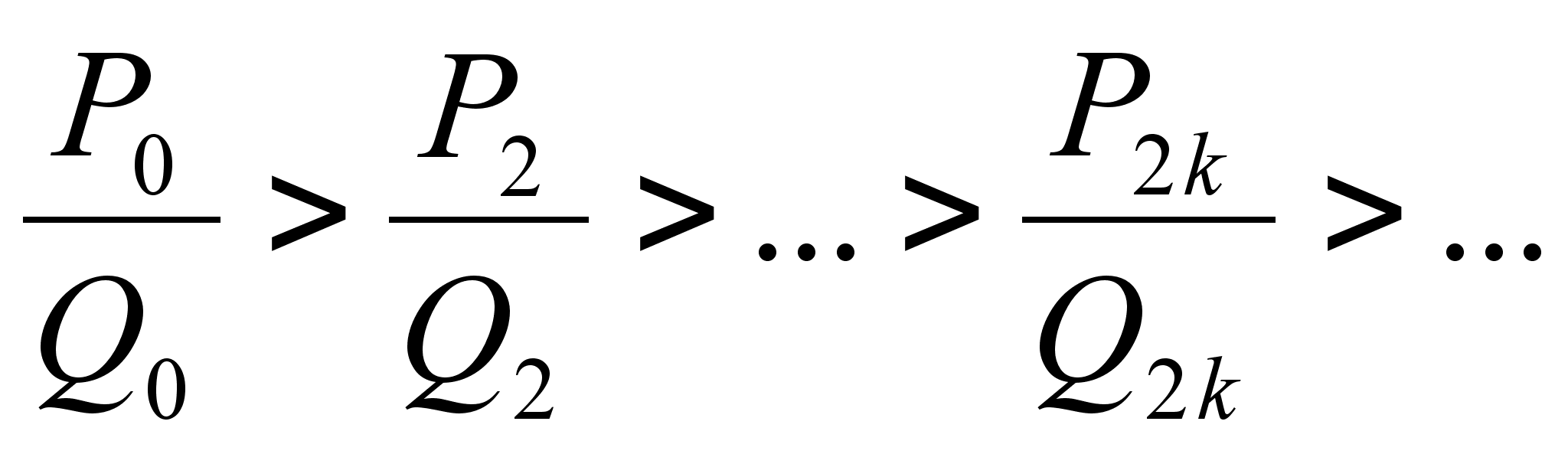 ;
;
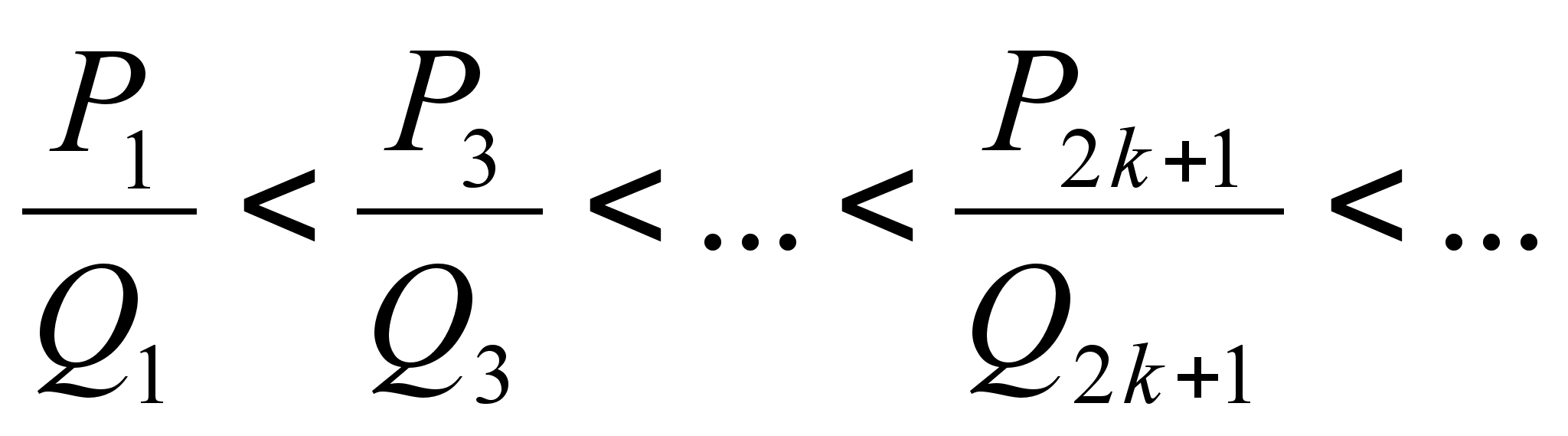 .
.
Две подходящие дроби 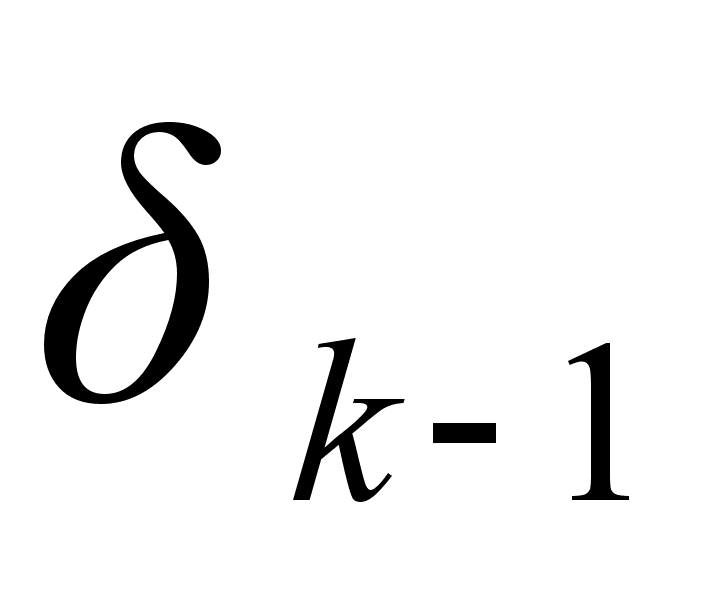 и
и 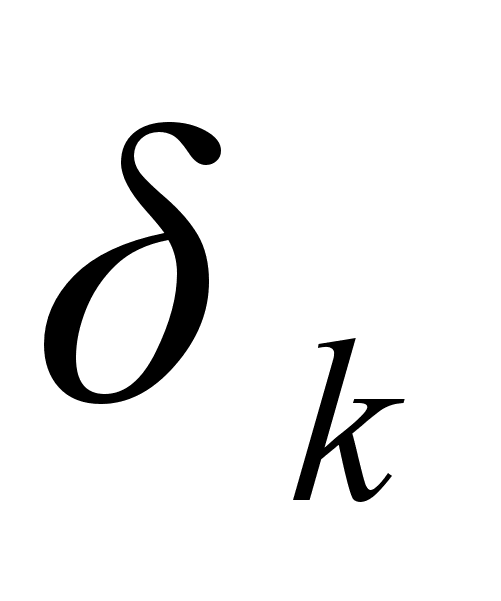 , у которых номер отличается на единицу, будем называть соседними.
, у которых номер отличается на единицу, будем называть соседними.
Теорема: Из двух соседних подходящих дробей четная дробь всегда больше нечетной.
Доказательство: По уже доказанному выше свойству имеем:
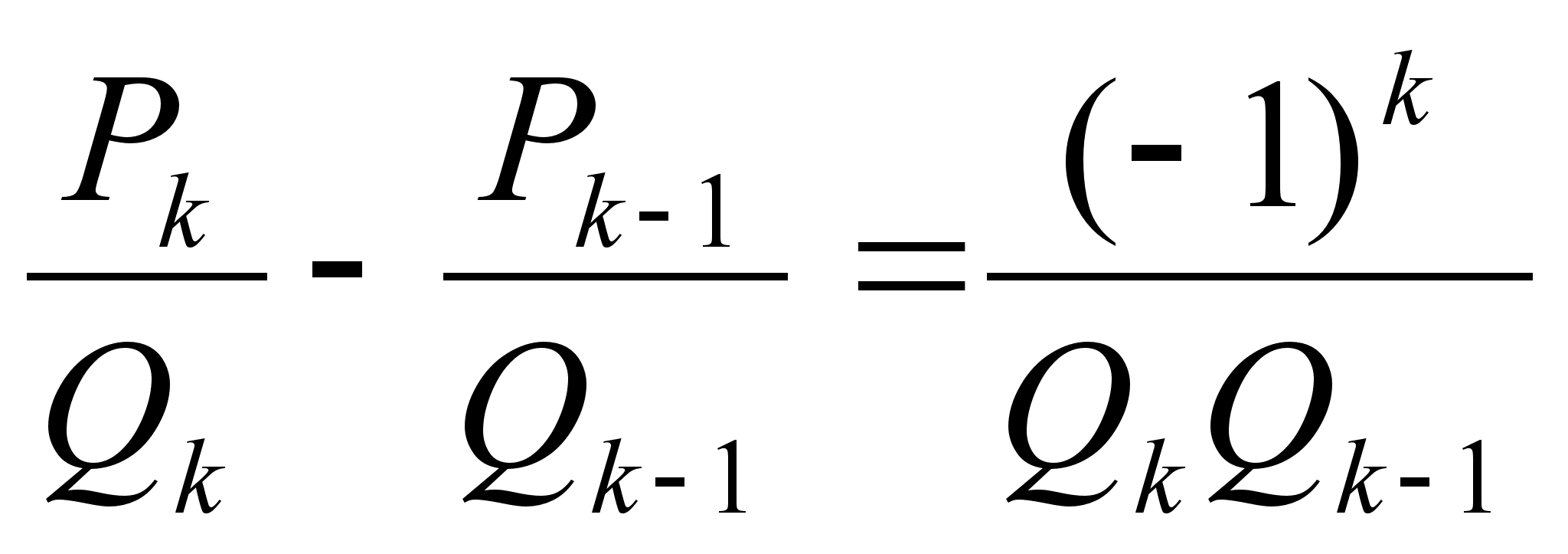 .
.
Если k тАУ четное, то 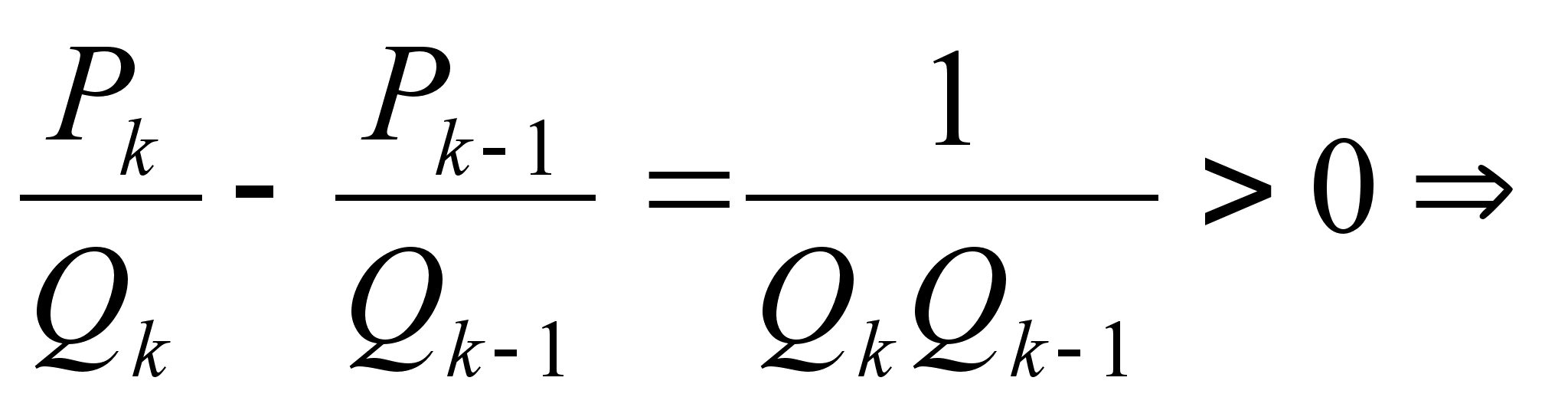
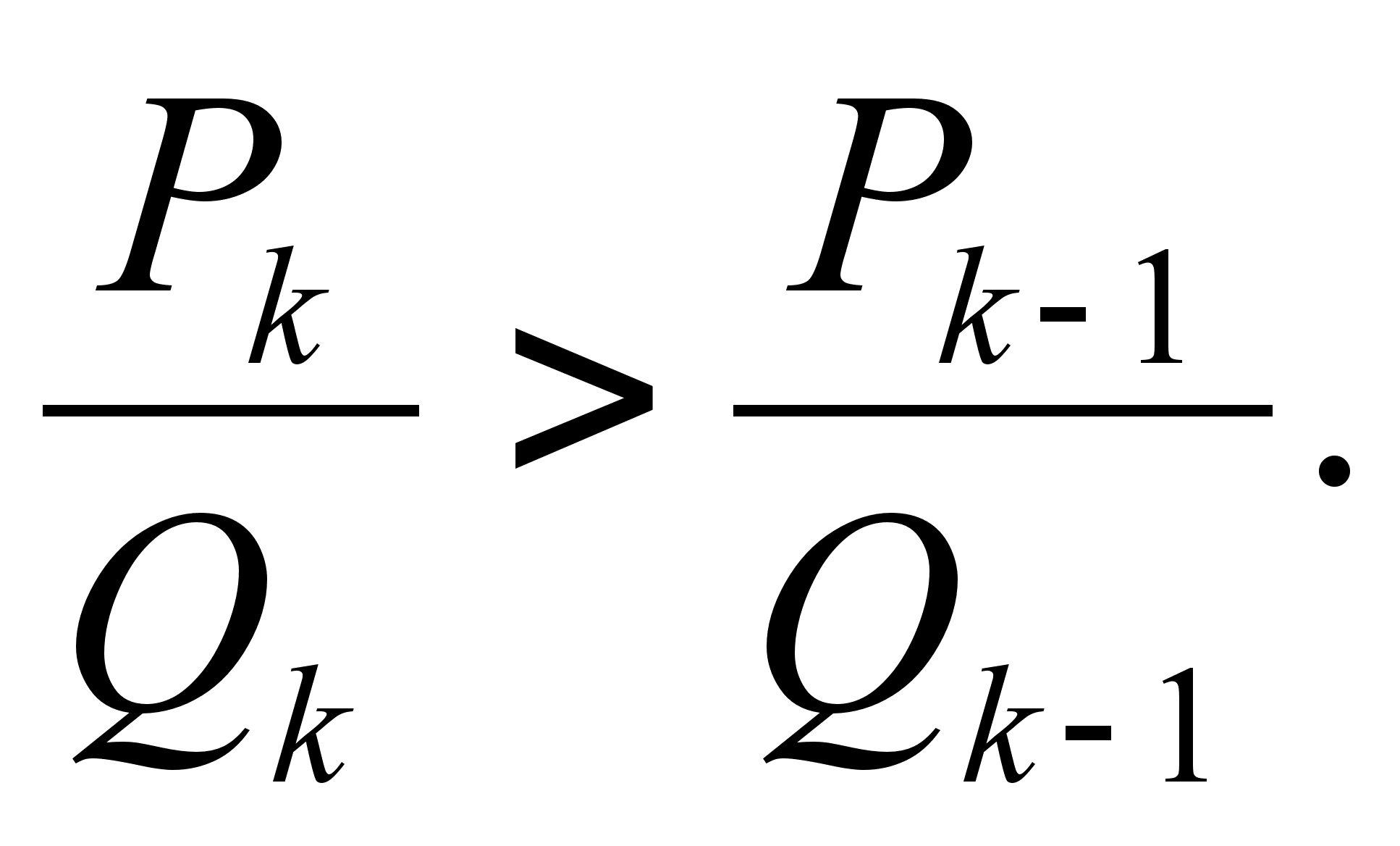
Если k тАУ нечетное, то 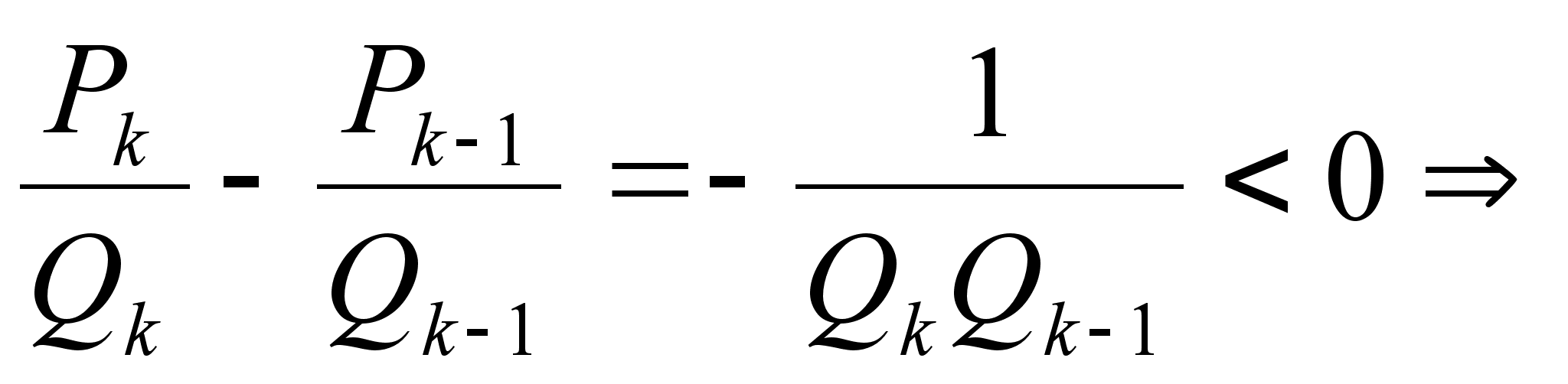

Значит, из двух соседних дробей 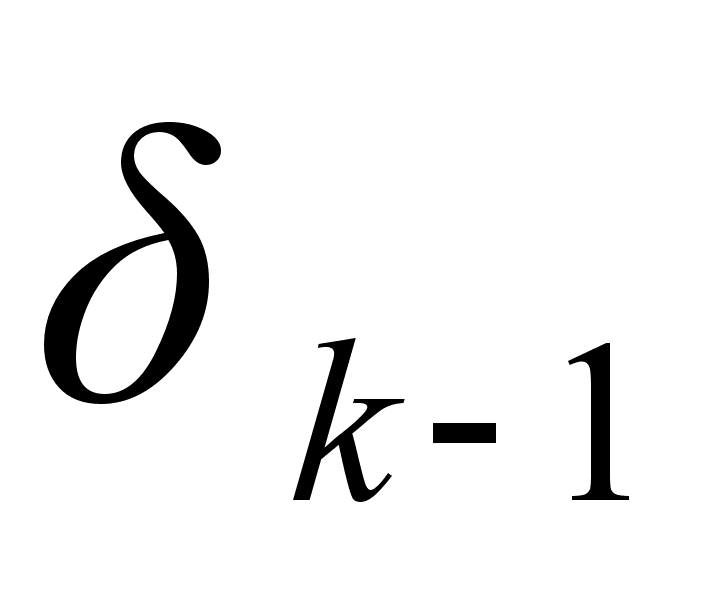 и
и 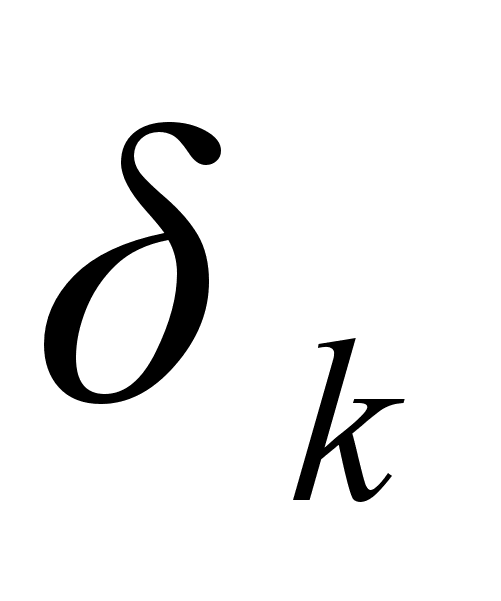 четная всегда больше нечетной, что и требовалось доказать.
четная всегда больше нечетной, что и требовалось доказать.
Теорема: Расстояние между двумя соседними подходящими дробями  .
.
Доказательство: Так как 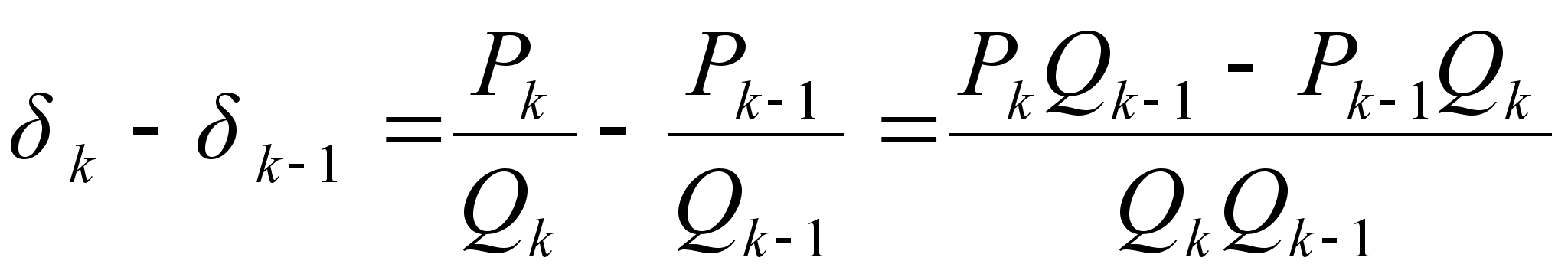 , то
, то 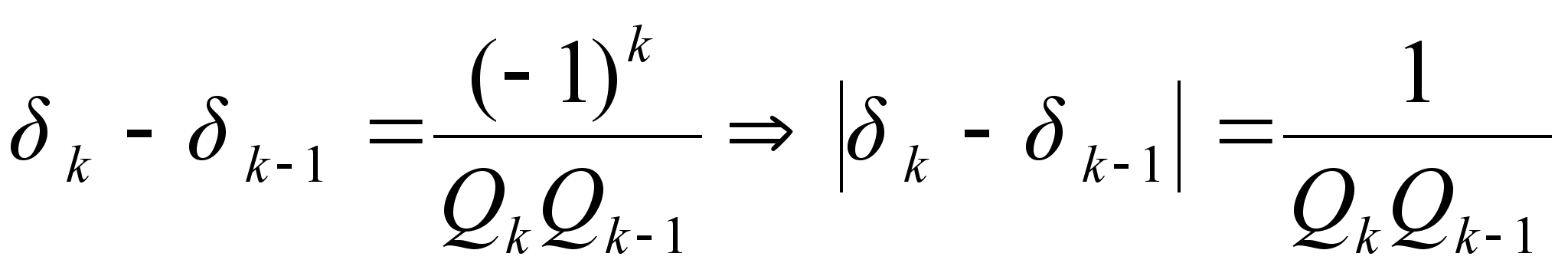 , что и требовалось доказать.
, что и требовалось доказать.
Глава II. Бесконечные цепные дроби.
Вз1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями.
Разложение действительного иррационального числа в правильную бесконечную цепную дробь.
В предыдущей главе мы рассмотрели, как в процессе последовательного выделения целой части и перевертывания дробной рациональная дробь  разлагается в конечную непрерывную дробь.
разлагается в конечную непрерывную дробь.
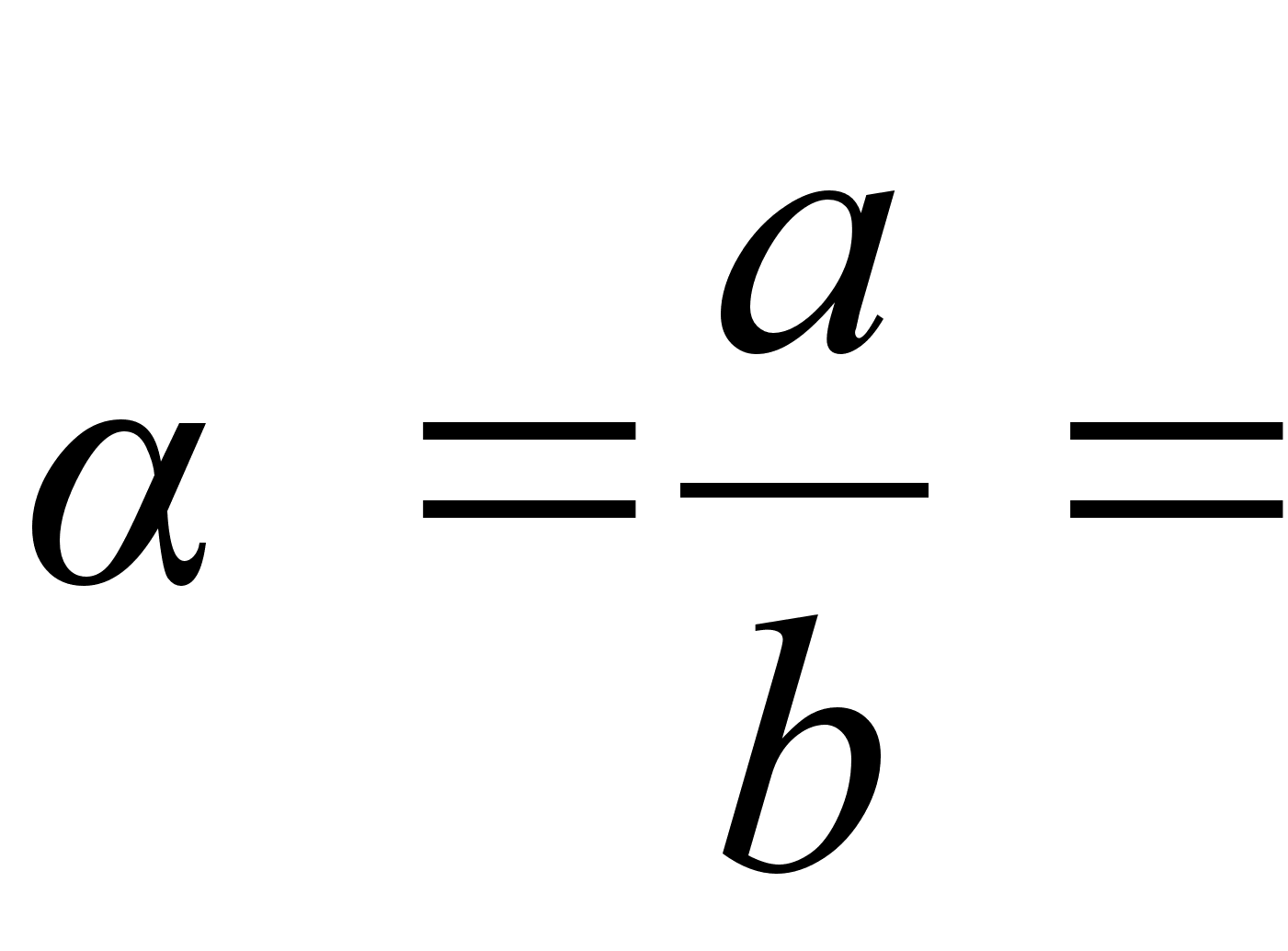
 =(
=(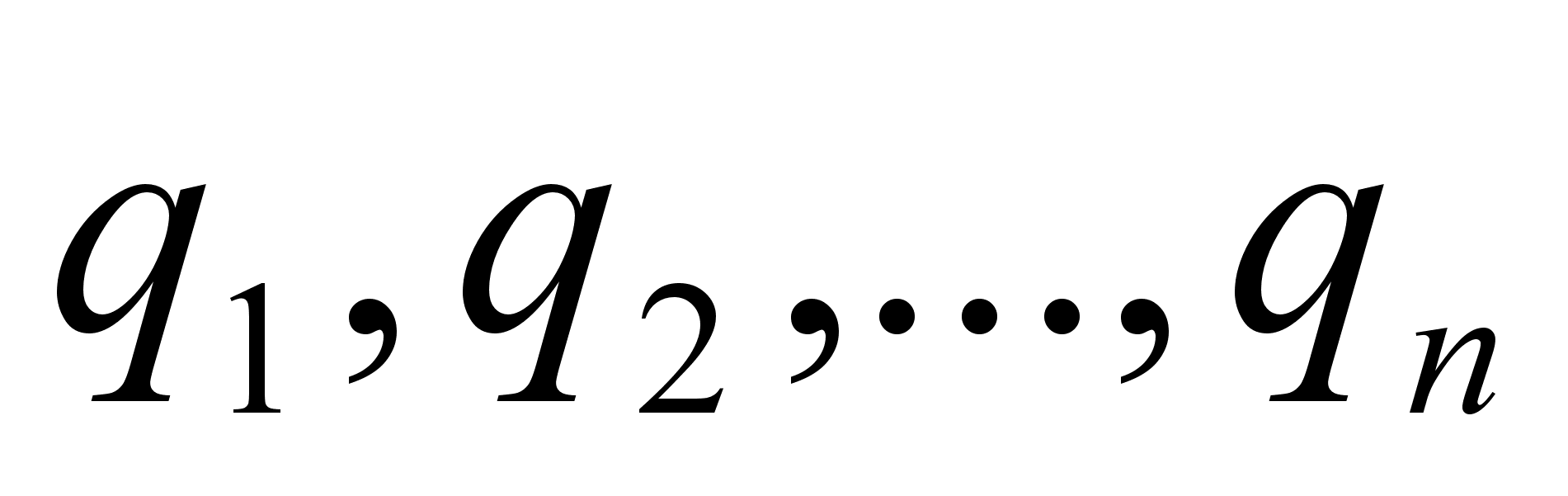 )
)
 (1)
(1)

и, наоборот, свертывание такой непрерывной дроби приводит к рациональной дроби.
Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу.
Для иррационального числа  указанный процесс должен быть бесконечным, так как конечная цепная дробь равна рациональному числу.
указанный процесс должен быть бесконечным, так как конечная цепная дробь равна рациональному числу.
Выражение  (где
(где  ,
, 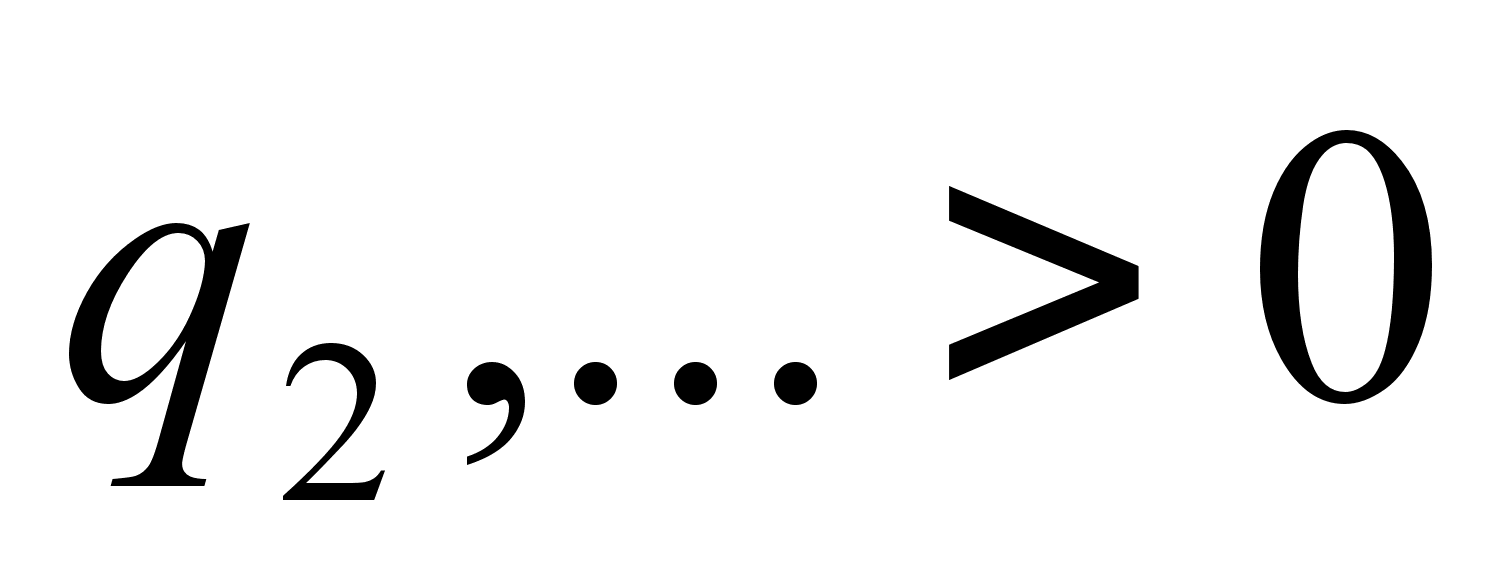 ) (2)
) (2)

возникающее в таком процессе или заданное формально, мы будем называть правильной бесконечной цепной, или непрерывной дробью, или дробью бесконечной длины и обозначать кратко через (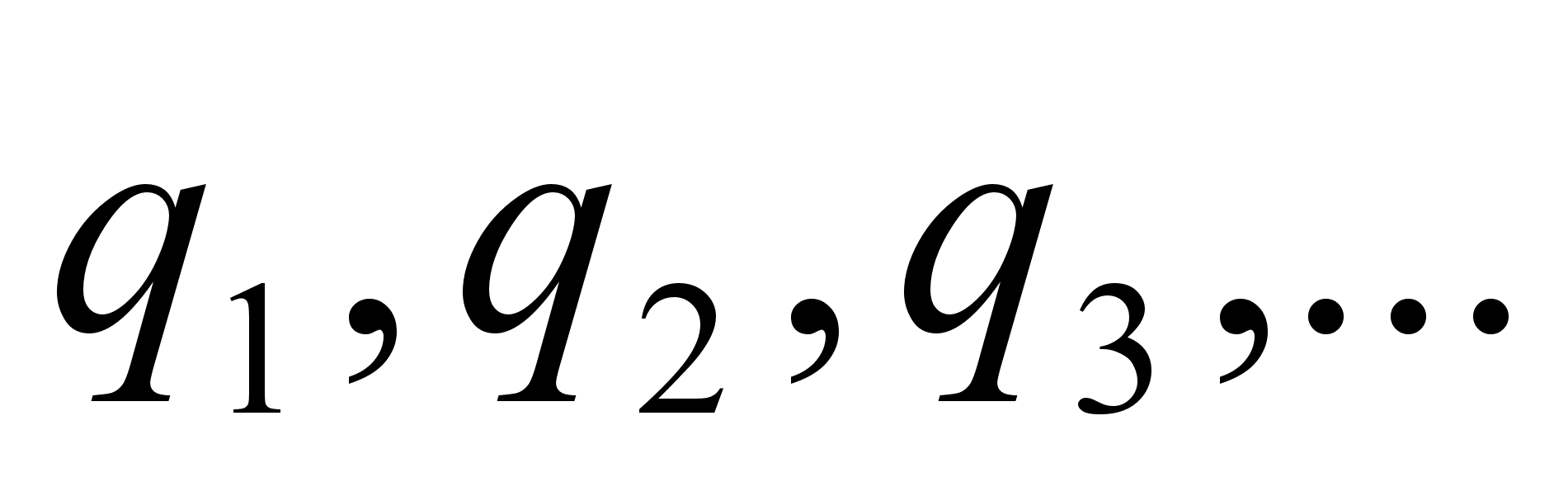 ), а числа
), а числа 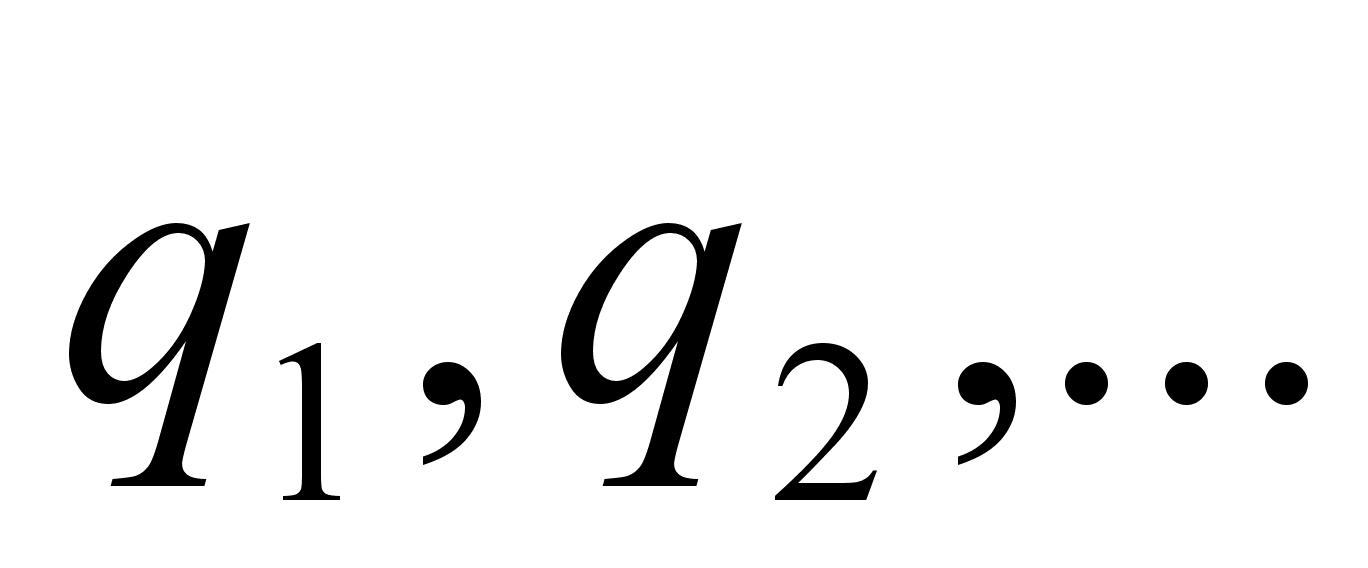 тАУ ее элементами или неполными частными.
тАУ ее элементами или неполными частными.
Отметим, что разложение  возможно только в единственном виде, так как процесс выделения целой части тАУ процесс однозначный.
возможно только в единственном виде, так как процесс выделения целой части тАУ процесс однозначный.
Рассмотрим пример разложения иррационального числа  .
.
Пусть  . Выделим из
. Выделим из 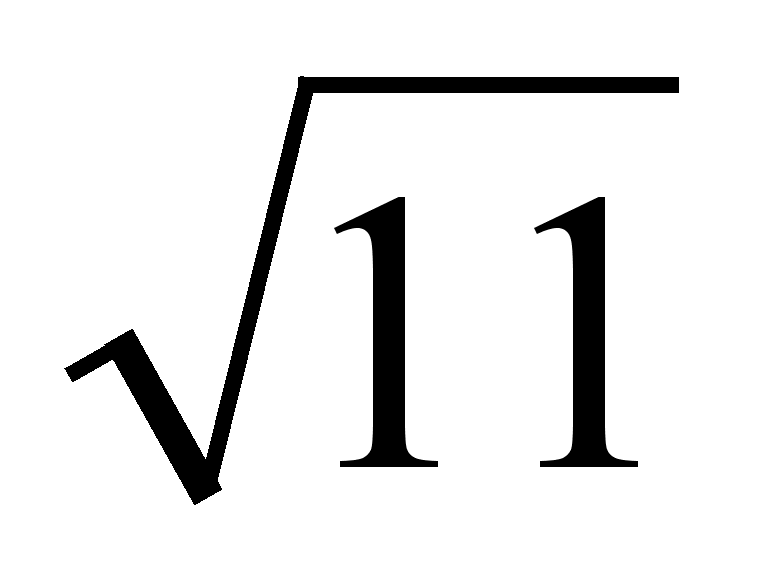 его целую часть.
его целую часть. 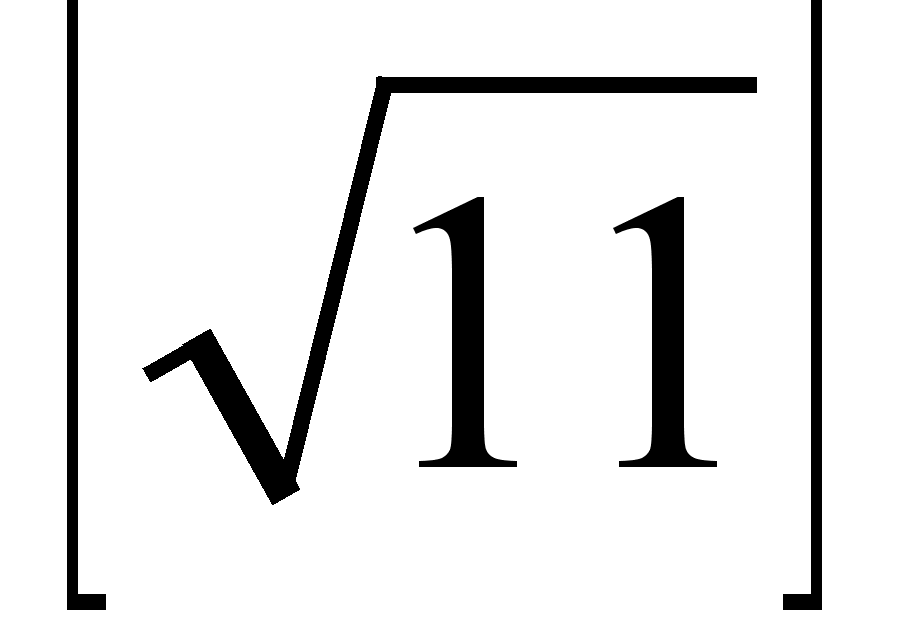 =3, а дробную часть
=3, а дробную часть 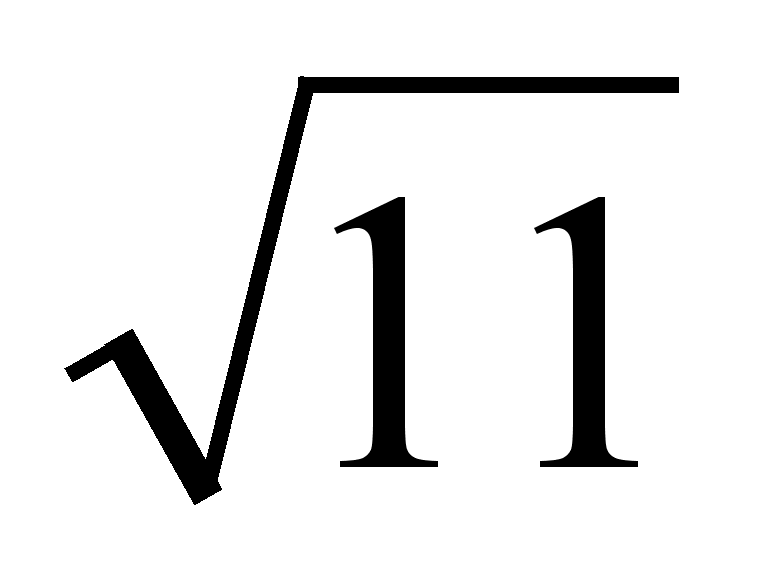 тАУ3, которая меньше 1, представим в виде
тАУ3, которая меньше 1, представим в виде 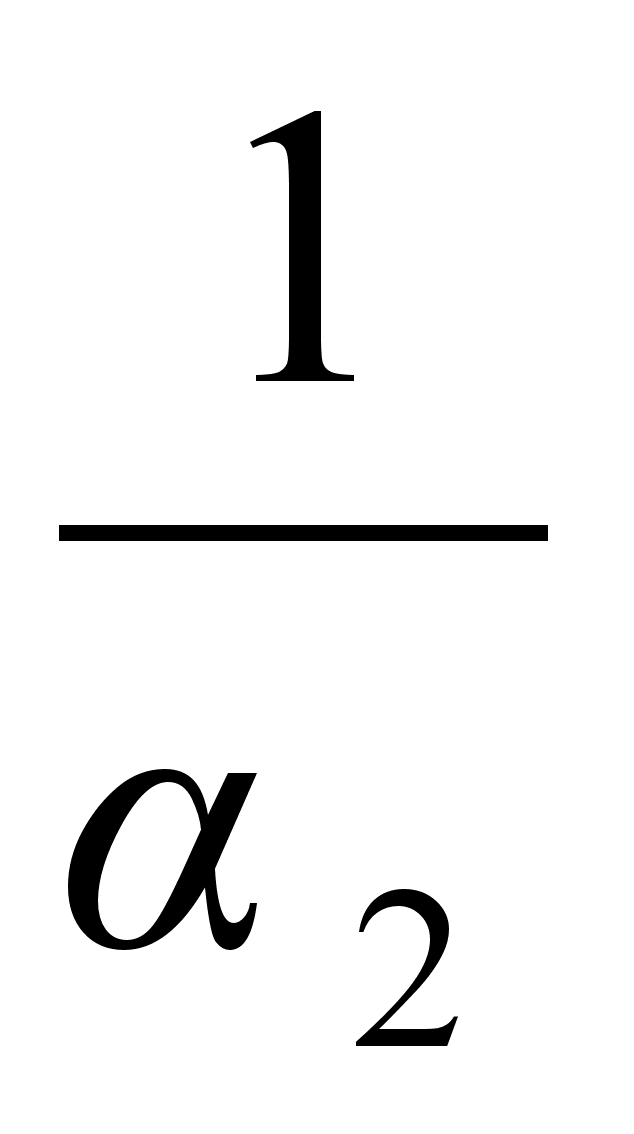 , где
, где 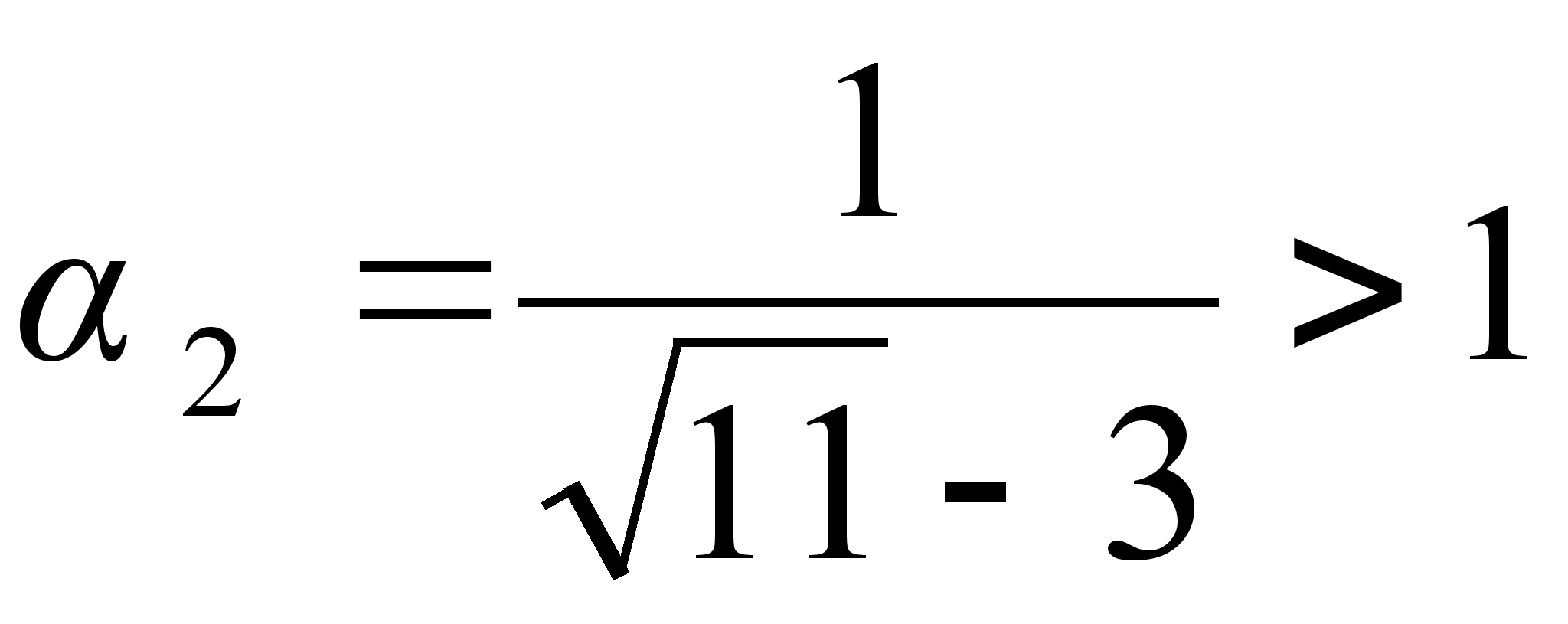 .
.
Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:
 ;
;
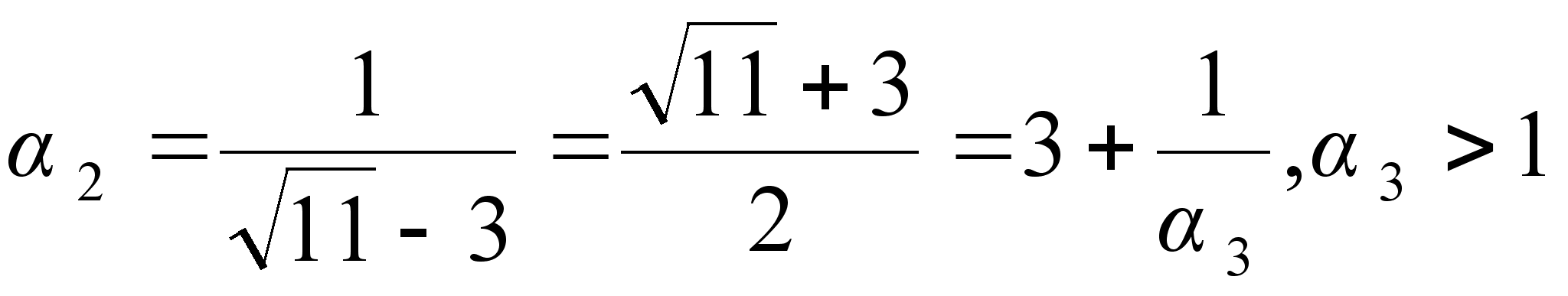 ;
;
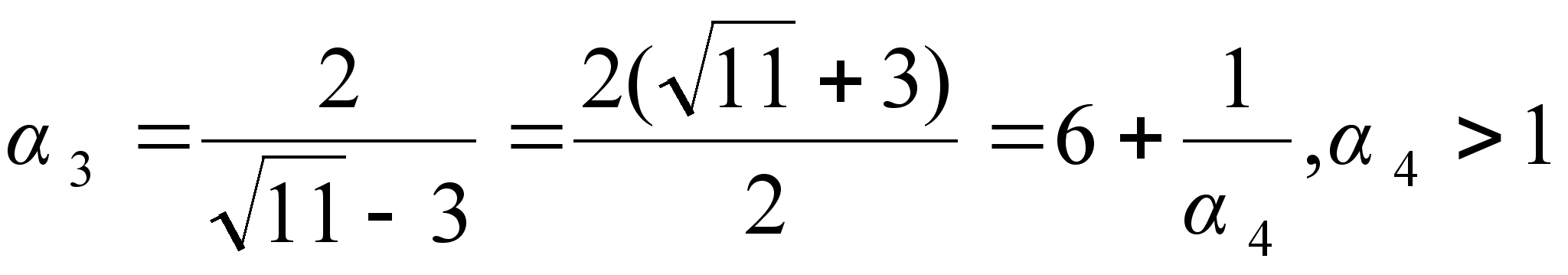 .
.
Если остановиться на этом шаге, то можно записать:

С другой стороны, из формулы для 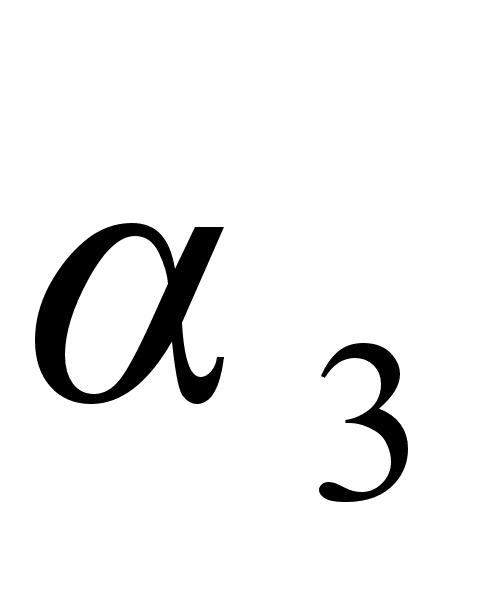 видно, что
видно, что 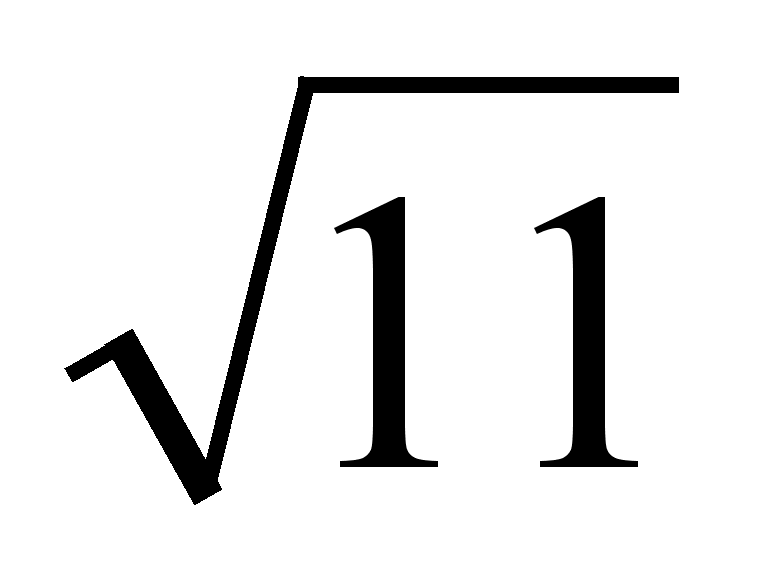 =3+
=3+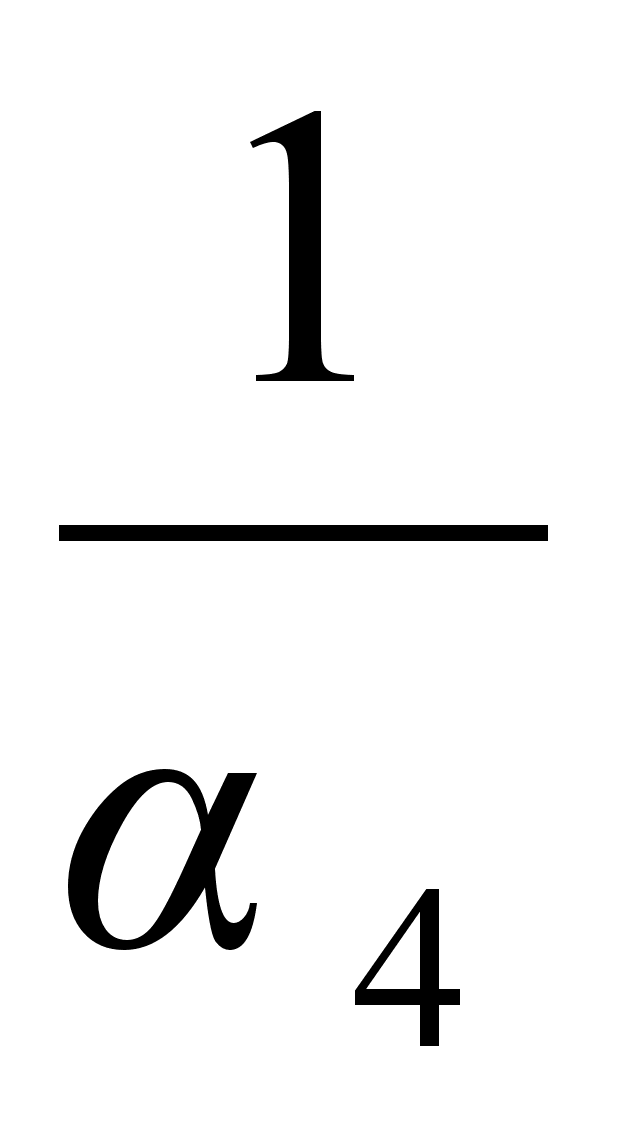 . Поэтому
. Поэтому 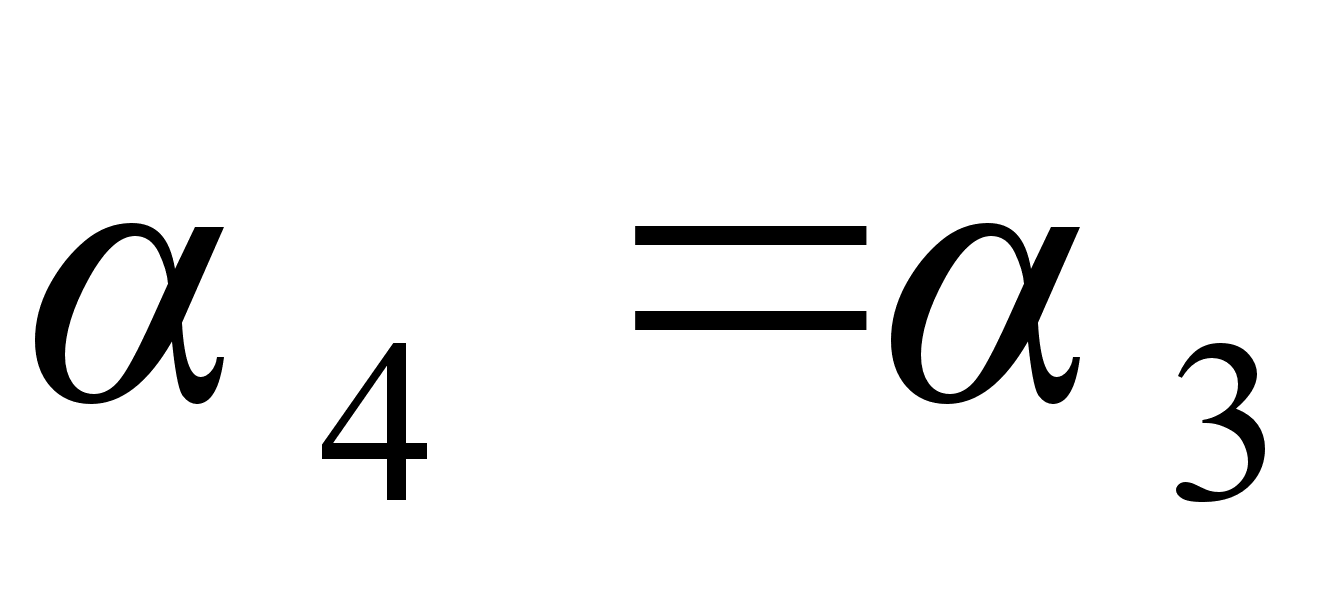 , вследствие чего, начиная с этого момента, неполные частные станут повторяться.
, вследствие чего, начиная с этого момента, неполные частные станут повторяться.
Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью.
Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае тАУ смешанной периодической.
Чисто периодическая дробь 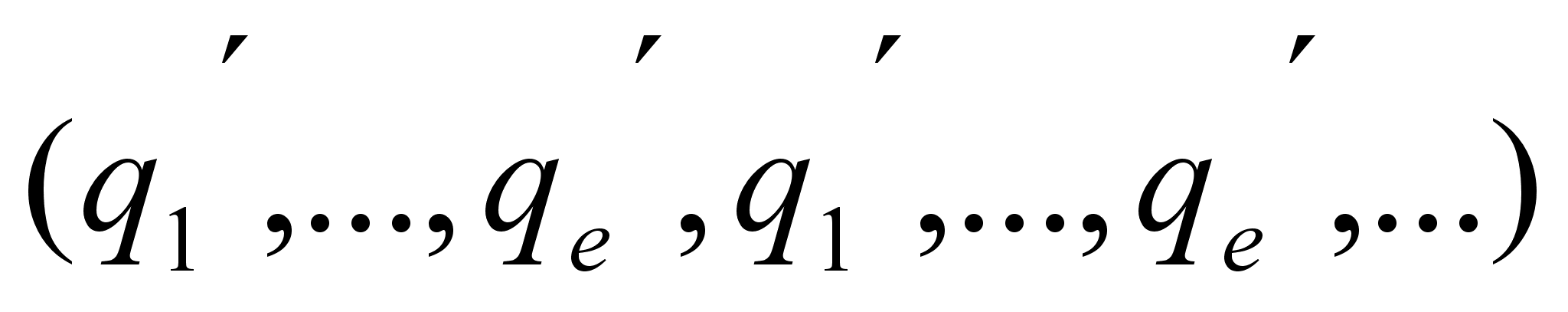 записывается в виде
записывается в виде  , а смешанная периодическая
, а смешанная периодическая 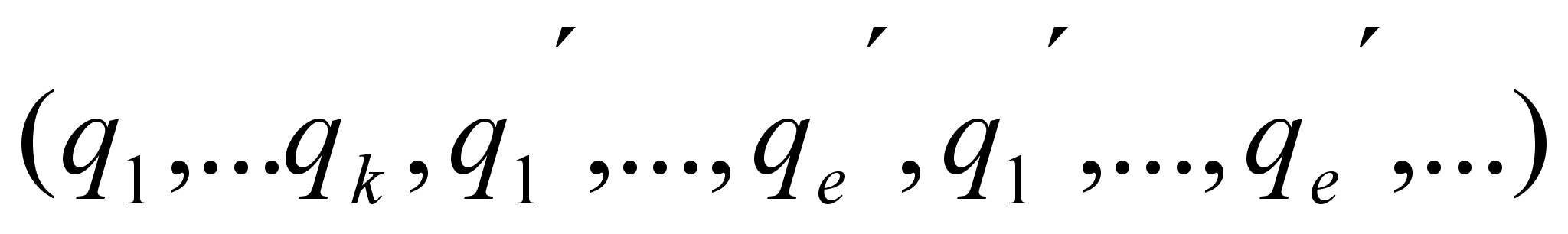 в виде
в виде 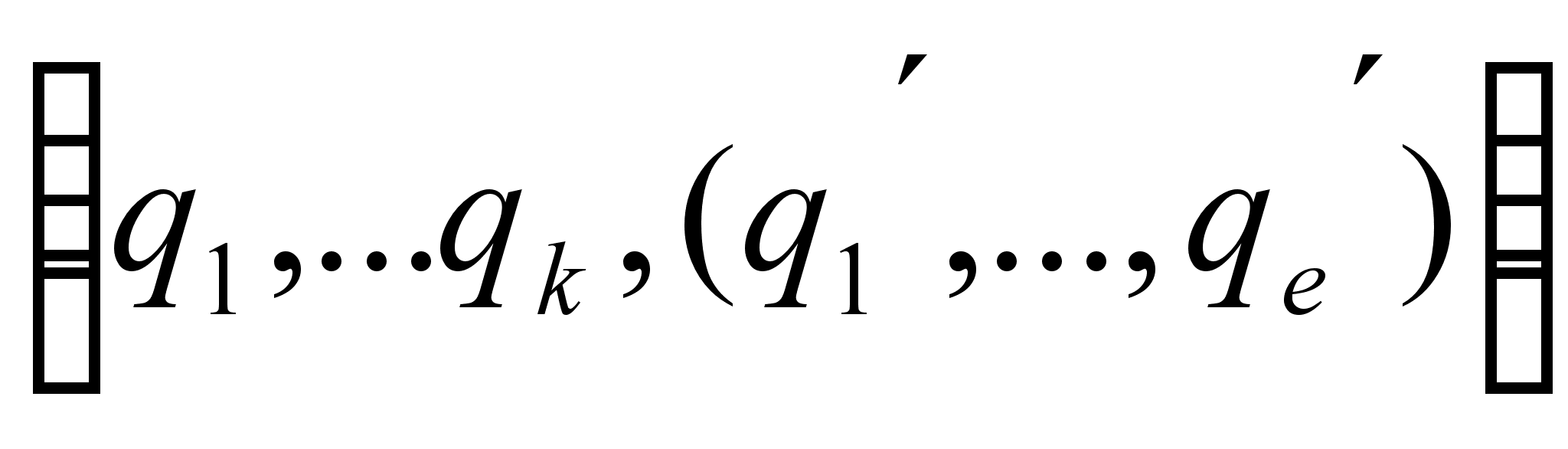 .
.
Итак, 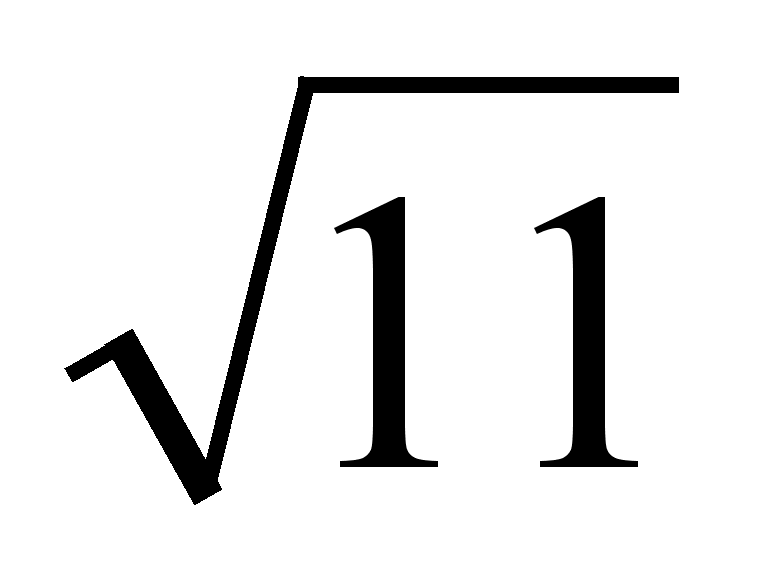 разлагается в смешанную периодическую дробь (3, 3, 6, 3, 6, тАж) или (3, (3, 6)).
разлагается в смешанную периодическую дробь (3, 3, 6, 3, 6, тАж) или (3, (3, 6)).
В общем случае разложения действительного иррационального числа  поступаем так же, как в примере. Останавливаясь при этом в процессе выделения целой части после kтАУго шага, будем иметь:
поступаем так же, как в примере. Останавливаясь при этом в процессе выделения целой части после kтАУго шага, будем иметь:
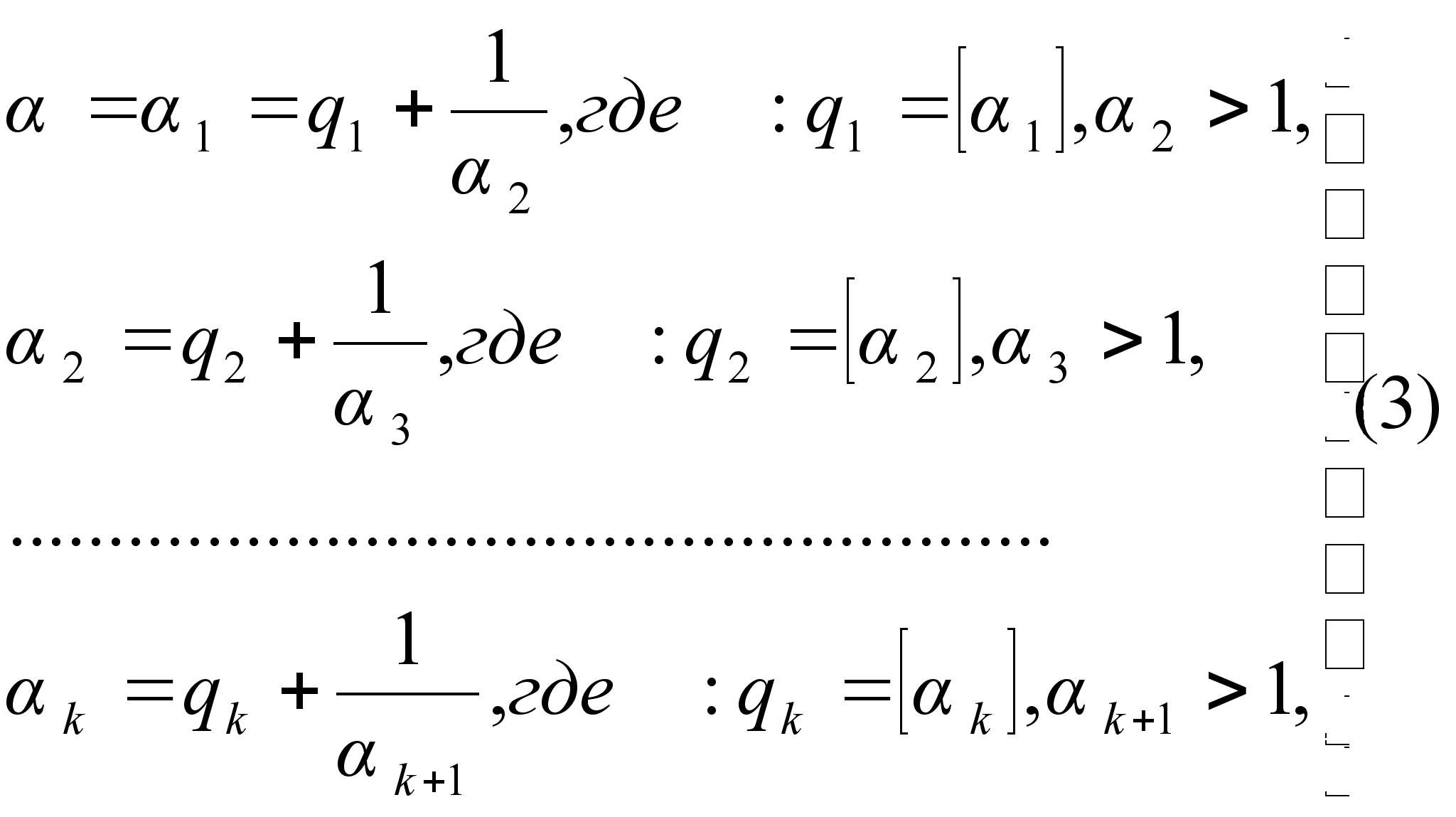
так что
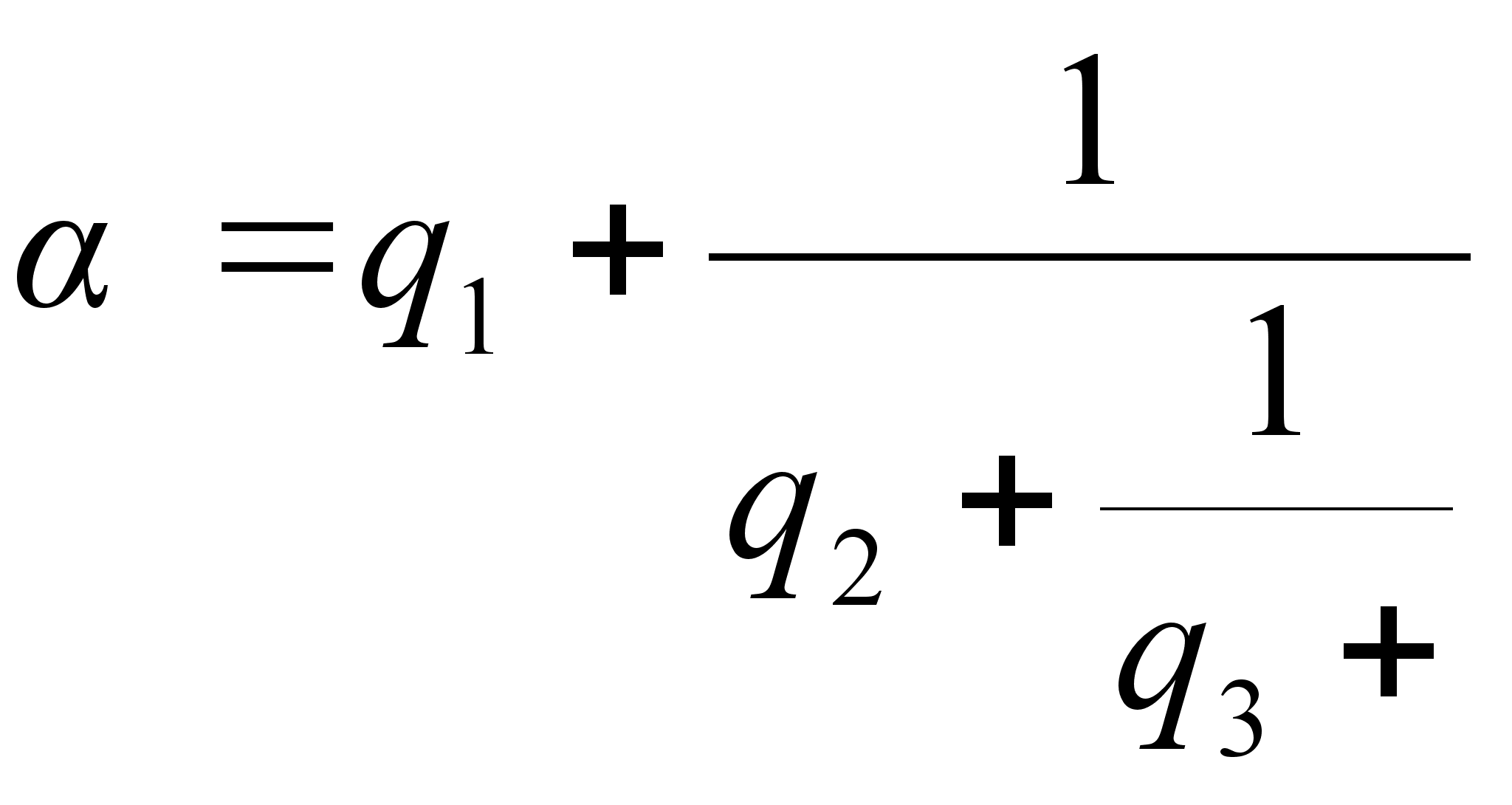

 .
.
Числа 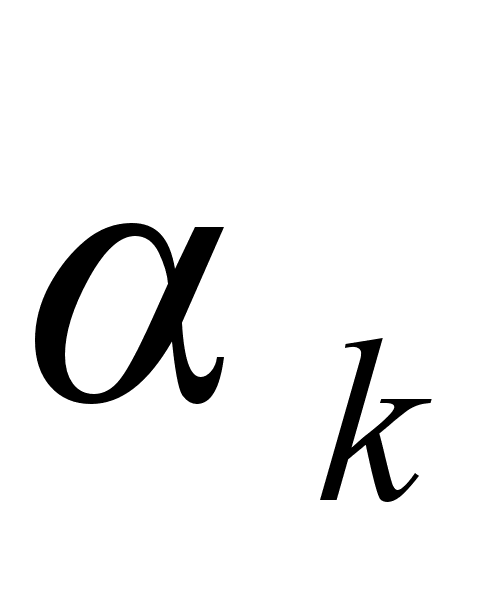 называются остаточными числами порядка k разложения
называются остаточными числами порядка k разложения  . В формуле (4) имеем кусок разложения до остаточного числа
. В формуле (4) имеем кусок разложения до остаточного числа 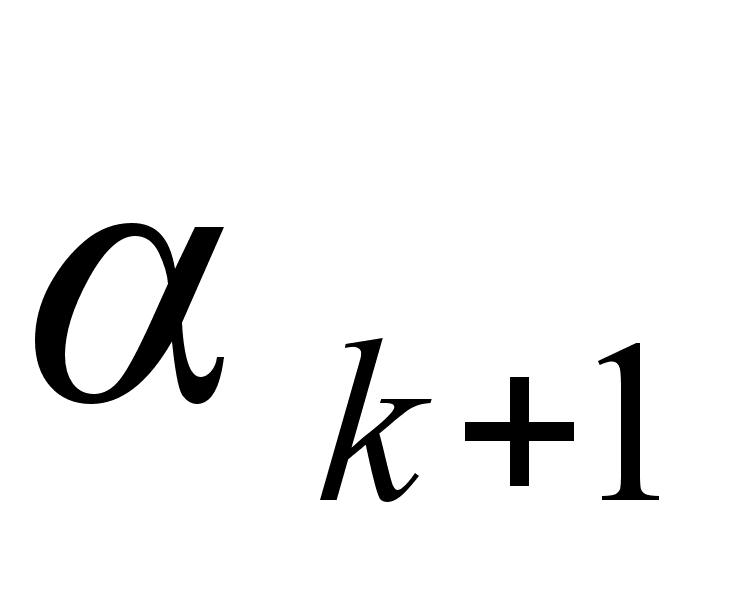 .
.
Для бесконечной цепной дроби (2) можно построить бесконечную последовательность конечных непрерывных дробей.
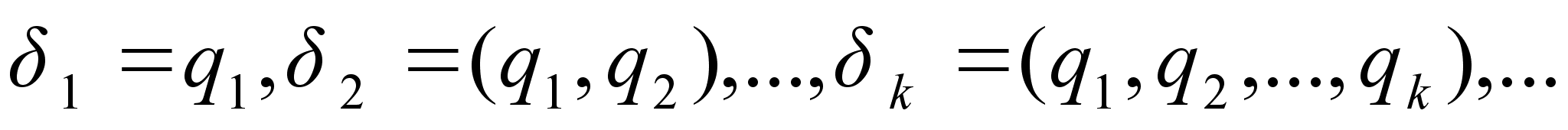
Эти дроби называют подходящими дробями. Закон образования соответствующих им простых дробей будет такой же, как и для подходящих дробей в случае конечных непрерывных дробей, так как этот закон зависит только от неполных частных 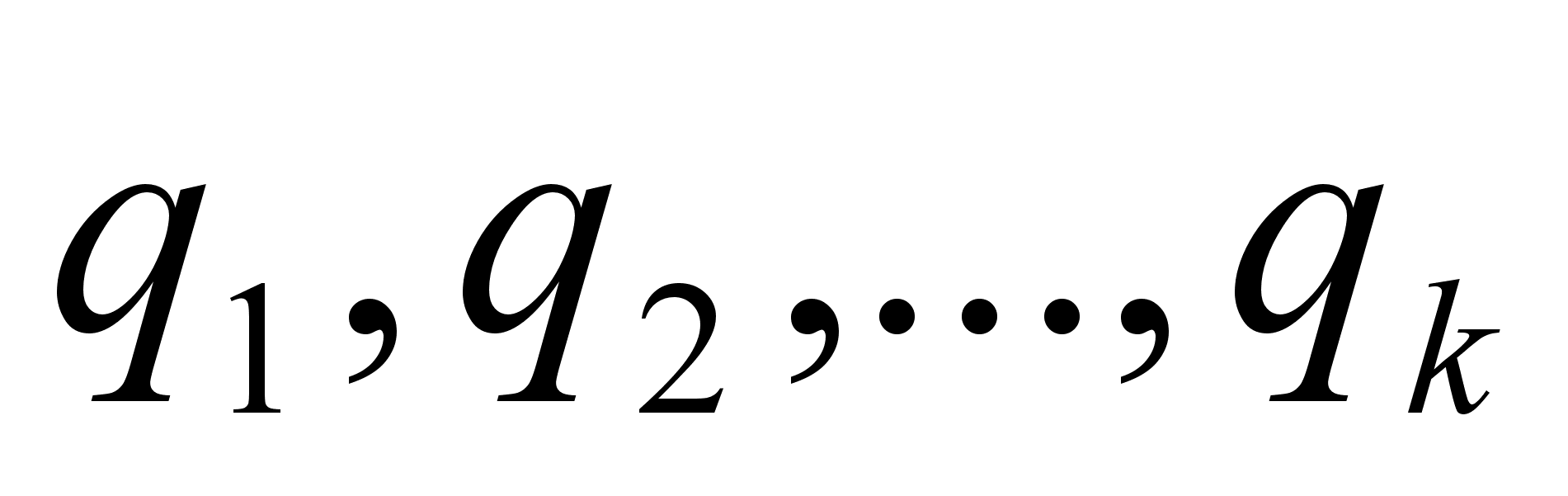 и совершенно не зависит от того, является ли
и совершенно не зависит от того, является ли 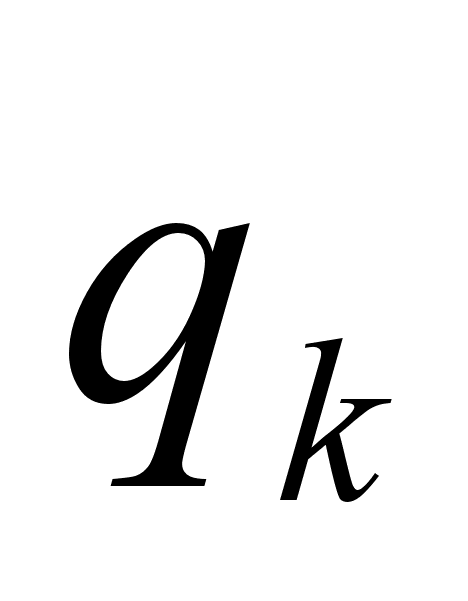 последним элементом или за ним следует еще элемент
последним элементом или за ним следует еще элемент 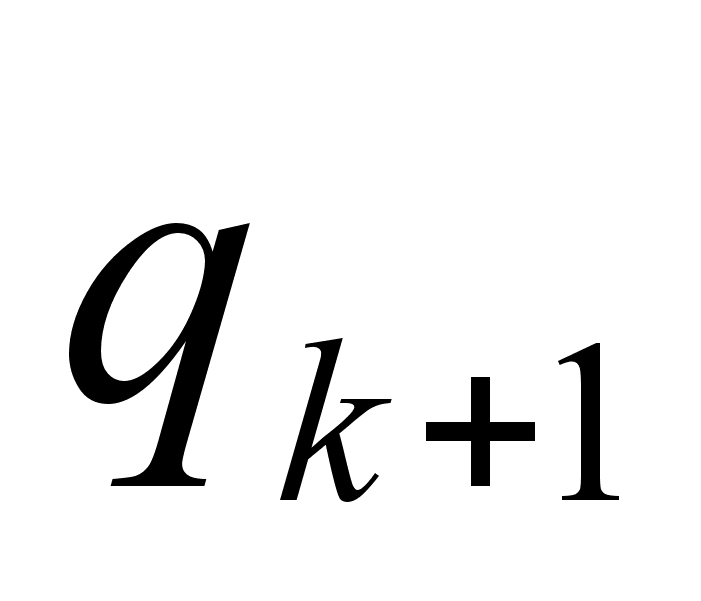 . Поэтому для них сохранятся также остальные свойства, которые выводятся из закона образования числителей и знаменателей подходящих дробей.
. Поэтому для них сохранятся также остальные свойства, которые выводятся из закона образования числителей и знаменателей подходящих дробей.
В частности, мы имеем:
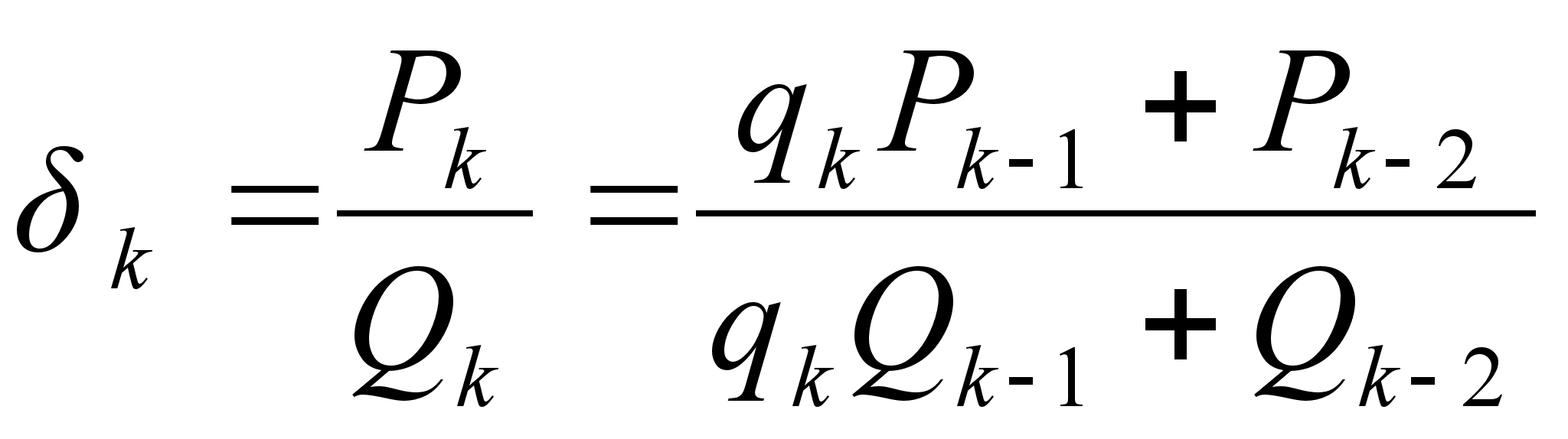 , причем
, причем 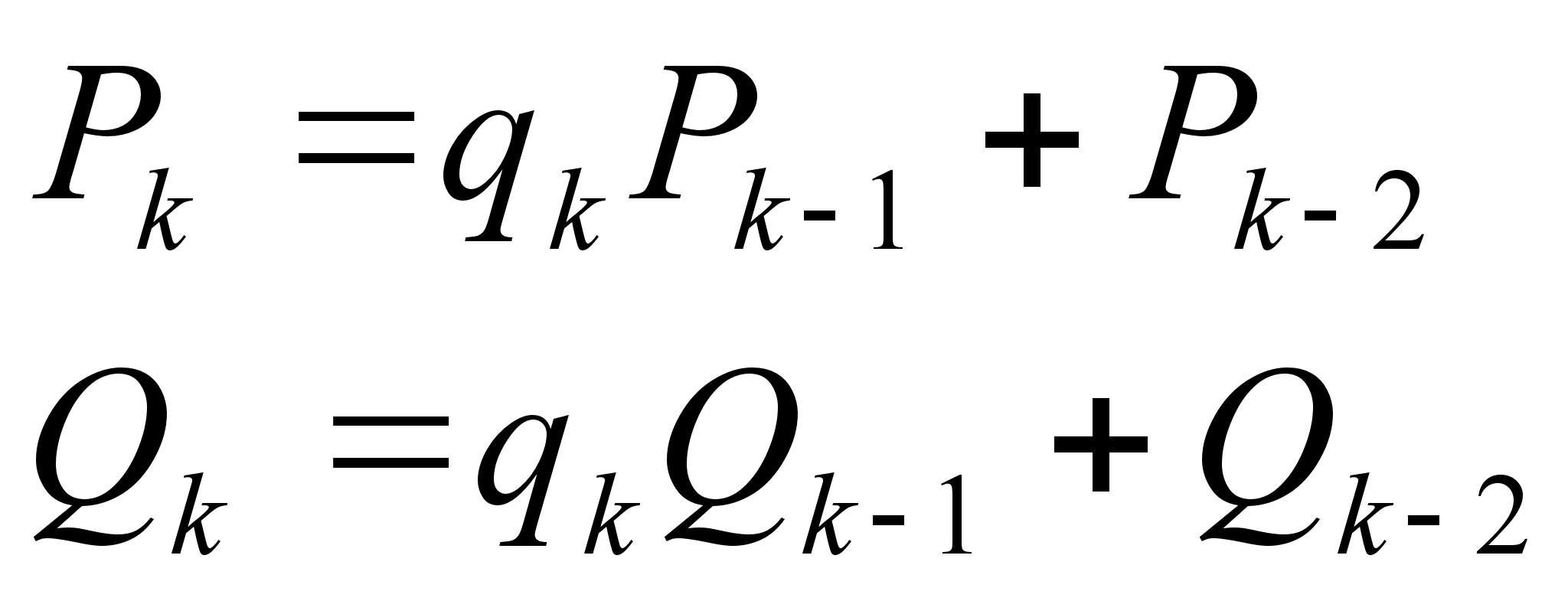 ;
;
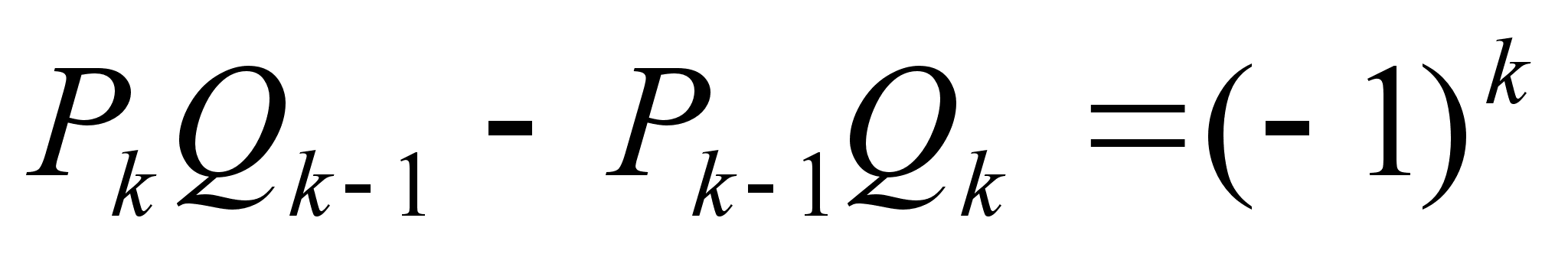 , откуда следует несократимость подходящих дробей
, откуда следует несократимость подходящих дробей 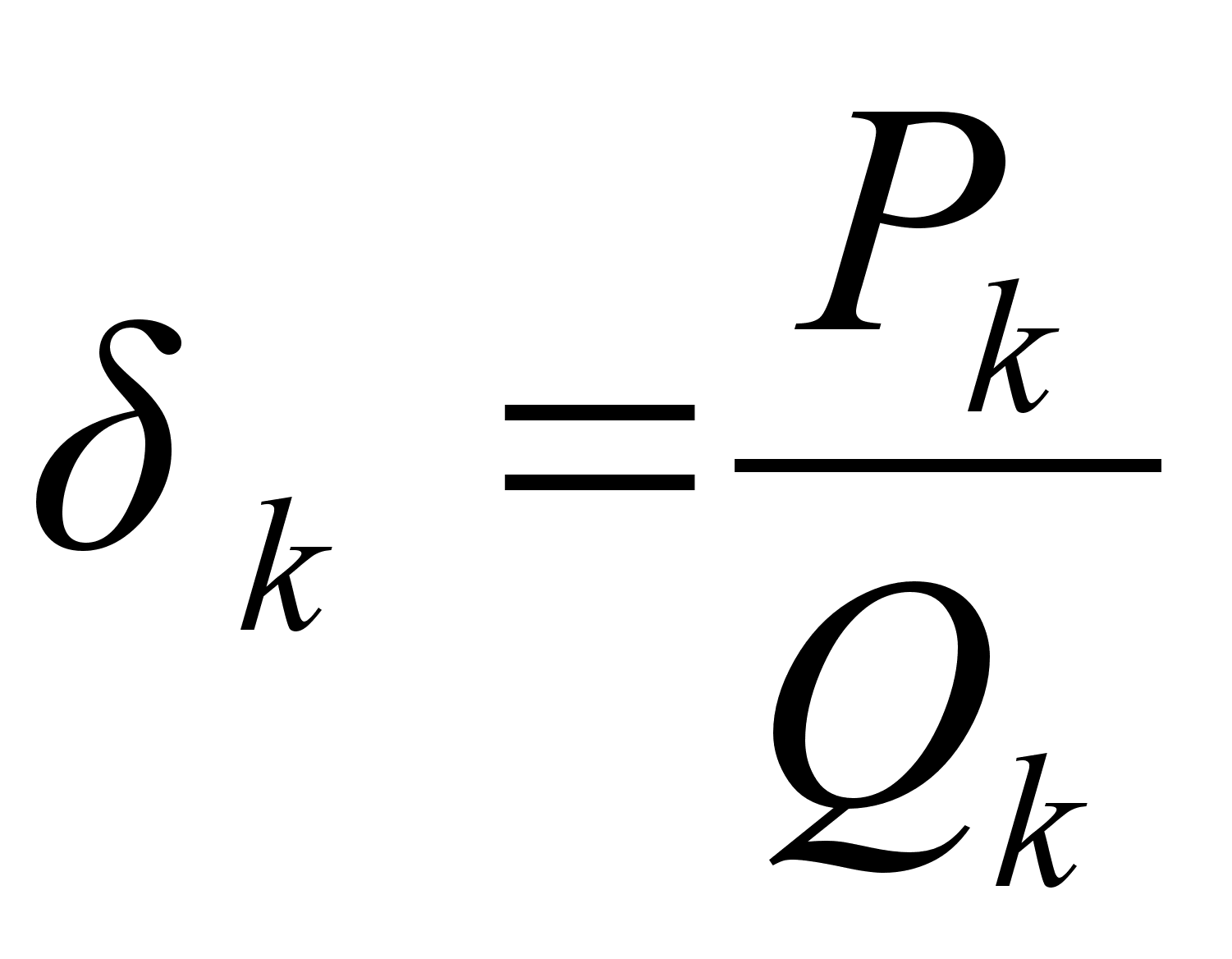 ;
;
 .
.
Сравним теперь подходящую дробь  и кусок разложения
и кусок разложения  до остаточного числа
до остаточного числа 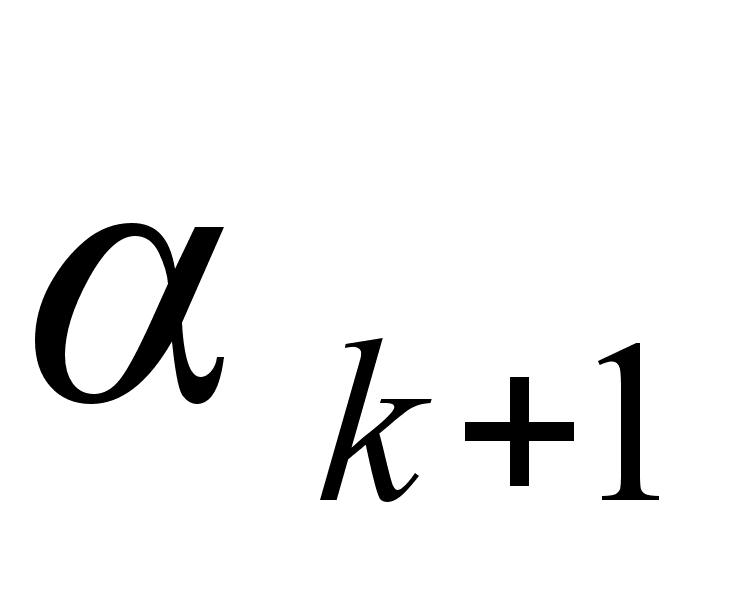 . Имеем
. Имеем
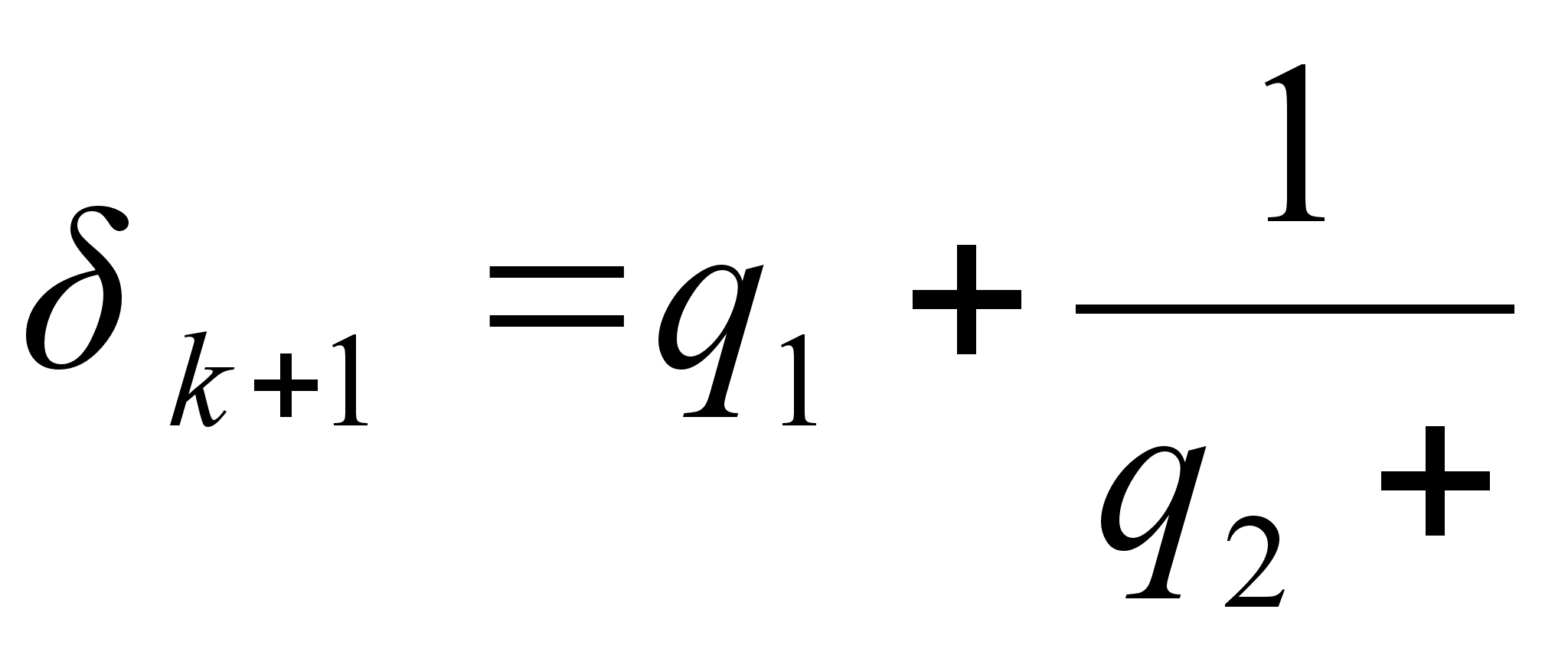
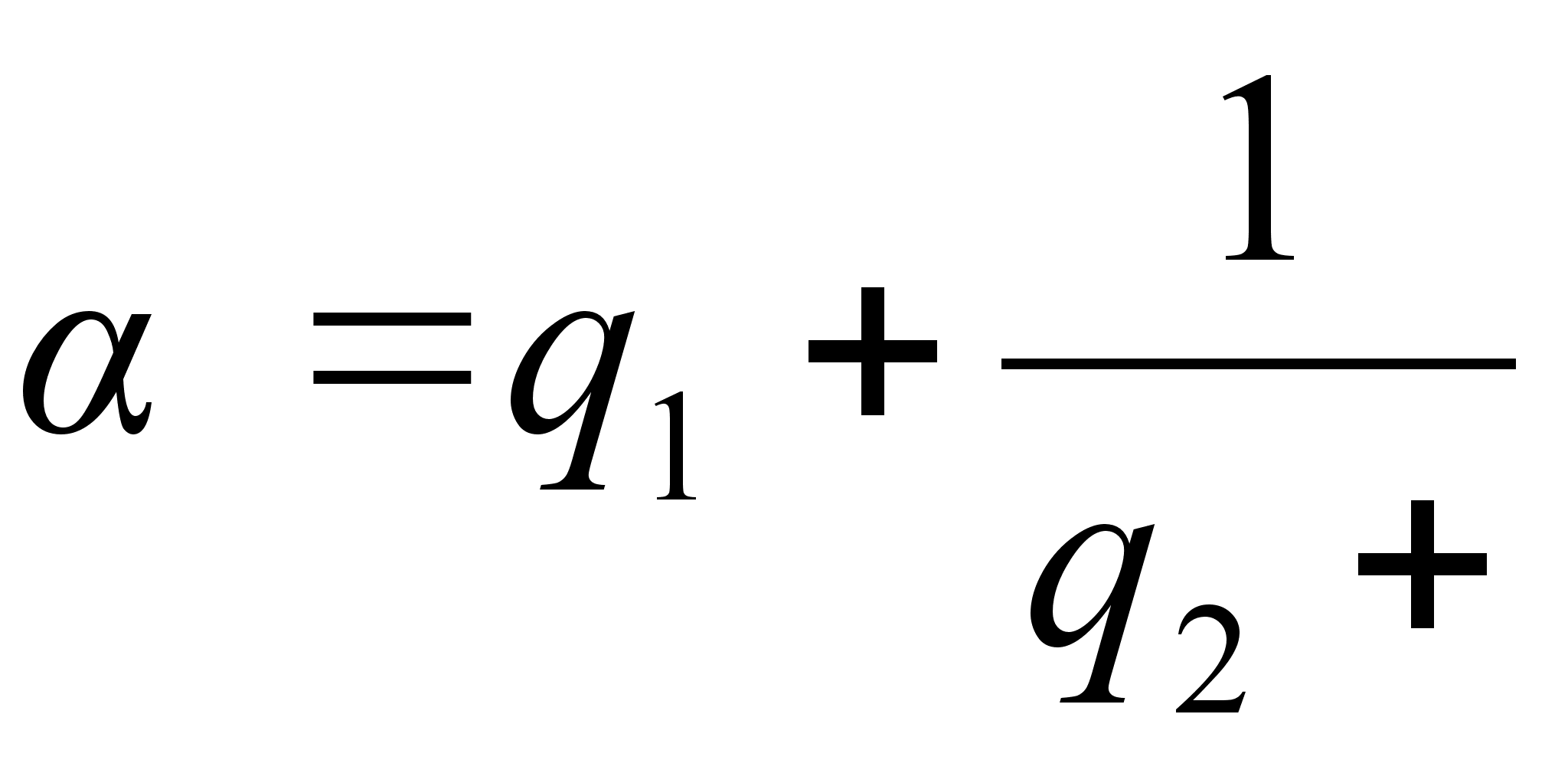


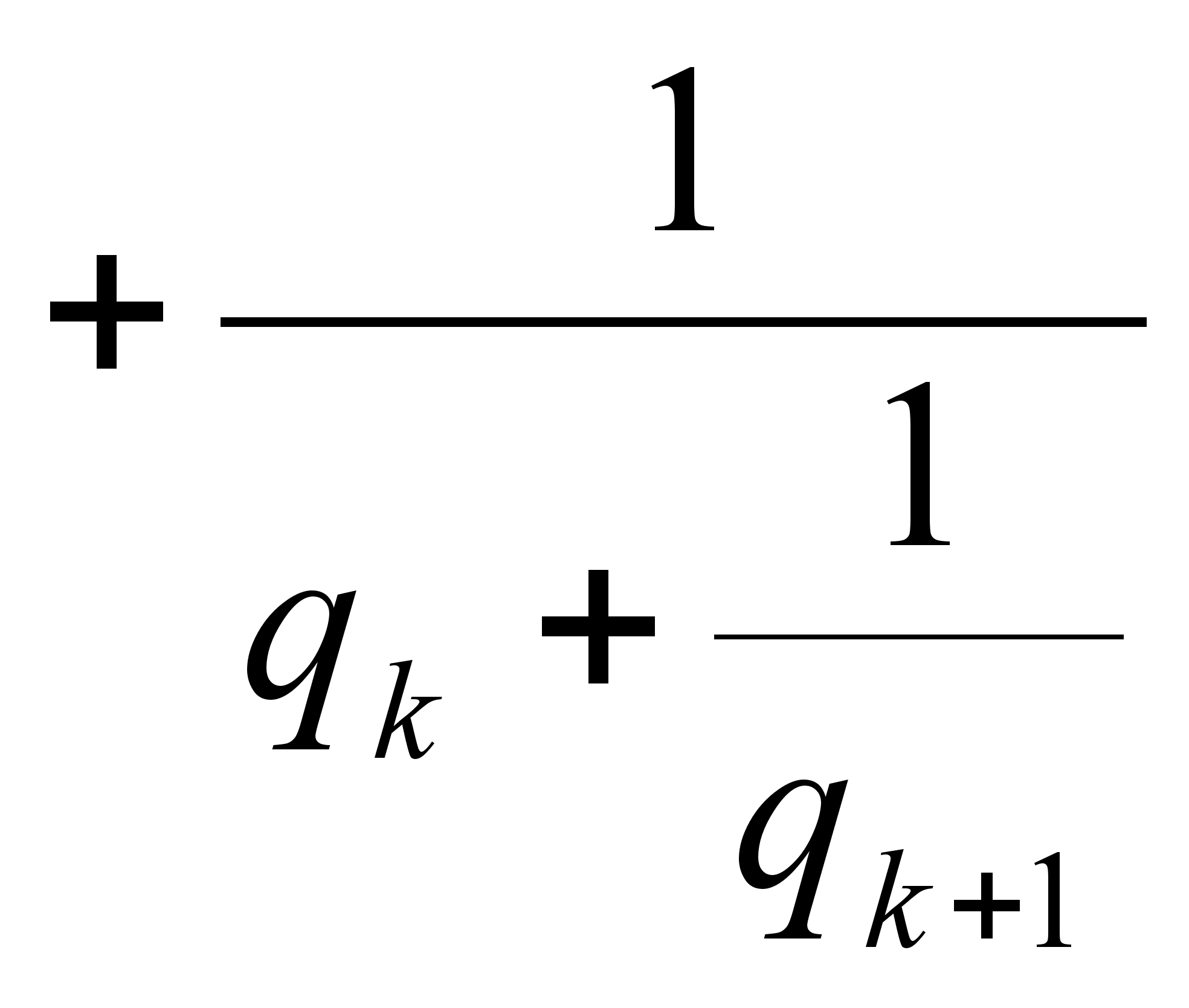
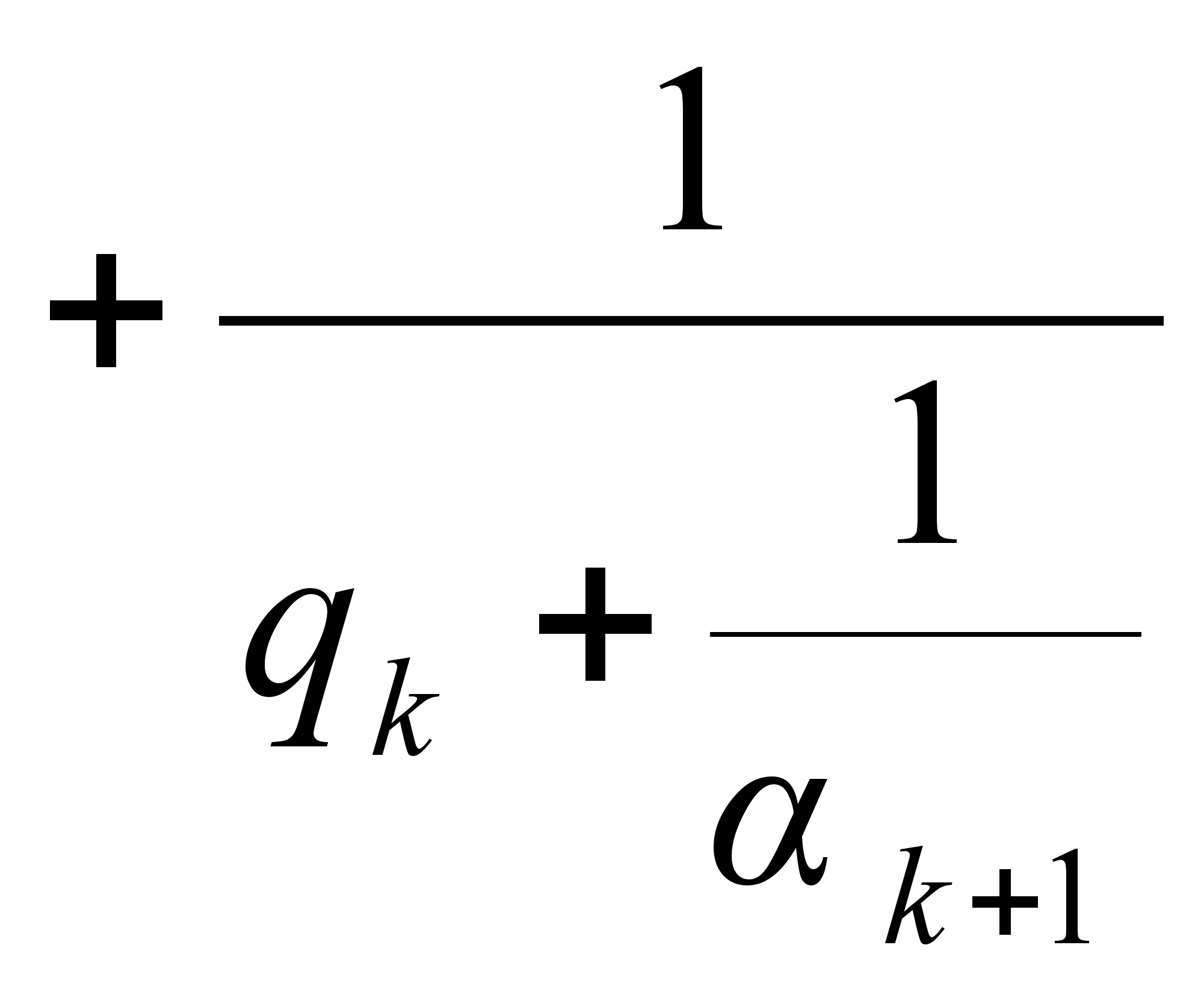 ,
,
откуда видно, что вычисление  по
по 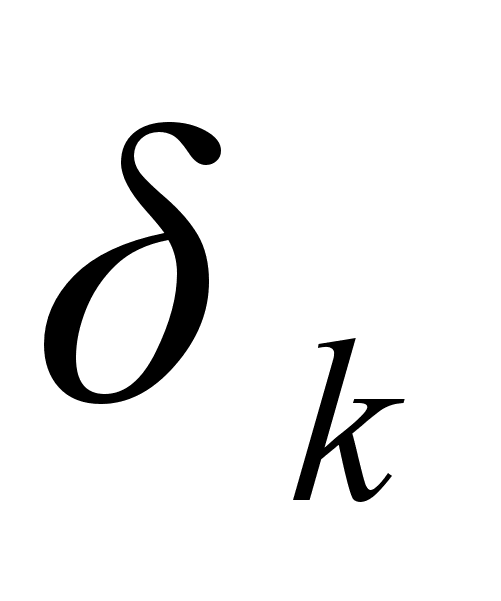 формально производится таким же образом, как вычисление
формально производится таким же образом, как вычисление  по
по 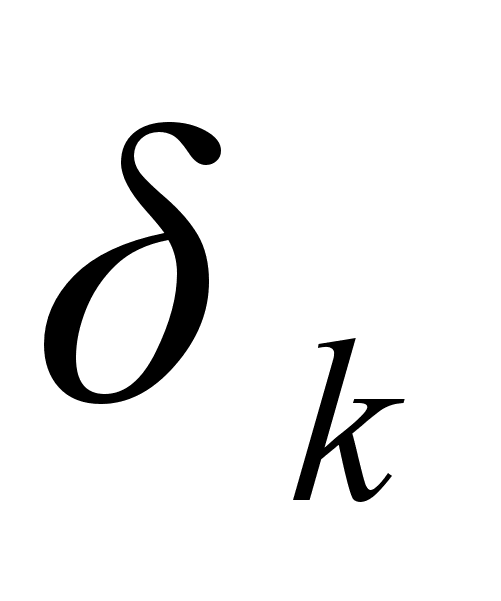 с тем лишь отличием, что в первом случае
с тем лишь отличием, что в первом случае 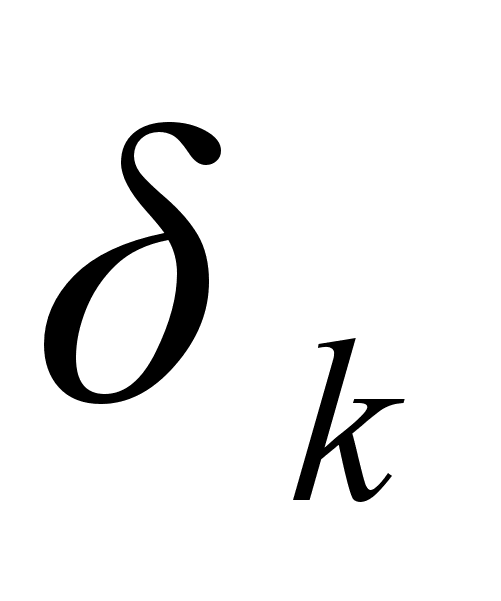 заменяется на
заменяется на 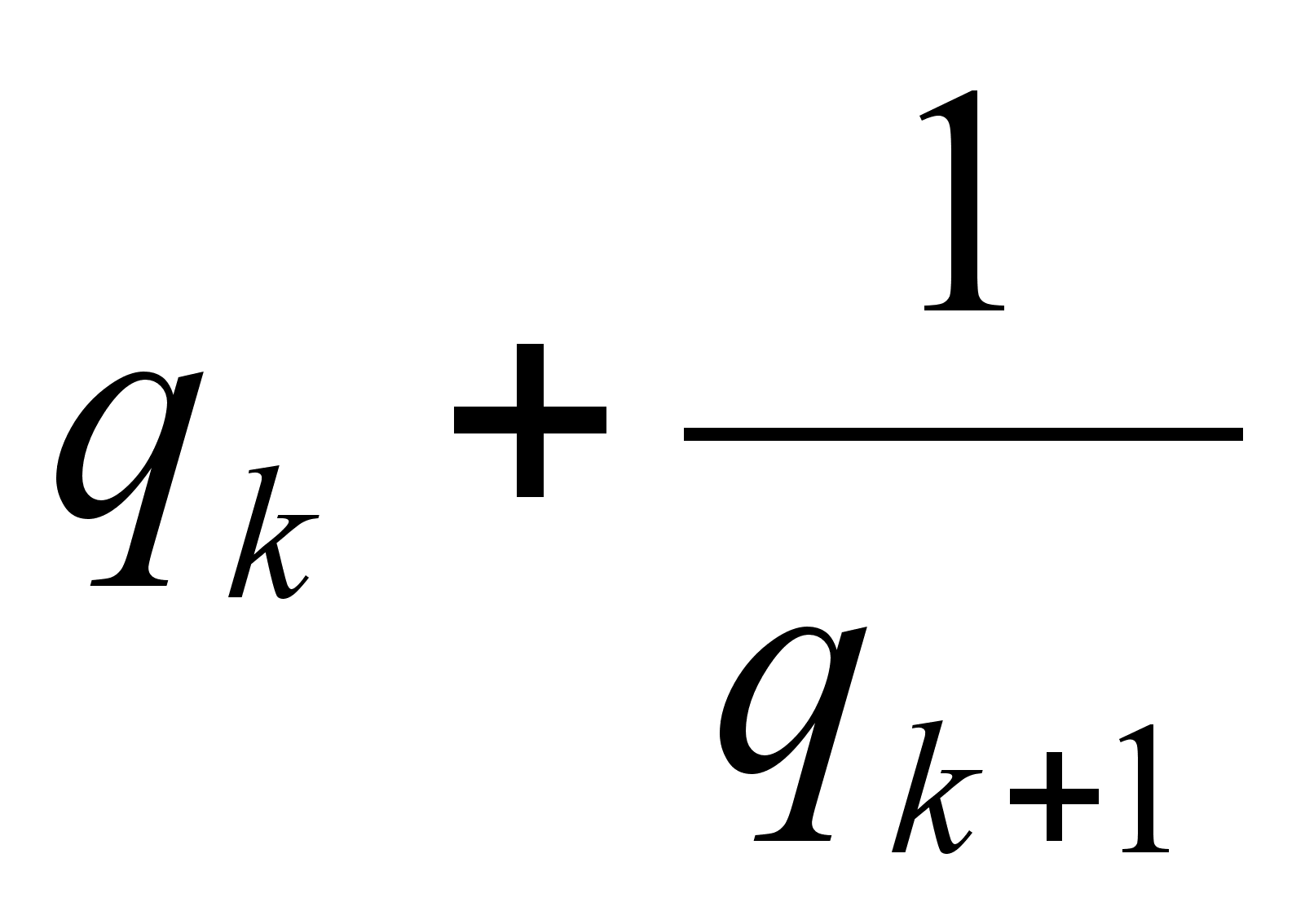 , а во втором
, а во втором 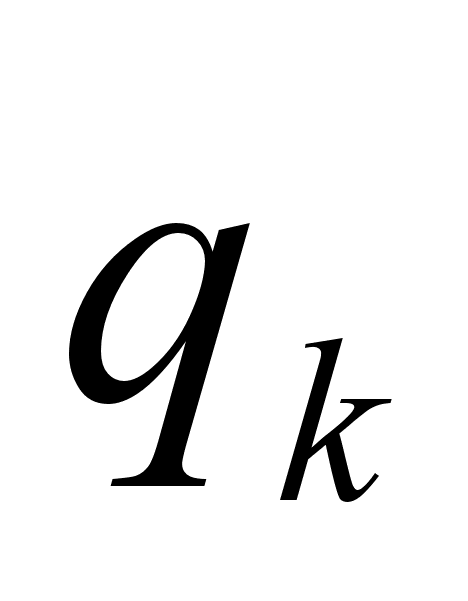 заменяется на
заменяется на 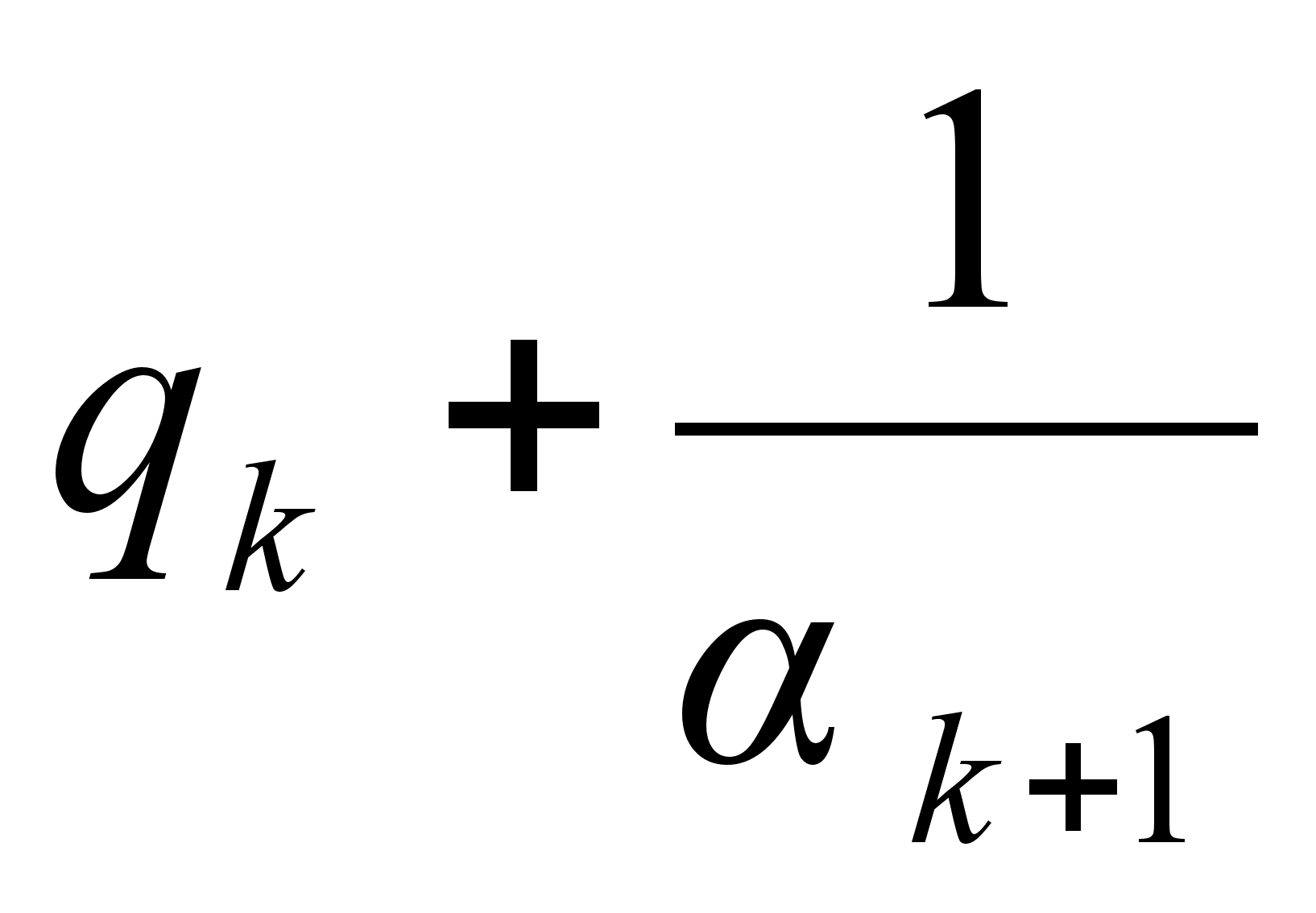 . Поэтому на основании формулы
. Поэтому на основании формулы  можно сделать вывод о справедливости следующего важного соотношения
можно сделать вывод о справедливости следующего важного соотношения
 . (5)
. (5)
По этой причине мы пишем также  , хотя
, хотя  не является здесь целым положительным числом.
не является здесь целым положительным числом.
При помощи формулы (5) можно вывести следующую теорему и расположении подходящих дробей разложения 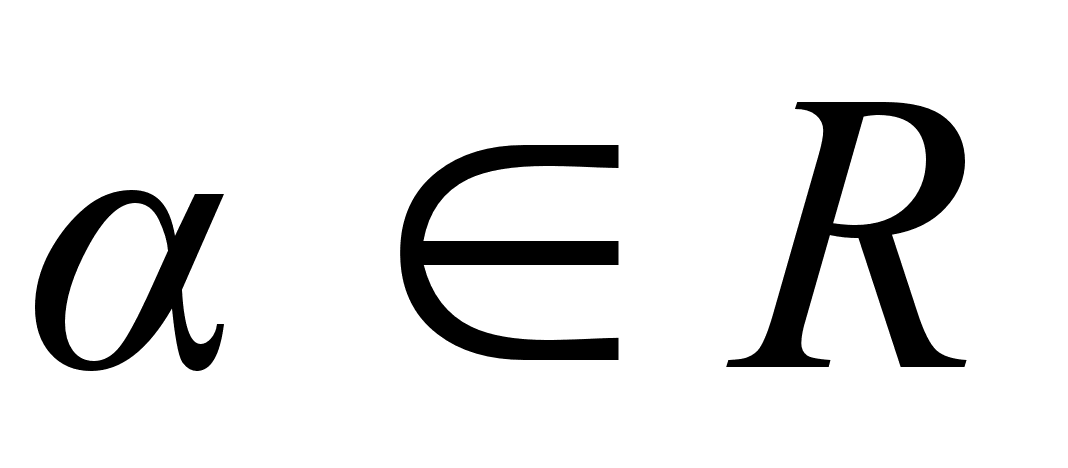 .
.
Теорема: Действительное число  всегда находится между двумя соседними подходящими дробями своего разложения, причем оно ближе к последующей, чем к предыдущей подходящей дроби.
всегда находится между двумя соседними подходящими дробями своего разложения, причем оно ближе к последующей, чем к предыдущей подходящей дроби.
Доказательство: Из формулы (5) следует

Но 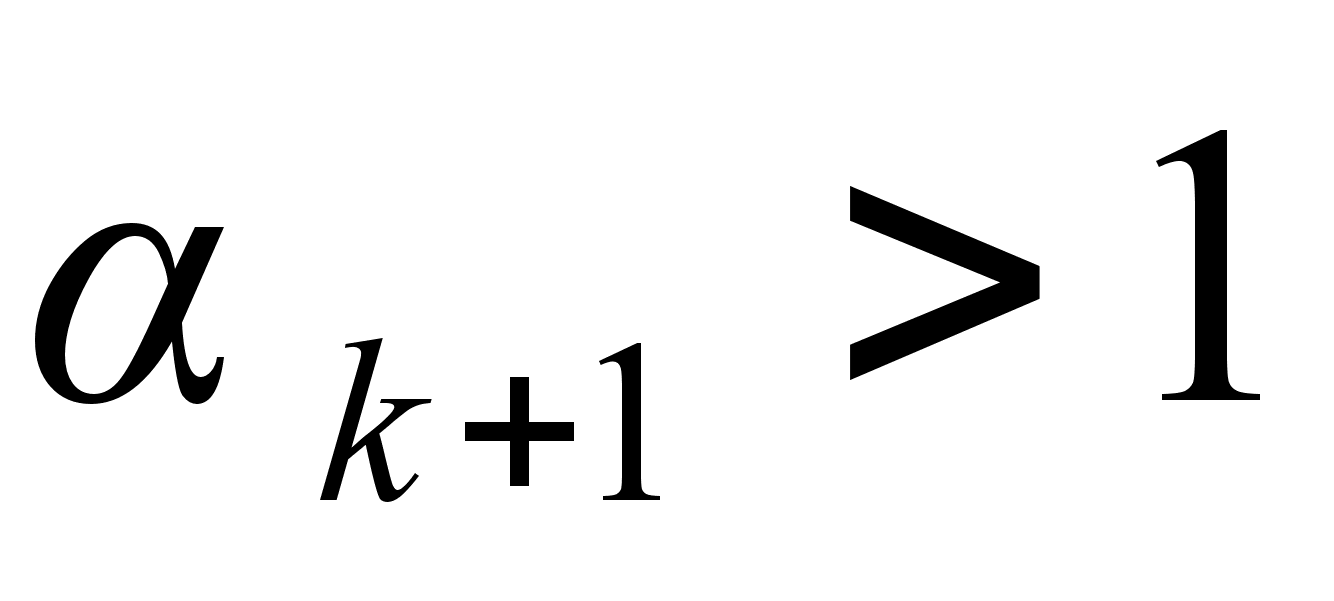 ,
, 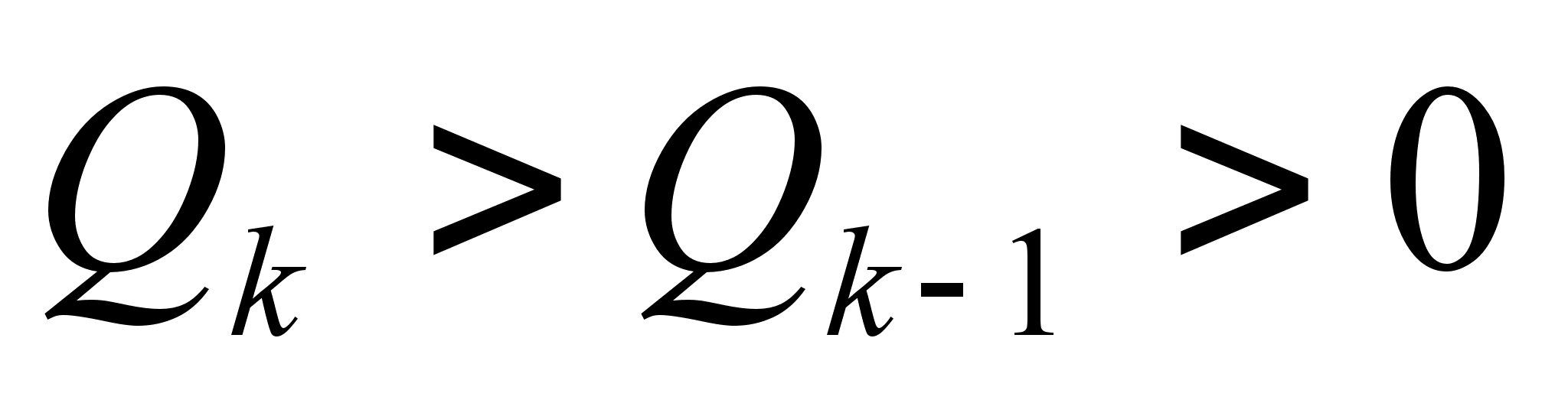 , так что
, так что 
(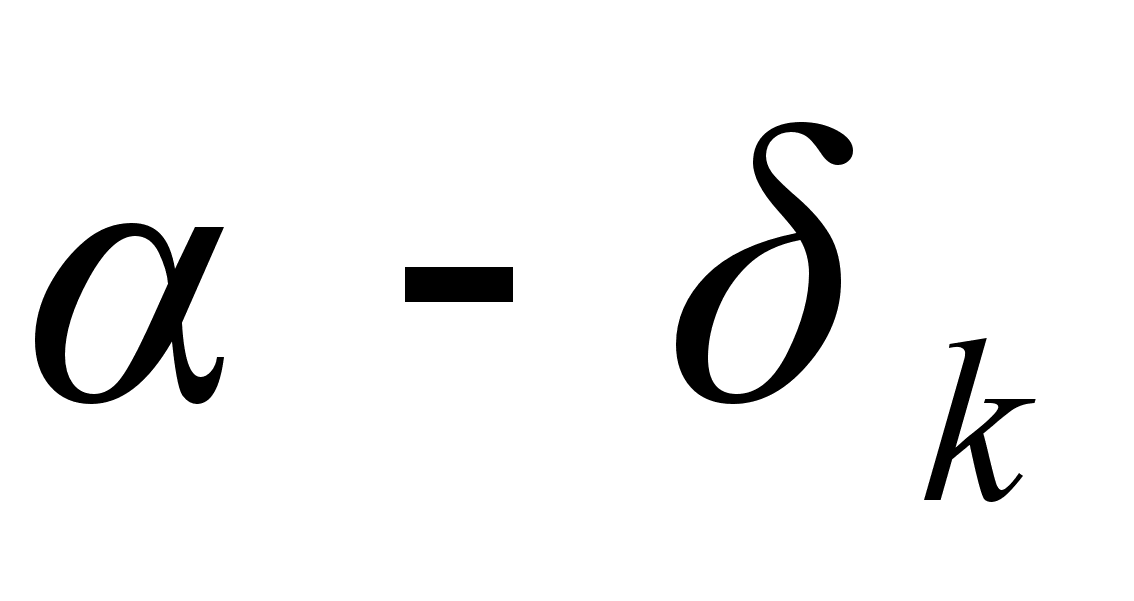 ) и (
) и (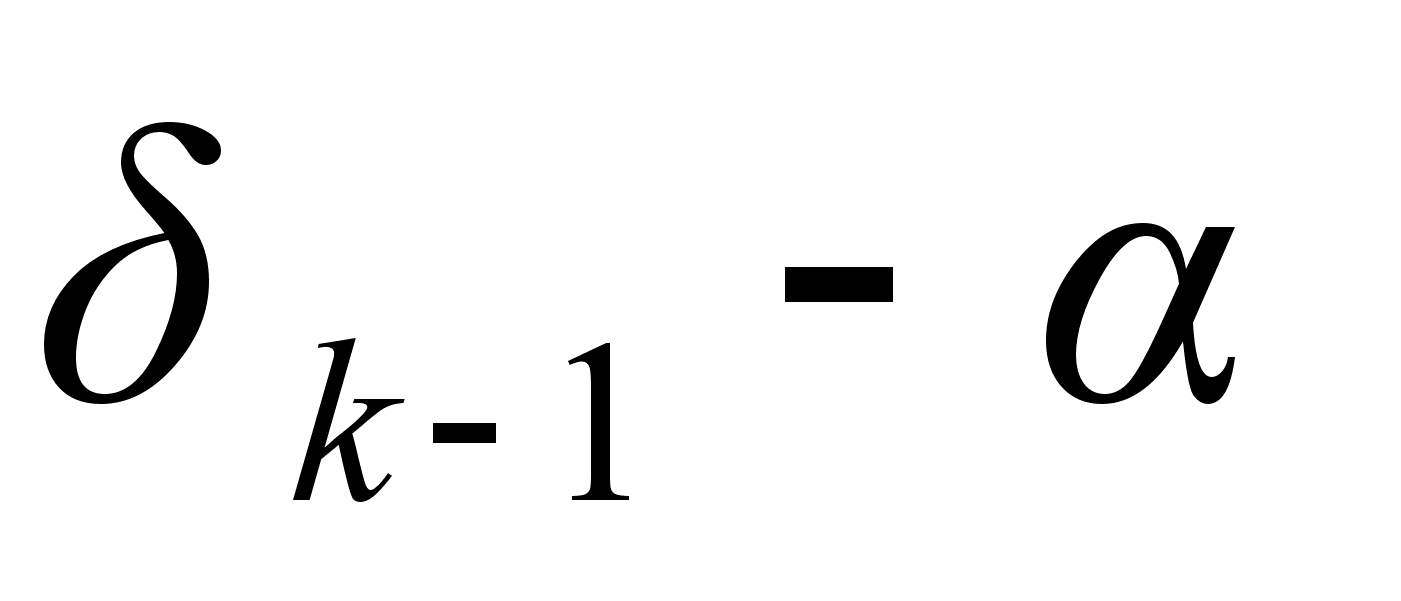 ) имеют одинаковый знак, а это значит, что
) имеют одинаковый знак, а это значит, что  находится между
находится между 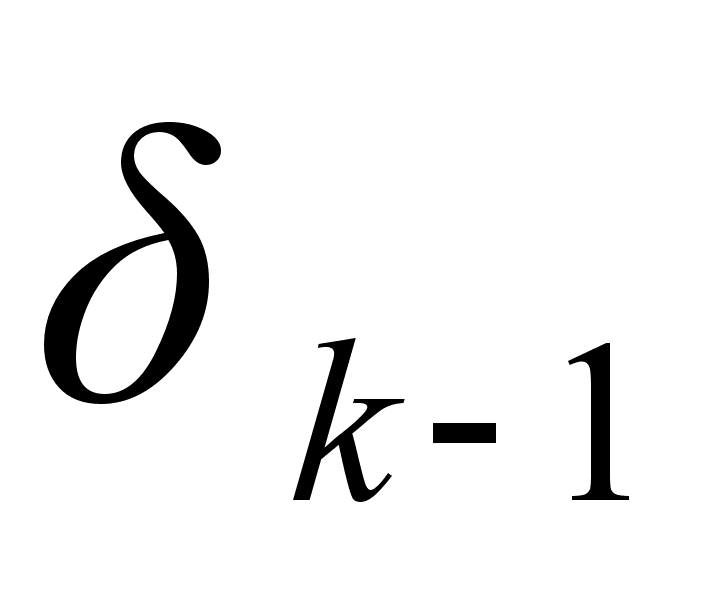 и
и 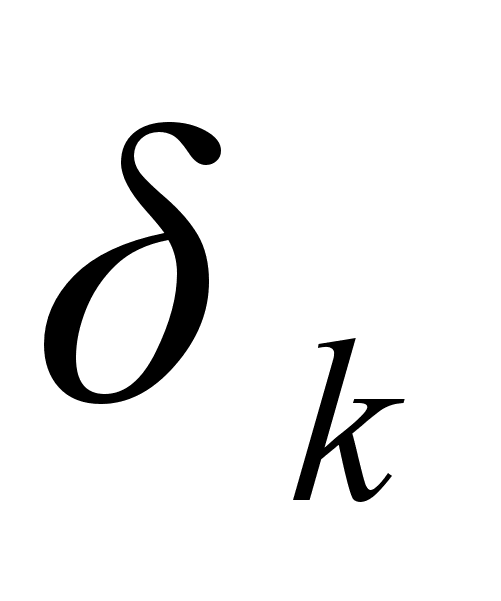 ;
;
 , то есть
, то есть  ближе к
ближе к 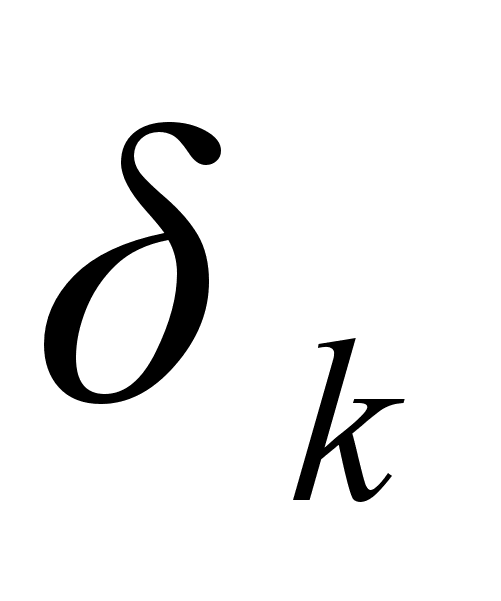 , чем к
, чем к 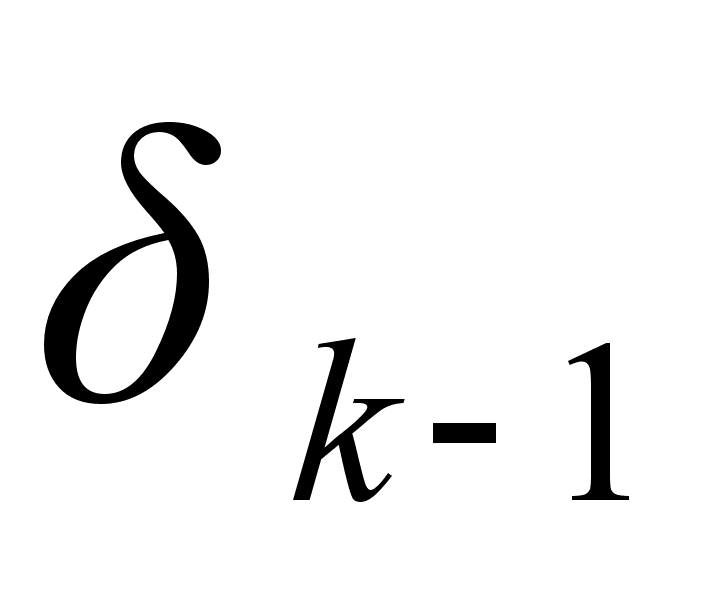 .
.
Теорема доказана.
Так как 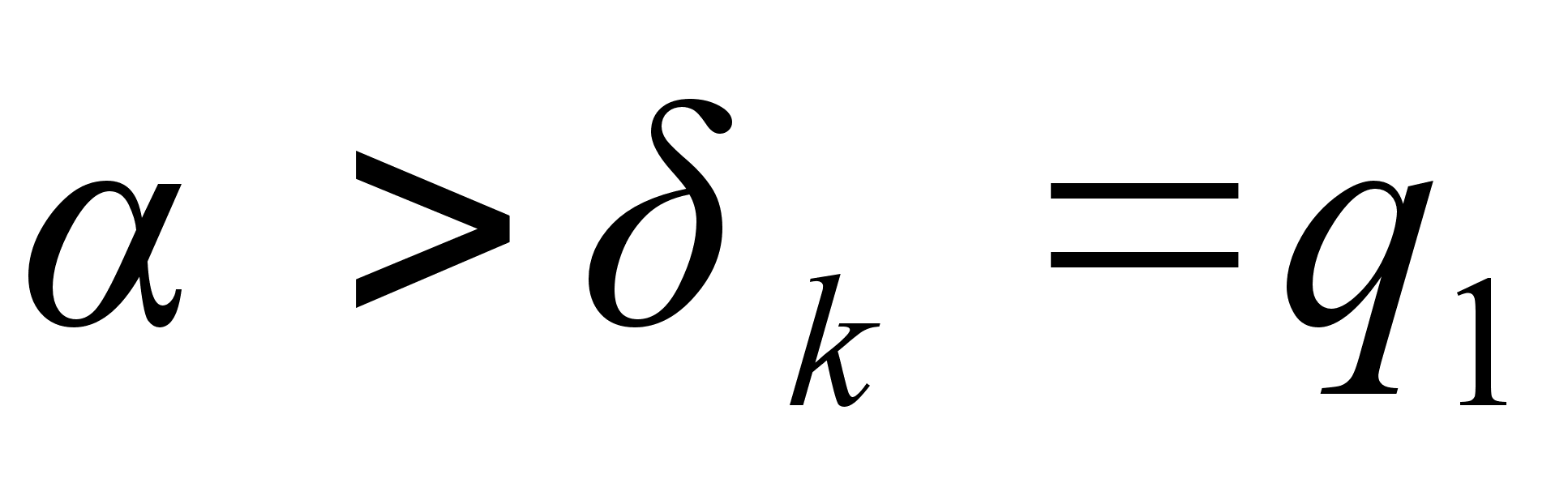 , то
, то 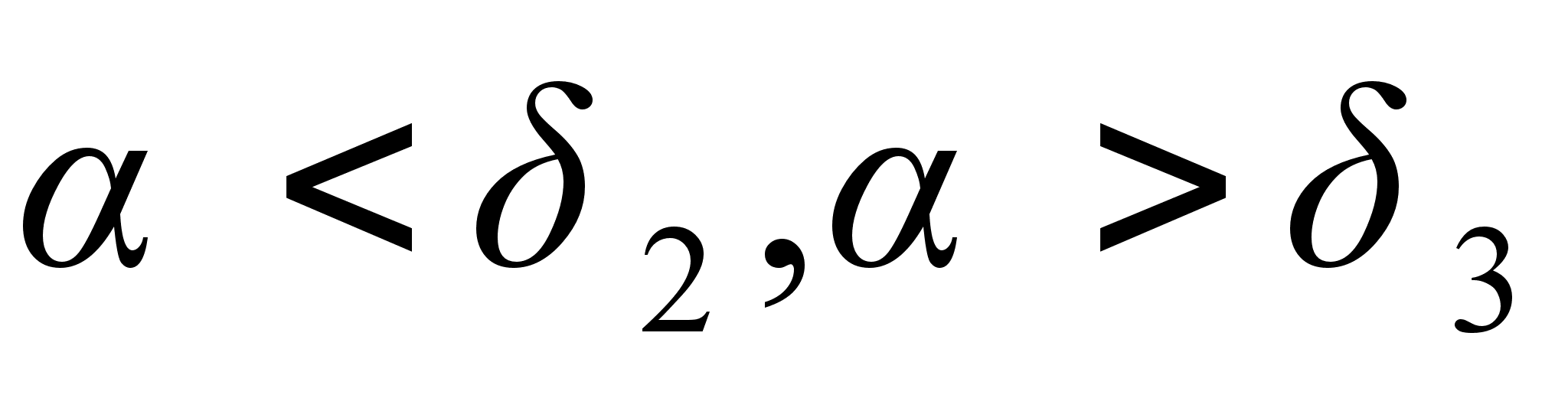 , и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
, и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
 больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка тАУ убывающую (в случае иррационального 
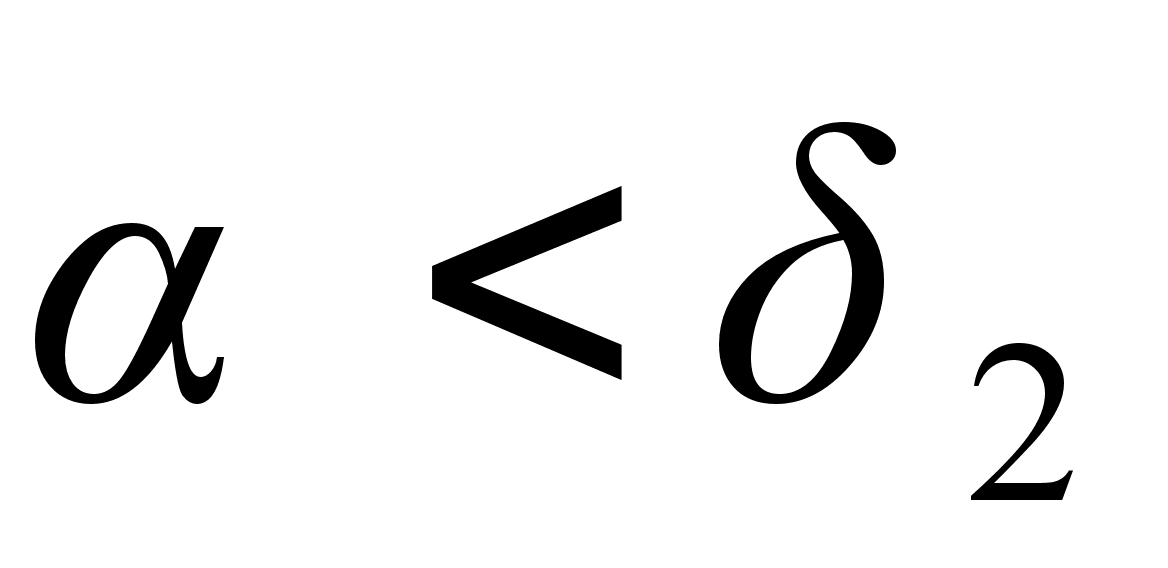
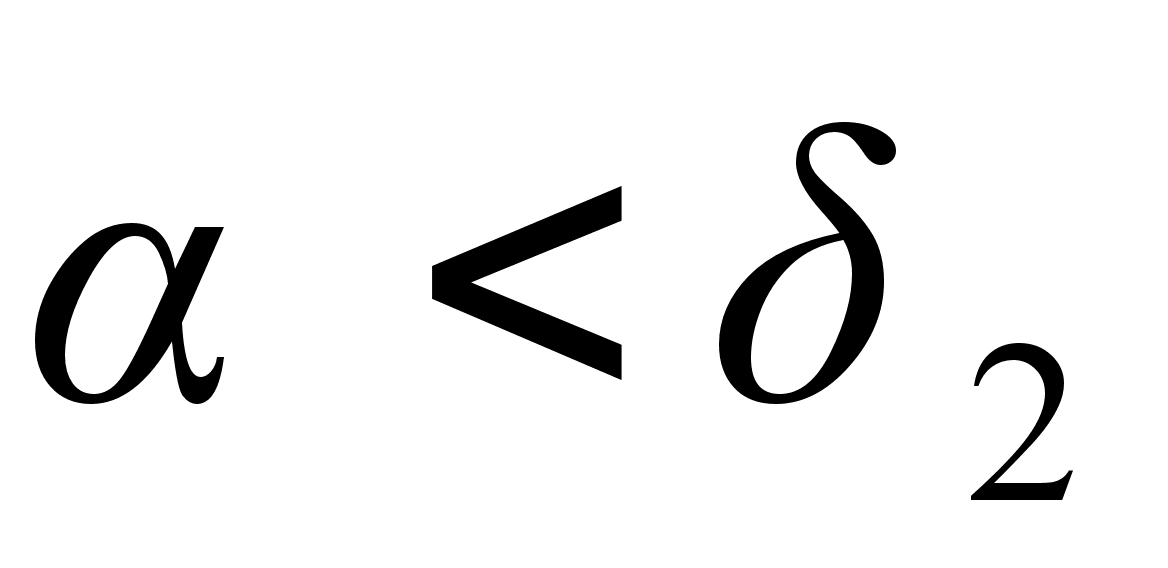
указанные последовательности являются бесконечными), то есть
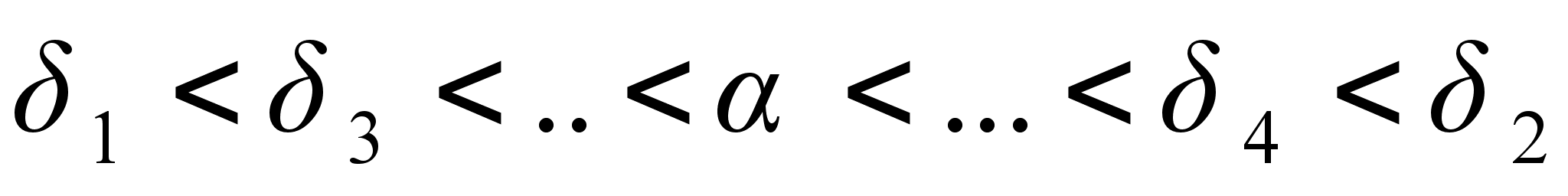
(в случае рационального 
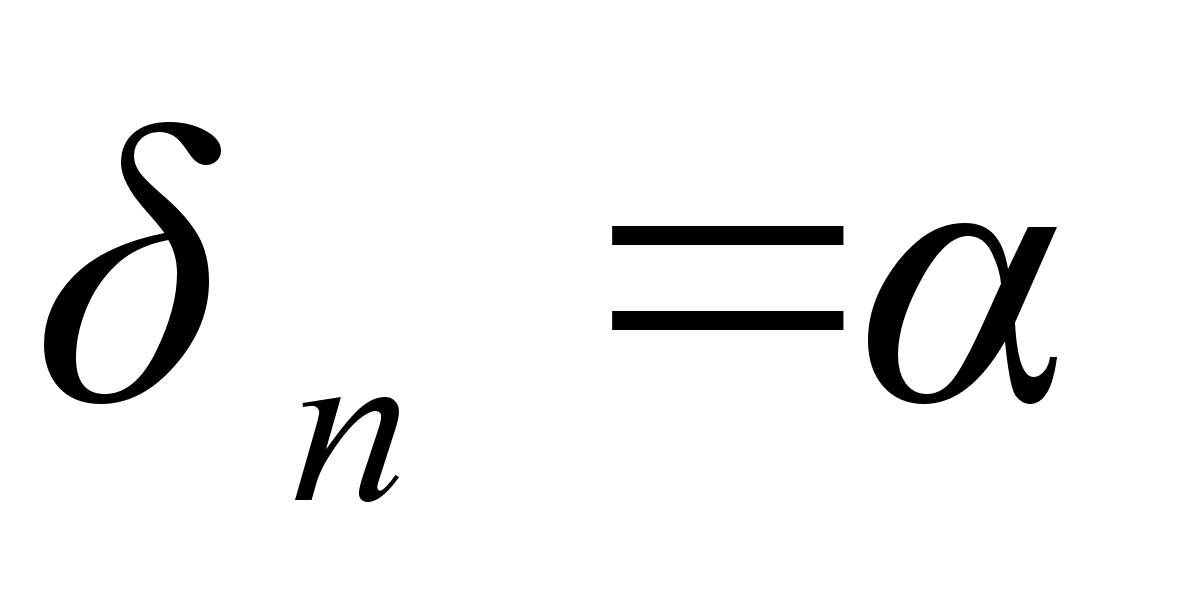 ).
).
тАФтАФтАФтАФ тАФтАФ
тАФтАФ тАФтАФтАФтАФ
тАФтАФтАФтАФ тАФтАФ
тАФтАФ тАФтАФтАФ
тАФтАФтАФ тАФтАФтАФтАФ
тАФтАФтАФтАФ
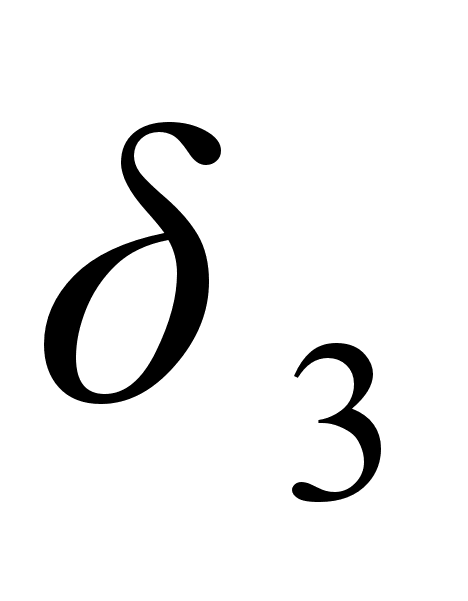

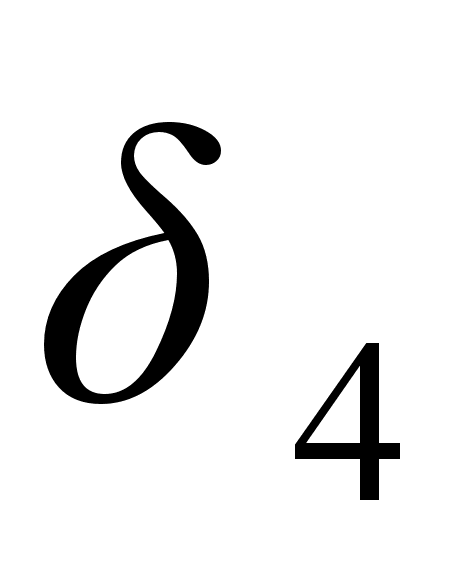
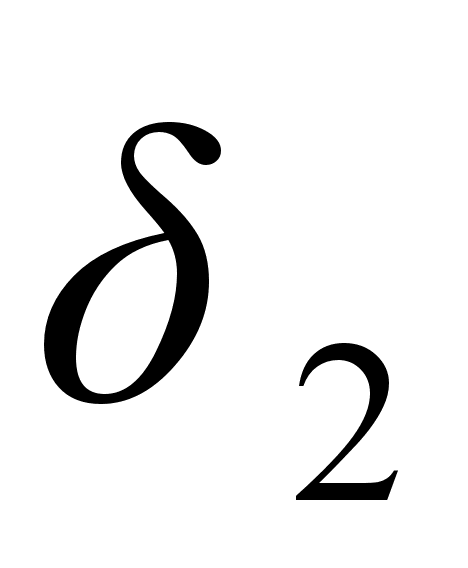
Учитывая то, что при 
 , вследствие чего
, вследствие чего 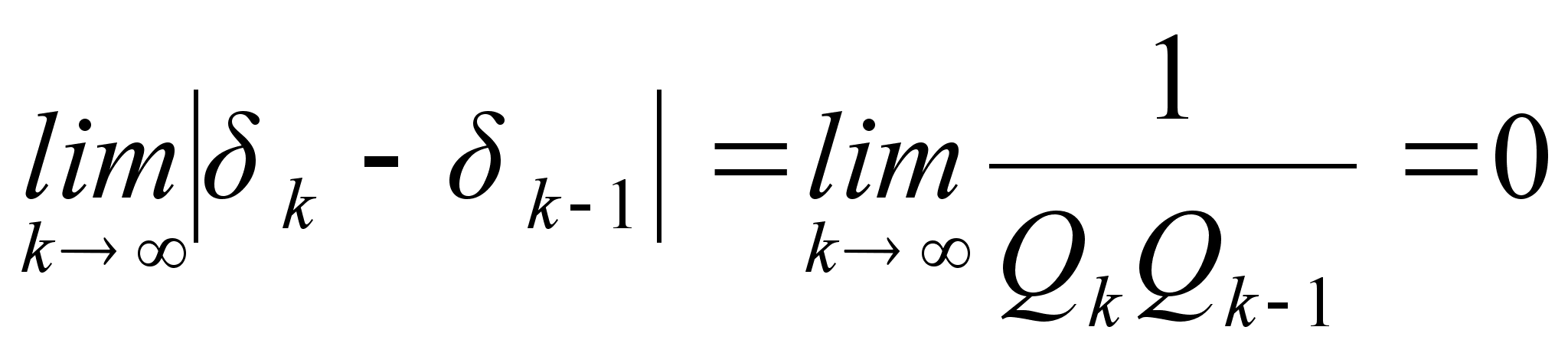 , переходим к дальнейшему выводу, что в случае иррационального
, переходим к дальнейшему выводу, что в случае иррационального  сегменты
сегменты 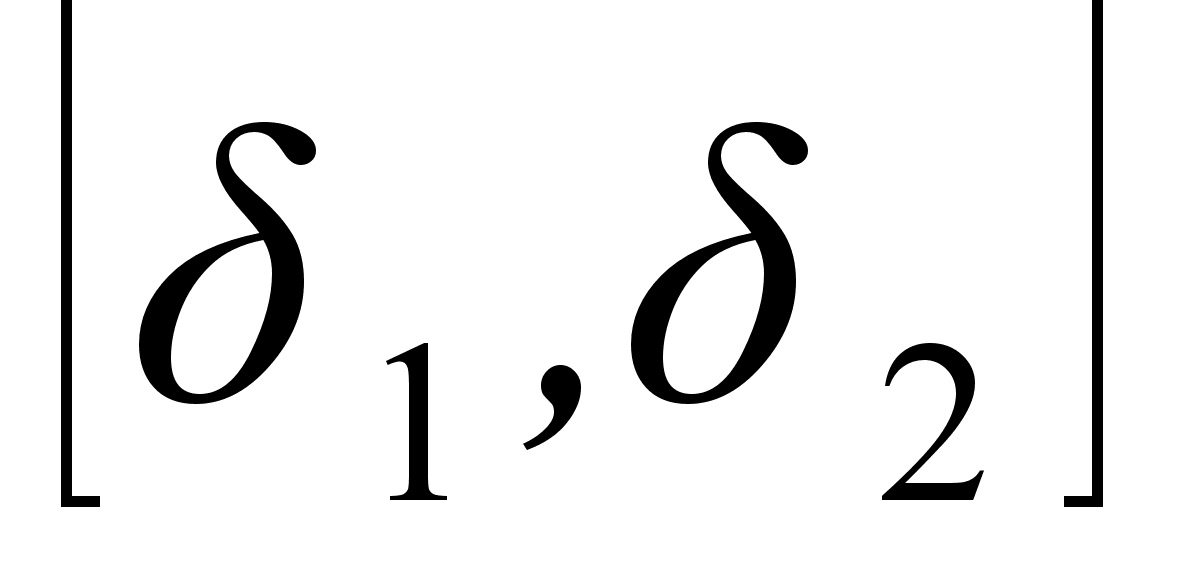 ,
, 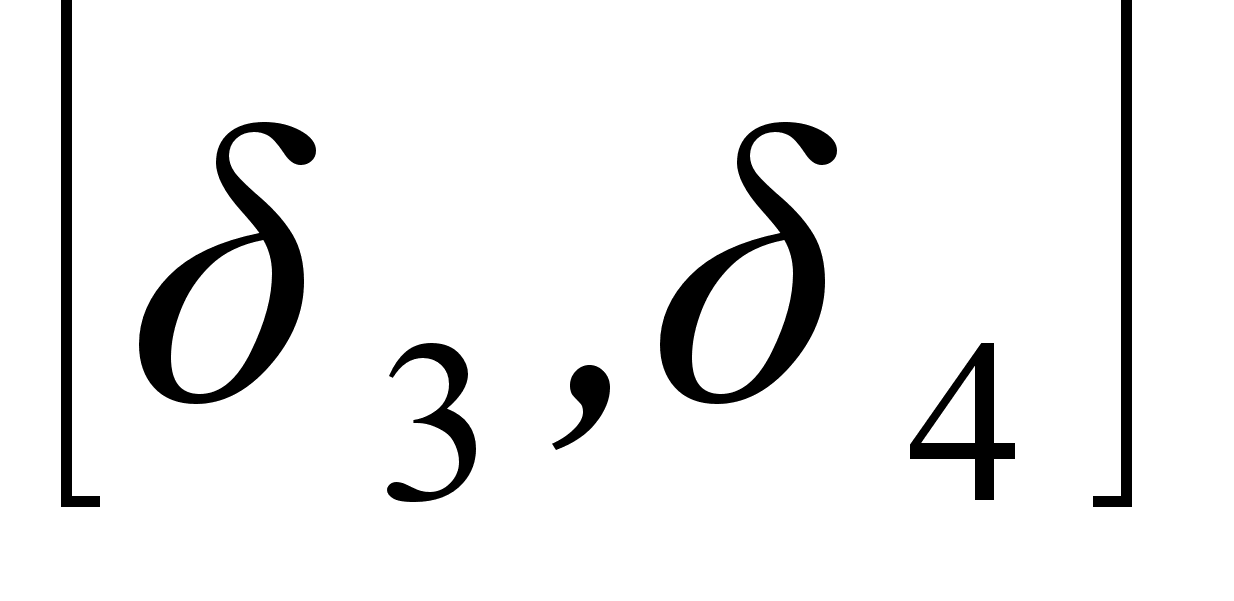 , тАж образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей
, тАж образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей 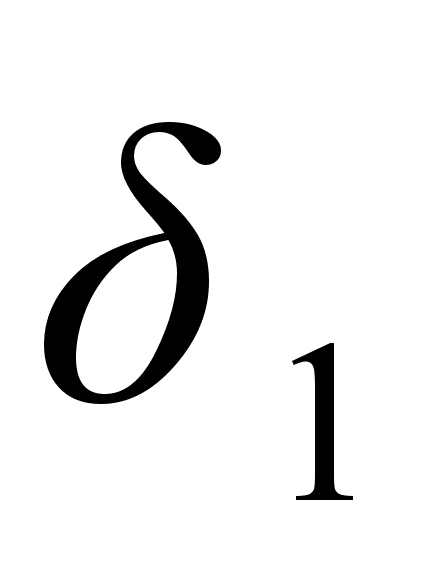 ,
, 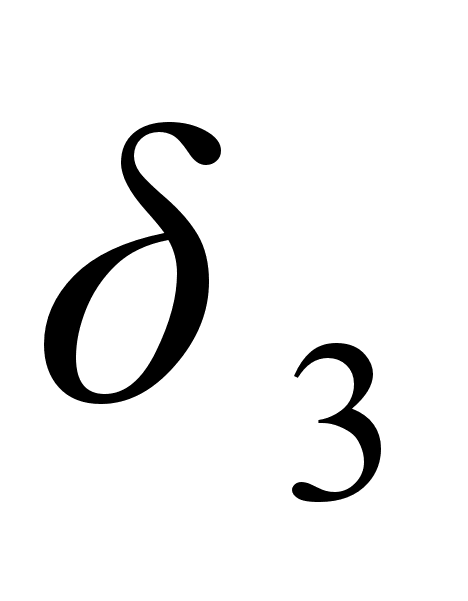 , тАж и
, тАж и 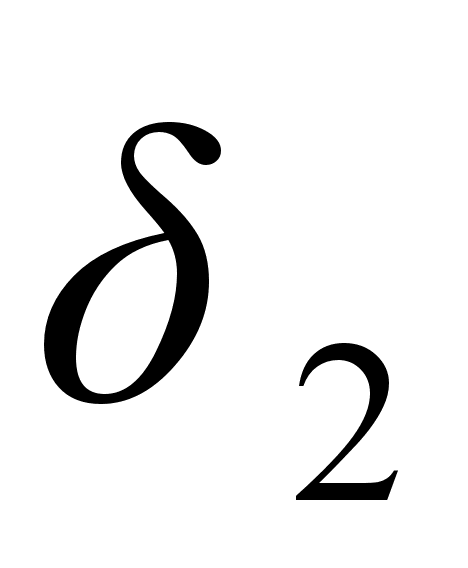 ,
, 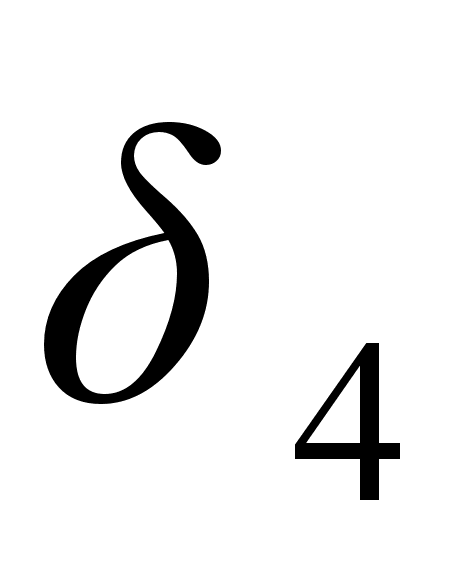 , тАж . Но так как
, тАж . Но так как  принадлежит всем сегментам последовательности, то
принадлежит всем сегментам последовательности, то  и совпадает с указанной точкой, так что
и совпадает с указанной точкой, так что  .
.
Итак, мы имеем следующий важный результат:
бесконечная последовательность подходящих дробей 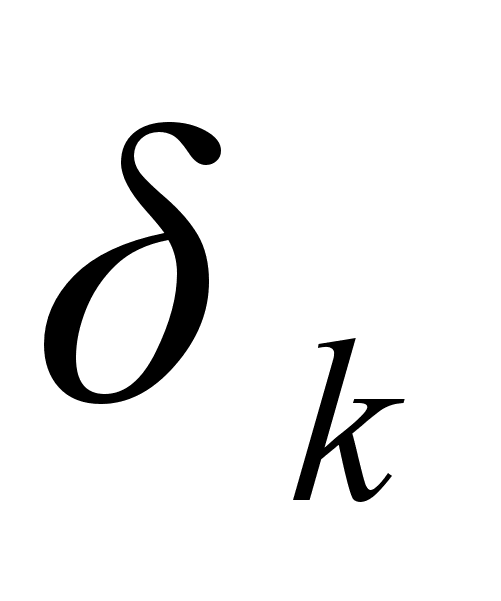 , которая возникает при разложении иррационального
, которая возникает при разложении иррационального  , сходится к
, сходится к  , колеблясь около него. Или: иррациональное действительное
, колеблясь около него. Или: иррациональное действительное  равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
Сходимость правильных бесконечных цепных дробей.
Теперь покажем, что сходящейся является последовательность подходящих дробей не только такой бесконечной непрерывной дроби, которая возникает при разложении иррационального числа  , но и любой бесконечной непрерывной дроби
, но и любой бесконечной непрерывной дроби 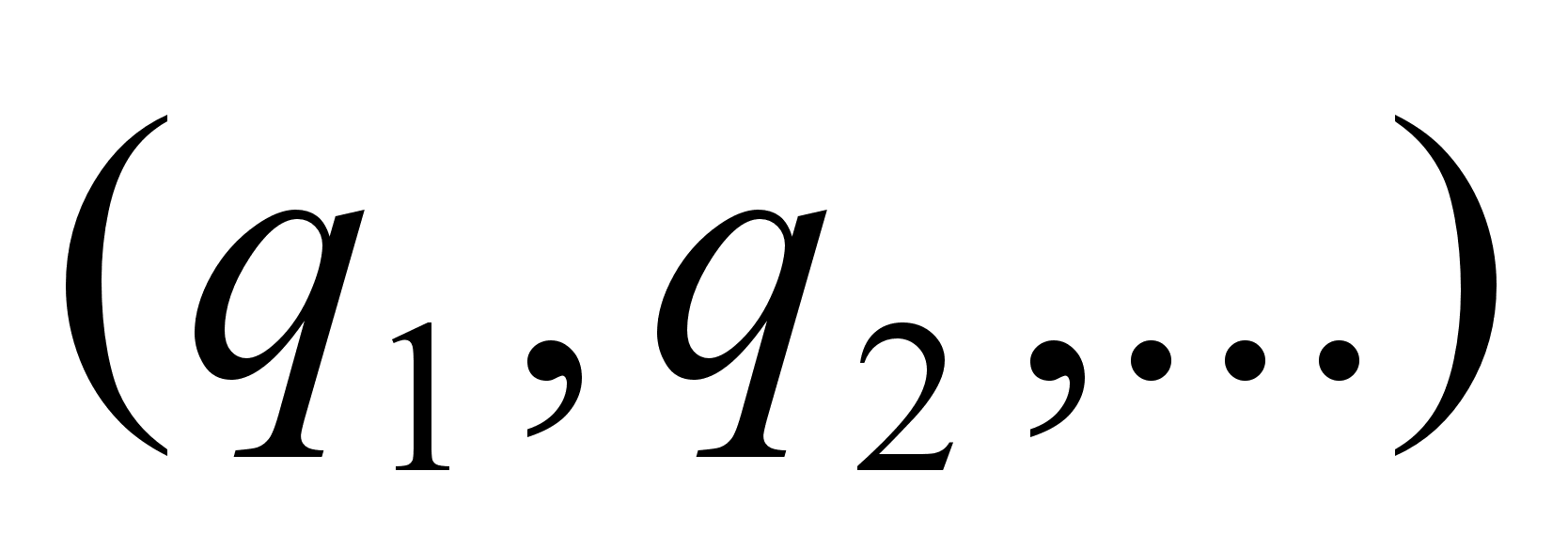 , где
, где  , а
, а 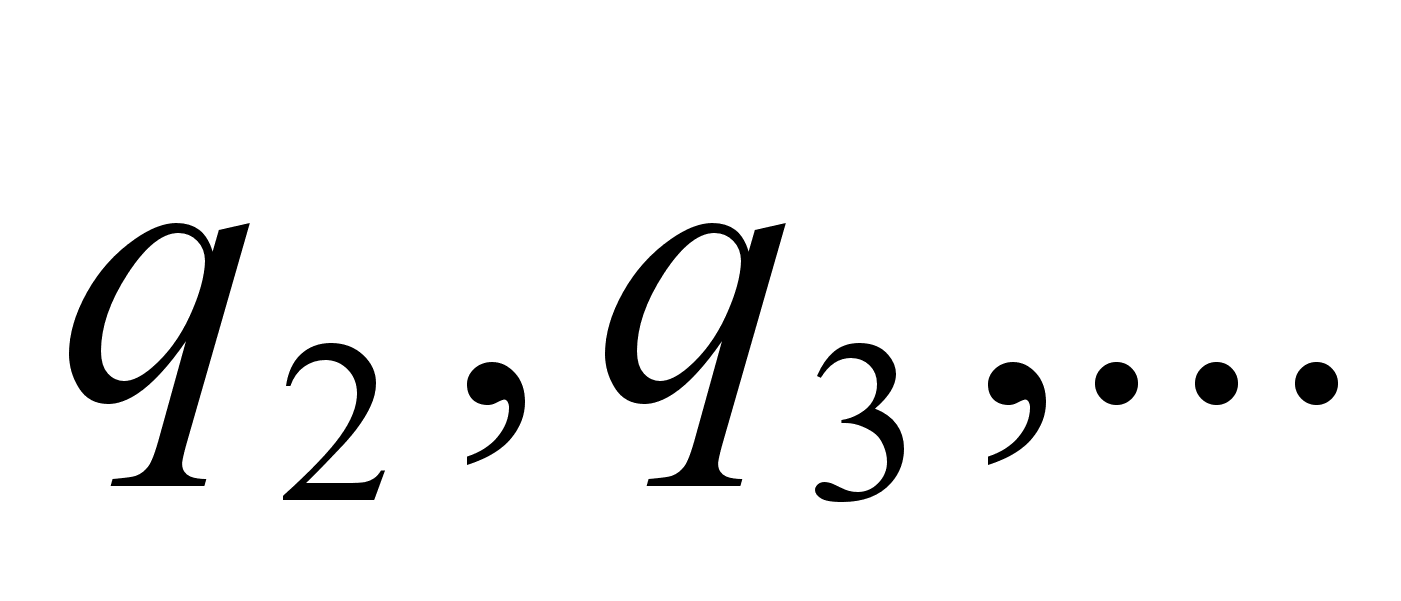 - произвольно выбранные целые положительные числа.
- произвольно выбранные целые положительные числа.
Но для этого мы заново исследуем взаимное расположение подходящих дробей.
С этой целью рассмотрим формулы:
 (1) и
(1) и  (2),
(2),
которые справедливы для любой бесконечной непрерывной дроби.
Формула (1) показывает, что любая подходящая дробь четного порядка больше двух соседних подходящих дробей, у которых порядок на единицу меньше или больше, чем у нее, то есть 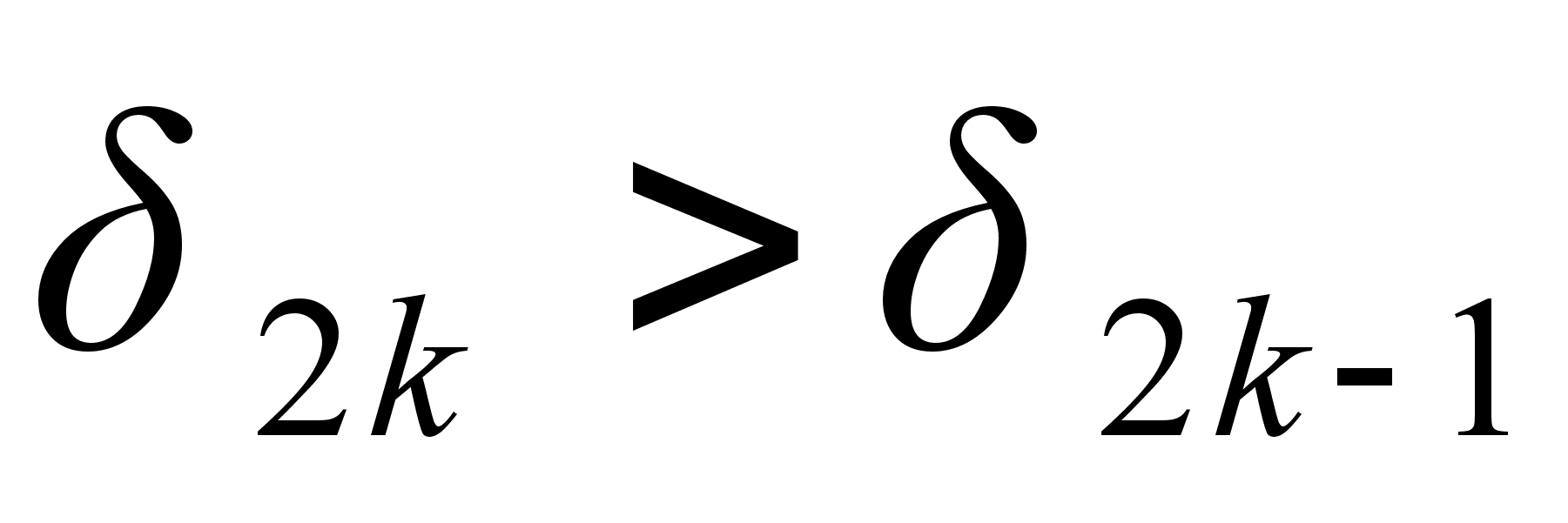 и
и 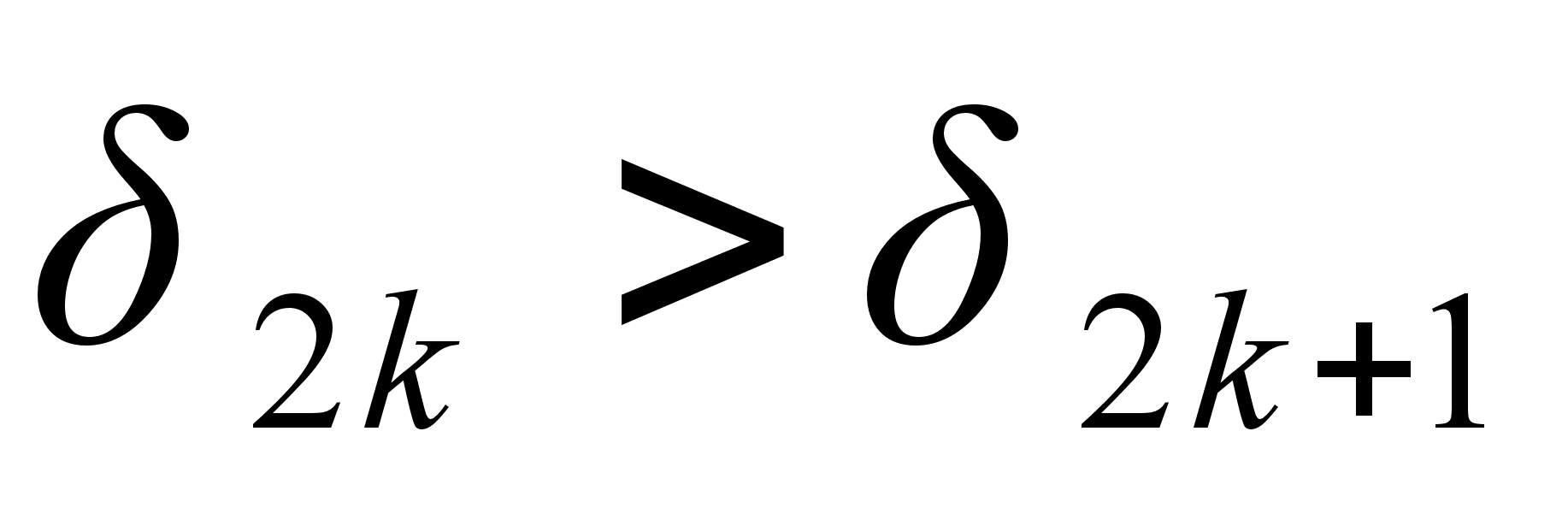 . Согласно этому
. Согласно этому 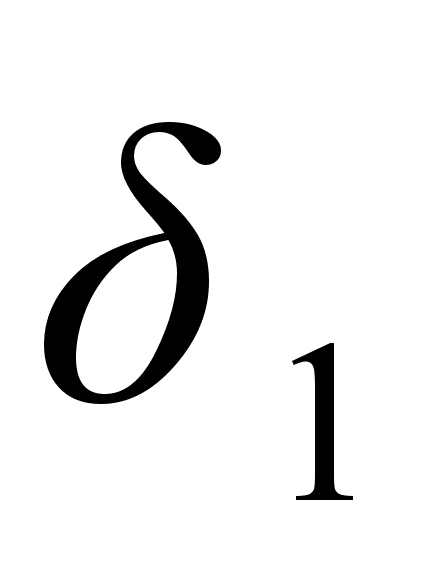 и
и 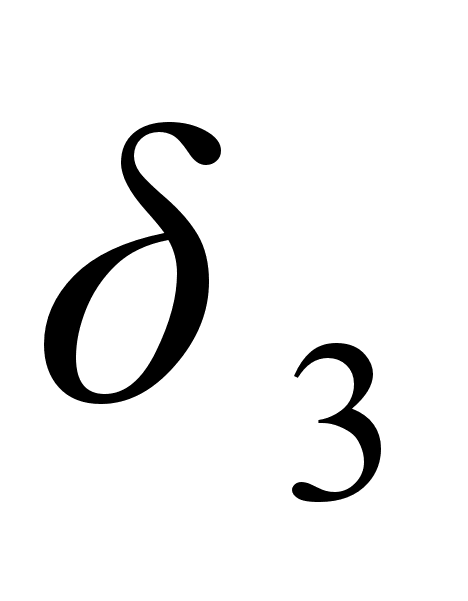 расположены слева от
расположены слева от 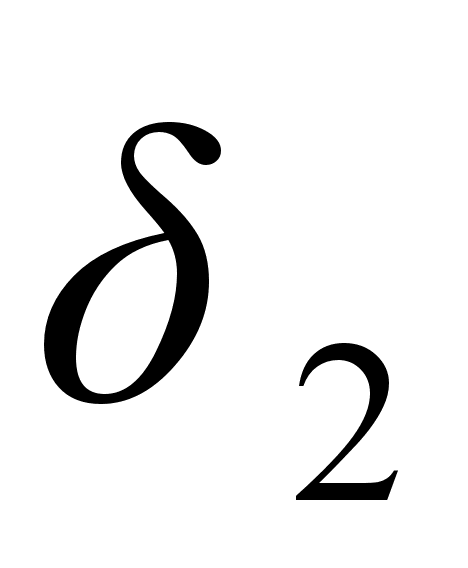 ,
, 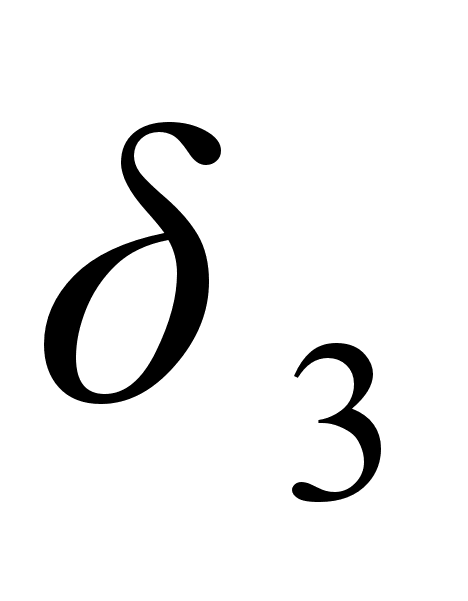 и
и 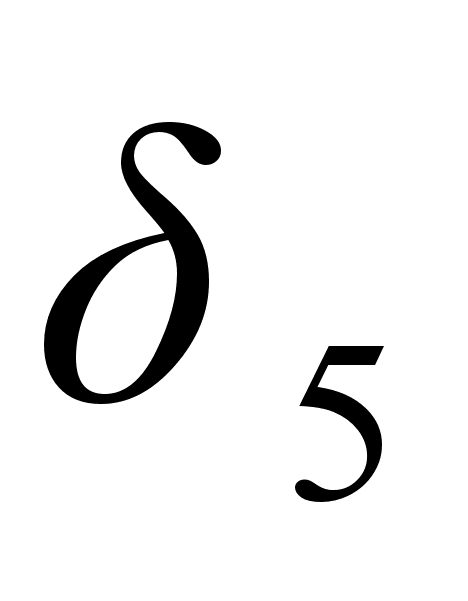 тАУ слева от
тАУ слева от 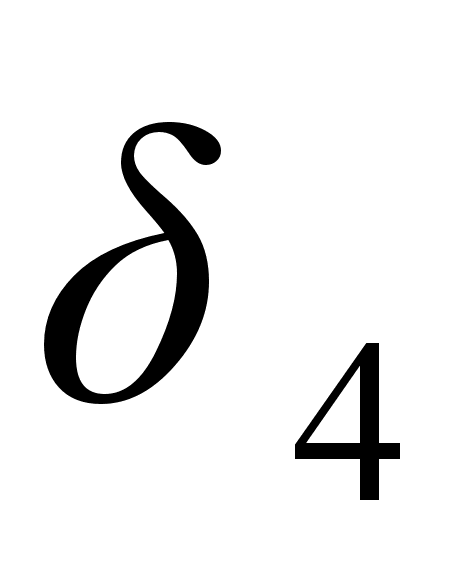 и так далее.
и так далее.
Формула (2) показывает, что расстояние между соседними подходящими дробями при увеличении k убывает. Действительно, так как 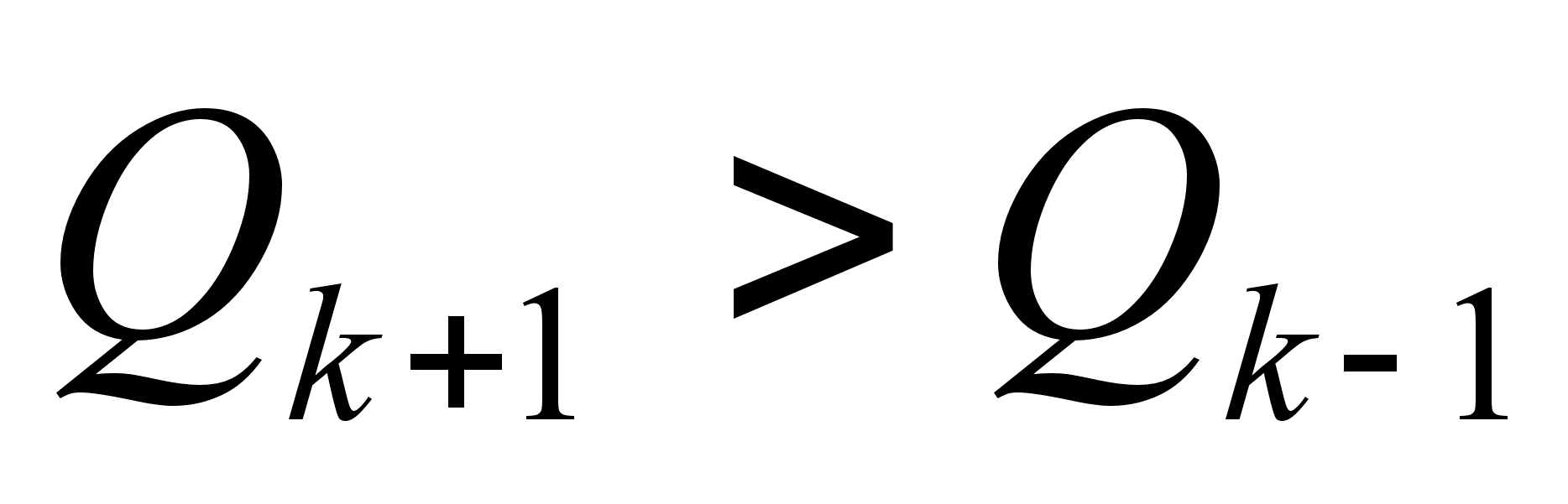 , то
, то
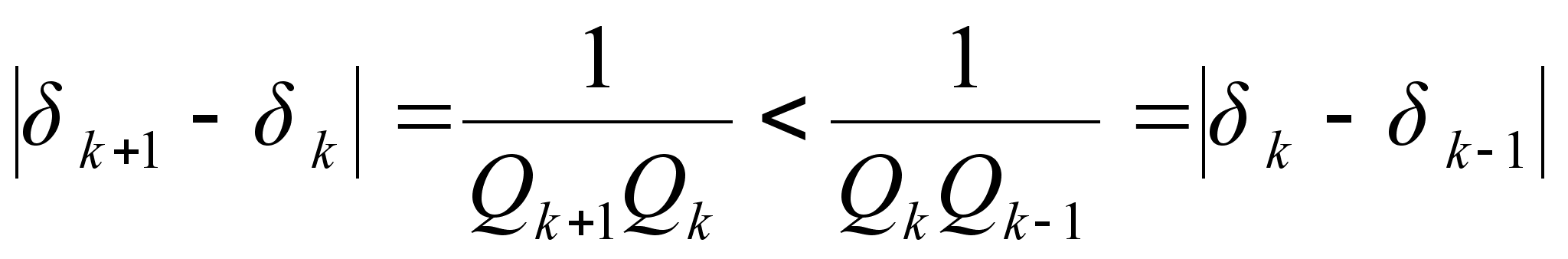
Согласно этому свойству 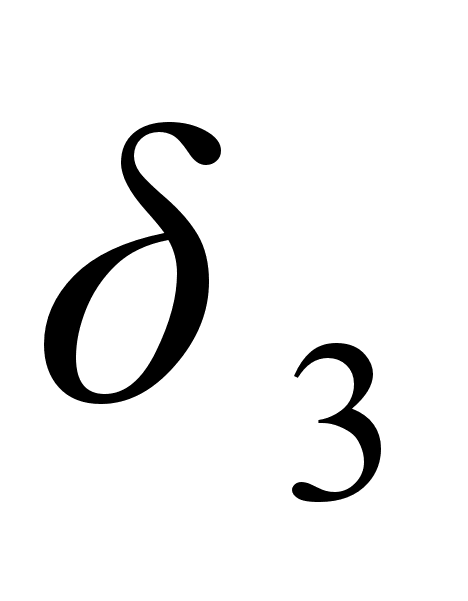 ближе к
ближе к 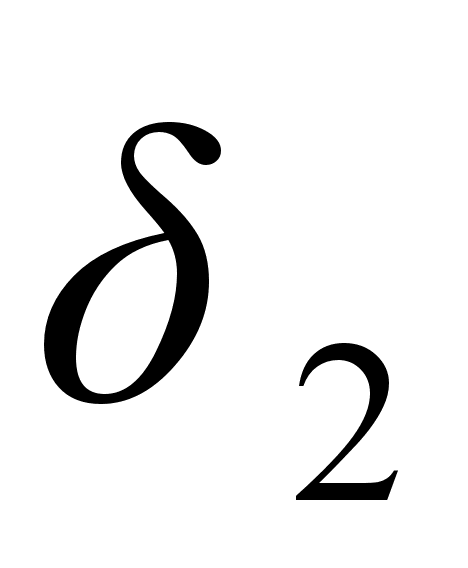 , чем
, чем 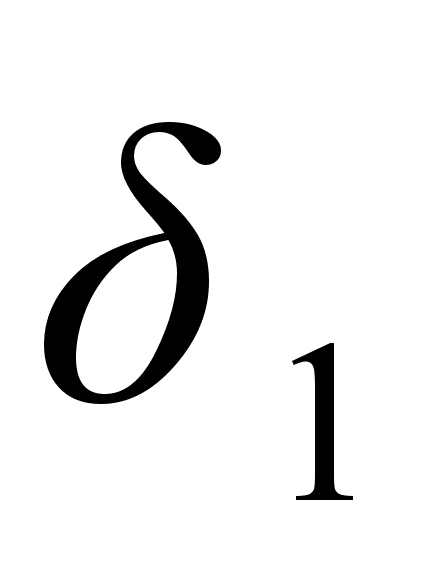 , а так как
, а так как 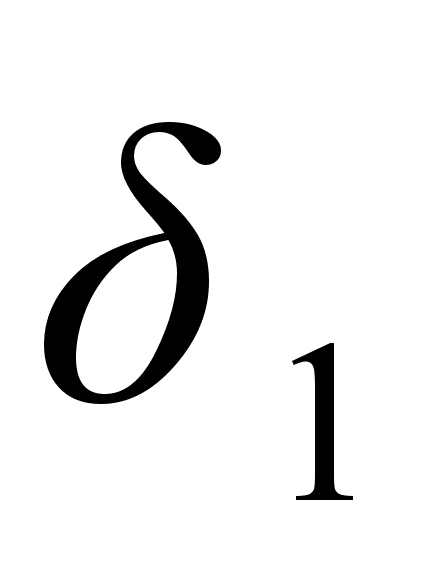 и
и 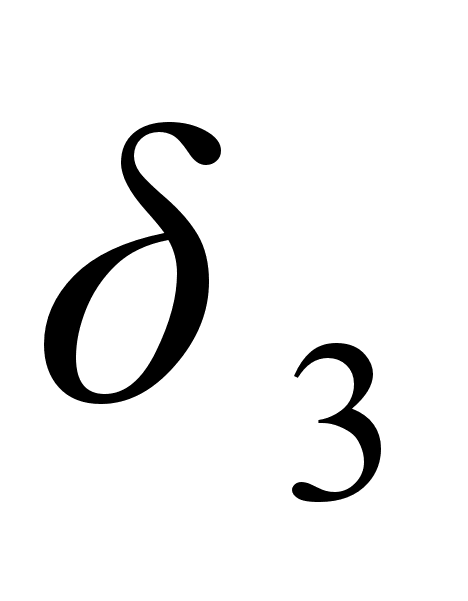 находятся слева от
находятся слева от 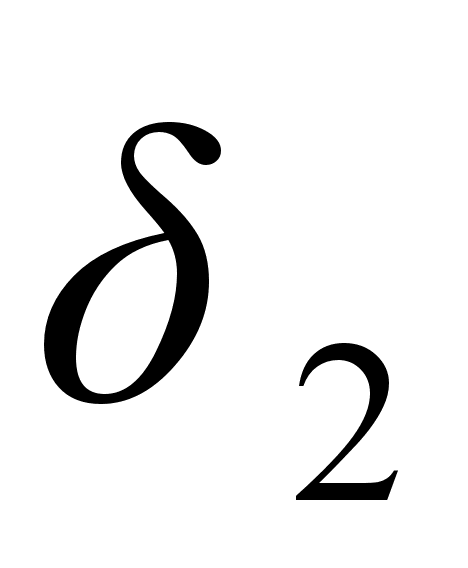 , то
, то 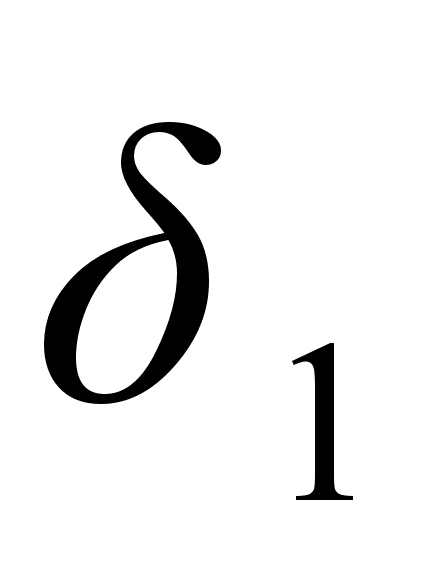
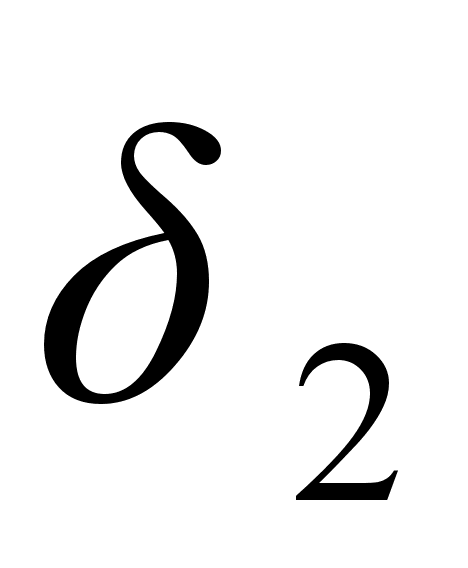 .
.
тАФтАФтАФтАФ тАФтАФтАФ
тАФтАФтАФ тАФтАФтАФ
тАФтАФтАФ тАФтАФтАФ
тАФтАФтАФ тАФтАФтАФтАФ
тАФтАФтАФтАФ
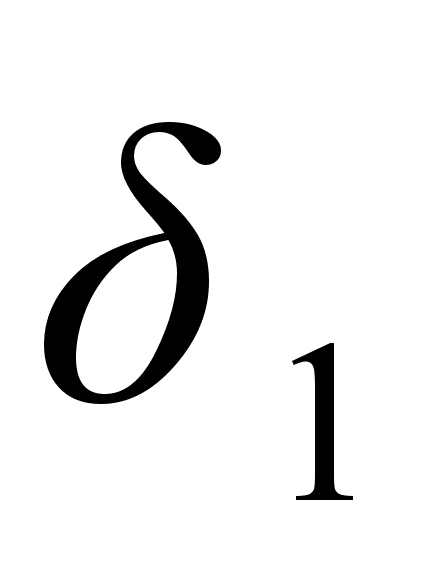
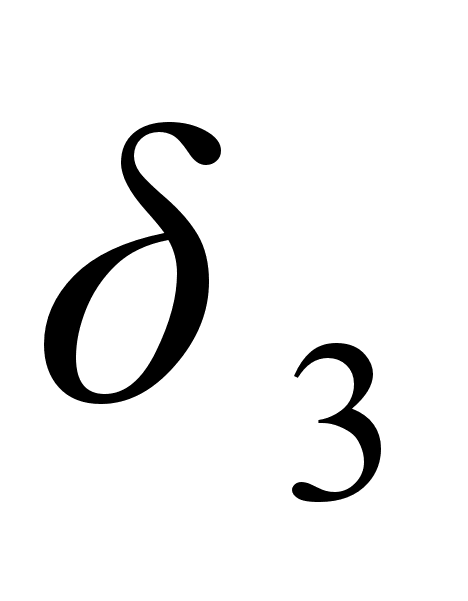
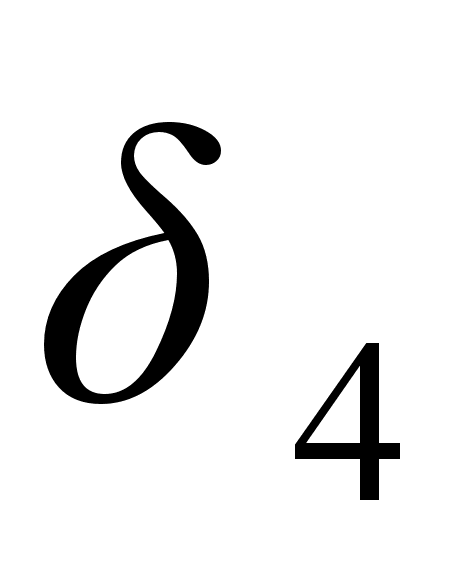
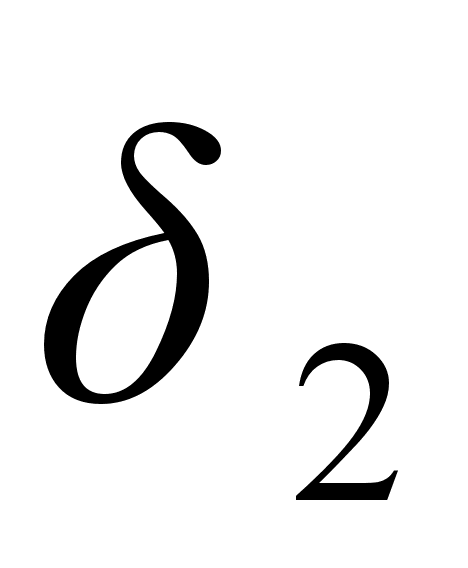
Из этого следует, что подходящая дробь 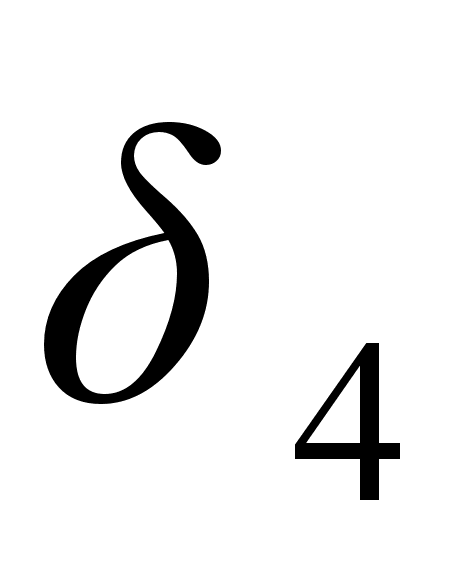 , которая, как и
, которая, как и 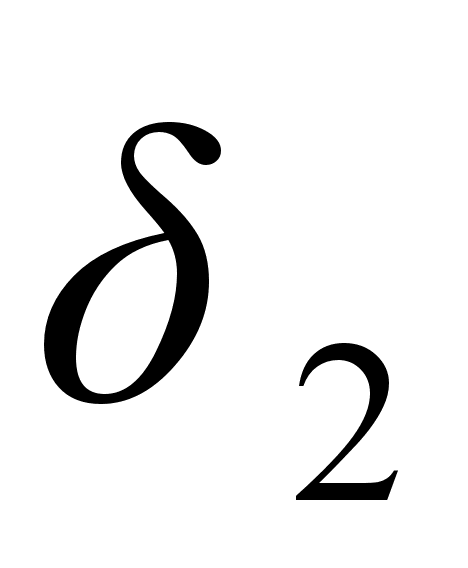 , расположена справа от
, расположена справа от 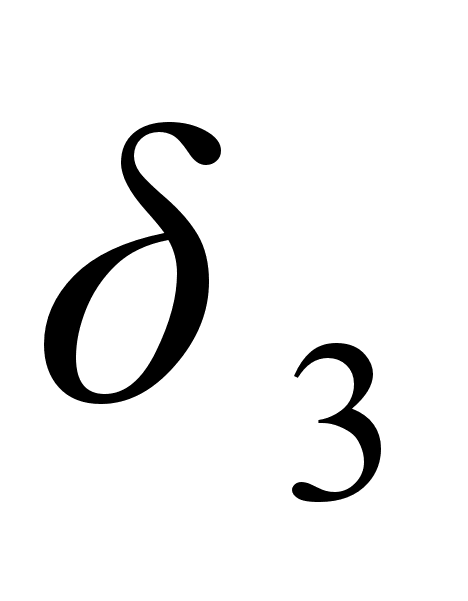 , ближе к
, ближе к 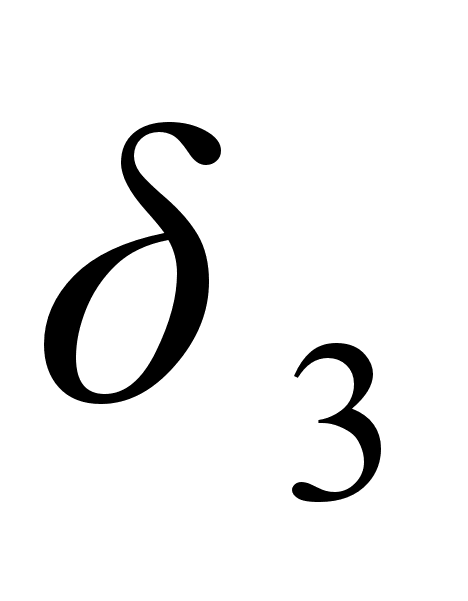 , чем к
, чем к 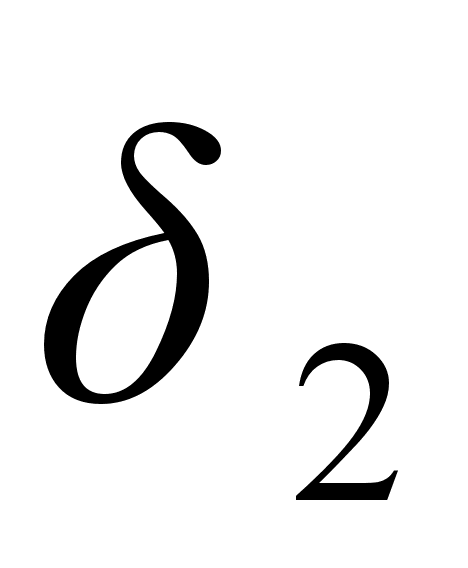 , то есть
, то есть 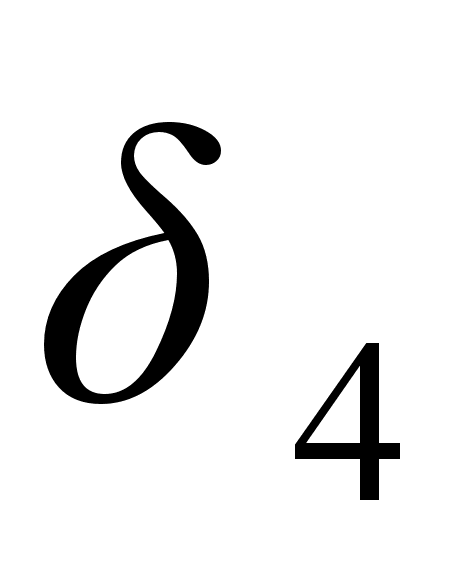
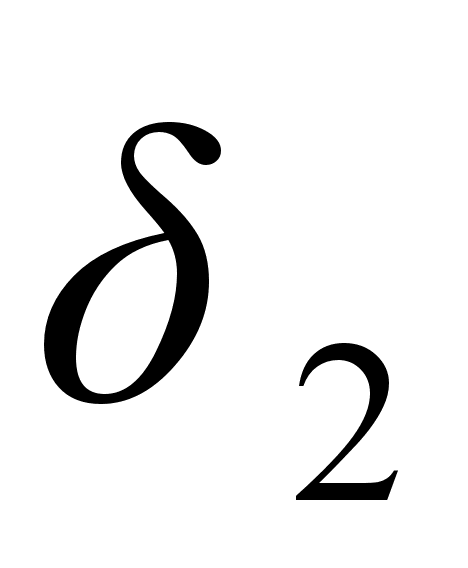 .
.
Подходящие дроби дальнейших порядков располагаются таким же образом.
Итак, подходящие дроби нечетного порядка увеличиваются с ростом порядка, а подходящие дроби четного порядка убывают с ростом порядка; при этом все подходящие дроби нечетного порядка меньше всех подходящих дробей четного порядка, то есть 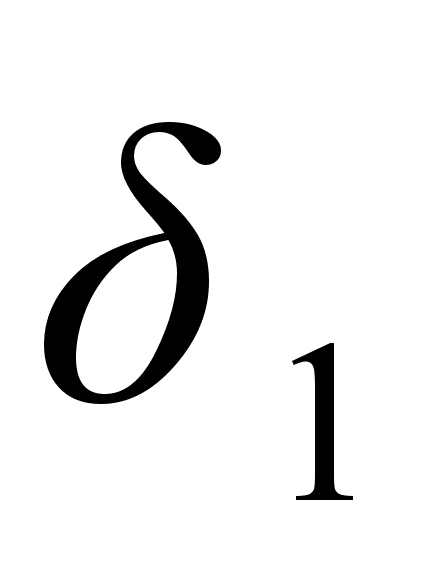
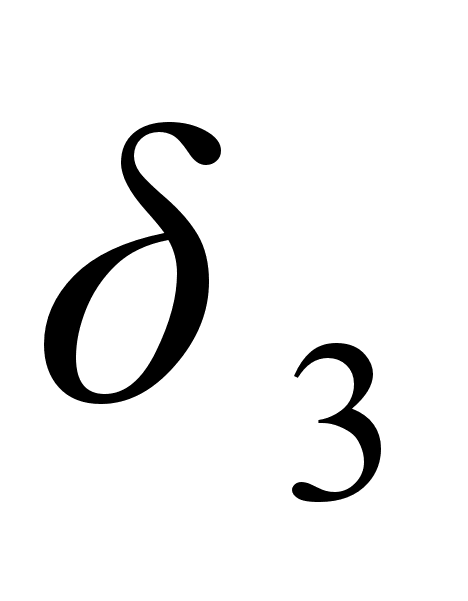
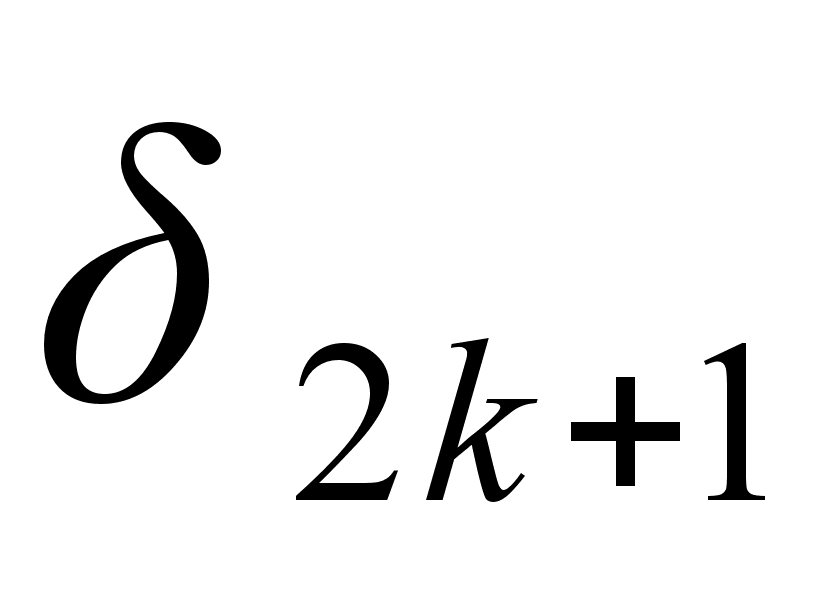
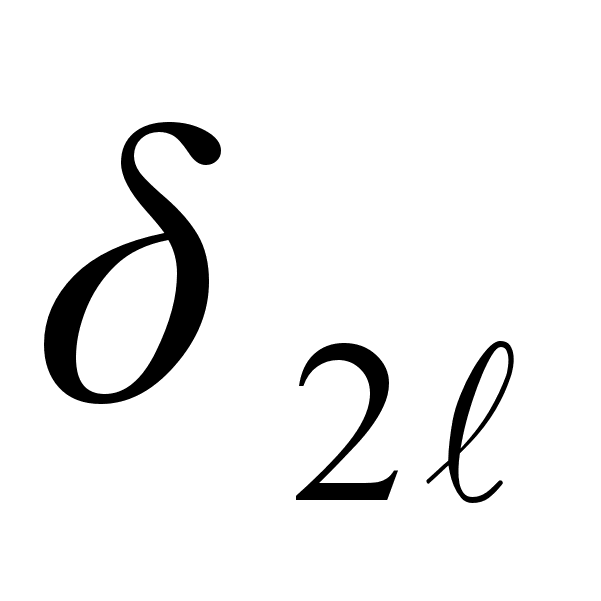
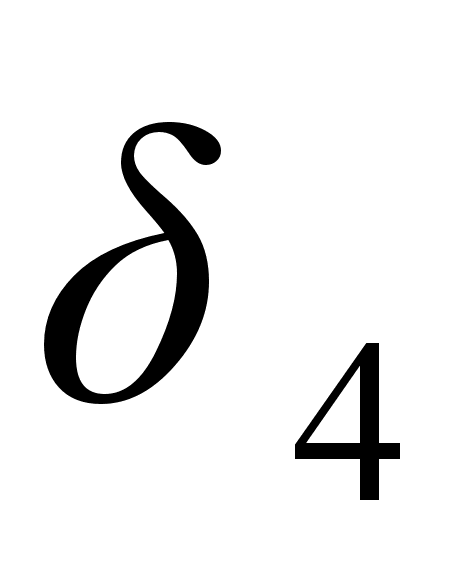
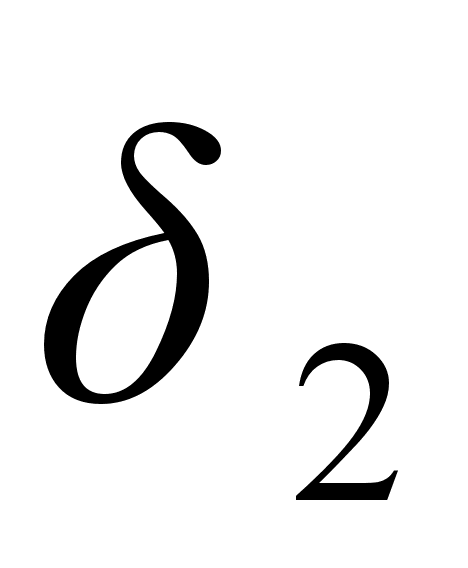 при любых k и
при любых k и  .
.
Так как 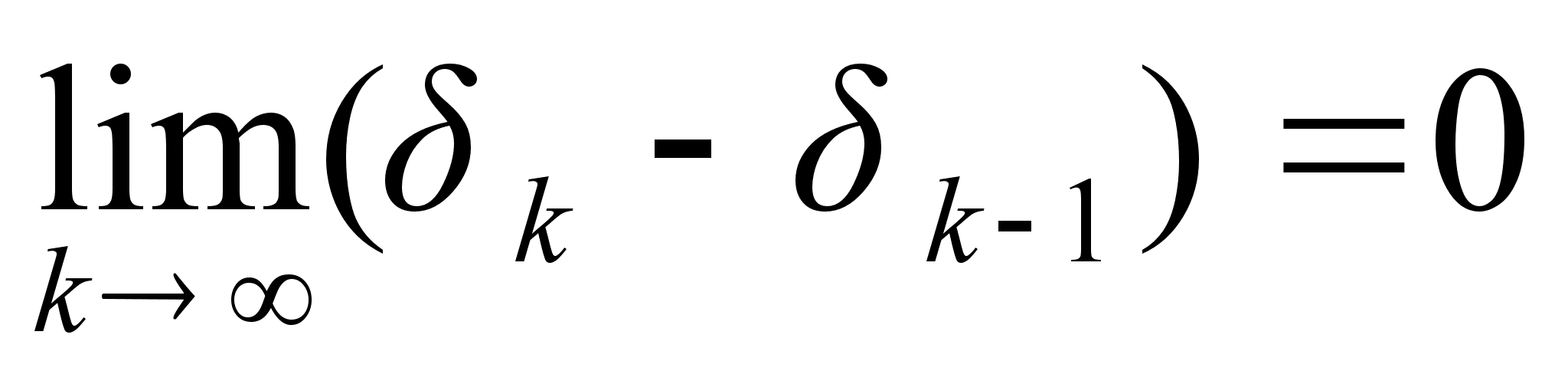 , то пары подходящих дробей
, то пары подходящих дробей 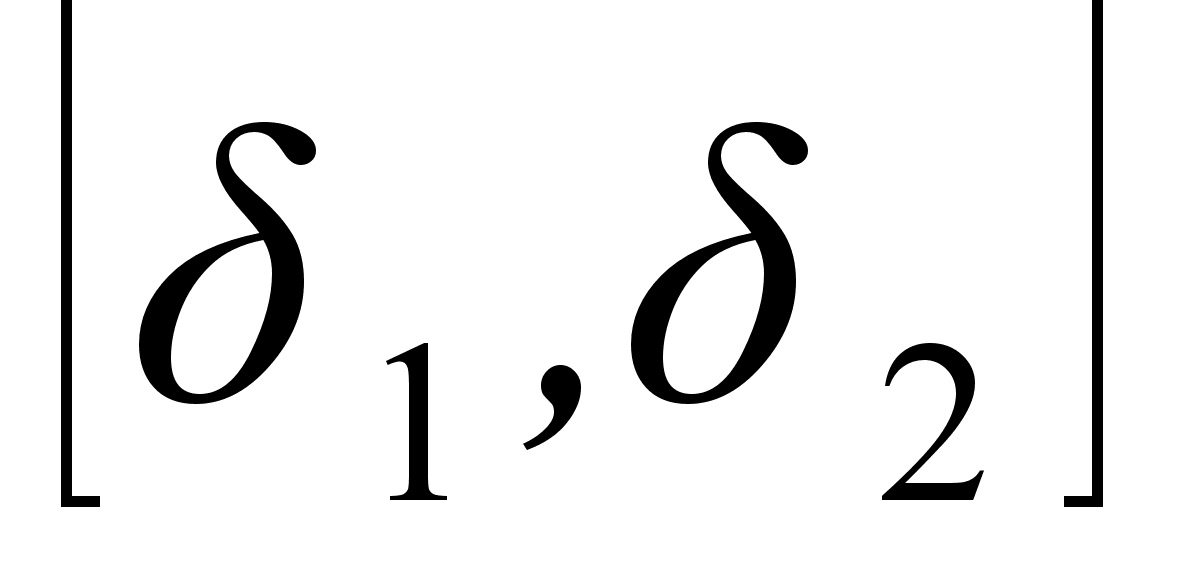 ,
, 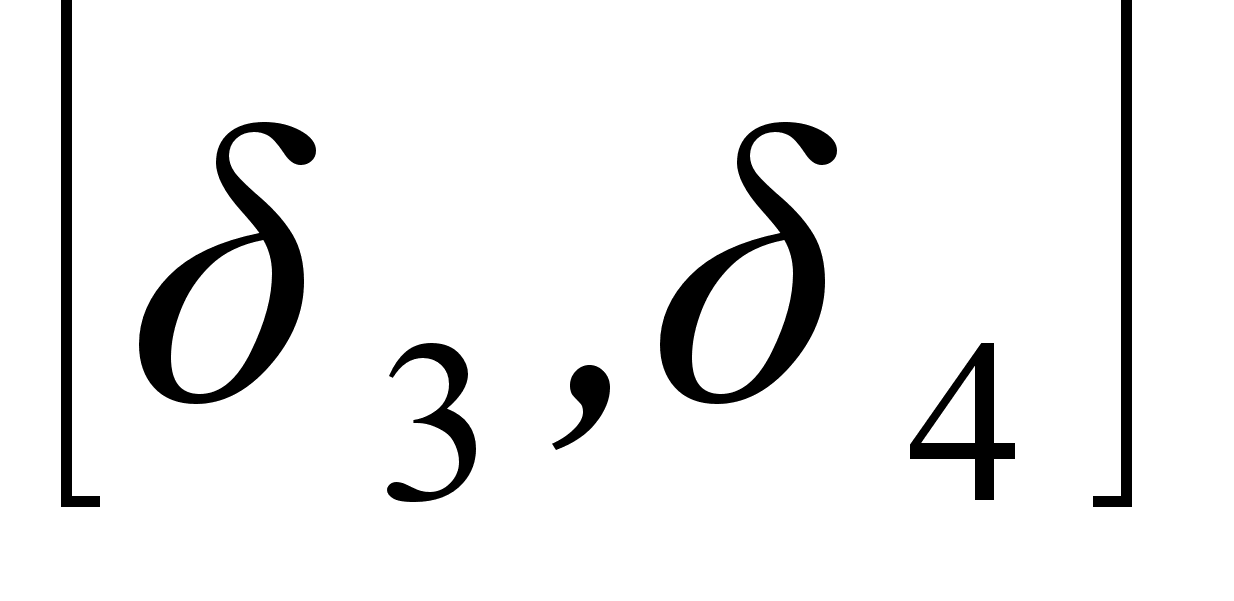 , тАж образуют стягивающуюся последовательность отрезков, которая должна иметь единственную общую точку, являющуюся общим пределом последовательностей
, тАж образуют стягивающуюся последовательность отрезков, которая должна иметь единственную общую точку, являющуюся общим пределом последовательностей 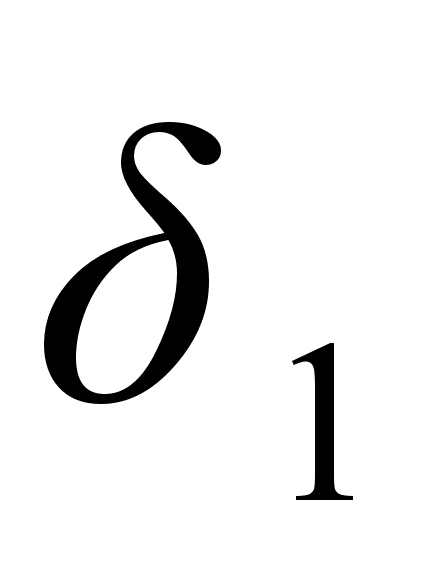 ,
, 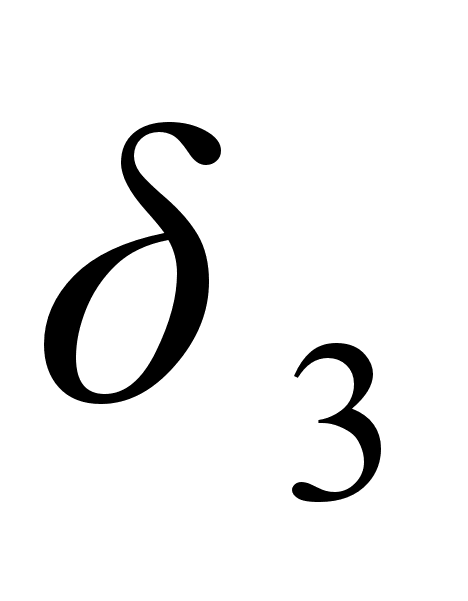 , тАж и
, тАж и 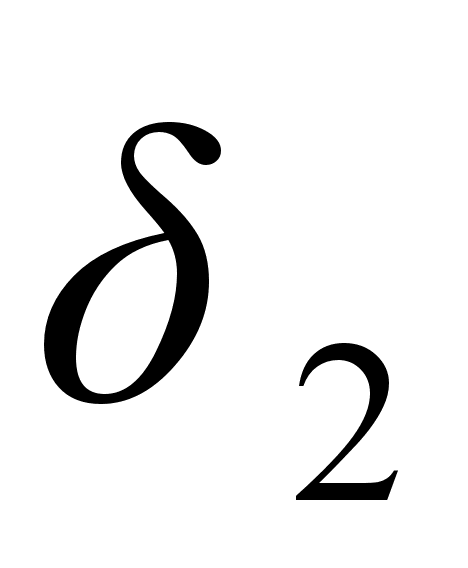 ,
, 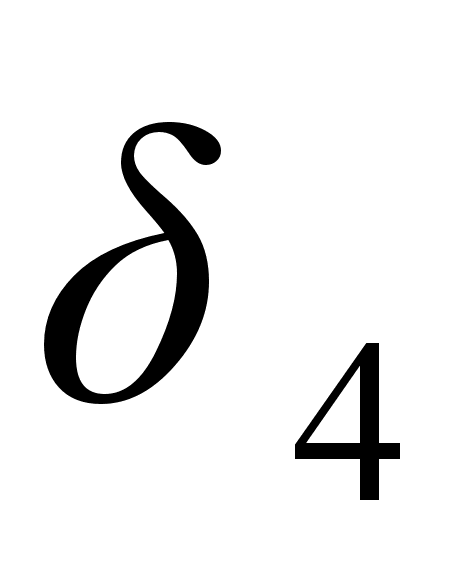 , тАж. Обозначим этот предел за
, тАж. Обозначим этот предел за  , имеем
, имеем  , причем, очевидно,
, причем, очевидно,  для любого k, то есть
для любого k, то есть  находится между любыми двумя соседними подходящими дробями.
находится между любыми двумя соседними подходящими дробями.
Следовательно, подходящие дроби любой бесконечной непрерывной дроби имеют некоторый предел  . Этот предел
. Этот предел  принимается в качестве значения бесконечной непрерывной дроби. Говорят, что бесконечная непрерывная дробь сходится к
принимается в качестве значения бесконечной непрерывной дроби. Говорят, что бесконечная непрерывная дробь сходится к  или представляет число
или представляет число  . Можно записать
. Можно записать  =
=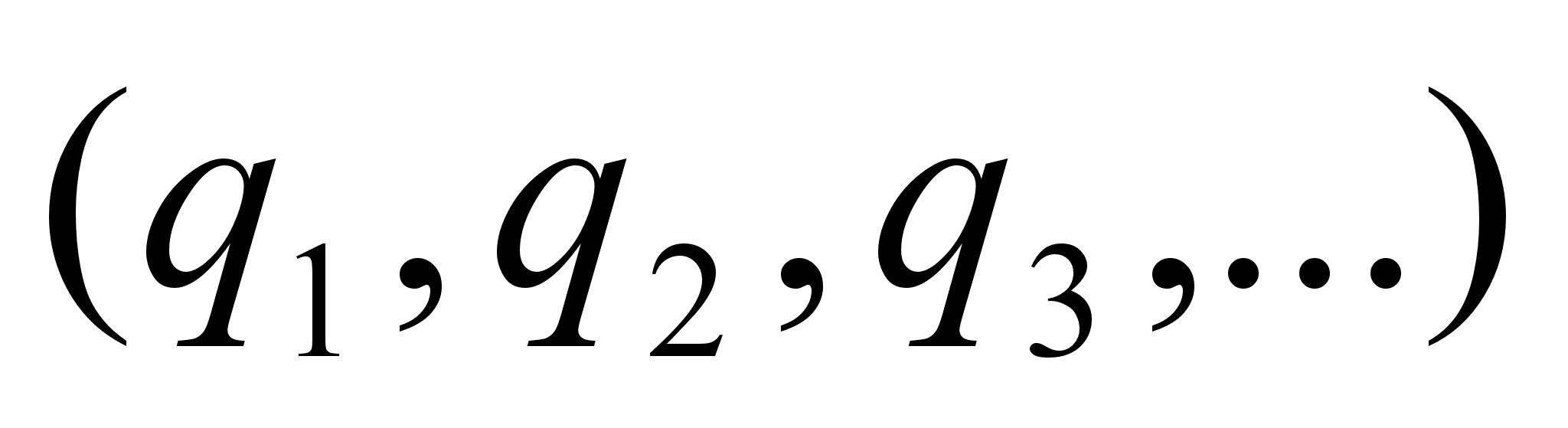 , подразумевая при этом, что
, подразумевая при этом, что  =
= .
.
Единственность представления действительного иррационального числа правильной бесконечной цепной дробью.
<
Вместе с этим смотрят:
"Инкарнация" кватернионов
* Алгебры и их применение
*-Алгебры и их применение
10 способов решения квадратных уравнений
Cпособы преобразования комплексного чертежа, применение при изображении предметов