Численные методы
МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛРЖНРЖЙНИХ АЛГЕБРАРЗЧНИХ РРЖВНЯНЬ.
Розглянемо чисельнi методи розв’язання систем лiнiйних алгебраiчних рiвнянь
Ax=f T (1)
де A- матриця m*m, x=(x1,x2,..,xm)- шуканийвектор,
Т
f=(f1, f2, .. , fm) -заданий вектор.
Припускаiмо, що 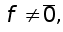 та визначник матрицi А вiдмiнний вiд нуля, так що iснуi iдиний розв’язок х. З курсу алгебри вiдомо, що систему (1) можна розв’язати за формулами Крамера*. Для великих m цей спосiб практично нереалiзований тому, що потребуi порядку m! aрифметичних дiй. Тому широко використовуються iншi методи розв’язання, наприклад, метод Гаусса**, який потребуi
та визначник матрицi А вiдмiнний вiд нуля, так що iснуi iдиний розв’язок х. З курсу алгебри вiдомо, що систему (1) можна розв’язати за формулами Крамера*. Для великих m цей спосiб практично нереалiзований тому, що потребуi порядку m! aрифметичних дiй. Тому широко використовуються iншi методи розв’язання, наприклад, метод Гаусса**, який потребуi 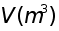 дiй.
дiй.
Методи чисельного розв’язання системи (1) подiляються на двi групи:
-прямi методи;
-iтерацiйнi методи.
У прямих (або точних) методах розв’язок x системи (1) вiдшукуiться за скiнченну кiлькiсть арифметичних дiй. Внаслiдок похибок заокруглення прямi методи насправдi не приводять до точного розв’язку системи (1) i назвати iх точними можливо лише залишаючи осторонь похибки заокруглення.
РЖтерацiйнi методи (iх також називають методами послiдовних наближень)полягають у тому, що розв’язок x системи (1) вiдшукуiться як границя при  послiдовних наближень
послiдовних наближень 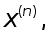 де n- номер iтерацii. Як правило, за скiнченну кiлькiсть iтерацiй ця границя не досягаiться.
де n- номер iтерацii. Як правило, за скiнченну кiлькiсть iтерацiй ця границя не досягаiться.
______________________
* Крамер Габрiiль (1704-1752)- швейцарський математик.
** Гаус Карл Фридрих (1777-1855)- нiмецький математик, астроном, фiзик, геодезист, професор Гетiнгенського унiверситету.
МЕТОД ГАУССА .
Запишемо систему (1) у розгорнутому виглядi:
а11x1+a12x2+..+a1mxm=f1 ,
a21x1+a22x2+..+a2mxm =f2 , (2)
...................
am1x1+am2x2+..+ammxm =fm .
Метод Гаусса розв’язання системи (2) полягаi у послiдовному вилученнi невiдомих x1, x2, .., xm-1 з цiii системи.
Припустимо, що a11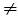 0 . Подiлив перше рiвняння на a11, одержимо
0 . Подiлив перше рiвняння на a11, одержимо
x1+c12x2 +..+c1m xm =y1 , (3)

де : c1j=a1j /a11 ; j=2,m ; y1=f1/a11 .
Розглянемо тепер рiвняння системи (2), що залишилися

ai1x1+ai2x2+..+aimxm=fi ; i= 2,m . (4)
 Помножимо (3) на ai1 та вiднiмемо одержане рiвняння з i-го рiвняння системи (4), i=2,m.
Помножимо (3) на ai1 та вiднiмемо одержане рiвняння з i-го рiвняння системи (4), i=2,m.
У результатi одержимо наступну систему рiвнянь:
x1+c12x2+..+c1jxj+..+c1mxm =y1 ,
(1) (1) (1) (1)
a22x2+.. +a2jxj+..+a2mxm=f2 ,
...................... (5)
(1) (1) (1) (1)
am2x2+..+amjxj+..+ammxm=fm .
Tут позначено:
 (1) (1)
(1) (1)
aij=aij-c1jai1; fi=fi -y1ai1; i,j=2,m . (6)
Матриця системи (5) маi вигляд:
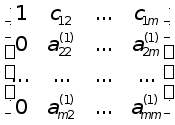 .
.
Матрицi такоi стуктури заведено позначати так:
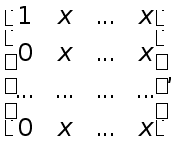
де хрестиками позначенi ненульовi елементи.
У системi (5) невiдоме х мiститься тiльки в першому рiвняннi, тому у подальшому достатньо мати справу iз скороченою системою рiвнянь:
(1) (1) (1) (1)
a22x2 +..+a2jxj +..+a2mxm =f2 ,
....................... (7)
(1) (1) (1) (1)
am2x2 +..+amjxj +..+ammxm =fm .
Тим самим ми здiйснили перший крок методу Гаусса . Коли 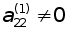 , то з системи (7) зовсiм аналогiчно можна вилучити невiдоме x2 i прийти до системи, еквiвалентнiй (2),що маi матрицю такоi структури:
, то з системи (7) зовсiм аналогiчно можна вилучити невiдоме x2 i прийти до системи, еквiвалентнiй (2),що маi матрицю такоi структури:
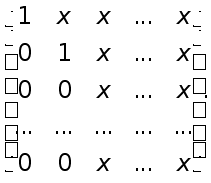
При цьому перше рiвняння системи (5) залишаiться без змiни.
Вилучая таким же чином невiдомi х 3, х4 ,.. ,xm-1,приходимо остаточно до системи рiвнянь виду:
x1 +c12x2 +..+c1,m-1xm-1+c1mxm =y1,
x2 +..+c2,m-1xm-1+c2mxm =y2 ,
................
xm-1+cm-1,mxm=ym-1,
xm=ym ,
що еквiвалентна початковiй системi (2) .
Матриця цiii системи
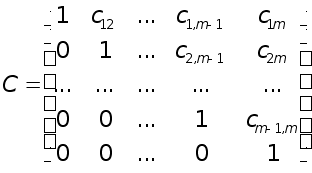
мiстить нулi усюди нижче головноi дiагоналi. Матрицi такого виду називаються верхнiми трикутними матрицями. Нижньою трикутною матрицею називаiться така матриця, у якоi дорiвнюють нулю усi елементи, що мiстяться вище головноi дiагоналi.
Побудова системи (8) складаi прямий хiд методу Гаусса. Зворотнiй хiд полягаi у вiдшуканнi невiдомих х1, .. ,хmз системи (8). Тому що матриця системи маi трикутний вигляд, можна послiдовно, починаючи з хm, вiдшукати всi невiдомi. Дiйсно, xm=ym,
x m-1 =ym-1 -cm-1,m x m i т. д.
Загальнi форми зворотнього ходу мають вигляд:
m
 xi =yi - е cijxj ; i=m-1,1; xm =ym . (10)
xi =yi - е cijxj ; i=m-1,1; xm =ym . (10)
j=i+1
При реалiзацii на ЕОМ прямого ходу методу Гаусса немаi необхiдностi дiяти iз змiнними x1 ,x2 ,.. ,xm. Досить вказати алгоритм,за яким початкова матриця А перетворюiться до трикутного вигляду (9), та вказати вiдповiдне перетворення правих частин системи.
Одержимо цi загальнi формули.
Нехай вже здiйсненi першi к-1 крокiв, тобто вже вилученi змiннi
x1 , x2,.., xk-1 .
Тодi маiмо систему:
x1+c12 x2 +..+c1,k-1xk-1+ c1kxk+..+c1mxm =y1 ,
x2 +..+c2,k-1xk-1+ c2kxk+..+c2mxm =y2 ,
.......................
xk-1+ck-1,kxk+..+ck-1,mxm=yk-1 , (11)
(k-1) (k-1) (k-1)
akkxk+..+akmxm =fk ,
..............
(k-1) (k-1) (k-1)
amkxk+..+ammxm =fm .
Розглянемо К-те рiвняння цiii системи:
(k-1) (k-1) (k-1)
akkxk+..+akmxm=fk ,
та припустимо, що 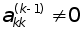 . Подiливши обидвi частини цього рiвняння на
. Подiливши обидвi частини цього рiвняння на 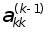 , одержимо
, одержимо
xk+ck,k+1xk+1+..+ckmxm=yk , (12)
(k-1) (k-1) (k-1) (k-1)
де ckj=akj / akk ; j=k+1,m ; yk=fk / akk .
Далi помножимо рiвняння (12) на 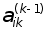 та вiднiмемо одержане спiввiдношення з i-го рiвняння системи (11). У результатi остання група рiвнянь системи (11) набуваi наступного вигляду:
та вiднiмемо одержане спiввiдношення з i-го рiвняння системи (11). У результатi остання група рiвнянь системи (11) набуваi наступного вигляду:
x k+ck,k+1xk+1 +..+ ckmxm=yk,
(k) (k) (k)
ak+1,k+1xk+1+..+ ak+1,mxm=fk+1,
....................
(k) (k) (k)
am,k+1xk+1+.. + ammxm=fm ,

 (k) (k-1) (k-1) (k) (k-1) (k-1)
(k) (k-1) (k-1) (k) (k-1) (k-1)
де: aij =aij - aikckj ; i,j=k+1,m ; fi= fi - aikyk ; i=k+1,m .
Таким чином, у прямому ходi методу Гаусса коефiцiiнти рiвнянь перетворюються за наступним правилом
 (0)
(0)
akj =akj ; k,j=1,m ;

 (k-1) (k-1)
(k-1) (k-1)
ckj=akj /akk ; j=k+1,m ; k=1,m ; (13)

 (k) (k-1) (k-1)
(k) (k-1) (k-1)
aij =aij - aikckj ; i,j=k+1,m ; k=1,m . (14)
Обчислення правих частин системи (8) здiйснюiться за формулами:
 (0) (k-1) (k-1)
(0) (k-1) (k-1)
fk=fk ; yk = fk / akk ; k=1,m ; (15)
 (k) (k-1) (k-1)
(k) (k-1) (k-1)
fi = fi - aikyk ; k=1,m . (16)


Коефiцiенти cij i правi частини yi ; i=1,m ; j=i+1,m зберiгаються у пам’ятi ЕОМ i використовуються при здiйсненнi зворотнього ходу за формулами (10).
Основним обмеженням методу i припущення, що усi елементи 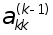 , на якi здiйснюiться дiлення, вiдрiзняються вiд нуля. Число
, на якi здiйснюiться дiлення, вiдрiзняються вiд нуля. Число 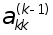 називаiться провiдним елементом на К-му кроцi вилучення. Навiть, якщо деякий провiдний елемент не дорiвнюi нулевi, а просто i близьким до нуля, в процесi обчислень може мати мiсце нагромадження похибок. Вихiд з цiii ситуацii полягаi в тому, шо як провiдний елемент вибираiться не
називаiться провiдним елементом на К-му кроцi вилучення. Навiть, якщо деякий провiдний елемент не дорiвнюi нулевi, а просто i близьким до нуля, в процесi обчислень може мати мiсце нагромадження похибок. Вихiд з цiii ситуацii полягаi в тому, шо як провiдний елемент вибираiться не 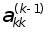 , а iнше число ( тобто на К-му кроцi вилучаiться не xk, а iнша змiнна xj ,
, а iнше число ( тобто на К-му кроцi вилучаiться не xk, а iнша змiнна xj , 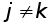 ) . Така стратегiя вибору провiдних елементiв здiйснюiться в методi Гаусса з вибором головного елементу, який буде розглянуто пiзнiш.
) . Така стратегiя вибору провiдних елементiв здiйснюiться в методi Гаусса з вибором головного елементу, який буде розглянуто пiзнiш.
А тепер пiдрахуiмо число арифметичних дiй, що необхiднi для розв’язання системи за допомогою методу Гаусса. Оскiльки виконання операцiй множення i дiлення на ЕОМ потребуi набагато бiльше часу, нiж виконання додавання i вiднiмання, обмежимось пiдрахуванням числа множень i дiлень.
1.Обчислення коефiцiiнтiв 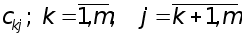 за формулами (13) потребуi:
за формулами (13) потребуi:
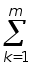 (m-k)=1+2+..+(m-1)=
(m-k)=1+2+..+(m-1)= 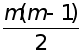 дiлень .
дiлень .
2.Обчислення усiх коефiцiiнтiв 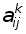 за формулами (14) потребуi
за формулами (14) потребуi
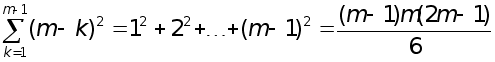
множень (тут ми використовуiмо легко перевiряiму за iндукцiiю рiвнiсть 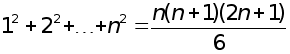 ).
).
Таким чином, обчислення ненульових елементiв 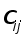 трикутноi матрицi С потребуi
трикутноi матрицi С потребуi
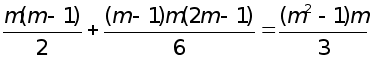
операцiй множення i дiлення.
3.Обчислення правих частин yk за формулами (15) потребуi m
дiлень, а вiдшукання 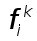 за формулами (16)
за формулами (16)
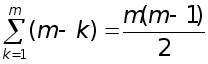
множень. Разом, обчислення правих частин перетвореноi системи (8) потребуi
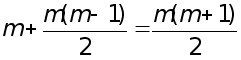
дiй множення i дiлення.
Усього для реалiзацii прямого ходу методу Гаусса необхiдно виконати
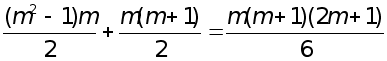
дiй.
4.Для реалiзацii зворотнього ходу методу Гаусса за формулами (10) необхiдно
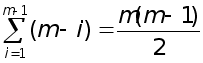
множень.
Всього, для реалiзацii методу Гаусса необхiдно виконати
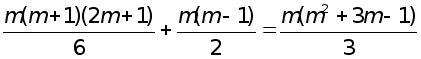
дiй множення i дiлення, причому основний час витрачаiться на прямий хiд. Для великих mчисло дiй множення i дiлення у методi Гаусса близьке до 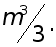 За витратами часу та необхiднiй машиннiй пам’ятi метод Гаусса придатний для розв’язання систем рiвнянь (2) загального вигляду з кiлькiстю змiнних m порядку 100.
За витратами часу та необхiднiй машиннiй пам’ятi метод Гаусса придатний для розв’язання систем рiвнянь (2) загального вигляду з кiлькiстю змiнних m порядку 100.
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ .
Пусть имеется функция 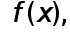 которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке.
которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке.
Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных ввобще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования.
Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена
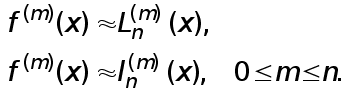
Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом.
Будем предполагать, что функция задана в равностоящих узлах
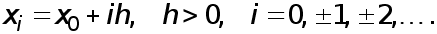
Ее значения и значения производных в узлах будем обозначать
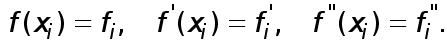
Пусть функция задана в двух точках  и
и 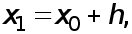 ее значения
ее значения 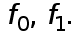
Посстроим интерполяционный многочлен первой степени
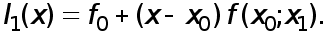
Производная 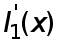 равна
равна
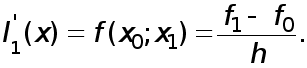

Производную функцию 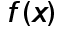 в точке
в точке 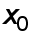 приближенно заменяем производной интерполяционного многочлена
приближенно заменяем производной интерполяционного многочлена
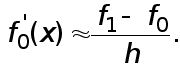 (1)
(1)
Величина  называется первой разностной производной.
называется первой разностной производной.
Пусть 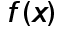 задана в трех точках
задана в трех точках 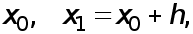
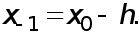
Интерполяционный многочлен Ньютона второй степени имеет вид
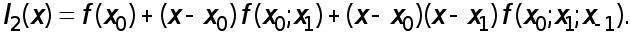
Берем производную
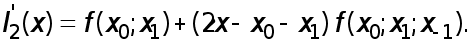
В точке 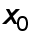 она равна
она равна
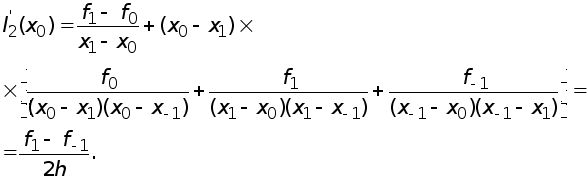
Получаем приближенную формулу
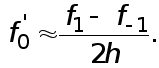 (2)
(2)
Величина 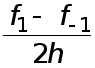 называется центральной разностной производной.
называется центральной разностной производной.
Наконец, если взять вторую производную
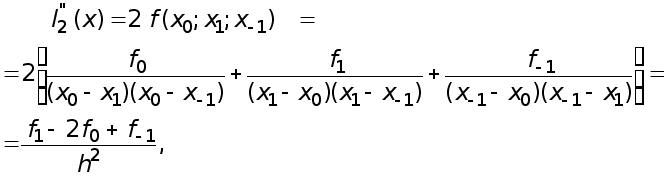 получаем приближенную формулу.
получаем приближенную формулу.
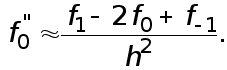 (3)
(3)
Величина 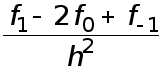 называется второй разностной производной.
называется второй разностной производной.
Формулы (1)-(3) называются формулами численного дифференцирования.
Предполагая функцию 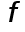 достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (1)-(3).
достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (1)-(3).
В дальнейшем нам понадобится следующая лемма.
Лемма 1. Пусть 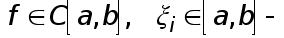 произвольные точки,
произвольные точки,  Тогда существует такая точка
Тогда существует такая точка 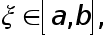 что
что
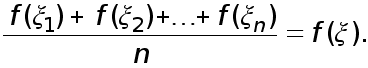
Доказательство. Очевидно неравенство
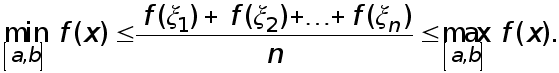
По теореме Больцано-Коши о промежуточных значениях непрерывной функции на замкнутом отрезке она принимает все значения между 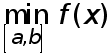 и
и 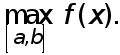 Значит существует такая точка
Значит существует такая точка 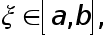 что выполняет указанное в лемме равенство.
что выполняет указанное в лемме равенство.
Погрешности формул численного дифференцирования дает следующая лемма.
Лемма 2.
1.Предположим, что 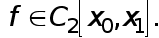 Тогда существует такая точка
Тогда существует такая точка 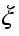 , что
, что
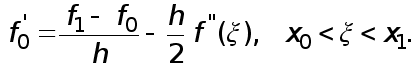 (4)
(4)
Если 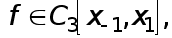 то существует такая точка
то существует такая точка 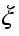 , что
, что
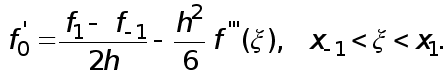 (5)
(5)
Когда  то существует
то существует 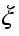 такая, что
такая, что
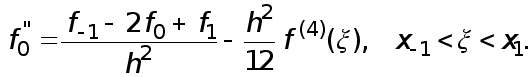 (6) Доказательство. По формуле Тейлора
(6) Доказательство. По формуле Тейлора
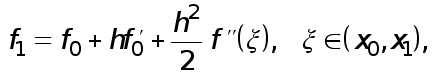
откуда следует (4).
Если 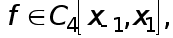 то по формуле Тейлора
то по формуле Тейлора
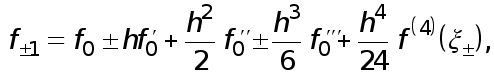 (7)
(7)
где 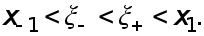
Подставим (7) в 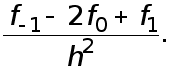 Получаем
Получаем
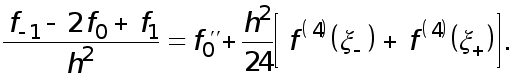
Заменяя в соответствии с леммою 1
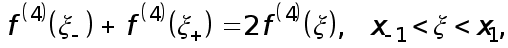
получаем
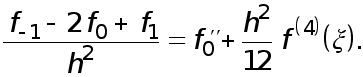
Откуда и следует (6).
Равенство (5) доказывается аналогично ( доказательство провести самостоятельно).
Формулы (4)-(6) называются формулами численного дифференцирования с остаточными членами.
Погрешности формул (1)-(3) оцениваются с помощью следующих неравенств, которые вытекают из соотношений (4)-(6):
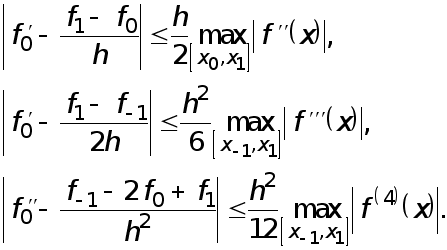
Говорят, что погрешность формулы (1) имеет первый порядок относительно  (или порядка
(или порядка  ), а погрешность формул (2) и (3) имеет второй порядок относительно
), а погрешность формул (2) и (3) имеет второй порядок относительно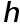 (или порядка
(или порядка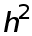 ). Также говорят, что формула численного дифференцирования (1) первого порядка точности (относительно
). Также говорят, что формула численного дифференцирования (1) первого порядка точности (относительно 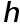 ), а формулы (2) и (3) имеют второй порядок точности.
), а формулы (2) и (3) имеют второй порядок точности.
Указанным способом можно получать формулы численного дифференцирования для более старших производных и для большего количества узлов интерполирования.
Выбор оптимального шага. Допустим, что граница абсолютной погрешности при вычислении функции 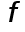 в каждой точке удовлетворяет неравенству
в каждой точке удовлетворяет неравенству
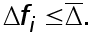 (8)
(8)
Пусть в некоторой окрестности точки 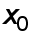 производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам
производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам
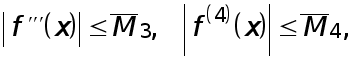 (9)
(9)
где 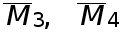 - некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин
- некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин 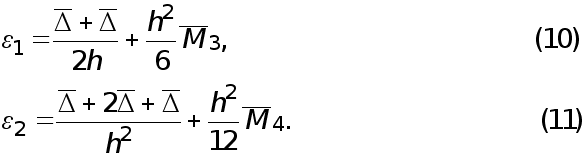
Минимизация по 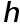 этих величин приводит к следующим значениям
этих величин приводит к следующим значениям 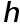 :
:
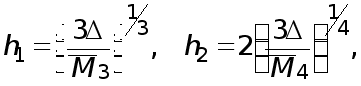 (12)
(12)
при этом
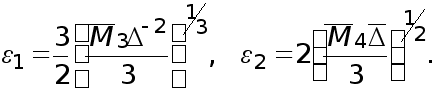 (13)
(13)
Если при выбранном для какой-либо из формул (2), (3) значении 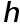 отрезок
отрезок 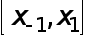 не выходит за пределы окрестности точки
не выходит за пределы окрестности точки 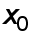 , в которой выполняется соответствующее неравенство (9), то найденное
, в которой выполняется соответствующее неравенство (9), то найденное 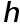 есть оптимальным и полная погрешность численного дифференцирования оценивается соответствующей величиной (13).
есть оптимальным и полная погрешность численного дифференцирования оценивается соответствующей величиной (13).
ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ.
Интерполирование многочленом Лагранжа или Ньютона на отрезке 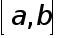 с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того, чтобы избежать больших погрешностей, весь отрезок
с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того, чтобы избежать больших погрешностей, весь отрезок 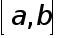 разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию
разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию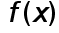 многочленом невысокой степени ( так называемая кусочно-полиномиальная интерполяция).
многочленом невысокой степени ( так называемая кусочно-полиномиальная интерполяция).
Одним из способов интерполяции на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке 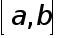 и имеющую на этом отрезке некоторое число непрерывных производных.
и имеющую на этом отрезке некоторое число непрерывных производных.
Слово ,,сплайн’’ (английское spline) означает гибкую линейку, используемую для проведения гладких кривых через заданные точки плоскости.
Преимущество сплайнов перед обычной интерполяцией является, во-первых, их сходимость, и, во-вторых, устойчивость процесса вычислений.
Рассмотрим частный, но распространенный в вычислительной практике случай, когда сплайн определяется с помощью многочленов третьей степени ( кубический сплайн).
Пусть на 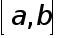 задана непрерывная функция
задана непрерывная функция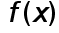 . Введем узлы ( сетку):
. Введем узлы ( сетку):
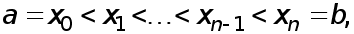
и обозначим 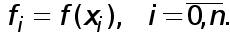
Интерполяционным кубическим сплайном, соответствующим данной функции 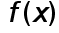 и данным узлам, называеться функция
и данным узлам, называеться функция 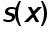 , удовлетворяющая следующим усовиям:
, удовлетворяющая следующим усовиям:
а) на кождом сегменте 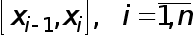 функция
функция 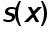 является многочленом третьей степени;
является многочленом третьей степени;
б) функция 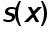 , а так же ее первая и вторая производные непрерывны на
, а так же ее первая и вторая производные непрерывны на 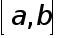 ;
;
в) 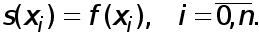
Последнее условие называется условием интерполирования.
Докажем существование и единственность сплайна, определяемого перечисленными условиями (плюс некоторые граничные условия, которые будут введены в процессе доказательства). Приводимое ниже доказательство содержит также способ построения сплайна.
На каждом из отрезков 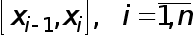 будем искать функцию
будем искать функцию  в виде многочлена третьей степени
в виде многочлена третьей степени
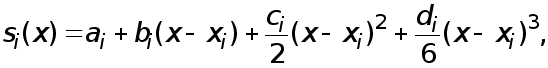 (1)
(1)
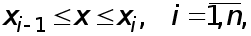
где 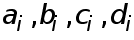 - коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов. Имеем
- коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов. Имеем
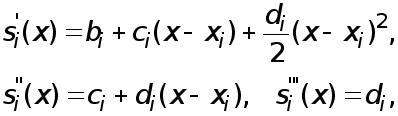
поэтому 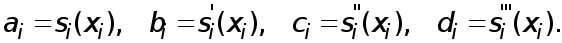
Из условий интерполирования 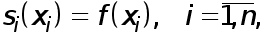 получаем, что
получаем, что
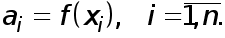
Доопределим , кроме того , 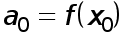 .
.
Далее , требование непрерывности функции 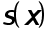 приводит к условиям
приводит к условиям
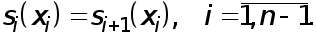
Отсюда,учитывая выражения для функций 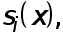 получаем при
получаем при 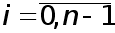 уравнения
уравнения
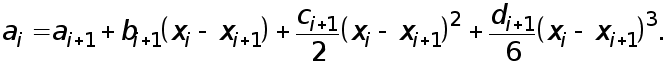 Обозначая
Обозначая 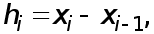 перепишем эти уравнения в виде
перепишем эти уравнения в виде
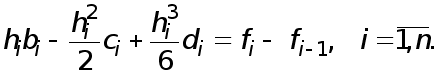 (2)
(2)
Условия непрерывности первой производной
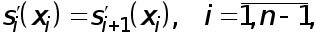
приводят к уравнениям
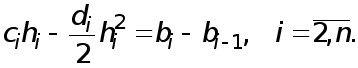 (3)
(3)
Из условий непрерывности второй производной получаем уравнения
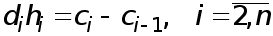 . (4)
. (4)
Объединяя (2) -(4) , получим систему 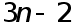 уравнений относительно
уравнений относительно 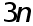 неизвестных
неизвестных 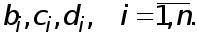
Два недостающих условия получают, задавая те или иные граничные условия для 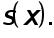 Предположим, например, что функция
Предположим, например, что функция 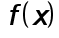 удовлетворяет условиям
удовлетворяет условиям 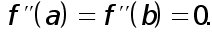 Тогда естественно требовать, чтобы
Тогда естественно требовать, чтобы 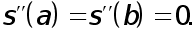 Отсюда получаем
Отсюда получаем 
т.е. 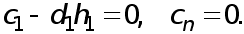
Заметим, что условие 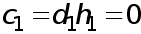 совпадает с уравнением (4) при
совпадает с уравнением (4) при 
 . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:
. Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:
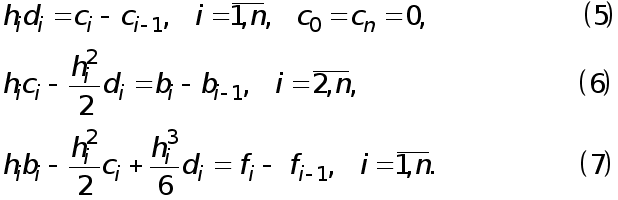 Убедимся в том, что эта система имеет единственное решение. Исключим из (5)- (7) переменные
Убедимся в том, что эта система имеет единственное решение. Исключим из (5)- (7) переменные 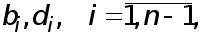 и получим систему, содержащую только
и получим систему, содержащую только  Для этого рассмотрим два соседних уравнения (7) :
Для этого рассмотрим два соседних уравнения (7) :
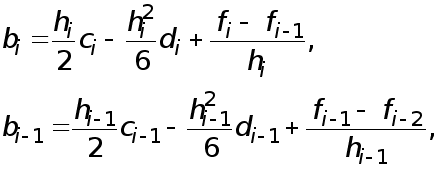
и вычтем второе уравнение из первого. Тогда получим
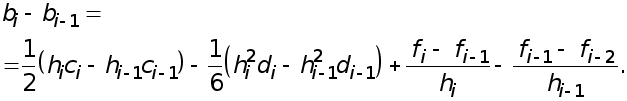
Подставляя найденное выражение для 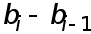 в правую часть уравнения (6), получим
в правую часть уравнения (6), получим
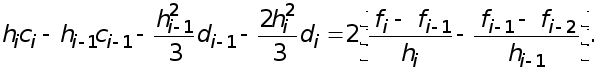 (8)
(8)
Далее, из уравнения (5) получаем

И подставляя эти выражения в (8) , приходим к уравнению
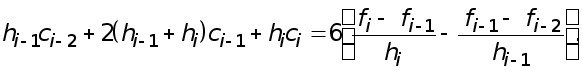
Окончательно для определения коэффициентов 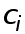 получаем систему уравнений
получаем систему уравнений
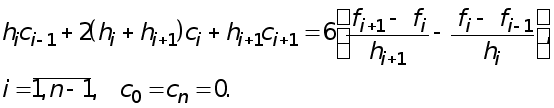 (9)
(9)
В силу диагонального преобладания система (9) имеет единственное решение. Так как матрица системы трехдиагональная, решение можно найти методом прогонки. По найденным коэффициентам 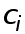 коэффициенты
коэффициенты 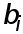 i
i 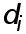 определяются с помощь явных формул
определяются с помощь явных формул
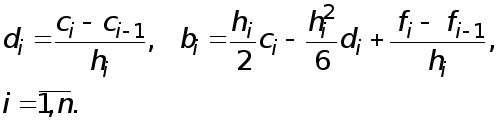 (10)
(10)
Таким образом, доказано, что существует единственный кубический сплайн, определяемый условиями а)-в) и граничными условиями 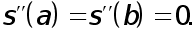 Заметим , что можно рассматривать и другие граничные условия.
Заметим , что можно рассматривать и другие граничные условия.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.
На практике редко удается вычислить точно определенный интеграл. Например, в элементарных функциях не вычисляется функция Лапласа
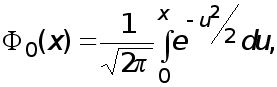
широко используемая в теории вероятностей для вычисления вероятностей, связанных с нормально распределенными случайными величинами.
Рассмотрим некотрые широко используемые приемы приближенного вычисления определенных интегралов.
Квадратурные формулы.
Введем понятие квадратурные формулы. Пусть дан определенный интеграл
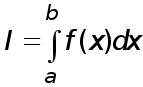 (1)
(1)
от непрерывной на отрезке 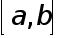 функции
функции 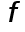 . Приближенное неравенство
. Приближенное неравенство
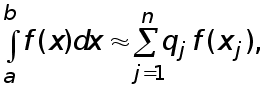 (2)
(2)
где  - некоторые числа,
- некоторые числа, 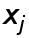 - некотрые точки отрезка
- некотрые точки отрезка 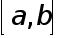 , называется квадратурной формулой, определяемой весами
, называется квадратурной формулой, определяемой весами и узлами
и узлами 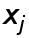 .
.
Говорят, что квадратурная формула точна для многочленов степени 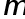 , если при замене
, если при замене 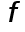 на произвольный алгебраический многочлен степени
на произвольный алгебраический многочлен степени  приближенное равенство (2) становится точным.
приближенное равенство (2) становится точным.
Рассмотрим наиболее простые квадратурные формулы.
Формула прямоугольников. Допустим, что 
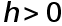 . Положим приближенно
. Положим приближенно
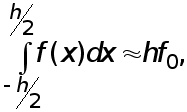 (3)
(3)
где 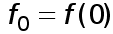 , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции
, т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции 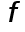 , аппроксимируется площадью прямоугольника, высота которого равна значению
, аппроксимируется площадью прямоугольника, высота которого равна значению 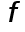 в средней точке основания трапеции .
в средней точке основания трапеции .

Найдем остаточный член , т.е. погрешность формулы (3) .
Пусть
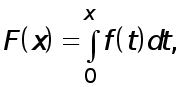 (4)
(4)
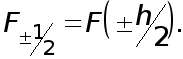 Так как
Так как 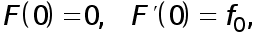
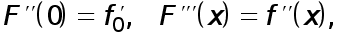 то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем
то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем

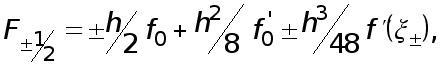 (5)
(5)
где 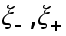 -некоторые точки ,
-некоторые точки , 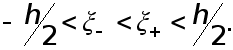
Функция 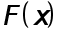 является первообразной для
является первообразной для 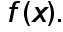 Поэтому для интеграла, стоящего в левой части приближенного равенства (3), из формулы Ньтона - Лейбница с расчетом (5) вытекает следующее соотношеие
Поэтому для интеграла, стоящего в левой части приближенного равенства (3), из формулы Ньтона - Лейбница с расчетом (5) вытекает следующее соотношеие
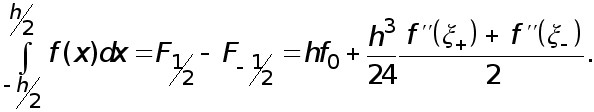
Отсюда с помощью ранее доказанной леммы получаем формулу прямоугольников с остаточным членом :
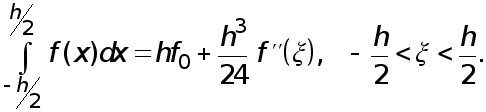 (6)
(6)
Формула трапеций. Пусть 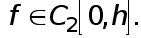 Полагаем
Полагаем
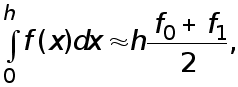 (7)
(7)
где 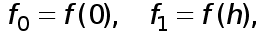 т.е. интеграл
т.е. интеграл  приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке.
приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке.
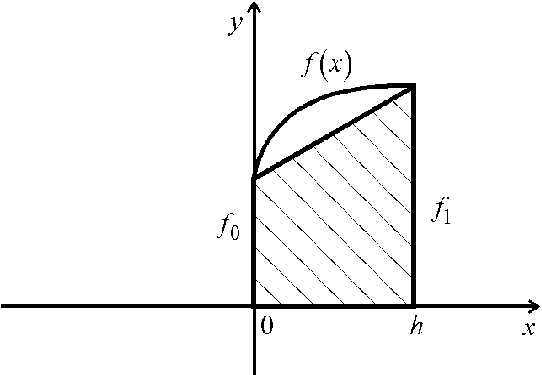
Найдем остаточный член, т.е. погрешность формулы (7). Выразим 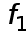 i
i 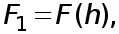 где
где 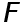 - функция (4), по формуле Тейлора с остаточным членом в интегральной форме
- функция (4), по формуле Тейлора с остаточным членом в интегральной форме  :
:
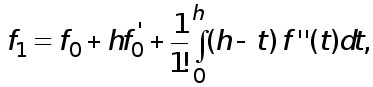 (8)
(8)
 (9)
(9)
Согласно (8) имеем
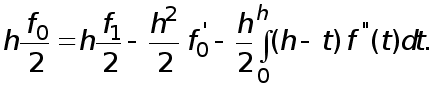 (10)
(10)
Отделив в правой части (9) слагаемое 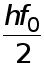 и заменив его выражением (10), с учетом того, что
и заменив его выражением (10), с учетом того, что 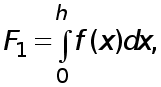 находим
находим
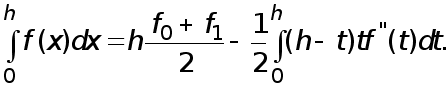

Преобразуем теперь второе слагаемое в правой части, используя обобщенную теорему о среднем.

* Формула Тейлора с остаточным членом в интегральной форме
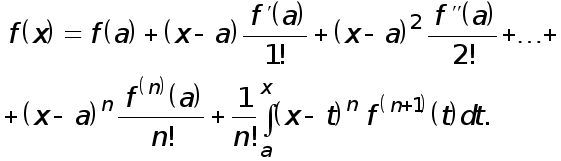
Теорема 1 (обобщенная теорема о среднем). Пусть 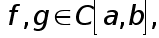 причем
причем 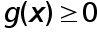 на
на 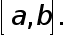 Тогда существует такая точка
Тогда существует такая точка 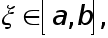 что
что

Доказательство. Положим
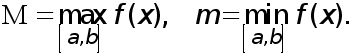 (11)
(11)
Тогд, так как 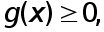 то
то
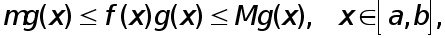
и, следовательно,
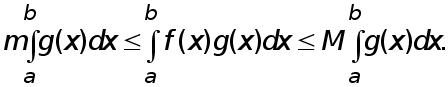

Если 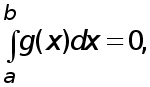 то
то 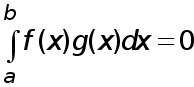 и в качестве
и в качестве 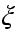 можн взять любую точку из
можн взять любую точку из 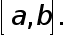
Если 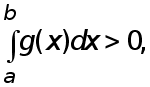 то вытекает существование такого числа с, удовлетворяющего неравенствам ( для этого делим все части
то вытекает существование такого числа с, удовлетворяющего неравенствам ( для этого делим все части  на
на 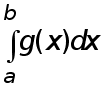 ):
):
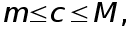 (12)
(12)
что
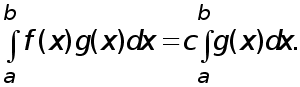 (13)
(13)
По теореме о промежуточных значениях непрерывной функции в силу (11) , (12) найдется точка 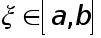 , в которой
, в которой  что вместе с равенством (13) доказывает теорему .
что вместе с равенством (13) доказывает теорему .
Теперь, так как 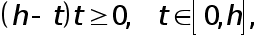 то по доказанной теоремою
то по доказанной теоремою
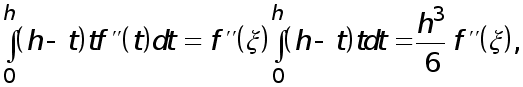
где 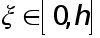 - некоторая точка . Подставляя полученное в
- некоторая точка . Подставляя полученное в  , приходим к формуле трапеций с остаточным членом :
, приходим к формуле трапеций с остаточным членом :
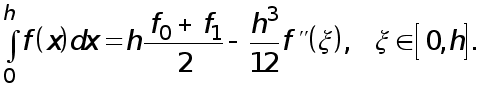 (14)
(14)
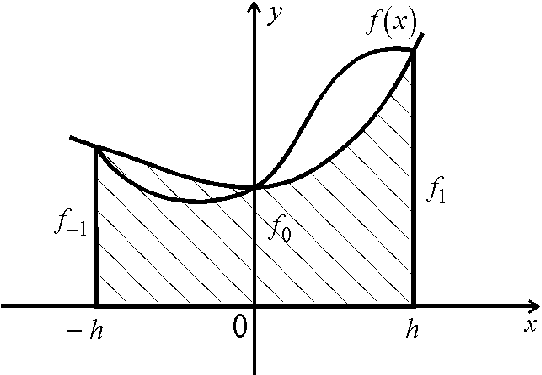
Формула Симпсона . Предположим, что 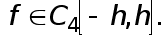 Интеграл
Интеграл 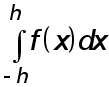 приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки
приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки 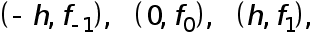 де
де 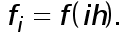
Указанная парабола задается уравнением
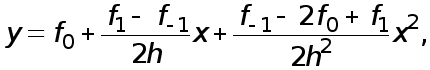
в чем нетрудно убедиться, положив поочередно 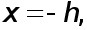
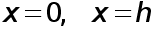 (ее можно также получить, построив интерполяционный многочлен второй степени и приводя подобные ) Отсюда находи ( проверить самостоятельно)
(ее можно также получить, построив интерполяционный многочлен второй степени и приводя подобные ) Отсюда находи ( проверить самостоятельно)
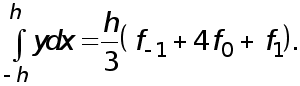
Таким образом , формула Симпсона , называемая также формулой парабол , имеет вид
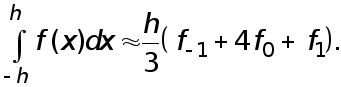 (15)
(15)
Положим 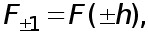 где
где 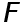 -функция (4). Поскольку
-функция (4). Поскольку
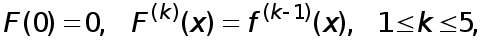
то согласно формул Тейлора с остаточным членом в интегральной форме имеем
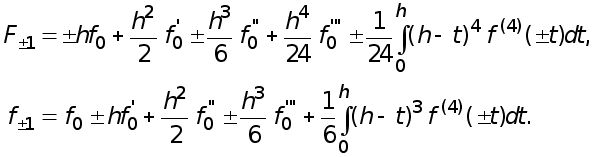 Отсюда получаем
Отсюда получаем
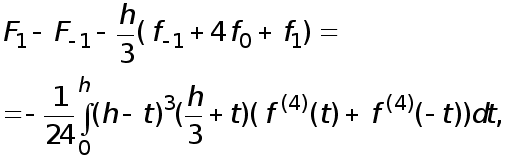 (16)
(16)
т.к. остальные члены взаимно уничтожаются.
Поскольку 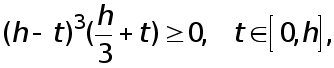 то применяя к интегралу (16) теорему 1 , а затем к полученному результату лемму, находим
то применяя к интегралу (16) теорему 1 , а затем к полученному результату лемму, находим
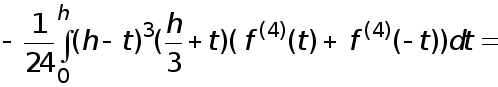
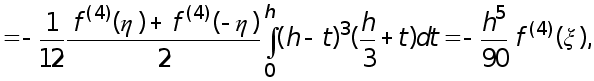 (17)
(17)
где 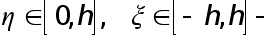 нектрые точки.
нектрые точки.
Принимая во внимание, что 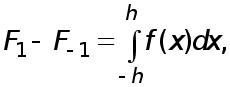 из (16), (17) приходим к формуле
из (16), (17) приходим к формуле
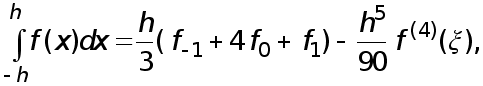 (18) т.е. к формуле Симпсона с остаточным членом.
(18) т.е. к формуле Симпсона с остаточным членом.
Рассмотрим квадратурные формулы прямоугольников (3), трапеций (7) и Симпсона (15) называются каноничными.
Усложненные квадратурные формулы.
На практике, если требуется вычислить приближенно интеграл (1) , обычно делят заданный отрезок 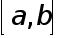 на
на 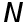 равных частей и на кождом частичном отрезке применяют какую-либо одну каноничную квадратурную формулу, а затем суммируют полученные результаты. Построенная таким путем квадратурная формула на отрезке
равных частей и на кождом частичном отрезке применяют какую-либо одну каноничную квадратурную формулу, а затем суммируют полученные результаты. Построенная таким путем квадратурная формула на отрезке 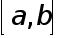 называется усложненной. При применении формул прямугольников и трапеций длину частичных отрезков удобно применять за
называется усложненной. При применении формул прямугольников и трапеций длину частичных отрезков удобно применять за 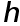 , а при использовании формулы Симпсона - за
, а при использовании формулы Симпсона - за 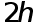 .
.
Остановимся сначала на применении формулы прямоугольников. Пусть  Обозначим частичные отрезки через
Обозначим частичные отрезки через 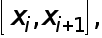
где 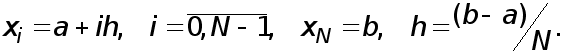
В соответствии с (3) полагаем
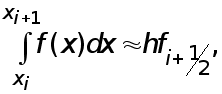 (19)
(19)
где 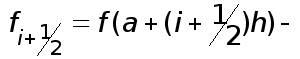 значение
значение 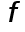 в середине частичного отрезка
в середине частичного отрезка 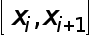 . При этом справедливо аналогичное (6) равенство
. При этом справедливо аналогичное (6) равенство
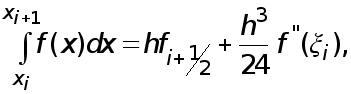 (20) где
(20) где 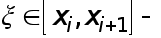 некоторая точка.
некоторая точка.
Суммирование по всем частичным отрезкам приближенного равенства (19) приводит к усложненной квадратурной формуле прямоугольников:
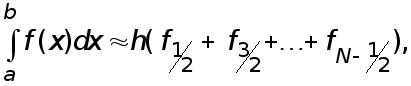 (21)
(21)
а суммирование равенств (20) с учетом того,что по лемме

где 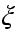 -некоторая точка отрезка
-некоторая точка отрезка 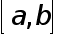 , дает усложненную формулу прямоугольников с остаточным членом:
, дает усложненную формулу прямоугольников с остаточным членом:

 (22)
(22)  Совершенно аналогично при услвии, что
Совершенно аналогично при услвии, что 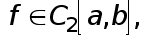 с использованием формул (7), (14) получается усложненная квадратурная формула трапеций
с использованием формул (7), (14) получается усложненная квадратурная формула трапеций
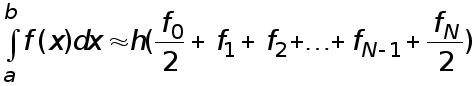 (23)
(23)
и отвечающая ей формула с остаточным членом
 (24)
(24)
где 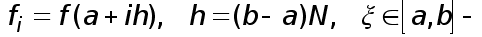 некоторая точка.
некоторая точка.
Пусть теперь 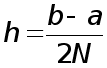 и, как обычно,
и, как обычно, 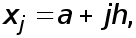
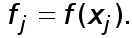 Перепишем каноническую квадратурную формулу Симпсона (15) применительно к отрезку
Перепишем каноническую квадратурную формулу Симпсона (15) применительно к отрезку 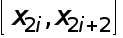 длины
длины 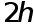 :
:

Суммируя левую и правую части этого соотношения от 0 до
N-1, получаем усложненную квадратурную формулу Симпсона (25)
Сответствующая ей формула с остаточным членом, полученная суммированием по частичным отрезкам 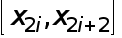 равенств вида (18), при условии, что
равенств вида (18), при условии, что 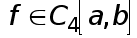 , такова :
, такова :
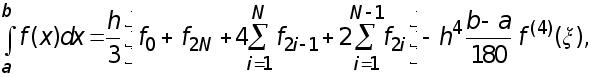 (26)
(26)
где 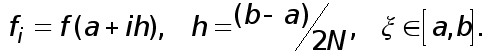
Введем краткие обозначения
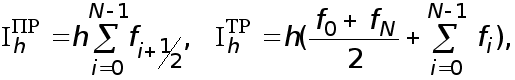 (27)
(27)
где 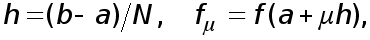 а также положим
а также положим
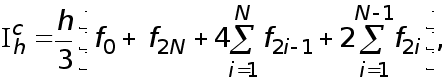 (28)
(28)
где 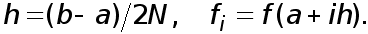
Приближенные равенства
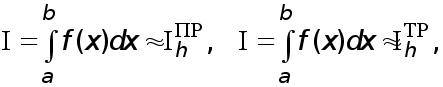 (29)
(29)
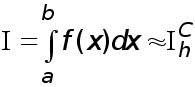 (30)
(30)
назовем сответственно формулами прямоугольников, трапеций и фор
Вместе с этим смотрят:
"Инкарнация" кватернионов
* Алгебры и их применение
*-Алгебры и их применение
10 способов решения квадратных уравнений
Cпособы преобразования комплексного чертежа, применение при изображении предметов