Шпоры по математическому анализу
1. Производные и дифференциалы высших порядков
Опр-ие: производной n-го порядка (n³2) функции у=f(х) называется производная (первого порядка) от производной (n-1)-го порядка.
Найдя 1-ю производную можно определить 2-ю производную по тем же формулам, по которым определяли первую.
Опр-ие: Дифференциалом n-го порядка функции у=f(х) называется дифференциал первого порядка от дифференциала (n-1)-го порядка. (обозначается dny)По определению dny= d(dn-1y). Иногда dy называют диф. Первого порядка. В общем случае, dny=f(n)(х)dxn, в предположении, что n-ая производная f(n)(х) сущ-ет, поэтому понятно, что n-e. Производную обозначают так
3. Теорема Ролля.
Теорема Ролля: Если функция
у=f(х) непрерывна на замкнутом промежутке [a,b], дифференцируема хотя бы в открытом промежутке (a,b) и на концах промежутка ее значения совпадают
f(a)=f(b), то внутри промежутка найдется такая точка x=c, что
f'(c)=0Док-во: Если функция сохраняет постоянное значение на промежутке [a,b], f(х)= f(a)=f(b), то f'(c)=0 и в качестве точки с можно взять любую точку интервала (a,b).
Пусть теперь функция f(x) не является постоянной. По теореме Вейштраса существуют точки х1 и х2на отрезке [a,b] , в которых достигаются наименьшее m и наибольшее М значения функции. Обе эти точки не могут быть концевыми для отрезка [a,b], т.к. из условия f(a)=f(b) вытекало бы, что m=М, следовательно, функция f(х) сохраняла бы постоянное значение, вопреки предположению.
Допустим, что не совпадает с концом отрезка точка х1, т.е. a< х1, тогда х1 является точкой локальности экстремума. По условия теоремы существует f'(х1). Из этих двух утверждений по теореме Ферма получаем f'(х1)=0, следовательно,
х1 можно принять за точку с.
2. Теорема Ферма (необходимое условие локального экстремума).
Опр-ие: Функция у=f(х) имеет в точке x0локальный максимум, если сущ-ет окрестность (х0-d, х0+d), для всех точек х которой выполняется неравенство f(х)£f(х0). Аналогично определяется локальный минимум, но выполняться должно равенство f(х)³f(х0).
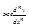
Теорема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю.
Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-d, х0+d) - та окрестность, для точек которой выполняется неравенство
Здесь возможно как 1 и 2 варианты, но | ∆х| <δ
При ∆х>0, будет ∆y:∆x ≤0, поэтому
При ∆х<0, будет ∆y:∆x ≥0, поэтому
По условию теоремы, существует производная f'(х0)А это означает, что правая производная fпр'(х0) и левая производная fл'(х0) равны между собой: fпр'(х0)= fл'(х0)= f'(х0). Таким образом, с одной стороны, f'(х0)≤0, с другой стороны, f'(х0)≥0, что возможно лишь, когда f'(х0)=0.
4. Теорема Коши.
Теорема Коши:Пусть функции
у=f(х) и у=g(х) неперырвны на отрезке [a,b],дифференцируемы хотя бы в открытом промежутке (a,b) и на этом промежутке g
'(х) не обращается в нуль. Тогда существует такая точка c Î (a,b), что выполняется равенство (1)
Докозательство: Вначале отметим, что знаменатель
g(b)-g(a) ≠ 0,т.к. из равенства
g(b)=g(a) следовало бы по теореме Ролля, что производная g
'(х) обратилась бы в нуль в какой-нибудь точке промежутка (a,b), что противоречит условию g
'(х)≠0. Образуем вспомогательную функцию:
К ней применима теорема Ролля: F(х) непрерывна в [a,b] и дифференцируема в (a,b) как сумма функций, непрерывных и дифференцируемых в соответствующих промежутках, кроме того, как легко проверить непосредственно, F(a)=F(b)=0. Следовательно, существует точка c Î (a,b), , такая, что F'(c)=0. Вычисляем:
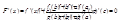
Подставляем x=c:
После деления на g'(х) (причем как говорилось раньше g'(х) ¹0), мы приходим к формуле (1)
5. Теорема Лагранжа.
Теорема Лагранжа: Если функция у=f(х) неперырвна на отрезке [a,b], дифференцируема хотя бы в интервале (a,b) то существует такая точка c Î (a,b), что f(b)-f(a)=f'(c)(b-a).
Доказательство: Применим теорему Коши к функциям f(x) и g(x)=x. Для них все условия этой теоремы выполняются, включая требование g'(х)¹0. Учитывая, что g(b)=b, g(a)=a, g'(x)=1, получим, (2)
Где точка с-точка, существующая в силу теоремы Коши в интервале (a,b). Умножив обе части на b-a, придем к формуле (2).
6. Правило Лопиталя.
Пусть выполнены следующие условия:
1. Функции f(x) и g(x) определены и дифференцируемы в выколотой окрестности точки a.
2. (1)
3. g(x) и f(x) не равны нулю в этой выколотой окрестности.
Если при этом существует (2)
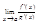
То существует и (3)
Причем, они равны между собой.(4)
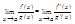
Доказательство: Доопределим функции f(x) и g(x) в точке x=a, положив f(a)=g(a)=0. Рассмотрим отрезок между числами a и x, где точка из упомянутой в условии выколотой окрестности. Для определенности будем считать, что x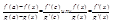
Так как f(a)=g(a)=0. При хВоа будет сВоа, потому xПо условию теоремы существует (2). Здесь х можно заменить любой другой буквой, в частности с. Переходя к пределу в равенстве (5) при хВоа, получим
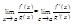
Или, что то же самое (4).
7. Необходимое условие локального экстремума функции одной переменной.
Опр-ие: Функция у=f(х) имеет в точке x0локальный максимум, если сущ-ет окрестность (х0-d, х0+d), для всех точек х которой выполняется неравенство f(х)£f(х0). Аналогично определяется локальный минимум, но выполняться должно равенство f(х)³f(х0).
Теорема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю.
Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-d, х0+d) - та окрестность, для точек которой выполняется неравенство
Здесь возможно как 1 и 2 варианты, но | ∆х| <δ
При ∆х>0, будет ∆y:∆x ≤0, поэтому
При ∆х<0, будет ∆y:∆x ≥0, поэтому
По условию теоремы, существует производная f'(х0)А это означает, что правая производная fпр'(х0) и левая производная fл'(х0) равны между собой: fпр'(х0)= fл'(х0)= f'(х0). Таким образом, с одной стороны, f'(х0)≤0, с другой стороны, f'(х0)≥0, что возможно лишь, когда f'(х0)=0.
Достаточные условия локального экстремума.
1. предположим, что в некоторой окрестности точки х0существует f'(х) ( в самой точке х0производной может не существовать). Допустим, что с приближением к точке х0слева функция f(х) возрастает (т.е. f'(х)>0), а после точки х0убывает (т.е. f'(х)<0). Очевидно, что в точке х0имеется максимум. Вывод: Если в достаточно малой окрестности точки х0 f'(х)>0 при х< х0 и f'(х)<0 при х > х0, то в точке х0 имеется максимум.
Если в достаточно малой окрестности точки х0 f'(х)<0 при х< х0 и f'(х)>0 при х > х0, то в точке х0 имеется минимум.
2. Перейдем к формулировке достаточного условия экстремума с помощью второй производной. Предполагается, что в некоторой окрестности точки х0, в том числе и в самой точке х0, существует первая производная f'(х). Кроме того, в точке х0существует вторая производная f''(х0). Исходя из выполнения необходимых условий экстремума, полагаем, что f''(х0)=0. Посмотрим теперь на f''(х)как на первую производную от функции
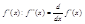
Допустим, что f''(х0)>0. Это означает, что f'(х) возрастает при переходе значений х < х0 к значениям х > х0 . Но f'(х0)=0, поэтому возрастание f'(х0)<0, при х < х0и f'(х0)>0, при х > х0 . (для значений х из достаточно малой окрестности х0 ). В соответствии с п.1 получается минимум в точке х0 . Аналогичное рассуждение при f''(х0)<0 приводит к существованию максимума в точке х0 . Вывод: если f'(х0)=0, а f''(х0)<0, то функция y=f(x) имеет локальный максимум в точке х0 . Если f'(х0)=0, а f''(х0)>0, то функция y=f(x) имеет локальный минимум в точке х0.
11. Формула Тейлора и Маклорена.
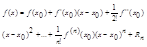
Этой формулой можно воспользоваться, когда в некоторой окрестности точки х0 существует непрерывная производная f(n+1)(x), и значения х принадлежат этой окрестности. Через Rn обозначен так называемый остаточный член. Его можно записывать в разных формах. Мы ограничимся формулой Лагранжа:

Здесь с - какое-то число, о котором известно только то, что оно находится между х0 и х.
При х0=0 формулу Тейлора называют формулой Маклорена, общий вид которой:
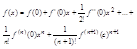
8. Нахождение наибольшего и наименьшего значений функции на отрезке.
Рассмотрим функцию у=f(х), непрерывную на отрезке [a,b]. По теореме Вейерштрасса эта функция принимает наибольшее и наименьшее значения на отрезке. Наибольшее и наименьшее значения могут достигаться либо в точках локального экстремума (x2, x3, x4, x5,), либо на концах промежутка. Находим точки, подозрительные на экстремум (х1, x2, x3, x4, x5,). Вычисляем значения функции в этих точках и на концах промежутка [a,b]. Из полученных чисел выбираем самое большое и самое маленькое. Это не предусматривает применения достаточных условий экстремума в точке х1, где локального экстремума не существует, т.е. проделана лишняя работа. Однако, как правило, экономнее вычислять значения функции во всех точках, подозрительных на экстремум, вместо того, что бы отбирать из них с помощью достаточных условий лишь те точки, в которых локальный экстремум действительно есть. Иногда описанную задачу называю глобальный экстремум.
9. Нахождение асимптот графиков функции.
Говорят, что точка движется по кривой в бесконечность, если расстояние этой точки до начала координат неограниченно возрастает.
Определение: Прямая называется асимптотой кривой, если расстояние от точки, движущейся по кривой в бесконечность, до этой прямой стремится к нулю.
Нахождение вертикальных ас:
Ищутся конечные значения х=а, при которых
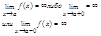
Существование такого значения часто связано с обращением в нуль знаменателя дроби.
Нахождение наклонных асимптот.
Пусть y = kx+b - асимптота кривой y=f(x) при x→+∞ (как на рисунке). Угол φ сохраняет постоянное значение, α=φ. Из ∆ KLMKM=MLּcos α. Поэтому KM и ML стремятся к нулю одновременно. ML=f(x)-(kx+b), следовательно (1):
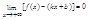
Преобразуем это равенство, вынеся х за скобки:
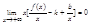
При x→∞ такое равенство возможно только тогда, когда: 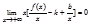
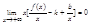
Здесь
Поэтому
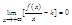
Следовательно (получаем (2)),
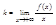
Вычислив k, находим b. Из равенства (1)(получаем (3)
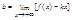
Существование пределов (2) и (3) не только необходимо, но и достаточно, чтобы прямая y=kx+b была асимтотой кривой y=f(x). В частности, при k=0 асимптота будет горизонтальной. Кривая не имеет наклонной асимптоты, если не существует хотя бы один из пределов (2) и (3).
13. Первообразная. Теорема о двух первообразных одной функции.
Определение: Функция F(x) называется первообразной для функции f(x) на интервале (a,b), если на этом интервале существует производная F'(x) и F'(x)=f(x).
Теорема: Если F1(x) и F2(x) - первообразные для одной и той же функции f(x), то их разность есть величина постоянная.
Докозательство: По условию F'1(x)=F'2(x)=f(x) обозначим: Ф(x)= F1(x) - F2(x). Очевидно, Ф'(x) равняется нулю во всем промежутке (a,b), где определены первообразные F1(x) и F2(x). Для любых х1, x2,Î (a,b) по формуле Лагранжа Ф(х1)-Ф(х2)=Ф'(c)(b-a). но Ф'(c)=0, т.к. сÎ (a,b), следовательно Ф(х1)=Ф(х2). Это означает, что Ф(х) сохраняет постоянное значение на промежутке (a,b), т.е. F1(x) - F2(x)=С.
Следствие: Если для функции f(x) первообразной на интервале (a,b) является функция F(x), то ее любая другая первообразная для f(x) имеет вид F(x)+C, где С - произвольная постоянная.
14. Неопределенный интеграл. Табличные интегралы.
Определение: Неопределенным интегралом от функции f(x) называется совокупность всех первообразных этой функции. Он изображается так: ∫ f(x)dx, где ∫- знак интеграла, f(x)dx - подынтегральное выражение,f(x) - подынтегральная функция.
Из определения вытекает, что
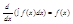
И следовательно d(∫f(x)dx)=f(x)dx. С другой стороны, ∫F'(x)dx=∫dF(x)=F(x)+C.
Если F(x) - какая-нибудь первообразная для f(x), то учитывая приведенное выше следствие, можно написать: ∫ f(x) dx = F(x)+C, где С- произвольная постоянная. Путем дифференцирования обеих частей равенства легко доказать справедливость следующих свойств:
1. ∫ Аf(x)dx = A ∫ f(x)dx (постоянный множитель можно выносить за знак интеграла).
2. ∫[f(x)-f(x)]dx=∫f(x)dx+∫f(x)dx (интеграл от суммы функций равен сумме интегралов от этих функций).
10. Схема исследования функции с помощью дифференциального исчисления и построения графика.
Исследование функции y=f(x) проводится по плану:
1. Находится ООФ.
2. Вычисляются нули функции y=f(x), т.е. значения х1, x2тАж, при которых f(x1)=0, f(x2)=0тАжМежду нулями функция, как правило сохраняет знак, так, непрерывная функция не может сменить знак не обратившись в ноль. Устанавливают где f(x)>0 и f(x)<0.
3. вычисляются производная f'(x) и находятся ее нули и знак в промежутках между нулями. В том промежутке, где f'(x)>0, функция возрастает, где f'(x)<0 - убывают. Попутно выявляются локальные экстремумы функции.
4. Вычисляется вторая производная f''(x) и с ее помощью находятся промежутки выпуклости (f''(x)<0), вогнутости (f''(x)>0) и точка перегиба (f''(x)=0).
5. Определяются вертикальные, горизонтальные и наклонные асимптоты.
Рекомендуется вычислять значения самой функции в тех точках, где f'(x) и f''(x) обращаются в нуль и наносить соответствующие точки на график. Затем нанесеные точки плавно соединяется прямой с учетом всех результатов исследования. Если функция обладает свойством четности или нечетности, то можно использовать это обстоятельство при исследовании (или после исследования для частичной проверки правильности построения графика).
21. Теорема о среднем значении для определенного интеграла.
Если функция y=f(x) непрерывна на отрезке [a,b], то найдется такая точка ξÎ(a,b), что справедливо равенство:
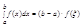
Теорема верна и при bДоказательство: Проведем его для случая a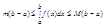
можно записать
Поделив это неравенство на полжительное число b-a, получим:
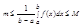
Непрерывная функция f(x) принимает всякое значение промежуточное между наименьшим m и наибольшим M значениями. Поэтому существует такое число x(a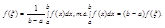
Чтд.
22. Классы интегрируемых функций. Функция Дирихле.
интегрируемость не является свойством, присущим всем функциям. В этом убеждает следующий пример. Рассмотрим функцию f(x), называемой функцией Дирихле:
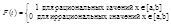
Сделаем произвольное разбиение R отрезка [a,b]. На любом частичном отрезке [xi, xi+1] найдетсяи как рациональная точка xi. Так, и иррациональная точка hi.Составим две интегральные суммы:sR и
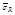
Пусть
При lR →0 предел интегральных сумм вида :sR равен b-a, в то время, как для
равен нулю. Итак, для интегральных сумм разного вида пределы получаются различные, зависящие от выбора точек на отрезках [xi, xi+1]. Это означает, что функция Дирихле не интегрируемая.
З класса функции:
1. Функции непрерывные на отрезке [a,b].
2. Функции имеющие не более конечного числа разрывов 1-го рода на отрезке [a,b]. (их называют кусочно-непрерывными)
3. Функции монотонные на отрезке [a,b] (у функции этого класса число разрывов может быть бесконечным).
23. Интеграл с переменным верхним пределом. Теорема о его непрерывности.
Теорма: Если функция f(x) интегрируема на отрезке [a,b], то функция
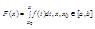
непрерывна на этом отрезке.
Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆хÎ[a,b]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек:

a x0 x х+∆х b
Получим:
По теореме (Если функция y=f(x) интегрируема на отрезке, то интегрируема и абсолютная величина |f(x)|, причем
тАж(на этом теорема закончилась, но неравенство относится к ней.) и следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства:
(на этом следствие из теоремы закончилось)
получаем:
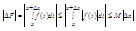
Отсюда следует, что при ∆х→0 будет ∆F→0. Это доказывает непрерывность функции F(x). Отметим, что для подынтегральной функции f(x) точка х может быть точкой разрыва.
24. Теорема о произвольной от интеграла с переменным верхним пределом.
Теорема: Если функция y=f(x) непрерывна на промежутке (a,b), то производная от интеграла
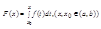
По переменному верхнему пределу x существует и равна подынтегральной функции с заменой переменной интегрирования верхним пределом х, т.е. F'(x)=f(x)
Доказательство: Дадим аргументу х приращение
∆х так, чтобы х+∆хÎ(a,b). Для приращения ∆F функции F(x) воспользуемся формулой
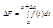
и применим теорему о среднем значении ( Если функция y=f(x) непрерывна на отрезке [a,b], то найдется такая точка ξÎ (a,b), что справедливо равенство:
Теорема верна и при b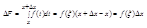
Число x заключено между числами х и х+∆х и при стремлении ∆х к нулю ξ стремится к х.
Перейдем к вычислению производной F'(x).
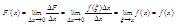
Последнее равенство основано на непрерывности функции f(x) в любой точке х промежутка (a,b).
Следствие: Всякая функция f(x), непрерывная на промежутке (a,b), имеет первообразную на этом промежутке.
Действительно, первообразной для такой функции является функция
Предыдущая теорема устанавливает связь между неопределенным и определенным интегралом. Можно написать:

25. Формула Ньютона-Лейбница.
Пусть F(x) -произвольная первообразная для функции f(x), заданной на промежутке [a,b]. Так как две первообразные одной и той же функции отличаются на постоянное слагаемое, то верно равенство (1):
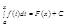
( в качестве числа х0 взято число а).
В этом тождестве положим х=а и получим ,
Откуда С = -F(a). Формула (1) примет вид:
Заменяя здесь х на b, приходим к формуле Ньютона-Лейбница:
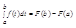
Иногда ее правую часть записывают короче с помощью двойной подстановки:
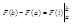
26. Интегрирование по частям в определнном интеграле.
Пусть u и v - непрерывно дифференцируемые функции. Проинтегрируем равенство d(uv)=udv+vdu в пределах от a до b.
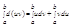
В левой части применим формулу Ньютона-Лейбница:
Получим:
Получим формулу интегрирования по частям:
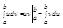
27. Замена переменной в определенном интеграле.
Теорема: при замене переменной х на t по формуле x=φ(t) равенство (1)
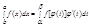
Справедливо при условиях:
1. φ(α) = а, φ(β) = b,
2. φ'(t) непрерывна на отрезке [α,β],
3 f(x) непрерывна на отрезке [a,b], а f[φ(t)] определена непрерывна на отрезке [α,β].
Доказательство: при наших предположениях левая и правая части равенства (1) существуют и существуют первообразные подынтегральные функции. Пусть ∫f(x)dx = F(x)+C. Тогда, как легко проверить дифференцированием обеих частей, справедливо равенство ∫f[φ(t)]φ'(t)dt = F[φ(t)]+C правая часть дифференцируется как сложная функция). Применяем формулу Ньютона-Лейбница
Получаем
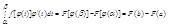
(по условию 1)
правые части этих двух равенств оказываются одинаковыми, следовательно, можно приравнять левые части. Приравнивая их, приходим к равенству (1). Ч.т.д.
30. Интегралы с бесконечными пределами.
Определение определенного интеграла по конечному промежутку [a,b] неприменимо к случаю бесконечного промежутка, например [a, +∞). Дело в том, что нельзя промежуток [a, +∞) разделить на конечное число частичных промежутков [xi, xi+1] конечной длины, чледовательно, нельзя составить сумму интегральную сумму. Понятие интеграла с бесконечным пределом вводится на основе понятий опредленного интеграла и понятия предела.
Определение: Предположим, что функция y=f(x) определена в промежутке [a, +∞) и интегрируема в любом промежутке [a,b] (b>a). Если существует конечный предел
То это предел называют несобственным интегралом от функции f(x) на промежутке от а до +∞ и обозначают
Аналогично определяется интеграл от -∞ до b:
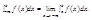
Интеграл от -∞ до +∞ можно определить так:
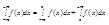
Где с - произвольное число.
Когда несобственный интеграл существует, говорят, что он существует или что он сходится. В противном случае несобственный интеграл расходится.
40. Необходимые условия абсолютного экстремума функции двух переменных.
Теорема: Пусть функция z=f(x,y) имеет экстремум в точке (x0, у0). Если в этой точке существуют частные производные по х и по у, то они равны нулю.
Докаательство: Оно может быть сведено к применению известной теоремы для функции одной переменной. В наших условиях функция f(x,y0) имеет экстремум в точке x0, т.к. неравенство f(х0+∆х, y0+∆у)≤f(х0, y0), иначе ∆f≤0
Или ∆f≥0 должно, в частности, выполнятся и при ∆у=0. Поэтому, d/dx∙f(x,y0)=0 при х=х0, а это то же самое, что f'x(х0, y0)=0. Аналогично устанавливается, что f'у(х0, y0)=0. Экстремум возможен и тогда, когда одна или обе частные производные не существуют, что тоже является необходимым условием экстремума. Т.о., необходимые условия экстремума формулируются так: для каждой из частных производных выполняется одно из двух - лиюл она существует и равна нулю, либо она не существует.
31. Предел и непрерывность функции двух переменных.
Определение: Число А называется пределом по совакупности переменных функции f(x,y) при стремлении х к х0 и у к у0, если для любого ε>0 существует такое δ>0, что для всех точек (x,y), координаты которых удовлетворяют неравенствам │ х - х0 │< δ, │ y - y0 │< δ ( за исключением, быть может, точки (х0, y0)), выполняется неравенство │f(x,y)-A│ < ε. Применяется обозначение
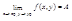
Заметим, что точка (х0, y0) может не принадлежать ООФ f(x,y).
Пусть функция f(x,y) определена в области D.
Определение. Если выполняются три условия:
1. (х0, y0)Î D;
2. существует
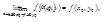
3.
то функция называется непрерывной в точке (х0, y0).
Определение: Если не выполняется хотя бы одно из этих условий, то функцию называют разрывной в точке (х0, y0), а саму точку называют точкой разрыва.
Определение: Функция называется непрерывной в области, если она непрерывна в каждой точке этой плоскости.
Определение: Функция z = f(x,y) называется непрерывной в точке (х0, y0), если при стремлении к нулю приращений ∆х, ∆у, независимых переменных стремится к нулю полное приращение ∆z функции f(x,y) (здесь предполагается выполнение условий 1 и 2.) (∆z - полное приращение).
42. Условный экстремум, метод множителей Лагранжа для функции двух переменных.
В этом методе не требуется выражать явно y через х , однако используется то обстоятельство, что в случае предполагаемой замены y на g(x) дело сводится к безусловному экстремуму функции одной переменной.
Итак, находим полную прозводную от z по х, считая y функцией х:
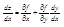
В точках экстремума dz: dx=0, следовательно (1),
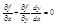
Применим снова правило дифференцирования сложной функции к уравнению φ(x,y)=0. Будем предполагать при этом, что у заменен той самой функцией х, которая неявно задается уравнением. Такая замена превращает уравнение φ(x,y)=0 в тождество. Получим (2):
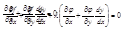
Умножим (2) на неопределенный множитель λ и сложим с (1):
Мы будем предполагать, что в точке экстремума
В¶j¸В¶у¹0. Тогда существует число l, при котором
В¶f¸В¶y + l(В¶j¸В¶у) = 0 в этой точке. Из равенства (3) следует, что в этой точке
В¶f¸В¶х + l(В¶j¸В¶х) = 0Мы приходим к необходимым условиям экстремума (4):

В этой системе из трех уранений три неизвестные величины x, y и l. Из системы находятся одна или несколько точек (х,у). Что касается l, то этот множитель играет вспомогательную роль и дальше не требуется. Найденные точки (х,у) проверяют на наличие в них экстремума и его вид (максимум или минимум). В случае необходимости вычисляются значения f(x,y) на концах промежутка, ограничивающего изменение х при описании кривой АВ. Часто из существа задачи легко решается вопрос, с каким из значений - наибольшим или наименьшим - мы имеем дело. Проведенные рассуждения обосновывают метод Лагранжа, который состоит в следующем.
Составляется вспомогательная функция
F (x,y,l) = f(x,y) + lj(x,y) (5), называемая функцией Лагранжа. Для нее выписываются как для функции трех переменных необходимые условия абсолютного экстремума:
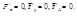
При этом получается в точности система (4).
Коэффициент l называют множителем Лагранжа.
Метод Лагранжа допускает обобщение на функции большего числа переменных. Так, в задаче на условный экстремум функции u=f(x,y,z) с ограничениями j1(x,y,z)=0 и j2(x,y,z)=0 функция Лагранжа имеет вид:
F(x,y,z, l1, l2) = f(x,y,z) + l1j1(x,y,z)+ l2j2(x,y,z).
Нулю приравниваются все произвоные по x,y,z, l1, l2.
41. Достаточные условия абсолютного экстермума функции двух переменных.
Обратимся к формуле Тейлора (вопр. 11). Нас интересует случай, когда необходимые условия экстремума выполняются, т.к. в противном случае вопрос решается однозначно - экстремума нет. Поэтому будем считать:
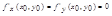
И, перенеся f(х0,y0) в левую часть, получим слева

Кроме того, обозначим
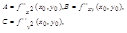
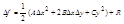
Приводим к формуле:
Положим u = AΔx2 + 2B∆xΔy +CΔy2При ρ→0 квадратичная форма u убывает со скоростью р2, т.е. быстрее. Поэтому в достаточно малой окрестности точки (х0,, y0) ,будет выполнятся неравенство 1/2│u│>│R│(если u не обратится в нуль). Это означает, что знак приращения совпадает со знаком u. Разумеется, в точках, где u=0, знаки ∆f и R совпадают. Имеются 3 возможности:
1. Величина u сохраняет знак, обращаясь в нуль только при ∆x=∆y=0. Такая квадратичная форма называется знакоопределенной. В этом случае сохраняет знак и приращение ∆f . При ∆f≤0 в точке (х0,, y0) имеется максимум, а при ∆f≥0 - минимум.
2. В любой оокрестности точки (х0,, y0) величина u принимает как положительные, так и отрицательные значения. Такая квадратичная форма называется знакопеременной. В этом случае меняет знак и приращение ∆f . Экстремума нет.
3. Величина u сохраняет знак, но обращается в нуль не только в начале координат. Такая квадратичная форма называется знакопостоянной. В этом случае никакого вывода сделать нельзя без исследования остаточного члена. Если в точках названной прямой остаточный член меняет знак, то экстремума нет, если сохраняет тот же знак, что и величина u - экстремум есть, если сохраняет знак противоположный u - экстремума нет.
Дело свелось теперь к установлению условий, при которых квадратичная форма u является знакоопределенной, знакопеременной или знакопостоянной. Если А = С = 0, В ¹ 0, то u = В∆х∆у, и квадратичная форма является знакопеременной. При совпадении знаков ∆х и ∆у она имеет знак В, при несовпалении - знак противоположный знаку В. В этом случае экстремума нет. Если к тому же В = 0, вопрос об экстремуме решается путем исследования остаточного члена R в каждом конкретном случае.

Пусть теперь хотя бы одна из величин А, С отлична от нуля. Положим для определенности, что А ≠ 0. Преобразуем форму u: вынесем за скобки А, прибавим и вычтем (В¸А ∆у)2. Первые три слагаемых представляют полный квадрат, два последних приводим к общему знаменателю:
1. Если В2 - АС <0, то форма знакоопределенная. Действительно,
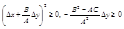
Поэтому выражение в квадратных скобках неотрицательно и может обратится в нуль только тогда, когда оба слагаемых равны нулю. Второе обращается в 0 лишь при ∆у=0. В этом случае первое слагаемое будет равно 0 только при ∆х=0. Очевидно, что знак знакоопределенной формы u совпадает со знаком числа А.
2. Если В2 - АС >0, то форма знакопеременная. Действительно, выражение в квадратных скобках останется ∆x2 и если ∆х≠0., то ∆x2 > 0; при ∆у≠0 можно взять ∆х = -В/А∆у и выражение в квадратных скобках будет отрицательным.
3. Если В2 - АС = 0, то форма знакопостоянная. В скобках останется выражение (∆х+В/А∆у)2, которое неотрицательно. Но в нуль оно обращается не только при ∆х=∆у=0, а и тогда, когда ∆х = -В/А∆у, при любом ∆у.
33. Частные производные.
Наряду с полным приращением функции вводится понятие частных приращений по х ∆хz и по у ∆уz. Они определяются формулами, где приращение дается только одной из переменных.
Определение: Частной производной функции f(x,y) по х называется предел отношения частного приращения ∆хz к приращению ∆х, когда х→0 (если этот предел существует)(1)

Аналогично определяется частная производная функции z=f(x,y) по у. Для частной производной функции нескольких переменных, производную функции одной переменной называют переменной иногда обыкновенной.
Формуле (1) можно дать такое толкование: у функции f(x,y) фиксируется значение переменной у и получается, что f(x,y) становится функцией одной переменной х, а частная производная - обыкновенной производной этой функции. Так же истолковывается формула для f'y(
Вместе с этим смотрят:
"Инкарнация" кватернионов
* Алгебры и их применение
*-Алгебры и их применение
10 способов решения квадратных уравнений
Cпособы преобразования комплексного чертежа, применение при изображении предметов