Использование корреляционных связей в комплексе с ядерно-геофизическими методами
(ягфм) каротажа при опробовании сред сложного состава
Красноперов Владимир Анатольевич, доктор геол.-мин. наук, профессор, академик РАЕН, Кульдеев Ержан Итеменович, инженер, Университет Сулеймана Демиреля, г. Алматы, Казахстан
Определенные преимущества ЯГФМ каротажа по сравнению с керновым опробованием повышают возможности комплексного исследования руд и вмещающих пород. В случаях, когда необходимо оценить содержания элементов, не обладающих благоприятными ядерными свойствами, используются эмпирические зависимости между химическими или минеральными компонентами изучаемых геологических сред, которые по своей природе могут быть кристаллохимическими и парагенетическими. Первые дают устойчивую, практически функциональную зависимость химических элементов в соединении (минерале), вторые объединяют минералы, образующиеся в одних геологических условиях, дают менее устойчивую корреляционную связь, зависящую от размеров элементов опробования, местоположения изучаемого участка и т.д. [6-10, 12, 13, 15, 16, 18-20, 21-27, 30- 33, 36, 38-40, 45, 47, 49, 51, 60, 261, 65, 67-69, 71, 72, 77, 84]. Наиболее устойчивыми из парагенетических являются связи минеральных компонент в закрытых системах, характеризующихся постоянством их суммы. К таким системам относятся, в частности кварц-карбонат-флюоритовые руды, пластовые фосфориты, фосфато-карбонаты, фосфато-кремнистые породы, карбонатно-терригенные образования.
Более чем вековая история развития учения о парагенезисе свидетельствует о неослабевающем интересе исследователей к этому разделу геологических знаний, оцененному В.И. Вернадским, как одно из крупнейших обобщений прошлого века, сыгравшего принципиально важную роль в создании основ генетической минералогии и современной геохимии. Отражая одну из кардинальных закономерностей природы - устойчивое сонахождение определенных минералов и химических элементов, парагенезис сейчас широко используется как мощное средство теоретического познания многокомпонентных минералогических и геохимических систем. Парагенетический метод в процессе изучения сложных природных объектов включает следующие этапы геологических исследований [77]:
1) постановку задачи с формированием общей цели исследований и выбором средств исследования;
2) определение компонентного состава геологического объекта, его описание как системы, выделение парагенезисов минералов и элементов;
3) генетическое истолкование результатов, конструирование модели объекта, формирование гипотез;
4) испытания моделей в реальных ситуациях, проверка гипотез практикой, превращение их в рабочую теорию для прогнозирования новых свойств объекта исследования.
Во многочисленных публикациях, посвященных парагенезису, чаще всего исследуются закономерные сообщества минералов и значительно реже- химических элементов. Это вполне закономерно, т.к. в породах химические элементы представлены в виде соединений-минералов. И практически один элемент может присутствовать в нескольких минералах, имеющих разные условия образования и составляющих изучаемую геологическую природную среду-породу. Поэтому в большинстве случаев целесообразно искать связи в геологических системах между минеральными компонентами, а не между элементами.
В работе Б.И. Смирнова [77] парагенезис рассмотрен как системное явление. Необходимость системного подхода в геологии обосновывалась в работах Ю.А. Косыгина, В.А. Соловьева, П.Ф. Иванкина, И.П. Шарапова, Р.А. Жукова, В.И. Оноприенко, Б.И. Смирнова. Характер системообразующих связей определяется, если рассматривать систему с наиболее общих позиций как взаимодействие элементов между собой, так и взаимодействие системы и среды. Единство компонентного состава и структурная однородность определяют целостность системы. Выбор методов обнаружения и описания связей между системными элементами существенно облегчается, если принять следующие определения системы: "..система - это множество объектов, на котором реализуется отношение с заранее заданным свойством" [77].
Формальная запись определения системы имеет вид:
S = def [R(m)] × P
где S-символ системы, def - дефиниция (определение); m- системообразующие элементы, R - некоторые фиксированное свойства, регулирующее выбор систематообразующего отношения R и играющее в связи с этим роль системной концепции. Процедуру конструирования системы можно представить в вид:
PВо R Во {m} = S
Таким образом, чтобы определить систему, вначале следует задать некоторое свойство Р, исходя из смысла решаемой задачи; затем на его основе найти класс отношений, обладающих этим свойством - R и перечислить множество элементов {m}, на которых реализованы отношения
R : {m} = S.
Выбор Р, вообще говоря произволен. Поэтому на одном и том же множестве, можно построить целый ряд различающихся систем:
{Р1S1; Р2S2; Р3S3; и тд. }
Множество вещественных компонентов {m} - субстрат системы, R - ее структура, Р- базовое свойство, системная концепция. Выбор Р имеет определяющее значение для успеха практической реализации системных исследований.
Основным видом геохимической информации являются сведения о количестве атомов того или иного химического элемента в некотором заданном объеме геологического объекта. Существуют различные формы фиксаций этих сведений, наиболее распространено представление в виде весовых процентов. Обычно объем геохимической пробы исчезающее мал в сравнении с размерами геологического объекта, что позволяет рассматривать ее как точку в этом объекте.
Следуя [77], обозначим символом J множество точек, в которых произведены измерения концентрации химических элементов (J {i}), символом А - множество химических элементов, обнаруженных в исследуемом геохимическом объекте
А = {aR: R=1,тАж Р}
Содержание R -го элемента в i-й точке объекта обозначим как yir; совокупность значений yir, относящихся к определенному элементу, образует множество
УR = { yir : i Î J}
Существует также более широкое множество:
У = {УR: R=1,2, тАж Р}
Таким образом, содержания элементов являются единственным объективно фиксируемым результатом эволюции любого геохимического объекта.
Значение концентрации R -го элемента в i -й точке объекта зависит как от величины текущих воздействий (xi), так и от состояния системы (Сi). Множество C= {Ci : i Î J} может трактоваться как совокупность внутренних факторов; в геохимических системах такими факторами являются состояния химических элементов, которые регулируются свойствами их атомов. Множество Х= {xi : i Î J} объединяет внешние факторы, действие которых связано с изменением условий среды.
Поскольку оценить степень участия каждого из множеств X и С в формировании yir затруднительно, то обычно оперируют объединенным множеством факторов F:
f = cux, f ={Fg.: g =1,2,3,тАжm}; Fg = {fgi : i Î J},
где Fg - множество значений некоторого природного фактора, управляющего поведением геохимического объекта (температура, давление, водородный показатель и т.п.), fgi - значения g-го фактора в i-той точке объекта, в принципе {fgi} с алгебраической точки зрения может рассматриваться как множество действительных чисел. Можно полагать, что концентрации элементов, различающихся по химическим и физическим свойствам, формируются под воздействием различных факторов. Подмножество Fs, объединяющее факторы, общие для некоторой группы элементов, выступает в качестве регулятора и если его вклад в F достаточно велик, то соответствующая группа элементов приобретает черты системного объекта. Непосредственно оценить количество и вес факторов в Fs практически невозможно, но в то же время, чем больше вклад факторов Fs в эволюцию геохимического объекта, тем выше степень общности геологической истории составляющих ее элементов. В свою очередь поведение химических элементов в геологических процессах во многом регулируется особенностями строения их атомов. Так формируется группы элементов, управляемых одними и теми же факторами, что фиксируется, в частности, сопряженностью их концентраций. Это позволяет рассматривать совокупность подобных элементов как геохимические системы. Понятие геохимической системы в соответствии с [32, 77] формируется как: тАЬтАж группа сонаходящихся в конкретном геологическом объекте химических элементов, характеризующихся сопряженностью их концентрацийтАЭ
В символах системного анализа это определение можно записать как:
АS = def [R(аR)] × P
где АS тАУ геохимическая система.
Применительно к геохимическим системам свойство Р, отражающее особый характер взаимодействия системных элементов с внешними и внутренними факторами, сформулировано как сопряженность концентраций химических элементов.
Для объединения элементов в парагенетическую ассоциацию требования сопряженности явно недостаточно, необходимо еще одно дополнительное условие, а именно однонаправленность изменения содержаний ассоциирующих химических элементов при тех или иных изменениях параметров среды. Именно при одновременном выполнении этих требований можно ожидать устойчивого появления одних и тех же наборов парагенетический связанных элементов в сходных геохимических обстановках. Элементы, реакция которых на одни и те же воздействия среды противоположна по знаку, характеризуются разнонаправленным изменением их концентраций и образуют "запрещенные" парагенезисы, состоящие из элементов антагонистов. Итак в соответствии с [77] "под парагенетической ассоциацией будем понимать группу сонаходящихся в конкретном геологическом объекте элементов, сходно (как по интенсивности, так и по знаку) реагирующих на изменения параметров среды и характеризующихся в связи с этим сопряженностью и однонаправленностью изменения их содержаний в пространстве объекта".
Используя терминологию теории определений, можно отметить,
что геохимическая система и парагенетическая ассоциация химических элементов соотносятся как родовое и видовое понятия. Это позволяет рассматривать парагенетическую ассоциацию как особым образом организованную геохимическую систему. Исходя из вышеизложенного, парагенетическая ассоциация может быть представлена в виде системы:
АП = def [RП (аR)] × PП
Здесь аR- элементы геохимической системы АS, слагающие парагенетическую ассоциацию
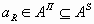
Концепция Р дополняется при переходе к парагенетическим ассоциациям требованием, чтобы элементы, объединяемые в АП, должны реагировать на изменения внешней среды сходным образом. Целостность геохимических систем обусловлена действием общих факторов FS. При переходе к парагенетическим ассоциациям, не все факторы из множества FS сохраняют системообразующие свойства. В связи с этим, возникает необходимость выделения из FS подмножества FП, объединяющего только те факторы, которые обеспечивают однонаправленность изменения состояния аR Î АП.
Таким образом, целостность и степень структурной однородности парагенетической ассоциации как системы особого рода определяется величиной вклада, связанного с действием факторов типа FП. Специфика факторов FП обусловливает сужение семейства системообразующих отношений. Если в геохимических системах допустима любая форма зависимости между концентрациями аR Î АS (как результат действия общих факторов FS), то для парагенетических ассоциаций, удовлетворяющих приведенному выше определению, приемлем только класс монотонных зависимостей. Обычно оперируют линейными зависимостями, использование которых в парагенетическом анализе вполне обосновано, т.к. факторы FП имеют причинный статус [1, 2, 4, 11, 14, 21, 29, 37, 44, 47, 48, 51, 61, 62, 73, 76- 79, 80, 84] .
Благодаря внедрению в практику геологических исследований математических методов и ЭВМ выделение парагенезисов и определение связей между их элементами все чаще осуществляется с помощью корреляционного и регрессионного методов [4, 21, 25, 28, 34, 35, 61, 63, 64, 66, 75- 78, 79, 84] .
В рамках системного подхода наиболее типична ситуация, когда неизвестны ни значения факторов F, ни реакция объекта на их воздействия. Неопределенность поведения объекта (с точки зрения исследователя) достигает крайних пределов. Но и в этом случае можно существенным образом снизить степень неопределенности, если от функциональных связей типа УR = j (F) (строго детерминированная модель) перейти к менее четким, но более реальным соотношениям типа:
П (F) Во П(У),
где П(F) - множество подмножеств множества значений F, П(У) -множество подмножеств множества выходных результатов У. Описание предложенной модели осуществляется на основании специально вводимой меры - вероятности Р. Допустимость вероятностной трактовки содержаний элементов, составляющих множества F и У, определяется, с одной стороны их случайным характером, а с другой тАУ относительно устойчивым появлением подмножества выходных результатов  Î П(У) при неоднократной реализации некоторого комплекса внешних условий
Î П(У) при неоднократной реализации некоторого комплекса внешних условий 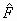 Î П(Р).
Î П(Р).
В геохимических системах в качестве случайности выступает частичная непредсказуемость результата эксперимента (при отборе и анализе проб). Действительно, истинное значение концентрации элемента в определенной точке геологического объекта совершенно определенное и является закономерным результатом геохимических процессов. Но при отборе и анализе проб (данный комплекс условий эксперимента) мы в каждой конкретной точке получаем значения концентраций, колеблющихся с определенной надежностью около определенного значения, т.е. имея многократное повторение процесса опробования можно рассматривать колеблющиеся в определенных пределах значения концентраций как случайные события. Рассматривая концентрации как случайные величины, можно выделить два случая:
а) изучаемая величина по своей природе не является случайной, но методы ее измерения (комплекс условий) обладают некоторой погрешностью, которая приводит к случайным значениям. Примером может служить анализ одной и той же пробы без расхода аналитического материала (ядерно-физический способ). Погрешность способа анализа будет выступать в качестве случайности в получении результата. Это классический пример применения вероятностных методов к теории ошибок, впервые изложенный Далласом [81];
б) Изучаемая величина является случайной относительно общего комплекса условий по своей природе. Задача определения среднего содержания в геологическом объекте по сериям отобранных проб при измерениях содержаний в отдельных пробах с абсолютной точностью. Колебания значений среднего содержания по сериям в этом случае также будут иметь место.
Таким образом, в геохимии имеют место случайные события, и это совершенно не противоречит физико-химическому подходу к изучению геологических объектов.
В общем случае значения концентраций в геохимических системах из-за частичной непредсказуемости результатов по вышеуказанным причинам могут рассматриваться как случайные величины, к которым применимы вероятностные методы изучения, с помощью статистических моделей, которые бывают двумерными и многомерными [44, 47] .
Для кристаллохимических связей характерна двумерная модель, в которой объект исследования рассматривается как двумерная статистическая совокупность с двумерной функцией распределения случайных величин X и У. В данном случае связи близки к функциональным, элемент случайности возникает из-за ошибок измерений коррелируемых величин. Между двумя случайными величинами проявляются стохастические (вероятностные) связи, когда заданному значению случайной величины X = х соответствует не определенное значение У, а некоторый набор ее значений тАУу1, у2, у3 тАжуn; каждое из которых характеризуется определенной вероятностью -p1, p2, p3 тАжpn. Функция распределения величины У, соответствующая значению Х=х характеризуется математическим ожиданием ` Ух и дисперсией 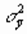 .
.
Распределения величины У соответствующие выбранным значениям величины X, называются условными распределениями, а дисперсии 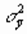 условными дисперсиями. Геометрическое место точек, соответствующих центрам условных распределений ` ух называется регрессионной зависимостью, а уравнение ее - уравнением регрессии. Аналогично каждому значению распределения величина У=у соответствует некоторая функция распределения величины X с математическим ожиданием ` ху и дисперсией
условными дисперсиями. Геометрическое место точек, соответствующих центрам условных распределений ` ух называется регрессионной зависимостью, а уравнение ее - уравнением регрессии. Аналогично каждому значению распределения величина У=у соответствует некоторая функция распределения величины X с математическим ожиданием ` ху и дисперсией 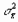 .
.
Система из двух случайных величин всегда будут соответствовать две регрессионных зависимости:
ух=f (x) и ху=f (у)
В частном случае зависимости могут быть линейными, в общем случае - нелинейными.
Для линейной регрессии система уравнений имеет вид:
у = а1+в1× х (регрессия у на х);
х = а2+в2× у (регрессия х на у).
Уравнения нелинейной регрессии соответствуют более сложной зависимости, но практически всегда могут быть аппроксимированы по частям уравнениями прямых или полиномами до третьего порядка.
В общем, регрессия может быть однозначно описана, если известей вид уравнения и значения коэффициентов при неизвестных. Остановимся на анализе линейной регрессии. В системе двух уравнений линейной регрессии коэффициенты а1 и а2, определяют положения начальных точек уравнений и называются коэффициентами пересечения или свободными членами уравнений [2, 34, 44, 48]. При а1 = а2, =0 уравнения исходят из начала координат.
Степень зависимости (тесноты связи) случайных величин определяется коэффициентами линейной регрессии - в1 и в2, геометрически они представляют собой тангенсы углов наклона прямых регрессии к осям абсцисс и ординат (a и b ). В общем случае прямые регрессии имеют общую точку пересечения с координатами в виде математических ожиданий величин X и У , а угол g между ними изменяется в пределах (0-90В°) и характеризует также связь между величинами (чем меньше g , тем теснее связь, g =0 связь - функциональная, т.к. обе линии сливаются, в1= 1 / в2 или в1× в2=1)
Основными числовыми характеристиками двумерного распределения случайных величин являются показатели их связи: для линейной регрессии - коэффициент корреляции и корреляционный момент (ковариация); для нелинейной регрессии - корреляционное отношение [2, 44, 75].
Коэффициентом корреляции r между случайными величинами х и у называется математическое ожидание произведения их нормированных отклонений:
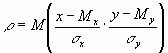
где Мх и Му тАУ центры распределения величин х и у, 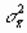 и
и 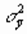 - их дисперсии. Коэффициент корреляции r может быть представлен в следующей форме:
- их дисперсии. Коэффициент корреляции r может быть представлен в следующей форме:
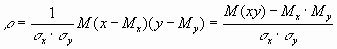
Величина М(х-Мх)(у-Му) называется корреляционными моментом (ковариацией) тАУ COV (x;y).
Коэффициент корреляции тАУ величина безразмерная с пределами изменения - В± 1. При r =0 линейная связь полностью отсутствует. Знак r (+) или (-) указывает на характер связи (прямая или обратная).
Равенства | r | =1 означает наличие линейной функциональной зависимости между величинами х и у.
Несмещенными и состоятельными оценками математических ожиданий Х= Мх и У=Му служат эмпирические средние значения:
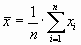 ;
; 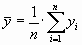
Несмещенными и состоятельными оценками дисперсии 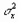 и
и 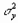 служат эмпирические дисперсии:
служат эмпирические дисперсии:

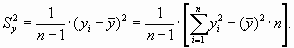
Несмещенной и состоятельной оценкой корреляционного момента служит эмпирический корреляционный момент (ковариация)
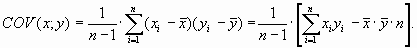
По этим оценкам определяют эмпирический коэффициент корреляции:
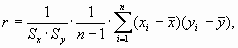
который дает состоятельную, но смещенную оценку теоретического коэффициента корреляции r (смещение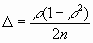 , при n>50 составляет менее 1%).
, при n>50 составляет менее 1%).
Значимость r проверяется путем сравнения величины |r| × 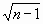 с его критическими значениями Н при заданной надежности r . При |r| ×
с его критическими значениями Н при заданной надежности r . При |r| × 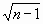 > H гипотеза о корреляционной связи подтверждается с надежностью r . Доверительные оценки r сложны и разработаны для случая нормального совместного распределения вероятностей величин X и У. Для приближенных доверительных оценок истинного значения коэффициента корреляции имеются номограммы[322]. Эмпирический коэффициент r может быть оценен оперативно графическим способом [44]. Доверительные интервалы для эмпирического коэффициента корреляции r, при малом количестве наблюдений n позволяет определить следующее преобразование, предложенное Р. Фишером:
> H гипотеза о корреляционной связи подтверждается с надежностью r . Доверительные оценки r сложны и разработаны для случая нормального совместного распределения вероятностей величин X и У. Для приближенных доверительных оценок истинного значения коэффициента корреляции имеются номограммы[322]. Эмпирический коэффициент r может быть оценен оперативно графическим способом [44]. Доверительные интервалы для эмпирического коэффициента корреляции r, при малом количестве наблюдений n позволяет определить следующее преобразование, предложенное Р. Фишером:
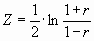
Величина Z при небольших n с хорошим приближением следует нормальному закону cо средним
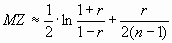 и дисперсией
и дисперсией 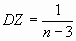
Это позволяет построить доверительный интервал [ Z1, Z2] для MZ по формуле:
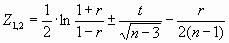
откуда следует, что истинное значение r с той же доверительной вероятностью ( 1-a ) заключено в пределах:
th Z1 < r< th Z2
где th - гиперболический тангенс аргумента, определяемый по таблицам. Использование Z-преобразованной величины r-оказывается более предпочтительным [76]. Параметры эмпирической прямой регрессии у на х оцениваются по формулам:
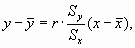
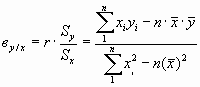
где ву/х - эмпирический коэффициент регрессии у на х.
Параметры линейной функции удовлетворяют принципу наименьших квадратов
по у: сумма квадратов отклонений наблюденных значений уi от
рассчитанных по уравнению прямой регрессии меньше, чем сумма квадратов отклонений их от любой другой прямой, т.е. имеет место не
равенство:
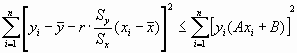
Наименьшая сумма квадратов отклонений наблюденных значений уi от линейной функции Ахi + B, т.е. сумма квадратов отклонений их от значений 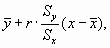 может быть выражена через эмпирический коэффициент регрессий по формуле:
может быть выражена через эмпирический коэффициент регрессий по формуле:
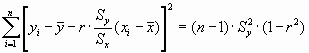
Аналогичен подход по оценке параметров прямой регрессии x на у. Доверительные оценки параметров прямой регрессии у на х (аналогично х на у) выполняются с использованием суммы квадратов отклонений измеренных значений yi от рассчитанных по уравнению прямой регрессии. Принято, что все ошибки измерения независимы и следуют нормальному закону распределения около нуля с дисперсией s 2. Для теоретической прямой регрессии y =` y тАУ ву/х (х-` х) доверительными границами для ` у служат:
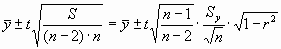
а доверительными границами для ву/х служат
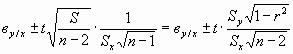
где t - значение коэффициента надежности из таблиц распределения Стьюдента при числе степеней свободы R =n-2 [134].
Доверительные оценки отклонения теоретической прямой регрессии от эмпирической для фиксированных значений аргумента x-x0 определяются как:

Необходимо отметить, что эта оценка значительно ухудшается при удалении от среднего значения Мх-` x, это указывает на опасность экстраполяции прямой регрессии за пределы интервала значений аргумента.
Для проверки гипотезы о том, что значения ` у /х подсчитанные по уравнению для каждого х, лежат на прямой, проводят поинтервальную оценку. Для каждого интервала (их количество l>8-10) подсчитывают условное среднее значение ` у /хj и условную дисперсию по формулам:
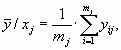

где mj - число точек ( xij, yij,) в j -том интервале, а затем вычисляют параметр:
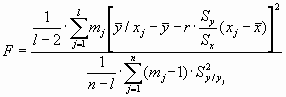
Если F превосходит критическое табличное значение при числах степеней свобода K1=l-2; K2=n-l надежностью P гипотезу о линейном характере усредненной зависимости y от x следует поставить под сомнение [70, 76, 80].
В случае нелинейной корреляции в качестве меры тесноты связи, т.е. меры концентрации экспериментальных точек около усредненных кривых регрессии, применяется корреляционное отношение h y/x для зависимости у от x или h y/x для зависимости x от y.
Корреляционные отношения вычисляются по формулам:
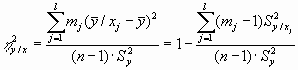
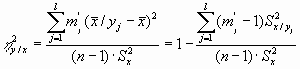
где обозначения, те же, что в приведенных выше выражениях, причем mjтАЩ и lтАЩ имеют тот же смысл для x, какой mJ и l - для у. Корреляционные отношения удовлетворяют неравенствам:
0 £ ç rç £ h y/x £ 1; 0 £ ç rç £ h x/y £ 1;
При отсутствии корреляционной связи r, в, h равны нулю. Поэтому проверка гипотезы о наличии корреляционной связи заключается в
расчете выборочных эмпирических оценок этих характеристик и значимости их отличия от нуля, причем из h у/х = 0 еще не следует, что h x/y =0 [2, 76]. Для криволинейных зависимостей по строение кривых регрессии проводится также методом наименьших квадратов, при расчетах ограничиваются полиномами до третьей степени [76,80].
Уравнение кривой регрессии удобно записывать в виде разложения по ортогональным полиномам П.Л. Чебышева [76]:
y = во× ро(х) + в1× р1(х) +тАжвvрv(x), где ро(х)=1, р1(х)=(х-` х),
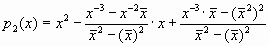
Параметры вj не зависят от степени искомого полинома и определяются по формуле:
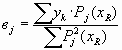 (j=0,1тАж.n)
(j=0,1тАж.n)
Истинные значения параметров вj с надежностью P лежат в доверительных интервалах:
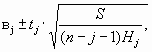 где tj =t(P,R) из таблиц распределения при числе степеней свободы R=n-j-1,
где tj =t(P,R) из таблиц распределения при числе степеней свободы R=n-j-1,
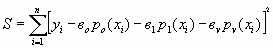 есть сумма квадратов отклонений опытных точек от расчетных,
есть сумма квадратов отклонений опытных точек от расчетных, 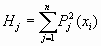 .
.
Все измерения предполагаются равноточными и независимыми с нормально распределенными ошибками. При оценке геохимических систем с парагенетическими корреляционными связями применяется метод множественной линейной корреляции для трех-шести компонент, уравнение множественной регрессии которого представляет линеаризированную функцию: 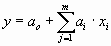 , где xi - значения i -ого признака.
, где xi - значения i -ого признака.
Найденное уравнение наилучшим образом, в смысле метода наименьших квадратов, соответствует имеющимся эмпирическим данным. Задача сводится к вычислению коэффициентов регрессии ao,a1,тАжaR по совокупности N наблюдений переменных x1,x2,тАжxm и зависимой переменной y. При вычислениях на ЭВМ определяются следующие показатели [44]:
Вычисление сумм взаимных произведений отклонений всех переменных
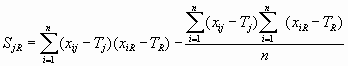
где j = 1, 2, 3,тАж m; 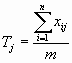
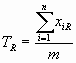 R=1, 2, 3,тАж m;
R=1, 2, 3,тАж m;
2. Вычисление средних для всех переменных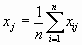
3. Вычисление парных эмпирических коэффициентов корреляции
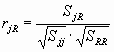
где j = 1, 2, 3,тАж m; R=1, 2, 3,тАж m;
4. Вычисление стандартных отклонений для всех переменных
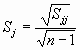
5. Подбор обратной матрицы парных эмпирических корреляционных коэффициентов, которая при умножении на данную матрицу дает единичную матрицу.
R . R-1 = R-1 .R = E
6. Вычисление коэффициентов регрессии 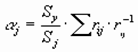
где Sy - стандартное отклонение зависимой переменной;
Sj - стандартное отклонение J -ой независимой переменной;
rij - парная корреляция i -ой независимой переменной с зависимой
переменной;
rij-1 - обратная корреляция независимых переменных.
7. Вычисление свободного члена 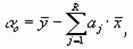
где ` y -среднее значение зависимой переменной y;
` xj - среднее значение j -той независимой переменной.
8. Вычисление множественного коэффициента корреляции
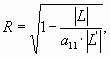
где ê Lê - определитель ковариационной матрицы;
a11 - первый член ковариационной матрицы;
ê LтАЩê - определитель ковариационной матрицы без первого столбца и первой
строки.
Такова рекомендуемая схема вычислений для оценки парагенетических
связей в многокомпонентных геохимических системах. Для настоящей
работы наиболее интересен случай трех величин: x={xi}, y={yi}, z={zi}.
Рассмотрим зависимости эмпирической регрессии z на x и y. Плоскость регрессии z на (x,y) описывается уравнением:
z-` z =вz/x(x-` x)+ вz/y(y-` y),
где коэффициенты регрессии вz/x, вz/y определяются через коэффициенты, корреляции nap (x,y), (x,z) и (y,z).
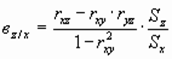 ;
; 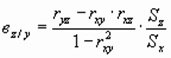
где Sx , Sy , Sz - эмпирические дисперсии при n результатах. Мерой связи Z и (x,y) служит сводный (множественный) коэффициент корреляции:
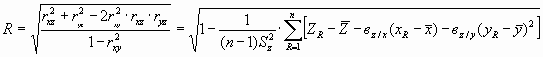
0 £ R £ 1.
При R=0 между z и величинами x, y нет линейной корреляционной зависимости (но может быть нелинейная). При R=1 (все точки лежит в плоскости (регрессии) имеет место случай линейной функциональной зависимости величины z от х и у. Для изучения корреляции между двумя компонентами (например х и z после устранения влияния у) можно ввести парциальный (частный) коэффициент корреляции:
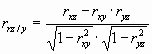
Таким образом, изложенные выше по литературным источникам рецепты указывают, что прикладная математика располагает достаточно мощным аппаратом для количественного анализа геохимических систем, и в частности для выявления, оценки и количественного выражения зависимостей между компонентами состава сложных сред.
При изучений состава геологических объектов, как геохимических систем, используется принцип относительной элементарности, представляющий собой общий методологический прием научного исследования материального мира. В соответствии с этой концепцией, объект исследования рассматривается в качестве сложной системы, состоящей из множества условно неделимых элементов, объединенных между собой совокупностью внутренних связей. Выявление взаимосвязей и пространственных взаимоотношений элементов неоднородности системы обеспечивает понимание ее структуры. При изучении Земли как планеты в качестве дискретных, условно неделимых элементов, рассматриваются ее оболочки. Для литосферы структурными элементами являются региональные участки пород различного состава. На уровне горной породы в качестве элементов выступают отдельные минералы, а на уровне минералов - слагающие их химические элементы. Таким образом, наличие нескольких дискретных качественно различных уровней в строении геологических объектов является их объективным природным свойством [42, 43, 46, 50, 74, 81-83].
При более детальных исследованиях геологических объектов в рамках каждого качественного однородного уровня появляется необходимость выделения уровней, различающихся по совокупности количественных критериев: состав и свойства. Подобную элементарность Л.И. Четвериков называет "количественной элементарностью" и отметил, что она определяется не только состоянием вещества слоеной системы, но и зависит от задачи исследований и детальности наблюдений. Специфика заключается в диспропорции между размерами дискретных наблюдений и размерами геологических элементов. Ослаблению неоднородности способствуют стабильные физико-химические условия процессов минералообразования, спокойная тектоника, хорошая проницаемость и выдержанность рудо подводящих и рудо локализующих структур. Для моделирования тел полезных ископаемых при решении различных геологоразведочных задач упрощенное формализованное представление об их строении было предложено Л.И. Четвериковым [83]. Условно им выделено пять структурных уровней: минерализованной зоны, тела полезного ископаемого, морфологически обособленного участка, текстуры руд и минерального агрегата. В соответствии с природными структурными уровнями при изучении месторождений определены уровни опробования, соответствующие этапам промышленного изучения: поисково-разведочному, предварительной, детальной и эксплуатационной разведкам; а также уровни отдельного замера (размера пробы). Изучение связей между компонентами должно выполняться на каждом уровне опробования с учетом конкретных задач в соответствии с этапами изучения объекта. Причем сила и характер связей, особенно парагенетических, могут меняться в зависимости от уровня опробования.
Детальность выявления структуры изучаемого объекта зависит от густоты сети дискретных наблюдений. Чем детальней эта сеть, тем более глубокий уровень в строении природных геологических образований может быть выявлен путем анализа и соответствующего группирования результатов единичных наблюдений.
Если группа единичных наблюдений располагается в пределах одного элемента неоднородности (структурного уровня, уровня опробования), то между значениями изучаемого признака в смежных пунктах наблюдений возникнут более или менее отчетливые автокорреляционные связи, а в характеристике наблюдаемой изменчивости признака отчетливо проявится неслучайная ее составляющая. Если ее проводить наблюдения по более редкой сети так, чтобы смежные пункты приходились на различные элементы неоднородности, корреляционные связи между значениями изучаемого признака в них ухудшатся или не проявятся, а в характеристике изменчивости признака будет доминировать случайная ее составляющая. Таким образом, изменчивость свойств одного и того же природного геологического объекта может быть оценена как случайная и как неслучайная после сгущения этой сети. Еще более заметное влияние на представления об изменчивости изучаемых свойств природных геологических образований оказывают размеры отбираемых проб. С увеличением размеров проб, их длины, наблюдаемая изменчивость значительно снижается. В частности, выравнивание средних содержаний происходит по закону "больших чисел" за счет резкого увеличения общего количества входящих в пробу элементов неоднородности.
Зависимость частных значений изучаемых признаков от густоты сети наблюдений и от размеров отбираемых проб свидетельствует о том, что задача полноценного и всестороннего количественного описания природной изменчивости свойств геологических образований практически невыполнима. Природная изменчивость существует объективно, отражая комплекс геологических и физико-химических условий формирования изучаемого объекта и представляет собой явление весьма сложного и многопланового характера. При решении конкретных геологических задач из всех возможных проявлений природной изменчивости оцениваются только те, знание которых необходимо для решения поставленных задач и только на тех уровнях строения, которые выявляются при данном масштабе проводимых исследований. Следовательно, понятие наблюдаемой изменчивости принципиально отличается от широко распространенного понятия природной изменчивости свойств геологических образований.
Наблюдаемая изменчивость отражает детальность наших представлений об изменчивости реально существующего геологического образования в зависимости не только от его природной сложности, но также и от условий экспериментальных наблюдений, положенных в основу ее характеристики.
При проведении статистической обработки экспериментальных геологических данных всегда следует помнить о том, что характеристики изменчивости, а также функции распределения изучаемых свойств отражают не только природную изменчивость, но и условия проводимого эксперимента. Это отчетливо видно при анализе распределения содержаний в объектах с повышенной степенью неравномерности (золото, ртуть, вольфрам). В работе [44] по материалам Д.А. Зенкова показано, что гиперболовидное распределение золота по секционным бороздовым пробам сменяется ассиметричным логнормальным для проб по подсечениям и почти симметричным для "площадных". Поэтому выводы по виду статистических характеристик необходимо делать с учетом уровня опробования и уровня проб.
При использовании методов корреляционного и регрессионного анализов при разведке также необходимо учитывать влияние геометрии проб - их объемов, размеров и ориентировки на количественные характеристики выборочных оценок связи. Для выявления характера и силы связей между содержаниями следует пользоваться данными анализов проб, геометрия которых отвечает решению практической задачи.
Если характеристики связи определяйся для целей подсчета одного элемента по содержанию другого в подсчетных блоках (вредные примеси, попутные полезные компоненты), то должны использоваться средние содержания исследуемых элементов в подсчетных бл
Вместе с этим смотрят:
"Нивхи"
32-я Стрелковая дивизия (результаты поисковой работы группы "Память" МИВлГУ)
4 capitals of Great Britain
About Canada
Description of Canada