Виявлення грубих результатiв вимiрювань

Виявлення грубих результатiв вимiрювань

При використаннi статистичних методiв для оцiнки результату i характеристик випадкових похибок вимiрювань за вибiркою (серiiю, рядом) результатiв спостережень обмеженого обтАЩiму повинна виконуватися вимога однорiдностi цiii вибiрки, тобто приналежнiсть усiх ii членiв до однiii генеральноi сукупностi. Проте на практицi дана вимога часто порушуiться, оскiльки до складу вибiрки можуть входити результати спостережень, якi мають грубi похибки i промахи, що може призвести до iстотного викривлення результату вимiрювань i його похибки.

При попередньому переглядi результатiв спостережень експериментатор мусить дiяти так. Якщо i результати спостережень (звичайно один-два), якi рiзко вiдрiзняються вiд iнших, то слiд уважно проаналiзувати, чи не допущена помилка при зняттi показiв ЗВТ або iх записi. Коли експериментатор переконався, що данi результати i промахами, то вони вилучаються з подальшого розгляду. В противному разi, тобто якщо не вдаiться пiдтвердити, що пiдозрiлi результати належать до промахiв, необхiдно перевiрити, чи не викликанi сумнiвнi результати спостережень грубими похибками. Така сама перевiрка необхiдна i в тому випадку, коли експериментальнi данi одержанi автоматично, а також за умови, що iх обробка виконуiться через деякий час пiсля закiнчення експерименту.

Для виявлення грубих результатiв (похибок) вимiрювань використовують статистичнi критерii.

При умовi, що вимоги до точностi результатiв прямих вимiрювань невисокi, можна користуватися найпростiшим критерiiм, яким i "правило ". Його сутнiсть полягаi в тому, що для вибiрки обчислюiться оцiнка СКВ i всi результати спостережень, якi задовольняють умову , визнаються такими, що мають грубi похибки. Дане правило в рядi випадкiв i надмiрно "жорстким". Так, якщо для нормального розподiлу поява результату спостереження свiдчить про наявнiсть у ньому грубоi похибки, то для рiвномiрного розподiлу аналогiчний висновок вiдповiдаi умовi . Це означаi, що критерiй виявлення грубих похибок повинен ураховувати не тiльки степiнь розсiювання результатiв вимiрювань, яке характеризуiться значенням СКВ , але й вид розподiлу випадкових похибок.

Для виявлення грубих похибок результатiв вимiрювань, якi пiдпорядковуються нормальному розподiлу, широке розповсюдження знаходить критерiй, що ТСрунтуiться на порiвняннi теоретичного (або граничного) i експериментального (або фактичного) значень параметра t, який характеризуi найбiльше вiдхилення результатiв спостережень вiд середнього арифметичного .

Методика застосування цього критерiю така.

1. Складають упорядкований (варiацiйний) ряд результатiв спостережень, розмiстивши вихiднi елементи ряду в порядку зростання (убування) i виконавши iх перенумерування, наприклад, .

2. Для початкового ряду результатiв спостережень обчислюють значення середнього арифметичного i незмiщеноi оцiнки СКВ згiдно з формулами (2.13) i (2.19).

3. Для крайнiх членiв упорядкованого ряду, якi найбiльш вiддаленi вiд центра розподiлу (визначаiться як середнi арифметичне цього ряду) i тому з найбiльшою ймовiрнiстю можуть мати грубi похибки, обчислюють вiдношення

де та .

4. За таблицею значень (додаток 10), входом якоi i заданий рiвень значущостi i число елементiв вибiрки n, знаходять теоретичне значення i порiвнюють його з обчисленим у п. 3 значенням t. Якщо виявиться, що , то вiдповiдний результат спостереження або , повинен бути вилучений з подальшоi обробки як грубий.

Потiм пп. 2-4 повторюють для (n-1) елементiв вибiрки до тих пiр, доки умова не перейде в умову . Проте при невеликiй кiлькостi спостережень, принаймнi при , указана методика може призвести до невiрноi оцiнки грубоi похибки i, як наслiдок, до помилкового вилучення результату спостереження , який насправдi не i грубим.

2.8. Методи вилучення систематичних похибок з результатiв вимiрювань

Систематичнi похибки, незалежно вiд характеру iх змiнювання в часi при постановцi i проведеннi вимiрювального експерименту, повиннi бути виявленi i вилученi з результатiв вимiрювань або хоча б зменшенi, для чого важливо знати джерела i причини iх виникнення. За цiiю ознакою розрiзняють такi систематичнi похибки: похибку через неадекватнiсть обтАЩiкта i фiзичноi моделi вимiрювання; похибки методу вимiрювання i ЗВТ; похибки, обумовленi дiiю впливних величин, i субтАЩiктивну похибку оператора. Систематичнi похибки можуть бути викликанi одночасно декiлькома причинами, якi треба враховувати при органiзацii вимiрювального експерименту i виробленнi заходiв щодо iх вилучення.

Наведемо основнi методи вилучення або зменшення систематичних похибок результатiв вимiрювань.

1. Застосування спецiальних конструктивних i схемотехнiчних рiшень, направлених на ослаблення або усунення дii на систематичну похибку ЗВТ впливних величин. Наприклад, термостатування i теплоiзоляцiя ЗВТ або окремих його вузлiв з метою зменшення температурноi похибки, екранування для захисту вiд зовнiшнiх електромагнiтних полiв, застосування спецiальних фундаментiв i вiброгасних пристроiв для ослаблення впливу механiчних дiй, застосування спецiальних схемотехнiчних рiшень при розробцi найбiльш критичних до дii зовнiшнiх факторiв вузлiв ЗВТ та iх виготовлення з високостабiльних комплектуючих елементiв.

2. Вилучення методичноi систематичноi похибки аналiтичним шляхом на основi розрахунку ii значення, виходячи з особливостей застосованого при експериментi методу вимiрювань i характеристик ЗВТ.

3. Використання методу замiщення для виключення iнструментальноi похибки вимiрювань, яка обумовлена вимiрювальним приладом. При цьому вимiрювання виконуються за два етапи. Спочатку на вхiд вимiрювального приладу подаiться вимiрювана фiзична величина i фiксуiться показ приладу. Потiм до входу вимiрювального приладу приiднуiться вихiд регульованоi зразковоi мiри, яка вiдтворюi фiзичну величину, однорiдну з вимiрюваною i, регулюючи мiру, добиваються того ж показу приладу. Результат вимiрювання, вiльний вiд систематичноi похибки, зчитуiться з вiдлiкового пристрою мiри.

Прикладом вилучення систематичноi похибки за допомогою методу замiщення служить вимiрювання активного опору омметром, який маi постiйну систематичну похибку, в тому числi за рахунок зтАЩiднувальних проводiв. Результат вимiрювання опору омметром подамо у виглядi , де - систематична похибка омметра. Пiсля цього замiсть вимiрюваного опору до омметра приiднуiться магазин опору, змiнюванням опору якого добиваються того ж показу омметра . При постiйнiй систематичнiй похибцi омметра для результатiв двох вимiрювань (а вони однаковi й дорiвнюють ) виконуiться умова , звiдки , тобто вiдлiк результату вимiрювання опору здiйснюiться з магазина опору, а постiйна систематична похибка омметра вилучаiться.

4. Застосування методу компенсацii систематичноi похибки за знаком. Метод дозволяi вилучити постiйну систематичну похибку, яка обумовлена впливною величиною i характеризуiться не тiльки ii значенням, але й напрямом. Для цього необхiдно провести два вимiрювання величини X таким чином, щоб систематична похибка , залишаючись незмiнною за модулем, увiйшла в результати вимiрювань з рiзними знаками: i . Тодi результат вимiрювання визначаiться середнiм значенням

Такий варiант методу компенсацii за знаком використовуiться, зокрема, для вилучення систематичних похибок, обумовлених впливом зовнiшнiх постiйних магнiтних полiв або термоЕРС, у цифрових фазометрах двопiвперiодноi дii (з усередненням двох результатiв вимiрювань, виконаних через пiвперiоду вхiдних сигналiв). Рiзновидом методу компенсацii i метод перiодичних спостережень, який дозволяi вилучити перiодичну систематичну похибку. Його суть зводиться до того, що вимiрювання проводять парне число разiв через iнтервали часу, що дорiвнюють пiвперiоду змiнювання систематичноi похибки, а результат вимiрювання знаходять усередненням одержаних результатiв.

5. Застосування методу протиставлення, який також передбачаi дворазове вимiрювання розмiру фiзичноi величини. При цьому умови експериментiв повиннi вiдрiзнятися так, щоб за вiдомими закономiрностями систематичноi похибки можна було б ii вилучити. Прикладом цього методу може служити вимiрювання активного опору за схемою моста постiйного струму (рис. 2.5), для якоi результат вимiрювання визначаiться з умови рiвноваги .

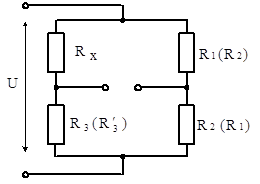
]Рис.2.5. До пояснення вилучення систематичноi похибки вимiрювань

за допомогою метода протиставлення

Результат вимiрювання може включати в себе систематичну похибку внаслiдок вiдмiнностi опорiв резисторiв вiд iх номiнального значення. Цю похибку можна вилучити, якщо резистори R₁ i R₂ помiняти мiсцями i знову зрiвноважити мiст тiльки резистором R₃. З умови рiвноваги моста одержимо , де - опiр резистора R₃ при новiй рiвновазi моста. Пiдставивши вiдношення , знайдене з однiii умови рiвноваги моста, в iншу умову його рiвноваги, одержимо . Таким чином, iз результату вимiрювання виключаiться вiдношення опорiв , а отже, i систематична похибка, що вноситься резисторами R₁ i R₂.

6. Проведення повiрки ЗВТ з метою визначення систематичноi похибки та ii компенсацii уведенням поправки в результат вимiрювання. Цей метод застосовуiться для вилучення постiйних у часi систематичних похибок, що мають ЗВТ, в окремих позначках шкали.

У сучасних ЗВТ, особливо в програмно-керованих, для визначення поправок або коригувальних коефiцiiнтiв усе ширше використовуiться калiбрування вiд внутрiшнього, iнколи зовнiшнього калiбратора, який являi собою або джерело зразкового (опорного) сигналу з параметрами, заданими з високою точнiстю, або зразковi елементи (резистори, конденсатори). Калiбрування здiйснюiться в декiлькох точках дiапазону вимiрювань, для кожноi з них визначаiться поправка (або коригувальний коефiцiiнт) i всi iх значення записують в ОЗП ЗВТ. Потiм результат вимiрювання уточнюiться за допомогою поправки або коригувального коефiцiiнта.

Таким чином, у принципi, систематичнi похибки вимiрювань можуть бути передбаченi, виявленi i тому i можливiсть для iх повного вилучення з результату вимiрювання, тобто перейти до виправленого результату вимiрювання. Проте, використовуючи на практицi описанi методи вилучення систематичних похибок, слiд памтАЩятати, що повною мiрою добитися цiii мети не можна. Отже, будь-який виправлений результат вимiрювання маi деякий залишок систематичноi похибки, названий невилученою систематичною похибкою, що i випадковою величиною, оцiнювання характеристик якоi ТСрунтуiться на методах математичноi статистики.

РЖнколи для пiдвищення правильностi вимiрювань, тобто зменшення систематичних похибок, використовують рандомiзацiю. Пiд рандомiзацiiю розумiють штучне переведення систематичних похибок у випадковi (в перекладi з англiйськоi термiн "рандомiзацiя" означаi перемiшування, створення хаосу). Для здiйснення рандомiзацii процес вимiрювання органiзуiться так, щоб фактори, якi впливають на результати вимiрювань, а точнiше, на iх похибки, дiяли випадково. Наприклад, неточне градуювання шкали вимiрювального приладу призводить до появи систематичних похибок для даного приладу. Якщо ж вимiрювання самоi фiзичноi величини провести декiлькома приладами даного типу, то цi похибки будуть змiнюватися вiд приладу до приладу випадково. Пiддаючи одержанi результати спостережень статистичнiй обробцi, можна iстотно зменшити систематичну складову результату вимiрювання.

2.9. Методи пiдсумовування похибок вимiрювань

2.9.1. Постановка задачi пiдсумовування похибок вимiрювань

При аналiзi похибок вимiрювань i ЗВТ можливi три основнi задачi:

1) кiлькiсна оцiнка окремих складових систематичноi i випадковоi похибок;

2) пiдсумовування кiлькiсних характеристик складових похибки одного виду (систематичних або випадкових);

3) пiдсумовування кiлькiсних характеристики систематичноi i випадковоi складових з метою одержання повноi похибки.

Вирiшення цих задач у сукупностi i дозволяi одержати кiлькiснi оцiнки характеристик похибки, тобто оцiнити похибку. Перш за все зауважимо, що термiн "пiдсумовування" використовують при оцiнюваннi похибок в узагальненому смислi, а не як найменування конкретноi математичноi операцii. Бiльш того, в останнiй час замiсть термiна "пiдсумовування" все частiше застосовують термiн "обтАЩiднання" похибок.

Повна похибка вимiрювань, як i ЗВТ, у загальному випадку створюiться рядом складових (систематичних i випадкових), оцiнку кожноi з яких знаходять розрахунковим або експериментальним шляхом. Метод пiдсумовування складових похибки визначаiться природою i взаiмозвтАЩязком iх джерел.

Сутнiсть задачi визначення розрахунковим шляхом повноi похибки вимiрювань або ЗВТ полягаi в пiдсумовуваннi (обтАЩiднаннi) ii окремих складових за установленим, загальноприйнятим правилом, що i одним iз заходiв забезпечення iдностi вимiрювань. Так, для визначення похибки навiть окремого вимiрювального пристрою необхiдно пiдсумовувати всi його складовi похибки, викликанi рiзними причинами. При створеннi вимiрювальних приладiв, установок i систем маi мiсце задача оцiнки похибки вимiрювальних каналiв, яка зводиться до пiдсумовування похибок ряду вимiрювальних пристроiв, що створюють даний вимiрювальний канал. Для визначення похибок будь-яких видiв вимiрювань необхiдно пiдсумовувати рiзнi складовi методичних, iнструментальних i субтАЩiктивних похибок, а також похибку обчислювань при опосередкованих, сукупних i сумiсних вимiрюваннях.

Таким чином, задача розрахункового пiдсумовування (або аналiтичного визначення) похибок - одна з основних задач як при створеннi ЗВТ, так i при оцiнюваннi похибок результатiв вимiрювань. Причому необхiднi якомога простiшi методи пiдсумовування похибок.

Труднiсть пiдсумовування похибок полягаi в тому, що всi складовi похибки треба розглядати як випадковi величини з найрiзноманiтнiшими значеннями в кожнiй конкретнiй реалiзацii. Найбiльш повно вони можуть бути описанi своiми законами розподiлу, а iх спiльна дiя - композицiiю цих законiв. Проте вирiшення задачi пiдсумовування похибок у такiй постановцi повтАЩязане з великими труднощами двоякого роду. По-перше, одержання композицii законiв розподiлу похибок уже для 3-4 складових вимагаi значного обтАЩiму обчислювань, якi часто можуть бути виконанi тiльки на ЕОМ. По-друге, при виконаннi технiчних i бiльшостi контрольно-повiрочних вимiрювань експериментатор, як правило, не маi iнформацii про закони розподiлу складових сумарноi похибки. Цi труднощi викликають необхiднiсть застосування для оцiнювання похибок спрощених правил пiдсумовування iх складових, якi дозволяють з достатнiм ступенем вiрогiдностi оцiнити сумарну похибку в умовах неповноi початковоi iнформацii.

Найбiльш розробленими методами оцiнювання випадкових похибок i методи, якi безпосередньо запозиченi з математичноi статистики. Основнi труднощi складають оцiнювання i пiдсумовування систематичних похибок. Звичайно iх характеризують границями, якi оцiнюють приблизними методами, в тому числi близькими до статистичних.

Для оцiнювання похибок використовуються три методи (правила, види, форми) пiдсумовування складових похибок: арифметичне, алгебраiчне i геометричне (квадратичне, статистичне) пiдсумовування.

2.9.2. Визначення сумарноi систематичноi похибки вимiрювань

При точних вимiрюваннях багато якi систематичнi похибки вилучаються або вiдповiдною постановкою експерименту, або введенням поправок. Як правило, це легше зробити для змiнних похибок, якi так чи iнакше проявляються у вимiрювальних сигналах (показах) ЗВТ. Труднiше вилучити постiйнi систематичнi похибки: потрiбен аналiз даних про обтАЩiкт, засоби i умови вимiрювань, як апрiорних, так i одержаних пiд час експерименту. Це i однiiю з основних задач при проведеннi вимiрювань. Методи iх вирiшення не достатньо формалiзованi i потребують високоi метрологiчноi культури.

Постiйнi систематичнi похибки можна подiлити на строго i умовно постiйнi, причому способи оцiнювання i пiдсумовування для них рiзнi. Для строго постiйних складових придатний лише детермiнiстський пiдхiд i вiдповiдно алгебраiчне та арифметичне пiдсумовування. Для умовно постiйних складових систематичноi похибки придатнi, залежно вiд умов, рiзнi квазiстатистичнi способи пiдсумовування.

Для визначення систематичноi складовоi повноi похибки, iнакше кажучи, при пiдсумовуваннi постiйних систематичних складових похибки, коли вiдомi iх значення i знаки, використовують алгебраiчне пiдсумовування. Це правило i наслiдком однiii з основних властивостей математичного сподiвання випадкових величин, згiдно з яким математичне сподiвання суми випадкових величин (похибок) дорiвнюi сумi математичних сподiвань цих випадкових величин (похибок). Ураховуючи, що математичне сподiвання повноi похибки являi собою ii систематичну складову, маiмо алгебраiчну суму

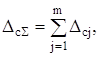
де - сумарна систематична похибка;

- складовi систематичноi похибки, - iх кiлькiсть.

Якщо для строго постiйних систематичних похибок заданi iх допустимi значення (або границi змiнювання) , то визначаiться допустиме значення сумарноi систематичноi похибки як арифметична сума за модулем допустимих значень складових

.

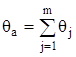Величину називають арифметичними границями систематичноi похибки.

На практицi нерiдко буваi вiдома додаткова iнформацiя про поведiнку систематичних похибок, зокрема, вiдомо, що невилученi систематичнi похибки змiнюються нерегулярно, залишаючись у границях . Тодi при пiдсумовуваннi такi похибки умовно розглядають як випадковi величини i звичайно вважають, що вони рiвномiрно розподiленi в заданих границях. Це припущення ТСрунтуiться на тому, що для випадковоi величини, яка змiнюiться в заданих границях, рiвномiрному розподiлу вiдповiдаi максимальна ентропiя (невизначенiсть). Тому таке припущення i досить обережним i на практицi приводить до реалiстичноi оцiнки похибок.

Зрозумiло, цей умовний прийом не i iдино можливим, проте вiн досить простий i широко застосовуiться на практицi. Можна використовувати i "нестатистичнi" методи, якi базуються, наприклад, на iнтервальному аналiзi або теорii нечiтких множин, проте цi методи не i строго обТСрунтованими i мiстять певнi припущення [8].

При квазiстатистичному методi границi довiрчого iнтервалу сумарноi невилученоi систематичноi похибки називають статистичними i знаходять за формулою

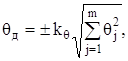(2.22)

де - коефiцiiнт, що залежить вiд числа m складових невилученоi систематичноi похибки i вiд спiввiдношення iх границь, а також вiд довiрчоi ймовiрностi P. Формула (2.22) i приблизною, вона одержана шляхом побудови композицii рiвномiрних розподiлiв складових на вiдповiдних iнтервалах . Значення коефiцiiнта для трьох поширених значень P наведено в табл. 2.2.

При значеннях довiрчоi ймовiрностi та залежнiсть коефiцiiнта вiд числа складових m незначна, тому рекомендуiться брати середнi значення коефiцiiнта : . При залежнiсть коефiцiiнта вiд числа складових m та iх спiввiдношення iстотнi, тому при рекомендуiться брати значення , а при можна уточнювати значення за графiком (наводиться в окремих працях) або за допомогою табл. 2.3.

Таблиця 2.2

Довiрча ймовiрнiсть, P	Значення коефiцiiнта при числi складових m, що дорiвнюi:
	2	3	4	5	..	¥	Середнi
0,90	0,97	0,96	0,95	0,95	..	0,95	0,95
0,95	1,10	1,12	1,12	1,12	..	1,13	1,13
0,99	1,27	1,37	1,41	1,42	..	1,49	1,4

Таблиця 2.3

Число cкладових, m	Значення коефiцiiнта kq при спiввiдношеннi границь , що дорiвнюi:
	0	1/2	1	2	3	4	5	6	7
2	0,98	1,15	1,27	1,22	1,15	1,12	1,08	1,07	1,05
3	1,27	1,32	1,37	1,32	1,24	1,18	1,15	1,12	1,08
4	1,38	1,40	1,41	1,36	1,28	1,23	1,18	1,15	1,11

Параметр , який характеризуi спiввiдношення складових невилученоi систематичноi похибки, дорiвнюi найменшому iз спiввiдношень границь 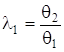та 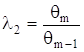, при цьому .

При малому числi складових () пiсля знаходження статистичноi границi q_д необхiдно порiвняти ii з арифметичною границею q_а i прийняти як остаточну найменшу з двох границь. Слiд зазначити, що для малого числа складових арифметичнi границi q_а звичайно незначно перевищують статистичнi q_д тАФ не бiльше як на 30 %, що в багатьох випадках цiлком припустимо.

Якщо невилученi систематичнi складовi похибки заданi своiми довiрчими границями , обчисленими за формулою (2.22), то довiрчу границю сумарноi систематичноi похибки знаходять iз виразу

,

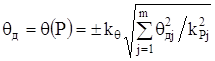де - довiрчi границi j-i невилученоi систематичноi складовоi похибки, що вiдповiдають довiрчiй ймовiрностi ;

- квантильний коефiцiiнт переходу, що вiдповiдаi довiрчiй iмовiрностi .

2.9.3. Визначення сумарноi випадковоi похибки вимiрювань

В основу пiдсумовування випадкових складових похибки вимiрювань покладена властивiсть дисперсii для суми залежних випадкових величин, яка стосовно похибок записуiться так:

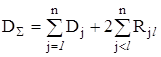, (2.23)

де - дисперсiя суми n випадкових похибок;

- дисперсiя j-i складовоi випадковоi похибки, ;

- взаiмна кореляцiйна функцiя, або взаiмний кореляцiйний момент j‑i та l-i складових випадковоi похибки, причому запис означаi, що пiдсумовування розповсюджуiться на всi можливi попарнi сполучення складових, для яких . Взаiмна кореляцiйна функцiя визначаiться рiвнянням

, (2.24)

де - вiдповiдно СКВ (або iх оцiнки ) j-i та l-i складових випадковоi похибки:

;

- нормована взаiмна кореляцiйна функцiя, або коефiцiiнт кореляцii:

.

Переходячи у формулi (2.23) до СКВ випадкових похибок з урахуванням (2.24), одержимо вираз для обчислення СКВ сумарноi випадковоi похибки за ii складовими

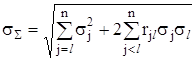. (2.25)

Звернемо увагу на те, що ця формула пiдсумовування випадкових похибок i унiверсальною, оскiльки СКВ (i дисперсiя) не залежить вiд закону розподiлу похибок.

Вiдзначимо, що строго врахувати всi кореляцiйнi звтАЩязки, а отже, i точно визначити коефiцiiнт кореляцii мiж похибками досить складно i не завжди можливо. Так, коефiцiiнт кореляцii мiж величинами визначаiться виразом

,

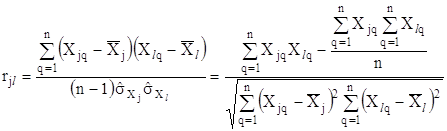де - результати q-го спостереження величин , вiдповiдно, ;

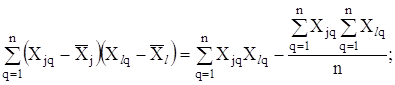
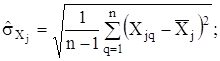
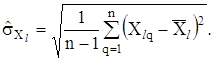
Застосування формули (2.25) потребуi ускладнення експерименту i обчислювань. Тому вона не знаходить широкого практичного застосування, а для ii спрощення користуються нижчевказаними рекомендацiями щодо задання коефiцiiнта кореляцii

За степенем корельованостi випадковi похибки слiд роздiлити лише на два види: сильно корельованi i слабко корельованi. Умовною границею мiж сильною i слабкою кореляцiями випадкових похибок вважають умову . Враховуючи це, до сильно корельованих належать похибки, для яких , i для них приймають . Прикладами сильно або жорстко корельованих похибок i похибки, викликанi однаковою причиною (загальним джерелом живлення, майже однаковим впливом змiнювання температури i т.п.), i в iнших випадках, коли тiснi кореляцiйнi звтАЩязки мiж похибками явно проглядаються. До слабко корельованих належать похибки, для яких i для них приймають . Такi похибки звичайно викликаються рiзними причинами, причому такими, що не мають мiж собою явного звтАЩязку. Вони також називаються незалежними. Промiжнi значення коефiцiiнта кореляцii, тобто крiм або , при оцiнюваннi випадковоi похибки, як правило, не використовуються.

У практицi вимiрювань здебiльшого мають справу з незалежними випадковими похибками, для яких i формула (2.25) набуваi вигляду

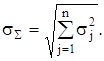(2.26)

Якщо СКВ похибки визначити у вiдносних одиницях, то

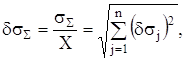(2.27)

де - вiдносне СКВ j-i складовоi похибки.

РЖнколи для спрощення розрахункiв переходять вiд пiдсумовування дисперсiй (або СКВ) випадкових похибок до пiдсумовування максимальних (допустимих) значень абсолютних похибок . Тодi аналогiчно формулам (2.22) i (2.26) маiмо

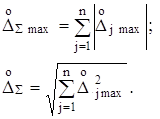(2.28)

Формула для СКЗ сумарноi випадковоi похибки даi завищену оцiнку в порiвняннi з (2.26), але ця оцiнка бiльш вiрогiдна, нiж "оцiнка зверху" .

Таким чином, арифметичне пiдсумовування використовуiться для грубоi оцiнки сумарноi похибки, названоi "оцiнкою зверху" (або за максимумом), i при випадковому характерi похибок. Воно зводиться до пiдсумовування максимальних значень окремих складових похибок. При такому пiдходi передбачаiться, що всi складовi випадковоi похибки мають одночасно i максимальне значення, i однаковий знак. Очевидно, ймовiрнiсть такого збiгу дуже мала, тому арифметичне пiдсумовування даi завищену оцiнку сумарноi випадковоi похибки, i похибка цiii оцiнки буде тим iстотнiша, чим бiльше число складових пiдсумовуiться. Тому арифметичне пiдсумовування випадкових похибок можливе при грубiй оцiнцi сумарноi похибки, коли вона мiстить 2-3 складових.

Переходячи в (2.28) до вiдносних похибок, маiмо

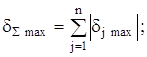
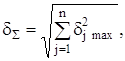
де

При умовi формула (2.25) набуваi вигляду

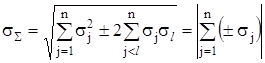, (2.29)

де знак "+" означаi, що для складових з позитивною кореляцiiю () СКВ треба брати зi знаком "+", а для складових з негативною кореляцiiю брати зi знаком "-". Знак модуля належить до .

Зокрема, при пiдсумовуваннi двох складових випадковоi похибки, СКВ яких , з (2.29) маiмо

,

тобто наявнiсть жорсткоi кореляцii () мiж випадковими складовими похибки приводить до переходу вiд геометричного iх пiдсумовування до алгебраiчного.

Таким чином, при виборi того або iншого методу (правила) пiдсумовування складових похибки визначальною ознакою i не роздiл iх на систематичнi i випадковi, а ступiнь (рiвень) кореляцiйних звтАЩязкiв: сильний або слабкий.

Якщо для складових випадковоi похибки задано границi довiрчих iнтервалiв i довiрчi ймовiрностi , то СКВ кожноi iз складових, згiдно з виразом (2.9), знаходять за формулою

.

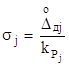Якщо всi складовi випадковоi похибки пiдлягають однаковому закону розподiлу i мають однакову довiрчу ймовiрнiсть P, тодi i .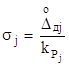

При нормальному законi розподiлу всiх складових або при кiлькостi складових n ³ 5 сумарна випадкова похибка маi нормальний закон розподiлу. Отже, ii границi довiрчого iнтервалу з довiрчою ймовiрнiстю P можна визначити так: .

Вместе с этим смотрят:

GPS-навигация

GPS-прийомник авиационный

IP-телефония и видеосвязь

IP-телефония. Особенности цифровой офисной связи

Unix-подобные системы