Загальнi уявлення про iндуктивнi фiльтри

Лекцiя

Загальнi уявлення про iндуктивнi фiльтри

Змiст

Вступ

1. Фiльтри верхнiх частот (ФВЧ)

2. Смуговi фiльтри та iншi типи iндукцiйних фiльтрiв

3. Вплив навантаження на характеристики фiльтрiв

Висновок

Вступ

В данiй лекцii будуть розглянутi фiзичнi процеси у фiльтрах верхнiх частот, смугових, загороджувальних, режекторних. Цi фiльтри як i фiльтри нижнiх частот широко використовуються в апаратурi радiозвтАЩязку, радiорелейному звтАЩязку, а особливо в системах передачi з частотним роздiлом каналiв.

Учбово-виховнi цiлi: Вивчити принципи побудови фiльтрiв верхнiх частот, смугових та режекторних фiльтрiв, областi iх використання; Виховати високу культуру iнженера-звтАЩязкiвця.

Учбово-матерiальне забезпечення: Принципiальнi схеми апаратури, ii функцiональнi вузли з ФВЧ та i\П-303\, Дiапроектор, дiапозитиви.

Виявляiться, що використовуючи так званий метод перетворення частоти, можна при розрахунках фiльтрiв верхнiх частот та iнших фiльтрiв використати всi методи, формули, малограми та таблицi, одержанi для фiльтрiв нижнiх частот.

У вступi акцентувати увагу курсантiв на важливiсть теми вивчення, використовуючи схеми та блоки реальноi апаратури звтАЩязку. Показати широке застосування рiзних видiв фiльтрiв.

У першому питаннi коротко викласти суть методу частотноi змiнноi та на його основi дати алгоритм одержання фiльтрiв верхнiх частот з фiльтрiв нижнiх частот.

У другому питаннi теж, використовуючи метод частотноi змiнноi, показати принцип одержання смугових фiльтрiв, загороджувальних, режекторних фiльтрiв з ФНЧ прототипiв.

У третьому питаннi показати, як змiнюються параметри та характеристики фiльтрiв при пiдключення до них навантаження та змiни ii другоi величини.

В заключнiй частинi узагальнити матерiал i ще раз акцентувати увагу на вузлових моментах теми.

1. Фiльтри верхнiх частот (фвч)

При розгляданнi принципiв побудови фiльтрiв верхнiх частот почнемо з розгляду сутностi методу перетворення частотноi змiнноi.

Практично всi фiльтри верхнiх частот можна одержати з фiльтрiв нижнiх частот, якщо в останнiх кожну iндуктивнiсть замiнити iмнiстю, а кожну iмнiсть тАУ iндуктивнiстю. (мал.1)

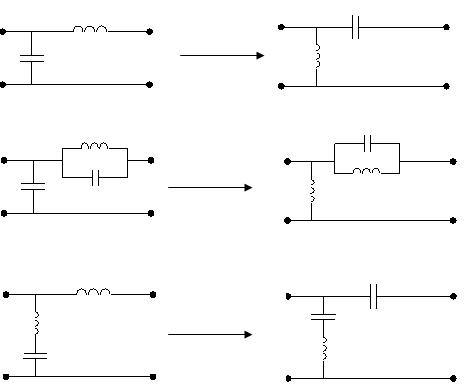
мал. 1 а ). б ). в ).

Затухання ФНЧ виражаiться спiввiдношенням дб., тобто i парною функцiiю частоти , з цього слiдуi тАУ крива затухання буде симетрична вiдносно осi ординат (мал. 2)

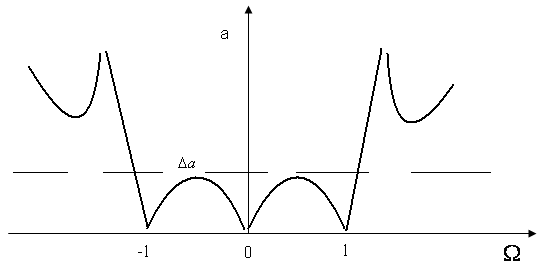
мал. 2

Лiва частина цього графiку вiдповiдаi взаiмному розмiщенню смуги затримки та смуги пропускання для фiльтрiв верхнiх частот. (мал. 3)

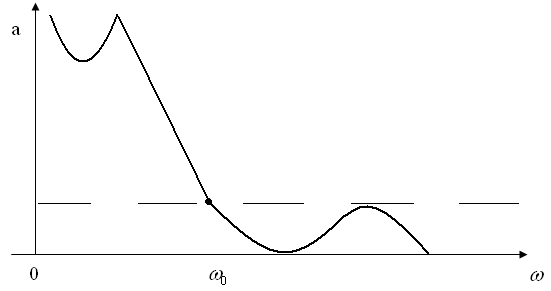
мал. 3

Пiдберемо таку функцiю, яка б перетворила вiдтАЩiмну пiввiсь (мал.2) в додатну (мал. 3) пiввiсь.

При цьому точцi (мал. 2) повинна вiдповiдати точка тАЬ0тАЭ (мал. 3)

"-1" ""

"0" ""

Очевидно, що такою функцiiю буде така:

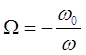(1)

Таким чином, всi вирази, одержанi ранiш для фiльтрiв нижнiх частот, будуть вiрнi i для фiльтрiв верхнiх частот, якщо в цих виразах визначатиметься iз спiввiдношення (1).

Нормуваннi по частотi дозволяi при розрахунках фiльтрiв верхнiх частот з характеристиками Баттерворта, Чебишева, Золотарьова або з довiльним розмiщенням сплескiв затухання повнiстю використовувати всi методи, формули, номограми та таблицi, одержанi для фiльтрiв верхнiх частот. В якостi прикладу на (мал. 4) наведенi схеми та характеристики деяких фiльтрiв верхнiх частот з рiвнохвильовими характеристиками затухання, а на (мал. 5) схема фiльтра к -2,0 апаратури П-303 та графiк частотноi залежностi робочого затухання цього фiльтру.

мал. 4

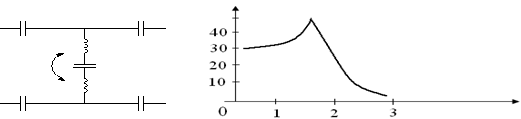
мал. 5

2. Смуговi фiльтри та iншi типи iндукцiйних фiльтрiв

Смуговий фiльтр може бути утворений з фiльтру нижнiх частот, якщо в останньому кожну iндуктивнiсть замiнити послiдовним коливальним контуром без втрат, а кожну iмнiсть тАУ паралельним, при чому резонанснi частоти всiх контурiв взяти однаковими (мал. 6)

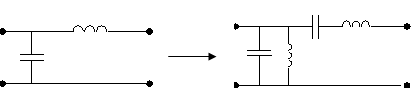
ФНЧ i

мал.6

Тодi до частоти резонансу характер опору вiток, одержаного фiльтра, буде таким самим як i у фiльтра верхнiх частот, а пiсля частоти резонансу тАУ таким самим як у фiльтра нижнiх частот. Фiльтр же в цiлому буде смуговим фiльтром, при ому частота резонансних контурiв буде очевидно знаходитись у смузi пропускання фiльтру.

Пiдберемо таку функцiю яка б перетворила вiсь частот () (мал. 2) у пiввiсь () (мал. 7)

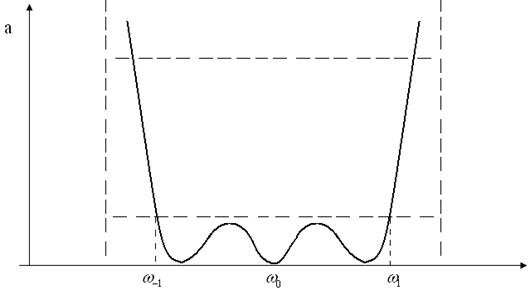
мал. 7

При цьому:

Точцi "-" (мал. 2) повинна вiдповiдати точка "0" (мал. 7).

"-1" ""

"0" ""

"1" ""

"" ""

Таке перетворення може зробити функцiя:

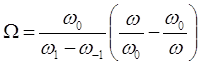(2)

Таким чином, всi вирази, одержанi ранiш для фiльтрiв нижнiх частот, залишаються справедливими i для розглядуваних смугових фiльтрiв, якщо в цих виразах визначати з вiдношення (2).

Важливо вiдмiтити, що частотнi характеристики розглянутих фiльтрiв володiють однiiю характерною особливiстю, яка обумовлена тим, що функцiя (2) приймаi рiвнi по абсолютнiй величинi i оберненi за знаком значення для будь-якоi пари частот та звтАЩязаних спiввiдношенням , тобто для будь-якоi пари частот, розмiщених симетрично вiдносно осi части , яка в свою чергу являiться середньою геометричною частотою смуги пропускання фiльтра.

Отже затухання фiльтра при частотах та 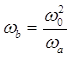буде однаковим, тобто характеристика затухання будь-якого речового фiльтра, одержаного з допомогою перетворення (2) завжди буде геометрично симетрична вiдносно частоти вiдповiдаi графiчна iлюстрацiя на (мал. 7)

Тому подiбнi фiгури одержали назви фiльтрiв з симетричними (геометричними) характеристиками загасання.

Практичне використання фiльтрiв, розглянутих вище, обмежено лише тими випадками, коли вимоги до характеристики затухання фiльтра по обидвi сторони вiд його смуги пропускання близькi до симетричних. В iншому випадку в деяких частотних областях буде мати мiсце невиправданий великий запас затухання, що говорить про iснування бiльш економiчного рiшення по числу елементiв. У вiдповiдностi з цим в загальному випадку смуговий фiльтр може мати рiзне число сплескiв злiва i справа вiд йог смуги пропускання, рiзну крутизну характеристики затухання при та при , що рiзко вiдрiзняються по широтi смуги переходу, коротшу характеристику затухання, яка суттiво вiдрiзняiться вiд симетричноi.

Одна й та сама передаточна функцiя смугового фiльтру може бути реалiзована тим бiльшим числом, зовнiшньо розрiзняючих ступiнчатих реактивних чотирьохполюсникiв, чим вище порядок функцii. Частiше iнших знаходять застосування фiльтри, схеми яких подiбнi до схем фiльтрiв з симетричними характеристиками, схеми у виглядi каскадного зтАЩiднання фiльтра нижнiх i верхнiх частот. Крiм ФНЧ, ФВЧ, i в технiцi часто використовуються режекторнi або, як iх iще називають, загороджувальнi фiльтри.

Характеристика загороджувального фiльтра маi вигляд, зображений на (мал. 8)

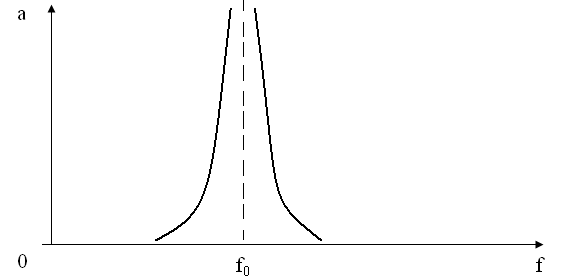
мал. 8

Якщо зрiвняти цю характеристику смугового фiльтра, то можна побачити, загороджувальний фiльтр маi характеристику затухання обернену до характеристики i, отже вiн також може бути одержаний з ФНЧ тАУ прототипу, однак в цьому випадку в ФНЧ кожну iмнiсть замiнити послiдовним коливальним контуром, а iндуктивнiсть тАУ паралельним (мал. 9) причому резонансна частота всiх контурiв повинна бути однаковою, тодi очевидно, що такий фiльтр буде вiльно (з малим затуханням) пропускати всi частоти нижчi i вище резонансноi частоти контурiв, а на частотах близьких до резонансу затухання фiльтру буде великим, так як послiдовнi контури будуть надавати штучну дiю на вхiдний сигнал, а паралельний контур буде мати для нього великий опiр.

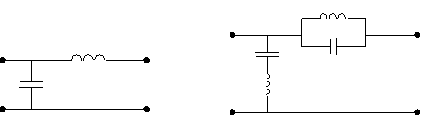
ФНЧ i \ ЗФ

мал. 9

У радiолокацiйнiй технiцi широко використовуiться гребiнчастi фiльтри, у яких смуги пропускання чергуються зi смугами затримки. Е багато способiв одержання гребiнчастоi характеристики затухання. Найпростiшим з них i спосiб утворення такоi характеристики з допомогою набору смугових або режекторних фiльтрiв. На (мал. 10(а,б)) зображений спосiб отримання гребiнчастоi характеристики затухання.

вих

мал. 10 а.

вх.

вих.

мал. 10 б.

3. Вплив навантаження на характеристики фiльтрiв

Вплив опору навантаження на характеристики фiльтрiв розглянемо на прикладi найпростiшого ФНЧ. Коли фiльтр навантажений на опiр z_н=z₀, тобто не характеристичне, такий режим називаiться режимом узгодження.

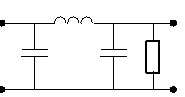
мал. 11

В цьому випадку характеристика фiльтра буде мати вигляд, показаний на мал. 12

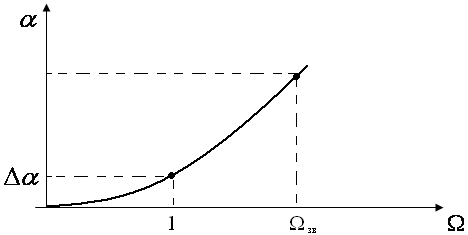
мал. 12

Необхiдно пiдкреслити, що такий вид характеристики фiльтр буде мати лише тодi, коли вiн буде навантажений на опiр, рiвний характеристичному. Щоб вияснити можливе iснування такого режиму, необхiдно знайти характеристичний опiр даного фiльтра.

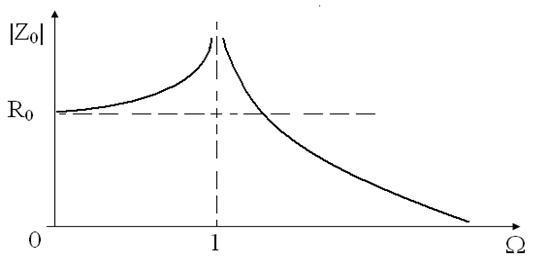
мал. 13

Користуючись теорiiю чотирьохполюсникiв можна написати для П-подiбноi схеми фiльтра формулу, яка виражаi залежнiсть характеристичного опору вiд частоти

,

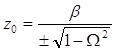де - хвильовий опiр. Графiк цiii залежностi представлений на мал. 13.

мал. 14

Як видно з мал. 13 опiр сильно залежить вiд частоти як по характеру так i по величинi. Це характерно для будь-якоi схеми фiльтру. Отже, бажаючи здiйснити узгодження навантаження, потрiбно було б для кожноi частоти пiдбирати свiй опiр навантаження \в смузi пропускання тАУ активне, в смузi затримки - реактивне. Мiж тим, в дiйсних умовах роботи опору навантаження, як правило, являiться практично не залежним вiд частоти активного опору R_н. Звiдси слiдуi, що в загальному випадку фiльтр працюi на неузгоджене навантаження, i до режиму узгодження можна лише наблизитись.

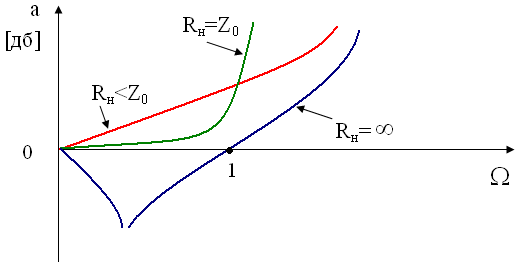
Користуючись тiiю ж теорiiю чотирьохполюсникiв можна визначити залежнiсть затухання фiльтру вiд опору навантаження.

При холостому ходi фiльтру R_н= в смузi пропускання затухання стаi вiдтАЩiмним, тобто коефiцiiнт передачi фiльтра бiльше одиницi. Це означаi пiдсилення сигналу по потужностi так як фiльтр i пасивним.

В загалi ж в реальних умовах частотнi характеристики фiльтра вiдрiзняються вiд тих, якi були б при умовi повного узгодження.

Висновок

Таким чином в данiй лекцii розглянутi фiзичнi процеси та принципи побудови фiльтрiв верхнiх частот, смугових та режекторних.

Використовуючи принципи перетворення частоти, ми впевнилися, що всi вирази, одержанi ранiше для фiльтрiв нижнiх частот, виявляються вiрними i для фiльтрiв верхнiх частот, якщо в цих виразах визначати з виразу (1) . Взагалi фiльтр верхнiх частот може бути утворений з фiльтру нижнiх частот, якщо у ньому кожну iндуктивнiсть замiнити на iмнiстю, а кожну iмнiсть тАУ iндуктивнiстю.

Всi вирази, одержанi ранiше для фiльтрiв нижнiх частот, залишаються вiрними i для смугових фiльтрiв, якщо в цих виразах визначити iз спiввiдношення (2).

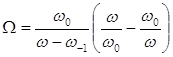
Смуговий фiльтр може бути утворений з фiльтра нижнiх частот, якщо в ньому кожну iндуктивнiсть замiнити послiдовним коливальним контуром, а кожну iмнiсть тАУ паралельним.

Режекторний фiльтр може бути утворений з ФНЧ тАУ прототипу, якщо в ньому кожну iндуктивнiсть замiнити паралельним коливальним контуром, а кожну iмнiсть послiдовним.

Для забезпечення активноi роботи фiльтра вiн повинен бути навантажений узгоджено як по воду так i по виходу.

Лiтература

1. Бiлицкий А.Ф. Лiнiйнi пристроi апаратури звтАЩязку, Л.ВАЗ, 1973р. с.70-78.

2. Качанов Н.С. ЛРТУ, М.Воениздат, с.311-325.

Вместе с этим смотрят:

GPS-навигация

GPS-прийомник авиационный

IP-телефония и видеосвязь

IP-телефония. Особенности цифровой офисной связи

Unix-подобные системы