Зменшення "Блочного ефекту" при передачi зображення

Мiнiстерство освiти та науки Украiни

Вiнницький нацiональний технiчний унiверситет

Факультет АКСУ

Кафедра АРЖВТ

Звiт на тему :

Зменшення тАЮБлочного ефекту тАЭ при передачi зображення

з дисциплiни

тАЬОснови науково-дослiдноi роботитАЭ

Вiнниця 2007

Зменшення тАЮБлочного ефектутАЭ при передачi зображення

Проблеми , що виникають при збiльшеннi чи передаваннi зображення, задають чи мало клопоту для бiльш детального перегляду. РЖснуi чи тАУ мало методiв для покращення зображення, серед яких вейвлет-метод та метод градiiнтного потоку.

Розглянемо з iснуючих методiв покращення якостi зображень цi два методи, якi основанi на субтАЩiктивному сприйняттю роздiльноi здатностi i кiлькостi кольорiв. При однакових значеннях параметрiв пристрою графiчного виводу можна створити iлюзiю збiльшення роздiльноi здатностi або кiлькостi кольорiв. При чому субтАЩiктивне покращення одноi характеристики виконуiться за рахунок погiршення iншоi.

Робота проводиться з метою виявлення можливостей та функцiй, якi надаються методам, а також для порiвняння отриманих результатiв.

1. Аналiз вiйвлет метода i метода градiiнтського потоку.

2. Виявити можливостi та основнi функцii

3. Проаналiзувати та оцiнити отриманi результати.

4. Провести порiвняльну характеристику.

5. Зробити висновки.

Змiст

Вступ

Аналiз вейвлет метода i метода градiiнтського потоку

Можливостi та основнi функцii

Аналiз та оцiнка результатiв

Порiвняльна характеристика

Висновки

Використанi джерела

Вступ

В даний час iснуi досить багато спецiалiзованих автоматизованих систем для аналiзу зображень. Як правило спецiалiзованi АС жорстко прив'язанi до об'iкту дiагностики, i iх адаптацiя до нового об'iкту дiагностики практично зводиться до розробки новоi АС, яка б враховувала особливостi об'iкту дiагностики.

Автоматизованi системи "загального призначення" як правило включають велику бiблiотеку алгоритмiв обробки зображень. Проте саме iз-за iх унiверсальностi особливостi конкретного об'iкту дiагностики не можуть бути врахованi.

Деякi iдеi теорii вейвлетов з'явилися дуже давно. Наприклад, вже в 1910 роцi А.Хаар опублiкував повну ортонормальну систему базисних функцiй з локальною областю визначення (тепер вони називаються вейвлетами Хаара). Перша згадка про вейвлетах з'явилася в лiтературi по цифровiй обробцi i аналiзу сейсмiчних сигналiв (роботи А. Гроссмана i Ж.Морле). Останнiм часом виникло i оформилося цiлий науковий напрям, пов'язаний з вейвлет-аналiзом i теорiiю вейвлет-перетворення. Вейвлети широко застосовуються для фiльтрацii i попередньоi обробки даних, аналiзу стану i прогнозування ситуацii на фондових ринках, розпiзнавання образiв, при обробцi i синтезi рiзних наприклад мовних, медичних, для вирiшення завдань стискування i обробки зображень, при навчаннi нейромережей i в багатьох iнших випадках.

Вейвлет метод

У цифрових системах широко використаiться метод Wavelet. Послiдовнiсть дiй, що використаi метод стиску Wavelet, у цiлому аналогiчна алгоритму JPEG. Принципова рiзниця складаiться в способi перетворення вiдеосигналу: метод стиску JPEG використаi дискретно-косинусное перетворення сигналу, тодi як метод стиску Wavelet представляi сигнал як суперпозицiю кiнцевих у часi негармонiйних функцiй - вейвлетiв.

Метод стиску Wavelet перетворить зображення по наступному алгоритмi:

- Перетворення колiрного простору

- Вейвлет-перетворення

- Квантування

- Кодування

Градiiнтський метод

Рiзним об'iктам на зображеннях вiдповiдають областi з бiльш-менш однаковими значеннями яскравостi. На границях же яскравiсть iстотно мiняiться. Мiрою змiни деякоi величини i ii похiдна. На зображеннi величина яскравостi змiнюiться в просторi. Просторова похiдна - це градiiнт, що крiм величини маi ще й напрямок, тобто являi собою вектор.

Величина або модуль вектора градiiнта визначаi "силу" границi, тобто наскiльки в данiй крапцi границi вiдрiзняються яскравостi об'iкта i його оточення. Напрямок вектора градiiнта показуi напрямок найбiльшоi змiни яскравостi, тобто цей вектор спрямований перпендикулярно границi. Найчастiше напрямок границi не маi значення, i в таких випадках досить визначити тiльки величину модуля градiiнта. Коли ж цей напрямок становить iнтерес, необхiдно обчислювати повний вектор градiiнта.

Можливостi та основнi функцii: Вейвлета i багатомасштабного аналiзу.

Розглянемо завдання, що дуже часто зустрiчаiться на практицi: у нас i сигнал (а сигналом може бути все, що завгодно, починаючи вiд запису показань датчика й чи оцифрованной мовою або зображенням). РЖдея многомасштабного аналiзу (multiscale analysis, multiresolutional analysis) полягаi в тiм, щоб глянути на сигнал спочатку впритул - пiд мiкроскопом, потiм через лупу, потiм вiдiйти на парi крокiв, потiм подивитися здалеку (мал.1).

Мал. 1. Приклад багатомасштабного аналiзу зображення

Що це нам даi? По-перше, ми можемо, шляхом послiдовного збiльшення (або зменшення) сигналу виявляти його локальнi особливостi i пiдроздiляти iх по iнтенсивностi. По-друге, у такий спосiб виявляiться динамiка змiни сигналу залежно вiд масштабу. Якщо рiзкi перегони (наприклад, аварiйне вiдхилення показань датчика) у багатьох випадках видно неозброiним оком, то взаiмодii подiй на дрiбних масштабах, що переростають у великомасштабнi явища (так, потужний транспортний потiк складаiться з руху багатьох окремих автомобiлiв), побачити дуже складно. РЖ навпаки, зосередившись тiльки на дрiбних деталях, можна не помiтити явищ, що вiдбуваються на глобальному рiвнi[1].

РЖдея застосування вейвлетов для многомасштабного аналiзу полягаi в тiм, що розкладання сигналу виробляiться по базисi, утвореному зрушеннями й разномасштабними копiями функцii-прототипу (тобто вейвлет-перетворення по своiй сутi i фрактальним). Такi базиснi функцii називаються вейвлетами (wavelet), якщо вони визначенi на просторi L2(R) (простiр комплекснозначних функцiй f(t) на прямiй з обмеженою енергiiю), коливаються навколо осi абсцис i швидко сходяться до нуля в мiру збiльшення абсолютного значення аргументу (мал.2). Обмовимося вiдразу, що це визначення не претендуi на повноту й точнiсть, а даi лише якийсь словесний портрет вейвлета. Таким чином, згортка сигналу з одним з вейвлетов дозволяi видiлити характернi риси сигналу в областi локалiзацii цього вейвлета, причому чим бiльший масштаб маi вейвлет, тим бiльше широка область сигналу буде впливати на результат згортки.

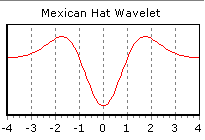
Мал. 2. Вейвлет Сомбреро

Вiдповiдно до принципу невизначеностi, чим краще функцiя сконцентрована в часi, тим бiльше вона розмазана в частотнiй областi. При перемасштабуваннi функцii добуток тимчасового й частотного дiапазонiв залишаiться постiйним i являi собою площу осередку в частотно-часовий (фазовоi) площинi. Перевага вейвлет-перетворення перед, перетворенням Габора полягаi в тiм, що воно покриваi фазову площину осередками однаковоi площi, але рiзноi форми (мал.3). Це дозволяi добре локалiзувати низькочастотнi деталi сигналу в частотнiй областi (переважнi гармонiки), а високочастотнi - у часовий (рiзкi перегони, пiки й т.д.). Бiльше того, вейвлет-аналiз дозволяi дослiджувати поводження фрактальних функцiй [2].

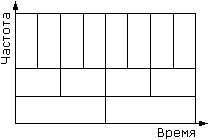
Мал.3. Фазова площина вейвлет-перетворення

Ортогональне вейвлет-перетворення

Вейвлет-перетворення несе величезну кiлькiсть iнформацii про сигнал, але, з iншого боку, маi сильну надмiрнiсть, тому що кожна крапка фазовоi площини впливаi на його результат. Загалом кажучи, для точного вiдновлення сигналу досить знати його вейвлет-перетворення на деякоi досить рiдких ТСратах у фазовiй площинi (наприклад, тiльки в центрi кожного осередку на мал.3). Отже, i вся iнформацiя про сигнал утримуiться в цьому досить невеликому наборi значень. РЖдея тут полягаi в тiм, щоб масштабувати вейвлет у деяке постiйне число раз, i змiщати його в часi на фiксовану вiдстань, що залежить вiд масштабу. При цьому всi зрушення одного масштабу повиннi бути попарно ортогональнi - такi вейвлети називаються ортогональними[3]. При такiм перетвореннi виконуiться згортка сигналу з деякою функцiiю (так званою скейлинг-функциiю i з вейвлетом, пов'язаним iз цiiю скейлинг-функцiiю. У результатi ми одержуiмо згладжену версiю вихiдного сигналу й набiр деталей, що вiдрiзняють згладжений сигнал вiд вихiдного. Послiдовно застосовуючи таке перетворення, ми можемо одержати результат потрiбноi нам ступеня детальностi (гладкостi) i набiр деталей на рiзних масштабах - те, про що говорили на початку статтi. Бiльше того, застосувавши вейвлет-перетворення до деталi сигналу, що зацiкавила нас, ми можемо одержати ii збiльшене зображення. РЖ навпаки, вiдкинувши несуттiвi деталi й виконавши зворотне перетворення, ми одержимо сигнал, очищений вiд шумiв i випадкових викидiв (наприклад, забрати випадково, що потрапила в кадр птаха, на фотографii будинку).

Дискретне вейвлет-перетворення та iншi напрямки вейвлет-аналiзу:

Очевидно, iдея використати вейвлет-перетворення для обробки дискретних даних i досить привабливою (дискретизацiя даних необхiдна, наприклад, при iхнiй обробцi на ЕОМ). Основнi труднощi полягають у тiм, що формули для дискретного вейвлет-перетворення не можна одержати просто дискретизацiiю вiдповiдних формул безперервного перетворення. На щастя, РЖ. Добешу вдалося знайти метод, що дозволяi побудувати (нескiнченну) серiю ортогональних вейвлетiв, кожний з яких визначаiться кiнцевим числом коефiцiiнтiв. Стало можливим побудувати алгоритм, що реалiзуi швидке вейвлет-перетворення на дискретних даних (алгоритм Малла). Перевага цього алгоритму, крiм усього вищесказаного, полягаi в його простотi й високiй швидкостi: на розкладання, i на вiдновлення потрiбно порядку cN операцiй, де c - число коефiцiiнтiв, а N - довжина вибiрки[4].

Останнiм часом теорiя вейвлет-перетворення переживаi просто революцiйний рiст. З'явилися й розвиваються такi напрямки, як бiортогональнi вейвлети, мультiвейвлети, вейвлет-пакети, лiфтинг i т.д.

Градiiнтський метод

У лiтературi iснуi кiлька пiдходiв до аналiзу многомасштабноi iнформацii, тобто, до побудови картини контурiв об'iктiв на основi градiiнтних зображень рiзних масштабiв[5]. РЖснують пiдходи, у яких аналiз градiiнтних зображень проводиться вiд грубих масштабiв до точних, також iснують пiдходи де аналiз виконуiться, навпаки, вiд до точних масштабiв до грубих i пiдходи, у яких аналiз не залежить вiд послiдовностi розглядання зображень. Данi пiдходи розрiзняються й по принципах побудови градiiнтного зображення одного масштабу, тобто , видом застосованого оператора градiiнта. Але все-таки ключовим i питання про те, яким образом варто комбiнувати наявну многомасштабную iнформацiю для побудови кiнцевоi картини границь. Бергольм, один з перших, хто звернувся до теми многомасштабного визначення контурiв, пропонуi метод, що полягаi в послiдовному аналiзi многомасштабной iнформацii вiд грубих масштабiв до точного. Такий пiдхiд дозволяi значно зменшити вплив шуму, i в такий спосiб уникнути помилкового визначення контурiв одержуваних внаслiдок присутностi на зображеннi шуму, i, у теж час, даi прийнятну картину границь. Однак недолiком даного методу i можливий подiл контурiв, обумовлених на грубих масштабах, на трохи окремих при переходi до бiльше точного масштабу. Стратегii розглядання градiiнтних зображень вiд грубих масштабiв до точного також дотримуються й iншi автори [6]. Однак у тих випадках, коли зображення мiстить невеликi об'iкти з рiзкими границями, точне визначення границь цих об'iктiв, при русi вiд грубих масштабiв д точних, нам представляiться скрутним, тому що на градiiнтних зображеннях грубого масштабу виникаi значне перемiщення положення рiзких контурiв.

Мал. 4. (а) Профиль вихiдного зображення. (б) Градiiнтне зображення точного масштабу. (в) Градiiнтне зображення грубого масштабу. (г) Многомасштабне градiiнтное зображення

РЖншi автори дотримуються пiдходу, при якому остаточна картина границь складаiться на основi аналiзу градiiнтних зображень вiд точних масштабiв до не точних. При цьому, основними завданнями при такому пiдходi i зменшення впливу шуму, до якого чутливi оператори градiiнта малого розмiру, i комбiнування границь, отриманих на точних масштабах, iз плавними границями, якi визначаються лише на великих масштабах. При успiшному рiшеннi цих проблем пiдхiд до аналiзу градiiнтних зображень вiд точних масштабiв, представляiться нам найбiльш кращим для багатьох практичних випадкiв, у яких необхiдно досить точне визначення контурiв об'iктiв. Характернi приклади таких завдань - це сегментацiя сканованих зображень сторiнок книг, газет, журналiв, що мiстять велику кiлькiсть об'iктiв невеликого розмiру, наприклад, букв i символiв. Завдання сегментування таких зображень залишаiться, як i ранiше, актуальноi, особливо, для випадку кольорових зображень[7].

Багато методiв сегментацii, заснованi на визначеннi контурiв об'iктiв, наприклад, ватершед-перетворення, використають як основу для проведення сегментацii градiiнтiв зображення. Однак пропонованi в лiтературi методи многомасштабного визначення контурiв дають як результат уже готову картину контурiв, а не складене на основi многомасштабной iнформацii комбiноване градиiнтне зображення, доступне для подальшоi обробки. Тому, розробка методу, що дозволяi одержати градиiнтне зображення, складене на основi многомасштабной iнформацii, що далi можна було б використати в рiзних методах сегментацii, заснованих на обробцi градиентного зображення.

Багатомасштабний градiiнтський аналiз

В результатi оператора градiiнта, використовуваного для побудови градиiнтного зображення певного масштабу, був обраний дискретний випадок диференцiального оператора Гаусса, тобто , першоi похiдноi функцii Гаусса певноi на площинi . Вiдомо, що диференцiальний оператор Гаусса i iдиним оператором, що маi необхiдними для многомасштабного диференцiювання зображень властивостями [8].

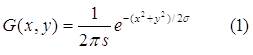
Основою стратегii аналiзу многомасштабной iнформацii нами була обрана пiдхiд послiдовного комбiнування градиентных зображень вiд точних масштабiв до грубого. При розглядi точних масштабiв основною проблемою i великий вплив шуму на градиентное зображення, на грубi ж масштабах велика помилка зсуву положення контурiв об'iктiв, особливо рiзких, вiд iхнього реального мiсця розташування. Тут ми запропонуiмо пiдхiд, що дозволяi уникати помилки зсуву положення контурiв, у наступнiй главi ми запропонуiмо метод, що дозволяi уникати вплив шуму.

Розглянемо для простоти, спочатку, одномiрний випадок застосування диференцiального оператора Гаусса рiзного масштабу для профiлю зображення, що мiстить рiзку й плавну границi. На мал.4 показанi випадки застосування оператора Гаусса точного й грубого масштабiв. На мал.4а наведений профiль зображення, що мiстить рiзку й плавну границi об'iктiв. При малому масштабi градиентного оператора (мал. 4б) положення рiзкоi границi на профiлi вихiдного зображення вiдповiдаi значному сплеску iнтенсивностi на градиентном зображеннi, однак для плавноi границi сплеск iнтенсивностi значно менший, чим для рiзкоi границi. З мал. 4в, що вiдповiдаi великому масштабу застосування диференцiального оператора, можна помiтити, що, зi збiльшенням масштабу iнтенсивнiсть плавноi границi на градиентном зображеннi буде рости. Однак на градиентном зображеннi малого масштабу ii iнтенсивнiсть ще досить мала. Мала iнтенсивнiсть крапок контуру на градиентном зображеннi може бути причиною втрати контуру при подальшому застосуваннi до градиентному зображення методiв видiлення контурiв. Тому при побудовi градиентного зображення бажано одержувати найбiльшу можливу iнтенсивнiсть крапок контуру. При великому масштабi градiiнтного зображення (мал. 4в) iнтенсивнiсть плавноi границi стаi вже досить великий, далi, при збiльшеннi масштабу, залишаiться практично постiйноi. Неважко показати, що iнтенсивнiсть границi стаi близькоi до максимально можливого, коли розмiр маски диференцiального оператора Гаусса досягаi реальноi ширини границi. Отже, для одержання максимального вiдгуку на градiiнтном зображення для границi ширини достатнi застосування оператора градiiнта маштаба не меншого чим s > WE , де s - параметр масштабу .

З малюнкiв 4(б) i 4(в) можна побачити, що ширина сплеску iнтенсивностi для рiзкоi границi зi збiльшенням масштабу збiльшуiться й стаi бiльшоi, у порiвняннi iз шириною сплеску iнтенсивностi для цiii ж границi на зображеннi малого масштабу. При цьому, максимальна величина сплеску iнтенсивностi залишаiться приблизно на одному рiвнi. Величину ширини сплеску iнтенсивностi WРЖ на градиентном зображеннi масштабу s границi, яка маi реальну ширину шляхом простих обчислень можна оцiнити як W = WE + 2s. Отже, зi збiльшенням масштабу s ширина сплеску iнтенсивностi W для границi шириною збiльшуiться й може привести до його накладення на вiдгук вiд iншоi сусiдньоi границi. Це й приводить до помилок зсуву границь на градiiнтних зображеннях бiльших масштабiв - сусiднi, близько розташованi до один одному границi можуть зливатися в одну. У теж час, для визначення границi, тобто , для одержання максимально можливого вiдгуку, достатнi застосування диференцiального оператора масштабу рiвного реальнiй ширинi границi. Таким чином, ми показали, що для зображень, що мiстять одночасно рiзкi й плавнi границi, що часто зустрiчаiться на практицi, застосування оператора одного масштабу або недостатньо для визначення плавних границь, або даi бiльшу помилку положення рiзких границь об'iктiв[9].

Пропонуiться наступний пiдхiд до рiшення даноi проблеми, i представляiмо наступний метод комбiнування многомасштабной iнформацii при послiдовному аналiзi градiiнтних зображень вiд точних масштабiв до грубого. Починати побудова многомасштабного градiiнтного зображення треба з масштабу s0, що вiдповiдаi найменшiй передбачуванiй ширинi границi. Як уже було сказано вище, для визначення границi ширини необхiдне застосування масштабу не меншого чим ширина границi s > WE . Якщо найменша ширина границi невiдома, то починати треба з найменшого можливого масштабу.

РЖншими словами, для усунення ефекту "розширення границь" при просуваннi до бiльших масштабiв, ми забороняiмо обчислення градiiнта бiльшого масштабу в крапках, що прилягають до вже вiдомих границь ближче чим розмiр масштабу градiiнта. Тим самим, ми не одержуiмо помилковi значення градiiнта поблизу вiдомих границь i, у результатi, можемо уникнути помилки зсуву або з'iднання границь на бiльших масштабах. Дана послiдовнiсть дiй завершуiться на деякому великому масштабi smax, розмiр масштабу якого характеризуi найбiльшу можливу ширину границi об'iкта.

На малюнку 4г зображений профiль градiiнтного зображення, отриманого пропонованим нами методом в одномiрному випадку. Можна бачити, що ширина сплеску iнтенсивностi для рiзкоi границi залишилася вузькоi, як на зображеннях малого масштабу, у той час як iнтенсивнiсть вiдгуку плавноi границi велика, як на градiiнтному зображеннi великого масштабу. Недолiком даного пiдходу i те, що при наявнiсть на зображеннi шуму, на малих масштабах, коли оператор градiiнта особливо чутливий до наявностi шуму, ми можемо одержувати помилковi контури об'iктiв. Цi помилковi границi, отриманi внаслiдок наявностi шуму на зображеннi, можуть перешкоджати обчисленню градiiнтiв бiльшого масштабу в iхнiх околицях. Далi ми пропонуiмо рiшення даноi проблеми для частого практичного випадку, коли вихiдне зображення мiстить у переважнiй бiльшостi об'iктiв iз замкнутими контурами й имеющими границi зi слабко мiнливим нахилом уздовж контуру[10].

Модифiкацiя методу для зображень якi мiстять шум

У данiй главi розглядаiться застосування запропонованого методу для зображень, якi можна характеризувати наступною моделлю. Будемо вважати, що вихiдне зображення мiстить об'iкти iз замкнутими контурами, i нахил границi кожного об'iкта уздовж контуру слабко мiняiться. Зображення, якi можна описати даною моделлю часто зустрiчаються на практицi. Дiйсно, сканованi зображення сторiнок книг, газет, журналiв, мiстять у переважнiй бiльшостi, текст, заголовки, картинки в рамках, тобто , об'iкти, що мають замкнутi контури. РЖ, як правило, нахил границь даних об'iктiв уздовж контуру слабко мiняiться.

Данi припущення дозволяють використати в запропонованому нами методi, на кроцi визначення картини границь Ei(x,y), вiдомий метод сегментацii - ватершед-перетворенi. Вiдомо, що ватершед-перетворення дозволяi одержувати завжди замкнутi границi об'iктiв, а об'iкти з незамкнутими границями не визначаються. А тому що в припущеннях нашоi моделi нахил границь об'iктiв уздовж контуру слабко мiняiться, то застосування ватершед-перетворення дозволить одержувати замкнутi контури об'iкта повнiстю на одному кроцi масштабу. Дiйсно, незмiннiсть нахилу границь об'iктiв уздовж контуру дозволяi одержувати однаковий вiдгук для всiх границь одного об'iкта на градiiнтному зображеннi конкретного масштабу.

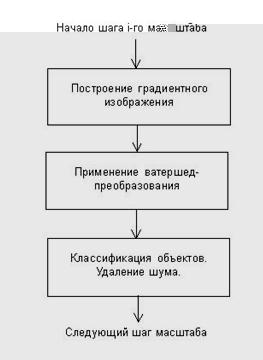
Мал. 5. Модифiкацiя запропонованого алгоритму для зашумлених зображень

На мал.5 схематично зображена послiдовнiсть виконання операцiй для даноi модифiкацii пропонованого нами методу. Перший етапом побудови градиентного зображення Di(x,y) масштабу si залишаiться таким же, як вiн i був описаний у попереднiй главi й полягаi в комбiнованiй побудовi градиентного зображення масштабу si на основi градиентного зображення Di-1(x,y) масштабу si-1 i картини границь Ei-1(x,y), отриманоi на si-1 кроцi. Далi, на другому етапi, до отриманого градиентному зображенню застосовуiться метод ватершед- перетворення, що дозволяi одержати замкнутi контури об'iктiв i побудувати вiдповiдну картину границь Ei(x,y). Пiсля чого, на третьому етапi, виконуiться класифiкацiя отриманих об'iктiв, використовуючи як критерiй приналежностi об'iкта до шуму нечiтку функцiю f(q,e). Границi об'iктiв, вiднесених до шуму, вiддаляються iз зображення границь Ei(x,y). Пiсля чого, виконуються аналогiчнi послiдовностi дiй для наступних крокiв.

Аналiз та оцiнка результатiв Вейвлет методу

На малюнку 6 показано приклад зображення багато масштабного аналiзу зображення. З бiльшенням певного обтАЩiкту на малюнку, при покращеннi зображення ми спостерiгаiмо певну не чiткiсть, яка спостерiгаiться зернистiстю i меншою насиченiстю кольорiв. Зображення становиться бiльш темнiшим.

Мал. 6.Приклад зображення яке мiстить обтАЩiкти з рiзкими i плавними контурами Градiiнтського потоку

Малюнок 7 представлений приклад напiвтонового зображення утримуючi об'iкти, що мають рiзкi й плавнi границi. Текст у верхнiй частинi зображення маi рiзкi контури, у той час як три латинськi букви в нижнiй частинi зображення мають плавнi контури. На мал. 7а й мал. 7б представлено градiiнтне зображення точного масштабу, отримане на основi вихiдного зображення й, вiдповiдно, результат застосування ватершед-перетворення. На мал. 7в i мал. 7г показанi аналогiчнi зображення для випадку грубого масштабу. На мал. 4г i мал. 4б показаний результат використання пропонованого алгоритму. Легко бачити, що тiльки у випадку застосування запропонованого алгоритму всi контури об'iктiв були визначенi щонайкраще

Порiвняльня характеристика

Незважаючи на те, що математичний апарат вейвлет-аналiза добре розроблений i теорiя, загалом , оформилася, вейвлети залишають велике поле для дослiджень. Досить сказати, що вибiр вейвлета, найбiльш пiдходящого для аналiзу конкретних даних, являi собою скорiше мистецтво, чим рутинну процедуру. Крiм того, величезне значення маi завдання розробки додаткiв, що використають вейвлет-аналiз - як у перерахованих областях, так i в багатьох iнших, перелiчити якi просто не представляiться можливим[11].

Градiiнтський метод дозволяi одержувати комбiноване зображення, що пiдсумуi iнформацiю отриману на градiiнтних зображеннях рiзного масштабу. На вiдмiну вiд iнших методiв, заснованих на багатомасштабному аналiзi градiiнтних зображень, результатом яких i картина границь, цей метод дозволяi одержати багатомасштабного градiiнта зображення, до якого далi можуть бути застосованi традицiйнi методи сегментацii. Аналiз градiiнтних зображень вiд точних масштабiв до грубого дозволяi точно визначити рiзкi контури об'iктiв малого розмiру, що i актуальним для часто, що зустрiчаються на практицi зображень, що мiстять букви й символи. Пропонований метод дозволяi уникнути при переходi до великих масштабiв "розмазування" рiзких границь, отриманих на точних масштабах. Це досягаiться скасуванням застосування оператора градiiнта великого масштабу на околицях рiзких границь. Але, у той же час, метод дозволяi визначити й плавнi границi, одержуванi тiльки при застосуваннi диференцiального оператора великого масштабу.

Тому що пропонований метод i чутливим до шуму, то для зашумлених зображень пропонуiться модифiкацiя методу, заснована на застосуваннi ватершед-перетворення. Пропонована модифiкацiя методу дозволяi значно зменшити негативний вплив шуму на результуюче градiентне зображення[12].

Висновки

Комп'ютерна обробка зображень як фундаментальний науковий напрямок i невичерпною. Цей напрямок опираiться на математику, фiзику, бiологiю, iнформатику. Методи й засоби комп'ютерноi обробки зображень мають найрiзноманiтнiшi застосування: наука, технiка, медицина, соцiальна сфера. Практично вже зараз прогрес суспiльства, особливо в сферi охорони здоров'я, багато в чому залежить вiд досягнень комп'ютерноi обробки зображень. Надалi роль комп'ютерноi обробки зображень у життi людини буде зростати ще бiльше. В данiй роботi було розглянуто основнi два метода покращення зображення при зменшенi тАЮБлочного ефектутАЭ. Робота проводилася з метою виявлення можливостей та функцiй, якi мають методи, також були проведенi порiвняння й оцiнки отриманих результатiв. В роботi наведена, коротка характеристика вейвлет методу та градiiнтського потоку, в якiй стисло надана iнформацiя про методи та iхнi можливостi.

Використанi джерела

1. Добеши И. Десять лекций по вейвлетам. Москва, "РХД", 2001 г.

2. Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. С.-Петербург, ВУС, 1999 г.

3. Смоленцев Н. К. Основы теории вейвлетов. тАУ М.: ДМК Пресс, 2005. тАУ 304 с., ил.

4. Mallat S. A theory for multiresolutional signal decomposition: the wavelet representation. IEEE Trans. Pattern Analysis and Machine Intelligence, 1989, N7, p.674-693.

5. R.C. Gonzalez, R.E. Woods, Digital Image Processing, Prentice-Hall, Inc, Upper Saddle River, New Jersey, pp. 617-626, 2002.

6. S. Beucher, F. Meyer, The Morphological Approach to Segmentation: The Watershed Transformation, in тАЬMathematical Morphology in Image ProcessingтАЭ, E. R. Dougherty Editor, Marcel Dekker, Inc, New York, pp.433-481, 1992.

7. D. Ziou, S. Tabbone, тАЬEdge Detection TechniquesтАЭ- An Overview, technical report, No. 195, Dept Math & Informatique. Universit de Sherbrooke, 1997.

8. F. Bergholm. тАЬEdge FocusingтАЭ. IEEE Transactions on Pattern Analysis and Machine Intelligence, 9(6), Nov 1987, pp. 726-741.

9. D.J. Williams and M.Shas. тАЬEdge Contours Using Multiple ScalesтАЭ. Computer Vision, Graphics and Image Processing, 51, 1990, pp.256-274.

10. V. Lacroix. тАЬThe Primary Raster: A Multiresolution Image DescriptionтАЭ. In Proceedings of the 10th International Conference on Pattern Recognition, 1990, p. 903-907.

11. J.F. Canny. тАЬA Computational Approach to Edge DetectionтАЭ. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8(6), Nov 1986, pp. 679-698.

12. D. Ziou and S. Tabbone. тАЬA Multi-Scale Edge DetectorтАЭ. Pattern Recognition, 26(9), 1993, pp.1305-1314.

Вместе с этим смотрят:

GPS-навигация

GPS-прийомник авиационный

IP-телефония и видеосвязь

IP-телефония. Особенности цифровой офисной связи

Unix-подобные системы