Конструювання обчислювальноi технiки

Дипломна робота

конструювання обчислювальноi технiки

Змiст

1. Тепловi процеси в РЕЗ

1.1 Теплообмiн

1.2 Передача тепловоi енергii теплопровiднiстю (кондукцiiю)

1.3 Теплопровiднiсть крiзь стiнку

1.4 Теплопровiднiсть вздовж стiнок та стержнiв

1.5 Способи збiльшення теплопровiдностi

1.6 Передача тепловоi енергii конвекцiiю

1.6.1 Конвективна тепловiддача

1.6.2 Вiльна конвекцiя в необмеженому просторi

1.6.3 Вiльна конвекцiя в обмеженому просторi

1.6.4 Конвективний теплообмiн при довiльному тиску

1.7 Передача тепловоi енергii випромiнюванням

1.8 Складний теплообмiн

1.9 Тепловi режими РЕЗ

1.9.1 Нагрiвання тiла зовнiшнiм середовищем

1.9.2 Нагрiвання тiла внутрiшнiм джерелом енергii

1.9.3 Розрахунок температури корпуса та нагрiтоi зони

1.9.4 Максимальна температура РЕЗ

1.9.5 Температура в довiльнiй точцi

1.10 Типовi тепловi моделi РЕЗ

1.11 Вибiр загальноi системи охолодження РЕЗ

2. ЕОМ як механiчна система

2.1 Динамiчна модель та ii параметри

2.1.1 Приведення мас

2.1.2 Приведення сил

2.1.3 Приведення пружних параметрiв

2.1.4 Приведення параметрiв дисипацii

2.2 Вiльнi коливання одномасовоi системи

2.3 Вимушенi коливання при гармонiчному збудженнi

2.4 Коефiцiiнт динамiчностi

2.5 Зменшення вимушених коливань

2.6 Вимушенi коливання при перiодичному збудженнi

2.7 Коливання елементiв РЕА типу балок

2.8 Коливання пластин

2.9 Вiброзахист обчислювальноi технiки

3. Електромагнiтна сумiснiсть радiоелектронних засобiв

3.1 Проблеми електромагнiтноi сумiсностi

3.2 Джерела, приймачi та звтАЩязки завад

3.3 Застосування еквiвалентних електричних схем

3.4 Приклад розрахунку еквiвалентноi схеми

3.5 Екранування

3.6 Екранування електростатичного поля

3.7 Магнiтостатичне екранування

3.8 Електромагнiтне екранування

3.9 Електромагнiтна сумiснiсть цифрових вузлiв

Висновки

Перелiк умовних позначень

Список лiтератури

Вступ

Конструювання i органiчною складовою бiльш широкого процесу, який повтАЩязаний iз розробкою технiчного проекту, виробництвом i експлуатацiiю виробу. Процес конструювання не можна звести до окремих конструкторських рiшень, прикладiв та рекомендацiй. Дуже важливо мати правильне й змiстовне уявлення про загальнi закономiрностi конструювання, його проблеми та перспективи. Тому конструювання обчислювальноi технiки (ОТ) розглянуто як прикладну наукову дисциплiну, що узагальнюi методи аналiзу та синтезу конструкцiй ОТ.

Теорiя конструювання обчислювальноi технiки формуiться на основi вивчення та врахування тих фiзичних процесiв, якi реально впливають на ii функцiональнi показники. В першу чергу, це електричнi, електромагнiтнi, тепловi та механiчнi процеси. Цi рiзнi за своiю фiзичною природою процеси певним чином взаiмоповтАЩязанi мiж собою. Сучасне проектування ОТ вимагаi системного пiдходу, при якому всi фiзичнi процеси розглядаються у взаiмодii. Такий пiдхiд потребуi створення складних фiзичних та математичних моделей.

Електрична енергiя, яку споживаi радiоелектронний засiб (РЕЗ), неминуче перетворюiться в теплову. При цьому елементи РЕЗ нагрiваються i погiршують своi характеристики. Боротьба з перегрiвом особливо актуальна в умовах мiнiатюризацii, що потребуi детального аналiзу трьох видiв теплообмiну: теплопровiдностi, конвекцii, випромiнювання. В багатьох випадках передача тепла вiдбуваiться через плоскi й цилiндричнi стiнки, при цьому важливими i способи збiльшення теплопровiдностi. У випадку складних теплових режимiв нормальна робота приладiв можлива завдяки використанню систем охолодження.

При певних обставинах на базi пружних елементiв в ЕОМ можуть виникати та розвиватись механiчнi коливання. Для визначення рiвня коливань складаiться вiдповiдна динамiчна модель. Динамiчна модель тАУ iдеалiзований в межах поставленоi задачi обтАЩiкт з певними характеристиками у виглядi iнерцiйних, пружних, дисипативних та силових параметрiв. Важливим питанням i вiброзахист обчислювальноi технiки, який реалiзуiться завдяки застосуванню рiзних видiв амортизаторiв.

Електромагнiтна сумiснiсть тАУ здатнiсть виробiв нормально функцiонувати поруч з iншими виробами в умовах дii мiж ними та на них додаткових електромагнiтних полiв при виготовленi та експлуатацii. Тому для надiйноi роботи приладiв важливими i способи зменшення завад, екранування електростатичного, магнiтного та електромагнiтного поля.

1. Тепловi процеси в РЕЗ

1.1 Теплообмiн

Електрична енергiя, яку споживаi РЕЗ, неминуче перетворюiться в теплову [1, 2]. При цьому елементи РЕЗ нагрiваються i погiршують своi характеристики. Боротьба з перегрiвом особливо актуальна в умовах мiнiатюризацii. РЖснують два принципово рiзнi методи боротьби з перегрiвом:

- зменшення споживаноi енергii, яка перетворюiться в теплову;

- iнтенсифiкацiя тепловiдведення з РЕЗ у навколишнi середовище.

Для успiшного розвтАЩязку проблеми треба вивчити процеси теплообмiну.

Теплообмiн тАУ це процес переносу тепловоi енергii iз однiii частини середовища в iншу. Важливо, що теплообмiн тАУ необоротний процес. Вiн визначаiться рiзницею температур i проходить в напрямку зменшення температури. Як правило, цей процес iде з середини апарату в зовнiшнi середовище.

Розрiзняють три види теплообмiну [1-3]:

В· теплопровiднiсть тАУ молекулярний чи електронний процес переносу тепла в суцiльному середовищi;

В· конвекцiя тАУ перенесення тепла, повтАЩязане з макроперемiщенням обтАЩiмiв рiдин та газiв;

В· випромiнювання (радiацiя) тАУ це явище переносу енергii у виглядi електромагнiтних хвиль.

Незалежно вiд виду теплообмiну, тобто незалежно вiд механiзму теплового процесу, його описують за допомогою аналiтичного виразу, який маi однакову лiнiйну форму.

Позначимо:

Q тАУ кiлькiсть тепла, Дж;

Ф тАУ тепловий потiк, Вт.

В такому випадку маi мiсце диференцiальна залежнiсть:

, (1.1)

де τ тАУ час.

Мiж рiзницею температур (перегрiвом θ) i тепловим потоком маi мiсце залежнiсть

, (1.2)

де R12 тАУ коефiцiiнт пропорцiональностi, який залежить вiд природи та стану середовища, а також вiд механiзму теплового процесу. В загальному випадку це складна функцiя, але досить часто R12 - константа. По аналогii з електричними колами R12 називають тепловим опором.

1.2 Передача тепловоi енергii теплопровiднiстю (кондукцiiю)

Мова йде про передачу тепла в твердих тiлах, нерухомих рiдинах i газах, коли температура iх окремих дiлянок рiзна. На рис.1.1. зображенi iзотермiчнi поверхнi та лiнii теплового потоку.

Рис.1.1. РЖзотермiчнi поверхнi та лiнii теплового потоку

Основним законом теплопровiдностi i закон ФуртАЩi:

, (1.3)

де q тАУ поверхнева густина теплового потоку, ;

- температурний градiiнт, ; - теплопровiднiсть, .

У диференцiальнiй формi звтАЩязок мiж тепловим потоком i поверхневою густиною теплового потоку маi вигляд

, (1.4)

де dА тАУ елементарна площа iзотермiчноi поверхнi, через яку проходить тепловий потiк.

Якщо тепловий потiк однорiдний (q=const), то

. (1.5)

Виведемо формулу для визначення теплового опору, якщо тепловий потiк однорiдний. З (1.3) та (1.5) слiдуi, що

.

Враховуючи останнi рiвняння, з формули (1.2) одержимо:

.

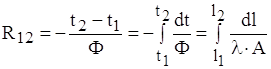Дуже часто . Тодi це рiвняння прийме вигляд:

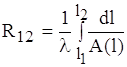. (1.6)

З допомогою формули (1.6), виходячи з геометричних особливостей тiла та знаючи коефiцiiнт теплопровiдностi матерiалу λ, можемо визначити тепловий опiр дiлянки. Знаючи тепловий опiр R12 та перегрiв θ12, iз формули (1.2) одержуiмо робочу формулу для визначення теплового потоку на заданiй дiлянцi:

, (1.7)

де - тепловий опiр дiлянки, ;

- теплова провiднiсть дiлянки, ; ;

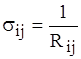- перепад температур (перегрiв).

1.3 Теплопровiднiсть крiзь стiнку

Стiнки i досить розповсюдженими елементами конструкцiй обчислювальноi технiки. Тепловий опiр стiнок можна визначати незалежно вiд умов роботи конструкцii та робочих режимiв. Розглянемо найбiльш типовi випадки та виведемо розрахунковi формули для визначення теплового опору.

Однорiдна поперечна плоска стiнка

На рис.1.2. зображена однорiдна плоска стiнка товщиною δ. Через неi в поперечному напрямку протiкаi однорiдний тепловий потiк Ф у напрямi зменшення температури; при цьому ti - температура лiвоi поверхнi стiнки, tj - температура правоi поверхнi стiнки, ti > tj.

Теплове коло i тепловим опором Rij з температурними потенцiалами на кiнцях ti, tj. Формула (1.6) у даному випадку набуде вигляду:

.

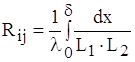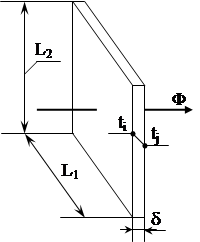а) б)

Рис. 1.2. Однорiдна поперечна плоска стiнка (а) та ii теплова модель (б)

Остаточно запишемо ii так:

. (1.8)

Отже, тепловий опiр пропорцiйний товщинi стiнки δ i обернено пропорцiйний ii площi А та теплопровiдностi матерiалу λ.

Цилiндрична стiнка

Нехай однорiдний тепловий потiк Ф напрямлений у напрямку зовнiшньоi стiнки (рис.1.3).

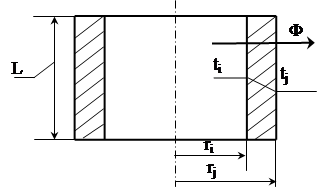Рис.1.3. Цилiндрична стiнка

Хоча теплове коло, як i в попередньому випадку, складаiться з одного теплового елемента Rij, розрахункова формула буде iншою. В даному випадку площа поверхнi, через яку проходить тепловий потiк Ф, i функцiiю . Тому формула (1.6) набуваi вигляду

.

Остаточно запишемо ii так:

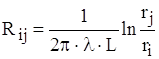. (1.9)

Поперечна багатошарова стiнка

На рис.1.4 зображена поперечна стiнка, що складаiться з трьох шарiв. Незмiнний однорiдний тепловий потiк Ф послiдовно проходить через кожний шар як через однорiдну поперечну стiнку площею А.

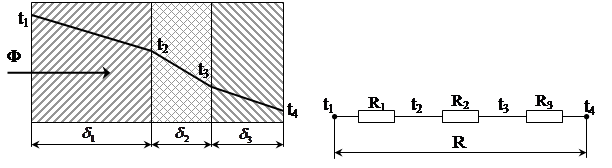а) б)

Рис.1.4. Поперечна багатошарова стiнка площею А (а) та ii теплова модель (б)

Теплове коло i послiдовним зтАЩiднанням теплових опорiв кожного шару. Тепловий опiр всiii стiнки визначаiться як сума теплових опорiв елементiв. У загальному випадку розрахункова формула набуваi вигляду:

. (1.10)

Поздовжня багатошарова стiнка

Всi шари стiнки мають однакову товщину δ (рис.1.5).

а) б)

Рис.1.5. Поздовжня багатошарова стiнка (а) та ii теплова модель (б)

Тепловий потiк Ф розподiляiться мiж кожним шаром стiнки площею Аk. Кожний шар маi свою теплопровiднiсть матерiалу λk. Через поверхню площею Аk проходить тепловий потiк Фk, при цьому 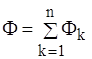. Теплове коло i паралельним зтАЩiднанням теплових опорiв кожного шару. Тепловий опiр всiii стiнки знайдемо по аналогii з визначенням опору електричного кола. Одержимо розрахункову формулу

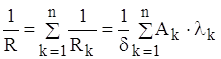. (1.11)

1.4 Теплопровiднiсть вздовж стiнок та стержнiв

Особливiстю стержнiв та пластин i одновимiрний характер розповсюдження тепла. Тепловий потiк у стержнi рухаiться вздовж його осi, а в стiнцi тАУ вздовж стiнки. В поперечному напрямку температурний градiiнт набагато менший, нiж уздовж стiнки чи стержня. До стержнiв можна вiднести провiдники, електроди термопар, тощо. До пластин можна вiднести робочий елемент напiвпровiдникового випрямляча радiаторного типу, окреме ребро радiатора, шасi, на якому змонтованi деталi, тощо.

На рис.1.6 зображений стержень, вздовж якого рухаiться тепловий потiк Ф

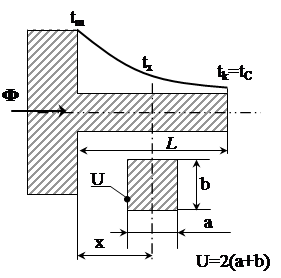Рис.1.6. Тепловий потiк стержня

Хоча тепловий потiк рухаiться вздовж стержня, його iнтенсивнiсть падаi, бо маi мiсце вiддача тепла з боковоi поверхнi стержня в оточуюче середовище. Тому, якщо на початку температура боковоi поверхнi стержня дорiвнювала tm, то в кiнцi стержня вона падаi до значення tk. Якщо L таке, що tk=tC (Фk=0), то для довiльного перерiзу з координатою х маi мiсце формула:

, (1.12)

де А тАУ площа поперечного перерiзу;

U тАУ периметр поперечного перерiзу;

;

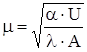α - коефiцiiнт тепловiддачi боковоi поверхнi стержня;

λ - теплопровiднiсть матерiалу;

, .

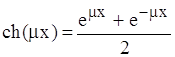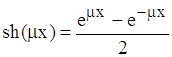1.5 Способи збiльшення теплопровiдностi

Ефективна робота теплопроводiв визначаiться не тiльки iх геометрiiю, але й властивостями матерiалу. В першу чергу мова пiде про теплопровiднiсть λ, яка входить у всi наведенi ранiше розрахунковi формули кондуктивноi теплопередачi.

Матерiал зi значенням теплопровiдностi вважаiться теплопровiдним. Тобто такi матерiали в загальному випадку здатнi забезпечити вiдвiд тепла вiд нагрiтого елемента, запобiгаючи його перегрiву. Матерiали зi значенням теплопровiдностi вважаються теплоiзоляцiйними. Розглянемо теплопровiдностi основних видiв матерiалiв бiльш детально.

Теплопровiднiсть газiв лежить у межах: (тiльки у гелiю i водню цi значення у птАЩять разiв бiльшi). З ростом абсолютноi температури Т iх теплопровiднiсть зростаi практично лiнiйно.

Теплопровiднiсть рiдин лежить в межах . Проте якщо в асоцiйованих рiдинах (вода та iн.) з ростом Т значення λ зростають згiдно параболiчного закону, то у неасоцiйованих рiдин (бензол та iн.) з ростом Т значення λ падають згiдно параболiчного закону.

Теплопровiднiсть металiв лежить в межах . У чистих металах при зростаннi Т значення λ падаi згiдно параболiчного закону, у сплавах тАУ зростаi лiнiйно.

Значення теплопровiдностi дiелектрикiв лежить в межах . З ростом абсолютноi температури Т значення λ зростаi майже параболiчно.

Особливе мiсце займають алмази (природнi i штучнi). Вони мають особливо високу теплопровiднiсть . Це визначаi iх широке застосування в електроннiй технiцi (напiвпровiдниковi прилади, iнтегральнi мiкросхеми, тощо). Алмази дозволяють зменшити тепловi опори мiж кристалами та корпусом.

Для зменшення теплового навантаження елементiв електронних приладiв потрiбно:

В· використовувати матерiали з високим значенням λ;

В· збiльшувати площу контакту елементiв теплопроводiв;

В· зменшувати шляхи теплопотокiв.

Для цього потрiбно знiмати з контактiв лаки, фарби, зменшувати шорсткiсть поверхонь i збiльшувати тиск мiж ними, в якостi прокладок використовувати пасти високоi провiдностi, застосовувати шини мiж елементами i корпусом, замiнювати гумовi прокладки на свинцевi, застосовувати самонарiзнi гвинти.

В якостi теплопровiдних найбiльше застосування знайшли такi матерiали:

В· мiдь i алюмiнiй для зниження контактного опору;

В· кадмiй i олово для покриття елементiв;

В· свинець, мiдь, алюмiнiй для виготовлення прокладок.

1.6 Передача тепловоi енергii конвекцiiю

1.6.1 Конвективна тепловiддача

Мова йде про передачу тепла з поверхнi твердого тiла в газ або рiдину, якi перемiщуються вiдносно поверхнi. Цей процес суттiво залежить вiд стану нагрiтого середовища. Конвекцiя завжди супроводжуiться теплопровiднiстю

,

де q- поверхнева густина теплового потоку;

- теплопровiдна складова;

- конвективна складова.

Якщо швидкiсть перемiщення V газу чи рiдини вiдносно поверхнi тiла падаi до нуля, то . Якщо ж ця швидкiсть досягаi високих значень, то . У бiльшостi практичних задач .

Процес конвекцii формально (математично) зводиться до процесу теплообмiну (тiло - рiдина). Цей процес називаiться конвективною тепловiддачею та виражаiться формулою Ньютона:

, (1.13)

де А - площа поверхнi тепловiддачi;

- конвективна теплопровiднiсть, ;

- коефiцiiнт конвективноi тепловiддачi, .

Формула Ньютона виглядаi як лiнiйна функцiя, але справа в тому, що коефiцiiнт конвективноi тепловiддачi складним чином суттiво залежить вiд багатьох теплофiзичних та гiдродинамiчних факторiв. Коефiцiiнт конвективноi тепловiддачi розглянемо як функцiю

, (1.14)

де - температура тiла;

- температура середовища;

- коефiцiiнт термiчного розширення середовища;

- теплопровiднiсть середовища;

- теплоiмнiсть середовища;

- коефiцiiнт динамiчноi втАЩязкостi середовища;

- густина середовища;

- визначальний розмiр тiла;

- прискорення земного тяжiння.

В залежностi вiд конкретних умов (1.14) може набути досить простого вигляду. Теорiя подiбностi даi ряд критерiiв, якi дозволяють класифiкувати задачу визначення αK по значеннях цих критерiiв. Формула (1.14) в залежностi вiд конкретних умов набуваi декiлькох характерних форм, кожна з яких значно простiша базовоi формули.

1.6.2 Вiльна конвекцiя в необмеженому просторi

Значення αK в першу чергу залежить вiд стану граничного шару рiдини. Для тiл з одним визначальним розмiром L (вертикальнi плити, стiнки, довгi провiдники) широкого застосування набула емпiрична формула:

,

деPr- число Прантля, , ;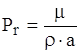

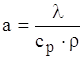Gr- число Грасгофа, ;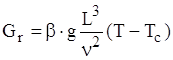

Nu- число Нуссельта, ;

c, n тАУ емпiричнi коефiцiiнти;

m тАУ iндекс, який означаi, що фiзичнi параметри рiдини беруться для середньоi температури

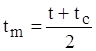. (1.15)

В залежностi вiд значення комплексного критерiю розрiзняють чотири типових ситуацii, якi характеризуються певним режимом руху рiдини та значеннями С i n (таблиця 1.1).

Таблиця. 1.1.

Режими руху рiдини

№	Значення	c	n	Режим руху рiдини
1		0,5	0	Плiвковий
2		1,18	1/8	Перехiдний до ламiнарного
3		0,54	1/4	Ламiнарний
4		0,135	1/3	Турбулентний

Формула (1.15) унiверсальна в тому розумiннi, що стосуiться рiзних середовищ (повiтря, водень, вуглекислий газ, мастила тощо). Нас ця формула цiкавить з точки зору застосування до електронних схем, тобто коли середовищем i повiтря.

Форма поверхонь тiл зводиться до трьох базових поверхонь: площина, сфера, цилiндр.

Цi поверхнi характеризуються одним визначальним розмiром L та орiiнтацiiю поверхнi в середовищi (повiтрi). Орiiнтацiя характеризуiться значенням параметра N. Основнi випадки орiiнтацii поверхнi наведемо у виглядi таблицi 1.2.

Чотири характернi режими конвективноi тепловiддачi повтАЩязують зi значенням емпiричного iндексу n i називають законом ступеня n. Розглянемо кожний з чотирьох законiв та дамо вiдповiднi формули визначення конвективноi тепловiддачi.

Таблиця 1.2.

Орiiнтацiя поверхнi в середовищi

№	Поверхня та орiiнтацiя	L	N
1	Горизонтальний цилiндр	d тАУ дiаметр	1,0
2	Вертикальна пластина чи цилiндр	H тАУ висота	1,0
3	Горизонтальна пластина: а) нижня площина б) верхня площина	Lmin - мiнiмальний розмiр площини	0,7 1,3

Закон ступеня нуль. Бiля поверхнi тiла утворюiться майже нерухома плiвка нагрiтого повiтря. Теплообмiн вiдбуваiться практично за рахунок теплопровiдностi. Такий режим теплообмiну маi мiсце при незначних перепадах температур (θ=Т-ТС) для тiл з малими розмiрами та плавними формами.

Закон ступеня 1/8. Такий закон маi мiсце при вiдносно невеликих перепадах температур для тiл з малими розмiрами та рiзкими формами. Наприклад, при охолодженнi тонких довгих стержнiв. Режим руху теплоносiя - перехiдний до ламiнарного. РЖнтенсивнiсть теплообмiну незначна. Маi мiсце формула:

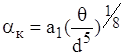, (1.16)

де d - дiаметр стержня;

. (1.17)

Закон ступеня 1/4. При цьому законi на поверхнi тiла вiдбуваiться ламiнарний рух. Здiйснюiться значний конвективний теплообмiн. Така картина спостерiгаiться бiля ребер радiаторiв, на поверхнi плоских та цилiндричних апаратiв середнього розмiру. Маi мiсце формула:

, (1.18)

де L - визначальний розмiр, м;

N - параметр, що визначаi орiiнтацiю тiла;

. (1.19)

Закон ступеня 1/3. При цьому законi на поверхнi тiла вiдбуваiться iнтенсивний турбулентний рух теплоносiя i вiдбуваiться iнтенсивний теплообмiн. Коефiцiiнт конвективноi тепловiддачi визначаiться за формулою

, (1.20)

. (1.21)

Для визначення коефiцiiнта а3 можна скористатись спецiальною таблицею.

Найбiльш часто зустрiчаються саме закони ступеня 1/4 та 1/3. Тому особливого значення для плоских i цилiндричних поверхонь набуваi спосiб швидкого визначення ступеня n:

якщо 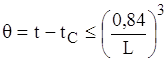, то n=1/4;

якщо 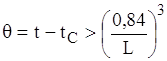, то n=1/3, (1.22)

де визначальний розмiр L береться в м.

Приклад 1.1. Корпус електричного приладу (рис.1.7) маi розмiр паралелепiпеда L1 = 0,3 м, L2 =0,4 м, Н = 0,2 м, . Знайти теплову потужнiсть корпусу при конвективнiй тепловiддачi.

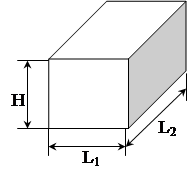а) б)

Рис.1.7. Корпус приладу та його теплова модель

Через гранi паралелепiпеда паралельно протiкають шiсть теплових потокiв. Оскiльки боковi поверхнi мають однаковий визначальний розмiр i розташованi вертикально, то iх можна обтАЩiднати в одну поверхню. Теплове коло (рис.1.7 б) i паралельним зтАЩiднанням трьох теплових опорiв: Rбок, Rкр, Rдно.

Конвективна провiднiсть системи визначаiться як сума трьох провiдностей:

,

де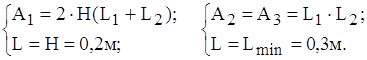

Розглянемо дно i кришку:

; ;

, тому n=1/4.

Оскiльки визначальнi розмiри бокових граней меншi визначального розмiру дна i кришки, то теплообмiн по всiх гранях маi ступiнь n=1/4. Отже маiмо такi данi для визначення коефiцiiнтiв конвективноi тепловiддачi бокових граней, кришки та дна вiдповiдно:

.

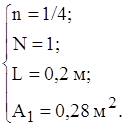
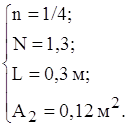
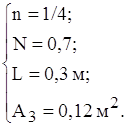
Згiдно формули (1.18) та формули (1.19)

;

;

.

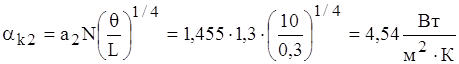Отже:

.

Теплова потужнiсть при конвективнiй тепловiддачi

.

1.6.3 Вiльна конвекцiя в обмеженому просторi

Мова йде про тонкий повiтряний прошарок, що розмiщений мiж двома близько розташованими площинами (рис.1.8). Складний процес в обмеженому замкнутому просторi прийнято розглядати по аналогii з передачею тепла кондуктивним способом. Це дозволяi уникнути визначення коефiцiiнтiв конвективноi тепловiддачi. У звтАЩязку з цим користуються ефективним коефiцiiнтом тепловiддачi.

У випадку, коли товщина прошарку набагато менша розмiрiв l1 та l2 (δ<<{l1, l2}), ефективний коефiцiiнт тепловiддачi визначаiться формулою:

.

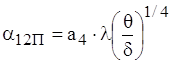Рис.1.8. Тонкий повiтряний прошарок

Для повiтряних прошаркiв добуток a2∙λ в широкому дiапазонi температур залишаiться практично сталим i рiвним 0,45. Тому:

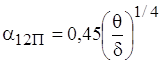. (1.23)

У випадку, коли товщина прошарку δ спiврозмiрна з розмiрами l1 та l2 (δ<{l1, l2}), ефективний коефiцiiнт тепловiддачi прошарку визначаiться формулою

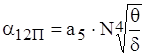, (1.24)

де 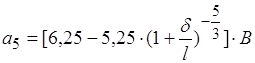, (1.25)

Значення В вибираiться для середньоi температури згiдно таблицi 1.3.

Таблиця 1.3.

Значення коефiцiiнта В

	0	50	100	200
B	0,63	0,58	0,56	0,44

1.6.4 Конвективний теплообмiн при довiльному тиску

Досi в усiх формулах передбачалося, що тиск середовища нормальний, тобто Па (760 мм. рт. ст.) Насправдi, тиск впливаi на значення коефiцiiнта тепловiддачi. Якщо , то

або 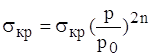, (1.26)

де n тАУ ступiнь закону теплообмiну (n=0, n=1/8, n=1/4, n=1/3).

Отже, вплив тиску можна врахувати пiсля того, як визначенi коефiцiiнти конвективноi тепловiддачi при нормальному тиску.

1.7 Передача тепловоi енергii випромiнюванням

Будь-яке тiло випромiнюi свiтлову енергiю у виглядi електромагнiтних хвиль широкого частотного спектру. Маi мiсце формула:

, (1.27)

де αВ - коефiцiiнт теплопередачi випромiнювання.

, (1.28)

де - приведена ступiнь чорноти;

- кутовий коефiцiiнт, що показуi, яка частина випромiнюваноi енергii тiла i попадаi на тiло j. В багатьох задачах, що стосуються радiоелектронних виробiв, можна прийняти ; f(ti, tj) - функцiя температур першоi поверхнi i та другоi поверхнi j. Згiдно закону Стефана-Больцмана значення цiii функцii можна обчислити за формулою

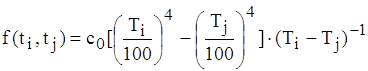, (1.29)

де с0 - стала Больцмана, с0 = 5,67.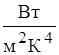

Значення функцii f(ti, tj) зручно визначати з допомогою спецiальноi таблицi. Потрiбно знати, що при пiдвищеннi температури доля тепловоi енергii, що випромiнюiться, збiльшуiться i перевищуi конвективну складову.

1.8 Складний теплообмiн

Незалежно вiд виду теплообмiну використовуiться одна розрахункова формула:

. (1.30)

РЖндекс m вказуi на механiзм переносу тепла: при iндукцii m≡т, при конвективному теплообмiнi m≡к та m≡в при випромiнюваннi. Тому в загальному випадку при наявностi всiх трьох теплових процесiв

. (1.31)

Вважаiмо, що всi три види теплових процесiв протiкають паралельно i незалежно.

1.9 Тепловi режими РЕЗ

1.9.1 Нагрiвання тiла зовнiшнiм середовищем

Будемо розрiзняти два типи температурних режимiв:

1) стацiонарний тАУ при якому температурне поле РЕЗ не змiнюiться з часом τ;

2) нестацiонарний тАУ поле РЕЗ змiнюiться з часом.

Нехай в тiлi довiльноi форми температура всiх точок однакова. Внутрiшнi джерела енергii вiдсутнi. Тiло з температурою переноситься в середовище з температурою .

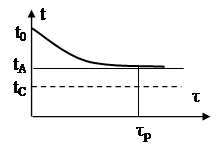
Рiзниця температури тiла i температури середовища змiнюiться з часом по експоненцiйному закону (рис.1.9)

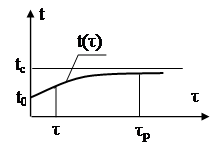а) б)

Рис.1.9. Графiк змiни температури при tc=const, Ф=0

Маi мiсце залежнiсть:

, (1.32)

де m0 тАУ деяка стала, яку називають темпом охолодження або нагрiвання тiла, 1/c.

При , тобто iснуi сталий режим, який називаiться регулярним режимом першого роду. З деякого часу значення i режим стаi практично сталим.

1.9.2 Нагрiвання тiла внутрiшнiм джерелом енергii

Нехай елементи РЕЗ видiляють тепло, яке утворюi тепловий потiк потужнiстю Ф, . При наступаi стацiонарний режим (рис.1.10). Температура тiла стаi рiвною

,

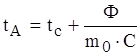де .

Маi мiсце формула аналогiчна формулi (1.32):

. (1.33)

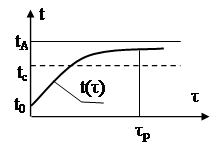а) б)

Рис.1.10. Графiк змiни температури при tc=const, Ф=const

1.9.3 Розрахунок температури корпуса та нагрiтоi зони

Середнiй тепловий потiк Ф, що проходить через корпус в оточуюче середовище, практично дорiвнюi потужностi Р, яку споживаi електронний пристрiй i яка задана. При цьому вiдомою вважаiмо температуру середовища tc, а потрiбно знайти температуру корпусу tк. Перегрiв корпус тАУ середовище вiдповiдаi потоку Ф згiдно формули

. (1.34)

Поверхня корпуса приймаiться iзотермiчною поверхнею i тому процес випромiнювання однаковий по всiй поверхнi корпуса площею А. Конвективна тепловiддача здiйснюiться по рiзному через боковi гранi площею Аб, кришку i дно площею Ак. Перегрiв θкс тАУ величина невiдома. Коефiцiiнт тепловiддачi можна визначити, якщо заданий перегрiв θкс. Отже температуру корпусу tk можна визначити, якщо знайти перегрiв θКС. Значення θКС шукають з допомогою тепловоi характеристики Ф=Ф(θКС), яку попередньо треба побудувати. Графiк Ф(θКС) проходить через початок координат: Ф(0)=0. Для побудови графiка (рис.1.11) знаходимо ще двi точки, бо графiк дещо вiдрiзняiться вiд лiнiйного. Спочатку задаiмось значенням перегрiву θ1. Тодi згiдно формули (1.34) можемо знайти значення теплового потоку Ф1, який для даного РЕЗ може забезпечити цей перегрiв θ1. Значення θ1 та Ф1 визначить точку 1 тепловоi характеристики. Задавшись значенням θ2 та повторивши розрахунки для визначення Ф2, знайдемо точку 2. Звичайно графiк теплово

Вместе с этим смотрят:

GPS-навигация

GPS-прийомник авиационный

IP-телефония и видеосвязь

IP-телефония. Особенности цифровой офисной связи

Unix-подобные системы