Методи нормування складових iнструментальноi похибки вимiрювань
Методи нормування складових iнструментальноi похибки вимiрювань
Згiдно з моделлю (3.3) iнструментальноi похибки вимiрювань i моделями (3.4), (3.5) похибки ЗВТ нормуванню пiдлягають такi похибки i властивостi ЗВТ:
- характеристики основноi похибки ЗВТ;
- характеристики чутливостi ЗВТ до впливних величин або похибки, викликанi впливними величинами i неiнформативними параметрами (додатковi похибки);
- динамiчнi властивостi ЗВТ, а отже, опосередковано i динамiчнi похибки ЗВТ;
- властивостi ЗВТ, якi визначають похибку взаiмодii ЗВТ з ОВ або iншими ЗВТ.
Нормування основноi похибки засобiв вимiрювальноi технiки
Основну похибку ЗВТ залежно вiд прийнятоi моделi похибки ЗВТ представляють або з подiлом на систематичнi i випадковi складовi (модель I), або без подiлу, коли вказуiться основна похибка (модель II).
Для встановлення нормованих характеристик основноi похибки кожного окремого екземпляра ЗВТ необхiдно вибрати таку математичну модель:
(3.6)
Ця модель записана для загального випадку - цифрових вимiрювальних засобiв i враховуi похибку квантування 
як випадкову складову основноi похибки. Очевидно, для переходу до моделi аналогових вимiрювальних засобiв необхiдно у формулi (3.6) припустити 
.
У моделi основноi похибки 
(3.6) для спрощення аналiзу i нормування випадковоi складовоi 
доцiльно видiлити, якщо це можливо, двi складовi - низькочастотну 
i високочастотну 
. Тодi остаточно узагальнена модель основноi похибки ЗВТ набираi вигляду:
+
+
. (3.7)
Такий подiл основноi похибки на складовi особливо необхiдний при аналiзi методiв зменшення iнструментальноi похибки ЗВТ.
У моделi (3.6) або (3.7) урахована принципова особливiсть властивостей основноi похибки всiii сукупностi ЗВТ даного типу. Змiст цiii особливостi такий. Основнi похибки окремих екземплярiв ЗВТ даного типу вiдрiзняються одна вiд одноi. Тому характеристики моделi похибки Do(t) слiд розглядати як випадковi величини, що мають своi реалiзацii для кожного ЗВТ. Виходячи з цього, для кожноi iз складових основноi похибки Do(t) слiд було б нормувати ii статистичнi характеристики, наприклад, оцiнки математичного сподiвання, СКВ та iн. Проте практика показуi, що розкид характеристик випадкових складових основноi похибки рiзних екземплярiв ЗВТ даного типу значно менший вiд цих характеристик. Тому розкид характеристик випадкових складових основноi похибки Do(t) вважаiться величиною другого порядку малостi i не нормуiться, а розкид характеристик систематичних похибок рiзних екземплярiв ЗВТ даного типу досить великий. Цим пояснюiться застосування ймовiрнiсних характеристик для опису систематичноi складовоi основноi похибки ЗВТ даного типу.
Характеристики систематичноi складовоi основноi похибки ЗВТ вибирають з таких: або значення систематичноi складовоi 
, або значення систематичноi складовоi , ii математичного сподiвання 
i СКВ 
, якi дозволяють при розрахунках характеристик iнструментальноi складовоi похибки вимiрювань ураховувати розкид значень систематичноi похибки для рiзних екземплярiв ЗВТ даного типу.
Установлювати значення математичного сподiвання i СКВ систематичноi складовоi похибки ЗВТ доцiльно тодi, коли можна знехтувати змiною iх у часi i залежно вiд змiни впливних величин або при можливостi одночасного нормування змiни даних характеристик як функцii часу та умов застосування. Отже, характеристики i вiдображають властивостi всiii сукупностi ЗВТ даного типу.
Характеристики випадковоi складовоi основноi похибки 
ЗВТ вибирають з таких: або значення СКВ 
випадковоi складовоi похибки, або значення СКВ , нормалiзованоi автокореляцiйноi функцii, або коефiцiiнта кореляцii 
, чи функцii спектральноi щiльностi потужностi 
випадковоi складовоi похибки.
При нормуваннi систематичноi i випадковоi складових основноi похибки ЗВТ указують границi перелiчених характеристик цих похибок.
Зважаючи на прагнення до максимально можливого спрощення системи нормування МХ, рекомендуiться:
- для ЗВТ з моделлю I iнструментальноi похибки нормувати тiльки границi допустимих значень основноi випадковоi похибки 
(iнодi, коли ЗВТ призначаiться для використання у вимiрювальних системах, коефiцiiнт кореляцii 
або спектральну щiльнiсть потужностi похибки) i границi допустимих значень основноi систематичноi похибки
;
- для ЗВТ з моделлю II нормувати границi допустимих значень абсолютноi основноi похибки 
Для обох моделей похибок ЗВТ рекомендуiться нормувати границi допустимих значень похибки гiстерезису 
Таке спрощення системи нормування призводить до деякого завищення розрахункових значень iнструментальноi складовоi похибки вимiрювань, якi визначаються за НМХ ЗВТ, оскiльки при розрахунках будуть ураховуватися максимально можливi, а не середнi для даного типу ЗВТ характеристики випадкових похибок. Одночасно указаний пiдхiд до нормування спрощуi процедуру проведення випробувань i повiрки ЗВТ.
При необхiдностi допускаiться нормувати:
- границю допустимоi систематичноi складовоi похибки ЗВТ для заданого iнтервалу часу;
- змiну в часi границi допустимоi систематичноi складовоi похибки;
- допустимi вiдхилення нормованоi кореляцiйноi функцii 
або функцii спектральноi щiльностi потужностi випадковоi складовоi похибки ЗВТ вiд iх номiнальних значень;
- функцiю або щiльнiсть розподiлу ймовiрностей систематичноi i випадковоi складових похибки ЗВТ;
- характеристику основноi похибки в iнтервалi впливноi величини (для моделi II похибки).
Похибка ЗВТ в iнтервалi впливноi величини - це похибка ЗВТ в умовах, коли одна з впливних величин набираi будь-яких значень у ii робочiй областi, а iншi впливнi величини знаходяться в границях, вiдповiдних до нормальних умов. Ця похибка не i додатковою, оскiльки вона обумовлена тiльки вiдмiннiстю значення впливноi величини вiд нормального значення.
При обчислюваннi випадковоi основноi похибки вiдповiдно до моделi I похибки ЗВТ маiться на увазi, що всi ii складовi незалежнi. Тодi дисперсiя випадковоi складовоi основноi похибки ЗВТ
,
причому 
(тобто приймаiться, що випадкова складова похибки ЗВТ вiд гiстерезису розподiлена за рiвномiрним законом).
Нормування додаткових похибок засобiв вимiрювальноi технiки
Як указувалось у Вз 3.2, додатковi похибки ЗВТ визначаються характеристиками чутливостi ЗВТ до впливних величин i неiнформативних параметрiв вхiдних сигналiв.
Враховуючи, що впливнi величини можуть викликати змiнювання не тiльки похибки ЗВТ, але й iнших МХ ЗВТ, в необхiдних випадках доцiльно передбачити нормування функцiй впливу i на цi МХ ЗВТ. При цьому як нормованi характеристики додаткових похибок ЗВТ можуть бути використанi:
а) або функцii впливу 
, якi являють собою залежностi змiни метрологiчних характеристик ЗВТ вiд змiни впливноi величини 
або вiд змiни сукупностi впливних величин;
б) або границi змiни значень метрологiчних характеристик ЗВТ, викликанi змiною впливних величин в установлених границях.
Для ЗВТ функцiя впливу може мати або певний вигляд, або при однаковому виглядi рiзнi значення параметрiв функцii. В усiх екземплярах ЗВТ даного типу функцii впливу повиннi бути iдентичними внаслiдок однакового принципу дii цих ЗВТ, а параметри функцiй впливу рiзних екземплярiв ЗВТ даного типу повиннi бути близькими мiж собою. Тому як основна характеристика додатковоi похибки береться деяка середня для ЗВТ даного типу функцiя впливу i деякi середнi значення ii параметрiв. Така функцiя впливу називаiться номiнальною функцiiю впливу, позначимо ii 
.
Змiна метрологiчноi характеристики ЗВТ, викликана змiною впливноi величини, - це рiзниця (без урахування знака) мiж значенням метрологiчноi характеристики, що вiдповiдаi деякому заданому значенню впливноi величини в границях робочих умов застосування, i значенням даноi метрологiчноi характеристики, яке вiдповiдаi нормальному значенню впливноi величини.
Для нормування функцiй впливу використовують два методи:
1) нормування номiнальноi функцii впливу i допустимих вiдхилень вiд неi;
2) нормування граничних функцiй впливу - верхньоi 
i нижньоi 
, якi обмежують область допустимих значень функцii впливу для будь-якого ЗВТ даного типу.
Другий метод нормування додаткових похибок застосовуiться для ЗВТ певного типу, для сукупностi яких розкид функцii впливу великий, в силу чого встановити номiнальну функцiю впливу неможливо.
Оскiльки функцii впливу визначенi як залежностi змiни МХ ЗВТ вiд змiн впливних величин в робочих умовах застосування ЗВТ, то iх слiд нормувати тiльки для тих МХ, що нормуються для нормальних (номiнальних) умов застосування ЗВТ. Якщо ж деякi МХ нормують для робочих умов застосування ЗВТ, то вiдповiднi функцii впливу не нормують. Проте далеко не всi МХ повиннi нормуватися для нормальних умов застосування ЗВТ, i ось чому. Майже всi МХ впливають лише на похибку вимiрювань, тому можна вважати, що змiна бiльшостi з МХ, яка здiйснюiться пiд дiiю впливних величин, призводить до вiдповiдноi змiни похибки вимiрювань другого порядку малостi, чим можна знехтувати. Тому вiдповiднi МХ слiд нормувати для робочих умов застосування ЗВТ, а функцii впливу на них не нормувати.
На цей час бiльш розповсюдженим i нормування не функцiй впливу, а характеристик якi традицiйно визначають додатковi похибки ЗВТ вiд впливних величин.
Серед таких характеристик найбiльш поширеною i границi допустимоi (найбiльшi допустимi змiни) додатковоi похибки В±DYxд, що мають мiсце при змiнi впливноi величини x на деяке встановлене (задане) значення В±Dx вiдносно ii нормального (номiнального) значення xном.
Якщо в реальних умовах експлуатацii ЗВТ впливна величина може приймати рiзнi (довiльнi) значення в межах вiд нижнього значення xнж до верхнього значення xв, причому xнж< xном< xв, то за вказаною вище характеристикою можна визначити лише граничнi (найбiльш можливi) змiни похибки ЗВТ:
;
.
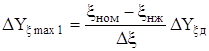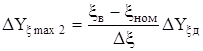При оцiнцi iнструментальноi складовоi похибки вимiрювань в реальних умовах експлуатацii ЗВТ, що обумовлена дiiю даноi впливноi величини x, i тiльки одна можливiсть: врахувати найбiльш можливу змiну додатковоi похибки ЗВТ DYxмах, яка дорiвнюi
або
при 
,
або
при 
.
Сумарна допустима iнструментальна статична похибка ЗВТ DYд в реальних умовах експлуатацii ЗВТ може бути визначена як арифметична сума границi допустимоi основноi похибки DYод та границь (найбiльших) допустимих змiн (значень) додаткових похибок ЗВТ вiд усiх впливних величин 
, що враховуються:
.
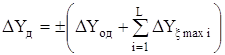Очевидно, значення похибки DYд практично завжди буде iстотно перевищувати значення дiйсноi похибки ЗВТ в реальних умовах експлуатацii, бо вона розраховуiться за припущенням, що всi похибки (основна i додаткова) мають найбiльше допустиме значення при будь-яких умовах експлуатацii, але вiрогiднiсть виконання такого припущення вкрай мала.
Отже, кiлькiсна характеристика додатковоi похибки DYxмах ЗВТ, яка традицiйно регламентуiться в технiчних описах ЗВТ, не дозволяi оцiнювати дiйсну iнструментальну похибку вимiрювань в реальних умовах експлуатацii (застосування) ЗВТ з допустимою вiрогiднiстю. Але вона i найбiльш простою для практичного використання.
Функцii впливу i границi допустимих додаткових похибок ЗВТ нормують, як правило, окремо для кожноi впливноi величини. РЖ тiльки при наявностi iстотноi взаiмноi залежностi декiлькох функцiй впливу рiзних величин 
допускаiться задання сумiсних (комплексних) функцiй впливу 
, якi й використовують при обчисленнi характеристик iнструментальноi складовоi похибки вимiрювань.
Критерiй iстотностi для впливних величин установлюiться в технiчнiй документацii на ЗВТ конкретних типiв. При вiдсутностi вказаних критерiiв визначають, що впливна величина iстотно впливаi на метрологiчну характеристику ЗВТ, якщо при змiнi цiii впливноi величини в границях робочого дiапазону дана метрологiчна характеристика ЗВТ змiнюiться бiльш як на 20% вiд значення, нормованого для номiнальних умов. Функцiю однiii впливноi величини приймають iстотно залежною вiд iншоi впливноi величини, при змiнi якоi в границях робочого дiапазону змiна функцii перевищуi 20% вiд ii номiнального значення.
РЖстотнiсть тiii чи iншоi складовоi сумарноi додатковоi похибки ЗВТ рекомендуiться визначати таким чином. Якщо найбiльш можливi значення всiх додаткових похибок ЗВТ 
, вiдповiдно до робочих умов застосування ЗВТ даного типу сумiрнi, то всi додатковi похибки визнаються iстотними при виконаннi умови
,
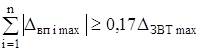де
- найбiльше можливе значення похибки ЗВТ у робочих умовах застосування.
Зауважимо, що додатковi похибки вважаються сумiрними, якщо iх значення вiдрiзняються одне вiд одного не бiльш як на 30%. Якщо серед додаткових похибок виявляються меншi або несумiрнi з iншими i iх сума менша вiд 
, то такi похибки належать до неiстотних.
Функцiю впливу рекомендуiться не нормувати за умови, що ii границi допустимих вiдхилень вiд номiнальноi функцii впливу не можуть бути встановленi меншими нiж 20% вiд номiнальноi функцii впливу. У цьому разi рекомендуiться нормувати границi допустимоi додатковоi похибки ЗВТ або допустимоi змiни iншоi НМХ ЗВТ у всьому робочому дiапазонi змiни впливноi величини вiдповiдно до робочих умов експлуатацii ЗВТ даного типу.
Значення допустимоi додатковоi похибки ЗВТ, як правило, задають у виглядi часткового або кратного значення допустимоi основноi похибки. Наприклад, додаткова похибка ЗВТ, яка викликана вiдхиленням його живлення на 
% вiд номiнального значення, не повинна перевищувати 0,5 границi основноi похибки ЗВТ.
Допустимi значення додаткових похибок, якi традицiйно застосовуються для розрахункiв iнструментальноi похибки вимiрювань, дають завищенi результати i тому придатнi для одержання тiльки досить приблизних оцiнок похибки вимiрювань. Для одержання бiльш точних оцiнок необхiдно враховувати функцiю впливу.
Методи нормування додаткових похибок i iх особливостi однаковi для всiх видiв ЗВТ i обох моделей похибки.
Перелiк нормованих неiнформативних параметрiв вхiдного i вихiдного сигналiв ЗВТ, iх номiнальнi значення i границi допустимих вiдхилень установлюються в ДСТУ та НТД.
Нормування динамiчноi похибки засобiв вимiрювальноi технiки
Динамiчнi похибки ЗВТ нормують опосередковано, шляхом нормування динамiчних характеристик (або властивостей) ЗВТ, у звтАЩязку з тим, що цi похибки залежать не тiльки вiд властивостей ЗВТ, але й вiд спектральних (частотних) характеристик вхiдного сигналу. В iснуючих стандартах передбачено нормування таких динамiчних характеристик ЗВТ, якi дозволяють оцiнювати похибки вимiрювань пiд час дii на входi ЗВТ будь-яких змiнних сигналiв. При цьому головними i вимоги, з одного боку, до детальностi опису метрологiчних характеристик ЗВТ, а з другого боку - до простоти iх нормування, експериментального визначення i контролю (повiрки).
Для задання динамiчних властивостей ЗВТ рекомендуiться використовувати iхнi повнi i частиннi динамiчнi характеристики (див. пiдп.3.3.4). Повнi динамiчнi характеристики нормуються або для системних ЗВТ, або для вимiрювальних перетворювачiв реiструвальних приладiв, якщо вони призначаються для роботи з вхiдними сигналами, в яких змiнюються в часi iнформативнi параметри. Для таких ЗВТ, якщо для них установленi нормальнi та робочi умови застосування, додатково нормують дiю впливних величин i неiнформативних параметрiв вхiдного сигналу на повнi динамiчнi характеристики (похибки, що при цьому виникають, належать до додаткових). Для показувальних приладiв, вимiрювальних перетворювачiв i реiструвальних приладiв, призначених для роботи з постiйними або з такими змiнними сигналами, для яких динамiчною похибкою можна знехтувати, нормують одну або декiлька частинних динамiчних характеристик, наприклад час реакцii ЗВТ.
Динамiчнi похибки визнаються неiстотними, а динамiчнi характеристики не нормуються, якщо виконуiться нерiвнiсть.
,
де
- найбiльше можливе значення динамiчноi похибки ЗВТ у робочих умовах застосування.
Основним методом нормування динамiчних властивостей ЗВТ i задання (вказування) таких повних i частинних характеристик:
1) номiнальних характеристик i границь допустимих вiдхилень вiд них;
2) границь допустимих значень параметрiв вхiдного сигналу.
Номiнальнi динамiчнi характеристики (повнi i частиннi) ЗВТ нормують у тих випадках, коли границi допустимих вiдхилень даноi динамiчноi характеристики не перевищують 20% ii номiнальноi характеристики.
Для ЗВТ, у значнiй кiлькостi екземплярiв яких розкид динамiчних характеристик (повних i частинних) великий, i в силу цього для них у НТД установлена необхiднiсть визначення i подальшого використання динамiчних характеристик кожного екземпляра ЗВТ, нормують граничну динамiчну характеристику (повну або частинну). У таких випадках застосовувати ЗВТ допускаiться тiльки за умови попереднього експериментального визначення динамiчноi характеристики для даного екземпляра ЗВТ. Граничну динамiчну характеристику використовують як критерiй придатностi ЗВТ i при розрахунках похибок вимiрювань.
Динамiчнi характеристики ЗВТ оцiнюють i контролюють при значеннях вхiдного сигналу, вiдповiдних усьому дiапазону вимiрювань (перетворень) або декiльком частинам дiапазону (пiддiапазонам), в яких допускають лiнiйну апроксимацiю динамiчних властивостей ЗВТ. Кiлькiсть таких динамiчних пiддiапазонiв повинна бути бiльша чотирьох.
Динамiчнi характеристики ЗВТ, властивостi яких залежать вiд напряму змiни вхiдного сигналу, оцiнюють для обох напрямiв змiни сигналу. Методики й алгоритми обробки результатiв контролю (оцiнки) динамiчних характеристик повиннi встановлюватися в стандартах i технiчних умовах на ЗВТ конкретних типiв i груп залежно вiд виду i порядку математичноi моделi iх динамiчних властивостей, яку називають динамiчною моделлю.
Якщо випадкова складова похибки ЗВТ iстотна, то частиннi динамiчнi характеристики контролюють за допомогою обробки серii з 
спостережень. Частинну характеристику приймають такою, що задовольняi вимоги технiчних умов, якщо максимальне значення iз серii n ii оцiнок не перевищуi допустимого значення.
Нормування похибки взаiмодii
З усiх складових iнструментальноi похибки вимiрювань найменш розробленi методи нормування похибки вiд взаiмодii ЗВТ з ОВ. Згiдно з фiзичним походженням похибки взаiмодii, для ii оцiнки необхiдно нормувати характеристики, що вiдображають властивостi ЗВТ вiдбирати енергiю через своi вхiднi або вихiднi кола i дозволяють визначити змiну вимiрюваноi фiзичноi величини, яка виникаi в результатi цього обмiну. Для засобiв електро - i радiотехнiчних вимiрювань ця задача вирiшуiться досить просто за допомогою нормування вхiдних i вихiдних повних опорiв ЗВТ, причому цi опори неважко контролювати пiд час повiрки.
У вимiрювальних засобах, призначених для вимiрювання i перетворення на постiйному струмi i в низькочастотному дiапазонi вхiдних сигналiв, вхiдний i вихiдний (для перетворювачiв) опори розглядаються i нормуються як активнi. У ЗВТ високочастотного дiапазону вхiднi i вихiднi опори i комплексними i повиннi нормуватися як повнi. В iснуючiй НТД вхiдний i вихiдний повнi опори для ЗВТ усiх типiв i обох моделей похибок нормуються однаково - заданням номiнального значення опорiв i границь iх допустимих значень або границь iх допустимих змiн.
Проте бiльш часто параметри вхiдного повного опору ЗВТ нормуються окремо. Оскiльки реактивна складова вхiдного повного опору ЗВТ маi, як правило, iмнiсний характер, то такий опiр представляють у виглядi паралельного (iнодi послiдовного) зтАШiднання резистора i конденсатора.
Значно складнiше нормувати похибки вiд взаiмодii ЗВТ неелектричних величин з ОВ. У цiй галузi вимiрювань явища обмiну енергiiю мiж ЗВТ i ОВ вивченi недостатньо. Але для багатьох ЗВТ неелектричних величин проблема може бути зведена до вже вирiшеноi, використовуючи теорiю електромеханiчних аналогiй i розрахунку еквiвалентних схем перетворювачiв неелектричних величин.
Нормування неiнформативних параметрiв вихiдних сигналiв засобiв вимiрювальноi технiки
Крiм указаних вище метрологiчних характеристик, що визначають результат i похибку вимiрювань, нормуються неiнформативнi параметри вихiдного сигналу ЗВТ.
Неiнформативнi параметри вихiдних сигналiв не належать до метрологiчних характеристик ЗВТ. Проте вони визначають можливiсть нормальноi роботи ЗВТ й iнших пристроiв, якi приiднуються до виходу даного ЗВТ. Наприклад, вихiдним сигналом перетворювача напруга-частота або генератора iмпульсiв i послiдовнiсть iмпульсiв, а ii iнформативним параметром - частота, вимiрювана частотомiром. У той самий час похибка частотомiра залежить вiд амплiтуди, тривалостi i форми iмпульсiв, якi належать до неiнформативних параметрiв. Отже, неiнформативнi параметри повиннi задовольняти певнi вимоги, тобто пiдлягають нормуванню. Це нормування здiйснюiться двома методами: встановленням або номiнальних характеристик (наприклад, значень iмпедансiв) зi вказанням границь допустимих вiдхилень вiд них, або граничних значень характеристик (iмпедансiв), якi визначають область iх допустимих значень. Найбiльш розповсюдженим з них i задання границь допустимих значень тiii чи iншоi характеристики. Цi границi визначають iнтервал, в якому значення характеристики кожного екземпляра ЗВТ конкретного типу повинно знаходитися з iмовiрнiстю, близькою до одиницi.
Укажемо також, що всi НМХ ЗВТ можуть представлятися у формi iменованого або неiменованого числа, формули або графiка. При цьому задання будь-якоi характеристики у виглядi графiка обовтАШязково треба супроводжувати одночасним поданням ii у виглядi формули або таблицi. Допускаiться застосування й iнших форм подання НМХ за умови, що цi формули дозволяють оцiнювати похибки ЗВТ даного типу, а також здiйснювати контроль вiдповiдностi цих засобiв установленим вимогам. У такому випадку форма подання НМХ конкретизуiться в НТД на даний тип або вид ЗВТ.
Класи точностi засобiв вимiрювальноi технiки
Бiльшiсть ЗВТ, якi знаходяться на теперiшнiй час в експлуатацii, мають переважно статичну похибку, тобто динамiчна похибка в них не враховуiться. Нормування статичноi похибки цих ЗВТ здiйснюiться, як правило, встановленням класу точностi.
Класом точностi називаiться узагальнена кiлькiсна характеристика ЗВТ, яка визначаiться гарантованими границями допустимих основноi i додаткових похибок, а також iншими характеристиками ЗВТ, що впливають на похибку (точнiсть) вимiрювань i значення яких установлюються стандартами на окремi види ЗВТ.
Дiйснi значення основноi повноi похибки окремих екземплярiв ЗВТ однакового типу можуть вiдрiзнятися одне вiд одного як систематичними, так i випадковими складовими, але в цiлому для даного типу ЗВТ вони не перевищують границi допустимоi основноi похибки. Таким чином, установленням i заданням класу точностi нормуiться основна статична похибка ЗВТ, а всi додатковi похибки й iншi метрологiчнi характеристики, що впливають на похибку ЗВТ, указуються окремо.
Вiдповiднiсть реального значення основноi похибки ЗВТ приписаному йому класу точностi перевiряiться при перiодичних повiрках. Якщо воно залишаiться менше вiд нормованого, то ЗВТ продовжуi експлуатуватися, якщо ж реальне значення основноi похибки ЗВТ бiльше вiд нормованого, то ЗВТ пiдлягаi ремонту та регулюванню.
Основна похибка ЗВТ нормуiться чотирма рiзними способами, вибiр яких обумовлений спiввiдношенням адитивноi i мультиплiкативноi складових похибки ЗВТ даного типу.
1. Для ЗВТ, абсолютна похибка яких визначаiться адитивною складовою i ii границi можна вважати практично незмiнними для будь-яких значень вимiрюваноi величини, тобто мультиплiкативною складовою похибки можна знехтувати, iнодi нормуються границi допустимоi абсолютноi основноi похибки
,
де a - постiйна додатна величина, виражена в одиницях вимiрюваноi величини.
Проте нормування допустимоi абсолютноi основноi похибки ЗВТ використовуiться рiдко, бо для засобiв з багатьма межами вимiрювань вона рiзна в кожному пiддiапазонi, що створюi певнi незручностi i для вказання всiх границь похибок (треба було б перелiчити значення похибок для всiх пiддiапазонiв), i для практичного застосування. Границi допустимих абсолютних похибок задають для ЗВТ тiльки тих фiзичних величин, похибки вимiрювань яких прийнято виражати в одиницях вимiрюваноi величини або в подiлках шкали, наприклад, для засобiв вимiрювань довжини, маси, фазового зсуву.
Для бiльшостi ЗВТ з переважною адитивною похибкою нормують границi допустимоi основноi зведеноi похибки ЗВТ, якi, згiдно з формулою (3.2), визначають за рiвнiстю
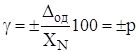, (3.8)
деp - стала додатна величина, виражена у вiдсотках. РЗi числове значення вибираiться з ряду: 
, де l = 1; 0; -1; -2 i т.д. Значення, якi вказанi в дужках, не рекомендуються при створеннi нових ЗВТ. Наведений ряд чисел установлений вiдповiдно до правила округлення значень похибок вимiрювань (див. Вз 2.11). При тому самому показнику степеня l допускаiться встановлювати не бiльш нiж птАЩять рiзних границь допустимоi основноi похибки для ЗВТ конкретного виду.
Слiд памтАШятати, що i при такiй формi нормування класу точностi ЗВТ характеристикою точностi вимiрювань залишаiться вiдносна похибка. Границi допустимоi вiдносноi похибки вимiрювань у функцii вимiрюваноi величини визначаються за формулою, одержаною з виразу (3.8) з урахуванням рiвностi (1.2):
. (3.9)
З формули (3.9) виходить, що зменшення розмiру вимiрюваноi величини 
призводить до збiльшення допустимоi вiдносноi похибки вимiрювань даним ЗВТ. Зокрема, при 
допустима вiдносна похибка 
дорiвнюi класу точностi ЗВТ лише на останнiй (кiнцевiй) позначцi дiапазону вимiрювань 
. При зменшеннi допустима вiдносна похибка вимiрювань 
зростаi i при 
, тому при виборi ЗВТ для проведення вимiрювань необхiдно враховувати не тiльки iх класи точностi, а й спiввiдношення 
. З цiii точки зору рекомендуiться межу вимiрювань вимiрювального приладу вибирати такою, щоб його покази знаходились у другiй половинi i навiть ближче до верхньоi межi вибраного дiапазону вимiрювань.
Зважаючи на залежнiсть вiдносноi похибки вимiрювань вiд значення Х, для ряду ЗВТ обмежують дiапазон вимiрювань такими значеннями вимiрюваноi величини Х, при яких допустима вiдносна похибка вимiрювань не перевищуi деякого, заздалегiдь заданого значення, яке дорiвнюi, наприклад, 4, 10 або 20%. Поза дiапазоном вимiрювань, особливо в початковiй частинi дiапазону показiв для ЗВТ, в яких вiн починаiться з нуля, вимiрювання не допустимi, оскiльки тут адитивна похибка може бути порiвняна з вимiрюваним значенням i навiть перевищувати його.
2. Для ЗВТ, в абсолютнiй похибцi яких переважаi мультиплiкативна складова, границю допустимоi основноi похибки виражають у вiдноснiй формi, через те, що у цьому випадку вона виявляiться практично постiйною величиною, не залежною вiд вимiрюваноi величини . Границi допустимоi вiдносноi основноi похибки ЗВТ установлюються за формулою:
, (3.10)
де
- границя допустимоi абсолютноi мультиплiкативноi похибки ЗВТ;
b - додатне безрозмiрне число;
- постiйна додатна величина, виражена у вiдсотках; вона вибираiться з того самого ряду, що й величина p.
Таким способом нормуються похибки масштабних перетворювачiв (подiльникiв напруги, шунтiв, вимiрювальних трансформаторiв струму i напруги та iн). РЖ якщо б спiввiдношення (3.10) залишалось справедливим для всього дiапазону можливих значень вимiрюваноi величини - вiд 0 до 
, то такi вимiрювальнi перетворювачi були б найбiльш досконалими, тому що вони мали б широкий робочий дiапазон, зокрема, забезпечували б з тiiю самою похибкою вимiрювання необмежено малого значення Х. Проте реально таких перетворювачiв не iснуi, оскiльки поки що неможливо створити перетворювачi, в яких повнiстю вилучена адитивна похибка в широкому дiапазонi значень вимiрюваноi величини. Тому для реальних ЗВТ завжди вказуiться дiапазон вимiрювань ЗВТ, в якому оцiнка (3.10) справедлива. Поза цим дiапазоном вплив адитивноi складовоi похибки ЗВТ зростаi настiльки, що нею знехтувати не можна i, як наслiдок, не можна використати допустиму вiдносну похибку (3.10) як норму основноi похибки ЗВТ.
3. Для ЗВТ, адитивна i мультиплiкативна складовi абсолютноi похибки яких сумiрнi, тобто жодною з них знехтувати не можна, нормуються або границi допустимоi абсолютноi основноi похибки, або границi допустимоi вiдносноi основноi похибки. У цьому разi границi допустимоi абсолютноi основноi похибки визначаються виразом.
.
Пiдставляючи це спiввiдношення в рiвнiсть (2.5), одержимо двочленну формулу для нормування границь допустимоi вiдносноi основноi похибки, вираженоi у вiдсотках:
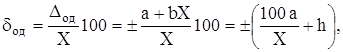(3.11)
де
- адитивна i мультиплiкативна складовi вiдносноi основноi похибки вiдповiдно.
Таким чином, особливiсть класифiкацii складових похибки ЗВТ полягаi в тому, що при переходi вiд абсолютноi похибки до вiдносноi форми ii вiдображення адитивна i мультиплiкативна складовi похибки мiняються мiсцями: вiдносне значення абсолютноi адитивноi похибки i мультиплiкативною похибкою, а вiдносне значення абсолютноi мультиплiкативноi похибки - адитивною похибкою.
Вираз (3.11) звичайно представляють в iншiй формi, яку одержують так. Нехай 
, де 
- модуль бiльшоi з меж вимiрювань. Додамо до правоi частини виразу (3.11) i вiднiмемо вiд неi величину d. Тодi одержимо
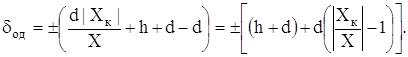
У цю рiвнiсть уведемо позначення 
i остаточно маiмо
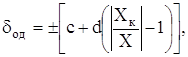(3.12)
деc, d - постiйнi додатнi величини, вираженi у вiдсотках; вибираються з того самого ряду, що й величина p. Спiввiдношення мiж числами c i d установлюються стандартами на конкретнi ЗВТ, причому звичайно 
Звернемо увагу на те, що складовi частини формули (3.12) формально схожi на адитивну i мультиплiкативну складовi похибки ЗВТ, але за своiю суттю вони не i такими, i тому використовувати цi термiни до даноi формули не можна. Аналiз двочленноi формули (3.12) показуi, що границi допустимоi вiдносноi основноi похибки при наявностi адитивноi i мультиплiкативноi складових звужуються iз зростанням вимiрюваноi величини , i при 
вони набирають мiнiмального значення, яке дорiвнюi 
(рис.3.8).
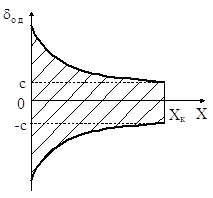
Рис.1. Графiк допустимоi вiдносноi похибки ЗВТ при нормуваннi за двочленною формулою.
Можливе також нормування зведеноi похибки за двочленною формулою, якщо в знаменник формули (3.11) замiсть пiдставити 
.
4. В окремих випадках границi допустимих абсолютноi i вiдносноi основноi похибок ЗВТ установлюються за бiльш складними, спецiальними формулами нормування, а також у виглядi графiка або таблицi.
Обумовлено це тим, що похибки ряду ЗВТ не можуть бути нормованi за описаними вище способами, оскiльки мають бiльш складний вигляд смуги похибок у порiвняннi з розглянутими варiантами. Як приклад можна навести цифровi частотомiри, похибка яких залежить вiд часу вимiрювання, параметрiв вхiдного сигналу i характеристик завад. Нормування похибок подiбних ЗВТ здiйснюiться за формулами, якi мають двi i бiльше складових, причому кiлькiсть складових i iх суть можуть бути рiзними як для окремих типiв ЗВТ, так i для рiзних режимiв роботи того самого засобу.
Нормування границь допустимих додаткових похибок ЗВТ здiйснюiться за однiiю з чотирьох форм:
- у виглядi постiйного значення додатковоi похибки вiд даноi впливноi величини для всiii робочоi областi або декiлькох постiйних значень по iнтервалах робочоi областi цiii впливноi величини;
- указанням вiдношення границi допустимоi додатковоi похибки, яка вiдповiдаi заданому iнтервалу впливноi величини, до цього iнтервалу;
- у виглядi залежностi границi допустимоi додатковоi похибки вiд впливноi величини, яку називають граничною функцiiю впливу;
- у виглядi функцiональноi залежностi границь допустимих вiдхилень вiд номiнальноi функцii впливу.
Першi двi форми нормування додаткових похибок не дозволяють визначити iх дiйснi значення для будь-якого значення впливних величин i забезпечують можливiсть iх оцiнки тiльки "зверху". Це i певним недолiком указаних форм нормування. Цього недолiку можна уникнути, якщо нормування додаткових похибок здiйснювати шляхом задання функцii впливу (третя i четверта форми). За iх допомогою можуть бути визначенi дiйснi значення додаткових похибок для будь-яких конкретних значень впливних величин, що вiдповiдають умовам виконання вимiрювань. Проте задання функцii впливу повтАШязано з великими труднощами, i тому в основному використовуються першi двi форми нормування додаткових похибок.
Нормуванню пiдлягаi також границя допустимоi варiацii (або похибки, обумовленоi гiстерезисом) вихiдного сигналу ЗВТ, яку задають у виглядi часткового або кратного значення границi основноi похибки або в подiлках шкали, як i границi допустимоi додатковоi похибки.
Норми метрологiчних характеристик у виглядi границь допустимих основноi i додаткових похибок наводяться в технiчнiй документацii на ЗВТ. Крiм того, умовнi позначення класiв точностi, що вiдбивають цi норми, наносять на циферблат, щитки, ш
Вместе с этим смотрят:
GPS-навигация
GPS-прийомник авиационный
IP-телефония и видеосвязь
IP-телефония. Особенности цифровой офисной связи
Unix-подобные системы