Оцiнка результату i похибки прямих вимiрювань

Залежно вiд розвтАЩязуваноi задачi прямi вимiрювання можуть проводитися з одноразовими i багаторазовими спостереженнями. Прямi одноразовi вимiрювання i найбiльш розповсюдженими в практицi технiчних вимiрювань, оскiльки точнiсть iх результатiв у звичайних умовах, як правило, достатня, i водночас вони вiдрiзняються простотою вимiрювального експерименту, високою продуктивнiстю (числом вимiрювань за одиницю часу) i незначними витратами, для iх проведення не ставляться високi вимоги до квалiфiкацii експериментатора. За цими показниками вони значно перевищують iншi методи вимiрювань. Прямi багаторазовi вимiрювання застосовуються у тому разi, коли необхiдно забезпечити пiдвищену точнiсть результатiв вимiрювань, яка досягаiться за рахунок зменшення випадковоi складовоi похибки вимiрювань усередненням (статистичною обробкою) результатiв спостережень вимiрюваноi величини того самого розмiру. РЗх доцiльно проводити тодi, коли випадкова похибка результату вимiрювань i переважаючою у порiвняннi з систематичною. Багаторазовi вимiрювання вiдрiзняються пiдвищеними складнiстю, трудомiсткiстю i витратами, тому iх доцiльнiсть мусить бути переконливо обТСрунтована. Найчастiше вони застосовуються, наприклад, при виконаннi наукових експериментiв i проведеннi метрологiчних робiт. Особливостi в органiзацii вимiрювального експерименту при виконаннi одноразових i багаторазових прямих вимiрювань визначають вiдмiннiсть у методиках оцiнки iх результатiв i похибок.

Перш нiж перейти до оцiнки похибок результату прямих вимiрювань ще раз пiдкреслимо таку важливу обставину: необхiдно чiтко вiдрiзняти похибку результату вимiрювання i похибку ЗВТ (див. Вз 3.3).

Оцiнка похибки прямих одноразових вимiрювань

Для прямих одноразових вимiрювань характернi двi головнi особливостi:

1. З множини можливих вiдлiкiв результату вимiрювання використовуiться лише один.

2. Потрiбен певний обсяг апрiорноi iнформацii та ii ретельний аналiз. Ця iнформацiя стосуiться всiх компонентiв процесу вимiрювання: властивостей фiзичноi моделi обтАЩiкта вимiрювання, методу вимiрювання i ЗВТ, умов виконання вимiрювання, квалiфiкацii експериментатора. Аналiз усiii цiii апрiорноi iнформацii виконуiться перед проведенням прямих одноразових вимiрювань i вiд його повноти залежить вiрогiднiсть результату вимiрювання. Основнi етапи цього аналiзу:

- слiд зтАЩясувати фiзичну сутнiсть дослiджуваноi властивостi обтАЩiкта вимiрювання, звернувши особливу увагу на вимiрюваний параметр;

- визначити впливнi величини i заходи, спрямованi на зменшення iх впливу (термостатування, екранування або компенсацiя електричних i магнiтних полiв тощо);

- прийняти рiшення на користь тiii чи iншоi методики виконання вимiрювань;

- вибрати ЗВТ, при цьому переконатися в справностi, в тому числi метрологiчнiй, вибраного ЗВТ i наявностi вiрогiдноi iнформацii про його НМХ;

- оцiнити похибку взаiмодii ЗВТ з обтАЩiктом вимiрювання i динамiчну похибку;

- дослiдити застосований метод вимiрювання з метою оцiнки методичноi похибки;

- оцiнити можливу похибку експериментатора, якщо вона iстотна.

Вибiр методу вимiрювання i ЗВТ проводиться так, щоб вилучити або зменшити до нехтовно малих значень методичну похибку, похибку взаiмодii i динамiчну похибку, тобто щоб похибка вимiрювання визначалась тiльки статичною похибкою ЗВТ (основною i додатковою, якщо вона i, складовими).

Приведенi етапи пiдготовки до виконання вимiрювань в якiйсь мiрi справедливi i для iнших методiв вимiрювань, але особливоi ретельностi вони потребують при одноразових вимiрюваннях, де роль одного вiдлiку результату вимiрювання надзвичайно висока.

Результат одноразового вимiрювання i випадковим числом i жоден з його окремих вiдлiкiв не даi повного уявлення про таке число, а отже, i про вимiрюваний параметр. Тому вже на етапi одержання вiдлiку ЗВТ (тобто результату вимiрювання) виникаi дефiцит вимiрювальноi iнформацii, що деякою мiрою може бути поповнений тiльки за рахунок апрiорноi iнформацii. РЖ в цьому багато що залежить вiд того, яка використовуiться апрiорна iнформацiя. Практично при вимiрюваннях мають мiсце два випадки:

1. РД тiльки iнформацiя про клас точностi ЗВТ, що використовуiться, i умови виконання вимiрювань.

2. На пiдставi накопиченого досвiду подiбних вимiрювань можуть бути вiдомi закон розподiлу ймовiрностей результатiв вимiрювань даноi фiзичноi величини, характеристики не вилучених систематичних i випадкових складових похибки вимiрювань.

У першому випадку при оцiнцi похибки вимiрювань ураховуються розсiяння (розкид) результатiв вимiрювань i поправка, обумовленi лише властивостями застосованого ЗВТ. Границi, в яких знаходиться значення вимiрюваноi величини, установлюються через iдиний вiдлiк показiв ЗВТ шляхом обчислення абсолютноi iнструментальноi похибки результату вимiрювання. Для ii оцiнки визначають границi допустимоi абсолютноi основноi похибки (за класом точностi) i додаткових похибок (за даними в технiчнiй документацii), якi обтАЩiднують за тим чи iншим правилом i одержують статичну похибку ЗВТ. Звичайно ця похибка i береться за границi довiрчого iнтервалу результату вимiрювання. Проте для пiдвищення iх вiрогiдностi слiд оцiнити (i при необхiдностi врахувати) останнi двi складовi iнструментальноi похибки вимiрювань (динамiчну похибку та похибку взаiмодii) i методичну похибку.

Границi допустимоi абсолютноi основноi похибки ЗВТ обчислюються залежно вiд форми кiлькiсного вiдображення похибки за формулами, наведеними в табл.3.2, при цьому довiрча ймовiрнiсть приймаiться за одиницю.

При прямих одноразових вимiрюваннях, коли маiмо апрiорну iнформацiю про характеристики випадкових i невилучених систематичних складових повноi похибки результату вимiрювання, ii оцiнювання проводиться вiдповiдно до методики, викладеноi в пiдп.2.9.4.

Оцiнка результату i похибки прямих багаторазових вимiрювань

Постiйно зростаючi вимоги до точностi прямих вимiрювань задовольняються не тiльки за рахунок пiдвищення точностi заново створених ЗВТ, але й використанням бiльш ефективних методiв обробки результатiв вимiрювань, наприклад статистичноi обробки багаторазових вимiрювань (або прямих вимiрювань з багаторазовими спостереженнями).

Головна особливiсть багаторазових вимiрювань, на вiдмiну вiд одноразових, полягаi в одержаннi i використаннi великого обсягу апостерiорноi вимiрювальноi iнформацii. Це не означаi, що необхiднiсть в аналiзi апрiорноi iнформацii вiдпадаi. Такий аналiз обовтАЩязково передуi багаторазовому вимiрюванню i маi ту саму мету, що й при одноразових вимiрюваннях, але з тiiю вiдмiннiстю, що при багаторазових вимiрюваннях розподiл iмовiрностей iх результатiв установлюiться експериментально. Визначення результату i похибки вимiрювань з багаторазовими спостереженнями ТСрунтуiться на статистичних оцiнках (див. Вз 2.5) або навпаки - статистичнi оцiнки одержують на пiдставi багаторазових рiвноточних вимiрювань. Методика обробки результатiв прямих вимiрювань з багаторазовими незалежними спостереженнями включаi чотири основнi етапи:

I. Аналiз апрiорноi iнформацii i пiдготовку до проведення багаторазових вимiрювань.

II. Виконання вимiрювальноi процедури. Експериментально одержують n незалежних результатiв спостережень вимiрюваного розмiру фiзичноi величини. Вимiрювальна процедура може бути органiзована по-рiзному. Якщо змiною вимiрюваноi величини в часi можна знехтувати, то всi результати спостережень простiше за все одержати шляхом багаторазових (послiдовних у часi) вимiрювань даноi величини тим самим ЗВТ. Якщо ж iз апрiорноi iнформацii можна зробити висновок, що за час такоi процедури вимiрювана величина буде iстотно змiнюватися, то ii вимiрюють одночасно (паралельно) декiлькома ЗВТ, кожний з яких даi один iз незалежних результатiв спостережень. У цьому випадку дещо порушуiться одна з умов рiвноточностi вимiрювань, але це вимушений захiд i вживаiться вiн досить рiдко. А зменшити ефект вiд використання не одного, а декiлькох ЗВТ можна iх ретельним попереднiм вiдбором.

Експеримент мусить бути добре продуманим i органiзованим так, щоб, в першу чергу, вилучити або зменшити вплив вiдомих чинникiв, якi призводять до систематичних похибок вимiрювань. Якщо цi причини невiдомi, то необхiдно якимось способом, здебiльшого експериментально, наприклад попередньою повiркою застосованих ЗВТ або на пiдставi виявлення зовнiшнiх чинникiв, одержати кiлькiсну оцiнку систематичноi складовоi похибки вимiрювань.

Результати проведеноi серii спостережень при вимiрюваннях позначимо . Вiдносно цих результатiв спостережень зробимо два припущення. По-перше, будемо вважати, що вони пiдлягають нормальному розподiлу (для пiдтвердження цього перевiряiться гiпотеза про нормальнiсть розподiлу результатiв спостережень), оскiльки це найбiльш розповсюджений на практицi випадок, для якого методи обробки експериментальних даних всебiчно вiдпрацьованi. По-друге, будемо також вважати, що результати спостережень мають систематичну i випадкову складовi похибки, тобто i невиправленими.

За одержаними експериментальними даними необхiдно знайти результат вимiрювання i оцiнити його похибку. Вирiшення цiii задачi зводиться до виконання операцiй, умовно видiлених у III i IV етапи методики.

III. Визначення результату прямих вимiрювань з багаторазовими незалежними рiвноточними спостереженнями.

1. З результатiв спостережень Вавилучають, якщо це можливо, систематичну похибку введенням поправки, використовуючи формулу (2.2), i одержують виправленi результати спостережень .

Систематичнi похибки (або iх залишки), якi не можна вилучити в процесi експерименту та при обробцi експериментальних даних введенням поправки, вiдносять до не вилучених систематичних похибок i оцiнюють iх як випадковi похибки при певних припущеннях (див. пiдп.2.9.2)

2. За виправленими результатами спостережень Вазнаходять результат прямих багаторазових вимiрювань, тобто оцiнку вимiрюваноi величини. Така оцiнка, одержана за експериментальними даними, вважаiться найкращою, якщо вона незмiщена, обТСрунтована та ефективна. Для експериментальних даних, якi вiдповiдають нормальному розподiлу, найкращою статистичною оцiнкою вимiрюваноi величини i середнi арифметичне , а найкращою оцiнкою характеристики випадковоi похибки тАУ ii СКВ (2.15).

IV. Обчислення оцiнок характеристик похибки результату прямих вимiрювань з багаторазовими спостереженнями.

1. Визначають незмiщену оцiнку СКВ Варезультатiв вимiрювань за формулою (2. 19), вводячи в неi позначення . Величину Ваназивають залишковою похибкою, або вiдхиленням q-го результату виправленого ряду спостережень вiд результату вимiрювань (середнього арифметичного значення ) цього ряду спостережень. РЖнакше кажучи, вiдхилення , показують, наскiльки результат Вакожного спостереження вiдрiзняiться вiд середнього арифметичного значення , прийнятого за результат вимiрювання, причому величини Ваможуть бути додатними або вiдтАЩiмними. Очевидно, якщо вiдхилення Вадуже малi за модулем, то результати спостережень Ваблизькi один до одного i можна вважати, що вимiрювання досить точнi. У протилежному разi, коли хоча б частина вiдхилень Вамаi досить великi значення, вимiрювання не такi вже й точнi.

Як видно iз спiввiдношення (2. 19) з урахуванням рiвностi , визначення оцiнки СКВ Вазводиться до послiдовного обчислення вiдхилень , пiднесення iх до квадрата, пiдсумовування цих квадратiв i добування квадратного кореня iз середнього значення одержаноi суми квадратiв. Для вiдхилень Васправедливе рiвняння 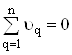, яке використовуiться для перевiрки правильностi iх обчислення.

2. Перевiряють гiпотезу про нормальнiсть розподiлу результатiв спостережень (див. Вз 2.6), попередньо вилучивши з експериментального ряду спостережень результати, якi i промахами. Якщо число спостережень , то застосовують критерiй Пiрсона (критерiй ), при 10 £ n < 50 використовують складений критерiй. Рiвень значущостi при цьому вибирають з iнтервалу 2..10%. При числi спостережень Ванормальнiсть розподiлу iх результатiв не перевiряiться.

3. Якщо гiпотеза про нормальнiсть розподiлу результатiв спостережень пiдтверджуiться, то визначають наявнiсть грубих результатiв спостережень (див. Вз 2.7). У тому випадку, коли грубi результати виявленi, вони вiдкидаються i для знов одержаного ряду обчислюють середнi арифметичне значення Ваi незмiщену оцiнку Варезультатiв спостережень.

4. Визначають границi довiрчого iнтервалу похибки результату прямих багаторазових вимiрювань, для цього:

- знаходять границi довiрчого iнтервалу випадковоi складовоi похибки (пiдп.2.4.2);

- обчислюють границi довiрчого iнтервалу невилученоi систематичноi складовоi похибки, якщо вона i (пiдп.2.9.2). До складових невилученоi систематичноi похибки можуть належати методична похибка i складовi iнструментальноi похибки ЗВТ, якщо iхнiми випадковими складовими можна знехтувати;

- обчислюють границi довiрчого iнтервалу повноi похибки результату вимiрювання (пiдп.2.9.4).

5. Записують результат вимiрювання (див. Вз 2.11). Якщо результат, одержаний при багаторазових вимiрюваннях, призначаiться в подальшому для аналiзу i зiставлення з iншими результатами або i промiжним для знаходження iнших величин, то необхiдно вказати роздiльно границi допустимоi невилученоi систематичноi похибки i оцiнку СКВ випадковоi похибки вимiрювань.

РЖнколи, при великому числi результатiв спостережень , для зменшення обсягу обчислень використовують групування даних, як i при побудовi гiстограми.

Очевидно, прямi одноразовi вимiрювання, для яких вiдома апрiорна iнформацiя про випадкову i не вилучену систематичну складовi похибки вимiрювань, можна вважати окремим випадком прямих багаторазових вимiрювань. Тому i для тих, i для iнших границi довiрчих iнтервалiв окремих складових i повноi похибки визначаються за однiiю методикою, однаково записуiться i результат вимiрювань. Вiдмiннiсть полягаi тiльки в тому, що при прямих одноразових вимiрюваннях характеристики похибок вiдомi апрiорно, а при багаторазових вимiрюваннях iх одержують за експериментальними даними, тобто вони i апостерiорними.

Основна iдея багаторазових вимiрювань того самого розмiру вимiрюваноi величини полягаi в переходi вiд результату окремого вимiрювання до середнього арифметичного значення Варяду вимiрювань. Згiдно зi спiввiдношенням (2.15) СКВ випадковоi похибки, а отже, i границi довiрчого iнтервалу середнього арифметичного значення Вав Варазiв меншi, нiж тi самi величини для окремого вимiрювання. Проте точнiсть багаторазових вимiрювань обмежуiться дефiцитом експериментальноi iнформацii i можливим часом ii одержання.

Обробка результатiв декiлькох серiй спостережень

РЖнколи за умовами вимiрювального експерименту багаторазовi спостереження (вимiрювання) фiзичноi величини незмiнного розмiру проводяться декiлькома етапами, розтягнутими на деякому тривалому iнтервалi часу, або серii (групи) вимiрювань цiii фiзичноi величини одержують за рiзних умов, з використанням рiзних ЗВТ i залученням для проведення експериментiв фахiвцiв рiзноi квалiфiкацii. Очевидно, точнiсть окремих серiй результатiв спостережень, одержаних у процесi проведення таких експериментiв, буде неоднаковою. Серii називаються однорiдними, якщо iх результати спостережень (значення фiзичноi величини) пiдлягають однаковому закону розподiлу ймовiрностей i задовольняють критерiй однорiдностi. У протилежному випадку серii спостережень вважаються неоднорiдними. В подальшому допускаiться, що результати спостережень усiх серiй пiдлягають нормальному закону розподiлу.

Задача обтАЩiднання результатiв декiлькох серiй спостережень

Задача обробки результатiв декiлькох серiй спостережень (вимiрювань) полягаi в тому, щоб, використовуючи увесь масив експериментальних даних, одержати найкращу оцiнку iстинного значення вимiрюваноi величини. Така задача називаiться обтАЩiднанням результатiв спостережень. Важливо вiдрiзняти ситуацii, при яких обтАЩiднання результатiв спостережень i виправданим, вiд тих, при яких воно не допустиме. Так, не маi рацii задача обтАЩiднання результатiв спостережень рiзних за розмiром фiзичних величин.

Задача обтАЩiднання результатiв спостережень розвтАЩязуiться двома етапами.

1. Здiйснюiться перевiрка однорiдностi i рiвноточностi серiй результатiв спостережень мiж собою. Вона i обовтАЩязковою, оскiльки визначаi вибiр методу сумiсноi обробки результатiв декiлькох серiй спостережень. Перевiрка зводиться до оцiнки допустимоi рiзницi мiж середнiми арифметичними значеннями (перевiрка на однорiднiсть) i СКВ (перевiрка на рiвноточнiсть, або на розкид, розсiювання) результатiв вимiрювань окремих серiй. Якщо обидва види вiдмiнностей, якi оцiнюються за певними критерiями, допустимi, то цi серii вимiрювань можна розглядати як iдину сукупнiсть експериментальних даних i статистично оброблювати як прямi вимiрювання з багаторазовими спостереженнями (див. пiдп.4.1.2).

2. Якщо проведена перевiрка на однорiднiсть показала недопустимiсть цього припущення, то необхiдно виконати такi двi операцii. По-перше, переконатися у тому, що в процесi проведення експерименту розмiр вимiрюваноi фiзичноi величини не змiнювався. По-друге, оцiнити границi систематичних похибок, якi мали мiсце при одержаннi кожноi серii результатiв спостережень. Використовуючи оцiнки границь систематичних похибок, слiд ввести вiдповiднi поправки в експериментальнi данi, внаслiдок чого рiзниця мiж середнiми арифметичними значеннями серiй стаi допустимою, а одержаний ряд виправлених результатiв вимiрювань однорiдним.

Критерii однорiдностi результатiв серiй спостережень

Перевiрка на однорiднiсть виконуiться для результатiв двох серiй спостережень з використанням критерiю Стьюдента, а для бiльшого числа серiй спостережень (вимiрювань) - критерiю Р. Фiшера.

Вiдповiдно до критерiю Стьюдента двi серii (L=2) з числом результатiв спостережень Вавизнаються однорiдними, якщо виконуiться нерiвнiсть

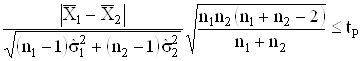, (4.1)

де - середнi арифметичнi результатiв спостережень першоi i другоi серiй вiдповiдно;

Ва- незмiщенi оцiнки дисперсiй результатiв спостережень першоi i другоi серiй;

Ва- коефiцiiнт Стьюдента, значення якого знаходять за таблицею додатка 6 при числi степенiв вiльностi , задаючись вiдповiдною довiрчою ймовiрнiстю P або рiвнем значущостi .

Отже, методика перевiрки однорiдностi результатiв двох серiй вимiрювань за критерiiм Стьюдента виконуiться так:

1) обчислюють середнi арифметичнi Варезультатiв першоi i другоi серiй вимiрювань;

2) обчислюють незмiщенi оцiнки дисперсiй Варезультатiв вимiрювань першоi i другоi серiй;

3) знаходять Ваза таблицею коефiцiiнтiв Стьюдента (додаток 6);

4) перевiряють виконання нерiвностi (4.1), тобто критерiю Стьюдента.

Вiдповiдно до критерiю Фiшера, який використовуiться при числi серiй , рiзницю середнiх арифметичних результатiв серiй спостережень вважають допустимою, якщо виконуiться умова

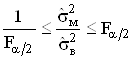, (4.2)

де - оцiнка мiжгруповоi дисперсii;

Ва- середнi значення оцiнок внутрiшньогрупових дисперсiй;

Ва- вiдсотковi значення розподiлу Фiшера. РЗх знаходять залежно вiд числа степенiв вiльностi Вадля рiзних рiвнiв значущостi (найбiльш широко використовуються 1% i 5%) за таблицями, якi приведенi у вiдповiднiй лiтературi [3,26]. Причому: Ва- число степенiв вiльностi чисельника ; Ва- число степенiв вiльностi знаменника , де Ва- число спостережень у всiх L серiях; Ва- число спостережень в j-й серii, .

Методика перевiрки однорiдностi результатiв Васерiй спостережень за критерiiм Фiшера:

1) обчислюють середнi арифметичне значення результатiв кожноi серii спостережень

, ;

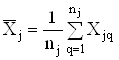2) обчислюють мiжгрупове (загальне) середнi арифметичне значення для всього обсягу N результатiв спостережень (в усiх серiях)

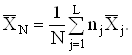Ва(4.3)

Якщо всi серii складаються з однакового числа спостережень , то формула (4.3) спрощуiться

;

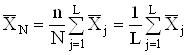3) знаходять незмiщену оцiнку мiжгруповоi дисперсii результатiв спостережень (розсiювання мiж груповими середнiми арифметичними)

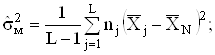
4) визначають середнi арифметичне значення незмiщених оцiнок внутрiшньогрупових дисперсiй результатiв спостережень (середнi розсiювання всерединi груп):

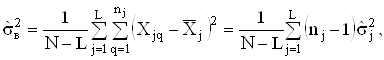Ва(4.4)

де Ва(4.5)

- незмiщена оцiнка внутрiшньогруповоi дисперсii результатiв спостережень j-i серii, ;

5) знаходять значення Ваза таблицею Фiшера i перевiряють виконання нерiвностi (4.2), тобто критерiю Фiшера. Якщо значення вiдношення Вазнаходиться поза iнтервалом, який визначаiться нерiвнiстю (4.2), то це означаi, що середнi арифметичнi результатiв спостережень серiй мають недопустимi змiщення. У такому разi приймають рiшення про неоднорiднiсть серiй спостережень, тобто про неприпустимiсть рiзницi мiж iхнiми середнiми арифметичними значеннями. Для усунення цього ефекту необхiдно знайти причину розходження мiж середнiми арифметичними значеннями Ваi в експериментальнi данi вiдповiдноi серii (серiй) внести додаткову поправку (поправки). РЖнколи, з метою виявлення за допомогою такоi перевiрки прогресуючого впливу будь-якого чинника, увесь масив експериментальних даних штучно розбивають на двi або бiльше серiй.

Для перевiрки однорiдностi двох серiй вимiрювань, розподiл яких вiдрiзняiться вiд нормального, доцiльно використовувати ранговi критерii Уiлкоксона i Сiджела-Тьюкi [25].

Критерii рiвноточностi результатiв серiй спостережень

Поряд з термiнами тАЬрiвноточнiтАЭ i тАЬнерiвноточнiтАЭ результати спостережень (вимiрювань) використовують також термiни тАЬрiвнорозсiянiтАЭ i тАЬнерiвнорозсiянiтАЭ результати спостережень, оскiльки вони ТСрунтуються на порiвняннi i допустимостi вiдмiнностей оцiнок внутрiшньогрупових дисперсiй (або СКВ) результатiв спостережень. Для перевiрки такоi допустимостi вiдмiнностей використовують критерiй Р. Фiшера (при числi серiй ) або критерiй М. Бартлетта (при числi серiй ).

Вiдповiдно до критерiю Фiшера вiдмiннiсть мiж незмiщеними оцiнками дисперсiй Варезультатiв двох серiй з числом спостережень Вавважаiться допустимою, якщо виконуiться умова

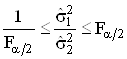. (4.6)

Значення Вазалежно вiд числа степенiв вiльностi для рiвнiв значущостi Ванаводяться в таблицях Фiшера. Число степенiв вiльностi для оцiнки дисперсii Вадорiвнюi , для оцiнки дисперсii Вавоно дорiвнюi . Оцiнки дисперсiй Ваобчислюють за формулою (4.5), пiсля цього перевiряють нерiвнiсть (4.6).

Критерiй М. Бартлетта справедливий для Ваi . Вiн ТСрунтуiться на обчисленнi - розподiлу

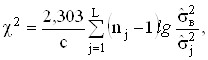Ва(4.7)

де 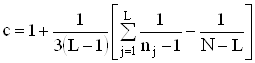. (4.8)

Оцiнки дисперсiй Ваi Ваобчислюють за формулами (4.4) i (4.5). Якщо в усiх серiях число спостережень , то можна вважати c = 1.

Критерiй Бартлетта визначаiться нерiвнiстю

Ва(4.9)

де - Ва- розподiл для рiвня значущостi , його знаходять за таблицею додатка 7. Вхiдними даними цiii таблицi i рiвень значущостi Ва(звичайно Ва= 1; 2,5 i 10%) i число степенiв вiльностi Ва(у даному випадку ).

Методика перевiрки рiвноточностi результатiв серiй спостережень за критерiiм Бартлетта:

1) обчислюють незмiщенi оцiнки внутрiшньогрупових дисперсiй Ваза формулою (4.5);

2) знаходять середнi значення цих оцiнок за формулою (4.4);

3) обчислюють значення Ваза формулою (4.7) iз застосуванням спiввiдношення (4.8);

4) задаючись рiвнем значущостi , знаходять за таблицею додатка 7 значення ;

5) перевiряють виконання нерiвностi (4.9), тобто критерiю Бартлетта. Якщо ця нерiвнiсть виконуiться, то вiдмiнностi мiж дисперсiями (i СКВ) результатiв вимiрювань вважаються допустимими i розвтАЩязуiться задача обтАЩiднання результатiв однорiдних рiвноточних серiй спостережень. В iншому разi (за умови, що результати спостережень однорiднi) мусить бути розвтАЩязана задача обтАЩiднання результатiв нерiвноточних серiй вимiрювань.

Вместе с этим смотрят:

GPS-навигация

GPS-прийомник авиационный

IP-телефония и видеосвязь

IP-телефония. Особенности цифровой офисной связи

Unix-подобные системы