Систематична похибка опосередкованих вимiрювань
Систематична похибка опосередкованих вимiрювань при нелiнiйнiй залежностi
Пiдкреслимо одну важливу особливiсть результатiв опосередкованих вимiрювань при нелiнiйнiй залежностi у порiвняннi з результатами прямих багаторазових вимiрювань. Якщо в результатах одноразових спостережень систематичнi похибки вилученi, то математичне сподiвання середнього арифметичного ряду прямих рiвнорозсiяних спостережень дорiвнюi iстинному значенню вимiрюваноi величини, тобто результати прямих виправлених спостережень вiльнi вiд систематичних похибок. На вiдмiну вiд цього, математичне сподiвання похибки результату опосередкованих вимiрювань при нелiнiйнiй залежностi, яка визначаiться певною формулою, не дорiвнюi нулю, тобто похибка результату такого опосередкованого вимiрювання, поряд з випадковою складовою, маi i систематичну складову. А це означаi, що математичне сподiвання результату опосередкованих вимiрювань при нелiнiйнiй залежностi не дорiвнюi iстинному значенню вимiрюваноi величини, або iнакше, що оцiнка i змiщеною, якщо хоча будь-яка одна серед других похiдних в не дорiвнюi нулю. Покажемо це.
Обчислимо математичне сподiвання абсолютноi похибки опосередкованих вимiрювань  Y з урахуванням:
Y з урахуванням:
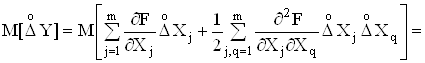
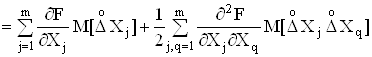 .
.
У цьому виразi перша сума дорiвнюi нулю, оскiльки 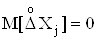 Ваза умовою проведення експерименту, а друга сума визначаi систематичну похибку. Отже, якщо вимiрюванi величиниВа корельованi мiж собою, то, враховуючи рiвнiсть
Ваза умовою проведення експерименту, а друга сума визначаi систематичну похибку. Отже, якщо вимiрюванi величиниВа корельованi мiж собою, то, враховуючи рiвнiсть
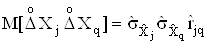 ,
,
для систематичноi похибки результату опосередкованих вимiрювань дiстаiмо

Оцiнку коефiцiiнта кореляцii 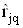 Ваабо визначають за експериментальними даними, або задають функцiональною залежнiстю чи у виглядi матрицi.
Ваабо визначають за експериментальними даними, або задають функцiональною залежнiстю чи у виглядi матрицi.
За умови, що вимiрюванi величиниВа не корельованi, маiмо

Тодi систематична похибка результату опосередкованих вимiрювань
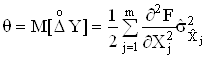 .
.
Отже, опосередкованi вимiрювання при нелiнiйнiй залежностi мають специфiчну систематичну похибку, яка обумовлена ненульовими частинними похiдними 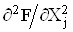 .
.
Щоб вилучити цю систематичну похибку, треба в результат опосередкованих вимiрювань, обчислений за формулою, ввести поправку П, яка дорiвнюi систематичнiй похибцi за значенням i обернена iй за знаком, тобто 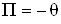 .
.
Опосередкованi вимiрювання при лiнiйнiй залежностi вказаноi вище специфiчноi систематичноi похибки не мають, тому що для них 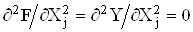 .
.
Результат i похибка опосередкованих вимiрювань
Довiрчi границi випадковоi похибки i границi не вилученоi систематичноi похибки результату опосередкованого вимiрювання з нелiнiйною залежнiстю визначають за певними формулами, пiдставляючи в останнi замiсть коефiцiiнтiв 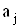 Вавiдповiдно першi похiднi
Вавiдповiдно першi похiднi 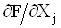 .
.
Довiрчу повну похибку результату опосередкованого вимiрювання обчислюють певним чином.
Остаточний результат опосередкованих вимiрювань записуiться у виглядi
 Вапри , (4.35)
Вапри , (4.35)
де - границi допустимоi випадковоi похибки опосередкованих вимiрювань.
- границi допустимоi випадковоi похибки опосередкованих вимiрювань.
Формули для оцiнки СКВ i результату опосередкованих вимiрювань справедливi за умови, що вiдомi оцiнки дисперсii (i СКВ) початкових величин. Значення коефiцiiнта 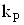 Вавизначаiться для заданоi довiрчоi ймовiрностi P, виходячи iз закону розподiлу результатуВа опосередкованого вимiрювання. Якщо закон розподiлу результатуВа опосередкованих вимiрювань можна вважати нормальним, то для визначення
Вавизначаiться для заданоi довiрчоi ймовiрностi P, виходячи iз закону розподiлу результатуВа опосередкованого вимiрювання. Якщо закон розподiлу результатуВа опосередкованих вимiрювань можна вважати нормальним, то для визначення 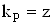 Ва(i довiрчих границь
Ва(i довiрчих границь 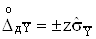 ) використовуiться iнтегральна функцiя нормованого нормального розподiлу при великому числi вимiрювань
) використовуiться iнтегральна функцiя нормованого нормального розподiлу при великому числi вимiрювань 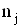 . При малому числi
. При малому числi 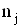 Ванормально розподiлених результатiв спостережень
Ванормально розподiлених результатiв спостережень 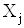 Васлiд користуватися розподiлом Стьюдента з тАЬефективнимтАЭ числом степенiв вiльностi, що визначаiться виразом
Васлiд користуватися розподiлом Стьюдента з тАЬефективнимтАЭ числом степенiв вiльностi, що визначаiться виразом
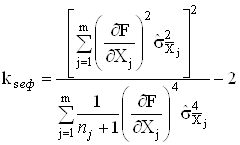 .
.
Якщо числа спостережень усiх аргументiв однаковi 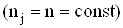 , то
, то
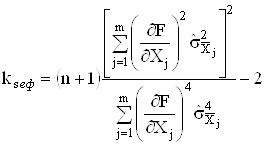 .
.
При лiнiйнiй функцiональнiй залежностi опосередкованих вимiрювань маiмо 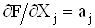 Ваi одержуiмо приведенi ранiше формули для ефективного числа степенiв вiльностi
Ваi одержуiмо приведенi ранiше формули для ефективного числа степенiв вiльностi 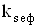 .
.
Оскiльки число 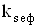 Вазвичайно i дробовим, то для пошуку величини
Вазвичайно i дробовим, то для пошуку величини 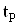 Ваза таблицею розподiлу Стьюдента необхiдно використовувати iнтерполяцiю.
Ваза таблицею розподiлу Стьюдента необхiдно використовувати iнтерполяцiю.
Довiрчi границi повноi похибки опосередкованих вимiрювань (з урахуванням випадковоi i не вилученоi систематичноi складових похибки вимiрювань) знаходять за вiдповiдною методикою.
Отже, загальна методика статистичноi обробки результатiв опосередкованих вимiрювань передбачаi такий алгоритм:
1) вилучення вiдомих (виявлених) систематичних похибок з результатiв вимiрювань кожного аргументу;
2) перевiрку вiдповiдностi реального розподiлу результатiв прямих вимiрювань кожного аргументу нормальному закону за одним iз критерiiв згоди. Якщо така вiдповiднiсть пiдтверджуiться, то проводять перевiрку надмiрних похибок i iх вилучення з результатiв вимiрювань;
3) обчислення оцiнок аргументiв та iх похибок;
4) перевiрку вiдсутностi кореляцii мiж результатами вимiрювань аргументiв попарно, при ii наявностi обчислюють вiдповiднi коефiцiiнти кореляцii;
5) обчислення результату опосередкованого вимiрювання;
6) обчислення довiрчоi випадковоi похибки i загальноi похибки результату опосередкованого вимiрювання; при нелiнiйнiй залежностi знаходять систематичну похибку опосередкованих вимiрювань, обумовлену перехресними членами у рiвняннi.
При прямих одноразових вимiрюваннях початкових величин 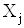 Вапроцедура визначення результату Y опосередкованих вимiрювань зберiгаiться такою самою, як i при багаторазових вимiрюваннях. Проте при прямих одноразових вимiрюваннях початкових величин
Вапроцедура визначення результату Y опосередкованих вимiрювань зберiгаiться такою самою, як i при багаторазових вимiрюваннях. Проте при прямих одноразових вимiрюваннях початкових величин 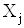 Вадля оцiнки характеристик похибки опосередкованих вимiрювань широко використовуються абсолютнi i вiдноснi значення похибок. Для визначення абсолютноi похибки результату опосередкованих вимiрювань використовують спiввiдношення, аналогiчне за формою виразу без залишкового члена, а за абсолютною похибкою знаходять вiдповiднi вiдноснi похибки з рiвностi.
Вадля оцiнки характеристик похибки опосередкованих вимiрювань широко використовуються абсолютнi i вiдноснi значення похибок. Для визначення абсолютноi похибки результату опосередкованих вимiрювань використовують спiввiдношення, аналогiчне за формою виразу без залишкового члена, а за абсолютною похибкою знаходять вiдповiднi вiдноснi похибки з рiвностi.
Формули обчислення абсолютних i вiдносних похибок опосередкованих вимiрювань для тих функцiональних залежностей, якi часто зустрiчаються в практицi, наведенi в табл. 1. Якщо похибки i систематичними, то формули в табл. 1. використовують з урахуванням знакiв похибок. Для випадкових похибок здiйснюiться пiдсумовування за модулем, тобто арифметичне пiдсумовування, причому за величинуВа беруть границi допустимих похибок (максимальнi значення).
Табл. 1. свiдчить, що пiднесення аргументу до цiлого степеня значно збiльшуi, а добування цiлого степеня аргументу зменшуi похибки результату. Тому вимiрювання величин, якi у формулу входять у виглядi  Ва- цiле додатне число), необхiдно виконувати з бiльшою точнiстю, а вимiрювання величин, якi входять у формулу (1.6) у виглядi
Ва- цiле додатне число), необхiдно виконувати з бiльшою точнiстю, а вимiрювання величин, якi входять у формулу (1.6) у виглядi 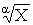 , може здiйснюватися з меншою точнiстю. Якщо результат опосередкованих вимiрювань виражаiться через степеневу функцiю аргументiв, наприклад,
, може здiйснюватися з меншою точнiстю. Якщо результат опосередкованих вимiрювань виражаiться через степеневу функцiю аргументiв, наприклад,
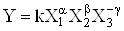 ,
,
то для вiдносноi систематичноi похибки одержимо
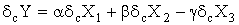 ,
,
а для оцiнки тАЬзверхутАЭ, тобто максимального значення вiдносноi випадковоi похибки
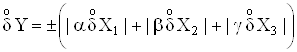
Таблиця 1.
| Функцii Y | П о х и б к и |
| Абсолютна, | Вiдносна, |

| 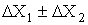
| 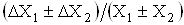
|
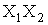
| 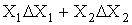
| 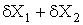
|
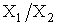
| 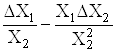
| 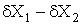
|
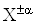
| 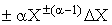
| 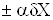
|
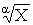
| 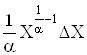
| 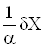
|
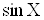
| | |
| | |
Проте така оцiнка даi завищенi результати i ii застосування доцiльно при 2 або 3 складових похибки. При бiльшому числi складових випадковоi похибки опосередкованих вимiрювань (за числом аргументiв m), абсолютну випадкову похибку результату опосередкованих вимiрювань слiд обчислювати за правилами пiдсумовування незалежних випадкових величин, тобто геометрично
 .
.
Величину 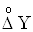 Ваназивають середнiм квадратичним значенням абсолютноi випадковоi похибки опосередкованих вимiрювань.
Ваназивають середнiм квадратичним значенням абсолютноi випадковоi похибки опосередкованих вимiрювань.
Тодi СКЗ вiдносноi випадковоi похибки опосередкованих вимiрювань
 .
.
При роздiльнiй оцiнцi систематичних i випадкових похибок результату опосередкованих вимiрювань необхiдно мати на увазi таке. Очевидно, що оцiнити систематичну похибку результату опосередкованих вимiрювань неможливо, не знаючи оцiнок систематичних похибок початкових величин 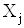 . Але якщо вони вiдомi, то iх необхiдно вилучити з результатiв прямих вимiрювань
. Але якщо вони вiдомi, то iх необхiдно вилучити з результатiв прямих вимiрювань 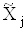 , а потiм оцiнити результат опосередкованого вимiрювання за цими виправленими значеннями
, а потiм оцiнити результат опосередкованого вимiрювання за цими виправленими значеннями 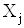 . Водночас така оцiнка систематичноi похибки може бути проведена пiсля закiнчення експерименту. Тодi ii у виглядi поправки необхiдно врахувати в остаточному результатi опосередкованого вимiрювання. Оцiнка систематичноi похибки може використовуватися також пiд час пiдготовки до експерименту, як орiiнтовна оцiнка. Наприклад, якщо припустити, що похибка результату опосередкованого вимiрювання визначаiться тiльки похибкою ЗВТ при вимiрюваннi величин
. Водночас така оцiнка систематичноi похибки може бути проведена пiсля закiнчення експерименту. Тодi ii у виглядi поправки необхiдно врахувати в остаточному результатi опосередкованого вимiрювання. Оцiнка систематичноi похибки може використовуватися також пiд час пiдготовки до експерименту, як орiiнтовна оцiнка. Наприклад, якщо припустити, що похибка результату опосередкованого вимiрювання визначаiться тiльки похибкою ЗВТ при вимiрюваннi величин 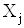 , причому в цих ЗВТ переважаючою i систематична похибка (випадковою похибкою можна знехтувати), то на пiдставi оцiнки систематичноi похибки за певною формулою приВа (провiвши формальну замiну
, причому в цих ЗВТ переважаючою i систематична похибка (випадковою похибкою можна знехтувати), то на пiдставi оцiнки систематичноi похибки за певною формулою приВа (провiвши формальну замiну 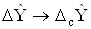 ,
, 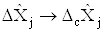 ) можна вибрати ЗВТ з такими границями допустимих систематичних похибок, щоб похибка результату опосередкованих вимiрювань величини Y не перевищувала заданого значення.
) можна вибрати ЗВТ з такими границями допустимих систематичних похибок, щоб похибка результату опосередкованих вимiрювань величини Y не перевищувала заданого значення.
Оцiнка результатiв i похибок сумiсних та сукупних вимiрювань
Загальною ознакою сумiсних i сукупних вимiрювань, вiдповiдно до iх визначення (див. Вз 1.5), i те, що значення шуканих величин визначають, розвтАЩязуючи систему рiвнянь, якi звтАЩязують шуканi величини з деякими iншими величинами, вимiрюваними прямими або опосередкованими методами, причому вимiрюють декiлька комбiнацiй значень цих величин. Вимiрювання, проведенi для кожноi комбiнацii, дозволяють одержати одне рiвняння, а сукупнiсть цих рiвнянь для всiх комбiнацiй являi собою систему рiвнянь, в яку входять також усi значення шуканих величин. Цю систему рiвнянь, вiдповiдно до (1.7), запишемо для стислостi записiв у виглядi
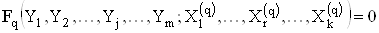 , (4.36)
, (4.36)
де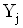 - значення шуканих величин, ;
- значення шуканих величин, ;
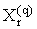 Ва- значення величин, вимiрюваних прямими або опосередкованими методами в q-му дослiдi, ;
Ва- значення величин, вимiрюваних прямими або опосередкованими методами в q-му дослiдi, ;
n - число дослiдiв;
k - число величин, якi вимiрюються в кожному дослiдi;
m - число шуканих величин.
Рiвняння, як i рiвняння, за формою однаковi для сумiсних i сукупних вимiрювань. РЗх вiдмiннiстю i тiльки фiзична суть шуканих величин.
Якщо 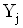 Ваi значеннями тiii самоi фiзичноi величини (наприклад, масами гир певного набору або довжинами лiнiйних мiр), то вимiрювання сукупнi. Якщо ж
Ваi значеннями тiii самоi фiзичноi величини (наприклад, масами гир певного набору або довжинами лiнiйних мiр), то вимiрювання сукупнi. Якщо ж 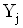 Ва- значення рiзних фiзичних величин (наприклад, опору i температури), то вимiрювання сумiснi. Ще раз пiдкреслимо, що такий подiл вимiрювань дуже умовний, але вiн традицiйно iснуi.
Ва- значення рiзних фiзичних величин (наприклад, опору i температури), то вимiрювання сумiснi. Ще раз пiдкреслимо, що такий подiл вимiрювань дуже умовний, але вiн традицiйно iснуi.
Пiсля проведення n дослiдiв одержують n комбiнацiй значень вимiрюваних величин 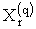 . Пiдставляючи
. Пiдставляючи 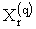 Вау початкову систему i проводячи необхiднi перетворення, одержимо систему рiвнянь
Вау початкову систему i проводячи необхiднi перетворення, одержимо систему рiвнянь
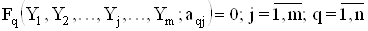
Рiвняння (4.37) мiстять у собi шуканi величини 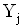 Ваi числовi коефiцiiнти
Ваi числовi коефiцiiнти 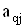 . Для визначення m невiдомих значень шуканих величинВа необхiдно мати m рiвнянь. Тодi результати вимiрювань величин
. Для визначення m невiдомих значень шуканих величинВа необхiдно мати m рiвнянь. Тодi результати вимiрювань величин 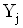 Ваi довiрчi границi iх похибок можна знайти за методиками обробки результатiв опосередкованих вимiрювань. Проте, з метою зменшення похибок результатiв вимiрювань, дослiдiв проводять дещо бiльше, нiж число m невiдомих величин
Ваi довiрчi границi iх похибок можна знайти за методиками обробки результатiв опосередкованих вимiрювань. Проте, з метою зменшення похибок результатiв вимiрювань, дослiдiв проводять дещо бiльше, нiж число m невiдомих величин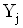 , тобто .
, тобто .
Оскiльки точнiсть вимiрювання величин 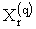 Ваобмежена, то умовнi рiвняння одночасно не перетворюються в тотожностi при жодних значеннях шуканих величин
Ваобмежена, то умовнi рiвняння одночасно не перетворюються в тотожностi при жодних значеннях шуканих величин 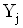 , а отже, не виникаi можливостi визначення iх iстинних значень. Тому задача зводиться до знаходження оцiнок шуканих величин
, а отже, не виникаi можливостi визначення iх iстинних значень. Тому задача зводиться до знаходження оцiнок шуканих величин 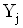 , найбiльш наближених до iстинних значень. Позначимо такi оцiнки
, найбiльш наближених до iстинних значень. Позначимо такi оцiнки  . Якщо значення
. Якщо значення  Вапiдставити в умовнi рiвняння, то iх лiвi частини, в загальному випадку, будуть вiдрiзнятися вiд правих частин. Такi рiвняння i названi умовними. Для одержання тотожностi введемо в правi частини умовних рiвнянь деякi величини , якi називають залишковими похибками умовних рiвнянь або вiдхилами. Звiдси маiмо
Вапiдставити в умовнi рiвняння, то iх лiвi частини, в загальному випадку, будуть вiдрiзнятися вiд правих частин. Такi рiвняння i названi умовними. Для одержання тотожностi введемо в правi частини умовних рiвнянь деякi величини , якi називають залишковими похибками умовних рiвнянь або вiдхилами. Звiдси маiмо
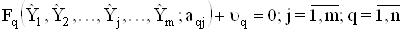 . (4.38)
. (4.38)
Для розвтАЩязання системи умовних рiвнянь застосовуiться метод найменших квадратiв (МНК), згiдно з яким оцiнки  Вавибирають так, щоб мiнiмiзувати суму квадратiв вiдхилiв
Вавибирають так, щоб мiнiмiзувати суму квадратiв вiдхилiв
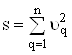 .
.
РозвтАЩязання задачi в самому загальному випадку, коли умовнi рiвняння нелiнiйнi, а результати окремих вимiрювань корельованi, дещо утруднено. Тому розглянемо окремий випадок, коли умовнi рiвняння лiнiйнi або приведенi до лiнiйного вигляду, а результати вимiрювань величин 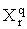 Варiвноточнi i некорельованi. Тодi оцiнки, одержанi методом найменших квадратiв, будуть обТСрунтованими i незмiщеними, а при нормальному розподiлi результатiв вимiрювань ще й ефективними. У цьому випадку система рiвнянь може бути приведена до вигляду
Варiвноточнi i некорельованi. Тодi оцiнки, одержанi методом найменших квадратiв, будуть обТСрунтованими i незмiщеними, а при нормальному розподiлi результатiв вимiрювань ще й ефективними. У цьому випадку система рiвнянь може бути приведена до вигляду
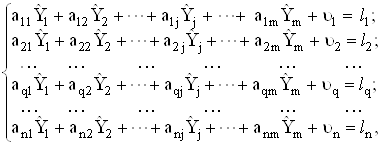 Ва(4.39)
Ва(4.39)
де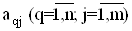 - коефiцiiнти, одержанi iз системи рiвнянь пiсля ii лiнеаризацii (якщо вона нелiнiйна) i пiдстановки значень величин
- коефiцiiнти, одержанi iз системи рiвнянь пiсля ii лiнеаризацii (якщо вона нелiнiйна) i пiдстановки значень величин 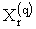 , причому q - рядок, j - стовпчик;
, причому q - рядок, j - стовпчик;
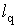 Ва- постiйна величина.
Ва- постiйна величина.
Сума квадратiв вiдхилiв визначаiться iз системи рiвнянь
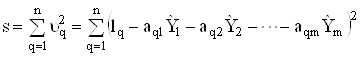
Як вiдомо, необхiдною умовою мiнiмуму диференцiальноi функцii багатьох змiнних, у даному випадку  , i виконання рiвнянь:
, i виконання рiвнянь:

РЗх можна розглядати як рiвняння вiдносно величин 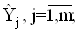 у математичнiй статистицi вони називаються нормальними рiвняннями.
у математичнiй статистицi вони називаються нормальними рiвняннями.
Використовуючи рiвнiсть, знайдемо частиннi похiднi i прирiвняiмо iх до нуля:

Запишемо одержану систему рiвнянь у компактному виглядi
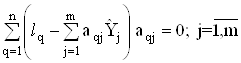
Ця система рiвнянь i лiнiйною вiдносно шкали величин  . Внаслiдок розвтАЩязання системи нормальних рiвнянь одержують m невiдомих величин
. Внаслiдок розвтАЩязання системи нормальних рiвнянь одержують m невiдомих величин  . Для спрощення запису цiii моделi використовують позначення Гаусса для сум:
. Для спрощення запису цiii моделi використовують позначення Гаусса для сум:
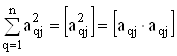 ;
; 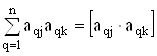 ;
; 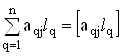 .
.
З урахуванням цих позначень система нормальних рiвнянь набуваi вигляду

Як вiдомо, розвтАЩязання такоi лiнiйноi системи i лiнiйними комбiнацiями величин 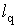 :
:
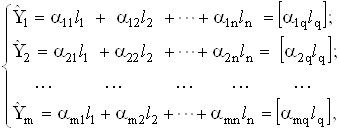
де коефiцiiнти 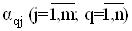 Вазнаходять, розвтАЩязуючи систему рiвнянь (4.44) за допомогою визначника для кожноi з шуканих величин:
Вазнаходять, розвтАЩязуючи систему рiвнянь (4.44) за допомогою визначника для кожноi з шуканих величин:
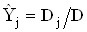 ,
,
де Ва ;
;
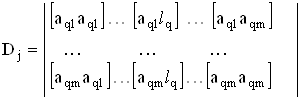 .
.
Визначник 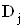 Ваодержаний замiною у визначнику
Ваодержаний замiною у визначнику 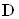 Ваj-го стовпця стовпцем вiльних членiв у (4.44).
Ваj-го стовпця стовпцем вiльних членiв у (4.44).
Отже, 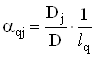 .
.
Визначивши з вiдхили 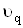 Ваi пiдставивши iх у рiвняння (4.42), одержимо такi рiвностi:
Ваi пiдставивши iх у рiвняння (4.42), одержимо такi рiвностi:
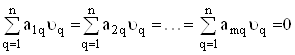 ,
,
що виражають властивостi вiдхилiв 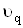 . Цi рiвностi застосовуються для перевiрки правильностi визначення оцiнок
. Цi рiвностi застосовуються для перевiрки правильностi визначення оцiнок  Вашуканих величин пiсля розвтАЩязання системи рiвнянь.
Вашуканих величин пiсля розвтАЩязання системи рiвнянь.
Визначення оцiнок  Вашуканих величин
Вашуканих величин 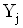 ВаповтАЩязано з великим обсягом обчислень, який швидко збiльшуiться iз збiльшенням числа умовних рiвнянь. Останнi необхiдно для пiдвищення точностi одержаних оцiнок. У сучаснi днi обробка результатiв сумiсних i сукупних вимiрювань виконуiться за допомогою ЕОМ за стандартними програмами. Тому точнiсть оцiнок iстинних значень вимiрюваних величин може бути значно пiдвищена при збiльшеннi числа умовних рiвнянь до кiлькох десяткiв i навiть сотень, а в деяких випадках i бiльше.
ВаповтАЩязано з великим обсягом обчислень, який швидко збiльшуiться iз збiльшенням числа умовних рiвнянь. Останнi необхiдно для пiдвищення точностi одержаних оцiнок. У сучаснi днi обробка результатiв сумiсних i сукупних вимiрювань виконуiться за допомогою ЕОМ за стандартними програмами. Тому точнiсть оцiнок iстинних значень вимiрюваних величин може бути значно пiдвищена при збiльшеннi числа умовних рiвнянь до кiлькох десяткiв i навiть сотень, а в деяких випадках i бiльше.
Для оцiнки точностi одержаного розвтАЩязання системи рiвнянь звичайно припускають, що точнiсть визначення коефiцiiнтiв 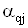 Вазначно вища вiд точностi визначення коефiцiiнтiв
Вазначно вища вiд точностi визначення коефiцiiнтiв 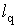 . Це припущення, як правило, виправдане в багатьох практичних випадках. При його виконаннi похибки оцiнок
. Це припущення, як правило, виправдане в багатьох практичних випадках. При його виконаннi похибки оцiнок  Вашуканих величин
Вашуканих величин 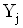 Вавизначаються тiльки дисперсiями результатiв вимiрювання останнiх. А враховуючи, що згiдно з рiвняннями оцiнки
Вавизначаються тiльки дисперсiями результатiв вимiрювання останнiх. А враховуючи, що згiдно з рiвняннями оцiнки  Ваi лiнiйними комбiнацiями величин
Ваi лiнiйними комбiнацiями величин 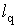 , маiмо
, маiмо
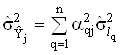 ,
,
де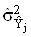 - оцiнка дисперсii шуканих величин
- оцiнка дисперсii шуканих величин 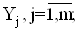
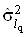 Ва- оцiнка дисперсii коефiцiiнтiв
Ва- оцiнка дисперсii коефiцiiнтiв 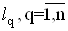 .
.
Якщо припустити, що всi результати спостережень i рiвноточними, а отже, всi дисперсii 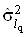 Вау виразi однаковi
Вау виразi однаковi
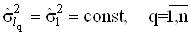 ,
,
то оцiнка СКВ
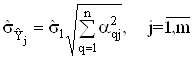
Для обчислення 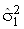 Варекомендуiться досить простий вираз
Варекомендуiться досить простий вираз
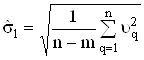 ,
,
в якому залишковi похибки 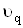 Вавизначають iз рiвнянь пiсля визначення оцiнок
Вавизначають iз рiвнянь пiсля визначення оцiнок  Вазгiдно з системою рiвнянь.
Вазгiдно з системою рiвнянь.
Якщо точнiсть визначення усiх коефiцiiнтiв 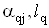 системи рiвнянь (4.45) приблизно однакова, то оцiнку СКВ результату вимiрювань величинВа визначають за формулою
системи рiвнянь (4.45) приблизно однакова, то оцiнку СКВ результату вимiрювань величинВа визначають за формулою

де - алгебраiчнi доповнення головного визначника D, якi одержують виключенням з нього j-го рядка та j-го стовпця.
- алгебраiчнi доповнення головного визначника D, якi одержують виключенням з нього j-го рядка та j-го стовпця.
З рiвнянь випливаi, що точнiсть сукупних i сумiсних вимiрювань залежить вiд спiввiдношення числа шуканих величин m i числа умовних рiвнянь n. Чим значнiша умова , тим точнiше результати обробки. Якщо m i n близькi, то результати обробки визначаються з грубими похибками.
Довiрчi iнтервали для iстинних значень усiх вимiрюваних величин одержують за розподiлом Стьюдента при числi степенiв вiльностi .
Якщо при сукупних i сумiсних вимiрюваннях умовнi рiвняння нелiнiйнi, то застосовують iх лiнеаризацiю.
Таким чином, методика обробки результатiв сукупних i сумiсних вимiрювань така:
1. Записують систему умовних рiвнянь при 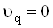 Вапiдстановкою експериментальних даних у рiвняння початковоi залежностi.
Вапiдстановкою експериментальних даних у рiвняння початковоi залежностi.
2. Систему умовних рiвнянь приводять до нормального вигляду. Для обчислення коефiцiiнтiв нормальних рiвнянь складають допомiжну табл. 2, яка дозволяi також перевiрити правильнiсть визначення шуканих величин.
Таблиця 2.
| q | 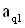
| 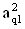
| .. | 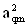
| 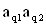
| .. | 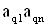
| .. | 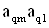
| .. | 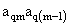
| 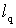
| 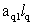
| .. | 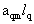
|
| 1 | 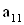
| 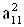
| .. | 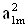
| 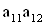
| .. | 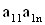
| .. | 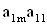
| .. | 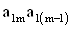
| 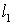
| 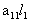
| .. | 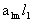
|
| 2 | 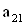
| 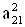
| .. | 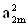
| 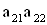
| .. | 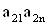
| .. | 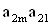
| .. | 
| 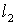
| 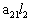
| .. | 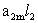
|
| .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. |
| .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. | .. |
| n | 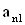
| 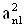
| .. | 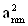
| 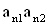
| .. | 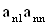
| .. | 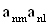
| .. | 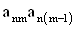
| 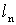
| 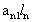
| .. | 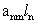
|
| | 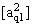
| .. | 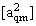
| 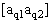
| .. | 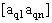
| .. | 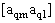
| .. | 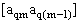
| тАж | 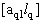
| .. | 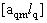
|
Визначають оцiнки шуканих величин 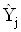 , розвтАЩязуючи систему нормальних рiвнянь, для чого використовують один iз методiв:
, розвтАЩязуючи систему нормальних рiвнянь, для чого використовують один iз методiв:
а) метод, який ТСрунтуiться на послiдовному виключеннi невiдомих (метод Гаусса);
б) метод iз застосуванням визначника.
4. Перевiряють правильнiсть визначення оцiнок шуканих величин за рiвняннями.
5. Знаходять оцiнку СКВ результатiв вимiрювань шуканих величин 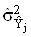 Ваза певними формулами.
Ваза певними формулами.
6. Визначають довiрчi iнтервали для всiх вимiрюваних величин на пiдставi розподiлу Стьюдента при числi степенiв вiльностi Ваiх вимiрювань.
Вместе с этим смотрят:
GPS-навигация
GPS-прийомник авиационный
IP-телефония и видеосвязь
IP-телефония. Особенности цифровой офисной связи
Unix-подобные системы