Теория автоматического управления
Министерство образования Российской Федерации
Ивановский государственный энергетический университет
кафедра АУЭС
Методические указания
к выполнению курсовой работы по дисциплине
тАЬТеория автоматического управлениятАЭ
(для студентов спец. 210400)
Иваново 2000
Составитель В.Ф. КОРОТКОВ
Редактировал А.А. ФОМИЧЕВ
Методические указания предназначены для студентов специальности 210400 "Автоматическое управление электроэнергетическими системами".
Утверждены цикловой методической комиссией ЭЭФ.
РЕЦЕНЗЕНТ
кафедра автоматического управления электроэнергетическими системами Ивановского государственного энергетического университета
СОДЕРЖАНИЕ
1. ЦЕЛИ И ЗАДАЧИ
2. ОБЩИЕ ЗАМЕЧАНИЯ
3. СТРУКТУРНАЯ СХЕМА САУ
4. СТАТИЧЕСКАЯ ХАРАКТЕРИСТИКА
5. ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА
6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
7. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В КОМПЛЕКСНОЙ ПЛОСКОСТИ
8. ОБЛАСТЬ УСТОЙЧИВОСТИ
9. ЗАПАС УСТОЙЧИВОСТИ
10. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ
ЛИТЕРАТУРА
ПРИЛОЖЕНИЕ
1. ЦЕЛИ И ЗАДАЧИ
Целью курсовой работы является закрепление и обобщение знаний, полученных студентами специальности 210400 при изучении дисциплины тАЬТеория автоматического управлениятАЭ, приобретение умений и навыков в использовании этих знаний при самостоятельном решении практических задач.
Задачи:
- обеспечить связь общей теории автоматического управления с конкретными проблемами автоматического управления в электроэнергетических системах;
- продемонстрировать влияние значений параметров на динамические и частотные свойства системы автоматического управления (САУ), а также на её устойчивость ;
- обеспечить получение умений и навыков в исследовании основных характеристик и показателей качества САУ.
2. ОБЩИЕ ЗАМЕЧАНИЯ
Объектом исследований в курсовой работе является фрагменты реальных САУ, используемых в электроэнергетике. Параметры САУ, задаваемых в качестве исходных данных, также близки к реальным и их различия в отдельных вариантах заданий определяется в основном необходимостью получения определенного числа вариантов.
Задания (см. Приложение) к курсовой работе в общем случае предполагают необходимость выполнения следующих работ:
- составление и преобразование структурной схемы замкнутой САУ и получение эквивалентной передаточной функции;
- обеспечение заданных статических характеристик САУ, в частности, заданного значения коэффициента статизма;
- исследование переходной характеристики САУ при заданном воздействии на входе и оценка динамических свойств (перерегулирование, время переходного процесса и др.);
- оценка частотных свойств САУ на основе частотных характеристик;
- расчёт и построение области устойчивости САУ в пространстве заданных параметров;
- определение запаса устойчивости САУ по модулю и по фазе.
При расчёте характеристик САУ предполагается возможность использования компьютерных программ тАЬClassicтАЭ (переходные и частотные характеристики) и тАЬРасчёт областей устойчивоститАЭ.
3. СТРУКТУРНАЯ СХЕМА САУ
Структурная схема САУ составляется с учётом заданных передаточных функций элементов САУ и их параметров. Она изображается в виде связанных между собой звеньев, с указанием их передаточных функций, точек приложения задающих и возмущающих воздействий, элементов суммирования и управляемой величины на выходе (см., например, рис.3.1)
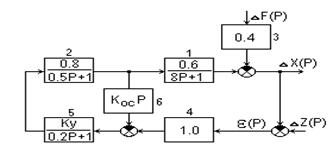
Рис.3.1. Пример структурной схемы САУ:
Dx(р) - изображение отклонения управляемой величины;
DZ(р)- изображение отклонения задающего воздействия;
DF(р) - изображение отклонения возмущающего воздействия.
De(p) - изображение ошибки воспроизведения задающего воздействия.
Звенья и соответствующие им передаточные функции нумеруются арабскими цифрами.
Если какой-либо параметр звена не задан и его значение предстоит выбрать в ходе работы, то в выражении передаточной функции звена он записывается в виде символа (например, Ку, Кос, и т.п.).
На основе правил эквивалентного преобразования структурная схема представляется в виде одного звена с эквивалентной передаточной функцией и с обязательным указанием рассматриваемого воздействия на входе и управляемой величины на выходе. Например, для схемы рис.3.1 возможны эквивалентные схемы, представленные на рис.3.2.
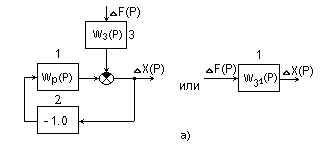
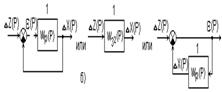
Рис 3.2. Варианты структурных схем, эквивалентных схеме рис.3.1
а - при входном воздействии DF(Р); б - при входном воздействии DZ(Р).
При этом следует иметь в виду, что для САУ, процессы в которых описываются линейными или линеаризованными (в отклонениях) дифференциальными уравнениями, справедлив принцип суперпозиции (наложения).
Поэтому при нахождении эквивалентной передаточной функции по какому-либо воздействию остальные воздействия могут считаться равными нулю.
Например, на рис.3.2,а принимается DZ(Р)=0, а на рис.3.2,б - DF(Р)=0. При этом в схеме рис.3.2,а звено с передаточной функцией - 1.0 отражает отрицательный знак главной обратной связи замкнутой САУ. Для структурных схем рис.3.2,а эквивалентные передаточные функции соответственно имеют вид:
DX(P) ВаВаВаВаВаВаВаВаВа W3(P)
Wз1(Р) =---------------- = --------------------- =
DF(P) ВаВаВаВаВаВаВаВаВа Ва1+Wp(P)
- 0.4 (0.8P3+(5.7+6.4KyKoc)P2+(8.7+0.8 KyKoc)P+1)
= ------------------------------------------------------------------------ ;(3.1)
0.8 P 3+(5.7+6.4 KyKoc)P2+(8.7+0.8 KyKoc)P+1+0.48Ку
DX(P) Ва ВаВаВаВаВаВаВаВа ВаWp(P)
Wз2(Р) =--------------- = --------------------- =
DZ(P) ВаВаВаВаВаВаВаВаВаВаВа Ва1+Wp(P)
0.48Ку
= ----------------------------------------------------------------------- ,(3.2)
0.8 P 3+(5.7+6.4 KyKoc)P2+(8.7+0.8 KyKoc)P+1+0.48Ку
Где ВаВаВаВаВаВаВаВаВаВаВа ВаDX(P) ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа W1(P) W2(P) W5(P) W4(P)
Wр(Р) =-------------- = ------------------------------------------------------------ =
DZ(P) ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1 + W2(P) W5(P) W6(P)
0.48Ку
= ---------------------------------------------------------------------------------- =
(8 P +1)[(0.5P+1)(0.2P+1)+0.8 KyKocР]
0.48Ку
= ------------------------------------------------------------------------- . (3.3)
0.8 P 3+(5.7+6.4 KyKoc)P2+(8.7+0.8 KyKoc)P+1
В выражении передаточной функции целесообразно выделить в явном виде характеристический оператор Д(Р) и операторный коэффициент Кр для передаточных функций (3.1), (3.2) и (3.3)
Дз(Р) = 0.8 P 3+(5.7+6.4 KyKoc)P2+(8.7+0.8 KyKoc)P+1+0.48Ку; (3.4)
Др(Р) = 0.8 P 3+(5.7+6.4 KyKoc)P2+(8.7+0.8 KyKoc)P+1; (3.5)
Кз1(Р) = - 0.4 (0.8 P 3+(5.7+6.4 KyKoc)P2+(8.7+0.8 KyKoc)P+1);
Кз2(Р)= Кр(Р) = 0.48Ку;
4. СТАТИЧЕСКАЯ ХАРАКТЕРИСТИКА
В большинстве заданий (см. Приложение) при оценке статических свойств САУ требуется обеспечить заданный коэффициент статизма по возмущающему воздействию, а также определить ошибку воспроизведения задающего воздействия.
Коэффициент статизма замкнутой САУ характеризует статическую ошибку, обусловленную влиянием возмущающего воздействия. Он численно равен статической ошибке (установившемуся отклонению) при возмущающем воздействии, равном одной относительной единице (в установившемся режиме). Значение его также равно значению коэффициента передачи замкнутой САУ по рассматриваемому возмущающему воздействию. Например, для схемы рис.3.1 с учётом (3.1)
- 0.4
Кс = Кз1 = lim Wз1(P) = --------------------------- (4.1)
PВо 0 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва1 + 0.48Ку
Физически это означает, что, например, при увеличении возмущающего воздействия на Df = 1.0, управляемая величина x изменяется в установившемся режиме на
- 0.4
Dx = Кс = -------------------------
1 + 0.48Ку
Знак минус указывает на то что величина x уменьшается по отношению к исходному значению x0.
Попутно следует заметить, что если бы в рассматриваемом случае отсутствовало управляющее устройство (регулятор) или САУ была разомкнутой (отсутствует главная обратная связь), то статическая ошибка и соответственно коэффициент статизма по возмущающему воздействию имели бы значение
Dx = Кс = - 0.4. При этом
x = x0 + Dx = 1.0 - 0.4 = 0.6.
Принято считать статизм положительным, если при увеличении возмущающего воздействия управляемая величина уменьшается. При этом знак минус в (4.1) обычно опускается, т.е. в рассматриваемом случае
0.4
Кс = ------------------------- (4.2)
1 + 0.48Ку
Если задан требуемый коэффициент статизма, то нетрудно определить коэффициент передачи регулятора, при котором он обеспечивается.
Например, из (4.2) следует
0.4 - Кс
Ку = ----------------------- (4.3)
0.48Кс
Найденное требуемое значение коэффициента передачи регулятора обычно округляется до ближайшего целого значения (чтобы легче было устанавливать) и определяется действительное значение коэффициента статизма.
По найденному значению коэффициента статизма легко может быть построена статическая (внешняя) характеристика САУ. Например, на рис.4.1, приведена статическая характеристика САУ, представленной на рис.3.1, при Ку = 20.
С целью сравнения дана также статическая характеристика объекта управления, что соответствует характеристике разомкнутой САУ.
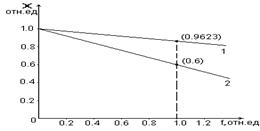
Рис.4.1. Статическая характеристика САУ по рис.3.1 при Ку=20 (линия 1) и объекта управления (линия2).
Для статических САУ коэффициент статизма по задающему воздействию, численно равный ошибке воспроизведения этого воздействия, зависит также от значения коэффициента передачи её по задающему воздействию. Так для САУ по рис.3.1 (см. также рис.3.2,б) с учётом (3.2)
1 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1
КтАЩc = = 1.0 - lim Wз2(P) = lim --------------------- = ------------------------
PВо0 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа PВо0 ВаВаВаВаВаВаВаВаВа 1+Wp(P)ВаВаВа 1 + 0.48Ку
При Ку = 20 КтАЩс = e = 0.094.
Это означает, что если при отсутствии возмущающего воздействия (например, холостой ход объекта управления) на вход рассматриваемой САУ подать задающее воздействие DZ = 1.0, то управляемая величина на выходе в установившемся режиме будет иметь значение
x = 1.0 - e = 1.0 - 0.094 = 0.906.
За счёт возмущающего воздействия Df это значение x ещё уменьшится на величину Кс Df.
Следует иметь в виду, что если замкнутая САУ имеет последовательно включенное интегрирующее звено, не охваченное жёсткой обратной связью, то она является астатической по задающему воздействию, т.е. безошибочно воспроизводит это воздействие (КтАЩс = e =0).
5. ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА
По переходной характеристике определяются динамические показатели качества управления (регулирования):
- время переходного процесса tп;
- перерегулирование g;
- колебательность G.
В реальных линейных САУ управляемая величина асимптотически приближается к установившемуся значению, т. е. теоретически tп = ¥. Поэтому, исходя из практических соображений, под временем переходного процесса понимают интервал времени, по истечении которого (от момента подачи воздействия) начинает выполняться условие
| Dx(t) - Dx | £ D,
где Dx(t) - текущее значение управляемой величины;
Dx - установившееся отклонение;
D - наперёд заданное значение допустимого отклонения управляемой величины от нового установившегося значения.
Часто принимают
D = 0.05Dx
Во время переходного процесса текущее значение отклонения управляемой величины может превышать установившееся отклонение. Разность между максимальным и установившимся отклонением, выраженная в процентах от установившегося отклонения, называется перерегулированием
|Dxмакс - Dx |
g = -------------------------------- 100%
| Dx |
Если переходная характеристика имеет колебательный характер, то оценивается так называемая колебательность.
Колебательность может быть определена отношением второго и первого максимумов переходной характеристики, выраженным в процентах
Dxмакс,2
ВаG =------------------------ 100%
Dxмакс,1
Незатухающие колебания при этом соответствуют колебательности 100%. Колебательность стремится к нулю при уменьшении до нуля второго максимума переходной характеристики.
В данной курсовой работе переходная характеристика может быть получена экспериментально путем математического моделирования САУ (программа тАЬCLASSICтАЭ). При этом имеется возможность легко настраивать САУ на заданные качественные показатели изменением параметров, значения которых не заданы и могут варьироваться (например, Кос на рис.3.1). В качестве примера на рис.5.1 приведен вариант структурной схемы САУ рис.3.1, реализованной на компьютере при входном воздействии Df, выходном - Dx, Ку = 20, Кос = 20.
При исследовании переходного процесса в САУ, обусловленного изменением задающего воздействия (уставки) на DZ(рис.3.1) тАЬвходтАЭ следует перенести на звено 4.
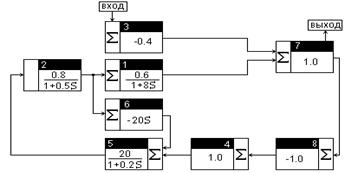
Рис.5.1. Вариант структурной схемы САУ рис.3.1.
Примечание. В программе тАЬCLASSICтАЭ оператор Лапласа обозначен S.
При исследовании переходной характеристики следует изменять параметры варьируемого звена САУ таким образом, чтобы характеристика по возможности имела монотонный характер без перерегулирования и колебательности. Если по каким-либо причинам этого достичь не удаётся, то можно считать допустимым
g £ 20 ¸ 25%; G £ 20%
На рис.5.2., 5.3. приведены переходные характеристики САУ рис.3.1 при Кос = 1.0; 10; 20 и Ку = 20 для воздействий Df и DZ соответственно.

Koc = 1.0
| Ваt,c | 0 | 2.06 | 4.1 | 6.2 | 8.2 | 10.3 | 11.33 | 14.42 | 20.6 | 23.69 | 34 |
| Dx | -0.4 | -0.35 | -0.23 | -0.09 | 0.013 | 0.072 | 0.083 | 0.057 | -0,06 | -0.08 | -0.02 |
Koc = 10
| Ваt,c | 0 | 4.7 | 7.8 | 10.9 | 14 | 20.2 | 26.4 | 29.5 | 35.7 | 42 | 45 |
| Dx | -0.4 | -0.37 | -0.33 | -0.29 | -0.25 | -0.16 | -0.09 | -0.07 | -0.04 | -0.02 | -0.02 |
Koc = 20
| Ваt,c | 0 | 4.6 | 9.13 | 15 | 20 | 25 | 29.6 | 38.7 | 47.8 | 59.2 | 68.3 |
| Dx | -0.4 | -0.38 | -0.36 | -0.3 | -0.26 | -0.23 | -0.19 | -0.14 | -0.10 | -0.07 | -0.06 |
Рис.5.2. Переходная характеристика САУ рис.3.1 при входном воздействии Df(t) = 1.0 и различных значениях Koc.
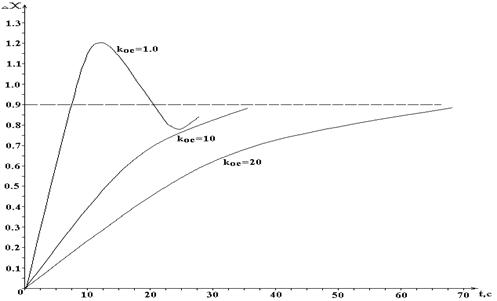
Koc = 1.0
| t,c | 0 | 2.25 | 4.5 | 6.2 | 9 | 10.1 | 11.3 | 11.8 | 13 | 14.6 | 18 |
| Dx | 0 | 0.154 | 0.49 | 0.77 | 1.1 | 1.17 | 1.21 | 1.21 | 1.19 | 1.13 | 0.95 |
Koc = 10
| Ваt,c | 0 | 4 | 6 | 8 | 10 | 11 | 14 | 16 | 18.5 | 20.5 | 24.5 |
| Dx | 0 | 0.05 | 0.1 | 0.16 | 0.23 | 0.28 | 0.38 | 0.45 | 0.54 | 0.6 | 0.7 |
Koc = 20
| Ваt,c | 0 | 4.4 | 10.3 | 14.7 | 19 | 23.5 | 29 | 38 | 45.5 | 48.4 | 57 |
| Dx | 0 | 0.3 | 0.13 | 0.22 | 0.31 | 0.4 | 0.51 | 0.64 | 0.71 | 0.74 | 0.8 |
Рис.5.3. Переходная характеристика САУ рис.3.1 при входном воздействии DZ = 1.0, Ку = 20 и различных значениях Koc.
При подаче воздействия Df(t) = 1.0 (например, включение номинальной нагрузки) управляемая величина x (например, напряжение) мгновенно изменяется на Dx = - 0.4, т. е. уменьшается. При этом x = xо + Dx = 1.0 - 0.4 = 0.6, т. е. при t = 0 и f = 1.0 управляемая величина имеет значение такое же, как при отсутствии управляющего устройства (см. рис.4.1). За счёт действия управляющего устройства (регулятора) после затухания переходного процесса отклонение управляемой величины приобретает значение Dx = - 0.0377.
При Кос = 1.0 переходный процесс имеет колебательный характер с большим перерегулированием. При Кос = 10 перерегулирование составляет
½-0.024 - (-0.0377)½
g = --------------------------------------------------- 100% = 36.3% ,
½-0.0377½
а время переходного процесса tп = 78с. При Кос = 20 перерегулирование отсутствует, но время переходного процесса увеличивается до tп = 120с (на рис.5.2 не показано).
При входном воздействии DZ(t) = 1.0 управляемая величина x = Dx (при xо = 0, Zо = 0 и f(t) = 0) стремится к значению x = 0.906. Причем, характер переходного процесса определяется значением Кос.
На основании анализа переходных характеристик рис.5.2 и 5.3 с целью исключения перерегулирования предварительно принимается Кос =20.
6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
Комплексную (амплитудно-фазовую) частотную характеристику (КЧХ, АФХ) W(jw) аналитически легко получить по соответствующей передаточной функции, если положить Р = jw.
Путём выделения в выражении КЧХ вещественной U(w) и мнимой V(w) частей, получаются соответственно вещественная (ВЧХ) и мнимая (МЧХ) частотные характеристики
U(w) = ReW(jw);
V(w) = ImW(jw).
Модуль А(w) и аргумент j(w) КЧХ определяют соответственно амплитудную (АЧХ) и фазовую (ФЧХ) частотные характеристики
U(w) = modW(jw);
V(w) = argW(jw).
Между всеми частотными характеристиками имеют место очевидные соотношения:
W(jw) = U(w) + jV(w) ;
W(jw) = А(w) e jj (w) ;
А(w) = ÖU2(w) + V2(w) ;
V(w)
j(w) = arctg -------------- ;
U(w)
U(w) = А(w)cosj(w);
V(w) = А(w)sinj(w).
Применительно к САУ рис.3.1 при входном воздействии Df(t) частотные характеристики приведены на рис.6.1 и 6.2.
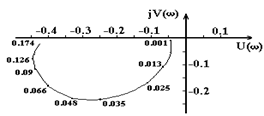 Ваа)
Ваа) 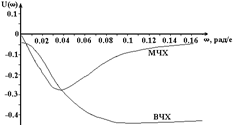 б)
б)
| U(w) | -0.03 | -0.04 | -0.06 | -0.08 | -0.11 | -0.17 | -0.25 | -0.33 | -0.4 | -0.44 | -0.44 |
| V(w) | -0.01 | -0.05 | -0.1 | -0.13 | -0.17 | -0.21 | -0.29 | -0.23 | -0.18 | -0.11 | -0.06 |
| w,рад/с | 0.001 | 0.005 | 0.01 | 0.013 | 0.018 | 0.025 | 0.035 | 0.48 | 0.066 | 0.09 | 0.13 |
Рис.6.1. Комплексная (а), вещественная (б) и мнимая (б) частотные характеристики САУ рис.3.1 при входном воздействии Df(t) и Ку = 20
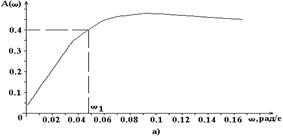
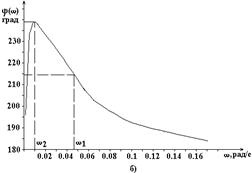
| w,рад/с | 0.001 | 0.005 | 0.01 | 0.013 | 0.018 | 0.025 | 0.035 | 0.048 | 0.066 | 0.09 | 0.13 |
| A(w) | 0.04 | 0.071 | 0.117 | 0.153 | 0.202 | 0.27 | 0.34 | 0.402 | 0.439 | 0.454 | 0.444 |
| j(w),град | 196 | 232 | 239 | 238 | 237 | 231 | 223 | 215 | 204 | 194 | 188 |
Рис.6.2. Амплитудная (а) и фазовая (б) частотные характеристики САУ рис.3.1 при входном воздействии Df(t) и Ку = 20, Кос = 20.
Из частотных характеристик следует, что при гармоническом характере возмущающего воздействия Df(t) влияние его на отклонение управляемой величины Dx(t) очень сильно возрастает с увеличением частоты. Например, при w1 = 0.047 рад/с и Df = 1.0sinw1t Dx(t) = 0.4sin(w1t + 2150), т. е. амплитуда колебаний Dxm = 0.4 имеет такое же значение, как и при отсутствии регулирования. Действительно, если в САУ рис.3.1 разорвать главную обратную связь, то будет
DX(P)
W(P) = ---------------- = - 0.4 ,
DF(P)
соответственно,
W(jw) = -0.4 и А(w) = 0.4.
При w > w1 влияние возмущающего воздействия сказывается ещё сильнее. Поэтому функционирование САУ рис.3.1 как системы регулирования будет эффективным только в том случае, если частота изменения возмущающего воздействия Df(t) будет достаточно малой (например, w1 < 0.01 рад/с). Из ФЧХ (рис.6.2,б) следует, что синусоидальные колебания величины на выходе Dx(t) опережают по фазе колебания Df(t) на угол больше 1800. Причем, при Ку = 20, Кос = 20 наибольший сдвиг фаз имеет место при w2 = 0.01 рад/с. Следует также отметить, что при w< w2 = 0.01 рад/с зависимость j(w) весьма рез
Вместе с этим смотрят:
GPS-навигация
GPS-прийомник авиационный
IP-телефония и видеосвязь
IP-телефония. Особенности цифровой офисной связи
Unix-подобные системы