Методи перетворення бiосигналiв та аналiз медико-бiологiчноi iнформацii

МЕТОДИ ПЕРЕТВОРЕННЯ БРЖОСИГНАЛРЖВ ТА АНАЛРЖЗ

МЕДИКО-БРЖОЛОГРЖЧНОРЗ РЖНФОРМАЦРЖРЗ


Сигнал тАУ процес змiни у часi фiзичного стану певного об'iкта, який можна зареiструвати, вiдобразити та передати.

Детермiнованi сигнали тАУ сигнали, значення яких у будь-який момент часу повнiстю вiдомi, тобто передбачуванi з iмовiрнiстю, що дорiвнюi одиницi.

Випадковi сигнали тАУ сигнали, значення яких у будь-який момент часу неможливо передбачити з iмовiрнiстю, що дорiвнюi одиницi.

Перiодичним називаiться будь-який сигнал, для якого виконуiться умова

,

де перiод Т i кiнцевим вiдрiзком, а k тАУ будь-яке цiле число.

Сигнали, що iснують в усi моменти часу, називають аналоговими.

Послiдовнiсть чисел, що подаi сигнал при цифровiй обробцi, називаiться дискретним сигналом. Числа, що складають послiдовнiсть, i значеннями сигналу в окремi (дискретнi) моменти часу й називаються вiдлiками. Переважно вiдлiки беруть через рiвнi промiжки часу Тд, що мають назву перiод дискретизацii (або крок дискретизацii). Величина, зворотна перiоду дискретизацii, називаiться частотою дискретизацii

,

вiдповiдна iй кругова частота

.

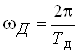Процес перетворення вiдлiкiв сигналу в числа називаiться квантуванням за рiвнем.

Сигнал, дискретний у часi та квантований за рiвнем, називають цифровим сигналом.

Динамiчним поданням називаiться спосiб подання сигналiв, при якому реальний сигнал приблизно подаiться сумою деяких елементарних сигналiв, що виникають у послiдовнi моменти часу. Якщо спрямувати до нуля тривалiсть окремих елементарних сигналiв, то границя суми дасть точне подання вихiдного сигналу.

Два сигнали u i v називають ортогональними, якщо iх скалярний добуток, а отже, i взаiмна енергiя дорiвнюють нулю:

.

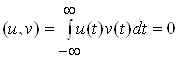Якщо в просторi сигналiв задана нескiнченна система ортогональних функцiй {a1, a2, тАж, an} з одиничними нормами

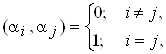
це означаi, що в просторi сигналiв заданий ортонормований базис.

Розкладання сигналу:

,

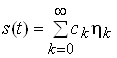де сk тАУ ВлпроекцiiВ» сигналу на координатнi вiсi, напрямок яких задаiться функцiями hk(t), називаiться узагальненим рядом Фур'i сигналу s(t) в обраному базисi.

Сукупнiсть коефiцiiнтiв ряду Фур'i {ck} тАУ спектр сигналу s(t).

Тригонометричний ряд Фур'i:

,

де t0 тАУ довiльна величина;

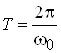ВатАУ перiод базисних функцiй;

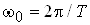ВатАУ кругова частота, що вiдповiдаi перiоду повторення сигналу Т; частоти, кратнi w0, що входять у формулу, називаються гармонiками;

;

;

.

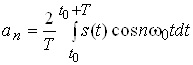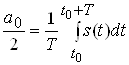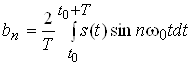Дiйсна форма тригонометричного ряду Фур'i:

,


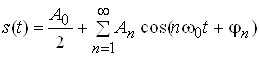де

;

;

.

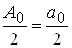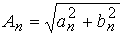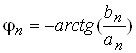Експоненцiйний ряд Фур'i:

; ,

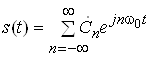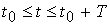де

.

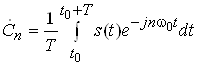Сукупнiсть амплiтуд гармонiк ряду Фур'i називають амплiтудним спектром.

Сукупнiсть фаз гармонiк ряду Фур'i називають фазовим спектром.

Коефiцiiнти ряду залежать тiльки вiд форми одиночного iмпульсу s(t) i характеризуються iнтегралом:

,

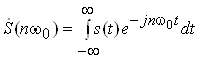який називаiться спектральна щiльнiсть одиночного iмпульсу s(t).

Перiодичне коливання маi дискретний або лiнiйчатий спектр.

Вiдношення перiоду послiдовностi прямокутних iмпульсiв до тривалостi iмпульсiв називають щiлиннiстю.

Амплiтудний спектр послiдовностi прямокутних iмпульсiв маi вигляд функцii 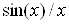, графiк якоi носить пелюстковий характер.

Важливою властивiстю спектра послiдовностi прямокутних iмпульсiв i те, що у ньому вiдсутнi (мають нульовi амплiтуди) гармонiки з номерами, кратними щiлинностi.

Вiдстань за частотою мiж сусiднiми гармонiками спектра перiодичного сигналу дорiвнюi частотi iмпульсiв 2p/Т.

Ширина пелюсток спектра послiдовностi прямокутних iмпульсiв, вимiряна в одиницях частоти, дорiвнюi 2p/t, тобто зворотно пропорцiйна тривалостi iмпульсiв.

Часове й частотне подання неперiодичного сигналу, що заданий на iнтервалi (-¥, ¥), складаi пару перетворень Фур'i:

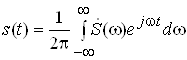ВатАУ зворотне перетворення Фур'i,

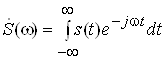ВатАУ пряме перетворення Фур'i.

Неперiодичнi сигнали мають безперервний (суцiльний) спектр.

Властивiсть спектра: чим коротше сигнал, тим ширше його спектр.

Добуток ефективних значень тривалостi сигналу й ширини його спектра називаiться базою сигналу.

Дуальнiсть перетворення Фур'i: якщо парнiй функцii часу f(t) вiдповiдаi спектральна функцiя g(w) (вона буде також парною), то функцii часу g(t) вiдповiдатиме спектральна функцiя 2pf(w).

Прямокутному iмпульсу вiдповiдаi спектральна функцiя, що маi вигляд sin(w)/w. Отже, спектральна функцiя сигналу sin(t)/t буде прямокутною.

Перетворення Фур'i i лiнiйним iнтегральним перетворенням, тобто спектр суми дорiвнюi сумi спектрiв або, математичною мовою, лiнiйна комбiнацiя сигналiв маi спектр у виглядi такоi самоi (з тими ж коефiцiiнтами) лiнiйноi комбiнацii iх спектральних функцiй.

При затримцi сигналу в часi амплiтудний спектр цього сигналу не змiнюiться, фазовий спектр здобуваi додатковий доданок, що лiнiйно залежить вiд частоти.

Змiна тривалостi сигналу приводить до змiни ширини спектра зворотним чином в поiднаннi зi збiльшенням (при розтяганнi, a<1) або зменшенням (при стиску, a>1) рiвня спектральних складових.

Спектр похiдноi отримують шляхом множення спектра вихiдного сигналу на jw. Отже, при диференцiюваннi низькi частоти послаблюються, а високi пiдсилюються. Фазовий спектр зсуваiться на 90В° для позитивних частот i на тАУ 90В° для негативних. Множник jw називають оператором диференцiювання сигналу в частотнiй зонi.

При iнтегруваннi вихiдного сигналу його спектр множиться на 1/(jw). Високi частоти послаблюються, а низькi пiдсилюються. Фазовий спектр сигналу зсуваiться на ‑90В° для позитивних частот i на 90В° для негативних. Множник 1/(jw) називають оператором iнтегрування в частотнiй зонi.

Спектр згортки сигналiв дорiвнюi добутку спектрiв.

Спектр добутку дорiвнюi згортцi спектрiв. РДдиною додатковою особливiстю i множник 1/(2p) перед iнтегралом згортки.

При множеннi сигналу на гармонiчну функцiю спектр ВлроздвоюiтьсяВ» тАУ розпадаiться на двi складовi вдвiчi меншого рiвня, зсунутих на w0 праворуч (w-w0) та лiворуч (w+w0) за вiссю частот. При кожному доданку i множник, що враховуi початкову фазу гармонiчного коливання.

Спектр дельта-функцii i константа, тобто i рiвномiрним у нескiнченнiй смузi частот.

Спектром константи i дельта-функцiя частоти.

Крок квантування:

,

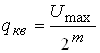де Umax тАУ максимальне значення аналогового сигналу на входi АЦП, що не викликаi переповнення арифметичного пристрою,

m тАУ кiлькiсть двiйкових розрядiв.

Теорема Котельникова: будь-який сигнал s(t), спектр якого не мiстить складових iз частотами вище wВ=2pfВ, може бути без втрат iнформацii поданий своiми дискретними вiдлiками {s(k)}, узятими з iнтервалом Т, що задовольняi наступнiй нерiвностi:

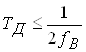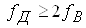Ва( або ).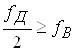

Частота Найквiста тАУ

.

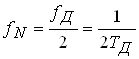Спектр дискретного сигналу i нескiнченним рядом зсунутих на величину частоти дискретизацii wд копiй спектра вихiдного безперервного сигналу s(t), тобто спектр дискретного сигналу перiодичний з перiодом, що дорiвнюi частотi дискретизацii.

сигнал аналоговий перетворення фур'i


Дискретне перетворення Фур'i (ДПФ):

,

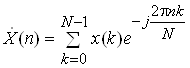де x(k) тАУ вiдлiки дискретного сигналу;

N тАУ кiлькiсть вiдлiкiв дискретного сигналу;

n тАУ номер коефiцiiнта ДПФ.

Перехiд вiд дискретного спектра до часових вiдлiкiв сигналу здiйснюiться за допомогою зворотного дискретного перетворення Фур'i (ЗДПФ):

.

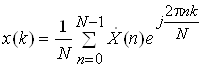ДПФ i лiнiйним перетворенням, тобто якщо послiдовностям {x(k)} i {y(k)} з перiодом N вiдповiдають набори гармонiк 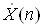Ваi 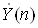, то послiдовностi {ax(k)+by(k)} вiдповiдатиме спектр .

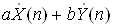Кiлькiсть рiзних коефiцiiнтiв ДПФ 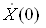, , 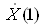, 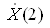тАж, 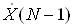Вадорiвнюi кiлькостi вiдлiкiв N за перiод; при n = N коефiцiiнт .

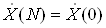Нульовий коефiцiiнт ДПФ 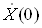Ва(постiйна складова) дорiвнюi сумi всiх вiдлiкiв сигналу.

Властивiсть симетричностi ДПФ: коефiцiiнти ДПФ, номери яких розташовуються симетрично вiдносно , утворюють спряженi пари.

Якщо кiлькiсть вiдлiкiв дискретного сигналу N не i простим числом i ii можна розкласти на множники, процес обчислень коефiцiiнтiв ДПФ можна прискорити, роздiливши набiр вiдлiкiв на частини, обчисливши iх ДПФ та об'iднавши результати. Такi способи обчислення ДПФ називаються швидким перетворенням Фур'i (ШПФ).

Залежно вiд способу розподiлу послiдовностi вiдлiкiв на частини при реалiзацii ШПФ можливо кiлька варiантiв органiзацii обчислень: прорiджування за часом; прорiджування за частотою. Можливi рiзнi варiанти також залежно вiд того, на скiльки фрагментiв розбивають послiдовностi на кожному кроцi (основа ШПФ).

Вибiр кiнцевого iнтервалу тривалiстю n секунд (Т тАУ iнтервал дискретизацii, n тАУ кiлькiсть вiдлiкiв) для заданого сигналу визначаi таку особливiсть спектрального розкладання: крiм основних спектральних складових з'являються ВлфальшивiВ» тАУ ВлрозмиванняВ» спектра. Причина ВлрозмиванняВ» спектра тАУ наявнiсть розривiв на межах iнтервалу спостережуваного сигналу i його перiодичного продовження.

Вiкна тАУ це ваговi функцii, що використовують для зменшення розмивання спектральних компонентiв, обумовленого скiнченнiстю iнтервалу спостереження.

Аналоговi фiльтри обробляють сигнали x(t), якi i безперервною величиною.

Цифровi фiльтри перетворюють вiдлiковi значення сигналу x(n) у дискретнi моменти часу n, де Т тАУ iнтервал дискретизацii.

Реакцiя системи на подану на вхiд дельта-функцiю називаiться iмпульсною характеристикою системи й позначаiться h(t).

Вихiдний сигнал лiнiйноi системи з постiйними параметрами дорiвнюi згортцi вхiдного сигналу й iмпульсноi характеристики системи:

.

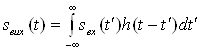Перехiдною характеристикою називають реакцiю системи на подану на вхiд функцiю одиничного стрибка. Позначаiться перехiдна характеристика як g(t).

У частотнiй зонi проходження сигналу через лiнiйну систему маi вигляд:

,

де 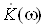ВатАУ перетворення Фур'i iмпульсноi характеристики системи

()

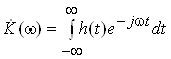Ця функцiя називаiться комплексним коефiцiiнтом передачi системи, а ii модуль i фаза тАУ амплiтудно-частотною (АЧХ) i фазочастотною (ФЧХ) характеристиками системи.

Фiльтри нижнiх частот (ФНЧ) пропускають частоти, меншi деякоi частоти зрiзу w0.

Фiльтри верхнiх частот (ФВЧ) пропускають частоти, бiльшi деякоi частоти зрiзу w0.

Смуговi фiльтри (i) пропускають частоти в деякому дiапазонi w1тАжw2 (вони можуть також характеризуватися середньою частотою w0=(w1+w2)/2 i шириною смуги пропускання Dw=w2-w1).

Режекторнi фiльтри (фiльтр-пробка) пропускають на вихiд всi частоти, крiм частот з деякого дiапазону w1тАжw2 (вони можуть також характеризуватися середньою частотою

w0=(w1+w2)/2

i шириною смуги затримування

Dw=w2-w1).

Дискретний фiльтр тАУ це довiльна система обробки дискретного сигналу, що маi властивостi лiнiйностi та стацiонарностi.

У загальному виглядi цифровий фiльтр пiдсумовуi (з ваговими коефiцiiнтами) деяку кiлькiсть вхiдних вiдлiкiв i деяку кiлькiсть вихiдних вiдлiкiв. Дана формула називаiться алгоритмом цифровоi фiльтрацii:

,

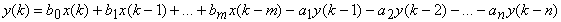де aj i bi тАУ дiйснi коефiцiiнти.

Якщо по-iншому згрупувати доданки, одержимо форму запису, що називаiться рiзницевим рiвнянням:

.

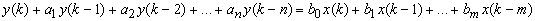Сутнiсть z-перетворення полягаi в тому, що послiдовностi чисел {x(k)} ставиться у вiдповiднiсть функцiя комплексноi змiнноi z, яка визначаiться так:

.

Зв'язок z-перетворення X(z) з перетворенням Фур'i :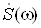

,

.


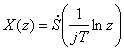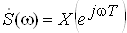Z-перетворення i лiнiйною комбiнацiiю вiдлiкiв, тому воно пiдлягаi принципу суперпозицii: якщо

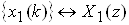Вай

,

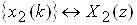то

.

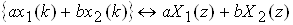Якщо z-перетворення послiдовностi {x(k)} дорiвнюi X(z), то z-перетворення послiдовностi, затриманоi на k0 тактiв

(y(k)=x(k-k0)),

матиме вигляд

,

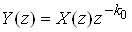тобто при затримцi послiдовностi на k0 тактiв необхiдно помножити ii z-перетворення на 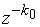(оператор затримки дискретноi послiдовностi на k0 тактiв).

Згортцi дискретних послiдовностей вiдповiдаi добуток iх z-перетворень.

Вихiдна реакцiя на одиничний iмпульс x0(k) називаiться iмпульсною характеристикою дискретноi системи й позначаiться h(k).

Вихiдний сигнал i лiнiйною комбiнацiiю iмпульсних характеристик, що випливаi з лiнiйностi та стацiонарностi розглянутоi системи. Цей вираз називаiться дискретною згорткою:

.

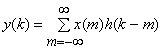Для системи, що фiзично реалiзуiться, формула дискретноi згортки маi вигляд:

.

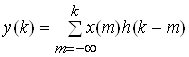Функцiя H(z), що дорiвнюi вiдношенню z‑перетворень вихiдного та вхiдного сигналiв i i z‑перетворенням iмпульсноi характеристики системи, називаiться функцiiю передачi або системною функцiiю дискретноi системи:

.

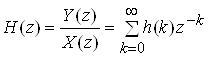Щоб одержати комплексний коефiцiiнт передачi (частотну характеристику) дискретноi системи, скористаiмося формулою, що описуi зв'язок z‑перетворення й перетворення Фур'i:

.

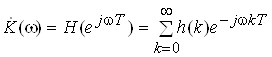Частотна характеристика дискретноi системи i перiодичною функцiiю частоти з перiодом, що дорiвнюi частотi дискретизацii.

Функцiя K(jw) i перетворенням Фур'i iмпульсноi характеристики ЦФ.

Модуль комплексноi частотноi характеристики A(w)=|K(jw)| називаiться амплiтудно-частотною характеристикою фiльтра (АЧХ).

Аргумент комплексноi частотноi характеристики j(w)=arg[K(jw)] називаiться фазо-частотною характеристикою фiльтра (ФЧХ).

Цифровi фiльтри, якi при обчисленнях не використовують попереднi вiдлiки вихiдного сигналу, називаються нерекурсивними (трансверсальнi фiльтри) (НЦФ):

.

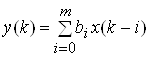Кiлькiсть попереднiх вiдлiкiв m, що використовуються у розрахунках, називаiться порядком фiльтра.

Цифровi фiльтри, якi при обчисленнях використовують попереднi вiдлiки вихiдного сигналу, називаються рекурсивними (РЦФ):

.

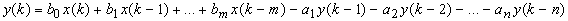Кiлькiсть попереднiх вхiдних та вихiдних вiдлiкiв, що використовуються для обчислень, може не збiгатися. У такому випадку порядком фiльтра вважаiться максимальне iз чисел m i n.

Рекурсiя тАУ математичний прийом, що становить циклiчне звертання до даних, якi отриманi на попереднiх етапах.

Характеристики випадкових сигналiв i статистичними.

РЖмовiрнiсть подii оцiнюють частотою сприятливих результатiв.

Якщо проведено N незалежних випробувань, причому в n iз них спостерiгалася подiя А, то емпiрична (вибiркова) оцiнка ймовiрностi Р(А):

.

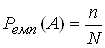Функцiя розподiлу випадковоi величини дорiвнюi ймовiрностi того, що випадкове число з Х прийме значення, рiвне або менше певного х:

;

;

; ,

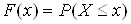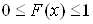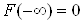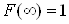де Х тАУ випадкова величина, тобто сукупнiсть дiйсних чисел х, що приймають випадковi значення.

Щiльнiсть iмовiрностi випадковоi величини тАУ iмовiрнiсть влучення випадковоi величини Х у пiвiнтервал (х, х + dx], тобто похiдна вiд функцii розподiлу:

;

;

; .

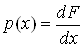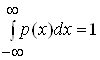Математичне очiкування (момент першого порядку) i теоретичною оцiнкою середнього значення випадковоi величини:

.

Дисперсiя (центральний момент):

.

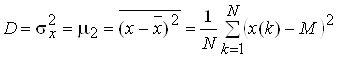Середньоквадратичне вiдхилення, необхiдне для кiлькiсного опису мiри розкиду результатiв окремих випадкових випробувань щодо математичного очiкування:

.

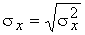Випадковий процес X(t) тАУ функцiя, що характеризуiться тим, що в будь-який момент часу t прийнятi нею значення i випадковими величинами.

Фiксуючи на певному промiжку часу миттiвi значення випадкового сигналу, одержуiмо реалiзацiю випадкового процесу.

Випадковий процес i нескiнченною сукупнiстю реалiзацiй, що утворюють статистичний ансамбль.

Випадковi процеси, статистичнi характеристики яких однаковi у всiх часових перетинах, називають стацiонарними випадковими процесами.

Стацiонарний випадковий процес називаiться ергодичним, якщо при визначеннi будь-яких його статистичних характеристик усереднення за ансамблем реалiзацiй еквiвалентно усередненню за часом однiii, теоретично довгоi, реалiзацii.

Кореляцiйний аналiз полягаi у кiлькiсному вимiрi ступеня подiбностi рiзних сигналiв.

Автокореляцiна функцiя (АКФ) дозволяi судити про ступiнь зв'язку (кореляцii) сигналу s(t) з його зсунутою за часом копiiю:

,

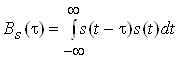де t тАУ величина часового зсуву сигналу.

Взаiмна кореляцiйна функцiя (ВКФ) дозволяi оцiнити ступiнь подiбностi двох сигналiв s1(t) i s2(t):


.

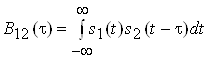ВКФ зв'язана перетворенням Фур'i iз взаiмним спектром сигналiв. Взаiмний спектр 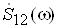Вадля сигналiв тАУ це s1(t) i s2(t) i добутком iх спектральних функцiй, одна з яких пiддана комплексному спряженню: 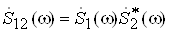. Якщо спектри сигналiв не перекриваються, то iх взаiмний спектр дорiвнюi нулю на всiх частотах, отже, дорiвнюi нулю i iх ВКФ при будь-яких часових зсувах t. Отже, сигнали зi спектрами, що не перекриваються, i некорельованими.

АКФ сигналу зв'язана перетворенням Фур'i iз квадратом модуля спектральноi функцii, або з енергетичним спектром сигналу.

Коварiацiйна функцiя тАУ це статистично усереднений добуток значень випадковоi функцii X(t) у моменти часу t1 i t2:

.

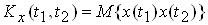Кореляцiйна функцiя i статистично усередненим добутком значень центрованоi випадковоi функцii X(t)-mx(t) у моменти часу t1 i t2:

.

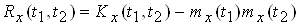Мiрою лiнiйного статистичного зв'язку мiж випадковими величинами i коефiцiiнт кореляцii:

,


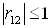, граничнi значення В±1 досягаються, якщо реалiзацii випадкових величин жорстко зв'язанi лiнiйним спiввiдношенням x2=ax1+b, де a i b тАУ деякi константи. Знак коефiцiiнта кореляцii збiгаiться зi знаком множника a. Рiвнiсть коефiцiiнта кореляцii нулю свiдчить про вiдсутнiсть лiнiйного статистичного зв'язку мiж випадковими величинами (тобто вони некорельованi).

Для стацiонарного випадкового процесу кореляцiйна функцiя залежить не вiд самих моментiв часу, а тiльки вiд iнтервалу мiж ними t=t2-t1:

.

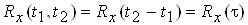Абсолютнi значення кореляцiйноi функцii при будь-яких t не перевищують ii значення при t=0 (це значення дорiвнюi дисперсii випадкового процесу):

.

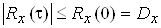Використовують коефiцiiнт кореляцii (його також називають нормованою кореляцiйною функцiiю):

;

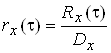rx(0) =1, |rx(t)|£1 i rx(-t)=rx(t).

Функцii Rx(t) i rx(t) характеризують зв'язок (кореляцiю) мiж значеннями X(t), роздiленими промiжком t. Чим повiльнiше убувають цi функцii з ростом абсолютного значення t, тим бiльше промiжок, протягом якого спостерiгаiться статистичний зв'язок мiж миттiвими значеннями випадкового процесу, i тим повiльнiше, плавнiше змiнюються в часi його реалiзацii. Усереднена спектральна щiльнiсть випадкового процесу i спектром його детермiнованоi складовоi (математичного очiкування). Для центрованих випадкових процесiв:

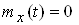Вата .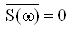

Усереднене значення спектральноi щiльностi не несе нiякоi iнформацii про флуктуацiйну, тобто випадкову, складову випадкового процесу.

Обчислення спектра випадкового процесу виконуiться на основi його кореляцiйноi функцii за допомогою теореми Вiнера-Хiнчина тАУ кореляцiйна функцiя випадкового процесу i його спектральна щiльнiсть потужностi зв'язанi перетворенням Фур'i:

,

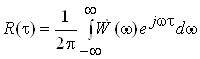де

тАУ спектральна щiльнiсть середньоi потужностi реалiзацii (Влспектральна щiльнiсть потужностiВ» або Влспектр потужностiВ»);

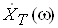ВатАУ спектральна щiльнiсть реалiзацii на iнтервалi часу Т, обчислена за допомогою прямого перетворення Фур'i.

Дискретний аналог теореми Вiнера-Хiнчина тАУ спектр дискретного випадкового процесу i перетворенням Фур'i вiд його кореляцiйноi функцii:

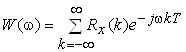
Вместе с этим смотрят: