Теория вероятности

Теория вероятностей возникла в середине XVII в. в связи с задачами расчета шансов выигрыша игроков в азартных играх. Страстный игрок в кости француз де Мере, стараясь разбогатеть, придумывал новые правила игры. Он предлагал бросать кость четыре раза подряд и держал пари, что при этом хотя бы один раз выпадет шестерка (6 очков). Для большей уверенности в выигрыше де Мере обратился к своему знакомому, французскому математику Паскалю, с просьбой рассчитать вероятность выигрыша в этой игре. Приведем рассуждения Паскаля. Игральная кость представляет собой правильный кубик, на шести гранях которого нанесены цифры 1, 2, 3, 4, 5 и 6 (число очков). При бросании кости "наудачу" выпадение какого-либо числа очков является случайным событием; оно зависит от многих неучитываемых воздействий: начальные положения и начальные скорости различных участков кости, движение воздуха на ее пути, те или иные шероховатости в месте падения, возникающие при ударе о поверхность упругие силы и т. д. Так как эти воздействия имеют хаотичный характер, то в силу соображений симметрии нет оснований отдавать предпочтение выпадению одного числа очков перед другим (если, конечно, нет неправильностей в самой кости или какой-то исключительной ловкости бросающего).

Поэтому при бросании кости имеется шесть исключающих друг друга равновозможных случаев, и вероятность выпадения данного числа очков следует принять равной 1/6 (или100/6 %). При двукратном бросании кости результат первого бросания - выпадение определенного числа очков - не окажет никакого влияния на результат второго бросания, следовательно, всех равновозможных случаев будет 6 В· 6 = 36. Из этих 36 равновозможных случаев в 11 случаях шестерка появится хотя бы один раз и в 5 В· 5 = 25 случаях шестерка не выпадет ни разу.

Шансы на появление шестерки хотя бы один раз будут равны 11 из 36, другими словами, вероятность события А, состоящего в том, что при двукратном бросании кости появится хотя бы один раз шестерка, равна11/100 , т. е. равна отношению числа случаев благоприятствующих событию А к числу всех равновозможных случаев. Вероятность того, что шестерка не появится ни разу, т. е. вероятность события 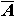, называемого противоположным событию A, равна25/36 . При трехкратном бросании кости число всех равновозможных случаев будет 36 В· 6 = 63, при четырехкратном 63 В· 6 = 64. При трехкратном бросании кости число случаев, в которых шестерка не появится ни разу, равно 25 В· 5 = 53, при четырехкратном 53 В· 5 = 54. Поэтому вероятность события, состоящего в том, что при четырехкратном бросании ни разу не выпадет шестерка, равна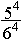, а вероятность противоположного события, т. е. вероятность появления шестерки хотя бы один раз, или вероятность выигрыша де Мере, равна .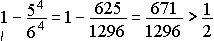

Таким образом, у де Мере было больше шансов выиграть, чем проиграть.

Рассуждения Паскаля и все его вычисления основаны на классическом определении понятия вероятности как отношения числа благоприятствующих случаев к числу всех равновозможных случаев.

Важно отметить, что произведенные выше расчеты и само понятие вероятности как числовой характеристики случайного события относились к явлениям массового характера. Утверждение, что вероятность выпадения шестерки при бросании игральной кости равна 1/6, имеет следующий объективный смысл: при большом количестве бросаний доля числа выпадений шестерки будет в среднем равна 1\6; так, при 600 бросаниях шестерка может появиться 93, или 98, или 105 и т. д. раз, однако при большом числе серий по 600 бросаний среднее число появлений шестерки в серии из 600 бросаний будет весьма близко к 100.

Отношение числа появлений события к числу испытаний называется частостью события. Для однородных массовых явлений частости событий ведут себя устойчиво, т. е. мало колеблются около средних величин, которые и принимаются за вероятности этих событий (статистическое определение понятия вероятности).

В XVII-XVIII вв. теория вероятностей развивалась незначительно, так как область ее применения, ввиду низкого уровня естествознания ограничивалась небольшим кругом вопросов (страхование, азартные игры, демография). В XIX в. и до настоящего времени, в связи с запросами практики, теория вероятностей непрерывно и быстро развивается, находя применения все в более разнообразных областях науки, техники, экономики (теория ошибок наблюдений, теория стрельбы, статистика, молекулярная и атомная физика, химия, метеорология, вопросы планирования, статистический контроль в производстве и т. д.)

Теория вероятностей является разделом математики, изучающим закономерности случайных массовых событий устойчивой частости.

Основное положение теории

Теория вероятности тАУ это наука, занимающаяся изучением закономерностей массовых случайных явлений. Такие же закономерности, только в более узкой предметной области социальноэкономических явлений, изучает статистика. Между этими науками имеется общность методологии и высокая степень взаимосвязи. Практически любые выводы сделанные статистикой рассматриваются как вероятностные.

Особенно наглядно вероятностный характер статистических исследований проявляется в выборочном методе, поскольку любой вывод сделанный по результатам выборки оценивается с заданной вероятностью.

С развитием рынка постепенно сращивается вероятность и статистика, особенно наглядно это проявляется в управлении рисками, товарными запасами, портфелем ценных бумаг и т.п. За рубежом теория вероятности и математическая статистика применятся очень широко. В нашей стране пока широко применяется в управлении качеством продукции, поэтому распространение и внедрение в практику методов теории вероятности актуальная задача.

Как уже говорилось, понятие вероятности события определяется для массовых явлений или, точнее, для однородных массовых операций. Однородная массовая операция состоит из многократного повторения подобных между собой единичных операций, или, как говорят, испытаний. Каждое отдельное испытание заключается в том, что создается определенный комплекс условий, существенных для данной массовой операции. В принципе должно быть возможным воспроизводить эту совокупность условий неограниченное число раз.

Пример1. При бросании игральной кости "наудачу" существенным условием является только то, что кость бросается на стол, а все остальные обстоятельства (начальная скорость, давление и температура воздуха, окраска стола и т. д.) в расчет не принимаются.

Пример 2. Стрелок многократно стреляет в определенную мишень с данного расстояния из положения "стоя"; каждый отдельный выстрел является испытанием в массовой операции стрельбы в данных условиях. Если же стрелку разрешено при разных выстрелах менять положение ("стоя", "лежа", "с колена"), то предыдущие условия существенно изменяются и следует говорить о массовой операции стрельбы с данного расстояния.

Возможные результаты единичной операции, или испытания S, называются случайными событиями. Случайное событие - это такое событие, которое может произойти, а может и не произойти при испытании S. Вместо "произойти" говорят также "наступить", "появиться", "иметь место".

Так, при бросании игральной кости случайными событиями являются: выпадение данного числа очков, выпадение нечетного числа очков, выпадение числа очков, не большего трех, и т. п.

При стрельбе случайным событием является попадание в цель (стрелок может как попасть в цель, так и промахнуться), противоположным ему случайным событием является промах. Из этого примера хорошо видно, что понятие случайного события в теории вероятностей не следует понимать в житейском смысле: "это чистая случайность", так как для хорошего стрелка попадание в цель будет скорее правилом, а не случайностью, понимаемой в обыденном смысле.

Пусть при некотором числе n испытаний событие A наступило m раз, т. е. m результатов единичной операции оказались "удачными", в том смысле, что интересующее нас событие A осуществилось, и n-m результатов оказались "неудачными" - событие A не произошло.

Вероятностью события A, или вероятностью ВлудачногоВ» исхода единичной операции, называется среднее значение частости, т. е. среднее значение отношения числа ВлудачныхВ» исходов к числу всех проведенных единичных операций (испытаний).

Само собой разумеется, что если вероятность события равна , то при n испытаниях событие A может наступить и более чем m раз, и менее чем m раз; оно лишь в среднем наступает m раз, и в большинстве серий по n испытаний число появлений события A будет близко к m, в особенности если n тАФ большое число.

Таким образом, вероятность P(A) есть некоторое постоянное число, заключенное между нулем и единицей:

0 РИ P(A) РИ 1

Иногда ее выражают в процентах: Р(А)

100% есть средний процент числа появлений события A. Конечно, следует помнить, что речь идет о некоторой массовой операции, т. е. условия S производства испытаний тАФ определенные; если их существенно изменить, то может измениться вероятность события A: то будет вероятность события A в другой массовой операции, с другими условиями испытаний. В дальнейшем будем считать, не оговаривая это каждый раз, что речь идет об определенной массовой операции; если же условия, при которых осуществляются испытания, меняются, то это будет специально отмечаться.

Два события A и B называются равносильными, если при каждом испытании они либо оба наступают, либо оба не наступают.

В этом случае пишут

A = B

и не делают различия между этими событиями. Вероятности равно- сильных событии A = B, очевидно, одинаковы:

P(A) = P(B)

Обратное утверждение, конечно, неверно: из того, что P(A) = P(B), отнюдь не следует, что A = B.

Событие, которое обязательно наступает при каждом испытании, называется достоверным.

Условимся обозначать его буквой D.

Для достоверного события число его наступлений m равно числу испытаний n, поэтому частость его всегда равна единице, т. е. вероятность достоверного события следует принять равной единице:

P(D) = 1

Событие, которое заведомо не может произойти, называется невозможным.

Условимся обозначать его буквой H.

Для невозможного события m = 0, следовательно, частость его всегда равна нулю, т. е. вероятность невозможного события следует считать равной нулю:

P(H) = 0

Чем больше вероятность события, тем чаще оно наступает, и наоборот, чем меньше вероятность события, тем реже оно наступает. Когда вероятность события близка к единице или равна единице, то оно наступает почти при всех испытаниях. О таком событии говорят, что оно практически достоверно, т. е. что можно наверняка рассчитывать на его наступление.

Наоборот, когда вероятность равна нулю или очень мала, то событие наступает крайне редко; о таком событии говорят, что оно практически невозможно.

На сколько мала должна быть вероятность события, чтобы практически можно было считать его невозможным? Общего ответа здесь дать нельзя, так как все зависит от того, насколько важно это событие.

Например.Если, например, вероятность того, что электрическая лампочка окажется испорченной, равна 0, 01, то с этим можно примириться. Но если 0, 01 есть вероятность того, что в банке консервов образуется сильный яд ботулин, то с этим примириться нельзя, так как примерно и одном случае из ста будет происходить отравление людей и человеческие жизни окажутся под угрозой.

Основные категории теории вероятности.

Как и всякая наука, теория вероятности и математическая статистика оперируют рядом основных категорий:

События;

Вероятность;

Случайность;

Распределение вероятностей и т.д.

События тАУ называется произвольное множество некоторого множества всех возможных исходов, могут быть:

Достоверные;

Невозможные;

Случайные.

Достоверным называется событие, которое заведомо произойдет при соблюдении определенных условий.

Невозможным называется событие, которое заведомо не произойдет при соблюдении определенных условий.

Случайным называют события, которые могут произойти либо не произойти при соблюдении определенных условий.

События называют единственновозможными, если наступление одного из них это событие достоверное.

События называют равновозможными, если ни одно из них не является более возможным, чем другие.

События называют несовместимыми, если появление одного из них исключает возможность появления другого в том же испытании.

Классическое и статистическое определение вероятности.

Вероятность тАУ численная характеристика реальности появления того или иного события.

Классическое определение вероятности: если множество возможных исходов конечное число, то вероятностью события Е считается отношение числа исходов благоприятствующих этому событию к общему числу единственновозможных равновозможных исходов.

Множество возможных исходов в теории вероятности называется пространством элементарных событий.

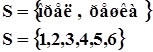
Пространство элементарных событий всегда можно описать числом nS=2, nS=6.

Если обозначить число исходов благоприятствующих событию n(E), то вероятность события Е будет выглядеть 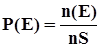. Для наших примеров .

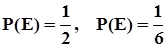Исходя из классического определения вероятности, можно вывести ее основные свойства:

Вероятность достоверного события равна 1.

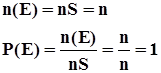
Вероятность невозможного события равна 0.

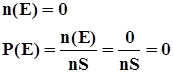
Вероятность случайного события находится в пределах от 0 до 1.

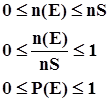
Классическое определение вероятности связано с непосредственным подсчетом вероятности, требует точного знания числа всех возможных исходов, и удобно для расчета вероятности достаточно простых событий.

Расчет вероятности более сложных событий - это сложная задача, требующая определения чисел всех возможных комбинаций появления этих событий. Подобными расчетами занимается специальная наука тАУ комбинаторика. Поэтому на практике часто используется статистическое определение вероятности.

Доказано, что при многократном повторении опыта частости довольно устойчивы и колеблятся около некоторого постоянного числа, представляющего собой вероятность события.

Таким образом, в условиях массовых испытаний распределение частостей превращается в распределение вероятности случайной перемены.

Достоинство статистического определения вероятности в том, что для ее расчета не обязательно знать конечное число исходов.

Если классическое определение вероятности осуществляется априори (до опыта), то статистическое апосториори (после опыта по результатам).

Распределение частостей дискретного ряда, выраженных конечными числами, называется дискретным распределением вероятности.

Если осуществляются исследования массовых событий частостей, которые распределяются непрерывно и могут быть выражены какой-либо функцией, называются непрерывным распределением вероятности.

На графике такое распределение отражается непрерывной плавной линией, а площадь ограниченная этой линией и осью абсцисс всегда равна 1.

Заключение

Таким образом, рассмотрев теорию вероятности, ее историю и положения и возможности, можно утверждать, что возникновение данной теории не было случайным явлением вы науке, а было вызвано необходимостью дальнейшего развития технологии и кибернетики, поскольку существующее программное управление не может помочь человеку в создании таких кибернетических машин, которые, подобно человеку, будут мыслить самостоятельно.

И именно теория вероятности может способствовать появлению искусственного разума.

ВлПроцессы управления , где бы они ни протекали тАУ живых организмах, машинах или обществе, - происходят по одним и тем же законамВ», - провозгласила кибернетика. А значит, и те, пусть еще не познанные до конца, процессы, что протекают в голове человека и позволяют ему гибко приспосабливаться к изменяющейся обстановке, можно воспроизвести искусственно в сложных автоматических устройствах.

Где же пределы, которых могут достичь кибернетические машины?

1.Г.И. Мишкевич ВлДоктор занимательных наукВ»

2.Е.П. Бударина ВлТеория вероятности и математическая статистикаВ»

3.И.В. Волков Вл Высшая математикаВ»

4. Гнеденко Б. В. и Хинчин А. Я., ВлЭлементарное введение в теорию вероятностейВ»

Для подготовки данной работы были использованы материалы с сайта http://referat.ru/

Вместе с этим смотрят:

Актуальные проблемы квантовой механики

Волоконно-оптические датчики температуры на основе решеток показателя преломления

Время и пространство - идеалистические понятия

Единое поле силового пространственного взаимодействия материальных тел

Интересные обьекты Вселенной