п.1. Аксиоматическая система натуральных чисел.
Определение. Системой натуральных чисел (системой Пеано) называется алгебра ![]() , где
, где ![]() - бинарные операции,
- бинарные операции, ![]() - унарная операция (функция ВлследованияВ»),
- унарная операция (функция ВлследованияВ»), ![]() - выделенный элемент в множестве
- выделенный элемент в множестве ![]() , для которой выполнены следующие аксиомы:
, для которой выполнены следующие аксиомы:
Для ![]() ,
, ![]() Ва(элемент
Ва(элемент ![]() Ваназывается следующим за
Ваназывается следующим за ![]() ).
).
Для ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Для ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Для ![]() ,
, ![]() .
.
Аксиома индукции: Пусть ![]() . Если множество
. Если множество ![]() Ваудовлетворяет условиям:
Ваудовлетворяет условиям:
а) ![]() ;
;
б) для ![]() ,
, ![]() ;
;
то ![]() .
.
Система аксиом Пеано обладает тем свойством, что ни одна из аксиом системы не является следствием других аксиом.
Из системы аксиом Пеано можно вывести все известные нам свойства натуральных чисел.
п.2. Теоремы математической индукции.
Теорема 1. (принцип полной математической индукции). Пусть ![]() - одноместный предикат на
- одноместный предикат на ![]() , который удовлетворяет условиям:
, который удовлетворяет условиям:
![]() - истина.
- истина.
![]() Ва(
Ва(![]() - истина Во
- истина Во ![]() - истина).
- истина).
Тогда предикат ![]() Ватождественно истинен на
Ватождественно истинен на ![]() .
.
Доказательство. Обозначим через ![]() Вамножество всех тех
Вамножество всех тех ![]() , для которых
, для которых ![]() Ваистина. Проверим, что
Ваистина. Проверим, что ![]() Ваудовлетворяет условиям аксиомы индукции.
Ваудовлетворяет условиям аксиомы индукции.
Т.к. ![]() - истина, то
- истина, то ![]() .
.
Если ![]() , то
, то ![]() - истина и по второму условию теоремы индукции
- истина и по второму условию теоремы индукции ![]() - истина. Поэтому
- истина. Поэтому ![]() .
.
Множество ![]() Ваудовлетворяет условиям аксиомы индукции. Поэтому
Ваудовлетворяет условиям аксиомы индукции. Поэтому ![]() .
.
Обозначение. Множество целых чисел ![]() Васостоит из натуральных чисел, нуля и чисел противоположных натуральным.
Васостоит из натуральных чисел, нуля и чисел противоположных натуральным.
Для ![]() Ваобозначим
Ваобозначим ![]() .
.
Теорема 2. (обобщение принципа полной математической индукции). Пусть ![]() - одноместный предикат на
- одноместный предикат на ![]() , где
, где ![]() , который удовлетворяет условиям:
, который удовлетворяет условиям:
![]() - истина.
- истина.
![]() Ва(
Ва(![]() - истина Во
- истина Во![]() - истина).
- истина).
Тогда предикат ![]() Ватождественно истинен на
Ватождественно истинен на ![]() .
.
Теорема 3. (сильная форма принципа полной математической индукции). Пусть ![]() - одноместный предикат на
- одноместный предикат на ![]() , который удовлетворяет условиям:
, который удовлетворяет условиям:
![]() - истина.
- истина.
![]() Ва(
Ва(![]() - истиныВо
- истиныВо ![]() - истина).
- истина).
Тогда предикат ![]() Ватождественно истинен на
Ватождественно истинен на ![]() .
.
Теорема 4. (обобщение сильной формы принципа полной математической индукции). Пусть ![]() - одноместный предикат на
- одноместный предикат на ![]() , где
, где ![]() , который удовлетворяет условиям:
, который удовлетворяет условиям:
![]() - истина.
- истина.
![]() Ва(
Ва(![]() - истины Во
- истины Во ![]() - истина).
- истина).
Тогда предикат ![]() Ватождественно истинен на
Ватождественно истинен на ![]() .
.
Определение. Числа Фибоначчи ![]() , для
, для ![]() , определяются рекуррентно
, определяются рекуррентно
(1) ![]() ,
, ![]() ;
;
![]() Вадля всех
Вадля всех ![]() .
.
Из определения чисел Фибоначчи следует, что
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для вычисления чисел Фибоначчи справедлива следующая формула Бине
(3) 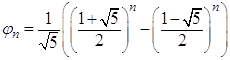 ,
, ![]() .
.
Из (1) и (2) следует, что индукционное предположение, при доказательстве формулы Бине, должно предполагать справедливость (3) для ![]() Ваи
Ваи ![]() , и значит, начальные условия должны требовать выполнение (3) для
, и значит, начальные условия должны требовать выполнение (3) для ![]() Ваи
Ваи ![]() . Поэтому доказательство формулы Бине может проводиться по следующей теореме математической индукции.
. Поэтому доказательство формулы Бине может проводиться по следующей теореме математической индукции.
Теорема 5. Пусть ![]() - одноместный предикат на
- одноместный предикат на ![]() , который удовлетворяет условиям:
, который удовлетворяет условиям:
![]() - истины.
- истины.
![]() Ва(
Ва(![]() - истины Во
- истины Во ![]() - истина).
- истина).
Тогда предикат ![]() Ватождественно истинен на
Ватождественно истинен на ![]() .
.
Проведём доказательство формулы Бине по теореме 5.
Для ![]() Ваи
Ваи ![]() Варавенство (3) принимает вид
Варавенство (3) принимает вид
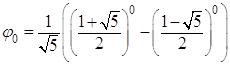 ,
, 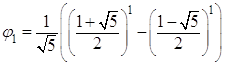 .
.
Очевидно, что эти равенства верны.
Предположим, что равенство (3) истинно для чисел ![]() Ваи
Ваи ![]() . Тогда из (2) следует, что
. Тогда из (2) следует, что
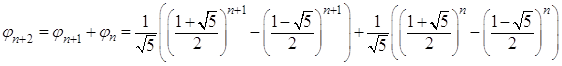 .
.
После простых преобразований правой части получим, что
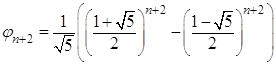
По индукции формула Бине доказана.
Теорема 6. Пусть ![]() - одноместный предикат на
- одноместный предикат на ![]() , который удовлетворяет условиям:
, который удовлетворяет условиям:
![]() - истина.
- истина.
![]() Ва(
Ва(![]() - истины Во
- истины Во ![]() - истина).
- истина).
Тогда предикат ![]() Ватождественно истинен на
Ватождественно истинен на ![]() .
.
п.3. Основное свойство ассоциативных операций.
Теорема. Если бинарная операция ![]() Вана множестве
Вана множестве ![]() Ваассоциативна, то
Ваассоциативна, то ![]()
![]() Вапри любой расстановке скобок, задающих порядок выполнения операций
Вапри любой расстановке скобок, задающих порядок выполнения операций ![]() Вав произведении
Вав произведении ![]() Вазначения произведений будут одинаковыми, то есть значение произведения не зависит от способа расстановки скобок.
Вазначения произведений будут одинаковыми, то есть значение произведения не зависит от способа расстановки скобок.
Доказательство. Проводится индукцией по ![]() . Проверим утверждения теоремы для
. Проверим утверждения теоремы для ![]() Ваи
Ваи ![]() .
.
Для ![]() - очевидно, так как порядок выполнения операций единственен.
- очевидно, так как порядок выполнения операций единственен.
Для ![]() Вапроизведение
Вапроизведение ![]() Ваможет быть вычислено двумя способами:
Ваможет быть вычислено двумя способами: ![]() Ваили
Ваили ![]() . В силу ассоциативности
. В силу ассоциативности ![]() - эти произведения равны.
- эти произведения равны.
Предположим, что теорема доказана для всех чисел ![]() , где
, где ![]() .
.
Докажем теорему для числа ![]() . При любой расстановке скобок в произведении
. При любой расстановке скобок в произведении ![]() , такое произведение есть произведение двух скобок
, такое произведение есть произведение двух скобок ![]() Ва(1), где
Ва(1), где ![]() . Внутри каждой скобки расставлены свои скобки. Так как в каждой скобке
. Внутри каждой скобки расставлены свои скобки. Так как в каждой скобке ![]() Вамножителей, то по индукционному предположению значение произведения в скобках не зависит от того, как в них расставлены скобки. Поэтому произведение (1) можно записать в виде
Вамножителей, то по индукционному предположению значение произведения в скобках не зависит от того, как в них расставлены скобки. Поэтому произведение (1) можно записать в виде ![]()
![]() , применяя закон ассоциативности и индукцирования к множителям. Получим, что произведение (1) равно
, применяя закон ассоциативности и индукцирования к множителям. Получим, что произведение (1) равно ![]()
![]() Ваи так далее продолжая, получим
Ваи так далее продолжая, получим ![]() , поэтому произведение (1) не зависит от способа расстановки скобок.
, поэтому произведение (1) не зависит от способа расстановки скобок.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал ВлАргументВ». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье тАУ М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Группы. Примеры групп. Простейшие свойства групп. Гомоморфизмы и изоморфизмы групп. Подгруппы
Даны определения группы, абелевой, бесконечной, аддитивной, мультипликативной и коммутативной групп, гомоморфизмов и изоморфизмов групп, приведены примеры групп и их простейшие свойства с доказательствами.
п.1. Понятие группы.
Определение. Алгебра ![]() , где
, где ![]() - бинарная операция,
- бинарная операция, ![]() - унарная операция,
- унарная операция, ![]() Ваназывается группой, если выполнены 3 аксиомы:
Ваназывается группой, если выполнены 3 аксиомы:
![]() - ассоциативно, то есть
- ассоциативно, то есть ![]()
![]() .
.
Аксиома существования правого нейтрального элемента: ![]()
![]()
Аксиома существования правого обратного элемента: ![]()
![]() ,
, ![]() - правый обратный элемент к
- правый обратный элемент к ![]() .
.
Определение. Группа ![]() Ваназывается коммутативной (абелевой), если операция
Ваназывается коммутативной (абелевой), если операция ![]() Вакоммутативна, то есть
Вакоммутативна, то есть ![]()
![]() .
.
Определение. Порядком группы ![]() Ваназывается число элементов в множестве
Ваназывается число элементов в множестве ![]() , если
, если ![]() - конечное множество. Если
- конечное множество. Если ![]() - бесконечное множество, то группа
- бесконечное множество, то группа ![]() Ваназывается бесконечной.
Ваназывается бесконечной.
Аддитивная форма записи группы.
Определение. Алгебра ![]() , где
, где ![]() - бинарная операция,
- бинарная операция, ![]() - унарная операция,
- унарная операция, ![]() Ваназывается аддитивной группой, если выполнены аксиомы:
Ваназывается аддитивной группой, если выполнены аксиомы:
операция ![]() Ваассоциативна, то есть
Ваассоциативна, то есть ![]()
![]()
существование правого нейтрального элемента, то есть ![]()
![]()
существование правого противоположного элемента, то есть ![]()
![]()
Определение. Группа называется абелевой, если операция ![]() - коммутативная операция, то есть
- коммутативная операция, то есть ![]()
![]() .
.
Мультипликативная форма записи группы.
Определение. Алгебра ![]() , где
, где ![]() - бинарная операция,
- бинарная операция, ![]() - унарная,
- унарная, ![]() Ваназывается мультипликативной группой, если выполняются следующие аксиомы:
Ваназывается мультипликативной группой, если выполняются следующие аксиомы:
Операция умножения ассоциативна, то есть ![]()
![]() .
.
Аксиома существования правого единичного элемента: ![]()
![]() .
.
Аксиома существования правого обратного элемента: ![]()
![]() .
.
Определение. Группа называется коммутативной, если операция ![]() - коммутативна, то есть
- коммутативна, то есть ![]()
![]() .
.
1) Рассмотрим множество натуральных чисел и операции ![]()
![]() .
. ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() Ва(сумма двух натуральных чисел тАУ натуральное число),
Ва(сумма двух натуральных чисел тАУ натуральное число), ![]() - не является унарной операцией на множестве
- не является унарной операцией на множестве ![]() ,
, ![]()
![]()
![]() - не является алгеброй
- не является алгеброй ![]() Ване группа.
Ване группа.
2) ![]() .
. ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() ,
, ![]() - унарная операция на множестве
- унарная операция на множестве ![]() ,
, ![]()
![]()
![]() Ваявляется алгеброй. Проверим аксиомы аддитивной группы:
Ваявляется алгеброй. Проверим аксиомы аддитивной группы:
![]()
![]() - выполняется по свойствам целых чисел.
- выполняется по свойствам целых чисел.
![]()
![]() - выполняется по свойствам целых чисел.
- выполняется по свойствам целых чисел.
![]()
![]() - выполняется по свойствам целых чисел.
- выполняется по свойствам целых чисел.
Значит, ![]() Ваявляются группой, абелева группа, так как
Ваявляются группой, абелева группа, так как ![]() Вабесконечная группа называется аддитивной группой целых чисел.
Вабесконечная группа называется аддитивной группой целых чисел.
3) ![]() .
. ![]() - бинарная операция,
- бинарная операция, ![]() - унарная операция,
- унарная операция, ![]()
![]()
![]() Ваявляется алгеброй.
Ваявляется алгеброй.
![]()
![]() - выполняется по свойствам действительных чисел.
- выполняется по свойствам действительных чисел.
![]()
![]() Вавыполняется по свойствам действительных чисел.
Вавыполняется по свойствам действительных чисел.
![]()
![]() .
.
Значит ![]() Ваявляется группой, абелева группа,
Ваявляется группой, абелева группа, ![]()
![]() , бесконечная группа называется аддитивной группой действительных чисел.
, бесконечная группа называется аддитивной группой действительных чисел.
4) ![]() .
. ![]()
![]() Ване является алгеброй
Ване является алгеброй ![]() Ване является группой.
Ване является группой.
1) ![]() .
. ![]() -бинарная операция на множестве
-бинарная операция на множестве ![]() ,
, ![]() - не является унарной операцией на множестве
- не является унарной операцией на множестве ![]() ,
, ![]()
![]() Ване является алгеброй
Ване является алгеброй ![]() Ване является группой.
Ване является группой.
2) ![]() Ване является алгеброй
Ване является алгеброй ![]() Ване является группой, так как
Ване является группой, так как ![]() Ване является унарной операцией.
Ване является унарной операцией.
3) ![]() .
. ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() ,
, ![]() - не является унарной операцией
- не является унарной операцией ![]() Ване является алгеброй
Ване является алгеброй ![]() Ване является группой.
Ване является группой.
4) ![]() .
. ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() ,
, ![]() - унарная операция на множестве
- унарная операция на множестве ![]() ,
, ![]()
![]()
![]() Ваявляется алгеброй
Ваявляется алгеброй ![]() Ваявляется группой, так как аксиомы выполняются по свойствам рациональных чисел коммутативная бесконечная группа называется мультипликативной группой не равных
Ваявляется группой, так как аксиомы выполняются по свойствам рациональных чисел коммутативная бесконечная группа называется мультипликативной группой не равных ![]() Варациональных чисел.
Варациональных чисел.
5) ![]() .
. ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() ,
, ![]() - не является унарной операцией на множестве
- не является унарной операцией на множестве ![]() ,
, ![]()
![]() Ване алгебра
Ване алгебра ![]() Ване группа.
Ване группа.
6) Симметрическая группа множества ![]() , где
, где ![]() .
. ![]() Вабиекция. Рассмотрим
Вабиекция. Рассмотрим ![]() , где
, где ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() Ва(по определению биекции),
Ва(по определению биекции), ![]() - унарная операция на множестве
- унарная операция на множестве ![]() ,
, ![]() Ва(из определения тождественной функции и биекции)
Ва(из определения тождественной функции и биекции) ![]() Ваявляется алгеброй.
Ваявляется алгеброй.
Проверим аксиомы групп:
![]() - ассоциативная операция.
- ассоциативная операция.
![]()
![]() Васвойство
Васвойство ![]()
![]()
![]() Васвойство обратной функции
Васвойство обратной функции ![]() Ва- группа.
Ва- группа.
Если множество ![]() - конечное множество, то группа
- конечное множество, то группа ![]() - конечная группа и её порядок равен
- конечная группа и её порядок равен ![]() . Если множество
. Если множество ![]() - бесконечное, то
- бесконечное, то ![]() - бесконечная группа. Если в множестве
- бесконечная группа. Если в множестве ![]() элементов, то группа коммутативна. Группа
элементов, то группа коммутативна. Группа ![]() Ваназывается симметричной группой множества
Ваназывается симметричной группой множества ![]() .
.
7) Группа вращений и симметрии правильного треугольника.

I - группа вращений правильного треугольника.
Под вращением треугольника понимается поворот, который вершины переводит в вершины.
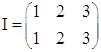 Ватождественное вращение.
Ватождественное вращение.
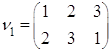
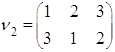
![]()
Составим таблицу умножения (роль умножения выполняет композиция)
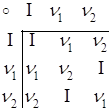
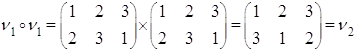
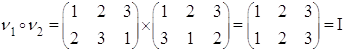
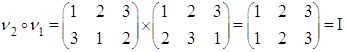
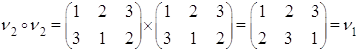
Из таблицы видим, что композиция элементов множества ![]() Вамножеству
Вамножеству ![]() , значит композиция тАУ бинарная операция.
, значит композиция тАУ бинарная операция.
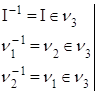
![]()
![]() Ваунарная операция на множестве
Ваунарная операция на множестве ![]() .
.
Тождественное вращение с ![]() , тогда
, тогда ![]() Ваявляется алгеброй.
Ваявляется алгеброй.
Проверим аксиомы группы:
Операция композиция ассоциативна на произведение множеств, а значит, ассоциативна на множестве ![]() .
.
![]()
![]() Вапо свойству тождественной функции.
Вапо свойству тождественной функции.
![]()
![]() Вапо свойству обратной функции.
Вапо свойству обратной функции.
Значит, ![]() Ваявляется группой, это конечная группа третьего порядка, коммутативная группа (таблица симметрична относительно главной диагонали).
Ваявляется группой, это конечная группа третьего порядка, коммутативная группа (таблица симметрична относительно главной диагонали).
II тАУ группа вращений и симметрии правильного треугольника.
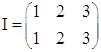
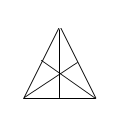
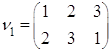
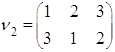
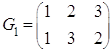
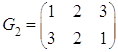
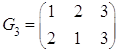
Рассмотрим множество ![]()
Рассмотрим ![]()
Построим таблицу умножения (для операции композиции)
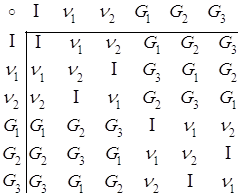
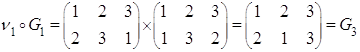
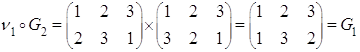
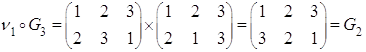
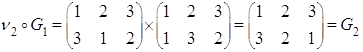
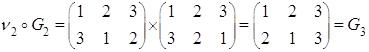
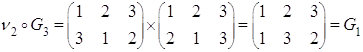
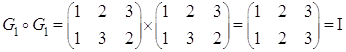
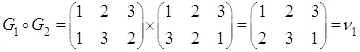
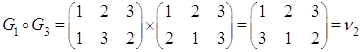
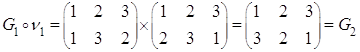
![]() - бинарная операция.
- бинарная операция.
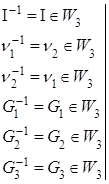
![]()
![]() Ваунарная операция.
Ваунарная операция.
![]() , значит
, значит ![]() - алгебра. Аксиомы группы на множестве выполняются.
- алгебра. Аксиомы группы на множестве выполняются.
Операция композиция не коммутативна (не симметрична) ![]()
Конечная группа шестого порядка называется группой вращения и симметрии правильного треугольника.
п.3. Простейшие свойства групп.
Пусть ![]() Вамультипликативная группа.
Вамультипликативная группа.
Свойства.
![]()
![]() , то есть правый обратный элемент
, то есть правый обратный элемент ![]() Ваявляется левым обратным элементом к
Ваявляется левым обратным элементом к ![]() .
.
Доказательство. Левая часть равна ![]()
![]()
![]() Варавна правой части.
Варавна правой части.
![]()
![]() Вато есть правый единичный является левым единичным элементом.
Вато есть правый единичный является левым единичным элементом.
Доказательство. Левая часть равна ![]()
![]() Варавна правой части.
Варавна правой части.
![]() , если
, если ![]()
Доказательство.
![]()
![]()
![]() Ваесли
Ваесли ![]()
Доказательство.
I способ:
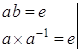
![]()
![]()
II способ:
![]()
I способ:
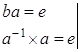
![]()
![]()
II способ:
![]() Ваправый
Ваправый
То есть существует и единственен правый, существует и единственен левый обратный элементы.
![]() Ваесли
Ваесли ![]()
Доказательство.
а) ![]()
![]()
![]()
б) ![]()
![]()
![]()
То есть существует и единственен правый, существует и единственен левый единичные элементы.
![]()
![]()
Доказательство.
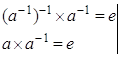
![]()
![]()
![]()
![]() ,
, ![]() Ваимеют в группе единственное решение.
Ваимеют в группе единственное решение.
Доказательство.
а) Проверим, что ![]() решение уравнения
решение уравнения ![]()
Левая часть равна ![]() Варавна правой части.
Варавна правой части.
Проверим, что решение единственно: пусть ![]() Ваи
Ваи ![]() Ва- решения уравнения
Ва- решения уравнения ![]() . Имеем
. Имеем 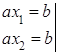
![]()
![]()
б) Проверим что ![]() - решение уравнения
- решение уравнения ![]() . Левая часть равна
. Левая часть равна ![]() Варавна правой части.
Варавна правой части.
Проверим, что решение уравнения единственно: Пусть ![]() Ваи
Ваи ![]() - два решения уравнения
- два решения уравнения ![]() . Имеем
. Имеем 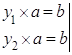
![]()
![]()
![]()
![]()
Доказательство.
![]()
![]()
Определение. Гомоморфизмом группы ![]() Вав группу
Вав группу ![]() Ваназывается отображение
Ваназывается отображение ![]() Ватакое, что:
Ватакое, что:
![]()
![]()
![]()
![]()
![]()
То есть ![]() Васохраняет операции в группе
Васохраняет операции в группе ![]() .
.
Определение. Гомоморфизмом группы ![]() Вав группу
Вав группу ![]() Ваназывается отображение
Ваназывается отображение ![]() Ватакое, что:
Ватакое, что:
![]()
![]()
![]()
![]()
![]()
Определение. Гомоморфизмом группы ![]() Вав группу
Вав группу ![]() Ваназывается отображение
Ваназывается отображение ![]() Ватакое, что:
Ватакое, что:
![]()
![]()
![]()
![]()
![]()
Определение. Гомоморфизмом группы ![]() Вав группу
Вав группу ![]() Ваназывается отображение
Ваназывается отображение ![]() Ватакое, что:
Ватакое, что:
![]()
![]()
![]()
![]()
![]()
Пример.
Пусть 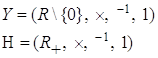
Рассмотрим функцию ![]() ;
; ![]()
Проверим, что ![]() - гомоморфизм:
- гомоморфизм:
1.![]()
![]()
2.![]()
![]()
3.![]()
Значит ![]() - гомоморфизм.
- гомоморфизм.
Пусть  .
.
Рассмотрим функцию ![]()
![]() Ваи
Ваи ![]() .
.
Проверим:
1) ![]()
![]()
2) ![]()
![]()
3) ![]()
Значит ![]() - гомоморфизм группы
- гомоморфизм группы ![]() Вав группе
Вав группе ![]() .
.
Теорема. Пусть ![]() ,
, ![]() - мультипликативные группы. Если
- мультипликативные группы. Если ![]() Ваи
Ваи ![]()
![]() , то
, то ![]() - гомоморфизм групп.
- гомоморфизм групп.
Доказательство. Проверим, что ![]() Ваобладает тремя свойствами определения гомоморфизма. Одно свойство дано в условии. Докажем, что
Ваобладает тремя свойствами определения гомоморфизма. Одно свойство дано в условии. Докажем, что ![]() :
: ![]()
![]()
![]()
![]()
![]()
![]() .
.
Докажем, что ![]() :
: ![]()
![]()
![]()
![]()
Значит ![]() - гомоморфизм групп.
- гомоморфизм групп.
Пусть ![]() - мультипликативные группы.
- мультипликативные группы.
Определение. Отображение ![]() Ваназывается изоморфизмом групп, если
Ваназывается изоморфизмом групп, если ![]() Ваобладает двумя свойствами:
Ваобладает двумя свойствами: ![]() - биекция и
- биекция и ![]() - гомоморфизм групп.
- гомоморфизм групп.
Если существует изоморфизм группы ![]() Вана
Вана ![]() , то группы называются изоморфными.
, то группы называются изоморфными.
Определение. Пусть ![]() - мультипликативная группа,
- мультипликативная группа, ![]() ,
, ![]() . Говорят, что множество
. Говорят, что множество ![]() - замкнуто относительно операции умножения, если
- замкнуто относительно операции умножения, если ![]()
![]() .
.
Говорят, что ![]() - замкнуто относительно операции
- замкнуто относительно операции ![]() , если
, если ![]()
![]() .
.
Определение. Пусть ![]() - аддитивная группа,
- аддитивная группа, ![]() ,
, ![]() .
.
Говорят, что ![]() - замкнуто относительно бинарной операции
- замкнуто относительно бинарной операции ![]() , если
, если ![]()
![]() .
.
Говорят, что ![]() - замкнуто относительно операции
- замкнуто относительно операции ![]() , если
, если ![]()
![]() .
.
Теорема. Пусть ![]() - мультипликативная группа,
- мультипликативная группа, ![]() ,
, ![]() .
.
Если ![]() - замкнуто относительно бинарной операции
- замкнуто относительно бинарной операции ![]() Ваи унарной операции
Ваи унарной операции ![]() , то
, то ![]() - группа, которая называется подгруппой группы
- группа, которая называется подгруппой группы ![]() .
.
Доказательство.
Так как ![]() - замкнуто относительно бинарной операции
- замкнуто относительно бинарной операции ![]() Ваи унарной операции
Ваи унарной операции ![]() , то
, то ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() , а
, а ![]() - унарная операция на множестве
- унарная операция на множестве ![]() .
.
Проверим, что ![]() . Так как
. Так как ![]() , то
, то ![]()
![]()
![]() Ва(так как операция
Ва(так как операция ![]() - унарная операция). Имеем
- унарная операция). Имеем ![]() Ва(так как
Ва(так как ![]() - бинарная операция на множестве
- бинарная операция на множестве ![]() )
) ![]()
![]() . Проверено, что
. Проверено, что ![]() - алгебра.
- алгебра.
Проверим, что ![]() - группа.
- группа.
Все аксиомы группы на множестве ![]() Вавыполнены, так как
Вавыполнены, так как ![]() . Поэтому
. Поэтому ![]() - группа.
- группа.
Пример.
Рассмотрим аддитивную группу целых чисел ![]() , найдём подгруппы этой группы. Из теории следует, что для того, чтобы найти подгруппу, необходимо найти
, найдём подгруппы этой группы. Из теории следует, что для того, чтобы найти подгруппу, необходимо найти ![]() , замкнутое относительно операций
, замкнутое относительно операций ![]() Ваи
Ваи ![]() .
.
Пусть ![]() ;
; ![]() - подгруппа.
- подгруппа.
![]()
![]() - подгруппа (то есть сама группа является своей подгруппой)
- подгруппа (то есть сама группа является своей подгруппой)
![]() - это множество не замкнуто относительно операции
- это множество не замкнуто относительно операции ![]() :
: ![]()
![]()
![]() - не образует подгруппу.
- не образует подгруппу.
Рассмотрим множество ![]() - множество целых чётных чисел (делящихся на целое число 2). Множество
- множество целых чётных чисел (делящихся на целое число 2). Множество ![]() - замкнуто
- замкнуто![]()
![]() - подгруппа аддитивной группы целых чисел.
- подгруппа аддитивной группы целых чисел.
Рассмотрим ![]() - множество целых чисел, кратных числу 3. Это множество замкнуто относительно операций
- множество целых чисел, кратных числу 3. Это множество замкнуто относительно операций ![]() Ваи
Ваи ![]() , значит
, значит ![]() - подгруппа аддитивной группы целых чисел.
- подгруппа аддитивной группы целых чисел.
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал ВлАргументВ». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кос
Вместе с этим смотрят:
Актуальные проблемы квантовой механики
Волоконно-оптические датчики температуры на основе решеток показателя преломления
Время и пространство - идеалистические понятия