Кольца. Примеры колец. Гомоморфизмы и изоморфизмы колец. Подкольца. Кольцо целых чисел
Для изучения предлагаются понятия кольца, коммутативного кольца и области целосности, гомоморфизма и изоморфизма колец, подкольца, а так же свойства кольца целых чисел.
п.1. Понятие кольца.
Определение. Алгебра  , где
, где  - бинарные операции,
- бинарные операции,  - унарная операция,
- унарная операция,  Ваназывается кольцом, если выполнены аксиомы.
Ваназывается кольцом, если выполнены аксиомы.
I.  - абелева группа.
- абелева группа.
1) 

2) 

3) 

4) 

II. 1) 
 - ассоциативность умножения.
- ассоциативность умножения.
2) законы дистрибутивности: 
 - левый дистрибутивный закон,
- левый дистрибутивный закон, 
 - правый дистрибутивный закон.
- правый дистрибутивный закон.
 - называется аддитивной группой кольца.
- называется аддитивной группой кольца.
Определение. Кольцо  Ваназывается кольцом с единицей
Ваназывается кольцом с единицей  , если существует
, если существует 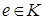

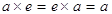
Определение. Кольцо  Ваназывается коммутативным, если
Ваназывается коммутативным, если 

Определение. Элементы  Ваназываются делителями
Ваназываются делителями  , если
, если 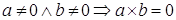
Определение. Кольцо  Ваназывается областью целостности, если оно обладает свойствами:
Ваназывается областью целостности, если оно обладает свойствами:
Кольцо  - коммутативно.
- коммутативно.
Кольцо  Вас единицей
Вас единицей  , где
, где 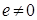 .
.
Кольцо не имеет делителей нуля.
п.2. Примеры колец.
Рассмотрим  . Операции
. Операции  - бинарная операция на множестве
- бинарная операция на множестве  , операция
, операция  - унарная операция на множестве
- унарная операция на множестве  ,
,  , значит
, значит  - алгебра. Аксиомы кольца на множестве
- алгебра. Аксиомы кольца на множестве  Вавыполнены, это следует из свойств целых чисел, значит
Вавыполнены, это следует из свойств целых чисел, значит  - кольцо. Это кольцо с единицей 1, так как
- кольцо. Это кольцо с единицей 1, так как  Ваи
Ваи 
 . Это коммутативное кольцо, так как
. Это коммутативное кольцо, так как 
 . Это кольцо без делителей нуля. Кольцо целых чисел является областью целостности.
. Это кольцо без делителей нуля. Кольцо целых чисел является областью целостности.
Пусть  - множество целых чётных чисел,
- множество целых чётных чисел,  - алгебра, кольцо без единицы, коммутативное, без делителей нуля, не является областью целостности.
- алгебра, кольцо без единицы, коммутативное, без делителей нуля, не является областью целостности.
 - проверим, будет ли на множестве
- проверим, будет ли на множестве  - кольцо.
- кольцо.



 - бинарная операция на множестве
- бинарная операция на множестве  .
.


 - бинарная операция на множестве
- бинарная операция на множестве  .
.


 - унарная операция на множестве
- унарная операция на множестве  .
. 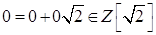
Значит  - алгебра.
- алгебра.
Аксиомы кольца для данной алгебры выполнены, так как 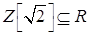 , а на
, а на  Вааксиомы выполнены (из свойств действительных чисел), значит
Вааксиомы выполнены (из свойств действительных чисел), значит  - это кольцо.
- это кольцо.
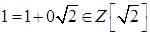 .
. 
 . Кольцо с единицей
. Кольцо с единицей  - это коммутативное кольцо без делителей нуля, является областью целостности.
- это коммутативное кольцо без делителей нуля, является областью целостности.
Пусть 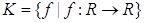 . Определим операции
. Определим операции 
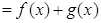 ,
,  ;
;  ,
,  .
.
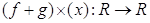

 - бинарные операции на множестве
- бинарные операции на множестве 
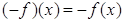
 Вазначит
Вазначит 

 - унарная операция на множестве
- унарная операция на множестве  .
.

 ,
,  , значит
, значит  - алгебра. Проверим, является ли эта алгебра кольцом. Для этого проверим аксиомы кольца. Равенство
- алгебра. Проверим, является ли эта алгебра кольцом. Для этого проверим аксиомы кольца. Равенство 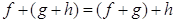 - равенство функции:
- равенство функции:  Ваиз определения операций. Рассмотрим произведение
Ваиз определения операций. Рассмотрим произведение  , вычислим значения левой и правой частей от
, вычислим значения левой и правой частей от  Ваа)
Ваа) б)
б)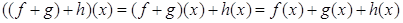


 . Аналогично проверяется, что все аксиомы кольца выполнены, значит
. Аналогично проверяется, что все аксиомы кольца выполнены, значит  Ваявляется кольцом. Это кольцо с единицей
Ваявляется кольцом. Это кольцо с единицей 
 . Действительно,
. Действительно, 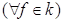
 Ва(свойство единицы). Это коммутативное кольцо, так как
Ва(свойство единицы). Это коммутативное кольцо, так как 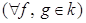
 . Покажем, что это кольцо с делителями нуля. Пусть
. Покажем, что это кольцо с делителями нуля. Пусть  ,
,  ,
,  ,
,  Ва(нулевая функция). Вычислим
Ва(нулевая функция). Вычислим  Ва(равно нулевой функции). Значит
Ва(равно нулевой функции). Значит  ,
, 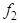 - делители нуля, значит кольцо
- делители нуля, значит кольцо  - не является областью целостности.
- не является областью целостности.
п.3. Простейшие свойства кольца.
Пусть  - кольцо. Выпишем и проверим аксиомы кольца:
- кольцо. Выпишем и проверим аксиомы кольца:

 .
.
Доказательство.  - абелева группа, имеем
- абелева группа, имеем 


 .
.
Доказательство.  - абелева группа, имеем
- абелева группа, имеем 
 .
.
 , если
, если  , если
, если  .
.
Доказательство. По закону сокращения в группе, определенной на множестве  .
.
 , если
, если  , если
, если  .
.
Доказательство. Следует из свойства 4 групп.
 Ваесли
Ваесли  , если
, если  .
.
Доказательство. Следует из 5 свойства групп.

 .
.
Доказательство. Следует из 6 свойства групп.

 .
.
Доказательство. Докажем, что  .
.


 .
.
Доказательство. Докажем, что 
 Варассмотрим сумму
Варассмотрим сумму  . Аналогично доказывается, что
. Аналогично доказывается, что  .
.

 . Обозначение:
. Обозначение: 
 .
.

 Ва(правый дистрибутивный закон),
Ва(правый дистрибутивный закон),  Ва(левый дистрибутивный закон).
Ва(левый дистрибутивный закон).
Доказательство. Правый дистрибутивный закон: левая часть равна 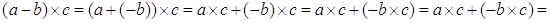
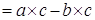 Варавна правой части. Аналогично доказывается левый дистрибутивный закон.
Варавна правой части. Аналогично доказывается левый дистрибутивный закон.

 .
.
Доказательство. Вычислим сумму 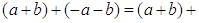
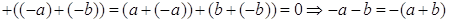 .
.
п.4. Гомоморфизмы и изоморфизмы колец.
Дано два кольца  Ваи
Ваи 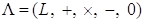 .
.
Определение. Гомоморфизмом кольца  Вав кольце
Вав кольце  Ваназывается функция
Ваназывается функция 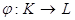 Ваи обладающая свойствами:
Ваи обладающая свойствами:

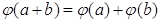





Другими словами, гомоморфизм колец тАУ это отображения, сохраняющие все операции кольца. Если  - гомоморфизм кольца
- гомоморфизм кольца  Вав
Вав  , то
, то  - гомоморфизм абелевых групп
- гомоморфизм абелевых групп  Вав группу
Вав группу  .
.
Теорема. Пусть  Ваи
Ваи 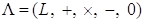 - кольца и
- кольца и 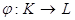 , обладающих свойствами:
, обладающих свойствами:

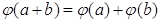

Тогда  - гомоморфизм колец.
- гомоморфизм колец.
Доказательство. Из свойства 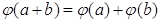

 Ваявляется гомоморфизмом групп
Ваявляется гомоморфизмом групп  Ваи
Ваи  , поэтому
, поэтому  Ваобладает свойствами:
Ваобладает свойствами:  ,
,  , значит по определению
, значит по определению  - гомоморфизм колец.
- гомоморфизм колец.
Определение. Отображение 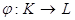 Ваназывается изоморфизмом кольца
Ваназывается изоморфизмом кольца  Вана
Вана  , если
, если  Ваобладает свойствами:
Ваобладает свойствами:
 - гомоморфизм колец.
- гомоморфизм колец.
 - биекция.
- биекция.
Другими словами: изоморфизм тАУ это гомоморфизм, являющийся биекцией.
п.5. Подкольца.
Пусть  - кольцо,
- кольцо,  ,
,  .
.
Определение. Множество  - замкнуто относительно операции
- замкнуто относительно операции  , если
, если 
 .
.
Множество  - замкнуто относительно операции
- замкнуто относительно операции  , если
, если 
 . Множество
. Множество  - замкнуто относительно операции
- замкнуто относительно операции  , если
, если 
 .
.
Теорема. Пусть  - кольцо,
- кольцо,  ,
,  , если
, если  - замкнуто относительно операции
- замкнуто относительно операции  , то
, то 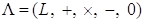 - кольцо, которое называется подкольцом, кольца
- кольцо, которое называется подкольцом, кольца  .
.
Доказательство.  - бинарные операции,
- бинарные операции,  - унарная операция, так как
- унарная операция, так как  - замкнутое множество. Так как
- замкнутое множество. Так как  , то существует
, то существует  , так как
, так как  - замкнуто относительно операции
- замкнуто относительно операции  , то
, то 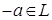

 , значит
, значит 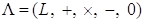 - алгебра, так как аксиомы выполнены на
- алгебра, так как аксиомы выполнены на  , то они выполнены и на
, то они выполнены и на  , потому алгебра
, потому алгебра  - кольцо.
- кольцо.
Теорема. Пусть 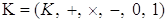 - числовое кольцо с единицей 1, тогда оно содержит подкольцо целых чисел.
- числовое кольцо с единицей 1, тогда оно содержит подкольцо целых чисел.
п.6. Аксиоматическое определение кольца целых чисел.
Алгебраическая система  , где
, где  Вабинарные операции,
Вабинарные операции,  - унарная операция,
- унарная операция,  ,
,  ,
,  Ваназывается системой целых чисел, если выполнены три группы аксиом:
Ваназывается системой целых чисел, если выполнены три группы аксиом:
I.  - кольцо.
- кольцо.
Абелева группа 





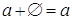


Аддитивная группа



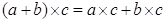


II. Множество  - замкнуто относительно операций
- замкнуто относительно операций  Ваи алгебраическая система
Ваи алгебраическая система  Ваявляется системой натуральных чисел (системой Пеано).
Ваявляется системой натуральных чисел (системой Пеано).
Для  ,
, 
Для  ,
, 
Для  ,
, 
Для  ,
, 
Для  ,
, 
Для  ,
, 
Аксиома индукции: пусть  . Если множество
. Если множество  Ваудовлетворяет условиям:
Ваудовлетворяет условиям:
а) 
б)  ,
,  , то
, то 
III. Аксиома минимальности.
Если  Ваи обладает свойствами:
Ваи обладает свойствами:
а) 
б) 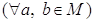
 , то
, то 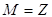 .
.
Свойства целых чисел.
Теорема 1. О делении с остатком.


 Ва|
Ва| 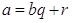 , где
, где  . Число
. Число  Ваназывается делимым,
Ваназывается делимым,  - делителем,
- делителем,  - частным,
- частным,  - остатком при делении
- остатком при делении  Вана
Вана  .
.
Доказательство. Докажем существование хотя бы одной пары чисел  ,
,  . Для этого рассмотрим множество
. Для этого рассмотрим множество  . Множество
. Множество  Васодержит как отрицательные, так и неотрицательные числа, пусть
Васодержит как отрицательные, так и неотрицательные числа, пусть  - наименьшее неотрицательное число в
- наименьшее неотрицательное число в  , тогда
, тогда  . Докажем, что
. Докажем, что  , предположим противное
, предположим противное  . Рассмотрим число
. Рассмотрим число  .
. 
 Вапротиворечие с выбором
Вапротиворечие с выбором  . Доказано, что
. Доказано, что  ,
, 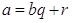 . Докажем единственность чисел
. Докажем единственность чисел  Ваи
Ваи  , пусть
, пусть 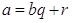
 .
.  ,
, 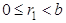 . Докажем, что
. Докажем, что  , предположим противное
, предположим противное 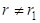 . Пусть
. Пусть 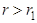 . Имеем
. Имеем 
 Вапротиворечие, так как между числами
Вапротиворечие, так как между числами 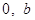 Ванет чисел, делящихся на
Ванет чисел, делящихся на  . Доказано, что
. Доказано, что  , если
, если  , то
, то  , а отсюда следует, что
, а отсюда следует, что  . Доказана единственность чисел
. Доказана единственность чисел  Ваи
Ваи  .
.
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал ВлАргументВ». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье тАУ М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Вместе с этим смотрят:
Актуальные проблемы квантовой механики
Волоконно-оптические датчики температуры на основе решеток показателя преломления
Время и пространство - идеалистические понятия
Интересные обьекты Вселенной
Коагуляция