Поле комплексных чисел
Вопросы поля комплексных чисел, описывается построение поля комплексных чисел, приводятся алгебраическая форма записи комплексных чисел, определение комплексного числа, действия над комплексными числами.
п.1. Построение поля комплексных чисел.
Рассмотрим множество 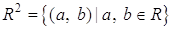 . Определим на
. Определим на  Вабинарные операции сложения
Вабинарные операции сложения  , умножения
, умножения  , унарную операцию
, унарную операцию  Ваи определим элементы
Ваи определим элементы  .
.
Для 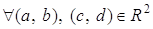 :
:
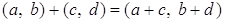 ;
;
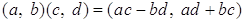 ;
;
 .
.
Обозначим: 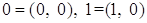 .
.
Теорема 1. Алгебра 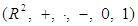 Ваявляется полем.
Ваявляется полем.
Доказательство. Проверим, что алгебра 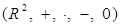 Ваесть абелева группа.
Ваесть абелева группа.
Для 
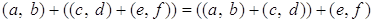 .
.
Для 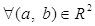
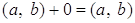 .
.
Для 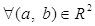
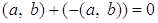 .
.
Для 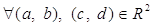
(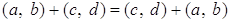 .
.
Проверим, что операция 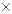 - ассоциативна, то есть
- ассоциативна, то есть 
 .
.
Действительно,
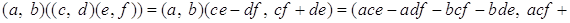
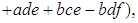

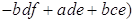 .
.
Проверим левый закон дистрибутивности, то есть для 
 .
.
Действительно,
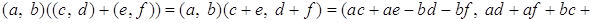
 ,
,
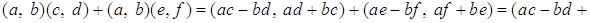
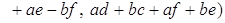 .
.
Аналогично проверяется справедливость правого закона дистрибутивности.
Из выше доказанного следует, что алгебра  Ваесть кольцо.
Ваесть кольцо.
Проверим, что кольцо  Вакоммутативно, то есть для
Вакоммутативно, то есть для 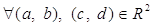
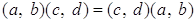 .
.
Действительно,
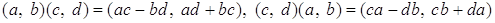 .
.
Проверим, что  Ва- кольцо с единицей 1, то есть
Ва- кольцо с единицей 1, то есть 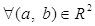
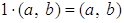 .
.
Действительно,
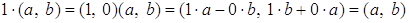 .
.
Так как 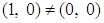 , то
, то 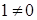 .
.
Докажем, что каждый ненулевой элемент кольца 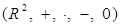 Ваобратим. Пусть
Ваобратим. Пусть 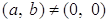 , что равносильно
, что равносильно 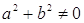 . Рассмотрим пару
. Рассмотрим пару 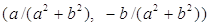 Ваи проверим, что эта пара является обратной к паре
Ваи проверим, что эта пара является обратной к паре 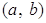 . Действительно,
. Действительно,
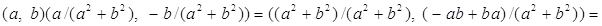
 .
.
Из выше доказанного следует, что алгебра 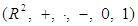 Ва- поле.
Ва- поле.
Определение. Поле 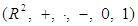 Ваназывается полем комплексных чисел, а его элементы - комплексными числами.
Ваназывается полем комплексных чисел, а его элементы - комплексными числами.
п.2. Алгебраическая форма записи комплексных чисел.
Обозначение. Множество комплексных чисел принято обозначать  , то есть
, то есть 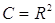 . Приняты также следующие обозначения:
. Приняты также следующие обозначения:
 Вадля
Вадля 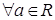 .
.
Теорема 2. Каждое комплексное число  Ваможет быть, и притом единственным образом, записано в виде:
Ваможет быть, и притом единственным образом, записано в виде:
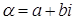 , где
, где 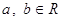 . (Такая запись называется алгебраической формой записи комплексного числа
. (Такая запись называется алгебраической формой записи комплексного числа  ).
).
Доказательство. Существуют 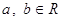 Ватакие, что
Ватакие, что 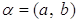 . Имеем
. Имеем
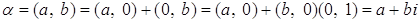 .
.
Теорема 3. Число 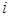 Ваобладает свойством:
Ваобладает свойством:  .
.
Доказательство. 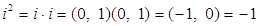 .
.
Из равенства  Васледует, что
Васледует, что 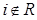 .
.
Определение. Пусть 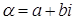 , где
, где 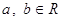 . Число
. Число 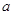 Ваназывается действительной частью,
Ваназывается действительной частью,  Ва- мнимой частью комплексного числа
Ва- мнимой частью комплексного числа  . Пишем
. Пишем 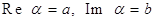 .
.
Пусть 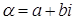 Ва- алгебраическая форма записи комплексного числа
Ва- алгебраическая форма записи комплексного числа  . Тогда:
. Тогда:
если  , то
, то 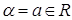 ;
;
если 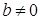 , то
, то 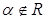 .
.
Определение. Если 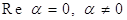 , то комплексное число
, то комплексное число  Ваназывают чисто мнимым числом.
Ваназывают чисто мнимым числом.
Действия над комплексными числами
в алгебраической форме
1) Для 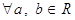
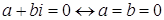 .
.
Другими словами: комплексное число равно нулю тогда и только тогда, когда у него действительная и мнимая части равны нулю.
Доказательство. 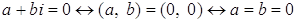 .
.
2) Для 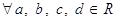
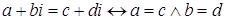 .
.
Другими словами: два комплексных числа равны тогда и только тогда, когда у них, соответственно, равны действительная и мнимая части.
Доказательство. 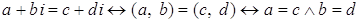 .
.
3) Для 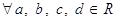
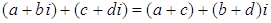 .
.
Другими словами: чтобы сложить два комплексных числа, нужно, соответственно, сложить их действительные и мнимые части.
Доказательство. 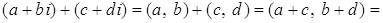
 .
.
4) Для 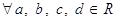
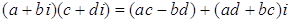 .
.
Доказательство. 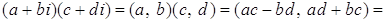
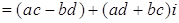 .
.
5) Для 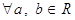
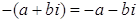 .
.
Доказательство. 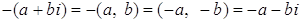 .
.
6) Для 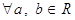 , если
, если 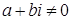 , то
, то
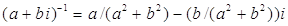 .
.
Доказательство. 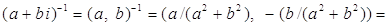
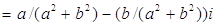 .
.
п.3. Операция сопряжения.
Определение. Пусть комплексное число 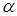 Вазаписано в алгебраической форме
Вазаписано в алгебраической форме 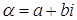 . Числом сопряжённым с
. Числом сопряжённым с 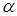 Ваназывается число
Ваназывается число 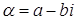 .
.
Свойства операции сопряжения
Для 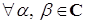 , где
, где 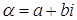 ,
,  ,
, 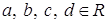 .
.
1).
Доказательство.
.
2) .
Доказательство. .
3) .
Доказательство.
.
.
4) Если a ¹ 0, то 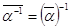 .
.
Доказательство. 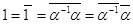 .
.
5) 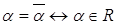 .
.
Доказательство.  .
.
6) 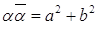 .
.
Доказательство.  .
.
С помощью операции сопряжения удобно производить деление комплексных чисел. Чтобы записать в алгебраической форме дробь с комплексными числителем и знаменателем нужно умножить числитель и знаменатель дроби на число, сопряжённое со знаменателем, и вычислить произведения в числителе и знаменателе.
п.4. Модуль комплексного числа.
Пусть  Вазаписано в алгебраической форме
Вазаписано в алгебраической форме 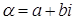 .
.
Определение. Модулем комплексного числа  Ваназывается неотрицательное действительное число
Ваназывается неотрицательное действительное число 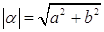 .
.
Свойства модуля.
Для 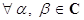 , где
, где 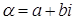 ,
, 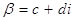 ,
, 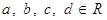 .
.
1) 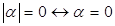 .
.
Доказательство. 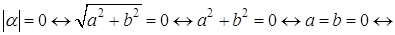
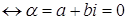 .
.
2) 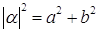 .
.
3) 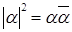 .
.
Доказательство. Свойство следует из свойства 6 операции сопряжения.
4) 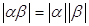 .
.
Доказательство. 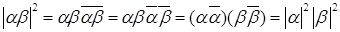 .
.
Отсюда следует нужное утверждение.
5) Если 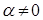 , то
, то 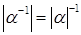 .
.
Доказательство. 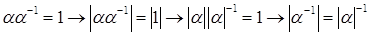 .
.
6) Неравенство треугольника: 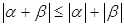 .
.
Доказательство. Докажем сначала неравенство
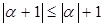 .
.
Имеем
(2) 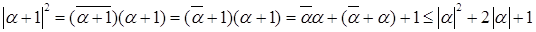 ,
,
так как
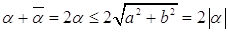 .
.
Из (2) следует, что
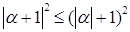 .
.
Из последнего неравенства следует неравенство (1).
Докажем теперь неравенство треугольника. Неравенство треугольника, очевидно, выполнено для 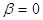 . Докажем неравенство треугольника для
. Докажем неравенство треугольника для 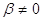 . Имеем
. Имеем
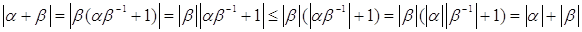 .
.
7) 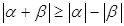 .
.
Доказательство.  . Отсюда следует нужное неравенство.
. Отсюда следует нужное неравенство.
8) 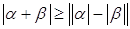 .
.
Доказательство. Справедливы неравенства
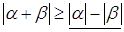 ,
,  .
.
Одно из подчёркнутых чисел совпадает с 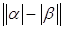 .
.
п.5. Геометрическая интерпретация комплексных чисел.
Пусть  Вазаписано в алгебраической форме
Вазаписано в алгебраической форме 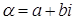 . Поставим в соответствие числу
. Поставим в соответствие числу  Ваточку плоскости с координатами
Ваточку плоскости с координатами 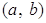 . Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
. Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
Числа  Ваи
Ваи 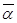 Варасположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
Варасположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
Геометрический смысл модуля
Из Рис.1 видно, что расстояние от начала координат до числа  Варавно
Варавно  . Поэтому геометрический смысл
. Поэтому геометрический смысл 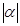 Ва- расстояние от
Ва- расстояние от  Вадо начала координат.
Вадо начала координат.
y

 Ваbi a
Ваbi a
i
 -1+i 1+i
-1+i 1+i
 Ва- 1 0 1 a
Ва- 1 0 1 a
x
- 1-i 1-i
- i
Рис.1.
 Ва- bi `a
Ва- bi `a
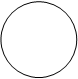
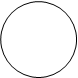
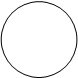
Пример. Изобразим на комплексной плоскости, на Рис.2, множества, заданные, соответственно, следующими условиями: 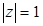 ;
; 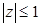 ;
; 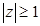 .
.


 Ваy | z | =1 y | z | £1 y | z | ³1
Ваy | z | =1 y | z | £1 y | z | ³1














 Ваi i i
Ваi i i






 Ва- 1 1 - 1 1 - 1 1
Ва- 1 1 - 1 1 - 1 1









 Ва0 0 0
Ва0 0 0












- i - i - i
Рис.2.
Пусть 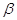 Вазаписано в алгебраической форме
Вазаписано в алгебраической форме 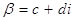 . Имеем
. Имеем
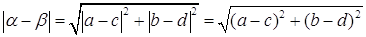 .
.
Из Рис.3 видно, что геометрический смысл модуля разности комплексных чисел - расстояние между этими числами.
 Ваy
Ваy

 Ваb a
Ваb a

d |b-d|



 Ваb |a-c|
Ваb |a-c|
Рис.3.
0 c a x
Пример. Изобразим на комплексной плоскости, на Рис.4, множества, заданные, соответственно, следующими условиями: 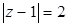 ;
; 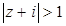 .
.
 Ваy y
Ваy y

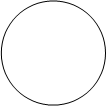
 Ва| z-1| =2 0
Ва| z-1| =2 0
x
- i
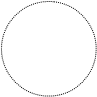
- 1 0 1 3 x |z+i | > 1
- 2i
Рис.4.
Геометрическая интерпретация комплексных чисел
векторами плоскости
Поставим в соответствие числу  Васвязаный вектор плоскости с началом в начале координат и с концом в точке
Васвязаный вектор плоскости с началом в начале координат и с концом в точке  . Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
. Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
 Ваy
Ваy


 Ваa+b
Ваa+b
 Ваb
Ваb

 Ваa
Ваa
0 Рис.5
x
Геометрический смысл модуля комплексного числа  , при интерпретации чисел векторами, - длина вектора
, при интерпретации чисел векторами, - длина вектора  . Сумма комплексных чисел находится как сумма векторов.
. Сумма комплексных чисел находится как сумма векторов.
п.6. Тригонометрическая форма записи
комплексного числа.
Определение. Аргументом комплексного числа  Ваназывается число
Ваназывается число 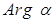 , равное величине угла между положительным направлением оси абсцисс и вектором
, равное величине угла между положительным направлением оси абсцисс и вектором  ,
, 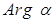 Ваопределяется с точность до углов, кратных
Ваопределяется с точность до углов, кратных 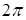 . Главным значением аргумента комплексного числа
. Главным значением аргумента комплексного числа  Ваназывается то значение
Ваназывается то значение 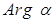 , которое принадлежит промежутку
, которое принадлежит промежутку 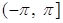 , оно обозначается
, оно обозначается  Ваи
Ваи 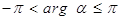 .
.
Пусть  Вазаписано в алгебраической форме
Вазаписано в алгебраической форме 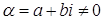 . Тогда из геометрической интерпретации
. Тогда из геометрической интерпретации  Васледует, что:
Васледует, что:
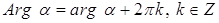 ;
;
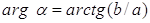 , если
, если 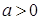 ;
;
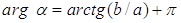 , если
, если 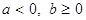 ;
;
 , если
, если 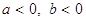 .
.
Заметим, что  Вавыражается только в радианах,
Вавыражается только в радианах, 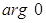 Ване определён.
Ване определён.
Теорема 4. Каждое комплексное число 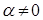 Ваможет быть записано в виде
Ваможет быть записано в виде
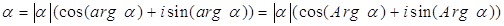 .
.
Доказательство. Изобразим  Вавектором комплексной плоскости,
Вавектором комплексной плоскости,
см. Рис.6.


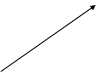


y
b a
Рис.6.
0 a x
Угол, образованный вектором  Ваи положительным направлением оси абсцисс, равен
Ваи положительным направлением оси абсцисс, равен  , следовательно,
, следовательно, 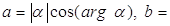
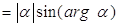 . Поэтому
. Поэтому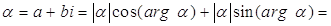
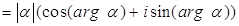 .
.
Определение. Если комплексное число  Вазаписано в виде
Вазаписано в виде 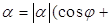
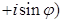 , то говорят, что
, то говорят, что  Вазаписано в тригонометрической форме.
Вазаписано в тригонометрической форме.
Правила действий с комплексными числами,
записанными в тригонометрической форме.
Пусть комплексные числа 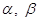 Вазаписаны в тригонометрической форме
Вазаписаны в тригонометрической форме
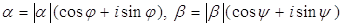 .
.
1) 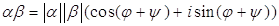 ,
,
то есть при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Доказательство.
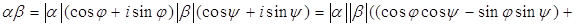
 .
.
2) Если 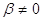 , то
, то
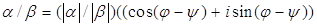 ,
,
то есть при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Доказательство. Обозначим 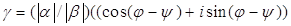 . Так как
. Так как 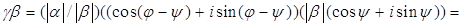
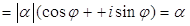 , то нужное утверждение доказано.
, то нужное утверждение доказано.
3) Если 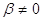 , то
, то
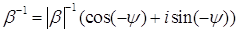 .
.
4) Формула Муавра. Для 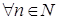 ,
,
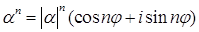 .
.
Доказательство. Формула Муавра является следствием правила 1.
5) Обобщённая формула Муавра. Для 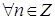 ,
,
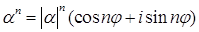 .
.
Доказательство. Обобщённая формула Муавра является следствием формулы Муавра и свойства 3).
п.7. Показательная форма записи комплексного числа.
Обозначение. Для 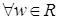 Ваобозначим
Ваобозначим
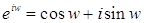 . (1)
. (1)
Равенство (1) называют формулой Эйлера. При этом обозначении, запись комплексного числа  Вав показательной форме принимает вид
Вав показательной форме принимает вид
 . (2)
. (2)
Из равенства (1) и правил действия с комплексными числами, записанными в тригонометрической форме, следует справедливость следующей теоремы .
Теорема 5. Для 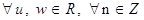 Васправедливы равенства:
Васправедливы равенства:
1) 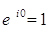 Ва;
Ва;
2) 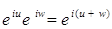 ;
;
3) 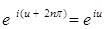 ;
;
4)  ;
;
5) 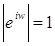 ;
;
6) 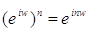 ;
;
7) 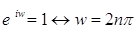
п.8. Связь между тригонометрическими и гиперболическими функциями.
Из формул Эйлера следует, что для 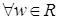
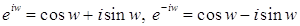 .
.
Складывая и вычитая эти равенства находим, что для 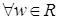 :
:
(1) 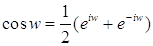 ;
;
(2) 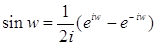 .
.
Как известно, из курса математического анализа, гиперболические косинус, синус, тангенс, котангенс, соответственно, 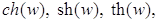
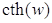 , для
, для 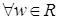 , определяются равенствами:
, определяются равенствами:
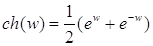 ;
; 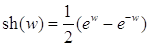 ;
;
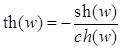 ;
; 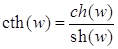 .
.
Если в формулах (1), (2), заменить 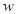 Вана
Вана  , то мы получим формулы для определения значений
, то мы получим формулы для определения значений 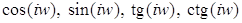 . Эти формулы выражают гиперболические формулы через тригонометрические. Для
. Эти формулы выражают гиперболические формулы через тригонометрические. Для 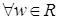 :
:
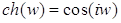 ;
; 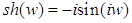 ;
;
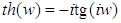 ;
;  .
.
п.9. Корни из комплексных чисел.
Определение. Пусть 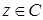 ,
, 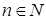 . Комплексное число
. Комплексное число 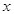 Ваназывается корнем степени
Ваназывается корнем степени 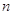 Ваиз
Ваиз 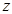 , если
, если 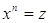 .
.
Теорема 6. Пусть 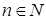 ,
,  Ва- множество всех корней степени
Ва- множество всех корней степени 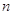 из 1. Тогда алгебра
из 1. Тогда алгебра 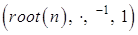 - группа, (которая называется группой корней степени
- группа, (которая называется группой корней степени 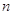 из 1).
из 1).
Доказательство. Пусть  .
.
Проверим, что умножение тАУ бинарная операция. Имеем 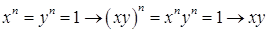 Ва- корень степени
Ва- корень степени 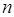 Ваиз 1.
Ваиз 1.
Проверим, что 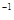 - унарная операция. Имеем
- унарная операция. Имеем 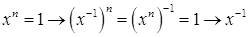 Ва- корень степени
Ва- корень степени 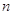 Ваиз 1.
Ваиз 1.
Очевидно, что 1 тАУ корень степени 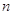 Ваиз 1.
Ваиз 1.
Доказано, что  Ва- алгебра.
Ва- алгебра.
То, что алгебра  Ва- группа, следует из свойств комплексных чисел.
Ва- группа, следует из свойств комплексных чисел.
Теорема 7. Для 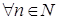 Васуществует точно
Васуществует точно 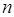 Варазличных корней
Варазличных корней 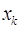 Вастепени
Вастепени 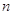 Ваиз 1,
Ваиз 1, 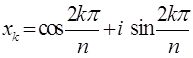 ,
, 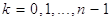 . (1)
. (1)
Все корни расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0).
Доказательство. Проверим сначала, что числа 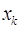 , заданные равенством (1), являются корнями степени
, заданные равенством (1), являются корнями степени 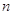 Ваиз 1. Действительно,
Ваиз 1. Действительно,  .
.
Докажем, что любой корень 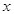 степени
степени 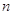 из 1 может быть вычислен по формуле (1). Т.к.
из 1 может быть вычислен по формуле (1). Т.к. 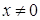 , то
, то 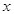 Ваможно записать в показательой форме
Ваможно записать в показательой форме  .
.
Имеем 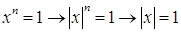 . Поэтому
. Поэтому 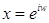 ,
, 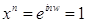 ,
, 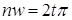 , где
, где 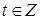 . По теореме о делении с остатком, существуют такие
. По теореме о делении с остатком, существуют такие 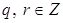 , что
, что  , где
, где 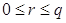 .
.
Значит, 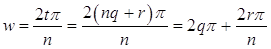 ,
, 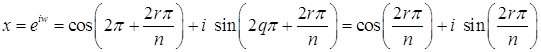 , т.е. вычисляется по формуле (1).
, т.е. вычисляется по формуле (1).
Изобразив числа, заданные формулой (1), на комплексной плоскости, мы увидим, что они расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0). В частности, числа, заданные формулой (1), попарно различны.
Теорема 8. Пусть 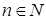 ,
, 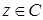 ,
, 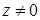 ,
, 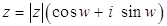 . Тогда существует точно
. Тогда существует точно  Варазличных корней
Варазличных корней 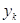 Вастепени
Вастепени 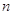 Ваиз
Ваиз 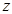 ,
,  ,
, 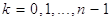 . (2)
. (2)
Доказательство. Проверим сначала, что числа 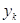 , заданные равенством (2), являются корнями степени
, заданные равенством (2), являются корнями степени 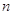 Ваиз
Ваиз 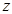 . Действительно,
. Действительно,  .
.
Пусть 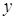 - корень степени
- корень степени 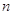 Ваиз
Ваиз 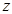 . Докажем, что он вычисляется по формуле (2). Рассмотрим число
. Докажем, что он вычисляется по формуле (2). Рассмотрим число 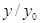 , где
, где 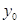 Ваопределено формулой (2). Имеем
Ваопределено формулой (2). Имеем 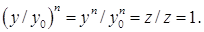
Следовательно 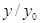 Ва- корень степени
Ва- корень степени 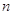 Ваиз 1, т.е.
Ваиз 1, т.е. 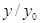 Васовпадает с одним из чисел
Васовпадает с одним из чисел 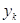 . Имеем
. Имеем 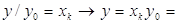
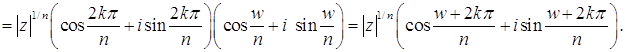
Из вышедоказанного следует, что числа  Вапопарно различны.
Вапопарно различны.
п.10. Мультисекция.
Теорема 1. (о мультисекции многочлена) Пусть
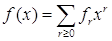 Ва- многочлен с числовыми коэффициентами,
Ва- многочлен с числовыми коэффициентами, 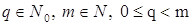 . Тогда
. Тогда
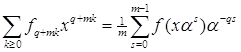 , (1)
, (1)
где 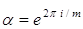 .
.
Доказательство. Для  Варавенство (1) очевидно выполнено. Докажем (1) для
Варавенство (1) очевидно выполнено. Докажем (1) для 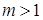 . Имеем
. Имеем
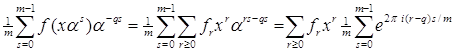 Ва(2)
Ва(2)
ЕслиВа - целое, то 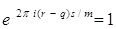 Ваи
Ваи 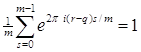 .
.
ЕслиВа - не целое, то 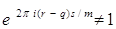 Ваи по формуле суммы членов геометрической прогрессии
Ваи по формуле суммы членов геометрической прогрессии
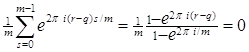 .
.
Поэтому в (2) суммирование нужно вести только по тем 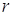 , для которых
, для которых 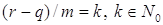 . Отсюда следует (1).
. Отсюда следует (1).
Заметим, что равенство (1) справедливо не только для многочленов, но и для рядов.
Следствие 1. Пусть 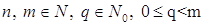 . Тогда
. Тогда
. (3)
Доказательство. Рассмотрим многочлен
.
Применяя мультисекцию к многочлену , получим, что
,
где . Полагая 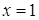 Вав последнем равенстве получим, что
Вав последнем равенстве получим, что
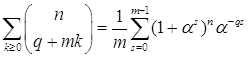 . (4)
. (4)
Имеем
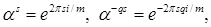
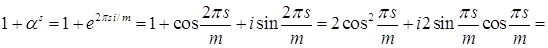
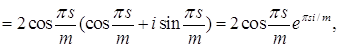

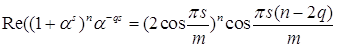 .
.
Приравнивая действительные части обеих частей равенства (4), получаем равенство (3).
п.11. Упорядоченные поля
.
Определение. Упорядоченным полем называется алгебраическая система
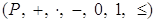 Ватакая, что:
Ватакая, что:
1) алгебра 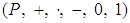 Ва- поле;
Ва- поле;
2) 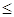 Ва- линейный порядок на
Ва- линейный порядок на 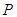 ;
;
3) для 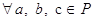
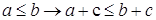 ;
;
4) для 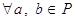
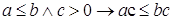 .
.
Другими словами, упорядоченное поле - это поле, на множестве элементов которого определён линейный порядок 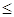 , согласованный условиями 3), 4), с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел.
, согласованный условиями 3), 4), с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел.
Примерами упорядоченных полей являются поле рациональных и поле действительных чисел.
Теорема 9. Если 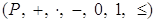 Ва- упорядоченное поле, то для
Ва- упорядоченное поле, то для 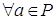 Ваиз условия
Ваиз условия  , следует, что
, следует, что 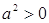 .
.
Доказательство. Так как 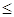 Ва- линейный порядок, то
Ва- линейный порядок, то 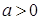 Ваили
Ваили  . Если
. Если 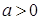 , то по условию 4)
, то по условию 4) 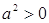 . Если
. Если  , то
, то 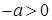 Ваи по условию 4),
Ваи по условию 4), 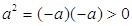 .
.
Теорема 10. Если 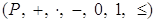 Ва- упорядоченное поле, то для
Ва- упорядоченное поле, то для 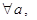
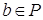 Ваиз условия
Ваиз условия  Васледует, что
Васледует, что 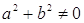 .
.
Доказательство. Из теоремы 9 следует, что 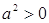 Ваи
Ваи 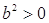 . Из условия 3 следует, что
. Из условия 3 следует, что 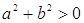 .
.
Теорема 11. Поле комплексных чисел 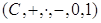 Ванельзя упорядочить.
Ванельзя упорядочить.
Доказательство. Предположим противное - поле комплексных чисел 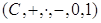 Ваупорядоченно. Так как
Ваупорядоченно. Так как 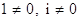 , то по теореме 10
, то по теореме 10  Ва- противоречие.
Ва- противоречие.
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал ВлАргументВ». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. тАУ М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье тАУ М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Вместе с этим смотрят:
Актуальные проблемы квантовой механики
Волоконно-оптические датчики температуры на основе решеток показателя преломления
Время и пространство - идеалистические понятия
Интересные обьекты Вселенной
Коагуляция