Пространство и время в современной научной картине мира

Страница 4

Правда, принцип эквивалентности справедлив только при строго локальных наблюдениях. Так, представим себе лифт, стоящий на Земле. Наблюдатель в лифте бросает два шара. Они будут двигаться по направлению к центру Земли и, следова­тельно, друг к другу. Если же мы будем тянуть лифт с ускоре­нием § в пустоте, то те же шары будут двигаться параллельно друг другу (см. рис. 2).

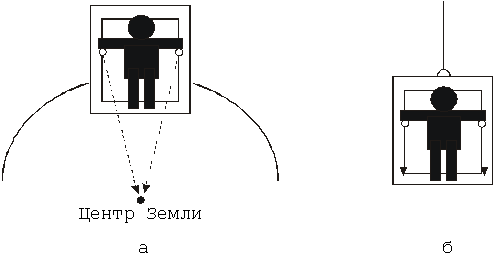
Рис. 2.

Но несмотря на это ограничение, принцип эквивалентности играет важную роль в науке. Мы всегда можем вычислить непо­средственно действие сил инерции на любую физическую систему, и это дает нам возможность знать действие поля тяготения, отвлека­ясь от его неоднородности, которая часто очень незначительна.

Расширение принципа относительности на неинсрциальные «.'истемы, казалось бы, противоречит нашему обыденному опы­ту. Находясь внутри инерциальной системы, никаким экспери­ментом нельзя определить, движется она или покоится. Те, кто летал в самолете, знают, что в нем, как и на Земле, можно де­лать вес: пить чай, играть в мячик и т. п. Даже если посмотреть в иллюминатор, то увидишь, что самолет как бы висит непод­вижно над облаками. Однако, когда самолет начинает сбавлять скорость и идет на посадку, пассажиры сразу же это замечают.

Эйнштейн предлагает провести мысленный эксперимент с лифтом, подвешенным над Землей. Наблюдатели, находящиеся внутри него, не смогут определить в некоторых ситуациях, на­ходятся они в покое или в движении. Представим себе, что в какой-то момент времени канат, на котором подвешен лифт, обрывается, и наблюдатели в нем оказываются в состоянии свободного падения. В этом случае они не смогут определить, какое из двух противоположных утверждений будет истинным: 1) лифт движется в поле тяготения Земли; 2) лифт покоится в отсутствии поля тяготения. Если же в отсутствие поля тяготе­ния Земли лифт будут тянуть вверх с ускорением §, то наблюдатели также не смогут выбрать истинное утверждение из двух противоположных: 1) лифт покоится в поле тяготения Земли; 2) лифт движется с ускорением в отсутствие поля тяготения.

Какие же следствия для пространства и времени вытекают из общей теории относительности? Для этого нужно обратиться вначале к геометрии, которая возникла прежде всего как уче­ние о физическом пространстве, измерении земельных площа­дей и строительных сооружений. Но уже в древности появилась теоретическая, аксиоматическая геометрия Евклида, которая оставалась единственной до XIX в. Правда, до конца XIX в. не делалось какого-либо различия между теоретической и физической геометрией.

С геометрией Евклида связывался тот взгляд, что простран­ство везде одно и то же. Она исходила из пяти аксиом или по­стулатов. Многих математиков не удовлетворял пятый постулат, который гласил, что из одной точки на плоскости можно про­несли только одну прямую, которая не будет пересекаться с джнип, сколько бы ее ни продолжали. Этот постулат не был очевиден, так как никто не мог бы его экспериментально под­твердить даже в воображении — нельзя же линию продолжать в бесконечность.

Ряд известных математиков пытались доказать, что этот по­стулат на самом деле является теоремой, т. е. его можно вывес­ти из четырех других. Но все их попытки оказались неудачны­ми. Они так или иначе неявно предполагали тот же самый пя­тый постулат. Например, в той форме, что сумма углов тре­угольника равна двум прямым. Великий математик К. Гаусс первый поставил под сомнение возможность такого доказатель­ства, т. е. признал, что постулат является аксиомой и, следова­тельно, его можно заменить другими аксиомами, построив но­вую геометрию. Но он на это не осмелился.

И лишь Н.И. Лобачевский в России, Б. Риман в Германии и Я. Больяй в Венгрии построили новые геометрии, отбросив пятый постулат и заменив его на другие. Б. Риман заменил его на аксиому, что через точку, лежащую вне данной прямой на плоскости, нельзя провести ни одной параллельной, все они будут пересекаться с данной. Н.И. Лобачевский и Я. Больяй до­пустили, что существует множество прямых, которые не пере­секутся с данной.

Для пояснения отличия этих геометрий возьмем простран­ство двух измерений, поверхность. Евклидова геометрия реали­зуется на плоскости, Римана — на поверхности сферы, на ко­торой прямая линия выглядит как отрезок дуги большого круга, центр которого совпадает с центром сферы. Геометрия Лоба­чевского осуществляется на так называемой псевдосфере. Так как пространство имеет три измерения, то для каждой геомет­рии вводится понятие кривизны пространства. В евклидовой геометрии кривизна нулевая, у Римана — положительная, у Ло­бачевского—Больяя — отрицательная.

Поскольку постулат параллельности эквивалентен положе­нию о сумме углов треугольника, то различие этих геометрий наглядно изображается на рисунке. В геометрии Евклида сумма углов треугольника равна 180°, у Римана — она больше, у Лоба­чевского — меньше. (Рис. 3, а, б, в соответственно).

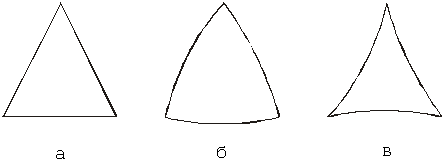
Рис. 3.

Под кривизной пространства не нужно понимать искривле­ние плоскости наподобие того, как искривлена поверхность евклидовой сферы, где внешняя поверхность отлична от внут­ренней. Изнутри ее поверхность выгладит вогнутой, извне — вы­пуклой. Если же брать плоскость в пространстве Лобачевского или Римана, обе ее стороны являются совершенно одинаковыми. Про­сто внутренняя структура плоскости такова, что мы измеряем ее с помощью некоторого коэффициента "кривизны". Кривизна пространства понимается в науке как отступление его метрики от евклидовой, что точно описывается в языке математики, но не проявляется каким-то наглядным образом.

Риман впоследствии показал единство и непротиворечи­вость всех неевклидовых геометрий, частным случаем которых является геометрия Евклида.

Создатели геометрий Лобачевский и Риман считали, что только физические эксперименты могут показать нам, какова геометрия нашего мира. Эйнштейн в общей теории относи­тельности сделал геометрию физической экспериментальной наукой, которая подтвердила характер пространства Римана. Здесь опять призовем на помощь мысленный эксперимент. Представим себе, что лифт покоится в отсутствие гравитацион­ного поля (см. рис. 4, а). В стене лифта сделано отверстие А, через которое луч света падает на его противоположную сторо­ну. Линия АВ — прямая. Пусть теперь лифт начинает движение вверх с ускорением §, т. е. 9,8 м/с2. За время, пока свет прохо­дит расстояние между стенками, лифт смещается вверх, и луч света попадает уже не в точку В, а в точку С (см. рис. 4, б).

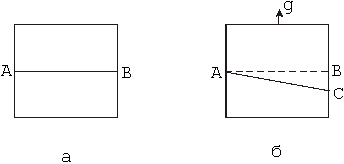
Рис. 4.

Линия АС сохраняет свойство быть кратчайшим расстояни­ем между двумя точками, но это будет уже не прямая, а пря­мейшая или геодезическая. На Земле, поверхность которой представляет собой сферу, такие линии и называются геодези­ческими. Общая теория относительности заменяет закон тяго­тения Ньютона новым уравнением тяготения. Закон Ньютона получается как предельный случай эйнштейновских уравнений. Рассчитанное теоретически Эйнштейном отклонение луча света было впоследствии экспериментально подтверждено наблюде­ниями во время солнечного затмения, когда луч света от звезды проходит вблизи поля тяготения Солнца.

В общей теории относительности Эйнштейн доказал, что структура пространства—времени определяется распределением масс материи. Когда корреспондент американской газеты "Нью-Йорк Тайме" спросил Эйнштейна в апреле 1921 г., в чем суть теории относительности, он ответил: "Сугь такова: раньше считали, что если каким-нибудь чудом все материальные вещи исчезли бы вдруг, то пространство и время остались бы. Со­гласно же теории относительности вместе с вещами исчезли бы и пространство, и время".

1.3. Свойства пространства и времени

Какие же основные свойства пространства и времени мы можем указать? Прежде всего пространство и время объективны и реальны, т. е. существуют независимо от сознания людей и познания ими этой объективной реальности. Человек все более и более углубляет свои знания о ней. Однако в исто­рии науки и философии существовал и другой взгляд на про­странство и время — как только субъективных всеобщих форм нашего созерцания.