Аксиоматика теории множеств

Страница 10

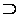6. Zorn (W. O.). Пусть z есть множество, а X есть класс всех взаимно однозначных функций f таких, что D(f)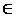Оп и R(f)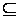z. Из теоремы Хартогса следует, что X есть множество. Очевидно также, что 0 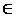X. Отношение 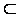частично упорядочивает X. Каковы бы ни были две функции, принадлежащие одной и той же цени в X, одна из них является продолжением другой. Поэтому для любой цепи в Х объеди­нение всех принадлежащих ей функций есть снова взаимно однозначная функция, принадлежащая той же цепи. Следовательно, на основании Zorn, в X имеется максимальный элемент g, представляющий собой взаимно однозначную функцию, определенную на некотором порядковом числе я и принимающую значения из z. Допустим, что z - g‘‘ α ≠ 0. Пусть b 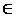z - g‘‘ α, и положим f = g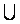{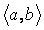}. Тогда f 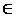X и g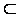f, что противоречит максимальности g. Следовательно, g‘‘ α = z, т. е. α 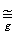z. Посредством функции g отношение Еα, вполне упорядочи­вающее множество α, преобразуется в некоторое отношение, вполне упорядочивающее z.

Заключение

Система аксиом теории множеств была создана для решения задачи обоснования базовых положений современной математики. Таким образом существующие разделы математики можно считать a priori непротиворечивыми, поскольку все их доказанные высказывания логически могут быть сведены к аксиомам. В этом отношении аксиоматика выполнила свое предназначение.

Список литературы

1. Мендельсон Э. Введение в математическую логику. – М.: Наука, 1984.

2. Ляпин Е. С. Полугруппы. – М.: Физматгиз, 1960.

3. Стол Роберт Р. Множества. Логика. Аксиоматические теории. Пер. с англ. Ю.А. Гастаева и И.Х. Шмаина. Под ред. Ю.А. Шихановича. М.: «Просвещение», 1968.