Алгебраические числа
Страница 3
Пример:
1) 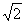 и
и 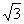 алгебраические числа 2-й степени, а
алгебраические числа 2-й степени, а 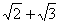 - алгебраическое число 4 степени. Действительно, если a=
- алгебраическое число 4 степени. Действительно, если a=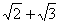 , то a2=5+
, то a2=5+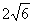 , 24-10a2+1=0, т.е. a корень многочлена f(x)=x4-10x2+1 с целыми коэффициентами, и f(x)=(x-
, 24-10a2+1=0, т.е. a корень многочлена f(x)=x4-10x2+1 с целыми коэффициентами, и f(x)=(x-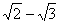 )(x-
)(x-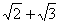 )(x+
)(x+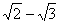 )(x+
)(x+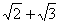 ) (4)
) (4)
Из теоремы единственности над полем рациональных чисел множители f(x) должны являться произведением каких-то множителей правой части равенства (4). Легко видеть, что из этих множителей нельзя составить многочлен с рациональными коэффициентами степени меньшей, чем 4, т.е. f(x) – неприводимый над полем рациональных чисел многочлен, а, следовательно, согласно теореме 3, 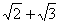 - алгебраическое число 4-й степени.
- алгебраическое число 4-й степени.
2) a=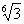 и b=
и b=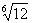 , как легко видеть, это алгебраические числа 6-й степени, а произведение ab=
, как легко видеть, это алгебраические числа 6-й степени, а произведение ab=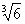 - алгебраическое число 3-й степени.
- алгебраическое число 3-й степени.
III. Рациональные приближения
алгебраических чисел.
3.1. Теорема Лиувилля.
Алгебраические числа не могут иметь слишком хороших рациональных приближений: погрешность при замене алгебраического числа рациональной дробью не может быть достаточно мала по порядку в сравнении с величиной, обратной знаменателю рациональной дроби.
Для алгебраического числа 1-й степени существует постоянная c>0, такая, что для любой рациональной дроби 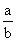 , отличной от a, будет выполняться неравенство:
, отличной от a, будет выполняться неравенство:
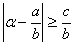 (5)
(5)
Для алгебраического числа 2-й степени можно подобрать c>0, такое, что для любой рациональной дроби, будет иметь место неравенство:
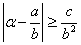 (6)
(6)
В 1844 г., французским математиком Лиувиллем, впервые была доказана общая теорема:
Теорема 5: Для любого действительного алгебраического числа a степени n можно подобрать положительноеc, зависящее только от a, такое, что для всех рациональных чисел 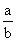 (
(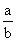 ¹a) будет иметь место неравенство:
¹a) будет иметь место неравенство:
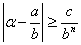 (7)
(7)
Доказательство:
Пусть f(x)=A0xn+ A1xn-1+An неприводимый многочлен с целыми коэффициентами, корнем которого является a. В качестве f(x) можно, например, взять многочлен, получающийся из минимального для a многочлена после умножения всех коэффициентов на наименьшее кратное их знаменателей.
Согласно теореме Безу, имеем:
f(x)=(x-a)g(x), (8)
где g(x) – многочлен с действительными коэффициентами.
Возьмем произвольное d>0. |g(x)| - непрерывная, а следовательно, ограниченная функция от x в сегменте [a-d; a+d], т.е. существует положительное число M, такое, что |g(x)|£M, для всех x из этого сегмента. Обозначим через c=min 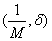 , так, что
, так, что 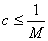 и
и 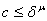 .
.
Для произвольного рационального числа 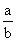 могут представиться две возможности:
могут представиться две возможности:
1) 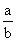 лежит вне сегмента |a-dm; a+dm|, тогда
лежит вне сегмента |a-dm; a+dm|, тогда 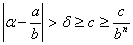
2) 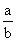 удовлетворяет неравенствам:
удовлетворяет неравенствам:
a-d£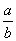 £a+d, тогда |g(
£a+d, тогда |g(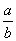 )|£M и, подставляя в (8) вместо x значение
)|£M и, подставляя в (8) вместо x значение 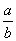 , получаем:
, получаем:
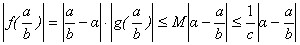 (9)
(9)
Неприводимый над полем рациональных чисел многочлен f(x) степени n³2 не имеет рациональных корней, а при n=1 не имеет корней, отличных от a, так что:
f(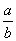 )=
)=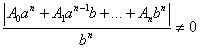
Поскольку числитель 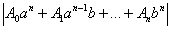 - целое неотрицательное, отличное от нуля, т.е. число большее или равное 1, то
- целое неотрицательное, отличное от нуля, т.е. число большее или равное 1, то 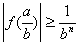 (10). Сравнивая неравенства (9) и (10) получаем
(10). Сравнивая неравенства (9) и (10) получаем 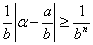 , так что и в этом случае имеем:
, так что и в этом случае имеем: 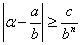 . Теорема доказана.
. Теорема доказана.
Пример:
Пусть z – неквадратное целое число. Найти c>0, такое, что для всех рациональных чисел 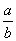 имело бы место неравенство:
имело бы место неравенство:
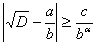 .
.
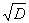 - корень многочлена xa-В. Деля x2-D на x-
- корень многочлена xa-В. Деля x2-D на x-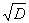 , находим g(x)=x+
, находим g(x)=x+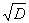 .
.
При 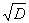 -d<x<
-d<x<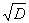 +d имеем
+d имеем 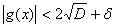 , т.е. M=
, т.е. M=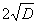 +d. В качестве c берем
+d. В качестве c берем 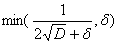 , при этом выгодней всего взять d так, что
, при этом выгодней всего взять d так, что 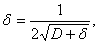 d2+
d2+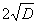 d-1=0, т.е. d=
d-1=0, т.е. d=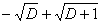 .
.
При таком d получаем 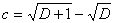 , так что при любых целых a и b имеем:
, так что при любых целых a и b имеем: 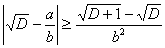 .
.
3.2. Трансцендентные числа Лиувилля.
Числа, являющиеся корнями уравнений с целыми коэффициентами, не исчерпывают все множество действительных чисел, т.е. существуют действительные числа отличные от алгебраических.
Определение 6: Любое неалгебраическое число называется трансцендентным.
Впервые существование трансцендентных чисел доказано Лиувиллем. Доказательство существования трансцендентных чисел у Лаувилля эффективно; на основе следующей теоремы, являющейся непосредственным следствием теоремы 5, строятся конкретные примеры трансцендентных чисел.
Теорема 6: Пусть a – действительное число. Если для любого натурального n³1 и любого действительного c>0 существует хотя бы одна рациональная дробь 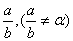 , такая, что
, такая, что 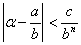 (11), то a – трансцендентное число.
(11), то a – трансцендентное число.
Доказательство:
Если бы a было алгебраическим, то нашлось бы (теорема 5) целое положительное n и действительное c>0 такие, что для любой дроби 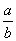 было бы
было бы 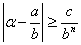 , а это противоречит тому, что имеет место (11). Предположение, что a алгебраическое число, т.е. трансцендентное число. Теорема доказана.
, а это противоречит тому, что имеет место (11). Предположение, что a алгебраическое число, т.е. трансцендентное число. Теорема доказана.