Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Содержание.
Введение… ………………………………………………………… 3
1. Классификация ошибок с примерами…………………………… .…… …5
1.1. Классификация по типам задач…… ……………………… … ……….5
1.2. Классификация по типам преобразований………………………………10
2. Тесты………………………… …………………….… .…………………….12
3. Протоколы решений……………… ……….….…………… ………… 18
3.1. Протоколы неверных решений……………………………… … 18
3.2. Ответы (протоколы верных решений)………………………………….34
3.3. Ошибки, допущенные в решениях…………………………………… 51
Приложение……………………….…………………………………………… 53
Литература……………………………………………………………………….56
ВВЕДЕНИЕ
“На ошибках учатся”, - гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи. Вследствие чего возникла идея провести исследование, цель которого - выявить типичные ошибки, совершаемые учащимися, а также как можно более полно классифицировать их.
В рамках этого исследования был рассмотрен и прорешен большой набор задач из вариантов апрельского тестирования, тестов и письменных заданий вступительных экзаменов в ОмГУ, различных пособий и сборников задач для поступающих в вузы, внимательно изучены материалы заочной школы при НОФ ОмГУ. Полученные данные подверглись подробному анализу, при этом большое внимание было уделено логике решений. На основе этих данных были выделены наиболее часто допускаемые ошибки, то есть типичные.
По результатам этого анализа была сделана попытка систематизировать характерные ошибки и классифицировать их по типам преобразований и типам задач, среди которых были рассмотрены следующие: квадратные неравенства, системы неравенств, дробно-рациональные уравнения, уравнения с модулем, иррациональные уравнения, системы уравнений, задачи на движение, задачи на работу и производительность труда, тригонометрические уравнения, системы тригонометрических уравнений, планиметрия.
Классификация сопровождается иллюстрацией в форме неверных протоколов решений, что дает возможность помочь школьникам развить умение проверять и контролировать себя, критически оценивать свою деятельность, находить ошибки и пути их устранения.
Следующим этапом стала работа с тестами. Для каждой задачи были предложены пять вариантов ответов, из которых один верный, а остальные четыре неверные, но взяты не случайным образом, а соответствуют решению, в котором допущена конкретная стандартная для задач данного типа ошибка. Это дает основание для прогнозирования степени “грубости” ошибки и развития основных мыслительных операций (анализ, синтез, сравнение, обобщение). Тесты имеют следующую структуру:
|
Тип задач | |
|
Условие задачи |
Варианты ответа |
|
Коды ошибок |
Коды ошибок делятся на три вида: ОК – верный ответ, цифровой код - ошибка из классификации по типам задач, буквенный код – ошибка из классификации по типам преобразований. Их расшифровку можно посмотреть в главе 1. Классификация ошибок с примерами.
Далее были предложены задания найти ошибку в решении. Эти материалы были использованы при работе со слушателями заочной школы при НОФ ОмГУ, а также на курсах повышения квалификации учителей г.Омска и Омской области, проводимых НОФ ОмГУ.
В перспективе на основе проделанной работы можно создать систему контроля и оценки уровня знаний и умений тестируемого. Появляется возможность выявить проблемные области в работе, зафиксировать удачные методы и приемы, проанализировать, какое содержание обучения целесообразно расширить. Но для наибольшей эффективности этих методов необходима заинтересованность учащегося. С этой целью мной совместно с Чубрик А.В. и был разработан небольшой программный продукт, генерирующий неверные решения линейных и квадратных уравнений (теоретическая база и алгоритмы – я и Чуубрик А.В., помощь в реализации – студент гр. МП-803 Филимонов М.В.). Работа с данной программой дает школьнику возможность выступить в роли учителя, учеником которого является компьютер.
Полученные результаты могут послужить началом более серьезного исследования, которое в ближайшей и отдаленной перспективе сможет внести необходимые корректировки в систему обучения математике.
1. КЛАССИФИКАЦИЯ ОШИБОК С ПРИМЕРАМИ
1.1. Классификация по типам задач
1. Алгебраические уравнения и неравенства.
1.1. Квадратные неравенства. Системы неравенств:
1.1.1. Неправильно найдены корни квадратного трехчлена: неверно использована теорема Виета и формула для нахождения корней;
![]()
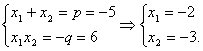
1.1.2. Неправильно изображен график квадратного трехчлена;
|
|
|
1.1.3. Неправильно определены значения аргумента, при которых неравенство выполняется;
![]()
![]()
1.1.4. Деление на выражение, содержащее неизвестную величину;
![]()
![]()
1.1.5. В системах неравенств неправильно взято пересечение решений всех неравенств;
|
|
|
1.1.6. Неправильно включены или не включены концы интервалов в окончательный ответ;
![]()
![]()
1.1.7. Округление.
![]()
1.2. Дробно-рациональные уравнения:
1.2.1. Неправильно указано или не указано ОДЗ: не учтено, что знаменатель дроби не должен быть равен нулю;
![]() ОДЗ:
ОДЗ: ![]() .
.
1.2.2. При получении ответа не учитывается ОДЗ;
![]() ОДЗ:
ОДЗ: ![]() . Ответ:
. Ответ: ![]()
1.2.3. Нерациональность в приведении к общему знаменателю;
![]()
![]()
1.2.4. Неправильно найдены корни уравнения;
![]()
1.2.5. Неэквивалентная замена переменной;
Замена переменной: ![]() .
.
1.2.6. Деление на выражение, содержащее неизвестную величину;
![]()
![]()
1.2.7. Не учтена кратность корня.
![]()
1.3. Уравнения с модулем:
1.3.1. При снятии знака модуля не учтено, при каких условиях был получен соответствующий корень;
![]() Один из случаев:
Один из случаев: ![]() . В этом случае получаем уравнение
. В этом случае получаем уравнение ![]() . Решение:
. Решение: ![]() .
.
