Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Страница 2
1.3.2. Неправильно снят знак модуля: неверно использовано определение модуля;
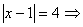 Один из случаев:
Один из случаев: 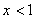 . Тогда уравнение примет вид:
. Тогда уравнение примет вид: 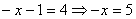 .
.
1.3.3. Перечислены не все случаи, возникающие при снятии знака модуля с выражений, стоящих в уравнении;
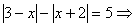 Т.к. в уравнении 2 знака модуля возможно 2 случая:
Т.к. в уравнении 2 знака модуля возможно 2 случая:
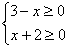 и
и 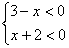 .
.
1.3.4. Деление на выражение, содержащее неизвестную величину.
Аналогично.
1.4. Иррациональные уравнения:
1.4.1. Неправильно указано или не указано ОДЗ: неучтено, что выражение под знаком корня четной степени должно быть неотрицательным;
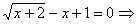 ОДЗ:
ОДЗ: 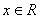 .
.
1.4.2. При получении ответа не учитывается ОДЗ;
Аналогично.
1.4.3. Не учтено, что квадратный арифметический корень - неотрицательная величина, что он определен только для неотрицательных чисел;
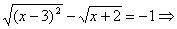
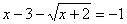 .
.
1.4.4. При возведении уравнения в квадрат не учтены знаки обеих его частей;
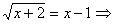
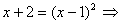
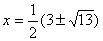 .
.
1.4.5. Неэквивалентная замена переменной;
Аналогично.
1.4.6. Деление на выражение, содержащее неизвестную величину.
Аналогично.
1.5. Системы уравнений:
1.5.1. Неправильно указано или не указано ОДЗ (см. конкретные уравнения);
1.5.2. При получении ответа не учитывается ОДЗ;
Аналогично.
1.5.3. Для каждого отдельного уравнения см. ошибки в предыдущих разделах;
1.5.4. Неправильно сформирован ответ.
Аналогично системам неравенств.
2. Текстовые задачи.
2.1. Задачи на движение:
2.1.1. Неправильно введены неизвестные величины: введены неизвестные величины, с помощью которых невозможно или трудно получить ответ, или несоответствующие смыслу задачи;
2.1.2. Составлено уравнение (неравенство), связывающее неизвестные величины с заданными величинами, несоответствующее условиям задачи;
…первый из А в С прошел на 12 км меньше, чем второй из В в С… 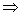
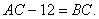
2.1.3. При решении полученных уравнений (неравенств) допущены ошибки, рассмотренные в предыдущих разделах;
2.1.4. Отобранные решения не соответствуют смыслу задачи;
Ответ: 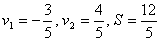 , где
, где 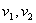 - скорости.
- скорости.
2.1.5. Неправильно поняты термины “позже”, “раньше” и т.д.;
Т.к. первый вышел на 6 часов раньше, то: 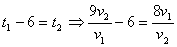 .
.
2.1.6. Неправильно применены формулы средней скорости, пути и т.д.;
Находим время, затраченное пешеходами от начала движения до их встречи: 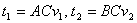 .
.
2.1.7. Выполнены преобразования с разными единицами измерения (км – м, ч – сек и т.д.)
…известно, что стоимость 4.5 м черной ткани = общей стоимости 3 м зеленой и 50 см синей… 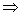 … уравнение, связывающее эти стоимости:
… уравнение, связывающее эти стоимости: 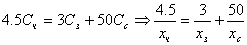 …
…
2.2. Задачи на работу и производительность труда:
2.2.1. Ошибки аналогичны допускаемым в задачах на движение.
3. Тригонометрия.
3.1. Тригонометрические уравнения:
3.1.1. Неправильно указано или не указано ОДЗ (аналогично алгебраическим уравнениям);
3.1.2. При получении ответа не учитывается ОДЗ;
3.1.3. Неправильно применены формулы: в формулах приведения получили неверный знак или функцию; в преобразовании суммы или разности в произведение (или наоборот) перепутали sin и cos, или полу сумму аргументов с полу разностью, или опустили множитель ½; в формулах сложения, понижения степени аналогично;
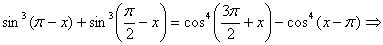
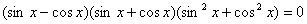 .
.
3.1.4. Неправильное преобразование сложной функции;
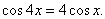
3.1.5. Использование неправильной области определения или свойств функции;
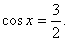
3.1.6. Допущены ошибки в преобразованиях, аналогичных алгебраическим уравнениям.
3.2. Системы тригонометрических уравнений:
3.2.1. Те же ошибки, что и в предыдущем разделе, при решении каждого уравнения;
3.2.2. Неправильный отбор корней: при получении ответа не учтено, что k и n, пробегающие множество целых чисел, могут быть как различными, так и одинаковыми;
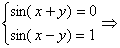
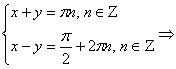 Ответ:
Ответ: 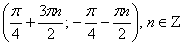 .
.
3.2.3. Те же ошибки, что и при решении систем алгебраических уравнений.
4. Планиметрия.
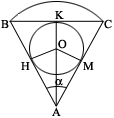
4.1. Неправильно сделан чертеж;
|
|
Окружность на чертеже – это окружность, вписанная в сектор.
|
4.2. Неправильно использованы формулы, теоремы или свойства фигур и тел;
…Радиус окружности можно найти с помощью теоремы синусов: 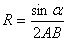 .
.
4.3. Не приведены величины к одной единице измерения;
Аналогично.
4.4. Ответ не соответствует смыслу задачи;
4.5. Могут быть допущены алгебраические ошибки.
1.2. Классификация по типам преобразований
A. Неправильно раскрыли скобки;
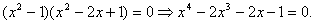
B. При переносе слагаемого в другую часть уравнения или неравенства не сменили его знак на противоположный;
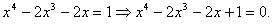
C. Неправильно привели подобные;
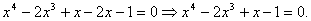
D. Перенос переместительного закона умножения / распределительного закона умножения относительно сложения на другие действия и преобразования;
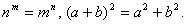
E. Ошибочное установление аналогии между объектами внешне сходными, но по сути различными;
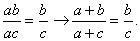
F. Неправильный порядок действий;
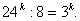
G. Перепутаны степень и коэффициент;
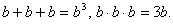
H. Неправильно перемножены многочлены и одночлены;
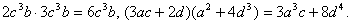
I. Неправильно поделены многочлены и одночлены;
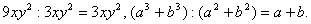
J. Неправильное разложение на множители;
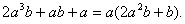
K. Неправильные тождественные преобразования иррациональных выражений;
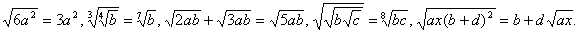
L. Арифметическая ошибка.
2. ТЕСТЫ
|
Алгебраические уравнения |
|
1. Разность между наибольшим и наименьшим корнями уравнения 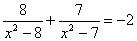 равна равна |
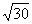
|
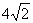
|
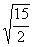
|
0 |
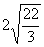
|
|
OK |
1.2.6. |
1.2.9. |
L. |
H. |
|
2. Сумма корней уравнения 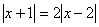 равна равна |
6 |
12 |
5 |
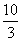
|
7 |
|
OK |
1.3.1. |
1.3.3. |
1.3.2. |
1.3.2 |
|
3. Среднее арифметическое всех действительных корней уравнения 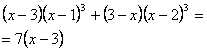 равно равно |
2 |
1,5 |
3 |
-3 |
4,5 |
|
OK |
1.2.6. |
1.2.7. |
H. |
L. |
|
4. Сумма корней уравнения 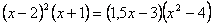 равна равна |
0 |
-4 |
-2 |
-8 |
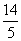
|
|
OK |
1.2.6. |
1.2.7. |
1.2.4. |
B. |
|
5. Сумма корней уравнения 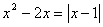 равна равна |
2 |
4 |
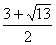
|
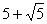
|
3 |
|
OK |
1.3.1. |
1.3.2. |
1.1.1. |
1.3.3. |
|
6. Сумма кубов действительных корней уравнения 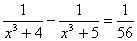 |
-9 |
6 |
36 |
15 |
-1701 |
|
OK |
E. |
1.1.1. |
E. |
1.2.5. |
|
7. Если 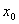 - корень уравнения - корень уравнения 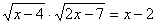 , то значение выражения , то значение выражения 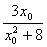 равно равно |
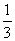
|
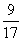
|
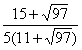
|
корней
нет |
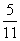
|
|
OK |
1.4.1. |
D. |
H. |
L. |
|
8. Разность между наибольшим и наименьшим корнями уравнения 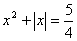 равна равна |
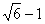
|
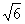
|
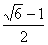
|
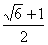
|
1 |
|
OK |
1.3.3. |
L. |
1.3.1. |
J. |
|
9. Произведение корней уравнения 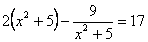 равно равно |
-4 |
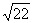
|
18 |
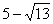
|
-1,5 |
|
OK |
1.1.1. |
1.4.3. |
H. |
1.2.5. |
|
10. Среднее арифметическое всех действительных корней уравнения 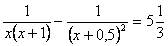 равно равно |
-0,5 |
0,5 |
корней
нет |
1 |
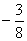
|
|
OK |
1.1.1. |
1.2.3. |
L. |
1.2.1. |
|
Текстовые |
|
1. Автобус из A в B ехал со скоростью 50 км в час, а обратно – со скоростью 30 км в час. Найти среднюю скорость движения автобуса. |
37,5 |
40 |
30 |
20 |
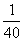
|
|
OK |
2.1.6. |
2.1.6. |
2.1.6. |
2.1.6. |
|
2. Два насоса, работая вместе, наполняют бак за 15 минут. В одиночку второй насос способен наполнить бак на 40 минут быстрее первого. За сколько минут первый насос наполняет бак в одиночку? |
60 |
20 |
27,5 |
12,5 |
35 |
|
OK |
2.1.5. |
2.1.2. |
2.1.6. |
2.1.2. |
|
3. 2 кг яблок и 3 кг груш стоят вместе 180 рублей, а 4 кг яблок и 1 кг груш стоят 160 рублей. Сколько стоят 2 кг груш и 1 кг яблок? |
110 |
100 |
285 |
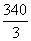
|
299 |
|
OK |
L. |
2.1.6. |
2.1.2. |
2.1.2. |
|
Тригонометрия |
|
1. Результат вычисления выражения 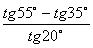 равен равен |
2 |
1 |
0,5 |
0 |
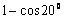
|
|
OK |
3.1.3. |
3.1.3. |
3.1.3. |
3.1.3. |
|
2. Результат вычисления выражения
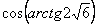 равен равен
|
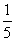
|
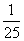
|
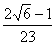
|
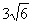
|
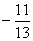
|
|
OK |
3.1.3. |
D. |
3.1.4. |
3.1.3. |
|
3. Результат вычисления выражения 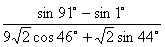 равен равен |
0,1 |
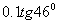
|
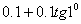
|
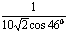
|
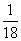
|
|
OK |
3.1.3. |
C. |
A. |
3.1.4. |
|
4. Результат вычисления выражения 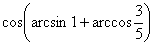 равен равен |
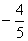
|
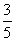
|
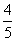
|
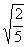
|
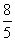
|
|
OK |
3.1.4. |
3.1.3. |
3.1.4. |
3.1.4., 3.1.5. |
|
5. Результат вычисления выражения 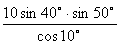 равен равен |
5 |
10 |
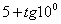
|
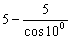
|
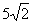
|
|
OK |
3.1.3. |
3.1.3 |
3.1.3.,
3.1.5 |
3.1.3., 3.1.4 |
|
6. Результат вычисления выражения 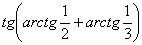 равен равен |
1 |
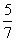
|
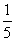
|
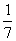
|
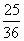
|
|
OK |
3.1.3. |
3.1.3. |
3.1.3. |
L. |
|
7. Результат вычисления выражения 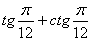 равен равен |
4 |
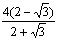
|
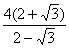
|
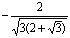
|
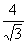
|
|
OK |
3.1.3. |
L. |
3.1.3. |
3.1.5. |
|
8. Результат вычисления выражения 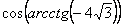 равен равен |
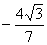
|
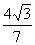
|
-0,5 |
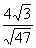
|
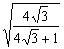
|
|
OK |
3.1.3. |
3.1.4. |
3.1.3. |
3.1.3. |
|
9. Если 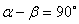 , то значение выражения , то значение выражения 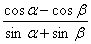 равно равно
|
-1 |
1 |
0 |
0,5 |
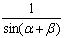
|
|
OK |
3.1.3. |
3.1.3. |
3.1.3. |
3.1.4. |
|
10. Если 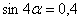 , то значение выражения , то значение выражения 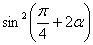 равно равно |
0,3 |
0,52 |
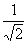
|
0,7 |
0,6 |
|
OK |
3.1.4. |
L. |
3.1.3. |
3.1.3. |
|
11. Укажите в градусах сумму корней уравнения 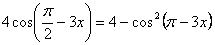 , принадлежащих промежутку , принадлежащих промежутку 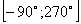 |
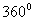
|
0 |
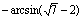
|
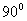
|
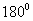
|
|
OK |
3.1.3. |
3.1.3. |
1.1.1. |
1.1.1. |
|
12. Укажите в градусах сумму корней уравнения 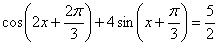 , принадлежащих промежутку , принадлежащих промежутку 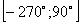 |
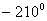
|
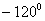
|
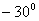
|
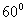
|
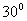
|
|
OK |
3.1.5. |
L. |
3.1.3., 3.1.4. |
L. |
|
13. Укажите количество корней уравнения 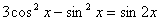 , принадлежащих промежутку , принадлежащих промежутку 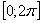 |
4 |
2 |
1 |
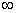
|
3 |
|
OK |
3.1.3. |
3.1.5. |
3.1.4. |
3.1.4. |
|
14. Укажите количество корней уравнения 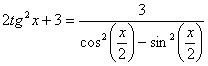 , принадлежащих промежутку , принадлежащих промежутку 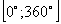 |
2 |
1 |
3 |
4 |
0 |
|
OK |
3.1.5. |
3.1.3. |
3.1.3. |
3.1.4. |
|
Укажите количество корней уравнения 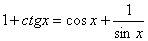 , принадлежащих промежутку , принадлежащих промежутку 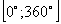 |
3 |
2 |
0 |
4 |
1 |
|
OK |
3.1.5. |
B., 1.3.4. |
1.3.4. |
1.3.4. |
|
16. Укажите в градусах сумму корней уравнения 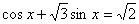 , принадлежащих промежутку , принадлежащих промежутку 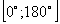 |
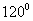
|
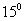
|
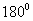
|
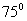
|
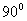
|
|
OK |
3.1.5. |
L. |
3.1.5. |
3.1.5., 3.1.3. |
|
17. Чему равно 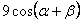 , если , если 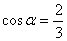 , , 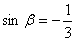 , , 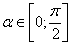 , , 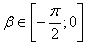 ? ? |
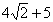
|
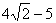
|
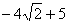
|
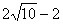
|
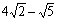
|
|
OK |
3.1.3. |
3.1.5. |
3.1.3. |
L. |
|
18. 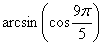 равно равно |
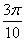
|
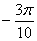
|
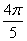
|
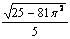
|
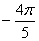
|
|
OK |
3.1.3. |
3.1.3. |
3.1.4. |
3.1.3. |
|
19. 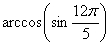 равно равно |
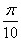
|
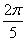
|
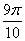
|
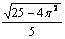
|
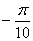
|
|
OK |
3.1.3. |
3.1.3. |
3.1.4. |
3.1.3. |
|
Планиметрия |
|
1. Если в треугольнике 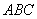 заданы заданы 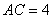 , , 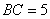 , , 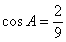 , то синус угла , то синус угла 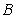 равен равен |
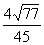
|
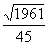
|
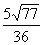
|
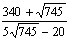
|
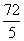
|
|
OK |
4.2. |
4.2. |
4.4. |
L. |
|
2. Если длины диагоналей ромба относятся как 1:2, а площадь ромба равна 12, то длина стороны ромба равна |
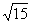
|
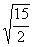
|
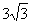
|
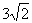
|
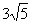
|
|
OK |
4.2. |
D. |
L. |
L. |
|
3. Если в окружность вписан правильный треугольник, площадь которого равна  , и в треугольник вписана окружность, то площадь кольца равна , и в треугольник вписана окружность, то площадь кольца равна |
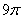
|
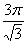
|
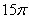
|
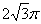
|
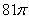
|
|
OK |
4.2. |
4.2. |
4.2. |
L. |
|
4. Если в треугольнике 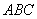 угол при вершине угол при вершине 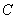 равен равен 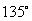 , , 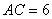 , высота , высота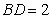 , то площадь треугольника , то площадь треугольника 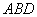 равна равна |
8 |
4 |
32 |
16 |
3 |
|
OK |
4.1. |
4.2. |
L. |
L. |
|
5. Если в треугольнике 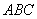 заданы заданы 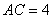 , , 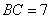 , , 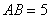 , то синус угла , то синус угла 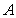 равен равен |
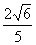
|
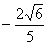
|
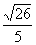
|
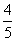
|
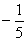
|
|
OK |
3.1.5. |
3.1.3. |
D. |
4.2. |
|
6. Если в треугольнике 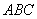 заданы заданы 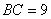 , , 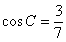 , , 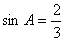 , то длина стороны , то длина стороны 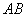 равна равна |
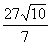
|
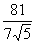
|
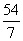
|
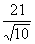
|
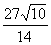
|
|
OK |
4.2. |
L. |
4.2. |
L. |
|
7. Если в окружности радиуса 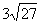 проведена хорда, которая стягивает дугу в проведена хорда, которая стягивает дугу в 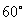 , то расстояние от центра окружности до данной хорды равно , то расстояние от центра окружности до данной хорды равно |
13,5 |
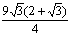
|
13,005 |
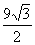
|
4,5 |
|
OK |
4.2. |
1.1.7. |
L. |
L. |
|
8. Если одна из диагоналей параллелограмма, длина которой равна 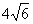 , составляет с основанием угол , составляет с основанием угол 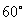 , а вторая диагональ составляет с тем же основанием угол , а вторая диагональ составляет с тем же основанием угол 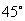 , то длина второй диагонали равна , то длина второй диагонали равна |
12 |
8 |
18 |
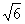
|
16 |
|
OK |
4.2. |
L. |
L. |
L. |
|
9. Если в круге, площадь которого равна 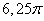 , проведена хорда длиной 3, то расстояние от центра круга до хорды равно , проведена хорда длиной 3, то расстояние от центра круга до хорды равно |
2 |
6,067 |
2,9 |
1 |
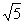
|
|
OK |
4.2.,
1.1.7. |
4.2., 1.1.7. |
D. |
L. |
|
10. Если в прямоугольном треугольнике длина гипотенузы равна 20, а радиус вписанной окружности – 4, то сумма длин катетов треугольника равна |
28 |
20 |
24 |
36 |
26 |
|
OK |
D. |
L. |
4.2. |
L. |
|
11. Если площадь ромба равна 18, а острый угол 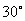 , то длина стороны ромба равна , то длина стороны ромба равна |
6 |
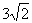
|
3 |
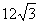
|
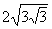
|
|
OK |
4.2. |
4.2. |
3.1.5., L. |
3.1.5. |
|
12. В прямоугольном треугольнике 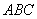 с катетом с катетом 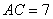 и медианой и медианой 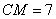 , проведенной к гипотенузе , проведенной к гипотенузе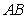 , расстояние между точкой , расстояние между точкой 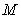 и основанием и основанием 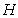 высоты высоты 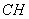 равно равно |
3,5 |
24,5 |
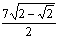
|
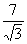
|
4,5 |
|
OK |
L. |
4.2. |
L. |
L. |
|
13. Отрезок длины 5, соединяющий боковые стороны равнобокой трапеции и параллельный ее основаниям, равным 2 и 7, делит площадь трапеции в отношении |
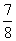
|
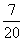
|
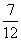
|
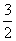
|
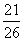
|
|
OK |
4.2. |
4.2. |
4.2. |
L. |
|
14. В круг радиуса 10 вписан равнобедренный треугольник с углом в 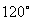 . Найти его периметр. . Найти его периметр. |
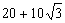
|
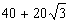
|
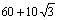
|
30 |
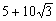
|
|
OK |
4.2. |
4.2. |
3.1.5. |
L. |
|
15. 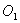 и и 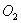 – центры кругов радиуса 6, – центры кругов радиуса 6, 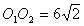 . Тогда площадь общей части этих кругов равна . Тогда площадь общей части этих кругов равна
|
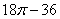
|
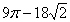
|
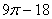
|
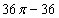
|
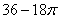
|
|
OK |
3.1.4. |
4.2. |
4.2. |
A. |
|
16. Если в равнобокой трапеции высота равна 14, основания равны 12 и 16, то площадь круга, описанного около трапеции, равна |
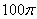
|
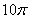
|
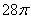
|
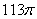
|
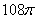
|
|
OK |
4.2. |
4.2. |
4.2. |
L. |
|
Алгебраические преобразования |
|
1. Результат упрощения выражения 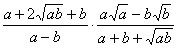 имеет вид имеет вид |
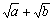
|
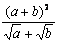
|
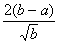
|
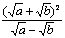
|
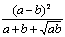
|
|
OK |
J. |
E. |
D. |
J. |
|
2. Результат упрощения выражения имеет вид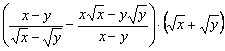 |
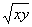
|
0 |
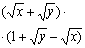
|
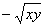
|
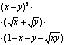
|
|
OK |
D. |
A., D. |
D. |
H. |
|
3. Результат сокращения дроби 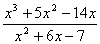 имеет вид имеет вид |
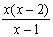
|
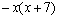
|
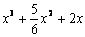
|
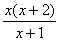
|
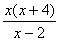
|
|
OK |
I. |
I. |
1.1.1. |
1.1.1. |
|
4. Результат упрощения выражения 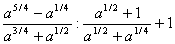 имеет вид имеет вид |
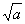
|
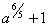
|
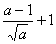
|
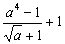
|
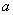
|
|
OK |
E. |
D., L. |
E. |
E. |
|
5. Результат упрощения выражения 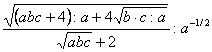 имеет вид имеет вид |
1 |
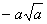
|
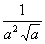
|
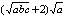
|
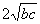
|
|
OK |
E. |
E. |
I. |
K. |
|
6. Результат упрощения выражения 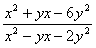 имеет вид имеет вид |
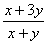
|
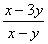
|
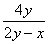
|
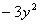
|
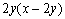
|
|
OK |
J. |
I. |
I., L. |
I. |
|
7. Результат упрощения выражения 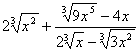 имеет вид имеет вид |
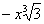
|
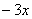
|
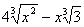
|
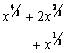
|
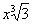
|
|
OK |
K. |
I. |
I., C. |
L. |
|
8. Результат упрощения выражения 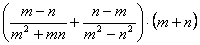 имеет вид имеет вид |
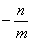
|
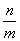
|
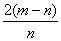
|
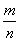
|
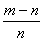
|
|
OK |
I., H. |
D. |
E. |
A. |
|
9. Результат вычисления 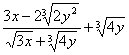 имеет вид имеет вид |
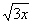
|
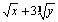
|
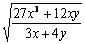
|
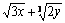
|
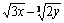
|
|
OK |
K., I. |
K., D. |
K., I. |
I., K. |
|
10. Результат упрощения выражения 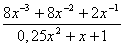 имеет вид имеет вид |
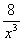
|
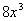
|
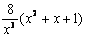
|
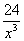
|
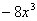
|
|
OK |
J. |
I. |
I. |
E. |
| | | | | | | | | | | | |