Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Страница 5
Решение:
Пусть 
-количество черной, зеленой и синей ткани соответственно.
Известно: 
. Используем формулу:
, где 
- цена ткани, S – стоимость куска, q – количество ткани.
Пусть S = 1. Получим 
- цены тканей. Составим уравнение, связывающее эти стоимости: 
.
Выразим 
и 
через 
: 
.
Подставляем в последнее уравнение: 
.
. Получили
.
Ответ: 
.
Задача 20.
Решить уравнение: 
.
Решение:
По формулам приведения приведем все функции к одному аргументу: 
. Получили уравнение: 
. По формулам сокращенного умножения разложим на множители: 
. По основному тригонометрическому тождеству 
, поэтому остается решить уравнение: 
.
Рассмотрим 2 случая:
1. 
. Разделим на
, причем 
. Тогда имеем уравнение: tg x = 1. Следовательно, 
.
2. 
. Разделим на, причем . Тогда имеем уравнение: tg x = -1. Следовательно, 
.
Получили ответ: 
.
Задача 21.
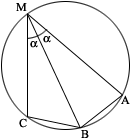
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1 см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.
Решение:
Отрезки 
и 
равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения второе и получим: 
. Значит, 
. Треугольник 
вписан в окружность, следовательно, радиус данной окружности можно найти с помощью теоремы синусов: 
. Ответ: 
.
Задача 22.
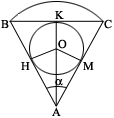
Решить задачу: В сектор радиуса 
с центральным углом 
вписан круг. Найти его радиус.
Решение:
Треугольник ABC – равнобедренный, т.к. AB=AC=R. Найдем BC по теореме косинусов: 
. 
, т.к. АК – высота треуг-ка АВС, следовательно, 
. Из прямоугольного треуг-ка АВК: 
. 
, где ОН=r. Из прямоугольного треуг-ка АОН: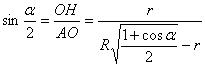 
, значит, ответ: 
.
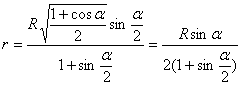Задача 23.
Решить уравнение: 
.
Решение:
ОДЗ:
.
Применяя формулы понижения степени, приведем это уравнение к более простому виду: 
, 
,
.
Отсюда, используя формулу преобразования суммы косинусов в произведение, получаем: 
,
,
.
Рассмотрим 2 случая:
1. 
;
2. 
, следовательно, используя вновь формулу преобразования суммы косинусов в произведение, имеем:
a) 
;
b) 
.
Таким образом, учитывая ОДЗ, получаем
Ответ: 
.
Задача 24.
Решить уравнение: 
.
Решение:
ОДЗ: .
Введем новую переменную, положив t = tg x. Так как 
, то уравнение примет вид:
или 
. Число 2 является корнем полученного уравнения, поэтому это уравнение можно преобразовать следующим образом: 
. Сократим на (t-2). Квадратный трехчлен во второй скобке не имеет действительных корней. Следовательно, исходное уравнение не имеет корней.
Ответ: решений нет.
Задача 25.
Решить уравнение: 
.