Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия
Страница 6
Решение:
Преобразуем уравнение следующим образом:
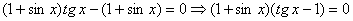 .
.
Рассмотрим 2 случая:
1. 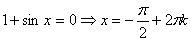 ;
;
2. 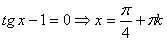 ;
;
Ответ: 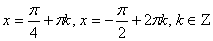 .
.
Задача 26.
Решить систему: 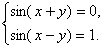
Решение:
Каждое из уравнений этой системы является простейшим, поэтому нетрудно заметить, что
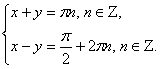
Решая последнюю систему, получаем
Ответ: 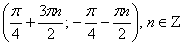 .
.
Задача 27.
Решить задачу: Основания трапеции 5 дм и 40 см. Найти длину отрезка, соединяющего середины диагоналей.
Решение:
|
|
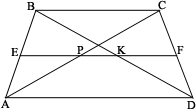
Пусть ABCD – трапеция, точка Р – середина диагонали АС, точка К – середина диагонали BD. |
Нетрудно заметить, что точки Р и К лежат на средней линии EF трапеции. Так как ЕК – средняя линия треугольника ABD, то 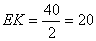 . Аналогично,
. Аналогично, 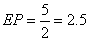 , поскольку является средней линией треугольника АВС. Следовательно,
, поскольку является средней линией треугольника АВС. Следовательно, 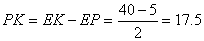 .
.
Ответ: 17.5 см.
Задача 28.
Решить задачу: Даны 2 стороны треугольника a, b и медиана 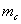 , проведенная к стороне c. Найти сторону с.
, проведенная к стороне c. Найти сторону с.
Решение:
|
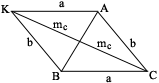
|
Достроим треугольник АВС до параллелограмма АВСК. При этом 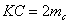 . По свойству параллелограмма сумма его диагоналей равна сумме его сторон. Поэтому из равенства . По свойству параллелограмма сумма его диагоналей равна сумме его сторон. Поэтому из равенства 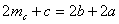 получаем получаем |
Ответ: 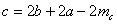 .
.
Задача 29.
Решить задачу: Даны 2 стороны треугольника a, b и медиана 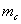 , проведенная к стороне c. Найти сторону с.
, проведенная к стороне c. Найти сторону с.
Решение:
Воспользуемся формулой 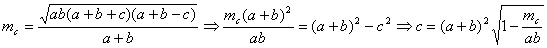 .
.
Ответ: 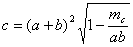 .
.
Задача 30.
Решить задачу: Несколько рабочих выполняют работу за 14 дней. Если бы их было на 4 человека больше и каждый работал в день на 1 час больше, то та же работа была бы сделана за 10 дней. Если бы их было еще на 6 человек больше и каждый работал бы еще на 1 час в день больше, то эта работа была бы сделана за 7 дней. Сколько было рабочих, и сколько часов в день они работали?
Решение:
Пусть w - число рабочих, х – число часов их работы в день. Пусть вся работа равна единице, а у – производительность (в час) каждого рабочего.
Тогда один рабочий за х часов (т.е. в день) выполняет ху единиц работы, а w рабочих за 14 дней выполнят 14wxy единиц работы. Согласно условию 14wxy = 1.
Аналогично, если рабочих стало w + 4, и они работают каждый день х + 1 час, то
10(w + 4)(x + 1)y = 1.
Для случая, когда рабочих еще на 6 человек больше (т.е. w + 6), и они работают еще на час дольше (т.е. х + 1 часа) каждый день, получаем уравнение 7(w + 6)(x + 1)y = 1.
Из системы
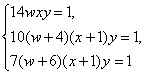
надо найти w, x.
Приравняв левые части первого и второго, а также первого и третьего уравнений и упростив, получим систему
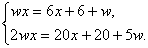
Отсюда легко получается, что 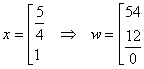 . Следовательно, второе значение х не подходит. Поэтому получили
. Следовательно, второе значение х не подходит. Поэтому получили
Ответ: всего было 54 рабочих; они работали 1,25 часов в день.
3.2. Ответы (протоколы верных решений)
Задача 1.
Решить неравенство: 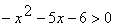 .
.
Решение:
Найдем корни квадратного уравнения 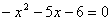 по теореме Виета:
по теореме Виета:
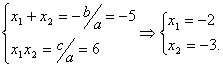 График функции
График функции 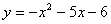 - это парабола, ветви которой направлены вниз:
- это парабола, ветви которой направлены вниз:
|
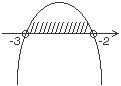
|
Нужно отметить те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 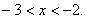 |
Задача 2.
Решить неравенство: 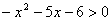 .
.
Решение:
Найдем корни квадратного уравнения 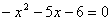 по теореме Виета:
по теореме Виета:
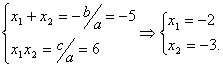 График функции
График функции 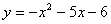 - это парабола, ветви которой направлены вниз:
- это парабола, ветви которой направлены вниз:
|

|
Нужно отметить те значения x, при которых график находится выше оси Ox. Следовательно, получаем ответ: 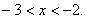 |
Задача 3.
Решить неравенство: 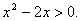
Решение:
Корни уравнения 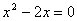 :
: 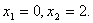 График функции
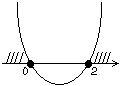
График функции 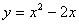 - это парабола, ветви которой направлены вверх.
- это парабола, ветви которой направлены вверх.
|
|
Выберем те значения x, при которых график находится выше оси Ox. Следовательно, получаем
ответ: 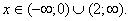 |
Задача 4.
Решить неравенство: 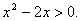
Решение:
Корни уравнения 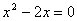 :
: 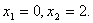 График функции
График функции 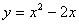 - это парабола, ветви которой направлены вверх.
- это парабола, ветви которой направлены вверх.
|

|
Выберем те значения x, при которых график находится выше оси Ox. Следовательно, получаем
ответ: 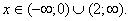 |
Задача 5.
Решить неравенство: 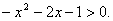
Решение:
Домножим неравенство на –1, получим: 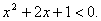 Выделим полный квадрат:
Выделим полный квадрат: 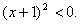 В левой части неравенства стоит неотрицательное число, а значит неравенство неверно при любых значениях x, т.е. не имеет решений.
В левой части неравенства стоит неотрицательное число, а значит неравенство неверно при любых значениях x, т.е. не имеет решений.