Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия

Страница 7

Запишем окончательный ответ: решений нет.

Задача 6.

Решить систему неравенств: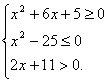

Решение:

Решаем каждое из неравенств системы в отдельности:

1.

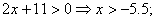
2.

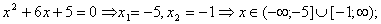
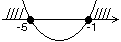
3.

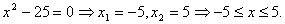
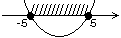
Для того, чтобы получить решение системы, возьмем пересечение всех полученных интервалов.

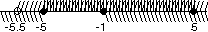
Ответ: .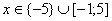

Задача 7.

Решить уравнение: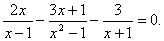

Решение:

ОДЗ: .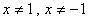

Приведем дроби к общему знаменателю и отбросим знаменатель:

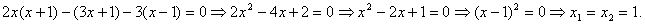Но x=1 не входит в ОДЗ, поэтому ответ: решений нет.

Задача 8.

Решить уравнение: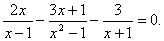

Решение:

ОДЗ: 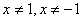, т.к. знаменатель не должен обращаться в ноль.

Приведем дроби к общему знаменателю и отбросим знаменатель:

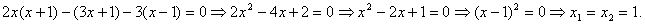Но x=1 не входит в ОДЗ, поэтому ответ: решений нет.

Задача 9.

Решить уравнение: .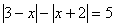

Решение:

Рассмотрим 4 возможных случая:

1. 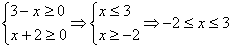. В этом случае получаем уравнение 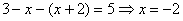. Это значение удовлетворяет уравнению, поэтому является корнем данного уравнения.

2. 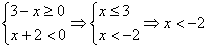. В этом случае получаем уравнение 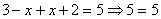. Решение: .

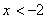3. 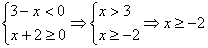. В этом случае получаем уравнение 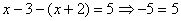. Решений нет.

4. 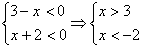- этот случай не возможен.

Объединяя найденные решения, получаем окончательный ответ: .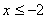

Задача 10.

Решить уравнение: .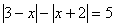

Решение:

Рассмотрим 4 возможных случая:

1. 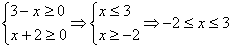. В этом случае получаем уравнение 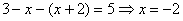. Это значение удовлетворяет уравнению, поэтому является корнем данного уравнения.

2. 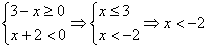. В этом случае получаем уравнение 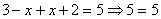. Решение: .

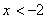3. 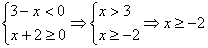. В этом случае получаем уравнение 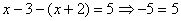. Решений нет.

4. 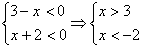- этот случай не возможен.

Объединяя найденные решения, получаем окончательный ответ: .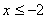

Задача 11.

Решить уравнение: .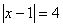

Решение:

Возможны 2 случая:

1. 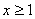. Тогда уравнение примет вид: 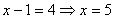- корень исходного уравнения.

2. 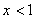. Тогда уравнение примет вид: 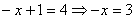- корень исходного уравнения.

Ответ: .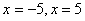

Задача 12.

Решить уравнение: .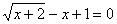

Решение:

ОДЗ: .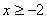

Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в правую: 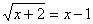. Затем возводим в квадрат: 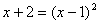, причем т.к. 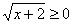, то для корректности возведения в квадрат необходимо, чтобы 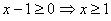. Получим уравнение 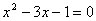. Найдем его корни:

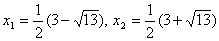. Оба корня удовлетворяют ОДЗ, но только один 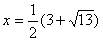удовлетворяет дополнительному ограничению 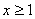. Поэтому ответ: .

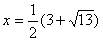Задача 13.

Решить уравнение: .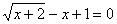

Решение:

ОДЗ: .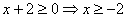

Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в правую: 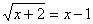. Затем возводим в квадрат: 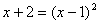, причем т.к. 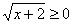, то для корректности возведения в квадрат необходимо, чтобы 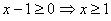. Получим уравнение 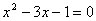. Найдем его корни: 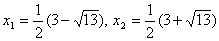. Оба корня удовлетворяют ОДЗ, но только один 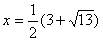удовлетворяет дополнительному ограничению 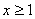. Поэтому ответ: .

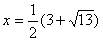Задача 14.

Решить уравнение: .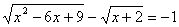

Решение:

ОДЗ: .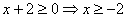

Выделим полный квадрат под первым знаком корня: .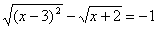

Получим уравнение: .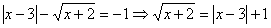

Рассмотрим 2 случая:

1. 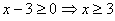. Получим 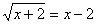. Возведем обе части уравнения в квадрат с учетом 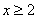, получим 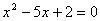. Найдем корни: 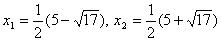. Учитывая ОДЗ и дополнительное ограничение 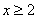, получаем корень: .

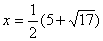2. x<3. Получим 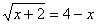. Возведем обе части уравнения в квадрат с учетом 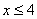, получим 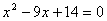. Найдем корни: 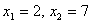. Учитывая ОДЗ и дополнительное ограничение 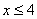, получаем корень: .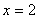