Введение во фракталы
Страница 2
Доказательство приводится в [1].
2.3. Ковер Серпинского.
Еще один пример простого самоподобного фрактала --- ковер Серпинского (рис. 2.3.1), придуманный польским математиком Вацлавом Серпинским в 1915 году. Сам термин ковер (gasket) принадлежит Мандельброту. В способе построения, следующем ниже, мы начинаем с некоторой области и последовательно выбрасываем внутренние подобласти. Позднее мы рассмотрим и другие способы, в частности с использованием L-систем, а также на основе итерированных функций.
Рис 2.3.1. Ковер Серпинского

Пусть начальное множество S0 --- равносторонний треугольник вместе с областью, которую он замыкает. Разобьем S0 на четыре меньшие треугольные области, соединив отрезками середины сторон исходного треугольника. Удалим внутренность маленькой центральной треугольной области. Назовем оставшееся множество S1 (рис. 2.3.2). Затем повторим процесс для каждого из трех оставшихся маленьких треугольников и получим следующее приближение S2. Продолжая таким образом, получим последовательность вложенных множеств Sn, чье пересечение образует ковер S.
Из построения видно, что весь ковер представляет собой объединение N = 3 существенно не пересекающихся уменьшенных в два раза копий; коэффициент подобия r = ½ (как по горизонтали, так и по вертикали). Следовательно, S --- самоподобный фрактал с размерностью:
d = log(3)/log(2) ~ 1,5850.
Рис. 2.3.2. Построение ковра Серпинского

Очевидно, что суммарная площадь частей, выкинутых при построении, в точности равна площади исходного треугольника. На первом шаге мы выбросили ¼ часть площади. На следующем шаге мы выбросили три треугольника, причем площадь каждого равна ¼ 2 площади исходного. Рассуждая таким образом, мы убеждаемся, что полная доля выкинутой площади составила:
1/4 + 3*(1/42) + 32*(1/43) + … + 3n-1*(1/4n) + … .
Эта сумма равна 1 (доказательство в [1]). Следовательно, мы можем утверждать, что оставшееся множество S, то есть ковер, имеет площадь меры нуль. Это выделяет множество S в разряд «совершенного», в том смысле, что оно разбивает свое дополнение на бесконечное число треугольных областей, обладая при этом нулевой толщиной.
3. L-системы.
Понятие L-систем, тесно связанное с самоподобными фракталами, появилось только в 1968 году благодаря Аристриду Линденмайеру. Изначально L-системы были введены при изучении формальных языков, а также использовались в биологических моделях селекции. С их помощью можно строить многие известные самоподобные фракталы, включая снежинку Коха и ковер Серпинского. Некоторые другие классические построения, например кривые Пеано (работы Пеано, Гильберта, Серпинского), также укладываются в эту схему. И конечно, L-системы открывают путь к бесконечному разнообразию новых фракталов, что и послужило причиной их широкого применения в компьютерной графике для построения фрактальных деревьев и растений. Рассмотренные в данной курсовой работе L-системы ограничиваются случаем детерминированных L-систем и графикой на плоскости.
Для графической реализации L-систем в качестве подсистемы вывода используется так называемая тертл-графика (turtle – черепаха). При этом точка (черепашка) движется по экрану дискретными шагами, как правило прочерчивая свой след, но при необходимости может перемещаться без рисования. В нашем распоряжении имеются три параметра (x,y,a), где (x,y) --- координаты черепашки, a --- направление, в котором она смотрит. Черепашка обучена интерпретировать и выполнять последовательность команд, задаваемых кодовым словом, буквы которого читаются слева направо. Кодовое слово представляет собой результат работы L-системы и может включать следующие буквы:
F --- переместиться вперед на один шаг, прорисовывая след.
b --- переместиться вперед на один шаг, НЕ прорисовывая след.
[ --- открыть ветвь (подробнее см. ниже)
] --- закрыть ветвь (подробнее см. ниже)
+ --- увеличить угол a на величину q
- --- уменьшить угол a на величину q
Размер шага и величина приращения по углу q задаются заранее и остаются неизменными для всех перемещений черепашки. Если начальное направление движения а (угол, отсчитываемый от положительного направления оси Х) не указано, то полагаем а равным нулю.
Несколько примеров иллюстрируют применение команд ветвления (обозначаются ],[) и вспомогательных переменных (обозначаются X, Y, и т.д.). Команды ветвления используются для построения деревьев растений, а вспомогательные переменные заметно облегчают построение некоторых L-систем.
Формально, детерминированная L-система состоит из алфавита, слова инициализации, называемого аксиомой или инициатором, и набора порождающих правил, указывающих, как следует преобразовывать слово при переходе от уровня к уровню (от итерации к итерации). К примеру, можно заменять букву F при помощи порождающего правила newf = F-F++F-F, что соответствует L-системе для снежинки Коха, рассматриваемой ниже. Символы +, -, ], [ не обновляются, а просто остаются на тех местах, где они встретились. Обновление букв в данном слове предполагается одновременным, то есть буквы слова одного уровня обновляются раньше любой буквы следующего уровня.
L-система, соответствующая снежинке Коха (рис. 2.2.1), задается следующим образом:
p = p/3
Аксиома: F++F++F
Порождающее правило: newf = F-F++F-F
Графическое представление аксиомы F++F++F --- равносторонний треугольник. Черепашка делает один шаг вперед, затем угол а увеличивается на 2p/3 и черепашка делает еще один шаг.
На первом шаге каждая буква F в слове-инициаторе F++F++F заменяется на F-F++F-F:
(F-F++F-F)+(F-F++F-F)+(F-F++F-F)
Повторяя этот процесс, на втором шаге получим:
F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F+F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F+ F-F++F-F- F-F++F-F++F-F++F-F-F-F++F-F
и т.д. Причем, убедившись на собственном опыте программирования L-систем знаю, что для снежинки Коха на 20-й итерации порождающее правило занимает несколько мегабайт текста !
Вот еще некоторые фракталы, построенные с использованием L-системы:
Рис. 3.1. Дракон Хартера-Хатвея после 12-ти итераций
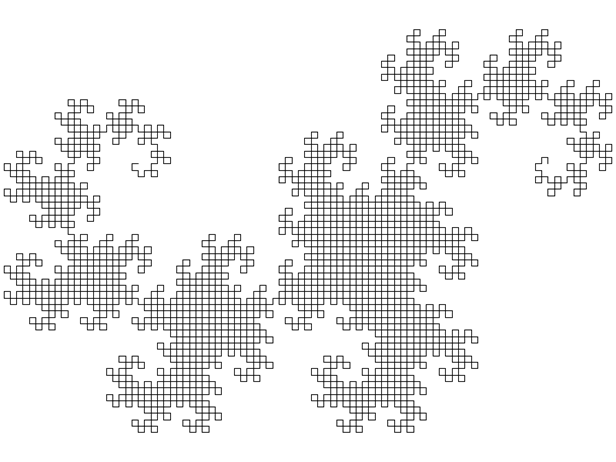
и его L-система:
p = p/4
Аксиома: FX
Порождающее правило: newf = F
newx = X+YF+
newy = -FX-Y
Рис 3.2. Дерево после 5-ти итераций

и его L-система:
p = p/7
Аксиома: F
Порождающее правило: newf = F[+F]F[-F]F
Рис. 3.3. Квадрат Госпера после 2-х итераций [2]
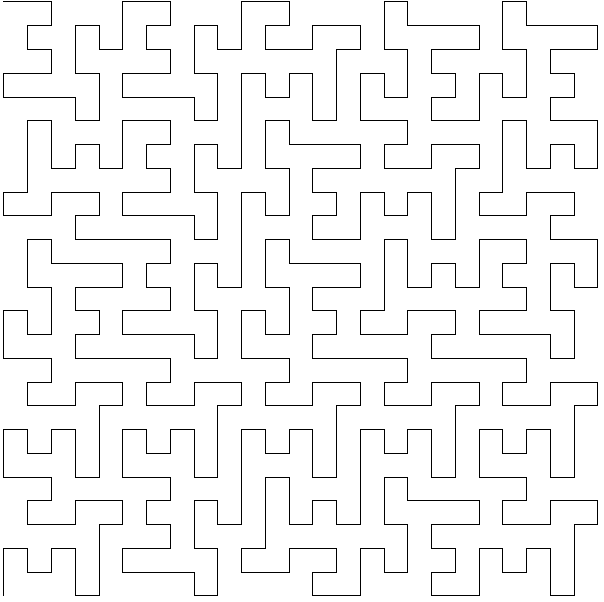
и его L-система:
p = p/2
Аксиома: -FX
Порождающее правило: newf = F
newx=+FYFY-FX-FX+FY+FYFX+FY-FXFX-FY-FX+FYFXFX-FY-FXFY+FY+FX-FX-FY+FY+FXFX
newy=FYFY-FX-FX+FY+FY-FX-FXFY+FX+FYFYFX-FY+FX+FYFY+FX-FYFX-FX-FY+FY+FXFX-
4. ХАОТИЧЕСКАЯ ДИНАМИКА
4.1. Аттрактор Лоренца
До настоящего момента мы изучали фракталы, которые являются статическими фигурами. Наш подход вполне приемлем до тех пор, пока не возникает необходимость рассмотрения таких природных явлений, как падающие потоки воды, турбулентные завихрения дыма, метеосистемы и потоки на выходе реактивных двигателей. В этих случаях один-единственный фрактал соответствует моментальному снимку данного феномена. Структуры, изменяющиеся во времени, мы определяем как динамические системы. Интуитивно понятно, что динамической противоположностью фрактала является хаос. Это означает, что хаос описывает состояние крайней непредсказуемости, возникающей в динамической системе, в то время как фрактальность описывает крайнюю иррегулярность или изрезанность, присущую геометрической конфигурации.
Достаточно скоро стало ясно, что многие хаотические динамические системы, описывающие феномены окружающего нас мира, устроены очень сложно и не могут быть представлены традиционными методами математического анализа. По-видимому, нет никакой возможности получить математические выражения для решений в замкнутом виде, даже если использовать бесконечные ряды или специальные функции.