Введение во фракталы

Страница 3

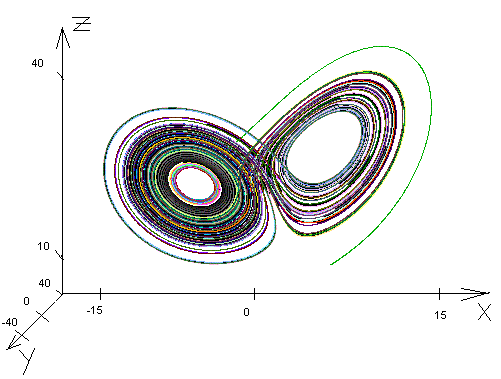
Рассмотрим знаменитый пример, весьма наглядно демонстрирующий, что стоит за термином «хаотическая динамика». Эдвард Лоренц из Массачусетского технологического института в 1961 году занимался численными исследованиями метеосистем, в частности моделированием конвекционных токов в атмосфере[1]. Он написал программу для решения следующей системы дифференциальных уравнений:

dx/dt = s(-x + y),

dy/dt = rx – y – xz,

dz/dt = -bz + xy.

В дальнейших расчетах параметры s, r и b постоянны и принимают значения s = -10, r = 28 и b = 8/3.

Согласно описанию эксперимента, принадлежащему самому Лоренцу, он вычислял значения решения в течение длительного времени, а затем остановил счет. Его заинтересовала некоторая особенность решения, которая возникала где-то в середине интервала счета, и поэтому он повторил вычисления с этого момента. Результаты повторного счета, очевидно, совпали бы с результатами первоначального счета, если бы начальные значения для повторного счета в точности были равны полученным ранее значениям для этого момента времени. Лоренц слегка изменил эти значения, уменьшив число верных десятичных знаков. Ошибки, введенные таким образом, были крайне невелики. Но самое неожиданное было впереди. Вновь сосчитанное решение некоторое время хорошо согласовывалось со старым. Однако, по мере счета расхождение возрастало, и постепенно стало ясно, что новое решение вовсе не напоминает старое (рисунки приведены в [1], стр. 149).

Лоренц вновь повторял и проверял вычисления (вероятно, не доверяя компьютеру), прежде чем осознал важность эксперимента. То, что он наблюдал, теперь называется существенной зависимостью от начальных условий --- основной чертой, присущей хаотической динамике. Существенную зависимость иногда называют эффектом бабочки. Такое название относится к невозможности делать долгосрочные прогнозы погоды. Сам Лоренц разъяснил это понятие в статье «Предсказуемость: может ли взмах крылышек бабочки в Бразилии привести к образованию торнадо в Техасе?», опубликованной в 1979 году [3, стр. 322].

Несмотря на большую значимость эксперимента Лоренца, в данной курсовой работе не будут рассматриваться модели, связанные с динамическими системами, описываемыми дифференциальными уравнениями. Напротив, мы будем рассматривать наиболее простые модели хаотической динамики --- дискретные, к которым относится знаменитое и вездесущее множество Мандельброта и сопутствующие ему множества Жюлиа.

Рис. 4.1.1. Аттрактор Лоренца.

4.2. Множества Мандельброта и Жюлиа.

Вероятно, нельзя привести пример такого компьютерного эксперимента, который впечатлением от результатов превосходил бы то чувство удивления, и восхищения, которое вызывает графическое построение множеств Мандельброта и множества Жюлиа на плоскости. Эти множества относятся к хаотической динамике на комплексной плоскости.

Множество Мандельброта и множество Жюлиа определяется как граница множества точек z, стремящихся к бесконечности при итерировании

f(z) = z2+c,

где с – комплексная константа. При этом множества Жюлиа (см. рис. 4.2.2) при разных с могут представляться как угодно сложно и красиво, но все они распределяются на два типа: связные или несвязные. Множество Мандельброта (см. рис. 4.2.1) служит индикатором для двух типов множеств Жюлиа функции z2+c. Каждая точка в множестве Мандельброта представляет значение с, для которого множество Жюлиа вполне связно и каждая точка из дополнения к множеству Мандельброта представляет значение с, для которого множество Жюлиа вполне несвязно.

Построение данных множеств сводится к построению орбит f(z), проверяемых на ограниченность. То есть на рисунок попадает только та точка на комплексной плоскости (представляемая плоским экраном монитора), которая при итерировании функции f(z0), последняя не стремится к бесконечности, а остается ограниченной на каком-то уровне. Проверка идет для каждой точки (x,y).

Несложно написать программу для построения множества Мандельброта. Единственная проблема, которая может возникнуть при использовании этой программы на маломощных ЭВМ --- большой объем вычислений. Для того, чтобы получить приемлемое изображение множества, желательно отображать по меньшей мере 256x256 пикселов. Более удачные визуализации получаются при использовании окна 400x400 пикселов и более. При этом количество итераций достаточно 20-ти. Для получения более качественного построения множества можно увеличить количество итераций до 50, 70, 100 и более.

Рис 4.2.1 Область 3-периодичности множества Мандельброта

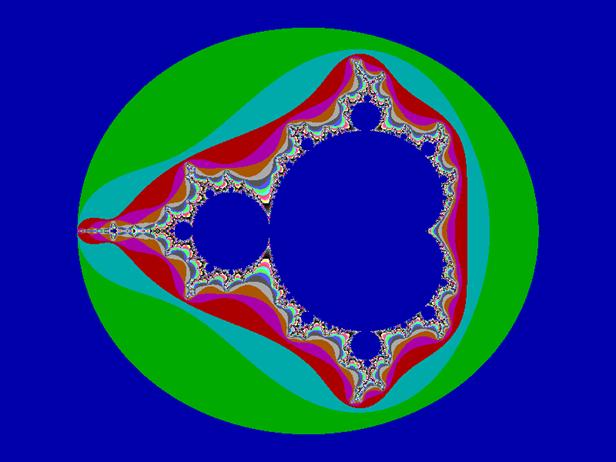
Рис. 4.2.2. Множество Жюлиа.

5. ЗАКЛЮЧЕНИЕ.

Данная курсовая работа является введением в мир фракталов. Мы рассмотрели только самую малую часть того, какие бывают фракталы, на основе каких принципов они строятся. Например в книгу [1] включено рассмотрение СИФ (систем итерированных функций), случайных фракталов, и многое другое из теории фракталов.

В дополнение хочется отметить применение фракталов в компьютерных технологиях, помимо просто построения красивых изображений на экране компьютера. Фракталы в компьютерных технологиях применяются в следующих областях:

1. Сжатие изображений и информации

2. Сокрытие информации на изображении, в звуке,…

3. Шифрование данных с помощью фрактальных алгоритмов

4. Создание фрактальной музыки

5. Моделирование систем

6. СПИСОК ЛИТЕРАТУРЫ

1. Фракталы и хаос в динамических системах. Основы теории. Москва: Постмаркет, 2000. – 352 с.

3. James Gleick, Chaos: Making a New Science, Viking, New York, 1987.

[1] Исследование аттрактора Лоренца включается сейчас в любой

математический пакет, например, Mathematica, Maple.