Векторы
Страница 4
Положим: а = СВ, в = СА,
![]() с = АВ (рис.10).
с = АВ (рис.10).
Тогда с = а – в, и мы имеем
(учитывая, что угол между векторами а и в равен С):
с2 = ( а – в )2 = а2 – 2ав + в2 = а2 – 2ав х соs С + в2.
Задача 4.
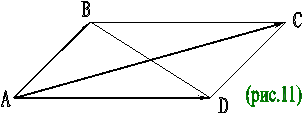
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Решение.
Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства
![]()
![]()
![]()
![]()
![]()
![]() АВ + AD = АС, АВ – АD = DВ.
АВ + AD = АС, АВ – АD = DВ.
Возведем эти равенства в квадрат. Получим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2
Сложим эти равенства почленно. Получим:
2АВ2 + 2 АD2 = АС2 + DВ2.
Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.
Задача 5.
![]()
![]() Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y), чтобы векторы АВ и СD были равны.
Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y), чтобы векторы АВ и СD были равны.
Решение.
![]()
![]()
![]()
![]() Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y –1. Так как АВ = СD, то х – 0 = -2, y –1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.
Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y –1. Так как АВ = СD, то х – 0 = -2, y –1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.
Задача 6.
![]()
![]() Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они друг другу или нет.
Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они друг другу или нет.
Решение.
![]()
![]() Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).
Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).
![]()
![]() Вычислим теперь скалярное произведение этих векторов:
Вычислим теперь скалярное произведение этих векторов:
![]()
![]() AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
![]() Последнее озночает, что АВ СD.
Последнее озночает, что АВ СD.
Рассмотренные выше примеры задач показывают, что векторный метод является весьма мощных средством решения геометрических и многих физических (и технических) задач.
Содержание:
1. Что такое вектор?
2. Сложение векторов.
3. Равенство векторов.
4. Скалярное произведение двух векторов и его свойства.
5. Свойства операций над векторами.
6. Доказательства и решение задач.
Используемая литература.
1. «Векторы в школьном курсе геометрии». (1976 г.)
В.А.Гусев. Ю.М.Колягин. Г.Л.Луканкин.
2. «Векторы в курсе геометрии средней школы. (1962 г.)
В.Г.Болтянский. И.М.Яглом.