Внеклассная работа по математике в школе

Страница 5

3. (ABDE)(BCEF)=(ABC)(DEF)(BE). Учитывая, что ABDE=BCEF=4, ABC=DEF=1, получаем равенство: 16=BE. Аналогично получим, что EH=16. Перемножаем полученные равенства: (BE)(EH)=(BEH)E. 1616=E.

Ответ: E=256.

4. Обозначим 2001=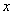. Тогда данное нам числовое выражение запишется в виде:.

Тогда .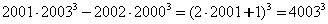

5. Пусть Nk, Ns и Nz - количество красных, синих и зелёных амёб, соответственно. В начальный момент времени 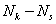, 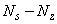- нечётны, 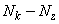- чётно. Нетрудно проверить, что при любом слиянии эти чётности сохраняются. Поэтому в конце концов 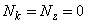, 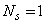. Ответ: последняя амёба - синяя.

РЕШЕНИЯ. 10 КЛАСС.

1. Пусть x$ - стоимость первого автомобиля, y$ - стоимость второго автомобиля. При продаже Вася получил 9000$ чистой прибыли. Составляем систему уравнений:

.

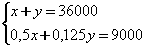Решив систему, найдём 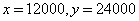. Тогда сумма штрафа составляет 12000$. 12000 - 9000=3000.

Таким образом, Вася потерял 3000$.

A1	A2	A3	A4	A5	A6	A7	A8
B1	B2	B3	B4	B5	B6	B7	B8
C1	C2	C3	C4	C5	C6	C7	C8

2. (A1A2A3B1B2B3C1C2C3) (A3A4A5B3B4B5C3C4C5) (A6A7A8B6B7B8C6C7C8)=(A1A2A3A4A5A6A7A8)

 (B1B2B3B4B5B6B7B8) (C1C2C3C4C5C6C7C8)(A3B3C3).

Т.е. A3B3C3=8. Аналогично - C1C2C3=8.

Произведение чисел в квадрате 66, стоящем на пересечении 3-8 столбцов и 3-8 строк равно 16, так как этот квадрат разбивается на 4 квадрата 33. В оставшемся уголке (на рисунке он заштрихован) произведение чисел равно 1/16, так как во всей таблице произведение равно 1. Но произведение чисел в закрашенном уголке можно также получить, перемножив числа первой и второй строк, первого и второго столбца и разделив всё это на A1A2B1B2. Отсюда A1A2B1B2=16.

(A1A2B1B2)( A3B3C3)( C1C2C3)=(A1A2A3B1B2B3C1C2C3)C3.

1688=2С3. Откуда С3=512, A3B3=8/512=1/64.

Ответ: 1/64.

3.

.

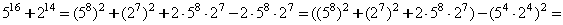
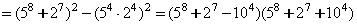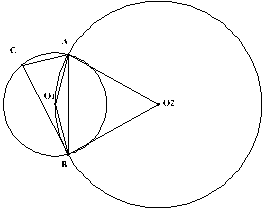
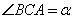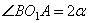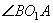4. Пусть вписанный в первую окружность . Соответствующий ему центральный угол . Но вписан во вторую окружность, поэтому 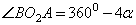. 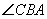- это угол между касательной BC и секущей AB, поэтому 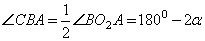. Тогда по теореме о сумме углов треугольника, 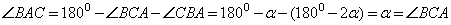. Значит, 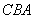- равнобедренный. AB=BC, что и требовалось доказать.

5. Каждому цвету поставим в соответствие один из остатков по модулю 4. Синий - 0, оранжевый - 1, фиолетовый - 2, зелёный - 3. Вместо хамелеонов будем рассматривать 2002 целых числа, стоящие по кругу. Операция смены цвета в новой трактовке будет равносильна прибавлению 1 к четырём последовательно стоящим числам. (При этом, если будет получаться число, большее 3, то оно заменяется на остаток от деления на 4.) В начальный момент времени по кругу стоят нули и нам требуется узнать, можно ли путём указанной операции сделать все числа, равные трём.

В начальный момент времени сумма равна 0 и на каждом шаге она может изменяться лишь на величину, кратную четырём, т.е. сумма всех чисел на каждом шаге будет делиться на 4. Поэтому 2002 тройки (которые в сумме дают 6006=41501+2) получить нельзя.

РЕШЕНИЯ. 11 КЛАСС.

1. Перенесём все слагаемые в левую часть.

.

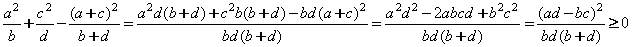2. ,

,

,

………

.

.

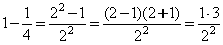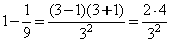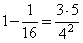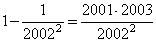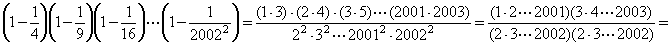
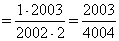3. Пусть x - количество мальчиков, y - количество девочек. - стоимость сникерса, 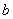- стоимость марса (в копейках). Составим уравнение.

.

.

.
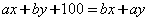
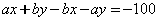
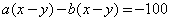