Возможности использования элементов теории вероят-ностей и статистики на уроках математики в начальной школе
Страница 5
В дальнейшем в задачах мы будем сталкиваться со случаями, когда несколько опытов проводятся независимо друг от друга. Как в предыдущем образце, можно показать, что вероятность события “исход первого опыта есть A, а второго — B” равно произведению вероятностей событий “исход первого опыта есть A” и “исход второго опыта есть B”.
Вернемся к задаче. В матче из четырех партий имеется 16 равновероятных исходов — последовательностей побед и поражений первого игрока. Событию “первый игрок победил в 3 партиях” благоприятны 4 исхода, поскольку единственное поражение может стоять на одном из четырех мест. Значит, вероятность выиграть 3 партии из 4-х у равносильного противника равна 1/4.
В матче из 8 партий имеется 28 = 256 равновозможных исходов — последовательностей побед и поражений первого игрока. В скольких из них ровно 5 побед? Другими словами, сколько существует подмножеств из 5 элементов в множестве из 8 элементов? Комбинаторика подсказывает нам, что это есть число сочетаний из 8 элементов по 5 элементов, которое подсчитывается по формуле: 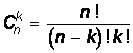 . Таким образом,
. Таким образом,
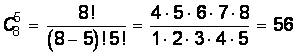 .
.
Значит вероятность выиграть 5 партий из 8 у равносильного противника равна 56/256 = 7/32, что меньше 1/4 = 8/32 — вероятности выиграть три партии из четырех.
Задача 8. Пусть вы забыли одну цифру нужного вам номера телефона и набираете ее наудачу. Какова вероятность того, что вам придется сделать не более двух звонков?
Обсуждение. Вероятность того, что первый же раз вы наберете правильный номер равна 1/10 , поскольку цифр всего десять; все десять исходов — набор 1, набор 2 и т. д. — равновозможны, а благоприятным является только один из них. Если первый раз забытая цифра была набрана неправильно, то при втором звонке вы будете набирать одну из девяти оставшихся цифр, и вероятность успеха будет равна 1/9. Ровно два звонка будут сделаны с вероятностью 9/10´1/9 = 1/10. Вероятность того, что придется сделать не более двух звонков, равна 1/10 + 1/10 = 0,2.
Задача 9. Бросают три игральные кубика. Что вероятнее: сумма очков на верхних гранях равна 11 или эта сумма равна 12? Каковы вероятности этих событий?[6]
Обсуждение. Прежде всего найдем, сколькими способами можно представить 11 и 12 в виде суммы трех натуральных слагаемых, каждое из которых не превосходит 6. Будем выписывать суммы в порядке возрастания слагаемых. Начнем с 11. Если наименьшее слагаемое — 1, то 11 = 1 + 4 + 6 либо 11 = 1 + 5 + 5. Если 2, то 11 = 2 + 3 + 6 либо 11 = 2 + 4 + 5. Если 3, то 11 = 3 + 4 + 4 либо 11 = 3 + 3 + 5. Этими случаями (6) исчерпываются все представления 11 в виде суммы трех чисел, нанесенных на грани кубиков. Число 12 можно представить шестью способами: 12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4. Шевелье де Мере заключил отсюда, что 12 в качестве суммы будет встречаться столь же часто, как и 11. Однако результаты многих игр показали, что, вопреки расчетам де Мере, 11 встречается чаще. Именно тогда Мере усомнился в теории вероятностей и обратился к Паскалю за разъяснениями. Паскаль решил задачу. Оказалось, что теория вероятностей верна, а рассуждения де Мере ошибочны. Шевалье не учел, что. скажем, 4 + 4 + 4 может выпасть одним способом: на всех трех кубиках 4, а 1 + 4 + 6 — многими: на первом — 1, на втором — 4, на третьем — 6 или на первом — 6, на втором — 4, на третьем — 1 и т. д.
Найдем вероятности того, что сумма очков на верхних гранях равна 11, и того, что эта сумма равна 12. При бросании трех кубиков имеется 6´6´6 = 216 равновозможных исходов. Событие “сумма очков равна 11” может осуществиться одним из шести способов: “выпали числа 1, 4, 6”, “выпали числа 1, 5, 5” и т. д. Посчитаем, сколько для каждого из этих способов имеется благоприятных исходов. Событию “выпали 1, 4, 6” соответствуют 6 исходов, которые можно записать так: 146 (на первом кубике на верхней грани 1, на втором — 4, на третьем — 6), 164, 416, 461, 614, 641. Точно так же 6 исходов благоприятны для любого способа представления суммы в виде трех различных слагаемых. Событию “выпали 1, 5, 5” соответствует три исхода: 155, 551, 515. Всего для события “сумма очков равна 11” благоприятны 6 + 3 + 6 + 6 + 3 + 3 = 27 исходов. А событию “сумма очков равна 12” благоприятны 6 + 6 + 3 + 3 + 6 + 1 = 25 исходов, поскольку представлению 4 + 4 + 4 соответствует только один исход — 444. Итак, вероятность того, что сумма очков равна 11, есть 27/216 = 1/8, а вероятность того, что эта сумма равна 12, есть 25/216 = 1/8 - 1/108 < 1/8. Решение этой задачи показывает, как важно правильно выделить равновозможные исходы.
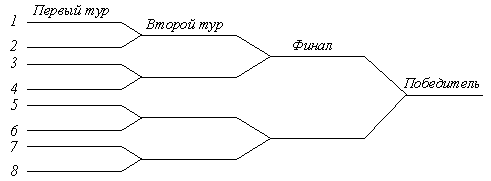
Задача 10. В шахматном турнире участвуют 8 игроков. Номера шести игроков распределяются по жребию. Номер определяет положение игрока в турнирной лестнице. Предположим, что лучший игрок всегда побеждает второго по мастерству, а тот в свою очередь побеждает всех остальных. Второе место занимает проигравший в финале. Какова вероятность того, займет второй по мастерству игрок?
Ðèñ. B
Обсуждение. Второй по мастерству игрок занимает второе место тогда и только тогда, когда он находится в той половине турнирной лестницы (верхней или нижней), в которой нет первого по мастерству игрока, поскольку в противном случае второй проиграет первому ранее финала. Поскольку имеется 7 ступеней турнирной лестницы (кроме ступени, занятой первым по мастерству игроком), которые может занимать второй по мастерству игрок, все эти исходы равновозможны, а 4 из них являются благоприятными для выхода в финал, то искомая вероятность равна 4/7.
Задача 11. Король Артур проводит рыцарский турнир, в котором порядок состязания определяется жребием (по турнирной лестнице). Среди восьми рыцарей, одинаково искусных в ратном деле, два близнеца. Какова вероятность того, что они встретятся в поединке?
Обсуждение. Обозначим близнецов A и B. Если A и B входят в одну пару в турнирной лестнице, что происходит с вероятностью 1/7 (для B равновозможны 7 мест, не занятых A), то близнецы заведомо встречаются в первом же туре. Вероятность того, что B находится в соседней паре, равна 2/7. В этом случае близнецы встречаются во втором туре) только тогда, когда они оба выиграют поединки первого тура, что происходит с вероятностью 1/4. Значит, вероятность события “близнецы встречаются во втором туре” равна 2/7´1/4 = 1/14. Наконец, вероятность того, что B находится в другой половине турнирной лестницы, равна 4/7, и в этом случае вероятность встречи равна 1/4´1/4 = 1/16, поскольку оба должны победить в обоих турах; вероятность события “близнецы встречаются в финале” есть 4/7´1/16 = 1/28. Все возможности перечислены, вероятность встречи в одном из туров есть сумма вероятностей встреч в первом, втором турах и финале, т. е. 1/7 + 1/14 + 1/28 = 1/4.
Задача 12. Задача о разделе ставки (вторая задача Шевалье де Мере, предложенная Паскалю). Подбрасывается монета. Первый игрок “набирает” гербы, а второй — решки. Тот, кто первым наберет три единицы, забирает ставку. Игра была прервана, когда у первого игрока имелось два герба, а у второго — одна решка. Ставка должна быть разделена пропорционально шансам на выигрыш. Как ее разделить?
Обсуждение. Полезно ввести опыт, состоящий в двукратном бросании монеты. Из четырех равновозможных исходов ГР (при первом бросании выпал герб, при втором — решка), ГГ, РГ, РР, в первых трех победа принадлежит первому игроку (в первых двух случаях в самой игре монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку.
Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы)
Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при одних и тех же условиях, а детям предлагают указать результат. Потом условия эксперимента изменяют.