Возможности использования элементов теории вероят-ностей и статистики на уроках математики в начальной школе

Страница 9

В эксперименте принимало участие 15 человек. Нету ни одного учащегося, решившего все задачи. Основной успех достигнут при решении задач №№ 1—3. Итак, как видим, результат невысок.

Причины низких результатов:

1. Подобные задачи редко встречались в практике учащихся.

2. Предложенные задачи чаще всего решаются нетрадиционными методами.

3. Учащиеся не знакомы с элементами теории вероятностей.

III.2. Методический (обучающий) эксперимент

Цель эксперимента: познакомить учеников с элементами теории вероятностей, логическим процессами, приемами решения задач, с проведением эксперимента, вычислением вероятности по формуле. Предлагались следующие задания.

1. В ящике имеются 3 черных и 5 белых шаров. Какое наименьшее количество шаров надо взять из ящика (не заглядывая в него) чтобы среди вынутых шаров оказался: а) хотя бы 1 черный; б) хотя бы 1 белый?

2. В ящике имеются 12 одинаковых шаров, отличающихся только цветом: 6 красных, 3 белых, 2 зеленых и 1 черный. Какое наименьшее количество шаров надо взять из ящика наугад, чтобы среди вынутых шаров было не менее двух шаров одного цвета?

Решение. Будем рассуждать следующим образом: вынув один шар, вынимаем следующий. Он может оказаться того же цвета, что и первый. Но возможно, что второй шар иного цвета, третий шар отличается по цвету от двух первых и т. д. Наихудший вариант: 4 первых шара оказались разных цветов. Тогда пятый шар составит одноцветную пару с одним из ранее вынутых.

Ответ: 5 шаров[7].

В методическом эксперименте учащихся познакомились с понятиями теории вероятностей, приемами вычислений по формуле, учились проводить опыты. Приведем несколько из них.

1. Опыты с пятью монетами, которые Буратино получил от Карабаса-Барабаса[8].

Велась таблица, куда заносились предположения детей об исходе опытов и данные опытов. Опыт проводился более 100 раз.

Учащиеся научились проводить эксперимент и заносить данные в таблицу, делать вывод.

2. Эксперимент с двумя белыми и одним черным шаром, где нужно было выяснить, каков может быть результат опыта, если вытаскивать один за другим 2 шара. Исходы опытов зарисовывались.

После знакомства детей с формулой, по которой вычисляется вероятность, были предложены задачи таких типов:

1. В урне 10 одинаковых шаров, из которых 4 красных и 6 голубых. Из урны извлекается 1 шар. Какова вероятность того, что извлеченный шар окажется голубым?

Решение. Событие “извлеченный шар окажется голубым” обозначим буквой A. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию A. В соответствии с формулой получаем:

.

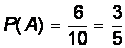2. В урне 3 черных и 4 белых шара. Вы вынимаете один из них, кладете обратно, перемешиваете и вынимаете другой. Возможен один из трех исходов: либо оба шара черные, либо оба белые, либо они различных цветов. Каковы вероятности этих событий?

Во время эксперимента дети учились применять формулу, придумывали и свои аналогичные задачи.

III.3. Контрольный эксперимент

Цель: 1. Окончательно проверить, доступны ли первоначальные логические понятия, элементы теории вероятностей, методика решения задач на нахождение вероятности какого-либо события учащимся начальных классов. 2. Проверить умения решать вероятностные задачи после получения некоторых теоретических и практических знаний и умений.

Были предложены задачи:

1. В пакете имеются конфеты трех сортов, не различимые на ощупь. Какое наименьшее число конфет надо взять наугад из пакета, чтобы среди вынутых были хотя бы 2 конфеты одного сорта?

2. Ключи от четырех чемоданов перемешались. Нужно определить, от какого чемодана какой ключ. Сколько для этого надо сделать попыток?

3. В мешочке 3 красных и 3 желтых шарика. Сколько надо вынуть наугад, не глядя в мешочек, шариков, чтобы быть уверенным в том, что:

а) будет 2 желтых шарика;

б) 3 шарика будут разного цвета.

4. В мешочке 3 черных и 4 белых шара. Вы вынимаете один из них, кладете обратно, перемешиваете и вынимаете другой. Найти вероятность того, что вынут черный шар (3/7), вынут белый шар (4/7).

5. Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы? (9/90)

Вывод. Результат контрольного эксперимента освещен в таблице.

№	Ф. И.	1	2	3	4	5	Всего решено
1	Ахремко Ксения	+	+	+	+	+	5
2	Беленко Юлия	+	+	+	+	+	5
3	Гедич Вадим	+	+	-	-	-	2
4	Грабун Максим	+	+	+	+	+	5
5	Иванов Роман	+	+	+	+	+	5
6	Киселев Кирилл	+	+	-	-	-	2
7	Куровская Ольга	+	+	+	-	-	3
8	Матеюк Андрей	+	-	-	-	-	1
9	Окунь Евгений	+	+	+	+	-	4
10	Панфилов Егор	+	+	-	-	-	2
11	Сидорик Анастасия	+	+	+	+	+	5
12	Сочан Анастасия	+	+	+	+	+	5
13	Тимохин Артем	+	+	+	+	+	5
14	Филипчик Виталий	+	+	+	+	-	4
15	Чищеня Ирина	+	+	-	-	-	2
	Итого	13	9	8	3	0	55