Высшая математика
Страница 5
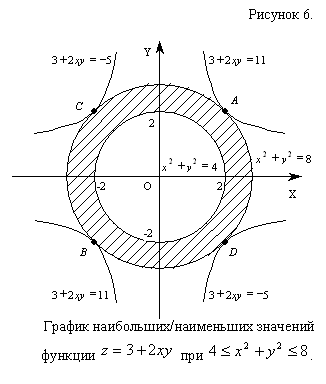
Следовательно, заданная функция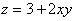 
в заданной области дифференцирования достигает наибольшего значения в точках 
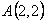и 
и 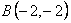наименьшего в точках 
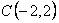и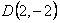 
при этом графики функци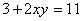й 
и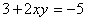 
касаются окружности 
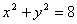в точках 
, 
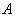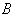и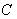 
, 
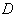соответственно (см. рис.6).
Задание №11. Вопрос №6.
Вычислить неопределенный интеграл: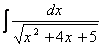 
.
Решение:
|
Ответ: |
Заданный неопределенный интеграл равен  . |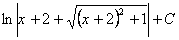
Задание №15. Вопрос №1.
Решить уравнение: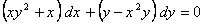 
.
Решение:
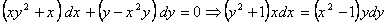. Разделив обе части на 
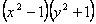, получим 
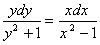. Проинтегрируем полученное уравнение:
.
|
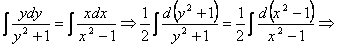
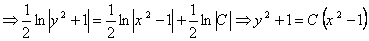Ответ: |
Решением данного уравнения является 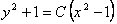 . |