Высшая математика
Высшая математика
Содержание
Часть I. 3
Задание №2. Вопрос №9. _ 3
Задание №3. Вопрос №1. _ 3
Задание №12. Вопрос №9. 5
Задание №13. Вопрос №2. 5
Задание №18. Вопрос №9 6
Часть II. _ 9
Задание №8. Вопрос №8. _ 9
Задание №12. Вопрос №9. _ 10
Задание №14. Вопрос №2. _ 10
Задание №15. Вопрос №6. _ 11
Задание №18. Вопрос №9. _ 12
Дополнительно Часть I. _ 13
Задание №7. Вопрос №1. 13
Задание №9. Вопрос №8. 13
Задание №11. Вопрос №6. _ 14
Задание №15. Вопрос №1. _ 15
Дополнительно Часть II. _ 15
Задание №7. Вопрос №1. 15
Задание №9. Вопрос №8. 16
Задание №11. Вопрос №6. _ 18
Задание №15. Вопрос №1. _ 18
Часть I.
Задание №2. Вопрос №9.
В штате гаража числится 54 водителя. Сколько свободных дней может иметь каждый водитель в месяц (30 дней), если ежедневно 25% автомашин из имеющихся 60 остаются в гараже для профилактического ремонта.
Решение: |
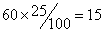
|
машин ежедневно остается в гараже на профилактическом ремонте. |
|
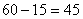
|
машин с водителями ежедневно уходят в рейс.
|
|
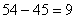
|
водителей из штата гаража ежедневно не выходит в рейс из-за профилактического ремонта автомашин. |
|
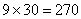
|
количество водителей в течение месяца, не выходящих в рейс из-за профилактического ремонта автомашин. |
|
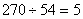
|
дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. |
|
Ответ: |
Каждый водитель из штата гаража в течение месяца может иметь 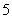 свободных дней. свободных дней. |
Задание №3. Вопрос №1.
Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если 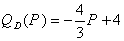 ,
, 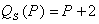 .
.
Решение:
Построим в плоскости POQ график функции спроса Q=QD(P) и предложения Q=QS(P). Для этого найдем координаты пересечения с осями координат:
|
С осью OP (Q=0): |
С осью OQ (P=0): |
|
Для Q=QS(P): |
Для Q=QD(P): |
|
|
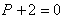
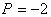
|
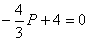
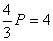
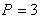
|
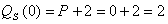
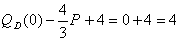
|
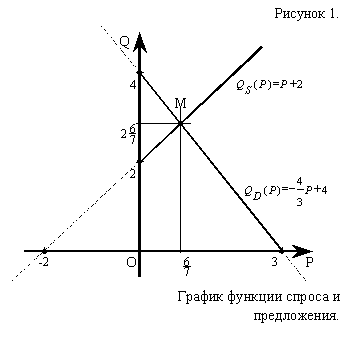 Т.к. функции QS(P) и QD(P) – линейные функции, то их графиками являются прямые, для построения которых достаточно определить их точки пересечения с осями координат. Они найдены, значит можно производить построение графика (рис.1).
Т.к. функции QS(P) и QD(P) – линейные функции, то их графиками являются прямые, для построения которых достаточно определить их точки пересечения с осями координат. Они найдены, значит можно производить построение графика (рис.1).
Найдем точку равновесия графиков функции спроса и предложения (М), в которой спрос равен предложению. Для этого решим систему:
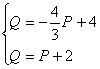 , из этой системы получаем:
, из этой системы получаем: 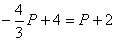
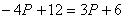
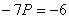
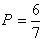 , тогда
, тогда 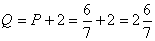 , значит координаты т.M
, значит координаты т.M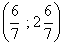 .
.
|
Ответ: |
Координаты точки равновесия равны 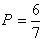 , ,  |
Задание №12. Вопрос №9.
Используя правила вычисления производных и таблицу, найдите производные следующих функций:
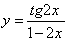
Решение:
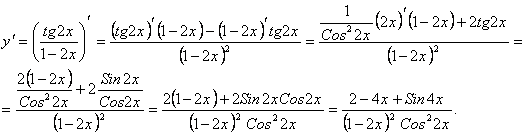
|
Ответ: |
Производная заданной функции равна 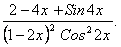 |
Задание №13. Вопрос №2.
Используя дифференциал функции, найдите приближенное значение
|
числа: |
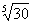
|
Решение:
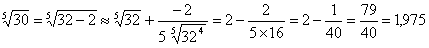
|
Ответ: |
Приближенное значение заданного числа равно 1,975. |
Задание №18. Вопрос №9 |
Исследуйте функцию и постройте ее график: |
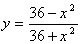
|
Решение:
1. Область определения данной функции: 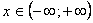 .
.
2. Найдем точки пересечения с осями координат:
|
С осью OY 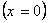 : : |
С осью OX 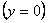 : : |
|
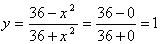
|
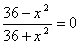 , дробь равна нулю, если ее числитель равен нулю, т.е. , дробь равна нулю, если ее числитель равен нулю, т.е.
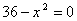
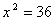
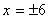
|
|
Точка пересечения: 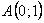 |
Точки пересечения: 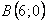 , ,  |