Вычисление двойных интегралов методом ячеек

Вычисление двойных интегралов методом ячеек

Содержание.

Теоретическая часть…………………………………………3

Задание……………………………………………………… 4

Текст программы. ……………………………………………5

Блок-схема программы…………………….……………… .6

Выполнение программы в математическом пакете……… 7

Список использованной литературы…………………… 8

Теоретическая часть.

Численные методы могут использоваться для вычисления кратных интегралов. Ограничимся рассмотрением двойных интегралов вида

I=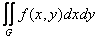 (1)

Одним из простейших способов вычисления этого интеграла является метод ячеек. Рассмотрим сначала случай, когда областью интегрирования G является прямоугольник: 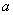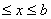, 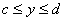.По теореме о среднем найдём среднее значение функции f(x,y):

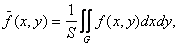S=(b-a)(d-c). (2)

Будем считать, что среднее значение приближённо равно значению функции в центре прямоугольника, т. е. 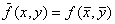. Тогда из (2) получим выражение для приближённого вычисления двойного интеграла:

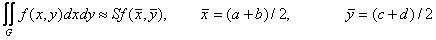(3)

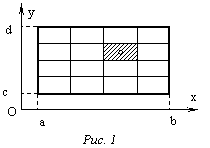
Точность этой формулы можно повысить, если разбить область G на прямоугольные ячейки D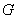ij (рис. 1): xi-1 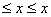i (i=1,2,…,M), yi-1 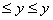i (j=1,2,…,N). Применяя к каждой ячейке формулу (3), получим

òòDGijf(x,y)dxdy»¦(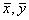)DxiDyi.

Суммируя эти выражения по всем ячейкам, находим значение двойного интеграла:

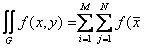I,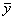j) (4)

В правой части стоит интегральная сумма; поэтому при неограниченном уменьшении периметров ячеек (или стягивания их в точки) эта сумма стремится к значению интеграла для любой непрерывной функции f(x,y).

Можно показать, что погрешность такого приближения интеграла для одной ячейки оценивается соотношением

Rij»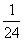DxiDyj.

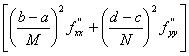Суммируя эти выражения по всем ячейкам и считая все их площади одинаковыми, получаем оценку погрешности метода ячеек в виде

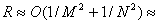O(Dx2+Dy2).

Таким образом, формула (4) имеет второй порядок точности. Для повышения точности можно использовать обычные методы сгущения узлов сетки. При этом по каждой переменной шаги уменьшают в одинаковое число раз, т. е. отношение M/N остаётся постоянным.

Если область G непрямоугольная, то в ряде случаев её целесообразно привести к прямоугольному виду путём соответствующей замены переменных. Например, пусть область задана в виде криволинейного четырёхугольника: 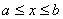, 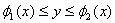. Данную область можно привести к прямоугольному виду с помощью замены 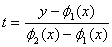, 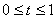. Кроме того, формула (4) может быть обобщена и на случай более сложных областей.

Задание. Найти при помощи метода ячеек значение интеграла 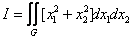, где 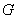– область, ограниченная функциями .

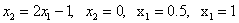Текст программы.

#include<conio.h>

#include<iostream.h>

float f(float,float);

void main() {

const float h1=.0005,h2=.001;

float s1,x,y,i,I;

clrscr();

s1=h1*h2;

I=0;

y=h2/2;

x=1-h1/2;

for(i=0;i<1/h2;i++) {

while (y<2*x-1) {

I+=s1*f(x,y);

x-=h1;

}

y+=h2;

x=1-h1/2;

}

cout<<"Площадь интеграла равна: "<<I;

getch();

}

float f(float x,float y){

return x*x+y*y;

}

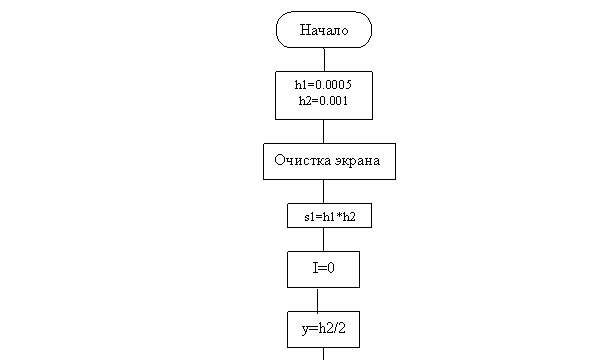
Блок-схема программы.

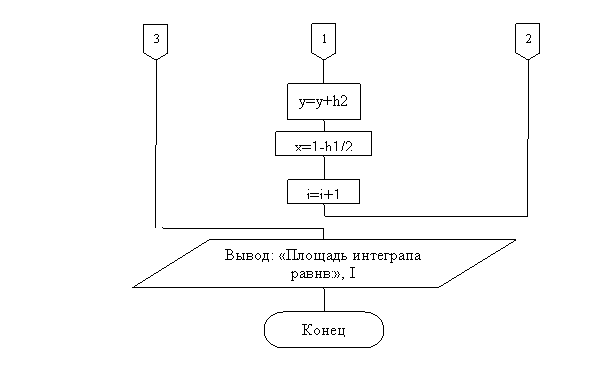
Выполнение программы в математическом пакете.

h1=.0005;

h2=.001;

s1=h1*h2;

I=0;

y=h2/2;

x=1-h1/2;

for i=1:1/h2

while y<2*x-1 I=I+s1*(x*x+y*y);

x=x-h1;

end

y=y+h2;

x=1-h1/2;

end

disp('Площадь интеграла равна:');

disp(I);

В зависимости от шагов сетки получаем с различной точностью значение искомого интеграла

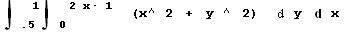
Площадь интеграла равна:

0.2190

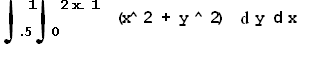
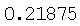
Список использованной литературы.

1. Бахвалов Н.С. Численные методы. т.1 – М.: Наука. 1975.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966.

3. Калиткин Н.Н Численные методы. – М.: Наука, 1978.

4. Турчак Л. И. Основы численных методов. – М.: Наука, 1987.