Вычисление интеграла фукции f(x) методом Симпсона
Страница 3
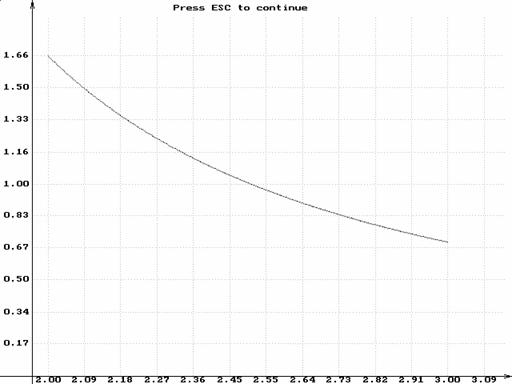
Результат по методу трапеций равен: 1.062
для получения необходимой точности интервал был разбит на 11 отрезков
Результат по методу Симпсона равен: 1.061
для получения необходимой точности интервал был разбит на 7 отрезков.
Анализ полученных в ходе работы программы результатов говорит о том, что поставленная задача успешно решается.
Метод трапеции является наиболее простым методом приближённого интегрирования , этот метод позволяет точно интегрировать многочлен первой степени , а для интегрирования данной функции требуется довольно много итераций. Более совершенным является метод Симпсона , который позволяет точно интегрировать многочлен второй производной и даже некоторые многочлены третьей степени, поэтому он требует почти в 2 раза меньше количества интервалов для получения результата.
Заключение
В данной курсовой работе решена задача приближённого интегрирования функции
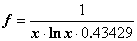
методами Симпсона и трапеции.
В процессе создания курсовой работы разработан алгоритм решения поставленной задачи. По этому алгоритму на языке Турбо Паскаль 7.0. составлена и отлажена программа.
В ходе тестирования были получены результаты работы метода трапеции и метода Симпсона, по которым видно, что результаты интегрирования обоими методами совпадают с достаточной точностью. Заметна лишь разница в качестве приближения интервалов.
Программа является полностью работоспособной, что подтверждается результатами её тестированием
Список использованных источников:
1.Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике для инженеров и учащихся втузов. - М.: Наука , 1981 . - 718 с.
2.Белецкий Я. Турбо Паскаль с графикой для персональных компьютеров перевод с польского Д.И.Юренкова. -М.: Машиностроение , 1991. - 320 с.
3.Сергиевский М.В., Шалашов А.В. Турбо Паскаль 7.0; язык, среда программирования. -М: Машиностроение.-1994,-254 с.ил.
4.Справочник по процедурам и функциям Borland Pascal 7.0. - Киев: Диалектика, 1993. - 272 с.
5.Самарский А.А, Гулин А.В. Численные методы.М.:Наука,1989. – 430 с.