Гамма функции
Страница 3
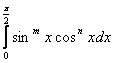
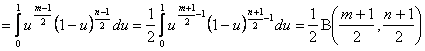
и на основании (2.2) имеем
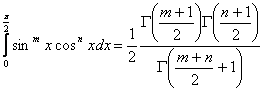 (3.1)
(3.1)
В интеграле
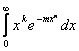
Где k > -1,n > 0,достаточно положить 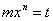
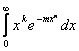
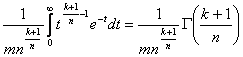
17
Интеграл
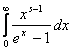
Где s > 0,разложить в ряд
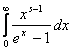
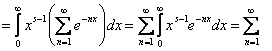
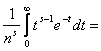
=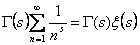
где 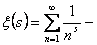 дзетта функция Римана
дзетта функция Римана
Рассмотрим неполные гамма функции (функции Прима)

связанные неравенством
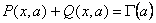

Разлагая,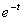 в ряд имеем
в ряд имеем
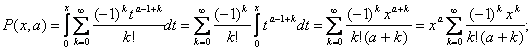
18

Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию
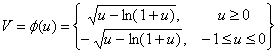 (3.2)
(3.2)
Непрерывна на интервале (-1,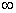 ) монотонно возрастает от
) монотонно возрастает от 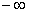 до
до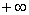 при изменении
при изменении 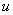 от
от 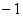 до
до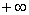 и обращаются в 0 при u = 0.Так как
и обращаются в 0 при u = 0.Так как
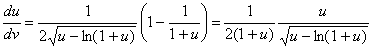
то 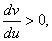 при u > 0 и при u < 0 , далее имеем
при u > 0 и при u < 0 , далее имеем
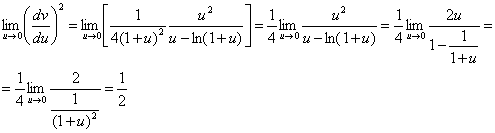
И так производная непрерывна и положительна во всем интервале  ,удовлетворяет условию
,удовлетворяет условию
19
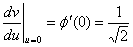
Из предыдущего следует, что существует обратная функция, 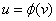 определенная на интервале
определенная на интервале 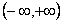 непрерывная и монотонно возрастающая в этом интервале,
непрерывная и монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие

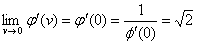 (3.3)
(3.3)
Формулу Стирлинга выведем из равенства
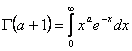
полагая 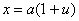 ,имеем
,имеем
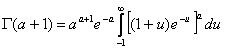
Положим далее 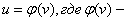 введенная выше обратная функция, удовлетворяющая условиям u = -1при
введенная выше обратная функция, удовлетворяющая условиям u = -1при 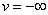 ,и
,и 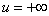 при
при 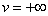 .Замечая что(см.3.2)
.Замечая что(см.3.2)
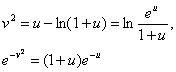
20
имеем
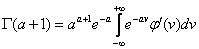 ,
,
полагая на конец ,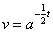 ,получим
,получим
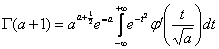
или
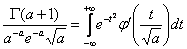
в пределе при 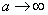 т.е. при
т.е. при 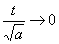 (см3.3)
(см3.3)
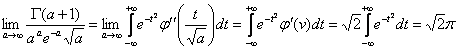
откуда вытекает формула Стирлинга
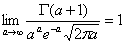
которую можно взять в виде
21
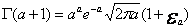 (3.4)
(3.4)
где 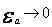 ,при
,при 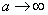

для достаточно больших 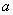 полагают
полагают
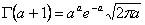 (3.5)
(3.5)
вычисление же производится при помощи логарифмов
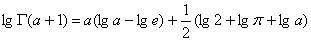
если 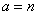 целое положительное число, то
целое положительное число, то 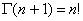 и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
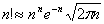
приведем без вывода более точную формулу
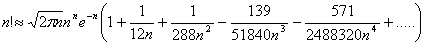
где в скобках стоит не сходящийся ряд.
5. Примеры вычисления интегралов 22
Для вычисления необходимы формулы:
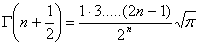

Г( )
)
Вычислить интегралы
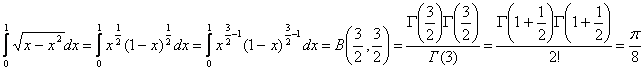
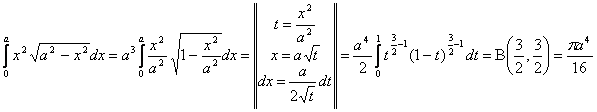
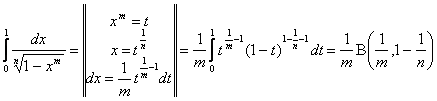


23

Міністерство освіти і науки України
Запорізький державний університет
ДО ЗАХИСТУ ДОПУЩЕНИЙ
Зав. каф. Математичного аналізу
д. т. н. проф. С.Ф. Шишканова
_ 2002р.
ПОЯСНЮВАЛЬНА ЗАПИСКА ДО КУРСОВОГО ПРОЕКТУ
ГАМА ФУНКЦІЇ
Розробив
Ст гр 8221-2
Садигов Р.А.
Керівник
Ст. викладач
Кудря В.І.
Запоріжжя 2002.
Содержание
Задание на курсовую работу .2
Реферат .4
введение .5
1. Бета функции…………………………………………… 6
2. Гамма функции .9
3. Производная гамма функции 11
4. Вычисление интегралов формула Стирлинга 16
5. Примеры вычеслений 22
вывод 24
Список литературы…………………………………………… 25
Реферат
Курсовая работа: 24 ст., 5 источников, 1 рис.
Обьект иследований: гамма и ее приложения.
В работе идет речь о представлении бета и гамма функций с помощью интегралов Эйлера соответствено первого и второго рода. И о их применении для вычисления интегралов.
Ключевые слова:
ГАММА И БЕТА ФУНКЦИЯ, ИНТЕГРАЛ ЭЙЛЕРА, ПРОИЗВОДНАЯ, ПРЕДЕЛ.
Введение
Выделяют особый класс функций, представимых в виде собственого либо несобственого интеграла, который зависит не только от формальной переменной, а и от параметра.