Гамма функции
Гамма функции
1. Бэта-функции 6
Бэта – функции определяются интегралом Эйлера первого рода:
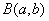 =
=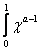
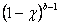
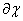 (1.1)
(1.1)
сходятся при 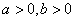 .Полагая
.Полагая 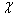 =1 – t получим:
=1 – t получим:
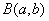 = -
= -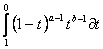 =
=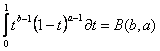
т.e. аргумент 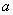 и
и 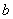 входят в
входят в 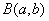 симетрично. Принимая во внимание тождество
симетрично. Принимая во внимание тождество
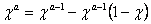
по формуле интегрирования почестям имеем

Откуда
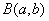 =
=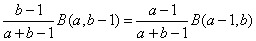 (1.2)
(1.2)
7
При целом b = n последовательно применяя(1.2)
Получим
 (1.3)
(1.3)
при целых 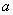 = m,
= m,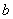 = n,имеем
= n,имеем
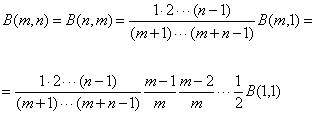
но B(1,1) = 1,следовательно:
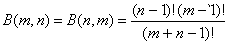


Положим в (1.1) 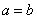 .Так как график функции
.Так как график функции 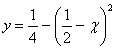 симметрична относительно прямой
симметрична относительно прямой 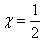 ,то
,то
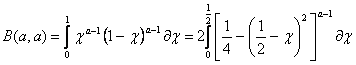
8
и в результате подстановки 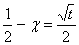 ,получаем
,получаем

полагая в(1.1) 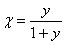 ,откуда
,откуда 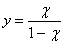 ,получим
,получим
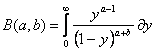 (1.4)
(1.4)
разделяя интеграл на два в пределах от 0 до 1 и от 1 до 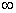 и применение ко второму интегралу подстановки
и применение ко второму интегралу подстановки 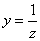 ,получим
,получим
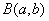 =
=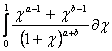
2. Гамма-функция9
Гамма функцию определяет интеграл Эйлера второго рода
G(a) =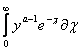

 (2.1)
(2.1)
сходящийся при 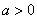 0.Положим
0.Положим 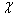 =ty,t > 0 ,имеем
=ty,t > 0 ,имеем
G(a) =
и после замены 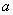 , через
, через 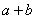 и t через 1+t ,получим
и t через 1+t ,получим
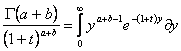
Умножая это равенство и интегрируя по t и пределах от 0 до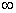 , имеем:
, имеем:
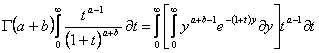
или на основании (1.4) и после изменения в правой части порядка интегрирования ,получаем:
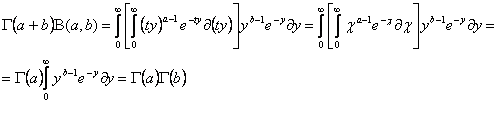
10
откуда
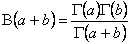 (2.2)
(2.2)
заменяя в (2,1) 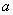 ,на
,на 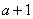 и интегрируем по частям
и интегрируем по частям
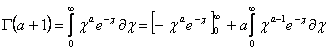
получаем рекурентною формулу

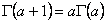 (2.3)
(2.3)

так как
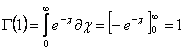
но при целом 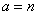 имеем
имеем
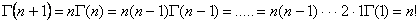 (2.4)
(2.4)
то есть при целых значениях аргумента гамма-функция превращается в факториал.Порядок которого на единицу меньше взятого значения аргумента.При n=1 в (2.4) имеем
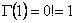
3. Производная гамма функции 11
Интеграл
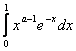

сходится при каждом 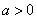 ,поскольку
,поскольку 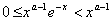 ,и интеграл
,и интеграл 
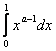 при
при 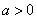 сходится.
сходится.
В области 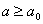 , где
, где 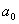 - произвольное положительное число, этот интеграл сходится равномерно, так как
- произвольное положительное число, этот интеграл сходится равномерно, так как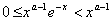 и можна применить признак Веерштраса. Сходящимся при всех значениях
и можна применить признак Веерштраса. Сходящимся при всех значениях 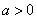 является и весь интеграл
является и весь интеграл 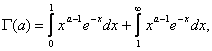 так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом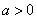 .Легко видеть что интеграл сходится по
.Легко видеть что интеграл сходится по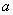 в любой области
в любой области 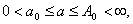 где
где 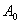 произвольно.Действительно для всех указаных значений
произвольно.Действительно для всех указаных значений 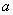 и для всех
и для всех 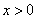
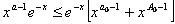 ,и так как
,и так как 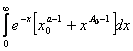 сходится, то выполнены условия признака Веерштрасса. Таким образом , в области
сходится, то выполнены условия признака Веерштрасса. Таким образом , в области 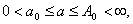 интеграл
интеграл 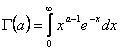 cходится равномерно.
cходится равномерно.
Отсюда вытекает непрерывность гамма функции при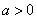 .Докажем дифференцируемость этой функции при
.Докажем дифференцируемость этой функции при 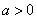 .Заметим что функция
.Заметим что функция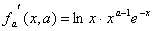 непрерывна при
непрерывна при 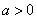 и
и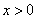 , и покажем ,что интеграл :
, и покажем ,что интеграл :