Геометрия в пространстве

Страница 8

A

C¹

C

A¹

Отметим интересное соотношение, связы­вающее площадь фигуры, площадь её проекции и угол между плоскостями:

· Площадь Sпр ортогональной проекцией многоугольника равна площади S многоугольника, умноженной на cos φ, где φ- угол между его плоскостью и плоскостью проекции:

φ

h

Это очевидно для треугольника, одна из сто­рон которого совпадает с линией пересечения двух плоскостей (рис. 17) или параллельна ей. А любой многоугольник можно разбить на та­кие треугольники. Приближая криволинейные фигуры многоу-гольниками, получим, что фор­мула площади проекции справедлива и для них. V. Несколько задач на построение, вооброжение, изображение и соображение.

ЗАДАЧА 1.

По правилам черчения принято изображать пунктиром ребра многоугольника, расположенные на его обратной стороне. Некоторый многоугольник спереди и сверху выглядит одинаково, как показано на рис 18. Пунктиров на изображении нет- значит нет и невидимых ребер. Как предмет выглядит сбоку?

ЗАДАЧА 2.

?

E

D

F

C

A

B

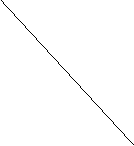
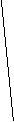
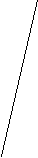
Может ли рисунок 19 служить изображением многогранника с тремя четырехугольными гранями и двумя треугольными?

ЗАДАЧА 3.

На рисунке 20 изображена треугольная пирамида, в которой проведены два отрезка, соединяющие точку на противоположных ребрах. Можно ли по рисунку определить, пересекаются эти отрезки в пространстве или нет? А если можно, то как?

ОТВЕТЫ.

1.

2. Нет. Прямые AD, BE, CF должны пересекаться в одной точке.

?